title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
JAVA | Kadane's | O(N) O(1) | maximum-sum-circular-subarray | 1 | 1 | # Intuition\n1. Find max sum subarray\n2. Find min sum subarray\n3. answer is max of (max sum subarray) && (totalSum - min sum subarray)\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n public int maxSubarraySumCircular(int[] nums) {\n boolean hasZeros = false;\n int sum=0; for(int i:nums) {sum+=i; if(i==0) hasZeros=true;}\n int maxSum = Integer.MIN_VALUE;\n int minSum = Integer.MAX_VALUE;\n int currSum = 0;\n //find maxSubarraySum\n for(int i:nums){\n currSum+=i;\n maxSum=Math.max(maxSum, currSum);\n if(currSum<0){\n currSum=0;\n }\n }\n //find minSubarraySum\n currSum=0;\n for(int i:nums){\n currSum+=i;\n minSum=Math.min(minSum, currSum);\n if(currSum>0){\n currSum=0;\n }\n }\n System.out.println(maxSum+":"+minSum);\n if(sum==minSum && !hasZeros){\n return maxSum;\n }\n return Math.max(maxSum, sum-minSum);\n }\n}\n``` | 1 | Given a **circular integer array** `nums` of length `n`, return _the maximum possible sum of a non-empty **subarray** of_ `nums`.
A **circular array** means the end of the array connects to the beginning of the array. Formally, the next element of `nums[i]` is `nums[(i + 1) % n]` and the previous element of `nums[i]` is `nums[(i - 1 + n) % n]`.
A **subarray** may only include each element of the fixed buffer `nums` at most once. Formally, for a subarray `nums[i], nums[i + 1], ..., nums[j]`, there does not exist `i <= k1`, `k2 <= j` with `k1 % n == k2 % n`.
**Example 1:**
**Input:** nums = \[1,-2,3,-2\]
**Output:** 3
**Explanation:** Subarray \[3\] has maximum sum 3.
**Example 2:**
**Input:** nums = \[5,-3,5\]
**Output:** 10
**Explanation:** Subarray \[5,5\] has maximum sum 5 + 5 = 10.
**Example 3:**
**Input:** nums = \[-3,-2,-3\]
**Output:** -2
**Explanation:** Subarray \[-2\] has maximum sum -2.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104` | null |
JAVA | Kadane's | O(N) O(1) | maximum-sum-circular-subarray | 1 | 1 | # Intuition\n1. Find max sum subarray\n2. Find min sum subarray\n3. answer is max of (max sum subarray) && (totalSum - min sum subarray)\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n public int maxSubarraySumCircular(int[] nums) {\n boolean hasZeros = false;\n int sum=0; for(int i:nums) {sum+=i; if(i==0) hasZeros=true;}\n int maxSum = Integer.MIN_VALUE;\n int minSum = Integer.MAX_VALUE;\n int currSum = 0;\n //find maxSubarraySum\n for(int i:nums){\n currSum+=i;\n maxSum=Math.max(maxSum, currSum);\n if(currSum<0){\n currSum=0;\n }\n }\n //find minSubarraySum\n currSum=0;\n for(int i:nums){\n currSum+=i;\n minSum=Math.min(minSum, currSum);\n if(currSum>0){\n currSum=0;\n }\n }\n System.out.println(maxSum+":"+minSum);\n if(sum==minSum && !hasZeros){\n return maxSum;\n }\n return Math.max(maxSum, sum-minSum);\n }\n}\n``` | 1 | Given an integer array of even length `arr`, return `true` _if it is possible to reorder_ `arr` _such that_ `arr[2 * i + 1] = 2 * arr[2 * i]` _for every_ `0 <= i < len(arr) / 2`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** arr = \[3,1,3,6\]
**Output:** false
**Example 2:**
**Input:** arr = \[2,1,2,6\]
**Output:** false
**Example 3:**
**Input:** arr = \[4,-2,2,-4\]
**Output:** true
**Explanation:** We can take two groups, \[-2,-4\] and \[2,4\] to form \[-2,-4,2,4\] or \[2,4,-2,-4\].
**Constraints:**
* `2 <= arr.length <= 3 * 104`
* `arr.length` is even.
* `-105 <= arr[i] <= 105` | For those of you who are familiar with the Kadane's algorithm, think in terms of that. For the newbies, Kadane's algorithm is used to finding the maximum sum subarray from a given array. This problem is a twist on that idea and it is advisable to read up on that algorithm first before starting this problem. Unless you already have a great algorithm brewing up in your mind in which case, go right ahead! What is an alternate way of representing a circular array so that it appears to be a straight array?
Essentially, there are two cases of this problem that we need to take care of. Let's look at the figure below to understand those two cases: The first case can be handled by the good old Kadane's algorithm. However, is there a smarter way of going about handling the second case as well? |
Python3 🔥🔥🔥 | Very Easy Solution | Kadane's Algorithem | O(n) complexity | maximum-sum-circular-subarray | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Using Kadane\'s Algorithem with small tweek we can solve this**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- So at start from simple kadane\'s algo from **maxi1** we can get maxsum without circular array constraint.\n\n---\n\n- Now to get circular max sum we have to think something differently, so if we flip sign of every element of array and then apply kadan\'s algo on it then we can get **maximum of minimum sum** that is effecting our original max sum that is **maxi2**\n\n---\n\n- Now parallelly calculate **totalsum** linearly of given array\n\n---\n- if **maxi1** **is < 0 return maxi1**\n- else return \n**maximum(maxi1, totalsum + maximumSumOfFlippedSignElement))**\n\n# Complexity\n- **Time complexity: $$O(n)$$**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSubarraySumCircular(self, nums: List[int]) -> int:\n arr = nums\n def kadanes_algo():\n maxi1 = arr[0]\n maxi2 = -arr[0]\n cont_sum = 0\n sum1 = 0\n sum2 = 0\n for i in arr:\n cont_sum += i\n sum1 += i\n sum2 += (-i)\n maxi1 = max(maxi1, sum1)\n maxi2 = max(maxi2, sum2)\n if sum1 < 0:\n sum1 = 0\n if sum2 < 0:\n sum2 = 0\n return maxi1,maxi2, cont_sum\n maxi1, maxi2, cont_sum = kadanes_algo()\n print(maxi1, maxi2, cont_sum)\n maxi2 *= -1\n return(maxi1 if maxi1 < 0 else max(maxi1, cont_sum - maxi2) )\n \n```\nPlease upvote this post if you find this solution helpful! \uD83D\uDE0A | 2 | Given a **circular integer array** `nums` of length `n`, return _the maximum possible sum of a non-empty **subarray** of_ `nums`.
A **circular array** means the end of the array connects to the beginning of the array. Formally, the next element of `nums[i]` is `nums[(i + 1) % n]` and the previous element of `nums[i]` is `nums[(i - 1 + n) % n]`.
A **subarray** may only include each element of the fixed buffer `nums` at most once. Formally, for a subarray `nums[i], nums[i + 1], ..., nums[j]`, there does not exist `i <= k1`, `k2 <= j` with `k1 % n == k2 % n`.
**Example 1:**
**Input:** nums = \[1,-2,3,-2\]
**Output:** 3
**Explanation:** Subarray \[3\] has maximum sum 3.
**Example 2:**
**Input:** nums = \[5,-3,5\]
**Output:** 10
**Explanation:** Subarray \[5,5\] has maximum sum 5 + 5 = 10.
**Example 3:**
**Input:** nums = \[-3,-2,-3\]
**Output:** -2
**Explanation:** Subarray \[-2\] has maximum sum -2.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104` | null |
Python3 🔥🔥🔥 | Very Easy Solution | Kadane's Algorithem | O(n) complexity | maximum-sum-circular-subarray | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Using Kadane\'s Algorithem with small tweek we can solve this**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- So at start from simple kadane\'s algo from **maxi1** we can get maxsum without circular array constraint.\n\n---\n\n- Now to get circular max sum we have to think something differently, so if we flip sign of every element of array and then apply kadan\'s algo on it then we can get **maximum of minimum sum** that is effecting our original max sum that is **maxi2**\n\n---\n\n- Now parallelly calculate **totalsum** linearly of given array\n\n---\n- if **maxi1** **is < 0 return maxi1**\n- else return \n**maximum(maxi1, totalsum + maximumSumOfFlippedSignElement))**\n\n# Complexity\n- **Time complexity: $$O(n)$$**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSubarraySumCircular(self, nums: List[int]) -> int:\n arr = nums\n def kadanes_algo():\n maxi1 = arr[0]\n maxi2 = -arr[0]\n cont_sum = 0\n sum1 = 0\n sum2 = 0\n for i in arr:\n cont_sum += i\n sum1 += i\n sum2 += (-i)\n maxi1 = max(maxi1, sum1)\n maxi2 = max(maxi2, sum2)\n if sum1 < 0:\n sum1 = 0\n if sum2 < 0:\n sum2 = 0\n return maxi1,maxi2, cont_sum\n maxi1, maxi2, cont_sum = kadanes_algo()\n print(maxi1, maxi2, cont_sum)\n maxi2 *= -1\n return(maxi1 if maxi1 < 0 else max(maxi1, cont_sum - maxi2) )\n \n```\nPlease upvote this post if you find this solution helpful! \uD83D\uDE0A | 2 | Given an integer array of even length `arr`, return `true` _if it is possible to reorder_ `arr` _such that_ `arr[2 * i + 1] = 2 * arr[2 * i]` _for every_ `0 <= i < len(arr) / 2`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** arr = \[3,1,3,6\]
**Output:** false
**Example 2:**
**Input:** arr = \[2,1,2,6\]
**Output:** false
**Example 3:**
**Input:** arr = \[4,-2,2,-4\]
**Output:** true
**Explanation:** We can take two groups, \[-2,-4\] and \[2,4\] to form \[-2,-4,2,4\] or \[2,4,-2,-4\].
**Constraints:**
* `2 <= arr.length <= 3 * 104`
* `arr.length` is even.
* `-105 <= arr[i] <= 105` | For those of you who are familiar with the Kadane's algorithm, think in terms of that. For the newbies, Kadane's algorithm is used to finding the maximum sum subarray from a given array. This problem is a twist on that idea and it is advisable to read up on that algorithm first before starting this problem. Unless you already have a great algorithm brewing up in your mind in which case, go right ahead! What is an alternate way of representing a circular array so that it appears to be a straight array?
Essentially, there are two cases of this problem that we need to take care of. Let's look at the figure below to understand those two cases: The first case can be handled by the good old Kadane's algorithm. However, is there a smarter way of going about handling the second case as well? |
Solution | complete-binary-tree-inserter | 1 | 1 | ```C++ []\nclass CBTInserter {\n TreeNode* root;\n int nodeCnt;\n int count(TreeNode* root) {\n if (!root) return 0;\n if (!root->left) root->right = NULL;\n return 1 + count(root->left) + count(root->right);\n }\npublic:\n CBTInserter(TreeNode* root) {\n this->root = root;\n this->nodeCnt = count(root);\n }\n int insert(int val) {\n int nextPos = this->nodeCnt + 1;\n int level = (int) log2(nextPos);\n int levelCnt = pow(2, level);\n int levelIdx = nextPos - levelCnt;\n\n TreeNode* cur = this->root;\n int curIdx = 0;\n\n for (int i = 0; i < level - 1; ++i) {\n if (levelIdx < levelCnt / 2) {\n cur = cur->left;\n curIdx = curIdx * 2;\n } else {\n cur = cur->right;\n curIdx = curIdx * 2 + 1;\n levelIdx -= (levelCnt / 2);\n }\n levelCnt /= 2;\n }\n if (!cur) return 0;\n TreeNode* newNode = new TreeNode(val);\n if (levelIdx < levelCnt / 2) {\n cur->left = newNode;\n } else {\n cur->right = newNode;\n }\n ++this->nodeCnt;\n return cur->val;\n }\n TreeNode* get_root() {\n return this->root;\n }\n};\n```\n\n```Python3 []\nclass CBTInserter:\n def __init__(self, root: Optional[TreeNode]):\n self.root = root\n self.deque = deque()\n queue = deque([root])\n while queue:\n node = queue.popleft()\n if not node.left or not node.right:\n self.deque.append(node)\n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n \n def insert(self, val: int) -> int:\n new_node = TreeNode(val)\n parent = self.deque[0]\n if not parent.left:\n parent.left = new_node\n else:\n parent.right = new_node\n self.deque.popleft()\n self.deque.append(new_node)\n return parent.val\n\n def get_root(self) -> Optional[TreeNode]:\n return self.root\n```\n\n```Java []\nclass CBTInserter {\n\tprivate Queue<TreeNode> queue;\n\tprivate TreeNode root;\n\n\tpublic CBTInserter(TreeNode root) {\n\t\tthis.root = root;\n\t\tthis.queue = new LinkedList<>();\n\t\tthis.queue.offer(this.root);\n\t\twhile (this.queue.peek().left != null && this.queue.peek().right != null) {\n\t\t\tTreeNode treeNode = this.queue.poll();\n\t\t\tthis.queue.offer(treeNode.left);\n\t\t\tthis.queue.offer(treeNode.right);\n\t\t}\n\t\tif (this.queue.peek().left != null) {\n\t\t\tthis.queue.offer(this.queue.peek().left);\n\t\t}\n\t}\n\tpublic int insert(int val) {\n\t\tTreeNode treeNode = this.queue.peek();\n\t\tif (treeNode.left == null) {\n\t\t\ttreeNode.left = new TreeNode(val);\n\t\t\tthis.queue.offer(treeNode.left);\n\t\t} else {\n\t\t\ttreeNode.right = new TreeNode(val);\n\t\t\tthis.queue.poll();\n\t\t\tthis.queue.offer(treeNode.right);\n\t\t}\n\t\treturn treeNode.val;\n\t}\n\tpublic TreeNode get_root() {\n\t\treturn this.root;\n\t}\n}\n```\n | 1 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
90% Tc easy python solution | complete-binary-tree-inserter | 0 | 1 | ```\nclass CBTInserter:\n def __init__(self, root: Optional[TreeNode]):\n self.d = dict()\n def dfs(node, i):\n if not(node): return 0\n self.d[i] = node\n return 1 + dfs(node.left, 2*i) + dfs(node.right, 2*i+1)\n self.root = root\n self.l = dfs(root, 1)\n\n def insert(self, val: int) -> int:\n self.l += 1\n self.d[self.l] = TreeNode(val)\n if(self.l % 2):\n self.d[self.l//2].right = self.d[self.l]\n else:\n self.d[self.l//2].left = self.d[self.l]\n return self.d[self.l//2].val\n\n def get_root(self) -> Optional[TreeNode]:\n return self.root\n``` | 1 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
Python O(n) init O(1) insert by queue. 80%+ [w/ Diagram] | complete-binary-tree-inserter | 0 | 1 | Python O(n) init O(1) insert by queue.\n\n---\n\n**Hint**:\n\nUtilize the nature of **numbering** in complete binary tree\nNumber each node, start from root as 1, 2, 3, ..., and so on.\n\nFor each node with of number *k*,\nnode with ( 2*k* ) is left child\nnode with ( 2*k* + 1 ) is right child\n\nMaintin a **queue** (i.e., First-in First-out ), to keep the **parent for next insertion** operation on-demand.\n\n---\n\n**Diagram** & **Abstract model**:\n\n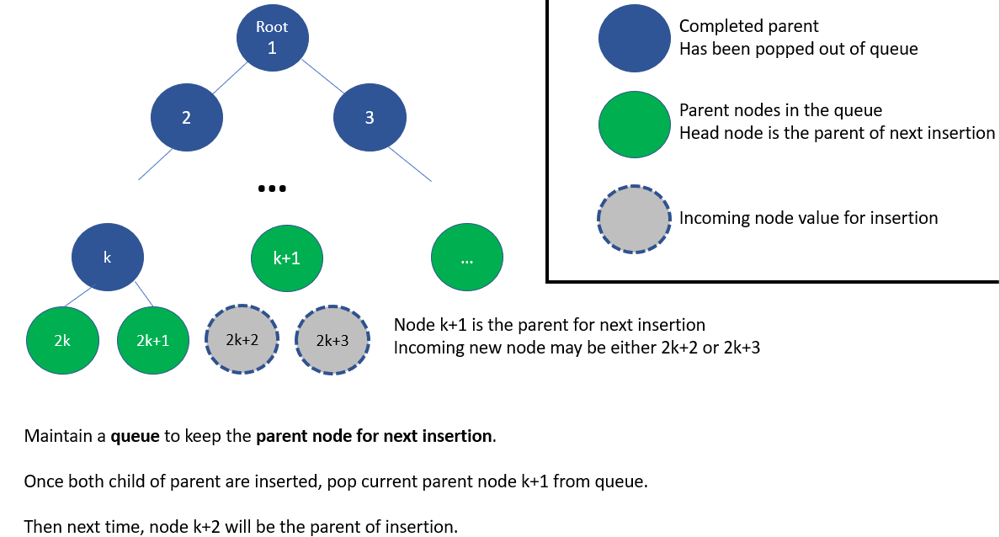\n\n---\n**Implementation**:\n```\nfrom collections import deque\n\nclass CBTInserter:\n\n \n def __init__(self, root: TreeNode):\n \n self.root = root\n \n self.parent_keeper = deque([root])\n\n while True:\n \n cur = self.parent_keeper[0]\n \n if cur:\n \n if cur.left:\n \n self.parent_keeper.append( cur.left )\n \n if cur.right:\n \n self.parent_keeper.append( cur.right )\n \n # cur is completed with two child, pop out\n self.parent_keeper.popleft()\n \n else:\n # parent of next insertion is found, stop\n break\n \n else:\n # parent of next insertion is found, stop\n break\n \n \n\n def insert(self, v: int) -> int:\n \n parent = self.parent_keeper[0]\n \n\t\t# Insert with leftward compact, to meet the definition of complete binary tree\n\t\t\n if not parent.left:\n parent.left = TreeNode( v )\n self.parent_keeper.append( parent.left )\n else:\n parent.right = TreeNode( v )\n self.parent_keeper.append( parent.right )\n \n # current parent is completed with two child now, pop parent from parent keeper on the head\n self.parent_keeper.popleft()\n \n return parent.val\n \n\n def get_root(self) -> TreeNode:\n \n return self.root\n```\n\n---\n\nRelated leetcode challenge:\n\n[Leetcode #958 Check Completeness of a Binary Tree](https://leetcode.com/problems/check-completeness-of-a-binary-tree/)\n\n[Leetcode #222 Count Complete Tree Nodes](https://leetcode.com/problems/count-complete-tree-nodes/)\n\n---\n\nReference:\n\n[1] [Wiki: Complete binary tree](https://en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees)\n\n[2] [GfG: Complete binary tree](https://bit.ly/3aFrrYQ) | 14 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
🔥 Rust, Go & Combinatorics | number-of-music-playlists | 0 | 1 | # Introduction\nIn this video, we\'re going to dive deep into a fascinating problem that combines dynamic programming, combinatorics, and music playlists! Imagine you\'re going on a trip and you want to create a playlist with a specific number of songs. However, you don\'t want to hear the same song again until `k` other songs have been played. How many different playlists can you create?\n\nThis problem might seem overwhelming at first, but fear not! By breaking it down step-by-step, we\'ll uncover the beautiful logic behind it. Let\'s crank up the volume and get started!\n\n# Approach\nOur solution uses a blend of dynamic programming and combinatorics. We\'ll use an array to keep track of the number of playlists for each possible combination of playlist length and number of unique songs. The combinatorial aspect comes into play when we calculate the number of ways we can add a new song or repeat a song. By cleverly using the modulo operator, we\'ll ensure that our calculations stay within manageable bounds.\n\n# Detailed Explanation\nWe start by initializing an array to store factorials and inverse factorials. This is a common trick in combinatorics problems to speed up our calculations. We then iterate over our songs, calculating the number of playlists for each possible number of unique songs.\n\nWe use the principle of inclusion-exclusion to avoid overcounting. In essence, we alternate between adding and subtracting the number of playlists to ensure that each valid playlist is counted exactly once.\n\nThe beauty of this approach lies in its efficiency. Despite the large input size, our algorithm handles it gracefully thanks to the power of combinatorics and dynamic programming.\n\n# Complexity Analysis\nOur approach runs in $$ O(n \\log \\text{{goal}}) $$ time, where `n` is the number of unique songs and `goal` is the total length of the playlist. The space complexity is $$ O(n) $$ because we need to store factorials and inverse factorials for each song.\n\nNow let\'s translate our approach into code! We\'ll use Python for its simplicity and expressiveness. Here\'s the complete code that implements our approach. It may seem short, but each line is packed with meaning. As we walk through the code, we\'ll highlight the key steps that correspond to our approach.\n\n# Code\n``` Python []\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n MOD = 10**9 + 7\n factorial = [1]*(n+1)\n inv_factorial = [1]*(n+1)\n \n # pre-calculate factorial and inverse factorial values\n for i in range(1, n+1):\n factorial[i] = factorial[i-1]*i % MOD\n inv_factorial[i] = pow(factorial[i], MOD-2, MOD)\n \n # initialization\n sign = 1\n answer = 0\n \n for i in range(n, k-1, -1):\n temp = pow(i-k, goal-k, MOD) * factorial[n] * inv_factorial[n-i] % MOD\n temp = temp * inv_factorial[i-k] % MOD\n answer = (answer + sign*temp) % MOD\n sign *= -1\n \n return answer\n\n```\n``` C++ []\nclass Solution {\npublic:\n int numMusicPlaylists(int n, int goal, int k) {\n long long MOD = 1e9 + 7;\n vector<long long> factorial(n+1, 1);\n vector<long long> inv_factorial(n+1, 1);\n\n auto power = [&](long long x, long long y) {\n long long res = 1;\n x %= MOD;\n while(y > 0) {\n if(y & 1)\n res = (res * x) % MOD;\n y >>= 1;\n x = (x * x) % MOD;\n }\n return res;\n };\n\n // pre-calculate factorial and inverse factorial values\n for(int i = 1; i <= n; ++i) {\n factorial[i] = (factorial[i - 1] * i) % MOD;\n inv_factorial[i] = power(factorial[i], MOD - 2);\n }\n\n // initialization\n int sign = 1;\n long long answer = 0;\n\n for(int i = n; i >= k; --i) {\n long long temp = power(i - k, goal - k) * factorial[n] % MOD * inv_factorial[n - i] % MOD;\n temp = temp * inv_factorial[i - k] % MOD;\n answer = (answer + sign * temp) % MOD;\n if (answer < 0) answer += MOD;\n sign *= -1;\n }\n\n return answer;\n }\n};\n```\n``` Go []\n\npackage main\n\nimport "fmt"\n\nconst MOD int = 1e9 + 7\n\nfunc power(x, y int) int {\n res := 1\n x %= MOD\n for y > 0 {\n if y & 1 == 1 {\n res = (res * x) % MOD\n }\n y >>= 1\n x = (x * x) % MOD\n }\n return res\n}\n\nfunc numMusicPlaylists(n, goal, k int) int {\n factorial := make([]int, n+1)\n inv_factorial := make([]int, n+1)\n factorial[0] = 1\n inv_factorial[0] = 1\n for i := 1; i <= n; i++ {\n factorial[i] = (factorial[i-1] * i) % MOD\n inv_factorial[i] = power(factorial[i], MOD-2)\n }\n\n sign := 1\n answer := 0\n for i := n; i >= k; i-- {\n temp := power(i-k, goal-k) * factorial[n] % MOD * inv_factorial[n-i] % MOD\n temp = temp * inv_factorial[i-k] % MOD\n answer = (answer + sign*temp) % MOD\n if answer < 0 {\n answer += MOD\n }\n sign *= -1\n }\n return answer\n}\n``` | 5 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
🔥 Rust, Go & Combinatorics | number-of-music-playlists | 0 | 1 | # Introduction\nIn this video, we\'re going to dive deep into a fascinating problem that combines dynamic programming, combinatorics, and music playlists! Imagine you\'re going on a trip and you want to create a playlist with a specific number of songs. However, you don\'t want to hear the same song again until `k` other songs have been played. How many different playlists can you create?\n\nThis problem might seem overwhelming at first, but fear not! By breaking it down step-by-step, we\'ll uncover the beautiful logic behind it. Let\'s crank up the volume and get started!\n\n# Approach\nOur solution uses a blend of dynamic programming and combinatorics. We\'ll use an array to keep track of the number of playlists for each possible combination of playlist length and number of unique songs. The combinatorial aspect comes into play when we calculate the number of ways we can add a new song or repeat a song. By cleverly using the modulo operator, we\'ll ensure that our calculations stay within manageable bounds.\n\n# Detailed Explanation\nWe start by initializing an array to store factorials and inverse factorials. This is a common trick in combinatorics problems to speed up our calculations. We then iterate over our songs, calculating the number of playlists for each possible number of unique songs.\n\nWe use the principle of inclusion-exclusion to avoid overcounting. In essence, we alternate between adding and subtracting the number of playlists to ensure that each valid playlist is counted exactly once.\n\nThe beauty of this approach lies in its efficiency. Despite the large input size, our algorithm handles it gracefully thanks to the power of combinatorics and dynamic programming.\n\n# Complexity Analysis\nOur approach runs in $$ O(n \\log \\text{{goal}}) $$ time, where `n` is the number of unique songs and `goal` is the total length of the playlist. The space complexity is $$ O(n) $$ because we need to store factorials and inverse factorials for each song.\n\nNow let\'s translate our approach into code! We\'ll use Python for its simplicity and expressiveness. Here\'s the complete code that implements our approach. It may seem short, but each line is packed with meaning. As we walk through the code, we\'ll highlight the key steps that correspond to our approach.\n\n# Code\n``` Python []\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n MOD = 10**9 + 7\n factorial = [1]*(n+1)\n inv_factorial = [1]*(n+1)\n \n # pre-calculate factorial and inverse factorial values\n for i in range(1, n+1):\n factorial[i] = factorial[i-1]*i % MOD\n inv_factorial[i] = pow(factorial[i], MOD-2, MOD)\n \n # initialization\n sign = 1\n answer = 0\n \n for i in range(n, k-1, -1):\n temp = pow(i-k, goal-k, MOD) * factorial[n] * inv_factorial[n-i] % MOD\n temp = temp * inv_factorial[i-k] % MOD\n answer = (answer + sign*temp) % MOD\n sign *= -1\n \n return answer\n\n```\n``` C++ []\nclass Solution {\npublic:\n int numMusicPlaylists(int n, int goal, int k) {\n long long MOD = 1e9 + 7;\n vector<long long> factorial(n+1, 1);\n vector<long long> inv_factorial(n+1, 1);\n\n auto power = [&](long long x, long long y) {\n long long res = 1;\n x %= MOD;\n while(y > 0) {\n if(y & 1)\n res = (res * x) % MOD;\n y >>= 1;\n x = (x * x) % MOD;\n }\n return res;\n };\n\n // pre-calculate factorial and inverse factorial values\n for(int i = 1; i <= n; ++i) {\n factorial[i] = (factorial[i - 1] * i) % MOD;\n inv_factorial[i] = power(factorial[i], MOD - 2);\n }\n\n // initialization\n int sign = 1;\n long long answer = 0;\n\n for(int i = n; i >= k; --i) {\n long long temp = power(i - k, goal - k) * factorial[n] % MOD * inv_factorial[n - i] % MOD;\n temp = temp * inv_factorial[i - k] % MOD;\n answer = (answer + sign * temp) % MOD;\n if (answer < 0) answer += MOD;\n sign *= -1;\n }\n\n return answer;\n }\n};\n```\n``` Go []\n\npackage main\n\nimport "fmt"\n\nconst MOD int = 1e9 + 7\n\nfunc power(x, y int) int {\n res := 1\n x %= MOD\n for y > 0 {\n if y & 1 == 1 {\n res = (res * x) % MOD\n }\n y >>= 1\n x = (x * x) % MOD\n }\n return res\n}\n\nfunc numMusicPlaylists(n, goal, k int) int {\n factorial := make([]int, n+1)\n inv_factorial := make([]int, n+1)\n factorial[0] = 1\n inv_factorial[0] = 1\n for i := 1; i <= n; i++ {\n factorial[i] = (factorial[i-1] * i) % MOD\n inv_factorial[i] = power(factorial[i], MOD-2)\n }\n\n sign := 1\n answer := 0\n for i := n; i >= k; i-- {\n temp := power(i-k, goal-k) * factorial[n] % MOD * inv_factorial[n-i] % MOD\n temp = temp * inv_factorial[i-k] % MOD\n answer = (answer + sign*temp) % MOD\n if answer < 0 {\n answer += MOD\n }\n sign *= -1\n }\n return answer\n}\n``` | 5 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
✅ 100% Dynamic Programming [VIDEO] Creating Unique Music Playlists | number-of-music-playlists | 1 | 1 | # Intuition\nThe task is to create a music playlist with `n` different songs and a total of `goal` songs, where each song must be played at least once, and a song can only be played again if `k` other songs have been played. The challenge is to calculate the total number of possible playlists.\n\nAt first glance, this might seem daunting. However, by using dynamic programming, we can break the problem down into manageable parts. We start by recognizing that the number of playlists of length `i` with `j` unique songs depends on the number of playlists of length `i-1` with `j-1` and `j` unique songs. This leads us to a dynamic programming solution.\n\n# Live Coding + Explenation\nhttps://youtu.be/EbBSwGM-NnU\n\n# Approach\n\n1. **Understanding the Problem**: The problem involves creating a playlist with `n` different songs, such that each song is played at least once, and a song can only be played again if `k` other songs have been played. We are required to find the number of possible playlists that can be created.\n\n2. **Identify the Approach**: We recognize this as a problem that can be solved using dynamic programming, a technique that breaks down a complex problem into simpler subproblems and avoids redundant computation by storing the results of these subproblems.\n\n3. **Initialization**: We initialize a 2D dynamic programming table, `dp`, with two rows and `n+1` columns. Each cell `dp[i][j]` represents the number of playlists of length `i` with `j` unique songs. \n\n - **Why only two rows in our DP table?** You might be wondering why we\'re using `i%2` and `(i - 1)%2` in our `dp` table. This is a memory optimization technique called "rolling array" or "sliding window". Since our current state only depends on the previous state, we don\'t need to store all the states. We only need a 2-row `dp` table: one row for the current state `i` and one row for the previous state `i - 1`. By using `i%2`, we ensure that `i` is always mapped to either `0` or `1`, effectively keeping our `dp` table within 2 rows.\n\n4. **Populating the DP Table**: We start populating the DP table from the first song to the goal. For each song, we consider two cases - adding a new song or adding an old song.\n\n - **Adding a New Song**: If we add a new song, it has to be one of the songs that have not yet been included in the playlist. Hence, the number of ways to do this is the number of ways to create a playlist of length `i - 1` with `j - 1` unique songs, times the number of new songs available, which is `n - (j - 1)`.\n \n - **Adding an Old Song**: If we add an old song, it has to be one of the songs that were not among the last `k` songs played. Hence, the number of ways to do this is the number of ways to create a playlist of length `i - 1` with `j` unique songs, times the number of old songs available, which is `j - k`.\n\n5. **Modulo Operation**: Since the number of ways can be very large, we take the modulo of the count of ways by `10^9 + 7` after each step to prevent overflow.\n\n6. **Return the Result**: Finally, the number of playlists that meet all conditions is represented by `dp[goal%2][n]`, and we return this as our answer.\n\n# Complexity\n- Time complexity: $$O(n \\times \\text{{goal}})$$, as we need to calculate a result for each combination of playlist lengths and song quantities.\n- Space complexity: $$O(n)$$, as we only maintain two rows of the `dp` table at any point in time, significantly optimizing our space usage.\n\n# Performance\n\n\n| Language | Runtime (ms) | Beats (%) | Memory (MB) | Beats (%) |\n|----------|--------------|-----------|-------------|-----------|\n| Rust | 0 | 100.00 | 2.1 | 100.00 |\n| C++ | 0 | 100.00 | 6.5 | 58.11 |\n| Go | 1 | 50.00 | 2.0 | 100.00 |\n| Java | 5 | 82.42 | 39.2 | 97.80 |\n| C# | 19 | 100.00 | 27.1 | 100.00 |\n| JavaScript| 50 | 100.00 | 44.6 | 100.00 |\n| Python | 55 | 83.46 | 16.3 | 90.98 |\n\n\n\n\n\n\n\n# Code\n``` Python []\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n MOD = 10**9 + 7\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\n dp[0][0] = 1\n\n for i in range(1, goal + 1):\n dp[i%2][0] = 0\n for j in range(1, min(i, n) + 1):\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD\n if j > k:\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD\n\n return dp[goal%2][n]\n```\n``` C++ []\nclass Solution {\npublic:\n int numMusicPlaylists(int n, int goal, int k) {\n const int MOD = 1e9 + 7;\n vector<vector<long long>> dp(2, vector<long long>(n+1, 0));\n dp[0][0] = 1;\n\n for (int i = 1; i <= goal; i++) {\n dp[i%2][0] = 0;\n for (int j = 1; j <= min(i, n); j++) {\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD;\n if (j > k)\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD;\n }\n }\n\n return dp[goal%2][n];\n }\n};\n```\n``` Java []\nclass Solution {\n public int numMusicPlaylists(int n, int goal, int k) {\n final int MOD = (int)1e9 + 7;\n long[][] dp = new long[2][n+1];\n dp[0][0] = 1;\n\n for (int i = 1; i <= goal; i++) {\n dp[i%2][0] = 0;\n for (int j = 1; j <= Math.min(i, n); j++) {\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD;\n if (j > k)\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD;\n }\n }\n\n return (int)dp[goal%2][n];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @param {number} goal\n * @param {number} k\n * @return {number}\n */\nvar numMusicPlaylists = function(n, goal, k) {\n const MOD = 1e9 + 7;\n let dp = Array.from({length: 2}, () => new Array(n + 1).fill(0));\n dp[0][0] = 1;\n\n for (let i = 1; i <= goal; i++) {\n dp[i%2][0] = 0;\n for (let j = 1; j <= Math.min(i, n); j++) {\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD;\n if (j > k)\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD;\n }\n }\n\n return dp[goal%2][n];\n};\n```\n``` C# []\npublic class Solution {\n public int NumMusicPlaylists(int n, int goal, int k) {\n int MOD = (int)1e9 + 7;\n long[][] dp = new long[2][];\n for (int i = 0; i < 2; i++)\n dp[i] = new long[n + 1];\n dp[0][0] = 1;\n\n for (int i = 1; i <= goal; i++) {\n dp[i%2][0] = 0;\n for (int j = 1; j <= Math.Min(i, n); j++) {\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD;\n if (j > k)\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD;\n }\n }\n\n return (int)dp[goal%2][n];\n }\n}\n```\n``` Go []\nfunc numMusicPlaylists(n int, goal int, k int) int {\n const MOD int = 1e9 + 7\n dp := make([][]int, 2)\n for i := range dp {\n dp[i] = make([]int, n + 1)\n }\n dp[0][0] = 1\n\n for i := 1; i <= goal; i++ {\n dp[i%2][0] = 0\n for j := 1; j <= min(i, n); j++ {\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD\n if j > k {\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD\n }\n }\n }\n\n return dp[goal%2][n]\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n```\n``` Rust []\nimpl Solution {\n pub fn num_music_playlists(n: i32, goal: i32, k: i32) -> i32 {\n const MOD: i64 = 1e9 as i64 + 7;\n let mut dp = vec![vec![0; n as usize + 1]; 2];\n dp[0][0] = 1;\n\n for i in 1..=goal {\n dp[i as usize % 2][0] = 0;\n for j in 1..=std::cmp::min(i, n) {\n dp[i as usize % 2][j as usize] = dp[(i - 1) as usize % 2][(j - 1) as usize] * (n - (j - 1)) as i64 % MOD;\n if j > k {\n dp[i as usize % 2][j as usize] = (dp[i as usize % 2][j as usize] + dp[(i - 1) as usize % 2][j as usize] * (j - k) as i64) % MOD;\n }\n }\n }\n\n dp[goal as usize % 2][n as usize] as i32\n }\n}\n```\n\nI hope you find this solution helpful in understanding how to generate all possible music playlists under the given constraints. If you have any further questions or need additional clarifications, please don\'t hesitate to ask. If you understood the solution and found it beneficial, please consider giving it an upvote. Happy coding, and may your coding journey be filled with success and satisfaction! \uD83D\uDE80\uD83D\uDC68\u200D\uD83D\uDCBB\uD83D\uDC69\u200D\uD83D\uDCBB | 70 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
✅ 100% Dynamic Programming [VIDEO] Creating Unique Music Playlists | number-of-music-playlists | 1 | 1 | # Intuition\nThe task is to create a music playlist with `n` different songs and a total of `goal` songs, where each song must be played at least once, and a song can only be played again if `k` other songs have been played. The challenge is to calculate the total number of possible playlists.\n\nAt first glance, this might seem daunting. However, by using dynamic programming, we can break the problem down into manageable parts. We start by recognizing that the number of playlists of length `i` with `j` unique songs depends on the number of playlists of length `i-1` with `j-1` and `j` unique songs. This leads us to a dynamic programming solution.\n\n# Live Coding + Explenation\nhttps://youtu.be/EbBSwGM-NnU\n\n# Approach\n\n1. **Understanding the Problem**: The problem involves creating a playlist with `n` different songs, such that each song is played at least once, and a song can only be played again if `k` other songs have been played. We are required to find the number of possible playlists that can be created.\n\n2. **Identify the Approach**: We recognize this as a problem that can be solved using dynamic programming, a technique that breaks down a complex problem into simpler subproblems and avoids redundant computation by storing the results of these subproblems.\n\n3. **Initialization**: We initialize a 2D dynamic programming table, `dp`, with two rows and `n+1` columns. Each cell `dp[i][j]` represents the number of playlists of length `i` with `j` unique songs. \n\n - **Why only two rows in our DP table?** You might be wondering why we\'re using `i%2` and `(i - 1)%2` in our `dp` table. This is a memory optimization technique called "rolling array" or "sliding window". Since our current state only depends on the previous state, we don\'t need to store all the states. We only need a 2-row `dp` table: one row for the current state `i` and one row for the previous state `i - 1`. By using `i%2`, we ensure that `i` is always mapped to either `0` or `1`, effectively keeping our `dp` table within 2 rows.\n\n4. **Populating the DP Table**: We start populating the DP table from the first song to the goal. For each song, we consider two cases - adding a new song or adding an old song.\n\n - **Adding a New Song**: If we add a new song, it has to be one of the songs that have not yet been included in the playlist. Hence, the number of ways to do this is the number of ways to create a playlist of length `i - 1` with `j - 1` unique songs, times the number of new songs available, which is `n - (j - 1)`.\n \n - **Adding an Old Song**: If we add an old song, it has to be one of the songs that were not among the last `k` songs played. Hence, the number of ways to do this is the number of ways to create a playlist of length `i - 1` with `j` unique songs, times the number of old songs available, which is `j - k`.\n\n5. **Modulo Operation**: Since the number of ways can be very large, we take the modulo of the count of ways by `10^9 + 7` after each step to prevent overflow.\n\n6. **Return the Result**: Finally, the number of playlists that meet all conditions is represented by `dp[goal%2][n]`, and we return this as our answer.\n\n# Complexity\n- Time complexity: $$O(n \\times \\text{{goal}})$$, as we need to calculate a result for each combination of playlist lengths and song quantities.\n- Space complexity: $$O(n)$$, as we only maintain two rows of the `dp` table at any point in time, significantly optimizing our space usage.\n\n# Performance\n\n\n| Language | Runtime (ms) | Beats (%) | Memory (MB) | Beats (%) |\n|----------|--------------|-----------|-------------|-----------|\n| Rust | 0 | 100.00 | 2.1 | 100.00 |\n| C++ | 0 | 100.00 | 6.5 | 58.11 |\n| Go | 1 | 50.00 | 2.0 | 100.00 |\n| Java | 5 | 82.42 | 39.2 | 97.80 |\n| C# | 19 | 100.00 | 27.1 | 100.00 |\n| JavaScript| 50 | 100.00 | 44.6 | 100.00 |\n| Python | 55 | 83.46 | 16.3 | 90.98 |\n\n\n\n\n\n\n\n# Code\n``` Python []\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n MOD = 10**9 + 7\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\n dp[0][0] = 1\n\n for i in range(1, goal + 1):\n dp[i%2][0] = 0\n for j in range(1, min(i, n) + 1):\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD\n if j > k:\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD\n\n return dp[goal%2][n]\n```\n``` C++ []\nclass Solution {\npublic:\n int numMusicPlaylists(int n, int goal, int k) {\n const int MOD = 1e9 + 7;\n vector<vector<long long>> dp(2, vector<long long>(n+1, 0));\n dp[0][0] = 1;\n\n for (int i = 1; i <= goal; i++) {\n dp[i%2][0] = 0;\n for (int j = 1; j <= min(i, n); j++) {\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD;\n if (j > k)\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD;\n }\n }\n\n return dp[goal%2][n];\n }\n};\n```\n``` Java []\nclass Solution {\n public int numMusicPlaylists(int n, int goal, int k) {\n final int MOD = (int)1e9 + 7;\n long[][] dp = new long[2][n+1];\n dp[0][0] = 1;\n\n for (int i = 1; i <= goal; i++) {\n dp[i%2][0] = 0;\n for (int j = 1; j <= Math.min(i, n); j++) {\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD;\n if (j > k)\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD;\n }\n }\n\n return (int)dp[goal%2][n];\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @param {number} goal\n * @param {number} k\n * @return {number}\n */\nvar numMusicPlaylists = function(n, goal, k) {\n const MOD = 1e9 + 7;\n let dp = Array.from({length: 2}, () => new Array(n + 1).fill(0));\n dp[0][0] = 1;\n\n for (let i = 1; i <= goal; i++) {\n dp[i%2][0] = 0;\n for (let j = 1; j <= Math.min(i, n); j++) {\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD;\n if (j > k)\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD;\n }\n }\n\n return dp[goal%2][n];\n};\n```\n``` C# []\npublic class Solution {\n public int NumMusicPlaylists(int n, int goal, int k) {\n int MOD = (int)1e9 + 7;\n long[][] dp = new long[2][];\n for (int i = 0; i < 2; i++)\n dp[i] = new long[n + 1];\n dp[0][0] = 1;\n\n for (int i = 1; i <= goal; i++) {\n dp[i%2][0] = 0;\n for (int j = 1; j <= Math.Min(i, n); j++) {\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD;\n if (j > k)\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD;\n }\n }\n\n return (int)dp[goal%2][n];\n }\n}\n```\n``` Go []\nfunc numMusicPlaylists(n int, goal int, k int) int {\n const MOD int = 1e9 + 7\n dp := make([][]int, 2)\n for i := range dp {\n dp[i] = make([]int, n + 1)\n }\n dp[0][0] = 1\n\n for i := 1; i <= goal; i++ {\n dp[i%2][0] = 0\n for j := 1; j <= min(i, n); j++ {\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD\n if j > k {\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD\n }\n }\n }\n\n return dp[goal%2][n]\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n```\n``` Rust []\nimpl Solution {\n pub fn num_music_playlists(n: i32, goal: i32, k: i32) -> i32 {\n const MOD: i64 = 1e9 as i64 + 7;\n let mut dp = vec![vec![0; n as usize + 1]; 2];\n dp[0][0] = 1;\n\n for i in 1..=goal {\n dp[i as usize % 2][0] = 0;\n for j in 1..=std::cmp::min(i, n) {\n dp[i as usize % 2][j as usize] = dp[(i - 1) as usize % 2][(j - 1) as usize] * (n - (j - 1)) as i64 % MOD;\n if j > k {\n dp[i as usize % 2][j as usize] = (dp[i as usize % 2][j as usize] + dp[(i - 1) as usize % 2][j as usize] * (j - k) as i64) % MOD;\n }\n }\n }\n\n dp[goal as usize % 2][n as usize] as i32\n }\n}\n```\n\nI hope you find this solution helpful in understanding how to generate all possible music playlists under the given constraints. If you have any further questions or need additional clarifications, please don\'t hesitate to ask. If you understood the solution and found it beneficial, please consider giving it an upvote. Happy coding, and may your coding journey be filled with success and satisfaction! \uD83D\uDE80\uD83D\uDC68\u200D\uD83D\uDCBB\uD83D\uDC69\u200D\uD83D\uDCBB | 70 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
Python short and clean. 4 solutions. DP and Combinatorics. Functional programming. | number-of-music-playlists | 0 | 1 | # Approach 1: Top-Down DP\nTL;DR, Similar to [Editorial solution Approach 2](https://leetcode.com/problems/number-of-music-playlists/editorial/) but shorter and cleaner.\n\n# Complexity\n- Time complexity: $$O(n * goal)$$\n\n- Space complexity: $$O(n * goal)$$\n\n# Code\n```python\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n @cache\n def num_lists(i: int, j: int) -> int:\n if not i and not j: return 1\n if not i or not j: return 0\n return (num_lists(i - 1, j - 1) * (n - j + 1) + num_lists(i - 1, j) * max(j - k, 0)) % 1_000_000_007\n \n return num_lists(goal, n)\n\n\n```\n\n---\n\n# Approach 2: Bottom-Up DP\nTL;DR, Similar to [Editorial solution Approach 1](https://leetcode.com/problems/number-of-music-playlists/editorial/) but shorter and cleaner.\n\n# Complexity\n- Time complexity: $$O(n * goal)$$\n\n- Space complexity: $$O(n * goal)$$\n\n# Code\n```python\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n num_lists = [[0] * (n + 1) for _ in range(goal + 1)]\n num_lists[0][0] = 1\n for i, j in product(range(1, goal + 1), range(1, n + 1)):\n num_lists[i][j] = (num_lists[i - 1][j - 1] * (n - j + 1) + num_lists[i - 1][j] * max(j - k, 0)) % 1_000_000_007\n return num_lists[-1][-1]\n\n\n```\n\n---\n\n# Approach 3: Bottom-Up DP Spacw optimized\nTL;DR, Similar to [Editorial solution Approach 1](https://leetcode.com/problems/number-of-music-playlists/editorial/) but shorter and cleaner with space optimization.\n\n# Complexity\n- Time complexity: $$O(n * goal)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n num_lists = [0] * (n + 1)\n num_lists[0] = prev = 1\n for i, j in product(range(1, goal + 1), range(1, n + 1)):\n prev, num_lists[j] = num_lists[j] * (j != n), (prev * (n - j + 1) + num_lists[j] * max(j - k, 0)) % 1_000_000_007\n return num_lists[-1]\n\n\n```\n\n---\n\n# Approach 4: Combinatorics\nTL;DR, Similar to [Editorial solution Approach 3](https://leetcode.com/problems/number-of-music-playlists/editorial/) but shorter, cleaner and functional.\n\n# Complexity\n- Time complexity: $$O(n * log(goal))$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n M = MOD = 1_000_000_007\n\n facts = tuple(accumulate(range(1, n + 1), lambda a, x: a * x % M, initial=1))\n ifacts = tuple((pow(x, M - 2, M) for x in facts)) # Fermat\'s little theorem\n\n terms = (pow(i - k, goal - k, M) * ifacts[n - i] * ifacts[i - k] % M for i in range(n, k - 1, -1))\n num_lists = facts[n] * sum(map(mul, terms, cycle((1, -1)))) % M\n\n return num_lists\n\n\n\n```\n\n | 1 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Python short and clean. 4 solutions. DP and Combinatorics. Functional programming. | number-of-music-playlists | 0 | 1 | # Approach 1: Top-Down DP\nTL;DR, Similar to [Editorial solution Approach 2](https://leetcode.com/problems/number-of-music-playlists/editorial/) but shorter and cleaner.\n\n# Complexity\n- Time complexity: $$O(n * goal)$$\n\n- Space complexity: $$O(n * goal)$$\n\n# Code\n```python\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n @cache\n def num_lists(i: int, j: int) -> int:\n if not i and not j: return 1\n if not i or not j: return 0\n return (num_lists(i - 1, j - 1) * (n - j + 1) + num_lists(i - 1, j) * max(j - k, 0)) % 1_000_000_007\n \n return num_lists(goal, n)\n\n\n```\n\n---\n\n# Approach 2: Bottom-Up DP\nTL;DR, Similar to [Editorial solution Approach 1](https://leetcode.com/problems/number-of-music-playlists/editorial/) but shorter and cleaner.\n\n# Complexity\n- Time complexity: $$O(n * goal)$$\n\n- Space complexity: $$O(n * goal)$$\n\n# Code\n```python\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n num_lists = [[0] * (n + 1) for _ in range(goal + 1)]\n num_lists[0][0] = 1\n for i, j in product(range(1, goal + 1), range(1, n + 1)):\n num_lists[i][j] = (num_lists[i - 1][j - 1] * (n - j + 1) + num_lists[i - 1][j] * max(j - k, 0)) % 1_000_000_007\n return num_lists[-1][-1]\n\n\n```\n\n---\n\n# Approach 3: Bottom-Up DP Spacw optimized\nTL;DR, Similar to [Editorial solution Approach 1](https://leetcode.com/problems/number-of-music-playlists/editorial/) but shorter and cleaner with space optimization.\n\n# Complexity\n- Time complexity: $$O(n * goal)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n num_lists = [0] * (n + 1)\n num_lists[0] = prev = 1\n for i, j in product(range(1, goal + 1), range(1, n + 1)):\n prev, num_lists[j] = num_lists[j] * (j != n), (prev * (n - j + 1) + num_lists[j] * max(j - k, 0)) % 1_000_000_007\n return num_lists[-1]\n\n\n```\n\n---\n\n# Approach 4: Combinatorics\nTL;DR, Similar to [Editorial solution Approach 3](https://leetcode.com/problems/number-of-music-playlists/editorial/) but shorter, cleaner and functional.\n\n# Complexity\n- Time complexity: $$O(n * log(goal))$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n M = MOD = 1_000_000_007\n\n facts = tuple(accumulate(range(1, n + 1), lambda a, x: a * x % M, initial=1))\n ifacts = tuple((pow(x, M - 2, M) for x in facts)) # Fermat\'s little theorem\n\n terms = (pow(i - k, goal - k, M) * ifacts[n - i] * ifacts[i - k] % M for i in range(n, k - 1, -1))\n num_lists = facts[n] * sum(map(mul, terms, cycle((1, -1)))) % M\n\n return num_lists\n\n\n\n```\n\n | 1 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
5 line Python solution, beats 100% | number-of-music-playlists | 0 | 1 | \nThis follows the exact same logic as the combinatorics solution in the editorial, so I won\'t try to shittily re-explain it here. I think that editorial is a great reference, but they made the actual implementation wayyyy more complicated than it needed to be, so here\'s a simpler one:\n\n# Code\n```\n# combinatorics solution!\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n # num playlists with i OR LESS unique songs\n def f(i):\n mults = [max(i - j, i - k) for j in range(goal)]\n return prod(mults)\n\n # calculate series\n curr, ans, sign = n, 0, 1\n while curr > k:\n ans += sign * comb(n, curr) * f(curr)\n sign *= -1\n curr -= 1\n return ans % (10**9 + 7)\n```\n\nHere\'s a 5 line version for shitts and giggles. I just put the stuff in the method in-line, but it\'s the same as above.\n```python\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n curr, ans, sign = n, 0, 1\n while curr > k:\n ans += sign * comb(n, curr) * prod([max(curr - j, curr - k) for j in range(goal)])\n sign, curr = sign * -1, curr - 1\n return ans % (10**9 + 7)\n```\n\nFor reference:\n- prod is from numpy.prod: it returns the product of all elements of an array. It would be very simple not to use it, it just makes the code so clean. \n- comb is from math.comb, it gives the answer to C(n, k) (n choose k). You could implement this method yourself in a few lines if you just look up / know the formula, so again, not too complicated to do without but makes the code so clean. | 1 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
5 line Python solution, beats 100% | number-of-music-playlists | 0 | 1 | \nThis follows the exact same logic as the combinatorics solution in the editorial, so I won\'t try to shittily re-explain it here. I think that editorial is a great reference, but they made the actual implementation wayyyy more complicated than it needed to be, so here\'s a simpler one:\n\n# Code\n```\n# combinatorics solution!\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n # num playlists with i OR LESS unique songs\n def f(i):\n mults = [max(i - j, i - k) for j in range(goal)]\n return prod(mults)\n\n # calculate series\n curr, ans, sign = n, 0, 1\n while curr > k:\n ans += sign * comb(n, curr) * f(curr)\n sign *= -1\n curr -= 1\n return ans % (10**9 + 7)\n```\n\nHere\'s a 5 line version for shitts and giggles. I just put the stuff in the method in-line, but it\'s the same as above.\n```python\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n curr, ans, sign = n, 0, 1\n while curr > k:\n ans += sign * comb(n, curr) * prod([max(curr - j, curr - k) for j in range(goal)])\n sign, curr = sign * -1, curr - 1\n return ans % (10**9 + 7)\n```\n\nFor reference:\n- prod is from numpy.prod: it returns the product of all elements of an array. It would be very simple not to use it, it just makes the code so clean. \n- comb is from math.comb, it gives the answer to C(n, k) (n choose k). You could implement this method yourself in a few lines if you just look up / know the formula, so again, not too complicated to do without but makes the code so clean. | 1 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
PYTHON3 THE BEST UZBEKISTAN | number-of-music-playlists | 0 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n MOD = 10**9 + 7\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\n dp[0][0] = 1\n\n for i in range(1, goal + 1):\n dp[i%2][0] = 0\n for j in range(1, min(i, n) + 1):\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD\n if j > k:\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD\n\n return dp[goal%2][n]\n``` | 1 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
PYTHON3 THE BEST UZBEKISTAN | number-of-music-playlists | 0 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n MOD = 10**9 + 7\n dp = [[0 for _ in range(n + 1)] for _ in range(2)]\n dp[0][0] = 1\n\n for i in range(1, goal + 1):\n dp[i%2][0] = 0\n for j in range(1, min(i, n) + 1):\n dp[i%2][j] = dp[(i - 1)%2][j - 1] * (n - (j - 1)) % MOD\n if j > k:\n dp[i%2][j] = (dp[i%2][j] + dp[(i - 1)%2][j] * (j - k)) % MOD\n\n return dp[goal%2][n]\n``` | 1 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
Recursion with memorization : Python with example | number-of-music-playlists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a hard problem to grasp.\nAt first it looks like we can easily solve it using permutaitons but no.\n\nAlso the conditions are not explained correctly.\n\nThe condition for k , is actually saying that if k = 2 and n = 3\nand we have [1] , then in order to play 1 again , we need to play 2 other songs first.\n[1,2,3,1]\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can make a choice diagram. There we will have choice each time to fill the spot either with a new song or a used song.\n\nin order to use the old song , we need to have atleask k used song.\n\nthe first spot will always be a unique song.\n\nso , our base conditions will be:\nif we have filled all the spots and we have used all the songs , then we return 1\nor if we have filled all the spots or we have used more songs than n , we return 0\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n\n mod = 10**9 + 7\n dic = {}\n\n def rec(lp , us):\n #base case\n if lp == 0 and us == n :\n return 1\n\n if lp == 0 or us > n :\n return 0\n if (lp , us) in dic :\n return dic[(lp , us)]\n # choosing a new/unique song\n res = (n-us) * rec(lp-1 , us+1)\n \n if us > k :\n # choosing a used/old song\n res += (us - k) * rec(lp-1 , us)\n \n dic[(lp , us)] = res\n return dic[(lp , us)]%mod\n\n return rec(goal , 0)\n\n``` | 1 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Recursion with memorization : Python with example | number-of-music-playlists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a hard problem to grasp.\nAt first it looks like we can easily solve it using permutaitons but no.\n\nAlso the conditions are not explained correctly.\n\nThe condition for k , is actually saying that if k = 2 and n = 3\nand we have [1] , then in order to play 1 again , we need to play 2 other songs first.\n[1,2,3,1]\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can make a choice diagram. There we will have choice each time to fill the spot either with a new song or a used song.\n\nin order to use the old song , we need to have atleask k used song.\n\nthe first spot will always be a unique song.\n\nso , our base conditions will be:\nif we have filled all the spots and we have used all the songs , then we return 1\nor if we have filled all the spots or we have used more songs than n , we return 0\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n\n mod = 10**9 + 7\n dic = {}\n\n def rec(lp , us):\n #base case\n if lp == 0 and us == n :\n return 1\n\n if lp == 0 or us > n :\n return 0\n if (lp , us) in dic :\n return dic[(lp , us)]\n # choosing a new/unique song\n res = (n-us) * rec(lp-1 , us+1)\n \n if us > k :\n # choosing a used/old song\n res += (us - k) * rec(lp-1 , us)\n \n dic[(lp , us)] = res\n return dic[(lp , us)]%mod\n\n return rec(goal , 0)\n\n``` | 1 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
Easy Explanation ever || Step-by-step Process || Python || Memoization | number-of-music-playlists | 0 | 1 | # Explanation\n1)We have to play goal No. of songs from n songs given that\n--->1.1)All n songs should be played atleast once and\n--->1.2)Replay of a song is only possible if there are k different songs played in between.\n2)So, at each song we can eighter play_new_song or replay_old_song\n--->2.1)if we play_new_song we multiply it with (No. of remaining new songs)\n------>2.1.1)This is because we can play any one out of remaining new songs. (so nC1 ways)\n--->2.2)similarly, if we replay_old_song we multiply it with (No. of possible songs that can be replayed)\n------>2.2.1)No. of possible songs that can be repalyed = n-k\n3)return play_new+replay_old\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Complexity\n- Time complexity: O(n*goal)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*goal)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n \n def solve(n, goal):\n if goal==0 and n==0:\n return 1\n if goal==0 or n==0:\n return 0\n if memo[n][goal] != -1:\n return memo[n][goal]\n replay_old_song = solve(n, goal-1)*max(n-k, 0)\n play_new_song = solve(n-1, goal-1)*n\n memo[n][goal] = (replay_old_song + play_new_song)%1000000007 \n return memo[n][goal]\n\n memo = [[-1 for j in range(goal+1)]for i in range(n+1)]\n return solve(n, goal)\n```\nThanks for viewing! | 1 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Easy Explanation ever || Step-by-step Process || Python || Memoization | number-of-music-playlists | 0 | 1 | # Explanation\n1)We have to play goal No. of songs from n songs given that\n--->1.1)All n songs should be played atleast once and\n--->1.2)Replay of a song is only possible if there are k different songs played in between.\n2)So, at each song we can eighter play_new_song or replay_old_song\n--->2.1)if we play_new_song we multiply it with (No. of remaining new songs)\n------>2.1.1)This is because we can play any one out of remaining new songs. (so nC1 ways)\n--->2.2)similarly, if we replay_old_song we multiply it with (No. of possible songs that can be replayed)\n------>2.2.1)No. of possible songs that can be repalyed = n-k\n3)return play_new+replay_old\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Complexity\n- Time complexity: O(n*goal)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*goal)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n \n def solve(n, goal):\n if goal==0 and n==0:\n return 1\n if goal==0 or n==0:\n return 0\n if memo[n][goal] != -1:\n return memo[n][goal]\n replay_old_song = solve(n, goal-1)*max(n-k, 0)\n play_new_song = solve(n-1, goal-1)*n\n memo[n][goal] = (replay_old_song + play_new_song)%1000000007 \n return memo[n][goal]\n\n memo = [[-1 for j in range(goal+1)]for i in range(n+1)]\n return solve(n, goal)\n```\nThanks for viewing! | 1 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
Python3 Solution | number-of-music-playlists | 0 | 1 | \n```\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n mod=10**9+7\n @cache\n def fn(i,x):\n if i==goal:\n return x==n\n\n ans=0\n if x<n:\n ans+=(n-x)*fn(i+1,x+1)\n\n if k<x:\n ans+=(x-k)*fn(i+1,x)\n\n return ans%mod\n\n return fn(0,0) \n``` | 1 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Python3 Solution | number-of-music-playlists | 0 | 1 | \n```\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n mod=10**9+7\n @cache\n def fn(i,x):\n if i==goal:\n return x==n\n\n ans=0\n if x<n:\n ans+=(n-x)*fn(i+1,x+1)\n\n if k<x:\n ans+=(x-k)*fn(i+1,x)\n\n return ans%mod\n\n return fn(0,0) \n``` | 1 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
Solution | number-of-music-playlists | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numMusicPlaylists(int n, int goal, int k) {\n \n const unsigned MOD = 1\'000\'000\'007;\n long dp[1+goal][1+n];\n memset( dp, 0, sizeof(dp) );\n dp[0][0] = 1;\n \n for( int i = 1; i <= goal; ++i )\n for( int j = 1; j <= n; ++j ) {\n dp[i][j] = dp[i-1][j-1] * ( n - (j-1) );\n dp[i][j] += dp[i-1][j] * max( j-k, 0 );\n dp[i][j] %= MOD;\n }\n return dp[goal][n];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n MOD = 10**9 + 7\n res, c = 0, 1\n\n def inv(x):\n return pow(x, MOD - 2, MOD)\n\n for x in range(1, n - k):\n c = (c * -x) % MOD\n c = inv(c)\n\n for j in range(1, n - k + 1):\n res += pow(j, goal - k - 1, MOD) * c\n c = c * (j - (n - k)) % MOD * inv(j) % MOD\n\n for j in range(1, n + 1):\n res = res * j % MOD\n return res\n```\n\n```Java []\nclass Solution {\n public int numMusicPlaylists(int n, int goal, int k) {\n int modulo = 1_000_000_007;\n\n long[] dp = new long[goal - n + 1];\n Arrays.fill(dp, 1);\n\n for (int p = 2; p <= n - k; ++p) {\n for (int i = 1; i <= goal - n; ++i) {\n dp[i] += dp[i - 1] * p;\n dp[i] %= modulo;\n }\n }\n long result = dp[goal - n];\n for (int key = 2; key <= n; ++key) {\n result = result * key % modulo;\n }\n return (int) result;\n }\n}\n```\n | 1 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Solution | number-of-music-playlists | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numMusicPlaylists(int n, int goal, int k) {\n \n const unsigned MOD = 1\'000\'000\'007;\n long dp[1+goal][1+n];\n memset( dp, 0, sizeof(dp) );\n dp[0][0] = 1;\n \n for( int i = 1; i <= goal; ++i )\n for( int j = 1; j <= n; ++j ) {\n dp[i][j] = dp[i-1][j-1] * ( n - (j-1) );\n dp[i][j] += dp[i-1][j] * max( j-k, 0 );\n dp[i][j] %= MOD;\n }\n return dp[goal][n];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n MOD = 10**9 + 7\n res, c = 0, 1\n\n def inv(x):\n return pow(x, MOD - 2, MOD)\n\n for x in range(1, n - k):\n c = (c * -x) % MOD\n c = inv(c)\n\n for j in range(1, n - k + 1):\n res += pow(j, goal - k - 1, MOD) * c\n c = c * (j - (n - k)) % MOD * inv(j) % MOD\n\n for j in range(1, n + 1):\n res = res * j % MOD\n return res\n```\n\n```Java []\nclass Solution {\n public int numMusicPlaylists(int n, int goal, int k) {\n int modulo = 1_000_000_007;\n\n long[] dp = new long[goal - n + 1];\n Arrays.fill(dp, 1);\n\n for (int p = 2; p <= n - k; ++p) {\n for (int i = 1; i <= goal - n; ++i) {\n dp[i] += dp[i - 1] * p;\n dp[i] %= modulo;\n }\n }\n long result = dp[goal - n];\n for (int key = 2; key <= n; ++key) {\n result = result * key % modulo;\n }\n return (int) result;\n }\n}\n```\n | 1 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
Python3 - Dead Simple DP - Beats 99% | number-of-music-playlists | 0 | 1 | \n```\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n @lru_cache(None)\n def dp(uniques, repeats, rem, songsTilNewRepeat):\n if songsTilNewRepeat == 0:\n repeats += 1\n songsTilNewRepeat = 1\n if uniques > rem:\n return 0\n if rem == 0:\n return 1\n \n res = 0\n # either pick from uniques, or from repeats\n if uniques > 0:\n res += dp(uniques - 1, repeats, rem - 1, songsTilNewRepeat - 1) * uniques\n if repeats > 0:\n res += dp(uniques, repeats - 1, rem - 1, songsTilNewRepeat - 1) * repeats\n return res\n\n \n return dp(n, 0, goal, k + 1) % (10 ** 9 + 7)\n\n``` | 10 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Python3 - Dead Simple DP - Beats 99% | number-of-music-playlists | 0 | 1 | \n```\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n @lru_cache(None)\n def dp(uniques, repeats, rem, songsTilNewRepeat):\n if songsTilNewRepeat == 0:\n repeats += 1\n songsTilNewRepeat = 1\n if uniques > rem:\n return 0\n if rem == 0:\n return 1\n \n res = 0\n # either pick from uniques, or from repeats\n if uniques > 0:\n res += dp(uniques - 1, repeats, rem - 1, songsTilNewRepeat - 1) * uniques\n if repeats > 0:\n res += dp(uniques, repeats - 1, rem - 1, songsTilNewRepeat - 1) * repeats\n return res\n\n \n return dp(n, 0, goal, k + 1) % (10 ** 9 + 7)\n\n``` | 10 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | number-of-music-playlists | 1 | 1 | # Intuition\nUsing dynamic programming to keep values that represent the number of valid playlists for different combinations of playlist length and unique songs.\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/6M7QoVTRgSE\n\n# Subscribe to my channel from here. I have 241 videos as of August 6th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Initialize `mod` with the value 10^9 + 7.\n\n2. Create a 2D array `dp` with dimensions `(goal + 1) x (n + 1)` and initialize all elements to 0. This array will be used to store the dynamic programming results, where `dp[i][j]` represents the number of possible playlists of length `i` containing exactly `j` unique songs.\n\n3. Set `dp[0][0]` to 1. This represents that there\'s exactly one way to create a playlist of length 0 with 0 unique songs, which is essentially an empty playlist.\n\n4. Loop from `i = 1` to `goal` (inclusive):\n - Inside this loop, iterate from `j = 1` to `min(i, n)` (inclusive). This loop calculates the possible playlists of length `i` with `j` unique songs.\n - Calculate `dp[i][j]` using the formula: `dp[i][j] = dp[i - 1][j - 1] * (n - j + 1) % mod`. This corresponds to the scenario where a new song is added to the playlist, increasing both the playlist length and the number of unique songs.\n - Check if `j` is greater than `k`. If true, it means we can replay old songs. In this case, update `dp[i][j]` again using the formula: `dp[i][j] = (dp[i][j] + dp[i - 1][j] * (j - k)) % mod`. This accounts for the scenario where an old song is replayed, increasing the playlist length but not the number of unique songs.\n\n5. Finally, the value in `dp[goal][n]` will represent the number of possible playlists of length `goal` using exactly `n` unique songs. This is the answer to the problem, so return this value.\n\nThe algorithm uses dynamic programming to iteratively fill the `dp` array with values that represent the number of valid playlists for different combinations of playlist length and unique songs.\n\n# Complexity\n- Time complexity: O(goal * n)\n\n\n- Space complexity: O(goal * n)\n\n```python []\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n mod = 10**9 + 7\n\n dp = [[0 for _ in range(n + 1)] for _ in range(goal + 1)]\n dp[0][0] = 1\n\n for i in range(1, goal + 1):\n for j in range(1, min(i, n) + 1):\n dp[i][j] = dp[i-1][j-1] * (n - j + 1) % mod\n \n if j > k:\n dp[i][j] = (dp[i][j] + dp[i-1][j] * (j-k)) % mod\n \n return dp[goal][n]\n```\n```javascript []\n/**\n * @param {number} n\n * @param {number} goal\n * @param {number} k\n * @return {number}\n */\nvar numMusicPlaylists = function(n, goal, k) {\n const MOD = 10**9 + 7;\n\n const dp = new Array(goal + 1).fill(0).map(() => new Array(n + 1).fill(0));\n dp[0][0] = 1;\n\n for (let i = 1; i <= goal; i++) {\n for (let j = 1; j <= Math.min(i, n); j++) {\n dp[i][j] = dp[i - 1][j - 1] * (n - j + 1) % MOD;\n\n if (j > k) {\n dp[i][j] = (dp[i][j] + dp[i - 1][j] * (j - k)) % MOD;\n }\n }\n }\n\n return dp[goal][n]; \n};\n```\n```java []\nclass Solution {\n public int numMusicPlaylists(int n, int goal, int k) {\n int MOD = 1000000007;\n\n int[][] dp = new int[goal + 1][n + 1];\n dp[0][0] = 1;\n\n for (int i = 1; i <= goal; i++) {\n for (int j = 1; j <= Math.min(i, n); j++) {\n dp[i][j] = (int)((long)dp[i - 1][j - 1] * (n - j + 1) % MOD);\n\n if (j > k) {\n dp[i][j] = (dp[i][j] + (int)((long)dp[i - 1][j] * (j - k) % MOD)) % MOD;\n }\n }\n }\n\n return dp[goal][n];\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numMusicPlaylists(int n, int goal, int k) {\n const int MOD = 1000000007;\n\n vector<vector<long long>> dp(goal + 1, vector<long long>(n + 1, 0));\n dp[0][0] = 1;\n\n for (int i = 1; i <= goal; i++) {\n for (int j = 1; j <= min(i, n); j++) {\n dp[i][j] = dp[i - 1][j - 1] * (n - j + 1) % MOD;\n\n if (j > k) {\n dp[i][j] = (dp[i][j] + dp[i - 1][j] * (j - k)) % MOD;\n }\n }\n }\n\n return dp[goal][n];\n\n }\n};\n```\n | 16 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | number-of-music-playlists | 1 | 1 | # Intuition\nUsing dynamic programming to keep values that represent the number of valid playlists for different combinations of playlist length and unique songs.\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/6M7QoVTRgSE\n\n# Subscribe to my channel from here. I have 241 videos as of August 6th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Initialize `mod` with the value 10^9 + 7.\n\n2. Create a 2D array `dp` with dimensions `(goal + 1) x (n + 1)` and initialize all elements to 0. This array will be used to store the dynamic programming results, where `dp[i][j]` represents the number of possible playlists of length `i` containing exactly `j` unique songs.\n\n3. Set `dp[0][0]` to 1. This represents that there\'s exactly one way to create a playlist of length 0 with 0 unique songs, which is essentially an empty playlist.\n\n4. Loop from `i = 1` to `goal` (inclusive):\n - Inside this loop, iterate from `j = 1` to `min(i, n)` (inclusive). This loop calculates the possible playlists of length `i` with `j` unique songs.\n - Calculate `dp[i][j]` using the formula: `dp[i][j] = dp[i - 1][j - 1] * (n - j + 1) % mod`. This corresponds to the scenario where a new song is added to the playlist, increasing both the playlist length and the number of unique songs.\n - Check if `j` is greater than `k`. If true, it means we can replay old songs. In this case, update `dp[i][j]` again using the formula: `dp[i][j] = (dp[i][j] + dp[i - 1][j] * (j - k)) % mod`. This accounts for the scenario where an old song is replayed, increasing the playlist length but not the number of unique songs.\n\n5. Finally, the value in `dp[goal][n]` will represent the number of possible playlists of length `goal` using exactly `n` unique songs. This is the answer to the problem, so return this value.\n\nThe algorithm uses dynamic programming to iteratively fill the `dp` array with values that represent the number of valid playlists for different combinations of playlist length and unique songs.\n\n# Complexity\n- Time complexity: O(goal * n)\n\n\n- Space complexity: O(goal * n)\n\n```python []\nclass Solution:\n def numMusicPlaylists(self, n: int, goal: int, k: int) -> int:\n mod = 10**9 + 7\n\n dp = [[0 for _ in range(n + 1)] for _ in range(goal + 1)]\n dp[0][0] = 1\n\n for i in range(1, goal + 1):\n for j in range(1, min(i, n) + 1):\n dp[i][j] = dp[i-1][j-1] * (n - j + 1) % mod\n \n if j > k:\n dp[i][j] = (dp[i][j] + dp[i-1][j] * (j-k)) % mod\n \n return dp[goal][n]\n```\n```javascript []\n/**\n * @param {number} n\n * @param {number} goal\n * @param {number} k\n * @return {number}\n */\nvar numMusicPlaylists = function(n, goal, k) {\n const MOD = 10**9 + 7;\n\n const dp = new Array(goal + 1).fill(0).map(() => new Array(n + 1).fill(0));\n dp[0][0] = 1;\n\n for (let i = 1; i <= goal; i++) {\n for (let j = 1; j <= Math.min(i, n); j++) {\n dp[i][j] = dp[i - 1][j - 1] * (n - j + 1) % MOD;\n\n if (j > k) {\n dp[i][j] = (dp[i][j] + dp[i - 1][j] * (j - k)) % MOD;\n }\n }\n }\n\n return dp[goal][n]; \n};\n```\n```java []\nclass Solution {\n public int numMusicPlaylists(int n, int goal, int k) {\n int MOD = 1000000007;\n\n int[][] dp = new int[goal + 1][n + 1];\n dp[0][0] = 1;\n\n for (int i = 1; i <= goal; i++) {\n for (int j = 1; j <= Math.min(i, n); j++) {\n dp[i][j] = (int)((long)dp[i - 1][j - 1] * (n - j + 1) % MOD);\n\n if (j > k) {\n dp[i][j] = (dp[i][j] + (int)((long)dp[i - 1][j] * (j - k) % MOD)) % MOD;\n }\n }\n }\n\n return dp[goal][n];\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numMusicPlaylists(int n, int goal, int k) {\n const int MOD = 1000000007;\n\n vector<vector<long long>> dp(goal + 1, vector<long long>(n + 1, 0));\n dp[0][0] = 1;\n\n for (int i = 1; i <= goal; i++) {\n for (int j = 1; j <= min(i, n); j++) {\n dp[i][j] = dp[i - 1][j - 1] * (n - j + 1) % MOD;\n\n if (j > k) {\n dp[i][j] = (dp[i][j] + dp[i - 1][j] * (j - k)) % MOD;\n }\n }\n }\n\n return dp[goal][n];\n\n }\n};\n```\n | 16 | You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.
You are given a collection of `rods` that can be welded together. For example, if you have rods of lengths `1`, `2`, and `3`, you can weld them together to make a support of length `6`.
Return _the largest possible height of your billboard installation_. If you cannot support the billboard, return `0`.
**Example 1:**
**Input:** rods = \[1,2,3,6\]
**Output:** 6
**Explanation:** We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.
**Example 2:**
**Input:** rods = \[1,2,3,4,5,6\]
**Output:** 10
**Explanation:** We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.
**Example 3:**
**Input:** rods = \[1,2\]
**Output:** 0
**Explanation:** The billboard cannot be supported, so we return 0.
**Constraints:**
* `1 <= rods.length <= 20`
* `1 <= rods[i] <= 1000`
* `sum(rods[i]) <= 5000` | null |
python3 solution beats 95% using stack O(N) SPACE | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe have the general way to find the validness of paranthesis we can use that and modify it a bit to solve this\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* if \'(\' is there append it\n* if \')\' is there then \n * we have a correct case where top of stack is \'(\' so just pop it\n * stack can be empty so we increase counter which keeps track of missing paranthesis\n * we can have \')\' itself as top of stack then we increment counter\n* further counter will have number of missing and any additional \')\' will be in stack, `return c + len(stack)` will get the required answer\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack=[]\n c=0\n for i in s:\n if i==\'(\':\n stack.append(i)\n continue\n if i==\')\':\n if not stack:\n c+=1\n else:\n if stack[-1]==\'(\':\n stack.pop()\n continue\n c+=1\n return c+len(stack)\n``` | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
python3 solution beats 95% using stack O(N) SPACE | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe have the general way to find the validness of paranthesis we can use that and modify it a bit to solve this\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* if \'(\' is there append it\n* if \')\' is there then \n * we have a correct case where top of stack is \'(\' so just pop it\n * stack can be empty so we increase counter which keeps track of missing paranthesis\n * we can have \')\' itself as top of stack then we increment counter\n* further counter will have number of missing and any additional \')\' will be in stack, `return c + len(stack)` will get the required answer\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack=[]\n c=0\n for i in s:\n if i==\'(\':\n stack.append(i)\n continue\n if i==\')\':\n if not stack:\n c+=1\n else:\n if stack[-1]==\'(\':\n stack.pop()\n continue\n c+=1\n return c+len(stack)\n``` | 1 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
Simple solution with using Stack DS, beats 72%/64% | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\nThe problem is the common as [Stack DS](https://en.wikipedia.org/wiki/Stack_(abstract_data_type)).\n\n# Approach\n1. initialize an empty `stack`\n2. iterate over all token in `s`\n3. check if token is `(` or if `stack` is empty, if last token in `stack` is a `)`\n4. return a length of a `stack` \n\n# Complexity\n- Time complexity: **O(n)**, because of iterating over all tokens in `s`\n\n- Space complexity: **O(n)**, because of storing tokens in string.\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n\n for token in s:\n if token == \'(\' or not stack or (stack and stack[-1] != \'(\'):\n stack.append(token)\n else:\n stack.pop()\n\n return len(stack)\n``` | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Simple solution with using Stack DS, beats 72%/64% | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\nThe problem is the common as [Stack DS](https://en.wikipedia.org/wiki/Stack_(abstract_data_type)).\n\n# Approach\n1. initialize an empty `stack`\n2. iterate over all token in `s`\n3. check if token is `(` or if `stack` is empty, if last token in `stack` is a `)`\n4. return a length of a `stack` \n\n# Complexity\n- Time complexity: **O(n)**, because of iterating over all tokens in `s`\n\n- Space complexity: **O(n)**, because of storing tokens in string.\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n\n for token in s:\n if token == \'(\' or not stack or (stack and stack[-1] != \'(\'):\n stack.append(token)\n else:\n stack.pop()\n\n return len(stack)\n``` | 1 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
Python || 96.41% Faster || Space - O(1) and O(n) | minimum-add-to-make-parentheses-valid | 0 | 1 | **Without Stack Soltuion:**\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n o=c=0\n for i in s:\n if i==\'(\':\n o+=1\n else:\n if o:\n o-=1\n else:\n c+=1\n return o+c\n```\n**With Stack Solution:**\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n st=[]\n c=0\n for i in s:\n if i==\'(\':\n st.append(i)\n else:\n if st and st[-1]:\n st.pop()\n else:\n c+=1\n return len(st) + c\n```\n**An upvote will be encouraging** | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Python || 96.41% Faster || Space - O(1) and O(n) | minimum-add-to-make-parentheses-valid | 0 | 1 | **Without Stack Soltuion:**\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n o=c=0\n for i in s:\n if i==\'(\':\n o+=1\n else:\n if o:\n o-=1\n else:\n c+=1\n return o+c\n```\n**With Stack Solution:**\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n st=[]\n c=0\n for i in s:\n if i==\'(\':\n st.append(i)\n else:\n if st and st[-1]:\n st.pop()\n else:\n c+=1\n return len(st) + c\n```\n**An upvote will be encouraging** | 1 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
Minimum add to make parentheses valid | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack=[]\n for i in s:\n if len(stack)==0:\n stack.append(i)\n elif i==\')\' and stack[-1]==\'(\':\n stack.pop()\n else:\n stack.append(i)\n return len(stack)\n``` | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Minimum add to make parentheses valid | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack=[]\n for i in s:\n if len(stack)==0:\n stack.append(i)\n elif i==\')\' and stack[-1]==\'(\':\n stack.pop()\n else:\n stack.append(i)\n return len(stack)\n``` | 1 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
Solution | minimum-add-to-make-parentheses-valid | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> st;\n int ans=0;\n for(auto x:s)\n {\n if(x==\'(\')\n st.push(x);\n else\n {\n if(!st.empty())\n st.pop();\n else\n {\n ans++;\n }\n }\n }\n while(!st.empty())\n {\n st.pop();\n ans++;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n counts=0\n counte=0\n for i in range(len(s)):\n if s[i]==\'(\':\n counts+=1\n elif counts>0:\n counts-=1\n else:\n counte+=1 \n return (counts+counte)\n```\n\n```Java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int a = 0, b = 0; \n for(char ch : s.toCharArray())\n {\n if(ch == \'(\')\n {\n a++;\n } \n else\n {\n if(a > 0)\n {\n a--;\n } \n else\n {\n b++;\n }\n }\n } \n return a+b;\n }\n}\n```\n | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Solution | minimum-add-to-make-parentheses-valid | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> st;\n int ans=0;\n for(auto x:s)\n {\n if(x==\'(\')\n st.push(x);\n else\n {\n if(!st.empty())\n st.pop();\n else\n {\n ans++;\n }\n }\n }\n while(!st.empty())\n {\n st.pop();\n ans++;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n counts=0\n counte=0\n for i in range(len(s)):\n if s[i]==\'(\':\n counts+=1\n elif counts>0:\n counts-=1\n else:\n counte+=1 \n return (counts+counte)\n```\n\n```Java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int a = 0, b = 0; \n for(char ch : s.toCharArray())\n {\n if(ch == \'(\')\n {\n a++;\n } \n else\n {\n if(a > 0)\n {\n a--;\n } \n else\n {\n b++;\n }\n }\n } \n return a+b;\n }\n}\n```\n | 1 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
stack | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n for ele in s:\n if stack: \n if stack[-1] == \'(\' and ele == \')\':\n stack.pop()\n else:\n stack.append(ele)\n else:\n stack.append(ele)\n return len(stack)\n\n``` | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
stack | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n for ele in s:\n if stack: \n if stack[-1] == \'(\' and ele == \')\':\n stack.pop()\n else:\n stack.append(ele)\n else:\n stack.append(ele)\n return len(stack)\n\n``` | 1 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
Simple Java & Python3 Solution | Beats 100 % in java and Python3| Explained | O(n) | minimum-add-to-make-parentheses-valid | 1 | 1 | The provided code takes a string s as input and calculates the minimum number of parentheses needed to make the string balanced. It does this by iterating over the string and keeping track of an integer variable total that represents the difference between the number of opening and closing parentheses encountered so far. Whenever an opening parenthesis is encountered, the code checks if there are any excess closing parentheses (i.e., if total is positive), and adds their absolute value to a running count final. Similarly, whenever a closing parenthesis is encountered, the total variable is incremented by 1. Finally, the absolute value of total is added to final to account for any remaining unbalanced parentheses. The final value of final is returned as the result of the function.\n# Complexity\n- Time complexity : O(n)\n\n- Space complexity : O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int f = 0;\n int t = 0;\n for(int i=0;i<s.length();i++){\n char c=s.charAt(i);\n if(c==\'(\'){\n if(t > 0){\n f += Math.abs(t);\n t = 0;\n }\n t -= 1;\n }\n else if(c==\')\'){\n t += 1;\n }\n }\n f += Math.abs(t);\n return f;\n }\n}\n```\n```python []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n final = 0\n total = 0\n for i in s:\n if i == "(":\n if total > 0:\n final += abs(total)\n total = 0\n total -= 1\n elif i == ")":\n total += 1\n final += abs(total)\n return final\n```\n\n\n | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Simple Java & Python3 Solution | Beats 100 % in java and Python3| Explained | O(n) | minimum-add-to-make-parentheses-valid | 1 | 1 | The provided code takes a string s as input and calculates the minimum number of parentheses needed to make the string balanced. It does this by iterating over the string and keeping track of an integer variable total that represents the difference between the number of opening and closing parentheses encountered so far. Whenever an opening parenthesis is encountered, the code checks if there are any excess closing parentheses (i.e., if total is positive), and adds their absolute value to a running count final. Similarly, whenever a closing parenthesis is encountered, the total variable is incremented by 1. Finally, the absolute value of total is added to final to account for any remaining unbalanced parentheses. The final value of final is returned as the result of the function.\n# Complexity\n- Time complexity : O(n)\n\n- Space complexity : O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n int f = 0;\n int t = 0;\n for(int i=0;i<s.length();i++){\n char c=s.charAt(i);\n if(c==\'(\'){\n if(t > 0){\n f += Math.abs(t);\n t = 0;\n }\n t -= 1;\n }\n else if(c==\')\'){\n t += 1;\n }\n }\n f += Math.abs(t);\n return f;\n }\n}\n```\n```python []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n final = 0\n total = 0\n for i in s:\n if i == "(":\n if total > 0:\n final += abs(total)\n total = 0\n total -= 1\n elif i == ")":\n total += 1\n final += abs(total)\n return final\n```\n\n\n | 1 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
🧠[C++/Java/Python]: One Pass Easy Solution | minimum-add-to-make-parentheses-valid | 1 | 1 | ## Approach\n> 1. Initialize an empty stack st to keep track of unmatched opening parentheses.\n> 2. Iterate through each character i in the input string s.\n\n> 3. For each character i:\n> * If the stack is empty, push the character onto the stack because there\'s nothing to match it with.\n> * If the stack is not empty and the current character i is a closing parenthesis \')\' and the top of the stack contains an opening parenthesis \'(\', then pop the opening parenthesis from the stack because a valid pair has been found.\n> * If none of the above conditions are met, push the current character i onto the stack.\n> 4. After processing all characters in the string, the remaining unmatched opening parentheses (if any) will be left on the stack. The size of the stack represents the minimum number of additions needed to make the string valid.\n> 5. Return the size of the stack as the result, which is the minimum number of additions required to make the string valid.\n\n---\n\n\n\n## Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n---\n\n\n\n## Code\n```C++ []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> st;\n\n for(auto i: s){\n if(st.empty())\n st.push(i);\n else if(st.top() == \'(\' and i == \')\')\n st.pop();\n else\n st.push(i);\n }\n return st.size();\n }\n};\n```\n```Java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n Stack<Character> stack = new Stack<>();\n\n for (char c : s.toCharArray()) {\n if (stack.isEmpty()) {\n stack.push(c);\n } else if (stack.peek() == \'(\' && c == \')\') {\n stack.pop();\n } else {\n stack.push(c);\n }\n }\n\n // At this point, the stack contains unmatched parentheses.\n // The size of the stack is the minimum number of additions required.\n return stack.size();\n }\n};\n```\n```Python []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n\n for char in s:\n if not stack:\n stack.append(char)\n elif stack[-1] == \'(\' and char == \')\':\n stack.pop()\n else:\n stack.append(char)\n\n # At this point, the stack contains unmatched parentheses.\n # The length of the stack is the minimum number of additions required.\n return len(stack)\n\n```\n\n---\n\n\n\n | 3 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
🧠[C++/Java/Python]: One Pass Easy Solution | minimum-add-to-make-parentheses-valid | 1 | 1 | ## Approach\n> 1. Initialize an empty stack st to keep track of unmatched opening parentheses.\n> 2. Iterate through each character i in the input string s.\n\n> 3. For each character i:\n> * If the stack is empty, push the character onto the stack because there\'s nothing to match it with.\n> * If the stack is not empty and the current character i is a closing parenthesis \')\' and the top of the stack contains an opening parenthesis \'(\', then pop the opening parenthesis from the stack because a valid pair has been found.\n> * If none of the above conditions are met, push the current character i onto the stack.\n> 4. After processing all characters in the string, the remaining unmatched opening parentheses (if any) will be left on the stack. The size of the stack represents the minimum number of additions needed to make the string valid.\n> 5. Return the size of the stack as the result, which is the minimum number of additions required to make the string valid.\n\n---\n\n\n\n## Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n---\n\n\n\n## Code\n```C++ []\nclass Solution {\npublic:\n int minAddToMakeValid(string s) {\n stack<char> st;\n\n for(auto i: s){\n if(st.empty())\n st.push(i);\n else if(st.top() == \'(\' and i == \')\')\n st.pop();\n else\n st.push(i);\n }\n return st.size();\n }\n};\n```\n```Java []\nclass Solution {\n public int minAddToMakeValid(String s) {\n Stack<Character> stack = new Stack<>();\n\n for (char c : s.toCharArray()) {\n if (stack.isEmpty()) {\n stack.push(c);\n } else if (stack.peek() == \'(\' && c == \')\') {\n stack.pop();\n } else {\n stack.push(c);\n }\n }\n\n // At this point, the stack contains unmatched parentheses.\n // The size of the stack is the minimum number of additions required.\n return stack.size();\n }\n};\n```\n```Python []\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n\n for char in s:\n if not stack:\n stack.append(char)\n elif stack[-1] == \'(\' and char == \')\':\n stack.pop()\n else:\n stack.append(char)\n\n # At this point, the stack contains unmatched parentheses.\n # The length of the stack is the minimum number of additions required.\n return len(stack)\n\n```\n\n---\n\n\n\n | 3 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
Python3 Solution | O(N) Time and Space Complexity | Stack | minimum-add-to-make-parentheses-valid | 0 | 1 | Approach:\nwe can use stack to solve this problem:\nThe problem is the same as checking the given set of parentheses are whether valid or not. if the given string parentheses are valid, then our stack will be empty. but if the string input is not a valid parentheses, then there will be some parentheses left in the stack. so to make the string valid we need to have a number of parentheses that are same as the length of the stack.\n```\ndef minAddToMakeValid(self, s: str) -> int:\n\tstack = []\n\ti = 0\n\tparentheses = {")":"("}\n\twhile i < len(s):\n\t\tif stack and stack[-1] == parentheses.get(s[i],None):\n\t\t\tstack.pop()\n\t\telse:\n\t\t\tstack.append(s[i])\n\t\ti +=1\n\treturn len(stack) | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Python3 Solution | O(N) Time and Space Complexity | Stack | minimum-add-to-make-parentheses-valid | 0 | 1 | Approach:\nwe can use stack to solve this problem:\nThe problem is the same as checking the given set of parentheses are whether valid or not. if the given string parentheses are valid, then our stack will be empty. but if the string input is not a valid parentheses, then there will be some parentheses left in the stack. so to make the string valid we need to have a number of parentheses that are same as the length of the stack.\n```\ndef minAddToMakeValid(self, s: str) -> int:\n\tstack = []\n\ti = 0\n\tparentheses = {")":"("}\n\twhile i < len(s):\n\t\tif stack and stack[-1] == parentheses.get(s[i],None):\n\t\t\tstack.pop()\n\t\telse:\n\t\t\tstack.append(s[i])\n\t\ti +=1\n\treturn len(stack) | 1 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
Using Stacks | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack=[]\n for i in s:\n if len(stack)==0:\n stack.append(i)\n else:\n if stack[-1]==\'(\' and i==\')\':\n del stack[-1]\n else:\n stack.append(i)\n return len(stack)\n``` | 2 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Using Stacks | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack=[]\n for i in s:\n if len(stack)==0:\n stack.append(i)\n else:\n if stack[-1]==\'(\' and i==\')\':\n del stack[-1]\n else:\n stack.append(i)\n return len(stack)\n``` | 2 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
Easy | Python Solution | Stack | Greedy | minimum-add-to-make-parentheses-valid | 0 | 1 | # Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n for i in s:\n if len(stack) == 0:\n stack.append(i)\n else:\n popp = stack.pop()\n if popp == "(" and i == ")":\n continue\n else:\n stack.append(popp)\n stack.append(i)\n return len(stack)\n``` | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Easy | Python Solution | Stack | Greedy | minimum-add-to-make-parentheses-valid | 0 | 1 | # Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n stack = []\n for i in s:\n if len(stack) == 0:\n stack.append(i)\n else:\n popp = stack.pop()\n if popp == "(" and i == ")":\n continue\n else:\n stack.append(popp)\n stack.append(i)\n return len(stack)\n``` | 1 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
Easy Intuition Python Single Pass Solution | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe number of opening/ brackets to add to make it a valid parentheses will be equal to the number of unbalanced "(" or ")". We can easily determine those by the exact same method by which we validate a string to be valid parentheses or not\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe shall use a stack to push the char in s and pop whenver we find a valid parenthesis. The unbalanced brackets will remain on the stack and thus the answer will be equal to the length of the final stack after iterating through s\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n q = deque()\n for i in s:\n if not q:\n q.append(i)\n else:\n if(i == "(") or (i == ")" and q[-1] != "("):\n q.append(i)\n continue\n if(i == ")" and q[-1] == "("):\n q.pop()\n continue\n return len(q)\n``` | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Easy Intuition Python Single Pass Solution | minimum-add-to-make-parentheses-valid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe number of opening/ brackets to add to make it a valid parentheses will be equal to the number of unbalanced "(" or ")". We can easily determine those by the exact same method by which we validate a string to be valid parentheses or not\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe shall use a stack to push the char in s and pop whenver we find a valid parenthesis. The unbalanced brackets will remain on the stack and thus the answer will be equal to the length of the final stack after iterating through s\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n q = deque()\n for i in s:\n if not q:\n q.append(i)\n else:\n if(i == "(") or (i == ")" and q[-1] != "("):\n q.append(i)\n continue\n if(i == ")" and q[-1] == "("):\n q.pop()\n continue\n return len(q)\n``` | 1 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
simple solution in python using replace | minimum-add-to-make-parentheses-valid | 0 | 1 | \n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n while "()" in s:\n s=s.replace("()","",1)\n return len(s)\n``` | 2 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
simple solution in python using replace | minimum-add-to-make-parentheses-valid | 0 | 1 | \n```\nclass Solution:\n def minAddToMakeValid(self, s: str) -> int:\n while "()" in s:\n s=s.replace("()","",1)\n return len(s)\n``` | 2 | There are `8` prison cells in a row and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
* If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
* Otherwise, it becomes vacant.
**Note** that because the prison is a row, the first and the last cells in the row can't have two adjacent neighbors.
You are given an integer array `cells` where `cells[i] == 1` if the `ith` cell is occupied and `cells[i] == 0` if the `ith` cell is vacant, and you are given an integer `n`.
Return the state of the prison after `n` days (i.e., `n` such changes described above).
**Example 1:**
**Input:** cells = \[0,1,0,1,1,0,0,1\], n = 7
**Output:** \[0,0,1,1,0,0,0,0\]
**Explanation:** The following table summarizes the state of the prison on each day:
Day 0: \[0, 1, 0, 1, 1, 0, 0, 1\]
Day 1: \[0, 1, 1, 0, 0, 0, 0, 0\]
Day 2: \[0, 0, 0, 0, 1, 1, 1, 0\]
Day 3: \[0, 1, 1, 0, 0, 1, 0, 0\]
Day 4: \[0, 0, 0, 0, 0, 1, 0, 0\]
Day 5: \[0, 1, 1, 1, 0, 1, 0, 0\]
Day 6: \[0, 0, 1, 0, 1, 1, 0, 0\]
Day 7: \[0, 0, 1, 1, 0, 0, 0, 0\]
**Example 2:**
**Input:** cells = \[1,0,0,1,0,0,1,0\], n = 1000000000
**Output:** \[0,0,1,1,1,1,1,0\]
**Constraints:**
* `cells.length == 8`
* `cells[i]` is either `0` or `1`.
* `1 <= n <= 109` | null |
Python3|| Easy solution. | sort-array-by-parity-ii | 0 | 1 | # Code\n```\nclass Solution:\n def sortArrayByParityII(self, nums: List[int]) -> List[int]:\n even = []\n odd = []\n lst=[]\n for i in range(len(nums)):\n if nums[i]%2 == 0:\n even.append(nums[i])\n else:\n odd.append(nums[i])\n for i in range(len(even)):\n lst.append(even[i])\n lst.append(odd[i])\n return lst\n```\n\n | 8 | Given an array of integers `nums`, half of the integers in `nums` are **odd**, and the other half are **even**.
Sort the array so that whenever `nums[i]` is odd, `i` is **odd**, and whenever `nums[i]` is even, `i` is **even**.
Return _any answer array that satisfies this condition_.
**Example 1:**
**Input:** nums = \[4,2,5,7\]
**Output:** \[4,5,2,7\]
**Explanation:** \[4,7,2,5\], \[2,5,4,7\], \[2,7,4,5\] would also have been accepted.
**Example 2:**
**Input:** nums = \[2,3\]
**Output:** \[2,3\]
**Constraints:**
* `2 <= nums.length <= 2 * 104`
* `nums.length` is even.
* Half of the integers in `nums` are even.
* `0 <= nums[i] <= 1000`
**Follow Up:** Could you solve it in-place? | null |
Python3|| Easy solution. | sort-array-by-parity-ii | 0 | 1 | # Code\n```\nclass Solution:\n def sortArrayByParityII(self, nums: List[int]) -> List[int]:\n even = []\n odd = []\n lst=[]\n for i in range(len(nums)):\n if nums[i]%2 == 0:\n even.append(nums[i])\n else:\n odd.append(nums[i])\n for i in range(len(even)):\n lst.append(even[i])\n lst.append(odd[i])\n return lst\n```\n\n | 8 | Given the `root` of a binary tree, determine if it is a _complete binary tree_.
In a **[complete binary tree](http://en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees)**, every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between `1` and `2h` nodes inclusive at the last level `h`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** true
**Explanation:** Every level before the last is full (ie. levels with node-values {1} and {2, 3}), and all nodes in the last level ({4, 5, 6}) are as far left as possible.
**Example 2:**
**Input:** root = \[1,2,3,4,5,null,7\]
**Output:** false
**Explanation:** The node with value 7 isn't as far left as possible.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `1 <= Node.val <= 1000` | null |
Solution | sort-array-by-parity-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n int n=nums.size();\n int i=0;\n int j=1;\n while(i<n && j<n){\n if(nums[i]%2==0)\n i=i+2;\n else if(nums[j]%2==1)\n j=j+2;\n else\n swap(nums[i],nums[j]);\n }\n return nums;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def sortArrayByParityII(self, nums: List[int]) -> List[int]:\n\n j=1\n\n for i in range(0,len(nums),2):\n if nums[i]%2:\n while nums[j]%2:\n j+=2\n nums[i],nums[j]=nums[j],nums[i]\n\n return nums\n```\n\n```Java []\nclass Solution {\n public int[] sortArrayByParityII(int[] nums) {\n int[] freq = new int[1001];\n for (int n : nums){\n freq[n]++;\n }\n for (int k = 0; k < 2; k++) {\n int cur = k;\n for (int i = k; i < nums.length; i += 2) {\n while (freq[cur] == 0) cur += 2;\n freq[cur]--;\n nums[i] = cur;\n }\n }\n return nums;\n }\n}\n```\n | 4 | Given an array of integers `nums`, half of the integers in `nums` are **odd**, and the other half are **even**.
Sort the array so that whenever `nums[i]` is odd, `i` is **odd**, and whenever `nums[i]` is even, `i` is **even**.
Return _any answer array that satisfies this condition_.
**Example 1:**
**Input:** nums = \[4,2,5,7\]
**Output:** \[4,5,2,7\]
**Explanation:** \[4,7,2,5\], \[2,5,4,7\], \[2,7,4,5\] would also have been accepted.
**Example 2:**
**Input:** nums = \[2,3\]
**Output:** \[2,3\]
**Constraints:**
* `2 <= nums.length <= 2 * 104`
* `nums.length` is even.
* Half of the integers in `nums` are even.
* `0 <= nums[i] <= 1000`
**Follow Up:** Could you solve it in-place? | null |
Solution | sort-array-by-parity-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n int n=nums.size();\n int i=0;\n int j=1;\n while(i<n && j<n){\n if(nums[i]%2==0)\n i=i+2;\n else if(nums[j]%2==1)\n j=j+2;\n else\n swap(nums[i],nums[j]);\n }\n return nums;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def sortArrayByParityII(self, nums: List[int]) -> List[int]:\n\n j=1\n\n for i in range(0,len(nums),2):\n if nums[i]%2:\n while nums[j]%2:\n j+=2\n nums[i],nums[j]=nums[j],nums[i]\n\n return nums\n```\n\n```Java []\nclass Solution {\n public int[] sortArrayByParityII(int[] nums) {\n int[] freq = new int[1001];\n for (int n : nums){\n freq[n]++;\n }\n for (int k = 0; k < 2; k++) {\n int cur = k;\n for (int i = k; i < nums.length; i += 2) {\n while (freq[cur] == 0) cur += 2;\n freq[cur]--;\n nums[i] = cur;\n }\n }\n return nums;\n }\n}\n```\n | 4 | Given the `root` of a binary tree, determine if it is a _complete binary tree_.
In a **[complete binary tree](http://en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees)**, every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between `1` and `2h` nodes inclusive at the last level `h`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** true
**Explanation:** Every level before the last is full (ie. levels with node-values {1} and {2, 3}), and all nodes in the last level ({4, 5, 6}) are as far left as possible.
**Example 2:**
**Input:** root = \[1,2,3,4,5,null,7\]
**Output:** false
**Explanation:** The node with value 7 isn't as far left as possible.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `1 <= Node.val <= 1000` | null |
Python3 O(n) || O(1) | sort-array-by-parity-ii | 0 | 1 | ```\nclass Solution:\n def sortArrayByParityII(self, nums: List[int]) -> List[int]:\n even, odd = 0, 1\n \n while even < len(nums) and odd < len(nums):\n while even < len(nums) and nums[even] % 2 == 0:\n even += 2\n while odd < len(nums) and nums[odd] % 2 != 0:\n odd += 2\n \n if even < len(nums) and odd < len(nums):\n nums[even], nums[odd] = nums[odd], nums[even]\n \n even += 2\n odd += 2\n \n return nums\n``` | 5 | Given an array of integers `nums`, half of the integers in `nums` are **odd**, and the other half are **even**.
Sort the array so that whenever `nums[i]` is odd, `i` is **odd**, and whenever `nums[i]` is even, `i` is **even**.
Return _any answer array that satisfies this condition_.
**Example 1:**
**Input:** nums = \[4,2,5,7\]
**Output:** \[4,5,2,7\]
**Explanation:** \[4,7,2,5\], \[2,5,4,7\], \[2,7,4,5\] would also have been accepted.
**Example 2:**
**Input:** nums = \[2,3\]
**Output:** \[2,3\]
**Constraints:**
* `2 <= nums.length <= 2 * 104`
* `nums.length` is even.
* Half of the integers in `nums` are even.
* `0 <= nums[i] <= 1000`
**Follow Up:** Could you solve it in-place? | null |
Python3 O(n) || O(1) | sort-array-by-parity-ii | 0 | 1 | ```\nclass Solution:\n def sortArrayByParityII(self, nums: List[int]) -> List[int]:\n even, odd = 0, 1\n \n while even < len(nums) and odd < len(nums):\n while even < len(nums) and nums[even] % 2 == 0:\n even += 2\n while odd < len(nums) and nums[odd] % 2 != 0:\n odd += 2\n \n if even < len(nums) and odd < len(nums):\n nums[even], nums[odd] = nums[odd], nums[even]\n \n even += 2\n odd += 2\n \n return nums\n``` | 5 | Given the `root` of a binary tree, determine if it is a _complete binary tree_.
In a **[complete binary tree](http://en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees)**, every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between `1` and `2h` nodes inclusive at the last level `h`.
**Example 1:**
**Input:** root = \[1,2,3,4,5,6\]
**Output:** true
**Explanation:** Every level before the last is full (ie. levels with node-values {1} and {2, 3}), and all nodes in the last level ({4, 5, 6}) are as far left as possible.
**Example 2:**
**Input:** root = \[1,2,3,4,5,null,7\]
**Output:** false
**Explanation:** The node with value 7 isn't as far left as possible.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `1 <= Node.val <= 1000` | null |
Solution | 3sum-with-multiplicity | 1 | 1 | ```C++ []\nstatic const int M = 1e9 + 7, N = 101;\n\nclass Solution {\npublic:\n int threeSumMulti(vector<int>& a, int target) {\n long ans = 0, cnt[N]{};\n for (int &x : a) ++cnt[x];\n for (int i = 0; i < N; ++i)\n for (int j = i + 1; j < N; ++j) {\n int k = target - i - j;\n if (j < k && k < N)\n (ans += cnt[i] * cnt[j] * cnt[k]) %= M;\n }\n for (int i = 0; i < N; ++i) {\n int k = target - 2 * i;\n if (i < k && k < N) (ans += cnt[i] * (cnt[i] - 1) / 2 * cnt[k]) %= M;\n }\n for (int i = 0; i < N; ++i)\n if (target % 2 == i % 2) {\n int j = (target - i) / 2;\n if (i < j && j < N) (ans += cnt[i] * cnt[j] * (cnt[j] - 1) / 2) %= M;\n }\n if (target % 3 == 0) {\n int i = target / 3;\n if (0 <= i && i < N) (ans += (cnt[i] * (cnt[i] - 1) % M) * (cnt[i] - 2) / 6) %= M;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def threeSumMulti(self, arr: List[int], target: int) -> int:\n counts = Counter(arr)\n sorted_arr = sorted(set(arr))\n res = 0\n \n for i, num1 in enumerate(sorted_arr):\n k, j = i + 1, len(sorted_arr) - 1\n \n if counts[num1] > 1 and target - num1 * 2 in counts:\n if num1 * 3 == target:\n res += math.comb(counts[num1], 3)\n else:\n res += ((counts[num1] * (counts[num1] - 1)) // 2) * counts[target - num1 * 2]\n \n while k < j:\n num2, num3 = sorted_arr[k], sorted_arr[j]\n total = num1 + num2 + num3\n \n if total == target:\n res += (counts[num1] * counts[num2] * counts[num3])\n k += 1\n j -= 1\n elif total < target:\n k += 1\n else:\n j -= 1\n \n return res % (10**9 + 7)\n```\n\n```Java []\nclass Solution {\n public int threeSumMulti(int[] A, int T) {\n long[] nmap = new long[101];\n long ans = 0;\n for (int num : A) nmap[num]++;\n for (int k = 100; k >= 0; k--)\n for (int j = k; j >= 0; j--) {\n int i = T - k - j;\n if (i > j || i < 0) continue;\n long x = nmap[i], y = nmap[j], z = nmap[k], res = x * y * z;\n if (res == 0) continue;\n if (i == k) res = x * (x-1) * (x-2) / 6;\n else if (i == j) res = x * (x-1) / 2 * z;\n else if (j == k) res = x * y * (y-1) / 2;\n ans += res;\n }\n return (int)(ans % 1000000007);\n }\n}\n```\n | 1 | Given an integer array `arr`, and an integer `target`, return the number of tuples `i, j, k` such that `i < j < k` and `arr[i] + arr[j] + arr[k] == target`.
As the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[1,1,2,2,3,3,4,4,5,5\], target = 8
**Output:** 20
**Explanation:**
Enumerating by the values (arr\[i\], arr\[j\], arr\[k\]):
(1, 2, 5) occurs 8 times;
(1, 3, 4) occurs 8 times;
(2, 2, 4) occurs 2 times;
(2, 3, 3) occurs 2 times.
**Example 2:**
**Input:** arr = \[1,1,2,2,2,2\], target = 5
**Output:** 12
**Explanation:**
arr\[i\] = 1, arr\[j\] = arr\[k\] = 2 occurs 12 times:
We choose one 1 from \[1,1\] in 2 ways,
and two 2s from \[2,2,2,2\] in 6 ways.
**Example 3:**
**Input:** arr = \[2,1,3\], target = 6
**Output:** 1
**Explanation:** (1, 2, 3) occured one time in the array so we return 1.
**Constraints:**
* `3 <= arr.length <= 3000`
* `0 <= arr[i] <= 100`
* `0 <= target <= 300` | null |
Solution | 3sum-with-multiplicity | 1 | 1 | ```C++ []\nstatic const int M = 1e9 + 7, N = 101;\n\nclass Solution {\npublic:\n int threeSumMulti(vector<int>& a, int target) {\n long ans = 0, cnt[N]{};\n for (int &x : a) ++cnt[x];\n for (int i = 0; i < N; ++i)\n for (int j = i + 1; j < N; ++j) {\n int k = target - i - j;\n if (j < k && k < N)\n (ans += cnt[i] * cnt[j] * cnt[k]) %= M;\n }\n for (int i = 0; i < N; ++i) {\n int k = target - 2 * i;\n if (i < k && k < N) (ans += cnt[i] * (cnt[i] - 1) / 2 * cnt[k]) %= M;\n }\n for (int i = 0; i < N; ++i)\n if (target % 2 == i % 2) {\n int j = (target - i) / 2;\n if (i < j && j < N) (ans += cnt[i] * cnt[j] * (cnt[j] - 1) / 2) %= M;\n }\n if (target % 3 == 0) {\n int i = target / 3;\n if (0 <= i && i < N) (ans += (cnt[i] * (cnt[i] - 1) % M) * (cnt[i] - 2) / 6) %= M;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def threeSumMulti(self, arr: List[int], target: int) -> int:\n counts = Counter(arr)\n sorted_arr = sorted(set(arr))\n res = 0\n \n for i, num1 in enumerate(sorted_arr):\n k, j = i + 1, len(sorted_arr) - 1\n \n if counts[num1] > 1 and target - num1 * 2 in counts:\n if num1 * 3 == target:\n res += math.comb(counts[num1], 3)\n else:\n res += ((counts[num1] * (counts[num1] - 1)) // 2) * counts[target - num1 * 2]\n \n while k < j:\n num2, num3 = sorted_arr[k], sorted_arr[j]\n total = num1 + num2 + num3\n \n if total == target:\n res += (counts[num1] * counts[num2] * counts[num3])\n k += 1\n j -= 1\n elif total < target:\n k += 1\n else:\n j -= 1\n \n return res % (10**9 + 7)\n```\n\n```Java []\nclass Solution {\n public int threeSumMulti(int[] A, int T) {\n long[] nmap = new long[101];\n long ans = 0;\n for (int num : A) nmap[num]++;\n for (int k = 100; k >= 0; k--)\n for (int j = k; j >= 0; j--) {\n int i = T - k - j;\n if (i > j || i < 0) continue;\n long x = nmap[i], y = nmap[j], z = nmap[k], res = x * y * z;\n if (res == 0) continue;\n if (i == k) res = x * (x-1) * (x-2) / 6;\n else if (i == j) res = x * (x-1) / 2 * z;\n else if (j == k) res = x * y * (y-1) / 2;\n ans += res;\n }\n return (int)(ans % 1000000007);\n }\n}\n```\n | 1 | An `n x n` grid is composed of `1 x 1` squares where each `1 x 1` square consists of a `'/'`, `'\'`, or blank space `' '`. These characters divide the square into contiguous regions.
Given the grid `grid` represented as a string array, return _the number of regions_.
Note that backslash characters are escaped, so a `'\'` is represented as `'\\'`.
**Example 1:**
**Input:** grid = \[ " / ", "/ "\]
**Output:** 2
**Example 2:**
**Input:** grid = \[ " / ", " "\]
**Output:** 1
**Example 3:**
**Input:** grid = \[ "/\\\\ ", "\\/ "\]
**Output:** 5
**Explanation:** Recall that because \\ characters are escaped, "\\/ " refers to /, and "/\\\\ " refers to /\\.
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 30`
* `grid[i][j]` is either `'/'`, `'\'`, or `' '`. | null |
[Python] 3Sum Approach with Explanation | 3sum-with-multiplicity | 0 | 1 | ### Introduction\n\nGiven an array of integers `arr`, determine how many tuples `(i, j, k)` exist such that `0 <= i < j < k < len(arr)` and `arr[i] + arr[j] + arr[k] == target`.\n\nThis problem is similar to [15. 3Sum](https://leetcode.com/problems/3sum/), except it differs in one major way: where the similar problem requires all unique tuples, this problem requires the number of all tuples (which need not be unique).\n\n---\n\n### Base Approach\n\nTo begin, let\'s understand how the 3-sum algorithm works. First, ensure that the array is sorted in ascending order (descending order works too, but we\'ll stick to ascending).\n\n```python\nclass Solution:\n def threeSumMulti(self, arr: List[int], target: int) -> int:\n arr.sort()\n\t\t# the rest of the code here\n```\n\nNext, we want a for-loop that will iterate through the array.\n\n```python\nclass Solution:\n def threeSumMulti(self, arr: List[int], target: int) -> int:\n arr.sort()\n\t\tfor i in range(len(arr)-2):\n\t\t\t# do something\n\t\t\tpass\n\t\t# the rest of the code here\n````\n\nNotice that we leave the last two indexes of the array untouched. This is because this for-loop will **serve as a pointer to the lowest value in the resulting tuple**; i.e., this pointer tries to find `i` in `(i, j, k)`. This also means that the resulting right end of the array (i.e., `arr[i+1:]`) will contain our remaining two pointers `j` and `k`.\n\nNotice now that we have simplified the problem from a 3-sum to a 2-sum; i.e., instead of finding `(i, j, k)` in `arr` where `arr[i] + arr[j] + arr[k] == target`, we now only need to find `(j, k)` in `arr[i+1:]` where `arr[j] + arr[k] == target - arr[i]`. The implementation that follows should then be similar to [1. Two Sum](https://leetcode.com/problems/two-sum/).\n\nIn case you are not familiar with the 2-sum algorithm: in a sorted ascending array, we have 2 pointers `j` and `k` pointing to the two ends of the array. Then, in binary-search fashion, **if `arr[j] + arr[k] < target`, we increment `j` to increase the value of `arr[j]`; if `arr[j] + arr[k] > target`, we decrement `k` to decrease the value of `arr[k]`; we continue doing this until we have found a suitable `(j, k)` or `j >= k`**.\n\nPutting it all together, we have:\n\n```python\nclass Solution(object):\n def threeSumMulti(self, arr: List[int], target: int) -> int:\n arr.sort()\n\t\tres, l = 0, len(arr)\n for i in range(l-2):\n\t\t\t# Initialise the 2-sum pointers\n j, k = i+1, l-1\n while j < k:\n if arr[j]+arr[k] < target-arr[i]: # arr[j] is too small\n j += 1\n elif arr[j]+arr[k] > target-arr[i]: # arr[k] is too large\n k -= 1\n\t\t\t\telse: # arr[i]+arr[j]+arr[k] == target\n\t\t\t\t\tres += 1\n\t\t\t\t\t# Shift both pointers by 1\n\t\t\t\t\tj += 1\n\t\t\t\t\tk -= 1\n\t\treturn res%1000000007\n```\n\n---\n\n### Tweaking the Algorithm\n\nIf you tried running the code above, it would give you the wrong answer. Let\'s use the testcase as an example:\n\n```text\ntarget = 8\narr: 1 1 2 2 3 3 4 4 5 5\n i j k --> arr[i] + arr[j] + arr[k] == target; j += 1, k -= 1.\n\t i j k --> arr[i] + arr[j] + arr[k] == target; j += 1, k -= 1.\n```\n\nThe problem comes when there are multiple instances of the same number. In the above example, after finding that `j=2, k=9` satisfies the equation, we simply shift the pointers and continue, **without realising that `j=3, k=9` and `j=2, k=8` are both valid tuples as well**. Hence, we end up missing some possible tuples if we shift the pointers. But how do we know when to shift the pointers and when not to?\n\nThe trick in this case is to **reconsider the way that we are counting the number of valid tuples**. In the above code, we simply increment the counter by 1 (`res += 1`), but we can do this more efficiently if we had the number of instances of `arr[j]` and `arr[k]` respectively. Of course, we will need to take into account different cases whereby `arr[i]`, `arr[j]`, and/or `arr[k]` may not be fully unqiue. Since `arr[i] <= arr[j] <= arr[k]`, we have the following cases:\n\n```text\nCases Result (note: count() is an arbitrary function)\n1) arr[i] != arr[j] != arr[k] --> res += count(arr[i]) * count(arr[j]) * count(arr[k])\n2) arr[i] == arr[j] != arr[k] --> res += math.comb(count(arr[i]), 2) * count(arr[k])\n3) arr[i] != arr[j] == arr[k] --> res += count(arr[i]) * math.comb(count(arr[j]), 2)\n4) arr[i] == arr[j] == arr[k] --> res += math.comb(count(arr[i]), 3)\n\nRelevant mathematical equations\nmath.comb(count(arr[i]), 2) = count(arr[i]) * (count(arr[i]) - 1) // 2\nmath.comb(count(arr[i]), 3) = count(arr[i]) * (count(arr[i]) - 1) * (count(arr[i]) - 2) // 6\n```\n\nTo incorporate this into our code, we then have to make sure that we do not check the same number twice. To do so, we can simply **shift our pointers by the number of instances of the number**, instead of incrementing or decrementing by 1 each time.\n\n```python\nclass Solution:\n def threeSumMulti(self, arr: List[int], target: int) -> int:\n arr.sort()\n cnt = Counter(arr) # obtain the number of instances of each number\n res, i, l = 0, 0, len(arr)\n while i < l: # in replacement of the for-loop, so that we can increment i by more than 1\n j, k = i, l-1 # j should be the leftmost index, hence j=i instead of j=i+1\n while j < k: # i <= j < k; arr[i] <= arr[j] <= arr[k]\n if arr[i]+arr[j]+arr[k] < target:\n j += cnt[arr[j]]\n elif arr[i]+arr[j]+arr[k] > target:\n k -= cnt[arr[k]]\n else: # arr[i]+arr[j]+arr[k] == target\n if arr[i] != arr[j] != arr[k]: # Case 1: All the numbers are different\n res += cnt[arr[i]]*cnt[arr[j]]*cnt[arr[k]]\n elif arr[i] == arr[j] != arr[k]: # Case 2: The smaller two numbers are the same\n res += cnt[arr[i]]*(cnt[arr[i]]-1)*cnt[arr[k]]//2 # math.comb(cnt[arr[i]], 2)*cnt[arr[k]]\n elif arr[i] != arr[j] == arr[k]: # Case 3: The larger two numbers are the same\n res += cnt[arr[i]]*cnt[arr[j]]*(cnt[arr[j]]-1)//2 # math.comb(cnt[arr[j]], 2)*cnt[arr[i]]\n else: # Case 4: All the numbers are the same\n res += cnt[arr[i]]*(cnt[arr[i]]-1)*(cnt[arr[i]]-2)//6 # math.comb(cnt[arr[i]], 3)\n\t\t\t\t\t# Shift pointers by the number of instances of the number\n j += cnt[arr[j]]\n k -= cnt[arr[k]]\n i += cnt[arr[i]] # Shift pointer by the number of instances of the number\n return res%1000000007\n```\n\n**TC: O(n<sup>2</sup>)**, where `n` is the length of `arr`, due to the nested while loop.\n**SC: O(n)**, due to the Counter object.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 98 | Given an integer array `arr`, and an integer `target`, return the number of tuples `i, j, k` such that `i < j < k` and `arr[i] + arr[j] + arr[k] == target`.
As the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[1,1,2,2,3,3,4,4,5,5\], target = 8
**Output:** 20
**Explanation:**
Enumerating by the values (arr\[i\], arr\[j\], arr\[k\]):
(1, 2, 5) occurs 8 times;
(1, 3, 4) occurs 8 times;
(2, 2, 4) occurs 2 times;
(2, 3, 3) occurs 2 times.
**Example 2:**
**Input:** arr = \[1,1,2,2,2,2\], target = 5
**Output:** 12
**Explanation:**
arr\[i\] = 1, arr\[j\] = arr\[k\] = 2 occurs 12 times:
We choose one 1 from \[1,1\] in 2 ways,
and two 2s from \[2,2,2,2\] in 6 ways.
**Example 3:**
**Input:** arr = \[2,1,3\], target = 6
**Output:** 1
**Explanation:** (1, 2, 3) occured one time in the array so we return 1.
**Constraints:**
* `3 <= arr.length <= 3000`
* `0 <= arr[i] <= 100`
* `0 <= target <= 300` | null |
[Python] 3Sum Approach with Explanation | 3sum-with-multiplicity | 0 | 1 | ### Introduction\n\nGiven an array of integers `arr`, determine how many tuples `(i, j, k)` exist such that `0 <= i < j < k < len(arr)` and `arr[i] + arr[j] + arr[k] == target`.\n\nThis problem is similar to [15. 3Sum](https://leetcode.com/problems/3sum/), except it differs in one major way: where the similar problem requires all unique tuples, this problem requires the number of all tuples (which need not be unique).\n\n---\n\n### Base Approach\n\nTo begin, let\'s understand how the 3-sum algorithm works. First, ensure that the array is sorted in ascending order (descending order works too, but we\'ll stick to ascending).\n\n```python\nclass Solution:\n def threeSumMulti(self, arr: List[int], target: int) -> int:\n arr.sort()\n\t\t# the rest of the code here\n```\n\nNext, we want a for-loop that will iterate through the array.\n\n```python\nclass Solution:\n def threeSumMulti(self, arr: List[int], target: int) -> int:\n arr.sort()\n\t\tfor i in range(len(arr)-2):\n\t\t\t# do something\n\t\t\tpass\n\t\t# the rest of the code here\n````\n\nNotice that we leave the last two indexes of the array untouched. This is because this for-loop will **serve as a pointer to the lowest value in the resulting tuple**; i.e., this pointer tries to find `i` in `(i, j, k)`. This also means that the resulting right end of the array (i.e., `arr[i+1:]`) will contain our remaining two pointers `j` and `k`.\n\nNotice now that we have simplified the problem from a 3-sum to a 2-sum; i.e., instead of finding `(i, j, k)` in `arr` where `arr[i] + arr[j] + arr[k] == target`, we now only need to find `(j, k)` in `arr[i+1:]` where `arr[j] + arr[k] == target - arr[i]`. The implementation that follows should then be similar to [1. Two Sum](https://leetcode.com/problems/two-sum/).\n\nIn case you are not familiar with the 2-sum algorithm: in a sorted ascending array, we have 2 pointers `j` and `k` pointing to the two ends of the array. Then, in binary-search fashion, **if `arr[j] + arr[k] < target`, we increment `j` to increase the value of `arr[j]`; if `arr[j] + arr[k] > target`, we decrement `k` to decrease the value of `arr[k]`; we continue doing this until we have found a suitable `(j, k)` or `j >= k`**.\n\nPutting it all together, we have:\n\n```python\nclass Solution(object):\n def threeSumMulti(self, arr: List[int], target: int) -> int:\n arr.sort()\n\t\tres, l = 0, len(arr)\n for i in range(l-2):\n\t\t\t# Initialise the 2-sum pointers\n j, k = i+1, l-1\n while j < k:\n if arr[j]+arr[k] < target-arr[i]: # arr[j] is too small\n j += 1\n elif arr[j]+arr[k] > target-arr[i]: # arr[k] is too large\n k -= 1\n\t\t\t\telse: # arr[i]+arr[j]+arr[k] == target\n\t\t\t\t\tres += 1\n\t\t\t\t\t# Shift both pointers by 1\n\t\t\t\t\tj += 1\n\t\t\t\t\tk -= 1\n\t\treturn res%1000000007\n```\n\n---\n\n### Tweaking the Algorithm\n\nIf you tried running the code above, it would give you the wrong answer. Let\'s use the testcase as an example:\n\n```text\ntarget = 8\narr: 1 1 2 2 3 3 4 4 5 5\n i j k --> arr[i] + arr[j] + arr[k] == target; j += 1, k -= 1.\n\t i j k --> arr[i] + arr[j] + arr[k] == target; j += 1, k -= 1.\n```\n\nThe problem comes when there are multiple instances of the same number. In the above example, after finding that `j=2, k=9` satisfies the equation, we simply shift the pointers and continue, **without realising that `j=3, k=9` and `j=2, k=8` are both valid tuples as well**. Hence, we end up missing some possible tuples if we shift the pointers. But how do we know when to shift the pointers and when not to?\n\nThe trick in this case is to **reconsider the way that we are counting the number of valid tuples**. In the above code, we simply increment the counter by 1 (`res += 1`), but we can do this more efficiently if we had the number of instances of `arr[j]` and `arr[k]` respectively. Of course, we will need to take into account different cases whereby `arr[i]`, `arr[j]`, and/or `arr[k]` may not be fully unqiue. Since `arr[i] <= arr[j] <= arr[k]`, we have the following cases:\n\n```text\nCases Result (note: count() is an arbitrary function)\n1) arr[i] != arr[j] != arr[k] --> res += count(arr[i]) * count(arr[j]) * count(arr[k])\n2) arr[i] == arr[j] != arr[k] --> res += math.comb(count(arr[i]), 2) * count(arr[k])\n3) arr[i] != arr[j] == arr[k] --> res += count(arr[i]) * math.comb(count(arr[j]), 2)\n4) arr[i] == arr[j] == arr[k] --> res += math.comb(count(arr[i]), 3)\n\nRelevant mathematical equations\nmath.comb(count(arr[i]), 2) = count(arr[i]) * (count(arr[i]) - 1) // 2\nmath.comb(count(arr[i]), 3) = count(arr[i]) * (count(arr[i]) - 1) * (count(arr[i]) - 2) // 6\n```\n\nTo incorporate this into our code, we then have to make sure that we do not check the same number twice. To do so, we can simply **shift our pointers by the number of instances of the number**, instead of incrementing or decrementing by 1 each time.\n\n```python\nclass Solution:\n def threeSumMulti(self, arr: List[int], target: int) -> int:\n arr.sort()\n cnt = Counter(arr) # obtain the number of instances of each number\n res, i, l = 0, 0, len(arr)\n while i < l: # in replacement of the for-loop, so that we can increment i by more than 1\n j, k = i, l-1 # j should be the leftmost index, hence j=i instead of j=i+1\n while j < k: # i <= j < k; arr[i] <= arr[j] <= arr[k]\n if arr[i]+arr[j]+arr[k] < target:\n j += cnt[arr[j]]\n elif arr[i]+arr[j]+arr[k] > target:\n k -= cnt[arr[k]]\n else: # arr[i]+arr[j]+arr[k] == target\n if arr[i] != arr[j] != arr[k]: # Case 1: All the numbers are different\n res += cnt[arr[i]]*cnt[arr[j]]*cnt[arr[k]]\n elif arr[i] == arr[j] != arr[k]: # Case 2: The smaller two numbers are the same\n res += cnt[arr[i]]*(cnt[arr[i]]-1)*cnt[arr[k]]//2 # math.comb(cnt[arr[i]], 2)*cnt[arr[k]]\n elif arr[i] != arr[j] == arr[k]: # Case 3: The larger two numbers are the same\n res += cnt[arr[i]]*cnt[arr[j]]*(cnt[arr[j]]-1)//2 # math.comb(cnt[arr[j]], 2)*cnt[arr[i]]\n else: # Case 4: All the numbers are the same\n res += cnt[arr[i]]*(cnt[arr[i]]-1)*(cnt[arr[i]]-2)//6 # math.comb(cnt[arr[i]], 3)\n\t\t\t\t\t# Shift pointers by the number of instances of the number\n j += cnt[arr[j]]\n k -= cnt[arr[k]]\n i += cnt[arr[i]] # Shift pointer by the number of instances of the number\n return res%1000000007\n```\n\n**TC: O(n<sup>2</sup>)**, where `n` is the length of `arr`, due to the nested while loop.\n**SC: O(n)**, due to the Counter object.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 98 | An `n x n` grid is composed of `1 x 1` squares where each `1 x 1` square consists of a `'/'`, `'\'`, or blank space `' '`. These characters divide the square into contiguous regions.
Given the grid `grid` represented as a string array, return _the number of regions_.
Note that backslash characters are escaped, so a `'\'` is represented as `'\\'`.
**Example 1:**
**Input:** grid = \[ " / ", "/ "\]
**Output:** 2
**Example 2:**
**Input:** grid = \[ " / ", " "\]
**Output:** 1
**Example 3:**
**Input:** grid = \[ "/\\\\ ", "\\/ "\]
**Output:** 5
**Explanation:** Recall that because \\ characters are escaped, "\\/ " refers to /, and "/\\\\ " refers to /\\.
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 30`
* `grid[i][j]` is either `'/'`, `'\'`, or `' '`. | null |
Python, 3 steps, O(N*W) | 3sum-with-multiplicity | 0 | 1 | # Idea\nThe idea is to keep counting the number of elements we have seen so far and keep `ones` and `twos` counters, which correspond to the number of ways given values can be constructed (as a sum) using one and two array elements respectively. So, we iterate over an array and do the following three steps as a pipeline:\n1. Update the total count by looking up the number of two-sums (`twos`) that if you add current value to would give you `target`.\n2. Update the number of twosums (`twos`) by looking at the numbers that have appeared before (`ones`).\n3. Update the counts of numbers that have appeared before (`ones`).\n\n# Complexity\nTime: O(NW), where N is the length of the array and W the number of unique numbers in our array (<= 100 in problem definition).\nMemory: O(W^2) because of twosum dictionary\n```\ndef threeSumMulti(self, arr: List[int], target: int) -> int:\n\ttotal = 0\n\tmod = 10 ** 9 + 7\n\n\tones = defaultdict(int)\n\ttwos = defaultdict(int)\n\n\tfor t, v in enumerate(arr): # O(N)\n\t\ttotal = (total + twos[target - v]) % mod\n\t\tfor k, c in ones.items(): # O(W)\n\t\t\ttwos[k+v] += c\n\t\tones[v] += 1\n\n\treturn total\n``` | 6 | Given an integer array `arr`, and an integer `target`, return the number of tuples `i, j, k` such that `i < j < k` and `arr[i] + arr[j] + arr[k] == target`.
As the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[1,1,2,2,3,3,4,4,5,5\], target = 8
**Output:** 20
**Explanation:**
Enumerating by the values (arr\[i\], arr\[j\], arr\[k\]):
(1, 2, 5) occurs 8 times;
(1, 3, 4) occurs 8 times;
(2, 2, 4) occurs 2 times;
(2, 3, 3) occurs 2 times.
**Example 2:**
**Input:** arr = \[1,1,2,2,2,2\], target = 5
**Output:** 12
**Explanation:**
arr\[i\] = 1, arr\[j\] = arr\[k\] = 2 occurs 12 times:
We choose one 1 from \[1,1\] in 2 ways,
and two 2s from \[2,2,2,2\] in 6 ways.
**Example 3:**
**Input:** arr = \[2,1,3\], target = 6
**Output:** 1
**Explanation:** (1, 2, 3) occured one time in the array so we return 1.
**Constraints:**
* `3 <= arr.length <= 3000`
* `0 <= arr[i] <= 100`
* `0 <= target <= 300` | null |
Python, 3 steps, O(N*W) | 3sum-with-multiplicity | 0 | 1 | # Idea\nThe idea is to keep counting the number of elements we have seen so far and keep `ones` and `twos` counters, which correspond to the number of ways given values can be constructed (as a sum) using one and two array elements respectively. So, we iterate over an array and do the following three steps as a pipeline:\n1. Update the total count by looking up the number of two-sums (`twos`) that if you add current value to would give you `target`.\n2. Update the number of twosums (`twos`) by looking at the numbers that have appeared before (`ones`).\n3. Update the counts of numbers that have appeared before (`ones`).\n\n# Complexity\nTime: O(NW), where N is the length of the array and W the number of unique numbers in our array (<= 100 in problem definition).\nMemory: O(W^2) because of twosum dictionary\n```\ndef threeSumMulti(self, arr: List[int], target: int) -> int:\n\ttotal = 0\n\tmod = 10 ** 9 + 7\n\n\tones = defaultdict(int)\n\ttwos = defaultdict(int)\n\n\tfor t, v in enumerate(arr): # O(N)\n\t\ttotal = (total + twos[target - v]) % mod\n\t\tfor k, c in ones.items(): # O(W)\n\t\t\ttwos[k+v] += c\n\t\tones[v] += 1\n\n\treturn total\n``` | 6 | An `n x n` grid is composed of `1 x 1` squares where each `1 x 1` square consists of a `'/'`, `'\'`, or blank space `' '`. These characters divide the square into contiguous regions.
Given the grid `grid` represented as a string array, return _the number of regions_.
Note that backslash characters are escaped, so a `'\'` is represented as `'\\'`.
**Example 1:**
**Input:** grid = \[ " / ", "/ "\]
**Output:** 2
**Example 2:**
**Input:** grid = \[ " / ", " "\]
**Output:** 1
**Example 3:**
**Input:** grid = \[ "/\\\\ ", "\\/ "\]
**Output:** 5
**Explanation:** Recall that because \\ characters are escaped, "\\/ " refers to /, and "/\\\\ " refers to /\\.
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 30`
* `grid[i][j]` is either `'/'`, `'\'`, or `' '`. | null |
Solution | minimize-malware-spread | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int find_p(vector<int>& ps, int i) {\n return ps[i] == i ? i : ps[i] = find_p(ps, ps[i]); \n }\n void union_p(vector<int>& ps, vector<int>& cs, int i, int j) {\n int pi = find_p(ps, i), pj = find_p(ps, j);\n if (pi != pj) {\n ps[pi] = pj;\n cs[pj] += cs[pi];\n }\n }\n int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) {\n int n = graph.size();\n vector<int> ps(n), cs(n, 1);\n iota(ps.begin(), ps.end(), 0);\n for (int i=0; i<n; ++i)\n for (int j=0; j<i; ++j)\n if (graph[i][j])\n union_p(ps, cs, i, j);\n \n vector<int> ct(n);\n for (int i : initial)\n ++ct[find_p(ps, i)];\n int msf_i = *min_element(initial.begin(), initial.end()), msf = 0;\n for (int i : initial) {\n if (ct[find_p(ps, i)] != 1) continue;\n int s = cs[find_p(ps, i)];\n if (s > msf) msf = s, msf_i = i;\n if (s == msf) msf_i = min(msf_i, i);\n }\n return msf_i;\n }\n};\n```\n\n```Python3 []\nclass Solution(object):\n\tdef minMalwareSpread(self, graph, initial):\n\t\tdef bfs(i):\n\t\t\tqueue, visited = [i], [i]\n\t\t\tpath_node = 0\n\t\t\twhile(queue):\n\t\t\t\tcur = queue.pop(0)\n\t\t\t\tfor idx, value in enumerate(graph[cur]):\n\t\t\t\t\t\n\t\t\t\t\tif value ==1 and idx not in visited:\n\t\t\t\t\t\tqueue.append(idx)\n\t\t\t\t\t\tpath_node += 1\n\t\t\t\t\t\tif idx!= cur and idx in initial:\n\t\t\t\t\t\t\treturn -1\n\t\t\t\t\t\tvisited.append(idx)\n\t\t\treturn path_node\n\n\t\trecord = dict()\n\n\t\tfor node in initial:\n\t\t\trecord[node] = bfs(node)\n\t\t\n\t\tcandidate = record[max(record, key=record.get)]\n\t\t\n\t\tres = []\n\t\tfor k, v in record.items():\n\t\t\tif v==candidate:\n\t\t\t\tres.append(k)\n\t\treturn min(res)\n```\n\n```Java []\nclass Solution {\n private int dfs(int[][] graph, int u, boolean[] visited, boolean[] initial) {\n if(initial[u]) return 0;\n visited[u] = true;\n int count = 1;\n for(int v = 0; v < graph[u].length; v++) {\n if(!visited[v] && graph[u][v] == 1) {\n int c = dfs(graph, v, visited, initial);\n if(c == 0) return 0;\n count += c;\n }\n }\n return count;\n }\n public int minMalwareSpread(int[][] graph, int[] initial) {\n Arrays.sort(initial);\n int n = graph.length, ans = initial[0], max = 0;\n boolean[] init = new boolean[n];\n for(int u: initial) init[u] = true;\n for(int u: initial) {\n init[u] = false;\n int count = dfs(graph, u, new boolean[n], init);\n if(count > max) {\n max = count;\n ans = u;\n }\n init[u] = true;\n }\n return ans;\n }\n}\n```\n | 1 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops. We will remove **exactly one node** from `initial`.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
Note that if a node was removed from the `initial` list of infected nodes, it might still be infected later due to the malware spread.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\], initial = \[0,2\]
**Output:** 0
**Example 3:**
**Input:** graph = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], initial = \[1,2\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length <= n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Solution | minimize-malware-spread | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int find_p(vector<int>& ps, int i) {\n return ps[i] == i ? i : ps[i] = find_p(ps, ps[i]); \n }\n void union_p(vector<int>& ps, vector<int>& cs, int i, int j) {\n int pi = find_p(ps, i), pj = find_p(ps, j);\n if (pi != pj) {\n ps[pi] = pj;\n cs[pj] += cs[pi];\n }\n }\n int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) {\n int n = graph.size();\n vector<int> ps(n), cs(n, 1);\n iota(ps.begin(), ps.end(), 0);\n for (int i=0; i<n; ++i)\n for (int j=0; j<i; ++j)\n if (graph[i][j])\n union_p(ps, cs, i, j);\n \n vector<int> ct(n);\n for (int i : initial)\n ++ct[find_p(ps, i)];\n int msf_i = *min_element(initial.begin(), initial.end()), msf = 0;\n for (int i : initial) {\n if (ct[find_p(ps, i)] != 1) continue;\n int s = cs[find_p(ps, i)];\n if (s > msf) msf = s, msf_i = i;\n if (s == msf) msf_i = min(msf_i, i);\n }\n return msf_i;\n }\n};\n```\n\n```Python3 []\nclass Solution(object):\n\tdef minMalwareSpread(self, graph, initial):\n\t\tdef bfs(i):\n\t\t\tqueue, visited = [i], [i]\n\t\t\tpath_node = 0\n\t\t\twhile(queue):\n\t\t\t\tcur = queue.pop(0)\n\t\t\t\tfor idx, value in enumerate(graph[cur]):\n\t\t\t\t\t\n\t\t\t\t\tif value ==1 and idx not in visited:\n\t\t\t\t\t\tqueue.append(idx)\n\t\t\t\t\t\tpath_node += 1\n\t\t\t\t\t\tif idx!= cur and idx in initial:\n\t\t\t\t\t\t\treturn -1\n\t\t\t\t\t\tvisited.append(idx)\n\t\t\treturn path_node\n\n\t\trecord = dict()\n\n\t\tfor node in initial:\n\t\t\trecord[node] = bfs(node)\n\t\t\n\t\tcandidate = record[max(record, key=record.get)]\n\t\t\n\t\tres = []\n\t\tfor k, v in record.items():\n\t\t\tif v==candidate:\n\t\t\t\tres.append(k)\n\t\treturn min(res)\n```\n\n```Java []\nclass Solution {\n private int dfs(int[][] graph, int u, boolean[] visited, boolean[] initial) {\n if(initial[u]) return 0;\n visited[u] = true;\n int count = 1;\n for(int v = 0; v < graph[u].length; v++) {\n if(!visited[v] && graph[u][v] == 1) {\n int c = dfs(graph, v, visited, initial);\n if(c == 0) return 0;\n count += c;\n }\n }\n return count;\n }\n public int minMalwareSpread(int[][] graph, int[] initial) {\n Arrays.sort(initial);\n int n = graph.length, ans = initial[0], max = 0;\n boolean[] init = new boolean[n];\n for(int u: initial) init[u] = true;\n for(int u: initial) {\n init[u] = false;\n int count = dfs(graph, u, new boolean[n], init);\n if(count > max) {\n max = count;\n ans = u;\n }\n init[u] = true;\n }\n return ans;\n }\n}\n```\n | 1 | You are given an array of `n` strings `strs`, all of the same length.
We may choose any deletion indices, and we delete all the characters in those indices for each string.
For example, if we have `strs = [ "abcdef ", "uvwxyz "]` and deletion indices `{0, 2, 3}`, then the final array after deletions is `[ "bef ", "vyz "]`.
Suppose we chose a set of deletion indices `answer` such that after deletions, the final array has **every string (row) in lexicographic** order. (i.e., `(strs[0][0] <= strs[0][1] <= ... <= strs[0][strs[0].length - 1])`, and `(strs[1][0] <= strs[1][1] <= ... <= strs[1][strs[1].length - 1])`, and so on). Return _the minimum possible value of_ `answer.length`.
**Example 1:**
**Input:** strs = \[ "babca ", "bbazb "\]
**Output:** 3
**Explanation:** After deleting columns 0, 1, and 4, the final array is strs = \[ "bc ", "az "\].
Both these rows are individually in lexicographic order (ie. strs\[0\]\[0\] <= strs\[0\]\[1\] and strs\[1\]\[0\] <= strs\[1\]\[1\]).
Note that strs\[0\] > strs\[1\] - the array strs is not necessarily in lexicographic order.
**Example 2:**
**Input:** strs = \[ "edcba "\]
**Output:** 4
**Explanation:** If we delete less than 4 columns, the only row will not be lexicographically sorted.
**Example 3:**
**Input:** strs = \[ "ghi ", "def ", "abc "\]
**Output:** 0
**Explanation:** All rows are already lexicographically sorted.
**Constraints:**
* `n == strs.length`
* `1 <= n <= 100`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Solved by using Disjoint Sets | minimize-malware-spread | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n n=len(graph)\n par=[-1]*n\n size=[1]*n\n \n for i in range(n):\n par[i]=i\n \n def findpar(i):\n if par[i]==i:\n return i\n else:\n par[i]=findpar(par[i])\n return par[i]\n\n def merge(i1,i2):\n if size[i1]>=size[i2]:\n par[i2]=i1\n size[i1]+=size[i2]\n else:\n par[i1]=i2\n size[i2]+=size[i1]\n \n for i in range(n):\n for j in range(n):\n if graph[i][j]==1:\n p1=findpar(i)\n p2=findpar(j)\n # print(i,p1,j,p2)\n if p1!=p2:\n merge(p1,p2)\n # print(par[i],size[i],par[j],size[j],56)\n \n inf=[0]*n\n for i in initial:\n p=findpar(i)\n inf[p]+=1\n \n mini=-1\n ans=-1\n # print(par)\n # print(size)\n initial.sort()\n for i in initial:\n # print(i)\n p=findpar(i)\n # print(i,p,size[p])\n if inf[p]==1 and size[p]>mini:\n ans=i\n mini=size[p]\n \n return initial[0] if ans==-1 else ans\n\n\n\n\n``` | 1 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops. We will remove **exactly one node** from `initial`.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
Note that if a node was removed from the `initial` list of infected nodes, it might still be infected later due to the malware spread.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\], initial = \[0,2\]
**Output:** 0
**Example 3:**
**Input:** graph = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], initial = \[1,2\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length <= n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Solved by using Disjoint Sets | minimize-malware-spread | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n n=len(graph)\n par=[-1]*n\n size=[1]*n\n \n for i in range(n):\n par[i]=i\n \n def findpar(i):\n if par[i]==i:\n return i\n else:\n par[i]=findpar(par[i])\n return par[i]\n\n def merge(i1,i2):\n if size[i1]>=size[i2]:\n par[i2]=i1\n size[i1]+=size[i2]\n else:\n par[i1]=i2\n size[i2]+=size[i1]\n \n for i in range(n):\n for j in range(n):\n if graph[i][j]==1:\n p1=findpar(i)\n p2=findpar(j)\n # print(i,p1,j,p2)\n if p1!=p2:\n merge(p1,p2)\n # print(par[i],size[i],par[j],size[j],56)\n \n inf=[0]*n\n for i in initial:\n p=findpar(i)\n inf[p]+=1\n \n mini=-1\n ans=-1\n # print(par)\n # print(size)\n initial.sort()\n for i in initial:\n # print(i)\n p=findpar(i)\n # print(i,p,size[p])\n if inf[p]==1 and size[p]>mini:\n ans=i\n mini=size[p]\n \n return initial[0] if ans==-1 else ans\n\n\n\n\n``` | 1 | You are given an array of `n` strings `strs`, all of the same length.
We may choose any deletion indices, and we delete all the characters in those indices for each string.
For example, if we have `strs = [ "abcdef ", "uvwxyz "]` and deletion indices `{0, 2, 3}`, then the final array after deletions is `[ "bef ", "vyz "]`.
Suppose we chose a set of deletion indices `answer` such that after deletions, the final array has **every string (row) in lexicographic** order. (i.e., `(strs[0][0] <= strs[0][1] <= ... <= strs[0][strs[0].length - 1])`, and `(strs[1][0] <= strs[1][1] <= ... <= strs[1][strs[1].length - 1])`, and so on). Return _the minimum possible value of_ `answer.length`.
**Example 1:**
**Input:** strs = \[ "babca ", "bbazb "\]
**Output:** 3
**Explanation:** After deleting columns 0, 1, and 4, the final array is strs = \[ "bc ", "az "\].
Both these rows are individually in lexicographic order (ie. strs\[0\]\[0\] <= strs\[0\]\[1\] and strs\[1\]\[0\] <= strs\[1\]\[1\]).
Note that strs\[0\] > strs\[1\] - the array strs is not necessarily in lexicographic order.
**Example 2:**
**Input:** strs = \[ "edcba "\]
**Output:** 4
**Explanation:** If we delete less than 4 columns, the only row will not be lexicographically sorted.
**Example 3:**
**Input:** strs = \[ "ghi ", "def ", "abc "\]
**Output:** 0
**Explanation:** All rows are already lexicographically sorted.
**Constraints:**
* `n == strs.length`
* `1 <= n <= 100`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Easy to understand with step wise explanation 😸😸 | minimize-malware-spread | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing BFS/DFS was first thought as Adjacency matrix is given. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo we need to minimize the infection in the connected graph. Only way is to find a connected graph which has only one node from initial state as we can remove it from intial infection and then its connected nodes will not get infected. So we need to find the maximum number of connected nodes from inital state nodes. \n\nTo do that I followed below steps:\n1. Used a dictionary to save max connected nodes from each node in initial state. \n2. BFS method to count the connected nodes count from each initial node. we can return -1 if we found some another node from the initial state as it can not be the answer. \n3. We can get the max value from dictionary and then find all nodes whiich have max number of connected nodes and then return which is smallest number. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nAs we might have to visit all the cells in graph if all values are 1. So it is upperboud by O(N^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwe using queue , visited , dict and will be bounded by O(N). \n\n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n res = []\n dict = {}\n max_value = float(\'-inf\')\n\n def bfs(node):\n queue = deque()\n visited = set()\n count = 0\n queue.append(node)\n visited.add(node)\n while(queue):\n cur = queue.popleft()\n\n # it will traverse the whole row of cur node\n for idx, value in enumerate(graph[cur]): \n if value ==1 and idx not in visited:\n queue.append(idx)\n visited.add(idx)\n count += 1\n # here we check if node \'idx\' is not curr and presentin initial nodes list - if yes then we return -1 \n if idx!= cur and idx in initial:\n return -1 \n return count\n\n for node in initial:\n dict[node] = bfs(node)\n # max connected node count \n max_value = max(max_value, dict[node])\n\n\n for k, v in dict.items():\n if v == max_value:\n res.append(k)\n return min(res)\n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops. We will remove **exactly one node** from `initial`.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
Note that if a node was removed from the `initial` list of infected nodes, it might still be infected later due to the malware spread.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\], initial = \[0,2\]
**Output:** 0
**Example 3:**
**Input:** graph = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], initial = \[1,2\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length <= n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Easy to understand with step wise explanation 😸😸 | minimize-malware-spread | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing BFS/DFS was first thought as Adjacency matrix is given. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo we need to minimize the infection in the connected graph. Only way is to find a connected graph which has only one node from initial state as we can remove it from intial infection and then its connected nodes will not get infected. So we need to find the maximum number of connected nodes from inital state nodes. \n\nTo do that I followed below steps:\n1. Used a dictionary to save max connected nodes from each node in initial state. \n2. BFS method to count the connected nodes count from each initial node. we can return -1 if we found some another node from the initial state as it can not be the answer. \n3. We can get the max value from dictionary and then find all nodes whiich have max number of connected nodes and then return which is smallest number. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nAs we might have to visit all the cells in graph if all values are 1. So it is upperboud by O(N^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwe using queue , visited , dict and will be bounded by O(N). \n\n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n res = []\n dict = {}\n max_value = float(\'-inf\')\n\n def bfs(node):\n queue = deque()\n visited = set()\n count = 0\n queue.append(node)\n visited.add(node)\n while(queue):\n cur = queue.popleft()\n\n # it will traverse the whole row of cur node\n for idx, value in enumerate(graph[cur]): \n if value ==1 and idx not in visited:\n queue.append(idx)\n visited.add(idx)\n count += 1\n # here we check if node \'idx\' is not curr and presentin initial nodes list - if yes then we return -1 \n if idx!= cur and idx in initial:\n return -1 \n return count\n\n for node in initial:\n dict[node] = bfs(node)\n # max connected node count \n max_value = max(max_value, dict[node])\n\n\n for k, v in dict.items():\n if v == max_value:\n res.append(k)\n return min(res)\n``` | 0 | You are given an array of `n` strings `strs`, all of the same length.
We may choose any deletion indices, and we delete all the characters in those indices for each string.
For example, if we have `strs = [ "abcdef ", "uvwxyz "]` and deletion indices `{0, 2, 3}`, then the final array after deletions is `[ "bef ", "vyz "]`.
Suppose we chose a set of deletion indices `answer` such that after deletions, the final array has **every string (row) in lexicographic** order. (i.e., `(strs[0][0] <= strs[0][1] <= ... <= strs[0][strs[0].length - 1])`, and `(strs[1][0] <= strs[1][1] <= ... <= strs[1][strs[1].length - 1])`, and so on). Return _the minimum possible value of_ `answer.length`.
**Example 1:**
**Input:** strs = \[ "babca ", "bbazb "\]
**Output:** 3
**Explanation:** After deleting columns 0, 1, and 4, the final array is strs = \[ "bc ", "az "\].
Both these rows are individually in lexicographic order (ie. strs\[0\]\[0\] <= strs\[0\]\[1\] and strs\[1\]\[0\] <= strs\[1\]\[1\]).
Note that strs\[0\] > strs\[1\] - the array strs is not necessarily in lexicographic order.
**Example 2:**
**Input:** strs = \[ "edcba "\]
**Output:** 4
**Explanation:** If we delete less than 4 columns, the only row will not be lexicographically sorted.
**Example 3:**
**Input:** strs = \[ "ghi ", "def ", "abc "\]
**Output:** 0
**Explanation:** All rows are already lexicographically sorted.
**Constraints:**
* `n == strs.length`
* `1 <= n <= 100`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Python DFS solution | minimize-malware-spread | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst, some background: a set of connected nodes forms a component. Nodes can be connected either directly via an edge or through other connected nodes.\n\nNow, let\'s assume we can find a component and how many infected nodes it has. A few scenarios to consider:\n\n1) Component has 0 infected nodes. In this case, "fixing" any of the nodes has no effect on the final count of infected nodes.\n2) Component has 2 or more infected nodes. In this case, "fixing" any of the infected nodes also will have no effect on the final count of infected nodes, because the malware will "spread" from one of the other infected nodes to contaminate the rest of the nodes in the component.\n3) Component has 1 infected node. Fixing the infected node means all the other nodes in this component will remain unaffected. The greater size the component is (i.e. more nodes it has), the greater the impact is of fixing the component\'s infected node.\n\n=> Our goal is to find the largest component satisfying `case 3`, i.e. the largest component containing exactly 1 infected node. And if there are multiple such components, return the smallest value from the `initial` malware nodes input.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDFS from each of the initial affected nodes in `initial`, if we have not visited that node already. Use a `visited` set to track visited nodes. The DFS function returns a tuple of `(component_size, num_infected_nodes)` so we can find the largest component with only one malware node.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n`O(N^2)` due to use of the adjacency matrix. In the worst case, all nodes are connected and form one component. Each call in DFS checks `n` nodes. This can be improved to `O(N+E)` (where `N` = number of nodes, `E` = number of edges) by using an adjacency list, though this requires additional space. \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n`O(N)`\nThe DFS call stack and `visited` set can grow to max size of N. Storing the sorted `initial` input also requires N space.\n\n# Code\n```\nclass Solution:\n def dfs(self, graph: List[List[int]], initial: Set[int], i: int, visited: Set[int]) -> Tuple[int, int]:\n visited.add(i)\n component_size = 1\n num_infected = 1 if i in initial else 0\n for neighbor, val in enumerate(graph[i]):\n if neighbor == i or neighbor in visited: continue\n elif val == 1:\n size, additional_infected = self.dfs(graph, initial, neighbor, visited)\n component_size += size\n num_infected += additional_infected\n return (component_size, num_infected)\n \n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n visited = set()\n initial_set = set(initial)\n max_component_size = 0\n result = -1\n initial = sorted(initial)\n for i in initial:\n if i in visited: continue\n component_size, num_infected = self.dfs(graph, initial_set, i, visited)\n if num_infected == 1 and component_size > max_component_size:\n max_component_size = component_size\n result = i\n if result >= 0: return result\n return initial[0]\n \n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops. We will remove **exactly one node** from `initial`.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
Note that if a node was removed from the `initial` list of infected nodes, it might still be infected later due to the malware spread.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\], initial = \[0,2\]
**Output:** 0
**Example 3:**
**Input:** graph = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], initial = \[1,2\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length <= n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Python DFS solution | minimize-malware-spread | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst, some background: a set of connected nodes forms a component. Nodes can be connected either directly via an edge or through other connected nodes.\n\nNow, let\'s assume we can find a component and how many infected nodes it has. A few scenarios to consider:\n\n1) Component has 0 infected nodes. In this case, "fixing" any of the nodes has no effect on the final count of infected nodes.\n2) Component has 2 or more infected nodes. In this case, "fixing" any of the infected nodes also will have no effect on the final count of infected nodes, because the malware will "spread" from one of the other infected nodes to contaminate the rest of the nodes in the component.\n3) Component has 1 infected node. Fixing the infected node means all the other nodes in this component will remain unaffected. The greater size the component is (i.e. more nodes it has), the greater the impact is of fixing the component\'s infected node.\n\n=> Our goal is to find the largest component satisfying `case 3`, i.e. the largest component containing exactly 1 infected node. And if there are multiple such components, return the smallest value from the `initial` malware nodes input.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDFS from each of the initial affected nodes in `initial`, if we have not visited that node already. Use a `visited` set to track visited nodes. The DFS function returns a tuple of `(component_size, num_infected_nodes)` so we can find the largest component with only one malware node.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n`O(N^2)` due to use of the adjacency matrix. In the worst case, all nodes are connected and form one component. Each call in DFS checks `n` nodes. This can be improved to `O(N+E)` (where `N` = number of nodes, `E` = number of edges) by using an adjacency list, though this requires additional space. \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n`O(N)`\nThe DFS call stack and `visited` set can grow to max size of N. Storing the sorted `initial` input also requires N space.\n\n# Code\n```\nclass Solution:\n def dfs(self, graph: List[List[int]], initial: Set[int], i: int, visited: Set[int]) -> Tuple[int, int]:\n visited.add(i)\n component_size = 1\n num_infected = 1 if i in initial else 0\n for neighbor, val in enumerate(graph[i]):\n if neighbor == i or neighbor in visited: continue\n elif val == 1:\n size, additional_infected = self.dfs(graph, initial, neighbor, visited)\n component_size += size\n num_infected += additional_infected\n return (component_size, num_infected)\n \n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n visited = set()\n initial_set = set(initial)\n max_component_size = 0\n result = -1\n initial = sorted(initial)\n for i in initial:\n if i in visited: continue\n component_size, num_infected = self.dfs(graph, initial_set, i, visited)\n if num_infected == 1 and component_size > max_component_size:\n max_component_size = component_size\n result = i\n if result >= 0: return result\n return initial[0]\n \n``` | 0 | You are given an array of `n` strings `strs`, all of the same length.
We may choose any deletion indices, and we delete all the characters in those indices for each string.
For example, if we have `strs = [ "abcdef ", "uvwxyz "]` and deletion indices `{0, 2, 3}`, then the final array after deletions is `[ "bef ", "vyz "]`.
Suppose we chose a set of deletion indices `answer` such that after deletions, the final array has **every string (row) in lexicographic** order. (i.e., `(strs[0][0] <= strs[0][1] <= ... <= strs[0][strs[0].length - 1])`, and `(strs[1][0] <= strs[1][1] <= ... <= strs[1][strs[1].length - 1])`, and so on). Return _the minimum possible value of_ `answer.length`.
**Example 1:**
**Input:** strs = \[ "babca ", "bbazb "\]
**Output:** 3
**Explanation:** After deleting columns 0, 1, and 4, the final array is strs = \[ "bc ", "az "\].
Both these rows are individually in lexicographic order (ie. strs\[0\]\[0\] <= strs\[0\]\[1\] and strs\[1\]\[0\] <= strs\[1\]\[1\]).
Note that strs\[0\] > strs\[1\] - the array strs is not necessarily in lexicographic order.
**Example 2:**
**Input:** strs = \[ "edcba "\]
**Output:** 4
**Explanation:** If we delete less than 4 columns, the only row will not be lexicographically sorted.
**Example 3:**
**Input:** strs = \[ "ghi ", "def ", "abc "\]
**Output:** 0
**Explanation:** All rows are already lexicographically sorted.
**Constraints:**
* `n == strs.length`
* `1 <= n <= 100`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Union Find in Py3 beating 97% in time | minimize-malware-spread | 0 | 1 | \n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n n = len(graph)\n p = [i for i in range(n)]\n def find(i):\n if i!=p[i]:\n p[i] = find(p[i])\n return p[i]\n for i in range(n):\n for j in range(i):\n if graph[i][j] == 1:\n pi,pj = find(i),find(j)\n if pi!=pj:\n pi,pj = sorted([pi,pj])\n p[pj] = pi\n freq = {}\n for i in range(n):\n pi = find(i)\n if pi not in freq:\n freq[pi] = 0\n freq[pi] += 1\n grpsz = 0\n res = min(initial)\n freqini = {}\n initial.sort() // if not sorted here it won\'t necessarily give the one with the smallest index\n for ini in initial:\n pi = find(ini)\n if pi not in freqini:\n freqini[pi] = 0\n freqini[pi] += 1\n for ini in initial:\n pi = find(ini)\n if freqini[pi] == 1: // we have to exclude the points which won\'t affect M(i) as some other initial points belong to the same union\n if freq[pi] > grpsz:\n grpsz = freq[pi]\n res = ini\n return res \n\n \n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops. We will remove **exactly one node** from `initial`.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
Note that if a node was removed from the `initial` list of infected nodes, it might still be infected later due to the malware spread.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\], initial = \[0,2\]
**Output:** 0
**Example 3:**
**Input:** graph = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], initial = \[1,2\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length <= n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Union Find in Py3 beating 97% in time | minimize-malware-spread | 0 | 1 | \n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n n = len(graph)\n p = [i for i in range(n)]\n def find(i):\n if i!=p[i]:\n p[i] = find(p[i])\n return p[i]\n for i in range(n):\n for j in range(i):\n if graph[i][j] == 1:\n pi,pj = find(i),find(j)\n if pi!=pj:\n pi,pj = sorted([pi,pj])\n p[pj] = pi\n freq = {}\n for i in range(n):\n pi = find(i)\n if pi not in freq:\n freq[pi] = 0\n freq[pi] += 1\n grpsz = 0\n res = min(initial)\n freqini = {}\n initial.sort() // if not sorted here it won\'t necessarily give the one with the smallest index\n for ini in initial:\n pi = find(ini)\n if pi not in freqini:\n freqini[pi] = 0\n freqini[pi] += 1\n for ini in initial:\n pi = find(ini)\n if freqini[pi] == 1: // we have to exclude the points which won\'t affect M(i) as some other initial points belong to the same union\n if freq[pi] > grpsz:\n grpsz = freq[pi]\n res = ini\n return res \n\n \n``` | 0 | You are given an array of `n` strings `strs`, all of the same length.
We may choose any deletion indices, and we delete all the characters in those indices for each string.
For example, if we have `strs = [ "abcdef ", "uvwxyz "]` and deletion indices `{0, 2, 3}`, then the final array after deletions is `[ "bef ", "vyz "]`.
Suppose we chose a set of deletion indices `answer` such that after deletions, the final array has **every string (row) in lexicographic** order. (i.e., `(strs[0][0] <= strs[0][1] <= ... <= strs[0][strs[0].length - 1])`, and `(strs[1][0] <= strs[1][1] <= ... <= strs[1][strs[1].length - 1])`, and so on). Return _the minimum possible value of_ `answer.length`.
**Example 1:**
**Input:** strs = \[ "babca ", "bbazb "\]
**Output:** 3
**Explanation:** After deleting columns 0, 1, and 4, the final array is strs = \[ "bc ", "az "\].
Both these rows are individually in lexicographic order (ie. strs\[0\]\[0\] <= strs\[0\]\[1\] and strs\[1\]\[0\] <= strs\[1\]\[1\]).
Note that strs\[0\] > strs\[1\] - the array strs is not necessarily in lexicographic order.
**Example 2:**
**Input:** strs = \[ "edcba "\]
**Output:** 4
**Explanation:** If we delete less than 4 columns, the only row will not be lexicographically sorted.
**Example 3:**
**Input:** strs = \[ "ghi ", "def ", "abc "\]
**Output:** 0
**Explanation:** All rows are already lexicographically sorted.
**Constraints:**
* `n == strs.length`
* `1 <= n <= 100`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
OMFG!! Beats 100 on both runtime and memory | minimize-malware-spread | 0 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n\tdef minMalwareSpread(self, graph, initial):\n\t\tdef bfs(i):\n\t\t\tqueue, visited = [i], [i]\n\t\t\tpath_node = 0\n\t\t\twhile(queue):\n\t\t\t\tcur = queue.pop(0)\n\t\t\t\tfor idx, value in enumerate(graph[cur]):\n\t\t\t\t\t\n\t\t\t\t\tif value ==1 and idx not in visited:\n\t\t\t\t\t\tqueue.append(idx)\n\t\t\t\t\t\tpath_node += 1\n\t\t\t\t\t\tif idx!= cur and idx in initial:\n\t\t\t\t\t\t\treturn -1\n\t\t\t\t\t\tvisited.append(idx)\n\t\t\treturn path_node\n\n\t\trecord = dict()\n\n\t\tfor node in initial:\n\t\t\trecord[node] = bfs(node)\n\t\t\n\t\tcandidate = record[max(record, key=record.get)]\n\t\t\n\t\tres = []\n\t\tfor k, v in record.items():\n\t\t\tif v==candidate:\n\t\t\t\tres.append(k)\n\t\treturn min(res)\n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops. We will remove **exactly one node** from `initial`.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
Note that if a node was removed from the `initial` list of infected nodes, it might still be infected later due to the malware spread.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,0,0\],\[0,1,0\],\[0,0,1\]\], initial = \[0,2\]
**Output:** 0
**Example 3:**
**Input:** graph = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], initial = \[1,2\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length <= n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
OMFG!! Beats 100 on both runtime and memory | minimize-malware-spread | 0 | 1 | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n\tdef minMalwareSpread(self, graph, initial):\n\t\tdef bfs(i):\n\t\t\tqueue, visited = [i], [i]\n\t\t\tpath_node = 0\n\t\t\twhile(queue):\n\t\t\t\tcur = queue.pop(0)\n\t\t\t\tfor idx, value in enumerate(graph[cur]):\n\t\t\t\t\t\n\t\t\t\t\tif value ==1 and idx not in visited:\n\t\t\t\t\t\tqueue.append(idx)\n\t\t\t\t\t\tpath_node += 1\n\t\t\t\t\t\tif idx!= cur and idx in initial:\n\t\t\t\t\t\t\treturn -1\n\t\t\t\t\t\tvisited.append(idx)\n\t\t\treturn path_node\n\n\t\trecord = dict()\n\n\t\tfor node in initial:\n\t\t\trecord[node] = bfs(node)\n\t\t\n\t\tcandidate = record[max(record, key=record.get)]\n\t\t\n\t\tres = []\n\t\tfor k, v in record.items():\n\t\t\tif v==candidate:\n\t\t\t\tres.append(k)\n\t\treturn min(res)\n``` | 0 | You are given an array of `n` strings `strs`, all of the same length.
We may choose any deletion indices, and we delete all the characters in those indices for each string.
For example, if we have `strs = [ "abcdef ", "uvwxyz "]` and deletion indices `{0, 2, 3}`, then the final array after deletions is `[ "bef ", "vyz "]`.
Suppose we chose a set of deletion indices `answer` such that after deletions, the final array has **every string (row) in lexicographic** order. (i.e., `(strs[0][0] <= strs[0][1] <= ... <= strs[0][strs[0].length - 1])`, and `(strs[1][0] <= strs[1][1] <= ... <= strs[1][strs[1].length - 1])`, and so on). Return _the minimum possible value of_ `answer.length`.
**Example 1:**
**Input:** strs = \[ "babca ", "bbazb "\]
**Output:** 3
**Explanation:** After deleting columns 0, 1, and 4, the final array is strs = \[ "bc ", "az "\].
Both these rows are individually in lexicographic order (ie. strs\[0\]\[0\] <= strs\[0\]\[1\] and strs\[1\]\[0\] <= strs\[1\]\[1\]).
Note that strs\[0\] > strs\[1\] - the array strs is not necessarily in lexicographic order.
**Example 2:**
**Input:** strs = \[ "edcba "\]
**Output:** 4
**Explanation:** If we delete less than 4 columns, the only row will not be lexicographically sorted.
**Example 3:**
**Input:** strs = \[ "ghi ", "def ", "abc "\]
**Output:** 0
**Explanation:** All rows are already lexicographically sorted.
**Constraints:**
* `n == strs.length`
* `1 <= n <= 100`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists of lowercase English letters. | null |
Solution | long-pressed-name | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isLongPressedName(string name, string typed) {\n int i=0,j=0;\n while(i< name.length() && j< typed.length()){\n if(name[i]==typed[j]){\n i++;\n j++;\n }\n else{\n if(i>0 &&name[i-1]==typed[j])\n j++;\n else{\n return false;\n }\n }\n }\n while(j< typed.length()){\n if(name[i-1]!=typed[j])\n return false;\n j++;\n }\n while(i< name.length()){\n if(name[i]!=typed[j])\n return false;\n i++;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n \n name = list(name)\n typed = list(typed)\n if name[0] != typed[0]:\n return False\n i = 1\n j = 1\n while i < len(name) and j < len(typed):\n if name[i] == typed[j]:\n i += 1\n j += 1\n elif name[i-1] == typed[j]:\n j += 1\n else:\n return False\n while j < len(typed):\n if name[i-1] == typed[j]:\n j += 1\n else:\n return False\n return i == len(name)\n```\n\n```Java []\nclass Solution {\n public boolean isLongPressedName(String name, String typed) {\n int n = name.length();\n int m = typed.length();\n int i=0;\n int j=0;\n if(name.charAt(0) != typed.charAt(0))\n return false;\n if(n>m){\n return false;\n }\n while(i<n && j<m){\n if(name.charAt(i) == typed.charAt(j)){\n i++;\n j++;\n }\n else if(name.charAt(i-1) == typed.charAt(j)){\n j++;\n }\n else{\n return false;\n }\n }\n while(j<m){\n if(name.charAt(i-1) == typed.charAt(j)){\n j++;\n }\n else{\n return false;\n }\n }\n if(i<n){\n return false;\n }\n return true; \n }\n}\n```\n | 3 | Your friend is typing his `name` into a keyboard. Sometimes, when typing a character `c`, the key might get _long pressed_, and the character will be typed 1 or more times.
You examine the `typed` characters of the keyboard. Return `True` if it is possible that it was your friends name, with some characters (possibly none) being long pressed.
**Example 1:**
**Input:** name = "alex ", typed = "aaleex "
**Output:** true
**Explanation:** 'a' and 'e' in 'alex' were long pressed.
**Example 2:**
**Input:** name = "saeed ", typed = "ssaaedd "
**Output:** false
**Explanation:** 'e' must have been pressed twice, but it was not in the typed output.
**Constraints:**
* `1 <= name.length, typed.length <= 1000`
* `name` and `typed` consist of only lowercase English letters. | null |
Solution | long-pressed-name | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isLongPressedName(string name, string typed) {\n int i=0,j=0;\n while(i< name.length() && j< typed.length()){\n if(name[i]==typed[j]){\n i++;\n j++;\n }\n else{\n if(i>0 &&name[i-1]==typed[j])\n j++;\n else{\n return false;\n }\n }\n }\n while(j< typed.length()){\n if(name[i-1]!=typed[j])\n return false;\n j++;\n }\n while(i< name.length()){\n if(name[i]!=typed[j])\n return false;\n i++;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n \n name = list(name)\n typed = list(typed)\n if name[0] != typed[0]:\n return False\n i = 1\n j = 1\n while i < len(name) and j < len(typed):\n if name[i] == typed[j]:\n i += 1\n j += 1\n elif name[i-1] == typed[j]:\n j += 1\n else:\n return False\n while j < len(typed):\n if name[i-1] == typed[j]:\n j += 1\n else:\n return False\n return i == len(name)\n```\n\n```Java []\nclass Solution {\n public boolean isLongPressedName(String name, String typed) {\n int n = name.length();\n int m = typed.length();\n int i=0;\n int j=0;\n if(name.charAt(0) != typed.charAt(0))\n return false;\n if(n>m){\n return false;\n }\n while(i<n && j<m){\n if(name.charAt(i) == typed.charAt(j)){\n i++;\n j++;\n }\n else if(name.charAt(i-1) == typed.charAt(j)){\n j++;\n }\n else{\n return false;\n }\n }\n while(j<m){\n if(name.charAt(i-1) == typed.charAt(j)){\n j++;\n }\n else{\n return false;\n }\n }\n if(i<n){\n return false;\n }\n return true; \n }\n}\n```\n | 3 | You are given an integer array `nums` with the following properties:
* `nums.length == 2 * n`.
* `nums` contains `n + 1` **unique** elements.
* Exactly one element of `nums` is repeated `n` times.
Return _the element that is repeated_ `n` _times_.
**Example 1:**
**Input:** nums = \[1,2,3,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,1,2,5,3,2\]
**Output:** 2
**Example 3:**
**Input:** nums = \[5,1,5,2,5,3,5,4\]
**Output:** 5
**Constraints:**
* `2 <= n <= 5000`
* `nums.length == 2 * n`
* `0 <= nums[i] <= 104`
* `nums` contains `n + 1` **unique** elements and one of them is repeated exactly `n` times. | null |
Python Elegant & Short | One line | itertools.groupby | long-pressed-name | 0 | 1 | ```\t\nfrom itertools import groupby, zip_longest\n\n\nclass Solution:\n\t"""\n\tTime: O(max(n, m))\n\tMemory: O(1)\n\t"""\n\n\tdef isLongPressedName(self, name: str, typed: str) -> bool:\n\t\tfor (a, a_gr), (b, b_gr) in zip_longest(groupby(name), groupby(typed), fillvalue=(None, None)):\n\t\t\tif a != b or sum(1 for _ in a_gr) > sum(1 for _ in b_gr):\n\t\t\t\treturn False\n\t\treturn True\n\n\nclass Solution:\n\t"""\n\tTime: O(max(n, m))\n\tMemory: O(1)\n\t"""\n\n\tdef isLongPressedName(self, name: str, typed: str) -> bool:\n\t\treturn all(\n\t\t\ta == b and sum(1 for _ in a_gr) <= sum(1 for _ in b_gr)\n\t\t\tfor (a, a_gr), (b, b_gr) in zip_longest(groupby(name), groupby(typed), fillvalue=(None, None))\n\t\t)\n```\n\nIf you like this solution remember to **upvote it** to let me know. | 4 | Your friend is typing his `name` into a keyboard. Sometimes, when typing a character `c`, the key might get _long pressed_, and the character will be typed 1 or more times.
You examine the `typed` characters of the keyboard. Return `True` if it is possible that it was your friends name, with some characters (possibly none) being long pressed.
**Example 1:**
**Input:** name = "alex ", typed = "aaleex "
**Output:** true
**Explanation:** 'a' and 'e' in 'alex' were long pressed.
**Example 2:**
**Input:** name = "saeed ", typed = "ssaaedd "
**Output:** false
**Explanation:** 'e' must have been pressed twice, but it was not in the typed output.
**Constraints:**
* `1 <= name.length, typed.length <= 1000`
* `name` and `typed` consist of only lowercase English letters. | null |
Python Elegant & Short | One line | itertools.groupby | long-pressed-name | 0 | 1 | ```\t\nfrom itertools import groupby, zip_longest\n\n\nclass Solution:\n\t"""\n\tTime: O(max(n, m))\n\tMemory: O(1)\n\t"""\n\n\tdef isLongPressedName(self, name: str, typed: str) -> bool:\n\t\tfor (a, a_gr), (b, b_gr) in zip_longest(groupby(name), groupby(typed), fillvalue=(None, None)):\n\t\t\tif a != b or sum(1 for _ in a_gr) > sum(1 for _ in b_gr):\n\t\t\t\treturn False\n\t\treturn True\n\n\nclass Solution:\n\t"""\n\tTime: O(max(n, m))\n\tMemory: O(1)\n\t"""\n\n\tdef isLongPressedName(self, name: str, typed: str) -> bool:\n\t\treturn all(\n\t\t\ta == b and sum(1 for _ in a_gr) <= sum(1 for _ in b_gr)\n\t\t\tfor (a, a_gr), (b, b_gr) in zip_longest(groupby(name), groupby(typed), fillvalue=(None, None))\n\t\t)\n```\n\nIf you like this solution remember to **upvote it** to let me know. | 4 | You are given an integer array `nums` with the following properties:
* `nums.length == 2 * n`.
* `nums` contains `n + 1` **unique** elements.
* Exactly one element of `nums` is repeated `n` times.
Return _the element that is repeated_ `n` _times_.
**Example 1:**
**Input:** nums = \[1,2,3,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,1,2,5,3,2\]
**Output:** 2
**Example 3:**
**Input:** nums = \[5,1,5,2,5,3,5,4\]
**Output:** 5
**Constraints:**
* `2 <= n <= 5000`
* `nums.length == 2 * n`
* `0 <= nums[i] <= 104`
* `nums` contains `n + 1` **unique** elements and one of them is repeated exactly `n` times. | null |
✅ [PYTHON] Compress strings then compare! | long-pressed-name | 0 | 1 | First I wrote a solution based on various conditions and it produced a good result. But I didn\'t like the way it looked. You can skip it, because the second solution is below and I like it much better.\n# My first solution (Beats 98.86% - skip it):\n```\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n if name[-1] != typed[-1] or len(set(name)) > len(set(typed)):\n return False\n name_pointer = 0\n typed_pointer = 0\n while name_pointer <= len(name) - 1:\n if (typed_pointer == len(typed) - 1 and name_pointer != len(name) - 1) or name[name_pointer] != typed[typed_pointer]:\n return False\n if name_pointer != len(name) - 1 and name[name_pointer] != name[name_pointer + 1]:\n while typed_pointer <= len(typed) - 1 and name[name_pointer] == typed[typed_pointer]:\n typed_pointer += 1\n name_pointer += 1\n elif name_pointer == len(name) - 1:\n if \'\'.join(set(typed[typed_pointer:])) == name[name_pointer]:\n return True\n else:\n return False\n else:\n typed_pointer += 1\n name_pointer += 1\n```\n# My second solution (Beats 92.68%)\nThen I remembered the string compression problem and decided to implement a solution based on it. I wrote a function that compresses, then splits the original strings, and then compares them.\nFor example:\n```\n>>>compress_split_string("saeed") \n[\'s1\',\'a1\',\'e2\',\'d1\']\n>>>compress_split_string("ssaaedd")\n[\'s2\',\'a2\',\'e1\',\'d2\']\n```\n```\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n if set(name) != set(typed):\n return False\n def compress_split_string(str_):\n char_counter = 1\n str_ += \' \'\n list_compress = []\n for idx, t_char in enumerate(str_):\n if idx == 0:\n continue\n if t_char != str_[idx - 1]:\n list_compress.append(str_[idx - 1] + str(char_counter))\n char_counter = 1\n else:\n char_counter += 1\n return list_compress\n name_compress = compress_split_string(name)\n typed_compress = compress_split_string(typed)\n if len(name_compress) != len(typed_compress):\n return False\n for n_num, t_num in zip(name_compress, typed_compress):\n if t_num < n_num:\n return False\n return True\n``` | 1 | Your friend is typing his `name` into a keyboard. Sometimes, when typing a character `c`, the key might get _long pressed_, and the character will be typed 1 or more times.
You examine the `typed` characters of the keyboard. Return `True` if it is possible that it was your friends name, with some characters (possibly none) being long pressed.
**Example 1:**
**Input:** name = "alex ", typed = "aaleex "
**Output:** true
**Explanation:** 'a' and 'e' in 'alex' were long pressed.
**Example 2:**
**Input:** name = "saeed ", typed = "ssaaedd "
**Output:** false
**Explanation:** 'e' must have been pressed twice, but it was not in the typed output.
**Constraints:**
* `1 <= name.length, typed.length <= 1000`
* `name` and `typed` consist of only lowercase English letters. | null |
✅ [PYTHON] Compress strings then compare! | long-pressed-name | 0 | 1 | First I wrote a solution based on various conditions and it produced a good result. But I didn\'t like the way it looked. You can skip it, because the second solution is below and I like it much better.\n# My first solution (Beats 98.86% - skip it):\n```\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n if name[-1] != typed[-1] or len(set(name)) > len(set(typed)):\n return False\n name_pointer = 0\n typed_pointer = 0\n while name_pointer <= len(name) - 1:\n if (typed_pointer == len(typed) - 1 and name_pointer != len(name) - 1) or name[name_pointer] != typed[typed_pointer]:\n return False\n if name_pointer != len(name) - 1 and name[name_pointer] != name[name_pointer + 1]:\n while typed_pointer <= len(typed) - 1 and name[name_pointer] == typed[typed_pointer]:\n typed_pointer += 1\n name_pointer += 1\n elif name_pointer == len(name) - 1:\n if \'\'.join(set(typed[typed_pointer:])) == name[name_pointer]:\n return True\n else:\n return False\n else:\n typed_pointer += 1\n name_pointer += 1\n```\n# My second solution (Beats 92.68%)\nThen I remembered the string compression problem and decided to implement a solution based on it. I wrote a function that compresses, then splits the original strings, and then compares them.\nFor example:\n```\n>>>compress_split_string("saeed") \n[\'s1\',\'a1\',\'e2\',\'d1\']\n>>>compress_split_string("ssaaedd")\n[\'s2\',\'a2\',\'e1\',\'d2\']\n```\n```\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n if set(name) != set(typed):\n return False\n def compress_split_string(str_):\n char_counter = 1\n str_ += \' \'\n list_compress = []\n for idx, t_char in enumerate(str_):\n if idx == 0:\n continue\n if t_char != str_[idx - 1]:\n list_compress.append(str_[idx - 1] + str(char_counter))\n char_counter = 1\n else:\n char_counter += 1\n return list_compress\n name_compress = compress_split_string(name)\n typed_compress = compress_split_string(typed)\n if len(name_compress) != len(typed_compress):\n return False\n for n_num, t_num in zip(name_compress, typed_compress):\n if t_num < n_num:\n return False\n return True\n``` | 1 | You are given an integer array `nums` with the following properties:
* `nums.length == 2 * n`.
* `nums` contains `n + 1` **unique** elements.
* Exactly one element of `nums` is repeated `n` times.
Return _the element that is repeated_ `n` _times_.
**Example 1:**
**Input:** nums = \[1,2,3,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,1,2,5,3,2\]
**Output:** 2
**Example 3:**
**Input:** nums = \[5,1,5,2,5,3,5,4\]
**Output:** 5
**Constraints:**
* `2 <= n <= 5000`
* `nums.length == 2 * n`
* `0 <= nums[i] <= 104`
* `nums` contains `n + 1` **unique** elements and one of them is repeated exactly `n` times. | null |
Python3 wasy-peasy solution | long-pressed-name | 0 | 1 | # Intuition\ntwo pointers\n\n# Approach\nIn this implementation, we are using two pointers i and j to traverse the name and typed strings respectively. We compare the characters at these pointers and move the pointers accordingly.\n\nIf the characters at the current positions are equal, we increment both i and j, and move on to the next character. If the characters are not equal, we check if the previous character in the typed string is the same as the current character, and if it is, we increment j and move on to the next character. If the previous character in the typed string is not the same as the current character, we can immediately return False as this means that the current character in typed is not part of the name.\n\nWe continue this process until we have traversed the entire typed string. Finally, we check if we have traversed the entire name string by comparing the value of i with n, the length of name.\n\n\n# Complexity\n- Time complexity:\nO(n), where n is the length of the typed string. This is already an optimal time complexity as we need to examine each character of the typed string at least once to compare it with the corresponding character in the name string.\n\n- Space complexity:\nThis implementation has a space complexity of O(1), as we are not using any additional data structures to store the counts of characters.\n\n# Code\n```\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n\n\n i, j = 0, 0\n while j < len(typed):\n\n if i < len(name) and name[i] == typed[j]:\n i += 1\n j += 1\n elif j > 0 and typed[j-1] == typed[j]:\n j += 1\n else:\n return False\n\n return i == len(name)\n``` | 5 | Your friend is typing his `name` into a keyboard. Sometimes, when typing a character `c`, the key might get _long pressed_, and the character will be typed 1 or more times.
You examine the `typed` characters of the keyboard. Return `True` if it is possible that it was your friends name, with some characters (possibly none) being long pressed.
**Example 1:**
**Input:** name = "alex ", typed = "aaleex "
**Output:** true
**Explanation:** 'a' and 'e' in 'alex' were long pressed.
**Example 2:**
**Input:** name = "saeed ", typed = "ssaaedd "
**Output:** false
**Explanation:** 'e' must have been pressed twice, but it was not in the typed output.
**Constraints:**
* `1 <= name.length, typed.length <= 1000`
* `name` and `typed` consist of only lowercase English letters. | null |
Python3 wasy-peasy solution | long-pressed-name | 0 | 1 | # Intuition\ntwo pointers\n\n# Approach\nIn this implementation, we are using two pointers i and j to traverse the name and typed strings respectively. We compare the characters at these pointers and move the pointers accordingly.\n\nIf the characters at the current positions are equal, we increment both i and j, and move on to the next character. If the characters are not equal, we check if the previous character in the typed string is the same as the current character, and if it is, we increment j and move on to the next character. If the previous character in the typed string is not the same as the current character, we can immediately return False as this means that the current character in typed is not part of the name.\n\nWe continue this process until we have traversed the entire typed string. Finally, we check if we have traversed the entire name string by comparing the value of i with n, the length of name.\n\n\n# Complexity\n- Time complexity:\nO(n), where n is the length of the typed string. This is already an optimal time complexity as we need to examine each character of the typed string at least once to compare it with the corresponding character in the name string.\n\n- Space complexity:\nThis implementation has a space complexity of O(1), as we are not using any additional data structures to store the counts of characters.\n\n# Code\n```\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n\n\n i, j = 0, 0\n while j < len(typed):\n\n if i < len(name) and name[i] == typed[j]:\n i += 1\n j += 1\n elif j > 0 and typed[j-1] == typed[j]:\n j += 1\n else:\n return False\n\n return i == len(name)\n``` | 5 | You are given an integer array `nums` with the following properties:
* `nums.length == 2 * n`.
* `nums` contains `n + 1` **unique** elements.
* Exactly one element of `nums` is repeated `n` times.
Return _the element that is repeated_ `n` _times_.
**Example 1:**
**Input:** nums = \[1,2,3,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,1,2,5,3,2\]
**Output:** 2
**Example 3:**
**Input:** nums = \[5,1,5,2,5,3,5,4\]
**Output:** 5
**Constraints:**
* `2 <= n <= 5000`
* `nums.length == 2 * n`
* `0 <= nums[i] <= 104`
* `nums` contains `n + 1` **unique** elements and one of them is repeated exactly `n` times. | null |
[Python3] 2 pointers | long-pressed-name | 0 | 1 | ```\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n ni = 0 # index of name\n ti = 0 # index of typed\n while ni <= len(name) and ti < len(typed):\n if ni < len(name) and typed[ti] == name[ni]:\n ti += 1\n ni += 1\n elif typed[ti] == name[ni-1] and ni != 0:\n ti += 1\n else:\n return False\n \n return ni == len(name) and ti == len(typed)\n \n``` | 13 | Your friend is typing his `name` into a keyboard. Sometimes, when typing a character `c`, the key might get _long pressed_, and the character will be typed 1 or more times.
You examine the `typed` characters of the keyboard. Return `True` if it is possible that it was your friends name, with some characters (possibly none) being long pressed.
**Example 1:**
**Input:** name = "alex ", typed = "aaleex "
**Output:** true
**Explanation:** 'a' and 'e' in 'alex' were long pressed.
**Example 2:**
**Input:** name = "saeed ", typed = "ssaaedd "
**Output:** false
**Explanation:** 'e' must have been pressed twice, but it was not in the typed output.
**Constraints:**
* `1 <= name.length, typed.length <= 1000`
* `name` and `typed` consist of only lowercase English letters. | null |
[Python3] 2 pointers | long-pressed-name | 0 | 1 | ```\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n ni = 0 # index of name\n ti = 0 # index of typed\n while ni <= len(name) and ti < len(typed):\n if ni < len(name) and typed[ti] == name[ni]:\n ti += 1\n ni += 1\n elif typed[ti] == name[ni-1] and ni != 0:\n ti += 1\n else:\n return False\n \n return ni == len(name) and ti == len(typed)\n \n``` | 13 | You are given an integer array `nums` with the following properties:
* `nums.length == 2 * n`.
* `nums` contains `n + 1` **unique** elements.
* Exactly one element of `nums` is repeated `n` times.
Return _the element that is repeated_ `n` _times_.
**Example 1:**
**Input:** nums = \[1,2,3,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,1,2,5,3,2\]
**Output:** 2
**Example 3:**
**Input:** nums = \[5,1,5,2,5,3,5,4\]
**Output:** 5
**Constraints:**
* `2 <= n <= 5000`
* `nums.length == 2 * n`
* `0 <= nums[i] <= 104`
* `nums` contains `n + 1` **unique** elements and one of them is repeated exactly `n` times. | null |
Python3 10-line code using 2-pointers | long-pressed-name | 0 | 1 | ```\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n i, j, m, n = 0, 0, len(name), len(typed)\n if n < m: return False\n while i < m and j < n:\n if name[i] == typed[j]:\n i += 1\n j += 1\n elif j == 0 or typed[j] != typed[j - 1]: return False\n else:\n j += 1\n return i == m and typed[j:] == typed[j - 1] * (n - j)\n``` | 2 | Your friend is typing his `name` into a keyboard. Sometimes, when typing a character `c`, the key might get _long pressed_, and the character will be typed 1 or more times.
You examine the `typed` characters of the keyboard. Return `True` if it is possible that it was your friends name, with some characters (possibly none) being long pressed.
**Example 1:**
**Input:** name = "alex ", typed = "aaleex "
**Output:** true
**Explanation:** 'a' and 'e' in 'alex' were long pressed.
**Example 2:**
**Input:** name = "saeed ", typed = "ssaaedd "
**Output:** false
**Explanation:** 'e' must have been pressed twice, but it was not in the typed output.
**Constraints:**
* `1 <= name.length, typed.length <= 1000`
* `name` and `typed` consist of only lowercase English letters. | null |
Python3 10-line code using 2-pointers | long-pressed-name | 0 | 1 | ```\nclass Solution:\n def isLongPressedName(self, name: str, typed: str) -> bool:\n i, j, m, n = 0, 0, len(name), len(typed)\n if n < m: return False\n while i < m and j < n:\n if name[i] == typed[j]:\n i += 1\n j += 1\n elif j == 0 or typed[j] != typed[j - 1]: return False\n else:\n j += 1\n return i == m and typed[j:] == typed[j - 1] * (n - j)\n``` | 2 | You are given an integer array `nums` with the following properties:
* `nums.length == 2 * n`.
* `nums` contains `n + 1` **unique** elements.
* Exactly one element of `nums` is repeated `n` times.
Return _the element that is repeated_ `n` _times_.
**Example 1:**
**Input:** nums = \[1,2,3,3\]
**Output:** 3
**Example 2:**
**Input:** nums = \[2,1,2,5,3,2\]
**Output:** 2
**Example 3:**
**Input:** nums = \[5,1,5,2,5,3,5,4\]
**Output:** 5
**Constraints:**
* `2 <= n <= 5000`
* `nums.length == 2 * n`
* `0 <= nums[i] <= 104`
* `nums` contains `n + 1` **unique** elements and one of them is repeated exactly `n` times. | null |
Python One Liner (Actually good, unexplained) | flip-string-to-monotone-increasing | 0 | 1 | ```\nclass Solution:\n def minFlipsMonoIncr(self, s: str) -> int:\n return min(0,*accumulate([[-1,1][int(c)]for c in s]))+s.count(\'0\')\n``` | 6 | A binary string is monotone increasing if it consists of some number of `0`'s (possibly none), followed by some number of `1`'s (also possibly none).
You are given a binary string `s`. You can flip `s[i]` changing it from `0` to `1` or from `1` to `0`.
Return _the minimum number of flips to make_ `s` _monotone increasing_.
**Example 1:**
**Input:** s = "00110 "
**Output:** 1
**Explanation:** We flip the last digit to get 00111.
**Example 2:**
**Input:** s = "010110 "
**Output:** 2
**Explanation:** We flip to get 011111, or alternatively 000111.
**Example 3:**
**Input:** s = "00011000 "
**Output:** 2
**Explanation:** We flip to get 00000000.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | null |
Python One Liner (Actually good, unexplained) | flip-string-to-monotone-increasing | 0 | 1 | ```\nclass Solution:\n def minFlipsMonoIncr(self, s: str) -> int:\n return min(0,*accumulate([[-1,1][int(c)]for c in s]))+s.count(\'0\')\n``` | 6 | A **ramp** in an integer array `nums` is a pair `(i, j)` for which `i < j` and `nums[i] <= nums[j]`. The **width** of such a ramp is `j - i`.
Given an integer array `nums`, return _the maximum width of a **ramp** in_ `nums`. If there is no **ramp** in `nums`, return `0`.
**Example 1:**
**Input:** nums = \[6,0,8,2,1,5\]
**Output:** 4
**Explanation:** The maximum width ramp is achieved at (i, j) = (1, 5): nums\[1\] = 0 and nums\[5\] = 5.
**Example 2:**
**Input:** nums = \[9,8,1,0,1,9,4,0,4,1\]
**Output:** 7
**Explanation:** The maximum width ramp is achieved at (i, j) = (2, 9): nums\[2\] = 1 and nums\[9\] = 1.
**Constraints:**
* `2 <= nums.length <= 5 * 104`
* `0 <= nums[i] <= 5 * 104` | null |
SIMPLE PYTHON SOLUTION | flip-string-to-monotone-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n \n def minFlipsMonoIncr(self, s: str) -> int:\n n=len(s)\n ones=[0]*(n)\n ct=0\n for i in range(n):\n if s[i]==\'1\':\n ct+=1\n ones[i]=ct\n prev=0\n for i in range(1,n+1):\n if s[i-1]==\'0\':\n curr=min(prev+1,ones[i-1])\n else:\n curr=min(prev,ones[i-1])\n prev=curr\n return prev\n``` | 5 | A binary string is monotone increasing if it consists of some number of `0`'s (possibly none), followed by some number of `1`'s (also possibly none).
You are given a binary string `s`. You can flip `s[i]` changing it from `0` to `1` or from `1` to `0`.
Return _the minimum number of flips to make_ `s` _monotone increasing_.
**Example 1:**
**Input:** s = "00110 "
**Output:** 1
**Explanation:** We flip the last digit to get 00111.
**Example 2:**
**Input:** s = "010110 "
**Output:** 2
**Explanation:** We flip to get 011111, or alternatively 000111.
**Example 3:**
**Input:** s = "00011000 "
**Output:** 2
**Explanation:** We flip to get 00000000.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | null |
SIMPLE PYTHON SOLUTION | flip-string-to-monotone-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n \n def minFlipsMonoIncr(self, s: str) -> int:\n n=len(s)\n ones=[0]*(n)\n ct=0\n for i in range(n):\n if s[i]==\'1\':\n ct+=1\n ones[i]=ct\n prev=0\n for i in range(1,n+1):\n if s[i-1]==\'0\':\n curr=min(prev+1,ones[i-1])\n else:\n curr=min(prev,ones[i-1])\n prev=curr\n return prev\n``` | 5 | A **ramp** in an integer array `nums` is a pair `(i, j)` for which `i < j` and `nums[i] <= nums[j]`. The **width** of such a ramp is `j - i`.
Given an integer array `nums`, return _the maximum width of a **ramp** in_ `nums`. If there is no **ramp** in `nums`, return `0`.
**Example 1:**
**Input:** nums = \[6,0,8,2,1,5\]
**Output:** 4
**Explanation:** The maximum width ramp is achieved at (i, j) = (1, 5): nums\[1\] = 0 and nums\[5\] = 5.
**Example 2:**
**Input:** nums = \[9,8,1,0,1,9,4,0,4,1\]
**Output:** 7
**Explanation:** The maximum width ramp is achieved at (i, j) = (2, 9): nums\[2\] = 1 and nums\[9\] = 1.
**Constraints:**
* `2 <= nums.length <= 5 * 104`
* `0 <= nums[i] <= 5 * 104` | null |
Explanation in laymens terms [Easy to understand] | flip-string-to-monotone-increasing | 1 | 1 | # Intuition\nBasically the idea is that once we reach a \'1\' we will start flipping \'0\'s to 1s until the count for zeros is less than ones but as an when the count for zero increases more than that of ones as we are logically supposed to flip the 1s instead of zeroes. \n\nThe way we will be able to acheive this is by considering count of 1 and number of flips(initially with the thought of flipping at 0s) and then we take a minimum of these two values to transition between these two flips min(counter_right, flips). \n\n```\n E.g. - \n s ="00110100" \n\n # string = "0" counter = 0, flips = 1 -> flips = min(0, 1) = 0\n - as bit is not \'0\' counter will be 0 and flips will be reset to zero as we don\'t need to flip anything yet\n\n # string = "00" counter = 0, flips = 1 -> flips = min(0, 1) = 0\n - as 1 is not reached counter will be 0 and flips will be reset to zero as we don\'t need to flip anything yet\n\n # string = "001" counter = 1, flips = 0 -> flips = min(1, 0) = 0\n - as we have a 1 now counter will be changed to 1 and the flip will still be zero as there is not to flip yet\n\n # string = "0011" counter = 2, flips = 0 -> flips = min(2, 0) = 0\n - as we have a 1 now counter will be changed to 2 and the flip will still be zero as there is not to flip yet\n\n # string = "00110" counter = 2, flips = 1 -> flips = min(2, 1) = 1\n - as bit is \'0\' counter will stay at 2 and the flip will changed to 1 with the idea that we need to have all 1s after the first 1 and as the minimum of counter and flips is 1 it will be saved\n\n # string = "001100" counter = 2, flips = 2 -> flips = min(2, 2) = 2\n - as bit is \'0\' counter will stay at 2 and the flip will changed to 2 and as the minimum of counter and flips is 2 it will be saved\n\n # string = "0011001" counter = 3, flips = 2 -> flips = min(3, 2) = 2\n - as now we encountered one more 1 our idea still holds true that we have to flip 0s to 1s so the value for flip will stay as 2 because of min and will be saved\n\n # string = "00110010" counter = 3, flips = 3 -> flips = min(3, 3) = 3\n - now we encountered \'0\' making its count same as the count for \'1\' (which means we will not care about if we are fliping 0 or 1) so we will increase the flips to 3. As min of counter and flips would be 3 which will be saved\n\n # string = "001100100" counter = 3, flips = 4 -> flips = min(3, 4) = 3\n - another \'0\' which makes its count more than that of \'1\' which will reset our idea that we have to flip 1s now. As we have the counter for 1s our min condition will support our idea and set the flips to min(3, 4) = 3\n\n\n This lands us to the conclusion that we had to flip 3 1s to make it binary monotonic and adds up to our solutions \n```\n\n# Approach\n- Take counter for 1s and flips\n- Increase counter for 1s at every \'1\' encountered\n- Increase the flips for every \'0\' encountered\n- reset flips to minimum of flips and counter for 1s(this will help us transition between fliping 0s ar 1s)\n- return flips\n\n> Note: Try to write your own code after this if you get the idea. :-)\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def minFlipsMonoIncr(self, s: str) -> int:\n counter = 0\n flips = 0\n for ch in s:\n if ch == \'1\':\n counter += 1\n else:\n flips += 1\n flips = min(counter, flips)\n return flips\n``` | 2 | A binary string is monotone increasing if it consists of some number of `0`'s (possibly none), followed by some number of `1`'s (also possibly none).
You are given a binary string `s`. You can flip `s[i]` changing it from `0` to `1` or from `1` to `0`.
Return _the minimum number of flips to make_ `s` _monotone increasing_.
**Example 1:**
**Input:** s = "00110 "
**Output:** 1
**Explanation:** We flip the last digit to get 00111.
**Example 2:**
**Input:** s = "010110 "
**Output:** 2
**Explanation:** We flip to get 011111, or alternatively 000111.
**Example 3:**
**Input:** s = "00011000 "
**Output:** 2
**Explanation:** We flip to get 00000000.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | null |
Explanation in laymens terms [Easy to understand] | flip-string-to-monotone-increasing | 1 | 1 | # Intuition\nBasically the idea is that once we reach a \'1\' we will start flipping \'0\'s to 1s until the count for zeros is less than ones but as an when the count for zero increases more than that of ones as we are logically supposed to flip the 1s instead of zeroes. \n\nThe way we will be able to acheive this is by considering count of 1 and number of flips(initially with the thought of flipping at 0s) and then we take a minimum of these two values to transition between these two flips min(counter_right, flips). \n\n```\n E.g. - \n s ="00110100" \n\n # string = "0" counter = 0, flips = 1 -> flips = min(0, 1) = 0\n - as bit is not \'0\' counter will be 0 and flips will be reset to zero as we don\'t need to flip anything yet\n\n # string = "00" counter = 0, flips = 1 -> flips = min(0, 1) = 0\n - as 1 is not reached counter will be 0 and flips will be reset to zero as we don\'t need to flip anything yet\n\n # string = "001" counter = 1, flips = 0 -> flips = min(1, 0) = 0\n - as we have a 1 now counter will be changed to 1 and the flip will still be zero as there is not to flip yet\n\n # string = "0011" counter = 2, flips = 0 -> flips = min(2, 0) = 0\n - as we have a 1 now counter will be changed to 2 and the flip will still be zero as there is not to flip yet\n\n # string = "00110" counter = 2, flips = 1 -> flips = min(2, 1) = 1\n - as bit is \'0\' counter will stay at 2 and the flip will changed to 1 with the idea that we need to have all 1s after the first 1 and as the minimum of counter and flips is 1 it will be saved\n\n # string = "001100" counter = 2, flips = 2 -> flips = min(2, 2) = 2\n - as bit is \'0\' counter will stay at 2 and the flip will changed to 2 and as the minimum of counter and flips is 2 it will be saved\n\n # string = "0011001" counter = 3, flips = 2 -> flips = min(3, 2) = 2\n - as now we encountered one more 1 our idea still holds true that we have to flip 0s to 1s so the value for flip will stay as 2 because of min and will be saved\n\n # string = "00110010" counter = 3, flips = 3 -> flips = min(3, 3) = 3\n - now we encountered \'0\' making its count same as the count for \'1\' (which means we will not care about if we are fliping 0 or 1) so we will increase the flips to 3. As min of counter and flips would be 3 which will be saved\n\n # string = "001100100" counter = 3, flips = 4 -> flips = min(3, 4) = 3\n - another \'0\' which makes its count more than that of \'1\' which will reset our idea that we have to flip 1s now. As we have the counter for 1s our min condition will support our idea and set the flips to min(3, 4) = 3\n\n\n This lands us to the conclusion that we had to flip 3 1s to make it binary monotonic and adds up to our solutions \n```\n\n# Approach\n- Take counter for 1s and flips\n- Increase counter for 1s at every \'1\' encountered\n- Increase the flips for every \'0\' encountered\n- reset flips to minimum of flips and counter for 1s(this will help us transition between fliping 0s ar 1s)\n- return flips\n\n> Note: Try to write your own code after this if you get the idea. :-)\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def minFlipsMonoIncr(self, s: str) -> int:\n counter = 0\n flips = 0\n for ch in s:\n if ch == \'1\':\n counter += 1\n else:\n flips += 1\n flips = min(counter, flips)\n return flips\n``` | 2 | A **ramp** in an integer array `nums` is a pair `(i, j)` for which `i < j` and `nums[i] <= nums[j]`. The **width** of such a ramp is `j - i`.
Given an integer array `nums`, return _the maximum width of a **ramp** in_ `nums`. If there is no **ramp** in `nums`, return `0`.
**Example 1:**
**Input:** nums = \[6,0,8,2,1,5\]
**Output:** 4
**Explanation:** The maximum width ramp is achieved at (i, j) = (1, 5): nums\[1\] = 0 and nums\[5\] = 5.
**Example 2:**
**Input:** nums = \[9,8,1,0,1,9,4,0,4,1\]
**Output:** 7
**Explanation:** The maximum width ramp is achieved at (i, j) = (2, 9): nums\[2\] = 1 and nums\[9\] = 1.
**Constraints:**
* `2 <= nums.length <= 5 * 104`
* `0 <= nums[i] <= 5 * 104` | null |
🐍 Python One Line 🏌️♂️ | flip-string-to-monotone-increasing | 0 | 1 | # Code\n```\nfrom itertools import accumulate\nfrom functools import reduce\n\nclass Solution:\n def minFlipsMonoIncr(self, s: str) -> int:\n return reduce(lambda acc, curr: acc if int(curr[0]) else min(curr[1], acc + 1), zip(s, accumulate(map(int, s))), 0)\n``` | 2 | A binary string is monotone increasing if it consists of some number of `0`'s (possibly none), followed by some number of `1`'s (also possibly none).
You are given a binary string `s`. You can flip `s[i]` changing it from `0` to `1` or from `1` to `0`.
Return _the minimum number of flips to make_ `s` _monotone increasing_.
**Example 1:**
**Input:** s = "00110 "
**Output:** 1
**Explanation:** We flip the last digit to get 00111.
**Example 2:**
**Input:** s = "010110 "
**Output:** 2
**Explanation:** We flip to get 011111, or alternatively 000111.
**Example 3:**
**Input:** s = "00011000 "
**Output:** 2
**Explanation:** We flip to get 00000000.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | null |
🐍 Python One Line 🏌️♂️ | flip-string-to-monotone-increasing | 0 | 1 | # Code\n```\nfrom itertools import accumulate\nfrom functools import reduce\n\nclass Solution:\n def minFlipsMonoIncr(self, s: str) -> int:\n return reduce(lambda acc, curr: acc if int(curr[0]) else min(curr[1], acc + 1), zip(s, accumulate(map(int, s))), 0)\n``` | 2 | A **ramp** in an integer array `nums` is a pair `(i, j)` for which `i < j` and `nums[i] <= nums[j]`. The **width** of such a ramp is `j - i`.
Given an integer array `nums`, return _the maximum width of a **ramp** in_ `nums`. If there is no **ramp** in `nums`, return `0`.
**Example 1:**
**Input:** nums = \[6,0,8,2,1,5\]
**Output:** 4
**Explanation:** The maximum width ramp is achieved at (i, j) = (1, 5): nums\[1\] = 0 and nums\[5\] = 5.
**Example 2:**
**Input:** nums = \[9,8,1,0,1,9,4,0,4,1\]
**Output:** 7
**Explanation:** The maximum width ramp is achieved at (i, j) = (2, 9): nums\[2\] = 1 and nums\[9\] = 1.
**Constraints:**
* `2 <= nums.length <= 5 * 104`
* `0 <= nums[i] <= 5 * 104` | null |
Clean Codes🔥|| Dynamic Programming ✅|| C++|| Java || Python3 | flip-string-to-monotone-increasing | 1 | 1 | # Request \uD83D\uDE0A :\n- If you find this solution easy to understand and helpful, then Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n# Code [C++| Java| Python3] :\n```C++ []\nclass Solution {\n public:\n int minFlipsMonoIncr(string S) {\n vector<int> dp(2);\n\n for (int i = 0; i < S.length(); ++i) {\n int temp = dp[0] + (S[i] == \'1\');\n dp[1] = min(dp[0], dp[1]) + (S[i] == \'0\');\n dp[0] = temp;\n }\n\n return min(dp[0], dp[1]);\n }\n};\n```\n```Java []\nclass Solution {\n public int minFlipsMonoIncr(String S) {\n int[] dp = new int[2];\n\n for (int i = 0; i < S.length(); ++i) {\n int temp = dp[0] + (S.charAt(i) == \'1\' ? 1 : 0);\n dp[1] = Math.min(dp[0], dp[1]) + (S.charAt(i) == \'0\' ? 1 : 0);\n dp[0] = temp;\n }\n\n return Math.min(dp[0], dp[1]);\n }\n}\n```\n```Python3 []\nclass Solution:\n def minFlipsMonoIncr(self, S: str) -> int:\n dp = [0] * 2\n\n for i, c in enumerate(S):\n dp[0], dp[1] = dp[0] + (c == \'1\'), min(dp[0], dp[1]) + (c == \'0\')\n\n return min(dp[0], dp[1])\n```\n | 10 | A binary string is monotone increasing if it consists of some number of `0`'s (possibly none), followed by some number of `1`'s (also possibly none).
You are given a binary string `s`. You can flip `s[i]` changing it from `0` to `1` or from `1` to `0`.
Return _the minimum number of flips to make_ `s` _monotone increasing_.
**Example 1:**
**Input:** s = "00110 "
**Output:** 1
**Explanation:** We flip the last digit to get 00111.
**Example 2:**
**Input:** s = "010110 "
**Output:** 2
**Explanation:** We flip to get 011111, or alternatively 000111.
**Example 3:**
**Input:** s = "00011000 "
**Output:** 2
**Explanation:** We flip to get 00000000.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.