title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Clean Codes🔥|| Dynamic Programming ✅|| C++|| Java || Python3 | flip-string-to-monotone-increasing | 1 | 1 | # Request \uD83D\uDE0A :\n- If you find this solution easy to understand and helpful, then Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n# Code [C++| Java| Python3] :\n```C++ []\nclass Solution {\n public:\n int minFlipsMonoIncr(string S) {\n vector<int> dp(2);\n\n for (int i = 0; i < S.length(); ++i) {\n int temp = dp[0] + (S[i] == \'1\');\n dp[1] = min(dp[0], dp[1]) + (S[i] == \'0\');\n dp[0] = temp;\n }\n\n return min(dp[0], dp[1]);\n }\n};\n```\n```Java []\nclass Solution {\n public int minFlipsMonoIncr(String S) {\n int[] dp = new int[2];\n\n for (int i = 0; i < S.length(); ++i) {\n int temp = dp[0] + (S.charAt(i) == \'1\' ? 1 : 0);\n dp[1] = Math.min(dp[0], dp[1]) + (S.charAt(i) == \'0\' ? 1 : 0);\n dp[0] = temp;\n }\n\n return Math.min(dp[0], dp[1]);\n }\n}\n```\n```Python3 []\nclass Solution:\n def minFlipsMonoIncr(self, S: str) -> int:\n dp = [0] * 2\n\n for i, c in enumerate(S):\n dp[0], dp[1] = dp[0] + (c == \'1\'), min(dp[0], dp[1]) + (c == \'0\')\n\n return min(dp[0], dp[1])\n```\n | 10 | A **ramp** in an integer array `nums` is a pair `(i, j)` for which `i < j` and `nums[i] <= nums[j]`. The **width** of such a ramp is `j - i`.
Given an integer array `nums`, return _the maximum width of a **ramp** in_ `nums`. If there is no **ramp** in `nums`, return `0`.
**Example 1:**
**Input:** nums = \[6,0,8,2,1,5\]
**Output:** 4
**Explanation:** The maximum width ramp is achieved at (i, j) = (1, 5): nums\[1\] = 0 and nums\[5\] = 5.
**Example 2:**
**Input:** nums = \[9,8,1,0,1,9,4,0,4,1\]
**Output:** 7
**Explanation:** The maximum width ramp is achieved at (i, j) = (2, 9): nums\[2\] = 1 and nums\[9\] = 1.
**Constraints:**
* `2 <= nums.length <= 5 * 104`
* `0 <= nums[i] <= 5 * 104` | null |
Solution | flip-string-to-monotone-increasing | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minFlipsMonoIncr(string s) {\n int ans = 0, ones = 0;\n for (char c : s) {\n if (c == \'0\')\n ans = min(ones, ans + 1);\n else\n ones++;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nfrom collections import Counter\n\nclass Solution:\n def minFlipsMonoIncrDP(self, s: str) -> int:\n res = 0\n ones = 0\n for c in s:\n if c == \'1\':\n ones += 1\n else:\n res = min(ones, 1 + res)\n return res\n\n def minFlipsMonoIncr(self, s: str) -> int:\n m = s.count(\'0\')\n if m == len(s) or m == 0:\n return 0\n\n ans = m\n for c in s:\n if c==\'0\':\n m -= 1\n if m<ans:\n ans = m\n else:\n m += 1\n\n return ans\n```\n\n```Java []\nclass Solution {\n public int minFlipsMonoIncr(String s) {\n int f1=0;\n int f2=0;\n for(char ch:s.toCharArray()){\n f1+=ch-\'0\';\n f2=Math.min(f1,f2+(1-(ch-\'0\')));\n }\n return f2;\n }\n}\n```\n | 1 | A binary string is monotone increasing if it consists of some number of `0`'s (possibly none), followed by some number of `1`'s (also possibly none).
You are given a binary string `s`. You can flip `s[i]` changing it from `0` to `1` or from `1` to `0`.
Return _the minimum number of flips to make_ `s` _monotone increasing_.
**Example 1:**
**Input:** s = "00110 "
**Output:** 1
**Explanation:** We flip the last digit to get 00111.
**Example 2:**
**Input:** s = "010110 "
**Output:** 2
**Explanation:** We flip to get 011111, or alternatively 000111.
**Example 3:**
**Input:** s = "00011000 "
**Output:** 2
**Explanation:** We flip to get 00000000.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | null |
Solution | flip-string-to-monotone-increasing | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minFlipsMonoIncr(string s) {\n int ans = 0, ones = 0;\n for (char c : s) {\n if (c == \'0\')\n ans = min(ones, ans + 1);\n else\n ones++;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nfrom collections import Counter\n\nclass Solution:\n def minFlipsMonoIncrDP(self, s: str) -> int:\n res = 0\n ones = 0\n for c in s:\n if c == \'1\':\n ones += 1\n else:\n res = min(ones, 1 + res)\n return res\n\n def minFlipsMonoIncr(self, s: str) -> int:\n m = s.count(\'0\')\n if m == len(s) or m == 0:\n return 0\n\n ans = m\n for c in s:\n if c==\'0\':\n m -= 1\n if m<ans:\n ans = m\n else:\n m += 1\n\n return ans\n```\n\n```Java []\nclass Solution {\n public int minFlipsMonoIncr(String s) {\n int f1=0;\n int f2=0;\n for(char ch:s.toCharArray()){\n f1+=ch-\'0\';\n f2=Math.min(f1,f2+(1-(ch-\'0\')));\n }\n return f2;\n }\n}\n```\n | 1 | A **ramp** in an integer array `nums` is a pair `(i, j)` for which `i < j` and `nums[i] <= nums[j]`. The **width** of such a ramp is `j - i`.
Given an integer array `nums`, return _the maximum width of a **ramp** in_ `nums`. If there is no **ramp** in `nums`, return `0`.
**Example 1:**
**Input:** nums = \[6,0,8,2,1,5\]
**Output:** 4
**Explanation:** The maximum width ramp is achieved at (i, j) = (1, 5): nums\[1\] = 0 and nums\[5\] = 5.
**Example 2:**
**Input:** nums = \[9,8,1,0,1,9,4,0,4,1\]
**Output:** 7
**Explanation:** The maximum width ramp is achieved at (i, j) = (2, 9): nums\[2\] = 1 and nums\[9\] = 1.
**Constraints:**
* `2 <= nums.length <= 5 * 104`
* `0 <= nums[i] <= 5 * 104` | null |
Full Solution Recursion --> Memoization --> Tabulation -->SpaceOptimization | flip-string-to-monotone-increasing | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def memo(self,s,ind,prev,dp):\n if ind>=len(s):\n return 0\n \n if dp[ind][prev]!=-1:\n return dp[ind][prev]\n flip=1000000\n notflip = 10000000\n ans=10000000\n if (s[ind]==\'0\'):\n if (prev==0):\n notflip= 0 + self.memo(s,ind+1,0,dp)\n flip= 1 + self.memo(s,ind+1,1,dp)\n else:\n flip= 1 + self.memo(s,ind+1,1,dp)\n #s[ind]==1\n if (s[ind]==\'1\'):\n if (prev==0):\n notflip= 0 + self.memo(s,ind+1,1,dp)\n flip= 1 + self.memo(s,ind+1,0,dp)\n else:\n notflip= 0 + self.memo(s,ind+1,1,dp)\n dp[ind][prev]= min(flip,notflip)\n \n return dp[ind][prev]\n \n def tabulation(self,s,n,prev):\n dp=[[0 for i in range(3)] for j in range (len(s)+2)]\n for ind in range (len(s)-1,-1,-1):\n for prev in range (0,2):\n flip=1000000\n notflip = 10000000\n ans=10000000\n if (s[ind]==\'0\'):\n if (prev==0):\n notflip= 0 + dp[ind+1][0]\n flip= 1 + dp[ind+1][1]\n else:\n flip= 1 + dp[ind+1][1]\n #s[ind]==1\n if (s[ind]==\'1\'):\n if (prev==0):\n notflip= 0 + dp[ind+1][1]\n flip= 1 + dp[ind+1][0]\n else:\n notflip= 0 + dp[ind+1][1]\n dp[ind][prev]= min(flip,notflip) \n return dp[0][0]\n \n def spaceOptimization(self,s,ind):\n curr=[0 for i in range (2+1)]\n ahead=[0 for j in range (2+1)]\n dp=[[0 for i in range(3)] for j in range (len(s)+2)]\n for ind in range (len(s)-1,-1,-1):\n for prev in range (0,2):\n flip=1000000\n notflip = 10000000\n ans=10000000\n if (s[ind]==\'0\'):\n if (prev==0):\n notflip= 0 + ahead[0]\n flip= 1 + ahead[1]\n else:\n flip= 1 + ahead[1]\n #s[ind]==1\n if (s[ind]==\'1\'):\n if (prev==0):\n notflip= 0 + ahead[1]\n flip= 1 + ahead[0]\n else:\n notflip= 0 + ahead[1]\n curr[prev]= min(flip,notflip) \n ahead=curr\n\n return ahead[0]\n \n def minFlipsMonoIncr(self, s: str) -> int:\n dp=[[-1 for i in range(2+1)] for j in range (len(s)+1)]\n return self.memo(s,0,0,dp)\n # return self.tabulation(s,len(s),0)\n # return self.spaceOptimization(s,len(s))\n\n\n\n\n``` | 1 | A binary string is monotone increasing if it consists of some number of `0`'s (possibly none), followed by some number of `1`'s (also possibly none).
You are given a binary string `s`. You can flip `s[i]` changing it from `0` to `1` or from `1` to `0`.
Return _the minimum number of flips to make_ `s` _monotone increasing_.
**Example 1:**
**Input:** s = "00110 "
**Output:** 1
**Explanation:** We flip the last digit to get 00111.
**Example 2:**
**Input:** s = "010110 "
**Output:** 2
**Explanation:** We flip to get 011111, or alternatively 000111.
**Example 3:**
**Input:** s = "00011000 "
**Output:** 2
**Explanation:** We flip to get 00000000.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | null |
Full Solution Recursion --> Memoization --> Tabulation -->SpaceOptimization | flip-string-to-monotone-increasing | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def memo(self,s,ind,prev,dp):\n if ind>=len(s):\n return 0\n \n if dp[ind][prev]!=-1:\n return dp[ind][prev]\n flip=1000000\n notflip = 10000000\n ans=10000000\n if (s[ind]==\'0\'):\n if (prev==0):\n notflip= 0 + self.memo(s,ind+1,0,dp)\n flip= 1 + self.memo(s,ind+1,1,dp)\n else:\n flip= 1 + self.memo(s,ind+1,1,dp)\n #s[ind]==1\n if (s[ind]==\'1\'):\n if (prev==0):\n notflip= 0 + self.memo(s,ind+1,1,dp)\n flip= 1 + self.memo(s,ind+1,0,dp)\n else:\n notflip= 0 + self.memo(s,ind+1,1,dp)\n dp[ind][prev]= min(flip,notflip)\n \n return dp[ind][prev]\n \n def tabulation(self,s,n,prev):\n dp=[[0 for i in range(3)] for j in range (len(s)+2)]\n for ind in range (len(s)-1,-1,-1):\n for prev in range (0,2):\n flip=1000000\n notflip = 10000000\n ans=10000000\n if (s[ind]==\'0\'):\n if (prev==0):\n notflip= 0 + dp[ind+1][0]\n flip= 1 + dp[ind+1][1]\n else:\n flip= 1 + dp[ind+1][1]\n #s[ind]==1\n if (s[ind]==\'1\'):\n if (prev==0):\n notflip= 0 + dp[ind+1][1]\n flip= 1 + dp[ind+1][0]\n else:\n notflip= 0 + dp[ind+1][1]\n dp[ind][prev]= min(flip,notflip) \n return dp[0][0]\n \n def spaceOptimization(self,s,ind):\n curr=[0 for i in range (2+1)]\n ahead=[0 for j in range (2+1)]\n dp=[[0 for i in range(3)] for j in range (len(s)+2)]\n for ind in range (len(s)-1,-1,-1):\n for prev in range (0,2):\n flip=1000000\n notflip = 10000000\n ans=10000000\n if (s[ind]==\'0\'):\n if (prev==0):\n notflip= 0 + ahead[0]\n flip= 1 + ahead[1]\n else:\n flip= 1 + ahead[1]\n #s[ind]==1\n if (s[ind]==\'1\'):\n if (prev==0):\n notflip= 0 + ahead[1]\n flip= 1 + ahead[0]\n else:\n notflip= 0 + ahead[1]\n curr[prev]= min(flip,notflip) \n ahead=curr\n\n return ahead[0]\n \n def minFlipsMonoIncr(self, s: str) -> int:\n dp=[[-1 for i in range(2+1)] for j in range (len(s)+1)]\n return self.memo(s,0,0,dp)\n # return self.tabulation(s,len(s),0)\n # return self.spaceOptimization(s,len(s))\n\n\n\n\n``` | 1 | A **ramp** in an integer array `nums` is a pair `(i, j)` for which `i < j` and `nums[i] <= nums[j]`. The **width** of such a ramp is `j - i`.
Given an integer array `nums`, return _the maximum width of a **ramp** in_ `nums`. If there is no **ramp** in `nums`, return `0`.
**Example 1:**
**Input:** nums = \[6,0,8,2,1,5\]
**Output:** 4
**Explanation:** The maximum width ramp is achieved at (i, j) = (1, 5): nums\[1\] = 0 and nums\[5\] = 5.
**Example 2:**
**Input:** nums = \[9,8,1,0,1,9,4,0,4,1\]
**Output:** 7
**Explanation:** The maximum width ramp is achieved at (i, j) = (2, 9): nums\[2\] = 1 and nums\[9\] = 1.
**Constraints:**
* `2 <= nums.length <= 5 * 104`
* `0 <= nums[i] <= 5 * 104` | null |
Flip String to Monotone Increasing | flip-string-to-monotone-increasing | 0 | 1 | # Intuition\nFlip string to monotonic increasing that all 0\'s and all 1\'s comes together \n# Approach\nfirst we iterate through the string and check the 1\'s present in string if we come across any 1\'s then we increase the countOne otherwise we take min of (ans+1,countOne) ans return the answer\n# Complexity\n- Time complexity:\nTime complexity will be O(N) \n- Space complexity:\nSpace complexity will be O(1)\n# Code\n```\nclass Solution:\n def minFlipsMonoIncr(self, s: str) -> int:\n ans = 0\n countOne = 0\n for char in s:\n if char == \'1\':\n countOne += 1\n else:\n ans = min(ans + 1, countOne)\n return ans\n``` | 1 | A binary string is monotone increasing if it consists of some number of `0`'s (possibly none), followed by some number of `1`'s (also possibly none).
You are given a binary string `s`. You can flip `s[i]` changing it from `0` to `1` or from `1` to `0`.
Return _the minimum number of flips to make_ `s` _monotone increasing_.
**Example 1:**
**Input:** s = "00110 "
**Output:** 1
**Explanation:** We flip the last digit to get 00111.
**Example 2:**
**Input:** s = "010110 "
**Output:** 2
**Explanation:** We flip to get 011111, or alternatively 000111.
**Example 3:**
**Input:** s = "00011000 "
**Output:** 2
**Explanation:** We flip to get 00000000.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | null |
Flip String to Monotone Increasing | flip-string-to-monotone-increasing | 0 | 1 | # Intuition\nFlip string to monotonic increasing that all 0\'s and all 1\'s comes together \n# Approach\nfirst we iterate through the string and check the 1\'s present in string if we come across any 1\'s then we increase the countOne otherwise we take min of (ans+1,countOne) ans return the answer\n# Complexity\n- Time complexity:\nTime complexity will be O(N) \n- Space complexity:\nSpace complexity will be O(1)\n# Code\n```\nclass Solution:\n def minFlipsMonoIncr(self, s: str) -> int:\n ans = 0\n countOne = 0\n for char in s:\n if char == \'1\':\n countOne += 1\n else:\n ans = min(ans + 1, countOne)\n return ans\n``` | 1 | A **ramp** in an integer array `nums` is a pair `(i, j)` for which `i < j` and `nums[i] <= nums[j]`. The **width** of such a ramp is `j - i`.
Given an integer array `nums`, return _the maximum width of a **ramp** in_ `nums`. If there is no **ramp** in `nums`, return `0`.
**Example 1:**
**Input:** nums = \[6,0,8,2,1,5\]
**Output:** 4
**Explanation:** The maximum width ramp is achieved at (i, j) = (1, 5): nums\[1\] = 0 and nums\[5\] = 5.
**Example 2:**
**Input:** nums = \[9,8,1,0,1,9,4,0,4,1\]
**Output:** 7
**Explanation:** The maximum width ramp is achieved at (i, j) = (2, 9): nums\[2\] = 1 and nums\[9\] = 1.
**Constraints:**
* `2 <= nums.length <= 5 * 104`
* `0 <= nums[i] <= 5 * 104` | null |
Solution | three-equal-parts | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n \n int countone=count(arr.begin(),arr.end(),1);\n int n=arr.size();\n if(countone%3)\n {\n return {-1,-1};\n }\n if(countone==0)\n {\n return {0,n-1};\n }\n int total=countone/3;\n int p1=0,p2=0,p3=0;\n int count=0;\n \n for(int i=0;i<n;i++)\n {\n if(arr[i]==1)\n {\n if(count==0)\n {\n p1=i;\n }\n else if(count==total)\n {\n p2=i;\n }\n else if(count==2*total)\n {\n p3=i;\n }\n count+=1;\n }\n }\n while(p3<n-1)\n {\n p1+=1;\n p2+=1;\n p3+=1;\n if(arr[p1]!=arr[p2] || arr[p2]!=arr[p3] || arr[p1]!=arr[p3])\n {\n return {-1,-1};\n }\n }\n return {p1,p2+1};\n } \n};\n```\n\n```Python3 []\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n \n ones = [i for i, j in enumerate(arr) if j==1]\n n=len(ones)\n\n if not ones:\n return [0, 2]\n if n%3:\n return [-1, -1]\n \n i,j,k = ones[0], ones[n//3], ones[n//3*2]\n l = len(arr)-k\n\n if arr[i:i+l]==arr[j:j+l]==arr[k:k+l]:\n return [i+l-1, j+l]\n\n return [-1, -1]\n```\n\n```Java []\nclass Solution {\n public int[] threeEqualParts(int[] arr) {\n int oneSum = 0;\n for(int x : arr) oneSum +=x;\n if(oneSum % 3 !=0)return new int[]{-1,-1};\n if(oneSum == 0)return new int[]{0,2};\n int oneCount = oneSum / 3;\n int i = 0;\n int firstOne = -1;\n int n= arr.length;\n int lastZeroCount = 0;\n i = n-1;\n while(arr[i] ==0){\n lastZeroCount++;\n i--;\n }\n i=0;\n while(oneCount > 0){\n if(arr[i] == 1 && firstOne == -1)firstOne = i;\n oneCount-=arr[i++];\n }\n while(lastZeroCount > 0){\n if(arr[i++] == 1)return new int[]{-1,-1};\n lastZeroCount--;\n }\n int k = i--;\n int t = firstOne;\n while(arr[k] == 0)k++;\n while(firstOne <=i){\n if(arr[firstOne++] != arr[k++])return new int[]{-1,-1};\n }\n int j = k;\n while(arr[k] == 0)k++;\n firstOne = t;\n while(firstOne <=i){\n if(arr[firstOne++] != arr[k++])return new int[]{-1,-1};\n }\n return new int[]{i,j};\n }\n}\n```\n | 1 | You are given an array `arr` which consists of only zeros and ones, divide the array into **three non-empty parts** such that all of these parts represent the same binary value.
If it is possible, return any `[i, j]` with `i + 1 < j`, such that:
* `arr[0], arr[1], ..., arr[i]` is the first part,
* `arr[i + 1], arr[i + 2], ..., arr[j - 1]` is the second part, and
* `arr[j], arr[j + 1], ..., arr[arr.length - 1]` is the third part.
* All three parts have equal binary values.
If it is not possible, return `[-1, -1]`.
Note that the entire part is used when considering what binary value it represents. For example, `[1,1,0]` represents `6` in decimal, not `3`. Also, leading zeros **are allowed**, so `[0,1,1]` and `[1,1]` represent the same value.
**Example 1:**
**Input:** arr = \[1,0,1,0,1\]
**Output:** \[0,3\]
**Example 2:**
**Input:** arr = \[1,1,0,1,1\]
**Output:** \[-1,-1\]
**Example 3:**
**Input:** arr = \[1,1,0,0,1\]
**Output:** \[0,2\]
**Constraints:**
* `3 <= arr.length <= 3 * 104`
* `arr[i]` is `0` or `1` | null |
Solution | three-equal-parts | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n \n int countone=count(arr.begin(),arr.end(),1);\n int n=arr.size();\n if(countone%3)\n {\n return {-1,-1};\n }\n if(countone==0)\n {\n return {0,n-1};\n }\n int total=countone/3;\n int p1=0,p2=0,p3=0;\n int count=0;\n \n for(int i=0;i<n;i++)\n {\n if(arr[i]==1)\n {\n if(count==0)\n {\n p1=i;\n }\n else if(count==total)\n {\n p2=i;\n }\n else if(count==2*total)\n {\n p3=i;\n }\n count+=1;\n }\n }\n while(p3<n-1)\n {\n p1+=1;\n p2+=1;\n p3+=1;\n if(arr[p1]!=arr[p2] || arr[p2]!=arr[p3] || arr[p1]!=arr[p3])\n {\n return {-1,-1};\n }\n }\n return {p1,p2+1};\n } \n};\n```\n\n```Python3 []\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n \n ones = [i for i, j in enumerate(arr) if j==1]\n n=len(ones)\n\n if not ones:\n return [0, 2]\n if n%3:\n return [-1, -1]\n \n i,j,k = ones[0], ones[n//3], ones[n//3*2]\n l = len(arr)-k\n\n if arr[i:i+l]==arr[j:j+l]==arr[k:k+l]:\n return [i+l-1, j+l]\n\n return [-1, -1]\n```\n\n```Java []\nclass Solution {\n public int[] threeEqualParts(int[] arr) {\n int oneSum = 0;\n for(int x : arr) oneSum +=x;\n if(oneSum % 3 !=0)return new int[]{-1,-1};\n if(oneSum == 0)return new int[]{0,2};\n int oneCount = oneSum / 3;\n int i = 0;\n int firstOne = -1;\n int n= arr.length;\n int lastZeroCount = 0;\n i = n-1;\n while(arr[i] ==0){\n lastZeroCount++;\n i--;\n }\n i=0;\n while(oneCount > 0){\n if(arr[i] == 1 && firstOne == -1)firstOne = i;\n oneCount-=arr[i++];\n }\n while(lastZeroCount > 0){\n if(arr[i++] == 1)return new int[]{-1,-1};\n lastZeroCount--;\n }\n int k = i--;\n int t = firstOne;\n while(arr[k] == 0)k++;\n while(firstOne <=i){\n if(arr[firstOne++] != arr[k++])return new int[]{-1,-1};\n }\n int j = k;\n while(arr[k] == 0)k++;\n firstOne = t;\n while(firstOne <=i){\n if(arr[firstOne++] != arr[k++])return new int[]{-1,-1};\n }\n return new int[]{i,j};\n }\n}\n```\n | 1 | You are given an array of points in the **X-Y** plane `points` where `points[i] = [xi, yi]`.
Return _the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes_. If there is not any such rectangle, return `0`.
Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[1,2\],\[2,1\],\[1,0\],\[0,1\]\]
**Output:** 2.00000
**Explanation:** The minimum area rectangle occurs at \[1,2\],\[2,1\],\[1,0\],\[0,1\], with an area of 2.
**Example 2:**
**Input:** points = \[\[0,1\],\[2,1\],\[1,1\],\[1,0\],\[2,0\]\]
**Output:** 1.00000
**Explanation:** The minimum area rectangle occurs at \[1,0\],\[1,1\],\[2,1\],\[2,0\], with an area of 1.
**Example 3:**
**Input:** points = \[\[0,3\],\[1,2\],\[3,1\],\[1,3\],\[2,1\]\]
**Output:** 0
**Explanation:** There is no possible rectangle to form from these points.
**Constraints:**
* `1 <= points.length <= 50`
* `points[i].length == 2`
* `0 <= xi, yi <= 4 * 104`
* All the given points are **unique**. | null |
Simple Python Solution with explanation 🔥 | three-equal-parts | 0 | 1 | # Approach\n\n> *divide the array into three non-empty parts such that all of these parts represent the same binary value*\n\nSame binary value means \n\n* each part has to have **<ins>equal number of ones<ins>** and zeroes\n* order of ones and zeroes should be same\n\n\n### Part 1: Equal number of ones and ending zeroes\n\n\nLets take below array as an example for understanding:\n\n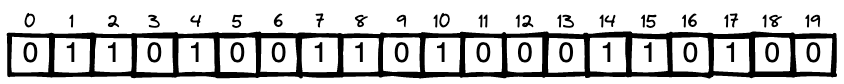\n\n\n* These binary values will have equal number of ones, which means the total count of ones should be a multiple of 3\n\n\n 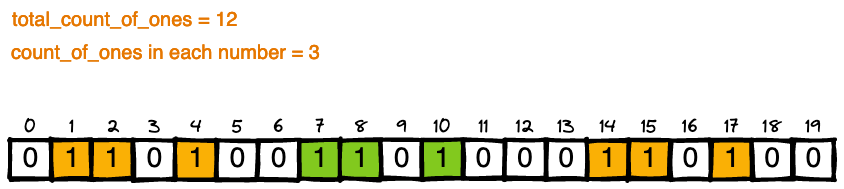\n\n\n\n* We know in a binary number, starting zeroes doesnt matter, however ending zeroes does matter. So I can find the `ending_zeroes` for my binary number using the location of last one:\n\n \n\n\n* We need to add these ending_zeroes count after every `total_count_of_ones // 3` ie in the example after every 3 count of ones\n\n 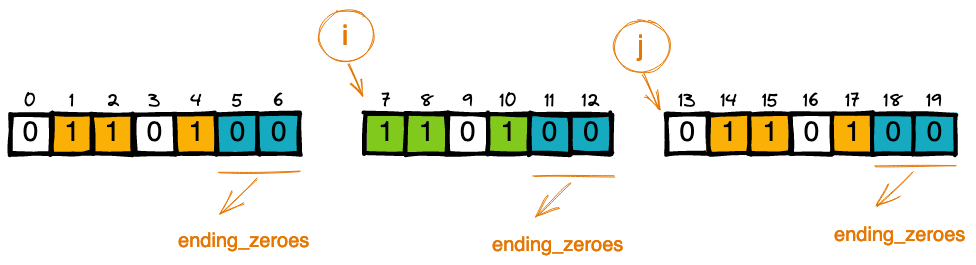\n\n* Now, we know the location of `i` and `j`\n\n\n\nNOTE:\n \n* All above steps can be done by traversing through the loop, \n\n however in my code below I have used prefix sum and binary search --> using modified binary_search to fetch index of the first occurrence in the prefix_sum \n\n for example: \n ```\n ending_zeroes = n - 1 - (index of first occurrence of total_count_of_ones in prefix_sum, ie 9 in this example)\n ```\n \n\n 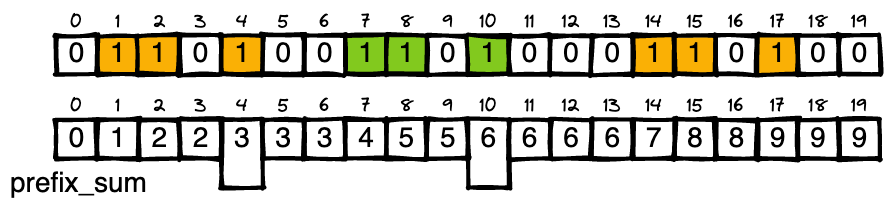\n\n\n Creation of prefix sum takes `O(n)` time, so no major optimisation with this, this just looked clean to me :)\n\n\n\n### Part 2: Order of ones and zeroes\n\nThis is simple, for each identified part\n\n* disregard starting zeroes\n* then, check if order of each ones and zeroes is same\n\n\n\n\n\n\n# Complexity\n- Time complexity:\n$$O(n + log(n))$$ = $$O(n)$$\n\n- Space complexity:\n$$O(n)$$ - for prefix_sum\n\n# Code\n\n```python []\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n n = len(arr)\n\n # part 1\n\n # get total_count and create prefix_sum\n total_count = 0\n prefix_sum = [0] * n\n for i in range(n):\n total_count += arr[i]\n prefix_sum[i] = total_count\n\n # checking if multiple of 3\n if total_count % 3 != 0:\n return [-1, -1]\n elif total_count == 0:\n return [0, n - 1]\n\n # binary search to get first occurrence of `val` using prefix_sum\n def bin_search(val):\n start = 0\n end = n - 1\n mid = 0\n\n while start <= end:\n mid = (start + end) // 2\n if prefix_sum[mid] >= val:\n if start == end:\n return mid\n end = mid\n else:\n start = mid + 1\n\n return mid\n\n \n # count of ones in each part and count of ending_zeroes\n part_count = total_count // 3\n ending_zeroes = n - 1 - bin_search(total_count)\n\n # value of i and j using binary_search and ending_zeroes\n i = bin_search(part_count) + ending_zeroes + 1\n j = bin_search(total_count - part_count) + ending_zeroes + 1\n\n\n\n # part 2\n\n # disregard starting zeroes in first part\n a = 0\n while a < n and arr[a] == 0:\n a += 1\n\n # disregard starting zeroes in second part\n b = i\n while b < n and arr[b] == 0:\n b += 1\n\n # disregard starting zeroes in third part\n c = j\n while c < n and arr[c] == 0:\n c += 1\n\n # check if indices have same order of ones and zeroes\n while c < n:\n if arr[a] == arr[b] and arr[b] == arr[c]:\n a += 1\n b += 1\n c += 1\n else:\n return [-1, -1]\n\n if a == i and b == j:\n return [i - 1, j]\n else:\n return [-1, -1]\n\n```\n | 1 | You are given an array `arr` which consists of only zeros and ones, divide the array into **three non-empty parts** such that all of these parts represent the same binary value.
If it is possible, return any `[i, j]` with `i + 1 < j`, such that:
* `arr[0], arr[1], ..., arr[i]` is the first part,
* `arr[i + 1], arr[i + 2], ..., arr[j - 1]` is the second part, and
* `arr[j], arr[j + 1], ..., arr[arr.length - 1]` is the third part.
* All three parts have equal binary values.
If it is not possible, return `[-1, -1]`.
Note that the entire part is used when considering what binary value it represents. For example, `[1,1,0]` represents `6` in decimal, not `3`. Also, leading zeros **are allowed**, so `[0,1,1]` and `[1,1]` represent the same value.
**Example 1:**
**Input:** arr = \[1,0,1,0,1\]
**Output:** \[0,3\]
**Example 2:**
**Input:** arr = \[1,1,0,1,1\]
**Output:** \[-1,-1\]
**Example 3:**
**Input:** arr = \[1,1,0,0,1\]
**Output:** \[0,2\]
**Constraints:**
* `3 <= arr.length <= 3 * 104`
* `arr[i]` is `0` or `1` | null |
Simple Python Solution with explanation 🔥 | three-equal-parts | 0 | 1 | # Approach\n\n> *divide the array into three non-empty parts such that all of these parts represent the same binary value*\n\nSame binary value means \n\n* each part has to have **<ins>equal number of ones<ins>** and zeroes\n* order of ones and zeroes should be same\n\n\n### Part 1: Equal number of ones and ending zeroes\n\n\nLets take below array as an example for understanding:\n\n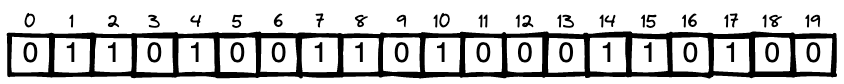\n\n\n* These binary values will have equal number of ones, which means the total count of ones should be a multiple of 3\n\n\n 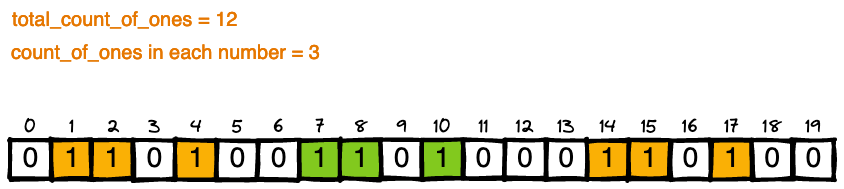\n\n\n\n* We know in a binary number, starting zeroes doesnt matter, however ending zeroes does matter. So I can find the `ending_zeroes` for my binary number using the location of last one:\n\n \n\n\n* We need to add these ending_zeroes count after every `total_count_of_ones // 3` ie in the example after every 3 count of ones\n\n 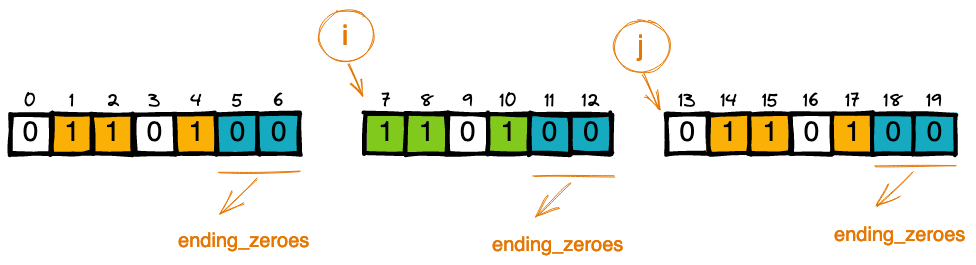\n\n* Now, we know the location of `i` and `j`\n\n\n\nNOTE:\n \n* All above steps can be done by traversing through the loop, \n\n however in my code below I have used prefix sum and binary search --> using modified binary_search to fetch index of the first occurrence in the prefix_sum \n\n for example: \n ```\n ending_zeroes = n - 1 - (index of first occurrence of total_count_of_ones in prefix_sum, ie 9 in this example)\n ```\n \n\n 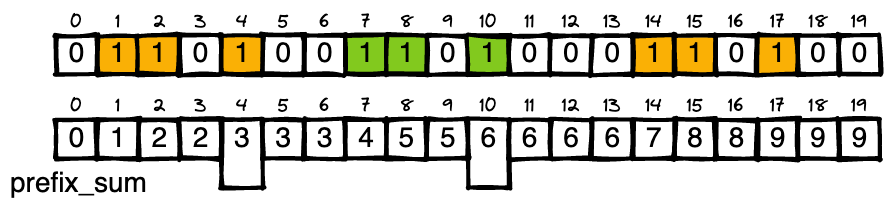\n\n\n Creation of prefix sum takes `O(n)` time, so no major optimisation with this, this just looked clean to me :)\n\n\n\n### Part 2: Order of ones and zeroes\n\nThis is simple, for each identified part\n\n* disregard starting zeroes\n* then, check if order of each ones and zeroes is same\n\n\n\n\n\n\n# Complexity\n- Time complexity:\n$$O(n + log(n))$$ = $$O(n)$$\n\n- Space complexity:\n$$O(n)$$ - for prefix_sum\n\n# Code\n\n```python []\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n n = len(arr)\n\n # part 1\n\n # get total_count and create prefix_sum\n total_count = 0\n prefix_sum = [0] * n\n for i in range(n):\n total_count += arr[i]\n prefix_sum[i] = total_count\n\n # checking if multiple of 3\n if total_count % 3 != 0:\n return [-1, -1]\n elif total_count == 0:\n return [0, n - 1]\n\n # binary search to get first occurrence of `val` using prefix_sum\n def bin_search(val):\n start = 0\n end = n - 1\n mid = 0\n\n while start <= end:\n mid = (start + end) // 2\n if prefix_sum[mid] >= val:\n if start == end:\n return mid\n end = mid\n else:\n start = mid + 1\n\n return mid\n\n \n # count of ones in each part and count of ending_zeroes\n part_count = total_count // 3\n ending_zeroes = n - 1 - bin_search(total_count)\n\n # value of i and j using binary_search and ending_zeroes\n i = bin_search(part_count) + ending_zeroes + 1\n j = bin_search(total_count - part_count) + ending_zeroes + 1\n\n\n\n # part 2\n\n # disregard starting zeroes in first part\n a = 0\n while a < n and arr[a] == 0:\n a += 1\n\n # disregard starting zeroes in second part\n b = i\n while b < n and arr[b] == 0:\n b += 1\n\n # disregard starting zeroes in third part\n c = j\n while c < n and arr[c] == 0:\n c += 1\n\n # check if indices have same order of ones and zeroes\n while c < n:\n if arr[a] == arr[b] and arr[b] == arr[c]:\n a += 1\n b += 1\n c += 1\n else:\n return [-1, -1]\n\n if a == i and b == j:\n return [i - 1, j]\n else:\n return [-1, -1]\n\n```\n | 1 | You are given an array of points in the **X-Y** plane `points` where `points[i] = [xi, yi]`.
Return _the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes_. If there is not any such rectangle, return `0`.
Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[1,2\],\[2,1\],\[1,0\],\[0,1\]\]
**Output:** 2.00000
**Explanation:** The minimum area rectangle occurs at \[1,2\],\[2,1\],\[1,0\],\[0,1\], with an area of 2.
**Example 2:**
**Input:** points = \[\[0,1\],\[2,1\],\[1,1\],\[1,0\],\[2,0\]\]
**Output:** 1.00000
**Explanation:** The minimum area rectangle occurs at \[1,0\],\[1,1\],\[2,1\],\[2,0\], with an area of 1.
**Example 3:**
**Input:** points = \[\[0,3\],\[1,2\],\[3,1\],\[1,3\],\[2,1\]\]
**Output:** 0
**Explanation:** There is no possible rectangle to form from these points.
**Constraints:**
* `1 <= points.length <= 50`
* `points[i].length == 2`
* `0 <= xi, yi <= 4 * 104`
* All the given points are **unique**. | null |
2 clean Python linear solutions | three-equal-parts | 0 | 1 | ```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # count number of ones\n ones = sum(arr)\n if ones % 3 != 0:\n return [-1, -1]\n elif ones == 0: # special case: all zeros\n return [0, 2]\n \n # find the start index of each group of ones\n c = 0\n starts = []\n for i, d in enumerate(arr):\n if d == 1:\n if c % (ones // 3) == 0:\n starts.append(i)\n c += 1\n\n # scan the groups in parallel to compare digits\n i, j, k = starts\n while k < len(arr): # note that the last/rightmost group must include all digits till the end\n if arr[i] == arr[j] == arr[k]:\n i += 1\n j += 1\n k += 1\n else:\n return [-1, -1]\n return [i-1, j]\n```\nRuntime: *O(n)*\nSpace: *O(1)*\n\n```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # gather the indices of the ones\n ones = [i for i, d in enumerate(arr) if d == 1]\n\n if not ones:\n return [0, 2]\n elif len(ones) % 3 != 0:\n return [-1, -1]\n\n # get the start indices of the 3 groups\n i, j, k = ones[0], ones[len(ones)//3], ones[len(ones)//3*2]\n\n # calculate the size/length of what each group should be\n length = len(arr) - k # note that the last/rightmost group must include all digits till the end\n # so we know that the size of each group is `len(arr) - k` (where `k` is start of third group)\n\n # compare the three groups\n if arr[i:i+length] == arr[j:j+length] == arr[k:k+length]:\n return [i+length-1, j+length]\n \n return [-1, -1]\n```\nRuntime: *O(n)*\nSpace: *O(n)* | 7 | You are given an array `arr` which consists of only zeros and ones, divide the array into **three non-empty parts** such that all of these parts represent the same binary value.
If it is possible, return any `[i, j]` with `i + 1 < j`, such that:
* `arr[0], arr[1], ..., arr[i]` is the first part,
* `arr[i + 1], arr[i + 2], ..., arr[j - 1]` is the second part, and
* `arr[j], arr[j + 1], ..., arr[arr.length - 1]` is the third part.
* All three parts have equal binary values.
If it is not possible, return `[-1, -1]`.
Note that the entire part is used when considering what binary value it represents. For example, `[1,1,0]` represents `6` in decimal, not `3`. Also, leading zeros **are allowed**, so `[0,1,1]` and `[1,1]` represent the same value.
**Example 1:**
**Input:** arr = \[1,0,1,0,1\]
**Output:** \[0,3\]
**Example 2:**
**Input:** arr = \[1,1,0,1,1\]
**Output:** \[-1,-1\]
**Example 3:**
**Input:** arr = \[1,1,0,0,1\]
**Output:** \[0,2\]
**Constraints:**
* `3 <= arr.length <= 3 * 104`
* `arr[i]` is `0` or `1` | null |
2 clean Python linear solutions | three-equal-parts | 0 | 1 | ```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # count number of ones\n ones = sum(arr)\n if ones % 3 != 0:\n return [-1, -1]\n elif ones == 0: # special case: all zeros\n return [0, 2]\n \n # find the start index of each group of ones\n c = 0\n starts = []\n for i, d in enumerate(arr):\n if d == 1:\n if c % (ones // 3) == 0:\n starts.append(i)\n c += 1\n\n # scan the groups in parallel to compare digits\n i, j, k = starts\n while k < len(arr): # note that the last/rightmost group must include all digits till the end\n if arr[i] == arr[j] == arr[k]:\n i += 1\n j += 1\n k += 1\n else:\n return [-1, -1]\n return [i-1, j]\n```\nRuntime: *O(n)*\nSpace: *O(1)*\n\n```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # gather the indices of the ones\n ones = [i for i, d in enumerate(arr) if d == 1]\n\n if not ones:\n return [0, 2]\n elif len(ones) % 3 != 0:\n return [-1, -1]\n\n # get the start indices of the 3 groups\n i, j, k = ones[0], ones[len(ones)//3], ones[len(ones)//3*2]\n\n # calculate the size/length of what each group should be\n length = len(arr) - k # note that the last/rightmost group must include all digits till the end\n # so we know that the size of each group is `len(arr) - k` (where `k` is start of third group)\n\n # compare the three groups\n if arr[i:i+length] == arr[j:j+length] == arr[k:k+length]:\n return [i+length-1, j+length]\n \n return [-1, -1]\n```\nRuntime: *O(n)*\nSpace: *O(n)* | 7 | You are given an array of points in the **X-Y** plane `points` where `points[i] = [xi, yi]`.
Return _the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes_. If there is not any such rectangle, return `0`.
Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[1,2\],\[2,1\],\[1,0\],\[0,1\]\]
**Output:** 2.00000
**Explanation:** The minimum area rectangle occurs at \[1,2\],\[2,1\],\[1,0\],\[0,1\], with an area of 2.
**Example 2:**
**Input:** points = \[\[0,1\],\[2,1\],\[1,1\],\[1,0\],\[2,0\]\]
**Output:** 1.00000
**Explanation:** The minimum area rectangle occurs at \[1,0\],\[1,1\],\[2,1\],\[2,0\], with an area of 1.
**Example 3:**
**Input:** points = \[\[0,3\],\[1,2\],\[3,1\],\[1,3\],\[2,1\]\]
**Output:** 0
**Explanation:** There is no possible rectangle to form from these points.
**Constraints:**
* `1 <= points.length <= 50`
* `points[i].length == 2`
* `0 <= xi, yi <= 4 * 104`
* All the given points are **unique**. | null |
Easiest Solution | three-equal-parts | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public int[] threeEqualParts(int[] arr) {\n int[] ans=new int[] {-1,-1};\n int ones=0;\n for(int x:arr) ones+=x;\n if(ones==0) return new int[] {0,2};\n if(ones%3!=0) return ans;\n int onesInEachPart=ones/3;\n int firstOneIndexPart1=-1;\n int firstOneIndexPart2=-1;\n int firstOneIndexPart3=-1;\n ones=0;\n for(int i=0; i<arr.length;i++) {\n if(arr[i]==1) {\n ones++;\n if(ones==1) firstOneIndexPart1=i;\n else if(ones==onesInEachPart+1) firstOneIndexPart2=i;\n else if(ones==2*(onesInEachPart)+1) firstOneIndexPart3=i;\n }\n }\n while(firstOneIndexPart3<arr.length) {\n if(arr[firstOneIndexPart3]==arr[firstOneIndexPart1] && arr[firstOneIndexPart3]==arr[firstOneIndexPart2]) {\n firstOneIndexPart1++;\n firstOneIndexPart2++;\n firstOneIndexPart3++;\n }\n else {\n return ans;\n }\n }\n return new int[] {firstOneIndexPart1-1,firstOneIndexPart2};\n }\n}\n```\n```python3 []\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # count number of ones\n ones = sum(arr)\n if ones % 3 != 0:\n return [-1, -1]\n elif ones == 0: # special case: all zeros\n return [0, 2]\n \n # find the start index of each group of ones\n c = 0\n starts = []\n for i, d in enumerate(arr):\n if d == 1:\n if c % (ones // 3) == 0:\n starts.append(i)\n c += 1\n\n # scan the groups in parallel to compare digits\n i, j, k = starts\n while k < len(arr): # note that the last/rightmost group must include all digits till the end\n if arr[i] == arr[j] == arr[k]:\n i += 1\n j += 1\n k += 1\n else:\n return [-1, -1]\n return [i-1, j]\n``` | 0 | You are given an array `arr` which consists of only zeros and ones, divide the array into **three non-empty parts** such that all of these parts represent the same binary value.
If it is possible, return any `[i, j]` with `i + 1 < j`, such that:
* `arr[0], arr[1], ..., arr[i]` is the first part,
* `arr[i + 1], arr[i + 2], ..., arr[j - 1]` is the second part, and
* `arr[j], arr[j + 1], ..., arr[arr.length - 1]` is the third part.
* All three parts have equal binary values.
If it is not possible, return `[-1, -1]`.
Note that the entire part is used when considering what binary value it represents. For example, `[1,1,0]` represents `6` in decimal, not `3`. Also, leading zeros **are allowed**, so `[0,1,1]` and `[1,1]` represent the same value.
**Example 1:**
**Input:** arr = \[1,0,1,0,1\]
**Output:** \[0,3\]
**Example 2:**
**Input:** arr = \[1,1,0,1,1\]
**Output:** \[-1,-1\]
**Example 3:**
**Input:** arr = \[1,1,0,0,1\]
**Output:** \[0,2\]
**Constraints:**
* `3 <= arr.length <= 3 * 104`
* `arr[i]` is `0` or `1` | null |
Easiest Solution | three-equal-parts | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public int[] threeEqualParts(int[] arr) {\n int[] ans=new int[] {-1,-1};\n int ones=0;\n for(int x:arr) ones+=x;\n if(ones==0) return new int[] {0,2};\n if(ones%3!=0) return ans;\n int onesInEachPart=ones/3;\n int firstOneIndexPart1=-1;\n int firstOneIndexPart2=-1;\n int firstOneIndexPart3=-1;\n ones=0;\n for(int i=0; i<arr.length;i++) {\n if(arr[i]==1) {\n ones++;\n if(ones==1) firstOneIndexPart1=i;\n else if(ones==onesInEachPart+1) firstOneIndexPart2=i;\n else if(ones==2*(onesInEachPart)+1) firstOneIndexPart3=i;\n }\n }\n while(firstOneIndexPart3<arr.length) {\n if(arr[firstOneIndexPart3]==arr[firstOneIndexPart1] && arr[firstOneIndexPart3]==arr[firstOneIndexPart2]) {\n firstOneIndexPart1++;\n firstOneIndexPart2++;\n firstOneIndexPart3++;\n }\n else {\n return ans;\n }\n }\n return new int[] {firstOneIndexPart1-1,firstOneIndexPart2};\n }\n}\n```\n```python3 []\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # count number of ones\n ones = sum(arr)\n if ones % 3 != 0:\n return [-1, -1]\n elif ones == 0: # special case: all zeros\n return [0, 2]\n \n # find the start index of each group of ones\n c = 0\n starts = []\n for i, d in enumerate(arr):\n if d == 1:\n if c % (ones // 3) == 0:\n starts.append(i)\n c += 1\n\n # scan the groups in parallel to compare digits\n i, j, k = starts\n while k < len(arr): # note that the last/rightmost group must include all digits till the end\n if arr[i] == arr[j] == arr[k]:\n i += 1\n j += 1\n k += 1\n else:\n return [-1, -1]\n return [i-1, j]\n``` | 0 | You are given an array of points in the **X-Y** plane `points` where `points[i] = [xi, yi]`.
Return _the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes_. If there is not any such rectangle, return `0`.
Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[1,2\],\[2,1\],\[1,0\],\[0,1\]\]
**Output:** 2.00000
**Explanation:** The minimum area rectangle occurs at \[1,2\],\[2,1\],\[1,0\],\[0,1\], with an area of 2.
**Example 2:**
**Input:** points = \[\[0,1\],\[2,1\],\[1,1\],\[1,0\],\[2,0\]\]
**Output:** 1.00000
**Explanation:** The minimum area rectangle occurs at \[1,0\],\[1,1\],\[2,1\],\[2,0\], with an area of 1.
**Example 3:**
**Input:** points = \[\[0,3\],\[1,2\],\[3,1\],\[1,3\],\[2,1\]\]
**Output:** 0
**Explanation:** There is no possible rectangle to form from these points.
**Constraints:**
* `1 <= points.length <= 50`
* `points[i].length == 2`
* `0 <= xi, yi <= 4 * 104`
* All the given points are **unique**. | null |
Solution based on substrings rather than subarrays. | three-equal-parts | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAfter my first couple of attempts to solve this problem, I realized that because of the limits of the inputs, it was possible to end up with three numbers of 10,000 digits each, which requires the use of expensive unlimited-precision integers. So, I changed my basic approach to convert the array into a string of "0"s and "1"s and to determine whether the three substrings are string-equivalent rather than comparing the numeric values of the subarrays. One thing that complicates this is the presence of the leading zeros, because it\'s necessary to treat the substrings "11" and "011" as numerically equivalent even though they\'re not string equivalent, but we\'ll handle this.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAlthough searching for three equivalent substrings should require a doubly-nested loop (think of it as looping over possible values of "i" and "j"), we can get away with a single loop over "i" because we\'re looking for substrings that are string-equivalent, hence the same length, so knowing "i", we have determined "j" -- basically 2 * i. However, as noted above, we have to consider leading zeros in any or all of the three substrings. We can eliminate the leading zeros for the left-most substring by searching for the first "1" in the string. For each value of "i" and discounting the leading 0\'s, we can compute "j" if we also take into account the leading 0\'s in the middle and right substrings. So, the basic logic is:\n```\nfor each i from 0 up to n:\n calculate left substring and "i", skipping leading zeros\n calculate mid substring and "j", skipping leading zeros\n calculate right substring, skipping leading zeros\n if left, mid and right substrings are ==, return [ i, j ]\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe iteration over ```i``` is $$O(n)$$ and within that loop,\nthe calculation does not depend on $$n$$, so the basic complexity\nis $$O(n)$$. However, there\'s another factor -- the comparison of\nleft, mid and right substrings. That is another factor of $$O(n)$$, so the overall complexity is $$O(n^2)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe only storage that depends on $$n$$ is for the String converted from the input array; its space complexity is $$O(n)$$\n\n# Code\n```\nclass Solution:\n # What we\'re going to do in this version is convert the array of 0\'s and 1\'s \n # into a string consisting of "0"s and "1"s.\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n n = len( arr )\n arr_str = \'\'.join( map( str, arr ) ) # Convert array of 0\'s and 1\'s to string of "0"s and "1"s\n left_leading_one_index = arr_str.find( "1" )\n if left_leading_one_index < 0: # No 1\'s anywhere\n return [ 0, 2 ] # Take left=first 0, mid=second 0, and right=the rest of the zero\'s \n for i in range( left_leading_one_index, n - 1 ):\n left_string = arr_str[ left_leading_one_index : i + 1 ]\n mid_leading_one_index = arr_str.find( "1", i + 1 )\n mid_stop_index = mid_leading_one_index + len( left_string )\n if mid_stop_index + len( left_string ) > n:\n return [ -1, -1 ] # No room for mid and right within "arr"\n right_leading_one_index = arr_str.find( "1", mid_stop_index )\n if right_leading_one_index < 0: # No 1\'s in right\n return [ -1, -1 ]\n mid_string = arr_str[ mid_leading_one_index : mid_stop_index ]\n right_string = arr_str[ right_leading_one_index : n ]\n if left_string == mid_string and left_string == right_string:\n return [ i, mid_stop_index ]\n return [ -1, -1 ]\n\n``` | 0 | You are given an array `arr` which consists of only zeros and ones, divide the array into **three non-empty parts** such that all of these parts represent the same binary value.
If it is possible, return any `[i, j]` with `i + 1 < j`, such that:
* `arr[0], arr[1], ..., arr[i]` is the first part,
* `arr[i + 1], arr[i + 2], ..., arr[j - 1]` is the second part, and
* `arr[j], arr[j + 1], ..., arr[arr.length - 1]` is the third part.
* All three parts have equal binary values.
If it is not possible, return `[-1, -1]`.
Note that the entire part is used when considering what binary value it represents. For example, `[1,1,0]` represents `6` in decimal, not `3`. Also, leading zeros **are allowed**, so `[0,1,1]` and `[1,1]` represent the same value.
**Example 1:**
**Input:** arr = \[1,0,1,0,1\]
**Output:** \[0,3\]
**Example 2:**
**Input:** arr = \[1,1,0,1,1\]
**Output:** \[-1,-1\]
**Example 3:**
**Input:** arr = \[1,1,0,0,1\]
**Output:** \[0,2\]
**Constraints:**
* `3 <= arr.length <= 3 * 104`
* `arr[i]` is `0` or `1` | null |
Solution based on substrings rather than subarrays. | three-equal-parts | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAfter my first couple of attempts to solve this problem, I realized that because of the limits of the inputs, it was possible to end up with three numbers of 10,000 digits each, which requires the use of expensive unlimited-precision integers. So, I changed my basic approach to convert the array into a string of "0"s and "1"s and to determine whether the three substrings are string-equivalent rather than comparing the numeric values of the subarrays. One thing that complicates this is the presence of the leading zeros, because it\'s necessary to treat the substrings "11" and "011" as numerically equivalent even though they\'re not string equivalent, but we\'ll handle this.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAlthough searching for three equivalent substrings should require a doubly-nested loop (think of it as looping over possible values of "i" and "j"), we can get away with a single loop over "i" because we\'re looking for substrings that are string-equivalent, hence the same length, so knowing "i", we have determined "j" -- basically 2 * i. However, as noted above, we have to consider leading zeros in any or all of the three substrings. We can eliminate the leading zeros for the left-most substring by searching for the first "1" in the string. For each value of "i" and discounting the leading 0\'s, we can compute "j" if we also take into account the leading 0\'s in the middle and right substrings. So, the basic logic is:\n```\nfor each i from 0 up to n:\n calculate left substring and "i", skipping leading zeros\n calculate mid substring and "j", skipping leading zeros\n calculate right substring, skipping leading zeros\n if left, mid and right substrings are ==, return [ i, j ]\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe iteration over ```i``` is $$O(n)$$ and within that loop,\nthe calculation does not depend on $$n$$, so the basic complexity\nis $$O(n)$$. However, there\'s another factor -- the comparison of\nleft, mid and right substrings. That is another factor of $$O(n)$$, so the overall complexity is $$O(n^2)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe only storage that depends on $$n$$ is for the String converted from the input array; its space complexity is $$O(n)$$\n\n# Code\n```\nclass Solution:\n # What we\'re going to do in this version is convert the array of 0\'s and 1\'s \n # into a string consisting of "0"s and "1"s.\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n n = len( arr )\n arr_str = \'\'.join( map( str, arr ) ) # Convert array of 0\'s and 1\'s to string of "0"s and "1"s\n left_leading_one_index = arr_str.find( "1" )\n if left_leading_one_index < 0: # No 1\'s anywhere\n return [ 0, 2 ] # Take left=first 0, mid=second 0, and right=the rest of the zero\'s \n for i in range( left_leading_one_index, n - 1 ):\n left_string = arr_str[ left_leading_one_index : i + 1 ]\n mid_leading_one_index = arr_str.find( "1", i + 1 )\n mid_stop_index = mid_leading_one_index + len( left_string )\n if mid_stop_index + len( left_string ) > n:\n return [ -1, -1 ] # No room for mid and right within "arr"\n right_leading_one_index = arr_str.find( "1", mid_stop_index )\n if right_leading_one_index < 0: # No 1\'s in right\n return [ -1, -1 ]\n mid_string = arr_str[ mid_leading_one_index : mid_stop_index ]\n right_string = arr_str[ right_leading_one_index : n ]\n if left_string == mid_string and left_string == right_string:\n return [ i, mid_stop_index ]\n return [ -1, -1 ]\n\n``` | 0 | You are given an array of points in the **X-Y** plane `points` where `points[i] = [xi, yi]`.
Return _the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes_. If there is not any such rectangle, return `0`.
Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[1,2\],\[2,1\],\[1,0\],\[0,1\]\]
**Output:** 2.00000
**Explanation:** The minimum area rectangle occurs at \[1,2\],\[2,1\],\[1,0\],\[0,1\], with an area of 2.
**Example 2:**
**Input:** points = \[\[0,1\],\[2,1\],\[1,1\],\[1,0\],\[2,0\]\]
**Output:** 1.00000
**Explanation:** The minimum area rectangle occurs at \[1,0\],\[1,1\],\[2,1\],\[2,0\], with an area of 1.
**Example 3:**
**Input:** points = \[\[0,3\],\[1,2\],\[3,1\],\[1,3\],\[2,1\]\]
**Output:** 0
**Explanation:** There is no possible rectangle to form from these points.
**Constraints:**
* `1 <= points.length <= 50`
* `points[i].length == 2`
* `0 <= xi, yi <= 4 * 104`
* All the given points are **unique**. | null |
[Python] 96% Straightforward Solution | three-equal-parts | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n n = sum(arr)\n if n % 3: return [-1, -1]\n if n == 0: return [0, 2]\n k, indices = n // 3, []\n for i, num in enumerate(arr):\n if num: indices.append(i)\n i1, i2, i3, i, j = *[indices[-(j * k)] for j in (3, 2, 1)], 0 ,0\n part1, part2, part3 = arr[i1: i2], arr[i2: i3], arr[i3:]\n l1, l2, l3 = i2 - i1, i3 - i2, len(part3)\n if l3 > l2 or part2[:l3] != part3 or l3 > l1 or part1[:l3] != part3: return [-1, -1]\n i, j = i1 + l3 - 1, i2 + l3\n return [i, j]\n \n \n \n``` | 0 | You are given an array `arr` which consists of only zeros and ones, divide the array into **three non-empty parts** such that all of these parts represent the same binary value.
If it is possible, return any `[i, j]` with `i + 1 < j`, such that:
* `arr[0], arr[1], ..., arr[i]` is the first part,
* `arr[i + 1], arr[i + 2], ..., arr[j - 1]` is the second part, and
* `arr[j], arr[j + 1], ..., arr[arr.length - 1]` is the third part.
* All three parts have equal binary values.
If it is not possible, return `[-1, -1]`.
Note that the entire part is used when considering what binary value it represents. For example, `[1,1,0]` represents `6` in decimal, not `3`. Also, leading zeros **are allowed**, so `[0,1,1]` and `[1,1]` represent the same value.
**Example 1:**
**Input:** arr = \[1,0,1,0,1\]
**Output:** \[0,3\]
**Example 2:**
**Input:** arr = \[1,1,0,1,1\]
**Output:** \[-1,-1\]
**Example 3:**
**Input:** arr = \[1,1,0,0,1\]
**Output:** \[0,2\]
**Constraints:**
* `3 <= arr.length <= 3 * 104`
* `arr[i]` is `0` or `1` | null |
[Python] 96% Straightforward Solution | three-equal-parts | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n n = sum(arr)\n if n % 3: return [-1, -1]\n if n == 0: return [0, 2]\n k, indices = n // 3, []\n for i, num in enumerate(arr):\n if num: indices.append(i)\n i1, i2, i3, i, j = *[indices[-(j * k)] for j in (3, 2, 1)], 0 ,0\n part1, part2, part3 = arr[i1: i2], arr[i2: i3], arr[i3:]\n l1, l2, l3 = i2 - i1, i3 - i2, len(part3)\n if l3 > l2 or part2[:l3] != part3 or l3 > l1 or part1[:l3] != part3: return [-1, -1]\n i, j = i1 + l3 - 1, i2 + l3\n return [i, j]\n \n \n \n``` | 0 | You are given an array of points in the **X-Y** plane `points` where `points[i] = [xi, yi]`.
Return _the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes_. If there is not any such rectangle, return `0`.
Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[1,2\],\[2,1\],\[1,0\],\[0,1\]\]
**Output:** 2.00000
**Explanation:** The minimum area rectangle occurs at \[1,2\],\[2,1\],\[1,0\],\[0,1\], with an area of 2.
**Example 2:**
**Input:** points = \[\[0,1\],\[2,1\],\[1,1\],\[1,0\],\[2,0\]\]
**Output:** 1.00000
**Explanation:** The minimum area rectangle occurs at \[1,0\],\[1,1\],\[2,1\],\[2,0\], with an area of 1.
**Example 3:**
**Input:** points = \[\[0,3\],\[1,2\],\[3,1\],\[1,3\],\[2,1\]\]
**Output:** 0
**Explanation:** There is no possible rectangle to form from these points.
**Constraints:**
* `1 <= points.length <= 50`
* `points[i].length == 2`
* `0 <= xi, yi <= 4 * 104`
* All the given points are **unique**. | null |
Python (Simple Maths) | three-equal-parts | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def threeEqualParts(self, arr):\n n = len(arr)\n\n res = [i for i in range(n) if arr[i] == 1]\n\n p = len(res)\n\n if p == 0:\n return [0,n-1]\n\n id1, id2, id3 = res[0], res[p//3], res[2*p//3]\n\n sub = n-id3\n\n if p%3 == 0 and arr[id1:id1+sub] == arr[id2:id2+sub] == arr[id3:]:\n return [id1-1+sub,id2+sub]\n\n return [-1,-1]\n\n\n\n \n\n\n\n\n\n \n``` | 0 | You are given an array `arr` which consists of only zeros and ones, divide the array into **three non-empty parts** such that all of these parts represent the same binary value.
If it is possible, return any `[i, j]` with `i + 1 < j`, such that:
* `arr[0], arr[1], ..., arr[i]` is the first part,
* `arr[i + 1], arr[i + 2], ..., arr[j - 1]` is the second part, and
* `arr[j], arr[j + 1], ..., arr[arr.length - 1]` is the third part.
* All three parts have equal binary values.
If it is not possible, return `[-1, -1]`.
Note that the entire part is used when considering what binary value it represents. For example, `[1,1,0]` represents `6` in decimal, not `3`. Also, leading zeros **are allowed**, so `[0,1,1]` and `[1,1]` represent the same value.
**Example 1:**
**Input:** arr = \[1,0,1,0,1\]
**Output:** \[0,3\]
**Example 2:**
**Input:** arr = \[1,1,0,1,1\]
**Output:** \[-1,-1\]
**Example 3:**
**Input:** arr = \[1,1,0,0,1\]
**Output:** \[0,2\]
**Constraints:**
* `3 <= arr.length <= 3 * 104`
* `arr[i]` is `0` or `1` | null |
Python (Simple Maths) | three-equal-parts | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def threeEqualParts(self, arr):\n n = len(arr)\n\n res = [i for i in range(n) if arr[i] == 1]\n\n p = len(res)\n\n if p == 0:\n return [0,n-1]\n\n id1, id2, id3 = res[0], res[p//3], res[2*p//3]\n\n sub = n-id3\n\n if p%3 == 0 and arr[id1:id1+sub] == arr[id2:id2+sub] == arr[id3:]:\n return [id1-1+sub,id2+sub]\n\n return [-1,-1]\n\n\n\n \n\n\n\n\n\n \n``` | 0 | You are given an array of points in the **X-Y** plane `points` where `points[i] = [xi, yi]`.
Return _the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes_. If there is not any such rectangle, return `0`.
Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[1,2\],\[2,1\],\[1,0\],\[0,1\]\]
**Output:** 2.00000
**Explanation:** The minimum area rectangle occurs at \[1,2\],\[2,1\],\[1,0\],\[0,1\], with an area of 2.
**Example 2:**
**Input:** points = \[\[0,1\],\[2,1\],\[1,1\],\[1,0\],\[2,0\]\]
**Output:** 1.00000
**Explanation:** The minimum area rectangle occurs at \[1,0\],\[1,1\],\[2,1\],\[2,0\], with an area of 1.
**Example 3:**
**Input:** points = \[\[0,3\],\[1,2\],\[3,1\],\[1,3\],\[2,1\]\]
**Output:** 0
**Explanation:** There is no possible rectangle to form from these points.
**Constraints:**
* `1 <= points.length <= 50`
* `points[i].length == 2`
* `0 <= xi, yi <= 4 * 104`
* All the given points are **unique**. | null |
Extremely simple explanation. (Solution included) | three-equal-parts | 0 | 1 | So the idea is pretty simple, and yes, like most of them, you have to count the number of ones first.\n1. Count the number of ones (let\'s call it `ones`). If it\'s zero, return (0,size-1). If it isn\'t a multiple of 3, return [-1,-1], and if it is a factor of 3, let\'s proceed. *\n\n* Think about the array this way: \n```\n0 1 0 1 ... 0 1 | 1 1 0 ... 0 1 | 0 0 0 0 1 1 1 ... 1\n left | middle | right\n```\n2. Get the right side first. Is the only side you can calculate by just passing a pointer and reaching `ones//3` ones. So the value that has to be obtained for the three sides is forced. Here you get the `j` index.\n3. Having the right side, now you can iterate a left index to see if you can reach the same value. If we surpass the value of the right side, we can just return `[-1,-1]`. If you reach the value, you get the index `i`.\n4. Now you can iterate over the middle to see if you can reach the same value as in the left and right sides. If you don\'t reach it, return `[-1,-1]`.\n5. If you got the value, the solution is done, because you got `ones` ones, so it\'s complete.\n\n\n* You need a multiple of three to be able to split the array into three equal bags since each of the subarrays will have `ones//3` ones. \n\n# Code\n```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # Step 1: count ones and store info\n ones = arr.count(1)\n if ones % 3 != 0: return [ -1, -1 ]\n oneSize = ones // 3\n\n # We start getting the right value\n size = len(arr)\n if not ones: return [0,size-1] # Particular case\n right = size\n rightValue = 0\n power = 1\n while oneSize > 0:\n right -= 1\n if arr[right] == 1:\n rightValue += power\n oneSize -= 1\n power <<= 1\n \n # We start getting the left value\n left = -1\n leftValue = 0\n while leftValue>>1 != rightValue:\n left += 1\n if arr[left] == 1:\n leftValue += 1\n leftValue <<= 1\n # If we can\'t reach the value we want, we leave the process\n if leftValue>>1 > rightValue: return [-1,-1] \n leftValue >>= 1\n\n # We start getting the third value\n third = 0\n answer = [left] # We got the last index we used for the left value\n left += 1 # We recycle the index from left\n while left < right:\n if arr[left] == 1:\n third += 1\n third <<= 1\n left += 1\n if third>>1 == rightValue: break\n third >>= 1\n # We got the three numbers. Now is matter of verifying.\n if third != rightValue: return [-1,-1]\n answer.append(left)\n return answer\n``` | 0 | You are given an array `arr` which consists of only zeros and ones, divide the array into **three non-empty parts** such that all of these parts represent the same binary value.
If it is possible, return any `[i, j]` with `i + 1 < j`, such that:
* `arr[0], arr[1], ..., arr[i]` is the first part,
* `arr[i + 1], arr[i + 2], ..., arr[j - 1]` is the second part, and
* `arr[j], arr[j + 1], ..., arr[arr.length - 1]` is the third part.
* All three parts have equal binary values.
If it is not possible, return `[-1, -1]`.
Note that the entire part is used when considering what binary value it represents. For example, `[1,1,0]` represents `6` in decimal, not `3`. Also, leading zeros **are allowed**, so `[0,1,1]` and `[1,1]` represent the same value.
**Example 1:**
**Input:** arr = \[1,0,1,0,1\]
**Output:** \[0,3\]
**Example 2:**
**Input:** arr = \[1,1,0,1,1\]
**Output:** \[-1,-1\]
**Example 3:**
**Input:** arr = \[1,1,0,0,1\]
**Output:** \[0,2\]
**Constraints:**
* `3 <= arr.length <= 3 * 104`
* `arr[i]` is `0` or `1` | null |
Extremely simple explanation. (Solution included) | three-equal-parts | 0 | 1 | So the idea is pretty simple, and yes, like most of them, you have to count the number of ones first.\n1. Count the number of ones (let\'s call it `ones`). If it\'s zero, return (0,size-1). If it isn\'t a multiple of 3, return [-1,-1], and if it is a factor of 3, let\'s proceed. *\n\n* Think about the array this way: \n```\n0 1 0 1 ... 0 1 | 1 1 0 ... 0 1 | 0 0 0 0 1 1 1 ... 1\n left | middle | right\n```\n2. Get the right side first. Is the only side you can calculate by just passing a pointer and reaching `ones//3` ones. So the value that has to be obtained for the three sides is forced. Here you get the `j` index.\n3. Having the right side, now you can iterate a left index to see if you can reach the same value. If we surpass the value of the right side, we can just return `[-1,-1]`. If you reach the value, you get the index `i`.\n4. Now you can iterate over the middle to see if you can reach the same value as in the left and right sides. If you don\'t reach it, return `[-1,-1]`.\n5. If you got the value, the solution is done, because you got `ones` ones, so it\'s complete.\n\n\n* You need a multiple of three to be able to split the array into three equal bags since each of the subarrays will have `ones//3` ones. \n\n# Code\n```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # Step 1: count ones and store info\n ones = arr.count(1)\n if ones % 3 != 0: return [ -1, -1 ]\n oneSize = ones // 3\n\n # We start getting the right value\n size = len(arr)\n if not ones: return [0,size-1] # Particular case\n right = size\n rightValue = 0\n power = 1\n while oneSize > 0:\n right -= 1\n if arr[right] == 1:\n rightValue += power\n oneSize -= 1\n power <<= 1\n \n # We start getting the left value\n left = -1\n leftValue = 0\n while leftValue>>1 != rightValue:\n left += 1\n if arr[left] == 1:\n leftValue += 1\n leftValue <<= 1\n # If we can\'t reach the value we want, we leave the process\n if leftValue>>1 > rightValue: return [-1,-1] \n leftValue >>= 1\n\n # We start getting the third value\n third = 0\n answer = [left] # We got the last index we used for the left value\n left += 1 # We recycle the index from left\n while left < right:\n if arr[left] == 1:\n third += 1\n third <<= 1\n left += 1\n if third>>1 == rightValue: break\n third >>= 1\n # We got the three numbers. Now is matter of verifying.\n if third != rightValue: return [-1,-1]\n answer.append(left)\n return answer\n``` | 0 | You are given an array of points in the **X-Y** plane `points` where `points[i] = [xi, yi]`.
Return _the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes_. If there is not any such rectangle, return `0`.
Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[1,2\],\[2,1\],\[1,0\],\[0,1\]\]
**Output:** 2.00000
**Explanation:** The minimum area rectangle occurs at \[1,2\],\[2,1\],\[1,0\],\[0,1\], with an area of 2.
**Example 2:**
**Input:** points = \[\[0,1\],\[2,1\],\[1,1\],\[1,0\],\[2,0\]\]
**Output:** 1.00000
**Explanation:** The minimum area rectangle occurs at \[1,0\],\[1,1\],\[2,1\],\[2,0\], with an area of 1.
**Example 3:**
**Input:** points = \[\[0,3\],\[1,2\],\[3,1\],\[1,3\],\[2,1\]\]
**Output:** 0
**Explanation:** There is no possible rectangle to form from these points.
**Constraints:**
* `1 <= points.length <= 50`
* `points[i].length == 2`
* `0 <= xi, yi <= 4 * 104`
* All the given points are **unique**. | null |
Python O(n) O(1) | pure logic deduction | three-equal-parts | 0 | 1 | # Intuition\r\nIf their are three equal parts, they must contain same amount of ones, and ends with same amount of zeros\r\nThe heading zeros is irrelevant\r\n\r\n# Approach\r\n- count ones, divide it by 3 to get ones count of each part\r\n- count tailing zeros, these zeros must contains in each part\r\n- hance we can get one and the only cut of I and J just in one parse\r\n- the last only thing we need to do, just check whether our cuts is legal\r\n\r\n# Complexity\r\n- Time complexity:\r\n$$O(n)$$\r\n- Space complexity:\r\n$$O(1)$$\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def threeEqualParts(self, arr):\r\n ones, remain = divmod(arr.count(1), 3)\r\n\r\n if remain != 0: return [-1, -1] # can not be divided equally\r\n if ones == 0: return [0, 2] # all zero\r\n\r\n L, tail_zero_cnts = len(arr), arr[::-1].index(1)\r\n\r\n I, J, cnt = 0, L - 1, 0\r\n for i in filter(arr.__getitem__, range(L)): # for all ones\r\n cnt += 1\r\n if cnt == ones:\r\n I = i + tail_zero_cnts\r\n if cnt == 2 * ones:\r\n J = i + tail_zero_cnts\r\n break\r\n\r\n if int(\'\'.join(map(str, arr[:I + 1]))) == int(\'\'.join(map(str, arr[I + 1:J + 1]))) == int(\'\'.join(map(str, arr[J + 1:]))):\r\n return [I, J + 1]\r\n\r\n return [-1, -1]\r\n\r\n\r\n``` | 0 | You are given an array `arr` which consists of only zeros and ones, divide the array into **three non-empty parts** such that all of these parts represent the same binary value.
If it is possible, return any `[i, j]` with `i + 1 < j`, such that:
* `arr[0], arr[1], ..., arr[i]` is the first part,
* `arr[i + 1], arr[i + 2], ..., arr[j - 1]` is the second part, and
* `arr[j], arr[j + 1], ..., arr[arr.length - 1]` is the third part.
* All three parts have equal binary values.
If it is not possible, return `[-1, -1]`.
Note that the entire part is used when considering what binary value it represents. For example, `[1,1,0]` represents `6` in decimal, not `3`. Also, leading zeros **are allowed**, so `[0,1,1]` and `[1,1]` represent the same value.
**Example 1:**
**Input:** arr = \[1,0,1,0,1\]
**Output:** \[0,3\]
**Example 2:**
**Input:** arr = \[1,1,0,1,1\]
**Output:** \[-1,-1\]
**Example 3:**
**Input:** arr = \[1,1,0,0,1\]
**Output:** \[0,2\]
**Constraints:**
* `3 <= arr.length <= 3 * 104`
* `arr[i]` is `0` or `1` | null |
Python O(n) O(1) | pure logic deduction | three-equal-parts | 0 | 1 | # Intuition\r\nIf their are three equal parts, they must contain same amount of ones, and ends with same amount of zeros\r\nThe heading zeros is irrelevant\r\n\r\n# Approach\r\n- count ones, divide it by 3 to get ones count of each part\r\n- count tailing zeros, these zeros must contains in each part\r\n- hance we can get one and the only cut of I and J just in one parse\r\n- the last only thing we need to do, just check whether our cuts is legal\r\n\r\n# Complexity\r\n- Time complexity:\r\n$$O(n)$$\r\n- Space complexity:\r\n$$O(1)$$\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def threeEqualParts(self, arr):\r\n ones, remain = divmod(arr.count(1), 3)\r\n\r\n if remain != 0: return [-1, -1] # can not be divided equally\r\n if ones == 0: return [0, 2] # all zero\r\n\r\n L, tail_zero_cnts = len(arr), arr[::-1].index(1)\r\n\r\n I, J, cnt = 0, L - 1, 0\r\n for i in filter(arr.__getitem__, range(L)): # for all ones\r\n cnt += 1\r\n if cnt == ones:\r\n I = i + tail_zero_cnts\r\n if cnt == 2 * ones:\r\n J = i + tail_zero_cnts\r\n break\r\n\r\n if int(\'\'.join(map(str, arr[:I + 1]))) == int(\'\'.join(map(str, arr[I + 1:J + 1]))) == int(\'\'.join(map(str, arr[J + 1:]))):\r\n return [I, J + 1]\r\n\r\n return [-1, -1]\r\n\r\n\r\n``` | 0 | You are given an array of points in the **X-Y** plane `points` where `points[i] = [xi, yi]`.
Return _the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes_. If there is not any such rectangle, return `0`.
Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[1,2\],\[2,1\],\[1,0\],\[0,1\]\]
**Output:** 2.00000
**Explanation:** The minimum area rectangle occurs at \[1,2\],\[2,1\],\[1,0\],\[0,1\], with an area of 2.
**Example 2:**
**Input:** points = \[\[0,1\],\[2,1\],\[1,1\],\[1,0\],\[2,0\]\]
**Output:** 1.00000
**Explanation:** The minimum area rectangle occurs at \[1,0\],\[1,1\],\[2,1\],\[2,0\], with an area of 1.
**Example 3:**
**Input:** points = \[\[0,3\],\[1,2\],\[3,1\],\[1,3\],\[2,1\]\]
**Output:** 0
**Explanation:** There is no possible rectangle to form from these points.
**Constraints:**
* `1 <= points.length <= 50`
* `points[i].length == 2`
* `0 <= xi, yi <= 4 * 104`
* All the given points are **unique**. | null |
100% TC easy python solution | three-equal-parts | 0 | 1 | Hint\nCount the num of ones, and think how they will be split between the 3 segments :)\n```\ndef threeEqualParts(self, arr: List[int]) -> List[int]:\n\tn = len(arr)\n\tpos = [i for i in range(n) if(arr[i])]\n\tl = len(pos)\n\tif(l == 0):\n\t\treturn [0, 2]\n\tif(l % 3):\n\t\treturn [-1, -1]\n\tones = l//3\n\tc = 0\n\tfor i in arr[::-1]:\n\t\tif(i == 1):\n\t\t\tbreak\n\t\tc += 1\n\tans = [-1, -1]\n\t# one hoga pos[ones-1] tak\n\t# uske bad chaiye meko c zeros\n\t# toh index pos[ones-1] + c tak first segment ho jayega\n\tans[0] = pos[ones-1] + c\n\tans[1] = pos[2*ones-1] + c + 1\n\tseg1, seg2, seg3 = arr[pos[0]:ans[0]+1], arr[pos[ones]:ans[1]], arr[pos[2*ones]:]\n\t# without leading zeros\n\tif(seg1 != seg2 or seg1 != seg3):\n\t\treturn [-1, -1]\n\treturn ans\n``` | 3 | You are given an array `arr` which consists of only zeros and ones, divide the array into **three non-empty parts** such that all of these parts represent the same binary value.
If it is possible, return any `[i, j]` with `i + 1 < j`, such that:
* `arr[0], arr[1], ..., arr[i]` is the first part,
* `arr[i + 1], arr[i + 2], ..., arr[j - 1]` is the second part, and
* `arr[j], arr[j + 1], ..., arr[arr.length - 1]` is the third part.
* All three parts have equal binary values.
If it is not possible, return `[-1, -1]`.
Note that the entire part is used when considering what binary value it represents. For example, `[1,1,0]` represents `6` in decimal, not `3`. Also, leading zeros **are allowed**, so `[0,1,1]` and `[1,1]` represent the same value.
**Example 1:**
**Input:** arr = \[1,0,1,0,1\]
**Output:** \[0,3\]
**Example 2:**
**Input:** arr = \[1,1,0,1,1\]
**Output:** \[-1,-1\]
**Example 3:**
**Input:** arr = \[1,1,0,0,1\]
**Output:** \[0,2\]
**Constraints:**
* `3 <= arr.length <= 3 * 104`
* `arr[i]` is `0` or `1` | null |
100% TC easy python solution | three-equal-parts | 0 | 1 | Hint\nCount the num of ones, and think how they will be split between the 3 segments :)\n```\ndef threeEqualParts(self, arr: List[int]) -> List[int]:\n\tn = len(arr)\n\tpos = [i for i in range(n) if(arr[i])]\n\tl = len(pos)\n\tif(l == 0):\n\t\treturn [0, 2]\n\tif(l % 3):\n\t\treturn [-1, -1]\n\tones = l//3\n\tc = 0\n\tfor i in arr[::-1]:\n\t\tif(i == 1):\n\t\t\tbreak\n\t\tc += 1\n\tans = [-1, -1]\n\t# one hoga pos[ones-1] tak\n\t# uske bad chaiye meko c zeros\n\t# toh index pos[ones-1] + c tak first segment ho jayega\n\tans[0] = pos[ones-1] + c\n\tans[1] = pos[2*ones-1] + c + 1\n\tseg1, seg2, seg3 = arr[pos[0]:ans[0]+1], arr[pos[ones]:ans[1]], arr[pos[2*ones]:]\n\t# without leading zeros\n\tif(seg1 != seg2 or seg1 != seg3):\n\t\treturn [-1, -1]\n\treturn ans\n``` | 3 | You are given an array of points in the **X-Y** plane `points` where `points[i] = [xi, yi]`.
Return _the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes_. If there is not any such rectangle, return `0`.
Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[1,2\],\[2,1\],\[1,0\],\[0,1\]\]
**Output:** 2.00000
**Explanation:** The minimum area rectangle occurs at \[1,2\],\[2,1\],\[1,0\],\[0,1\], with an area of 2.
**Example 2:**
**Input:** points = \[\[0,1\],\[2,1\],\[1,1\],\[1,0\],\[2,0\]\]
**Output:** 1.00000
**Explanation:** The minimum area rectangle occurs at \[1,0\],\[1,1\],\[2,1\],\[2,0\], with an area of 1.
**Example 3:**
**Input:** points = \[\[0,3\],\[1,2\],\[3,1\],\[1,3\],\[2,1\]\]
**Output:** 0
**Explanation:** There is no possible rectangle to form from these points.
**Constraints:**
* `1 <= points.length <= 50`
* `points[i].length == 2`
* `0 <= xi, yi <= 4 * 104`
* All the given points are **unique**. | null |
Python 9 lines O(kn^2) BFS | minimize-malware-spread-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n # the key observation for me is the fact that we don\'t need to\n # really delete the initial in the graph. We can simply ignore\n # the deleted initial while we are doing BFS. So basically we\n # do BFS with each deleted value on initial, and we get the\n # minimal count of the connected graph. Note if two deleted\n # values give same count of connected graph, then we choose\n # smaller value. that\'s why I used a tuple, (BFS(a), a) this \n # will first compare BFS(a), if they are equal then it compares\n # a.\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n def BFS(delval):\n seen, lst = set(), list(initial)\n while lst:\n node = lst.pop()\n if node == delval or node in seen: continue\n seen.add(node)\n lst += [i for i, val in enumerate(graph[node]) if val]\n return len(seen)\n return min(initial, key=lambda a: (BFS(a), a))\n \n``` | 1 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops.
We will remove **exactly one node** from `initial`, **completely removing it and any connections from this node to any other node**.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,1,0\],\[1,1,1\],\[0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Example 3:**
**Input:** graph = \[\[1,1,0,0\],\[1,1,1,0\],\[0,1,1,1\],\[0,0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length < n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Solution | minimize-malware-spread-ii | 1 | 1 | ```C++ []\nclass Solution {\n bool vis[300];\npublic:\n void dfs(const vector<vector<int>>&v,int node,const int nhi_dekhna,int &ans)\n {\n vis[node] = true;\n ++ans;\n for(auto &x : v[node])\n if(!vis[x] and x != nhi_dekhna)\n dfs(v,x,nhi_dekhna,ans);\n } \n int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) {\n int n = graph.size();\n vector<vector<int>> v(n);\n for(int i = 0 ; i < n ; ++i)\n for(int j = 0 ; j < n ; ++j)\n if(graph[i][j] == 1 and i != j)\n v[i].push_back(j);\n sort(initial.begin(),initial.end());\n int res = 1e9;\n int res1 = initial[0];\n for(auto &x : initial)\n {\n int ans = 0;\n memset(vis,false,sizeof vis);\n for(auto &y : initial)\n {\n if(x != y and !vis[y])\n dfs(v,y,x,ans);\n }\n if(ans < res)\n {\n res1 = x;\n res = ans;\n }\n }\n return res1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n N = len(graph)\n uf = UF(N)\n\n clean = set(range(N)) - set(initial)\n\n for u, v in itertools.combinations(clean, 2):\n if graph[u][v]:\n uf.union(u,v)\n\n infect_node = collections.defaultdict(set)\n infected_by = collections.Counter()\n\n ans = min(initial)\n max = -1\n\n for i in initial:\n for c in clean:\n if graph[i][c]==1:\n infect_node[i].add(uf.find(c))\n # infected[uf.find(c)] += [i]\n for idx in infect_node[i]:\n infected_by[idx] += 1\n \n size = collections.Counter(uf.find(i) for i in clean)\n\n for key, nodes in infect_node.items():\n cnt = 0\n for node in nodes:\n if infected_by[node]==1:\n cnt += size[node]\n if cnt > max:\n max = cnt\n ans = key\n elif cnt==max:\n ans = min(ans, key)\n return ans\n \nclass UF:\n def __init__(self, n):\n self.parent = [-1]*n\n self.unique = n\n\n def find(self, a):\n if self.parent[a]>=0:\n self.parent[a] = self.find(self.parent[a])\n return self.parent[a]\n else:\n return a\n \n def union(self, a, b):\n pa = self.find(a)\n pb = self.find(b)\n\n if pa==pb: return False\n\n if pa<pb:\n self.parent[pa] += self.parent[pb]\n self.parent[pb] = pa\n else:\n self.parent[pb] += self.parent[pa]\n self.parent[pa] = pb\n self.unique-=1\n return True\n```\n\n```Java []\nclass Solution {\n private int dfs(int[][] graph, int u, boolean[] visited, boolean[] infected) {\n if(infected[u]) return 0;\n visited[u] = true;\n int count = 1;\n for(int v = 0; v < graph[u].length; v++) {\n if(!visited[v] && graph[u][v] == 1) {\n int c = dfs(graph, v, visited, infected);\n if(c == 0) {\n infected[u] = true;\n return 0;\n }\n count += c;\n }\n }\n return count;\n }\n public int minMalwareSpread(int[][] graph, int[] initial) {\n int n = graph.length, ans = initial[0], max = 0;\n boolean[] infected = new boolean[n];\n for(int u: initial) infected[u] = true;\n for(int u: initial) {\n boolean[] visited = new boolean[n];\n visited[u] = true;\n int count = 0;\n for(int i = 0; i < n; i++) {\n if(!visited[i] && graph[u][i] == 1) {\n count += dfs(graph, i, visited, infected);\n }\n }\n if(count > max || count == max && u < ans) {\n max = count;\n ans = u;\n }\n }\n return ans;\n }\n}\n```\n | 1 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops.
We will remove **exactly one node** from `initial`, **completely removing it and any connections from this node to any other node**.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,1,0\],\[1,1,1\],\[0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Example 3:**
**Input:** graph = \[\[1,1,0,0\],\[1,1,1,0\],\[0,1,1,1\],\[0,0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length < n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
[Python] DFS Solution- O(n ^ 2) => The cost of adjacency matrix | minimize-malware-spread-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to count the nodes which are infected by **only one** initial node.\nSo traversal from the initial nodes and stop until it encounter another initial nodes or already visited nodes.\n<br>\nDFS would pass each node once, so the complexcity is every node pass its adjacency array from the adjacency matrix = O(n ^ 2).\n# Code\nRuntime 793 ms || 94.87%\nMemory 23.5 MB || 5.13%\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n # O(n ^ 2) => the cost of adjacency matrix\n # Three types of node:\n # -1 -> not visit\n # i -> first pass by node i\n # [0 ~ n-1] -> another infected node\n n = len(graph)\n vis = [-1] * n\n for i in initial:\n vis[i] = i\n \n def dfs(node, cur):\n vis[node] = cur \n cnt = 1\n for i, v in enumerate(graph[node]):\n if not v: continue\n if vis[i] == -1:\n cnt += dfs(i, cur)\n elif vis[i] != cur:\n # The set is infected by another node\n vis[cur] = n\n return cnt\n \n ans = [-1, -1]\n for i in initial:\n count = 0\n for j, v in enumerate(graph[i]):\n if not v or vis[j] != -1: \n continue\n # reset\n vis[i] = i\n k = dfs(j, i)\n if vis[i] == i:\n count += k\n if count > ans[1]:\n ans = [i, count]\n if count == ans[1]:\n ans[0] = min(ans[0], i)\n\n return ans[0]\n```\nMemory optimization:\n\nRuntime: 787 ms || 96.15% \nMemory 18.8 MB || 96.15%\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n # O(n ^ 2) => the cost of adjacency matrix\n # Three types of node:\n # -1 -> not visit\n # i -> first pass by node i\n # [0 ~ n-1] -> another infected node\n n = len(graph)\n vis = [-1] * n\n for i in initial:\n vis[i] = i\n \n ans = [-1, -1]\n for i in initial:\n count = 0\n for j, v in enumerate(graph[i]):\n if not v or vis[j] != -1: \n continue\n q = [j]\n vis[i] = vis[j] = i\n cnt = infected = 0\n while q:\n node = q.pop()\n cnt += 1\n for nxt, v in enumerate(graph[node]):\n if not v: continue\n if vis[nxt] == -1:\n q.append(nxt)\n vis[nxt] = i\n elif vis[nxt] != i:\n # The set is infected by another node\n infected = 1\n if not infected:\n count += cnt\n if count > ans[1]:\n ans = [i, count]\n if count == ans[1]:\n ans[0] = min(ans[0], i)\n\n return ans[0]\n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops.
We will remove **exactly one node** from `initial`, **completely removing it and any connections from this node to any other node**.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,1,0\],\[1,1,1\],\[0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Example 3:**
**Input:** graph = \[\[1,1,0,0\],\[1,1,1,0\],\[0,1,1,1\],\[0,0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length < n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Python3 FT 90%, O(V+E) time and space: Union-Find and Cut/Articulation Point Detection | minimize-malware-spread-ii | 0 | 1 | # The Idea\n\nWe can use union-find to find infected clusters.\n* if a cluster has one infected node, deleting it saves the whole cluster. So the reduction is size(component)\n* if a cluster has 2+ infected nodes, then we can still save some nodes if some of them are cut points (articulation points), and the new clusters created are full of only uninfected nodes\n\nUnion-find and finding cut/articulation points both run in O(V+E) time.\n\nSee the code for details and more explanation.\n\nIn a way this solution is more complicated than the union-find-merge-clusters solutions because you need to find articulation points. And that\'s a relatively advanced algorithm.\n\nBut on the other hand, that algorithm (`findCuts`) isn\'t too hard to code up once you know it.* And you benefit from a simpler explanation - the code very directly answers the question "if I deleted this infected node, would I create a new cluster(s) of uninfected nodes?"\n\n*be VERY careful of replacing `v` with `p`, etc. though!\n\n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n debug = False\n\n # if we delete node u:\n # if u is not a cut point: reduction is componentSize if u is the only infected node, else 0\n # if u is a cut point: removing u isolates 1 or more child components from the rest of the graph\n # if the component that would be isolated has zero infected nodes, removing u saves all nodes\n # from infection. So we\'ll add those nodes to a running total for u\n # otherwise there is 1+ infected node, so eventually the whole component will become infected.\n # So no nodes in that component will be saved.\n\n # Finding cut points is a known DFS algo, onto which we can bolt on summing up clean and total node counts easily\n\n # So the steps are\n # 1. identify the connected components with union find\n # 2. for each connected component with an infected vertex: what infected vertices are in there\n # 3. scan over those infected components\n # a. if there\'s only one infected node, deleting it saves the whole cluster\n # b. if there are 2+, find cut points in the component. Then if an infected\n # vertex u is a cut point, then number of nodes saved is\n # i. clean nodes in "sub-components" that become isolated if we delete u\n # ii. plus 1 for the infected vertex we delete\n\n N = len(graph)\n\n ### (1) UNION-FIND\n p = [-1]*N # -size if root, else parent\n\n def getRoot(u: int) -> int:\n if p[u] < 0:\n return u\n\n p[u] = getRoot(p[u])\n return p[u]\n\n def union(u: int, v: int) -> None:\n ru = getRoot(u)\n rv = getRoot(v)\n\n if ru == rv:\n return\n\n # union smaller component into larger component\n if p[rv] < p[ru]:\n ru, rv = rv, ru\n\n p[ru] += p[rv]\n p[rv] = ru\n\n adj = defaultdict(list)\n for u in range(N):\n for v in range(u):\n if graph[u][v]:\n union(u, v)\n adj[u].append(v)\n adj[v].append(u)\n\n if debug: \n for i in range(N): \n js = list(j for j in adj[i])\n print(f"adj {i}: {js}")\n\n ### (2) FIND INFECTED COMPONENTS AND THEIR INFECTED VERTICES\n ccs = defaultdict(list) # infected CC root -> infected vertices\n for u in initial:\n ccs[getRoot(u)].append(u)\n\n ### (3) PROCESS EACH INFECTED COMPONENT\n time = [-1]*N\n lo = [-1]*N\n reductions = defaultdict(int) # infected index => the total reduction we get\n infset = set(initial)\n\n def findCuts(u: int, p: int, t: int, sz: int, ninf: int) -> tuple[int, int]:\n """\n Detects if u is a cut point. If so, and it isolates\n a cluster of all uninfected nodes from a cluster of infected nodes,\n then it increments reductions by that that number.\n\n Returns the number of clean and total nodes reachable from u without visiting p.\n\n Updates time and lo.\n """\n\n # This is a variation on identifying cut points, see https://cp-algorithms.com/graph/cutpoints.html,\n # modified to return node counts; the "plain vanilla" algo just identifies vertices that are\n # cut points.\n\n time[u] = t\n lo[u] = t\n total = 1\n clean = 0 if u in infset else 1\n for v in adj[u]:\n if v == p: continue\n \n if time[v] == -1:\n if debug: print(f" time[{u}] = {time[u]}, visiting {v} with time {t+1}")\n cl, ttl = findCuts(v, u, t+1, sz, ninf)\n if lo[v] >= time[u]:\n # deleting v isolates u and all reachable except via u-v\n if cl == ttl:\n reductions[u] += cl\n \n clean += cl\n total += ttl\n\n # regardless\n if lo[v] < lo[u]:\n if debug: print(f" {u}: non-parent(=={p}) neighbor {v} has lo[{v}] {lo[v]} < lo[{u}] {lo[u]}. Updating lo[{u}]")\n lo[u] = lo[v]\n\n # NOTE: we don\'t need this (and thus sz and numInf as params either) by always picking\n # an infected node as the root. this way the "ancestor cluster" and yet-unvisited\n # nodes will contain at least one infected node so we know that isolating them\n # won\'t reduce the solution (well yet-unvisited nodes might, but they\'ll be picked\n # up when visited later on)\n # (this was a bug I had to fix!!)\n # if lo[u] == time[u]:\n # # DFS from u never touched p and other ancestor nodes,\n # # so we include the "ancestor cluster" will all other nodes\n # cl = (sz - ninf) - clean\n # ttl = sz - total\n # if cl == ttl:\n # reductions[u] += cl\n\n if debug: print(f"node {u}: time[u] = {time[u]}, lo[u] = {lo[u]}, clean={clean}, total={total}, sz={sz}, numInf={numInf}")\n\n return clean, total\n\n bestReduction = 0\n bestVertex = min(initial)\n for r, inf in ccs.items():\n sz = -p[r]\n numInf = len(inf)\n if numInf == 1:\n u = inf[0]\n \n if sz > bestReduction or (sz == bestReduction and u < bestVertex):\n bestReduction = sz\n bestVertex = u\n\n if debug: print(f"iso: deleting {u} would reduce inf by {sz}")\n\n else:\n maxReductionPossible = sz - numInf + 1 # isolate all size(CC)-len(inf), plus 1 for deleting an infected node\n if maxReductionPossible < bestReduction: continue\n if maxReductionPossible == bestReduction and all(u > bestVertex for u in inf): continue # same reduction, but worse index\n\n # BUG FIX: start from an infected node\n # that way we don\'t have to handle the edge case where a cut point isolates all len(inf) infected\n # nodes from the "ancestor cluster" with only clean nodes\n if debug: print(f"finding cut points starting from {inf[0]}")\n findCuts(inf[0], -1, 0, sz, numInf)\n for u in inf:\n if reductions[u] + 1 > bestReduction or (reductions[u] + 1 == bestReduction and u < bestVertex):\n # +1 because we isolate all the clean nodes, and also delete an infected node\n bestReduction = reductions[u] + 1\n bestVertex = u\n\n if debug: print(f"cut: deleting {u} would reduce inf by {reductions[u] + 1}")\n\n return bestVertex\n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops.
We will remove **exactly one node** from `initial`, **completely removing it and any connections from this node to any other node**.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,1,0\],\[1,1,1\],\[0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Example 3:**
**Input:** graph = \[\[1,1,0,0\],\[1,1,1,0\],\[0,1,1,1\],\[0,0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length < n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Strongly connected components | minimize-malware-spread-ii | 0 | 1 | \n# Complexity\n- Time complexity:$$O(V+E)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(V)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n adj=collections.defaultdict(list)\n for i in range(len(graph)):\n for j in range(len(graph[0])):\n if graph[i][j]!=1 or i==j:continue\n adj[i].append(j)\n\n visited=set(initial)\n d=set()\n low=[-1]*len(graph)\n disc=[-1]*len(graph)\n time=0\n d=[min(initial),-1]\n\n def dfs(node,par):\n nonlocal time\n time+=1\n low[node]=disc[node]=time\n yes=False\n count=1\n for nei in adj[node]:\n if par==nei:continue\n if low[nei]!=-1:low[node]=min(low[node],disc[nei])\n else:\n yest,count2=dfs(nei,node)\n if not yest:count+=count2\n yes=yes or yest\n low[node]=min(low[node],low[nei])\n if disc[node]<=low[nei] and node in visited and not yest:\n if count>d[-1]:\n d[-1]=count\n d[0]=node\n elif count==d[-1]:d[0]=min(d[0],node)\n \n return (yes or node in visited,count)\n for i in initial:\n if low[i]==-1:dfs(i,-1)\n return d[0]\n\n \n \n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops.
We will remove **exactly one node** from `initial`, **completely removing it and any connections from this node to any other node**.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,1,0\],\[1,1,1\],\[0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Example 3:**
**Input:** graph = \[\[1,1,0,0\],\[1,1,1,0\],\[0,1,1,1\],\[0,0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length < n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Union Find Algorithm || Graph || Python3 | minimize-malware-spread-ii | 0 | 1 | # Complexity\n- Time complexity: O(N * N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\n\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n n = len(graph)\n initials = set()\n\n for i in initial:\n initials.add(i)\n\n parent = [i for i in range(n)]\n size = [1] * n\n\n for i in range(n):\n for j in range(n):\n if(graph[i][j] == 1 and i not in initials and j not in initials and i != j):\n self.union(i, j, parent, size)\n \n map = {}\n\n infected = [0] * n\n for i in initial:\n map[i] = set() # this will create a map for all components vs the infected numbe rof nodes in that component apart from i\n for j in range(n):\n if(graph[i][j] == 1 and i != j and j not in initials):\n p = self.find(j, parent)\n map[i].add(p)\n for c in map[i]:\n infected[c] += 1\n \n ans_node = -1\n ans_size = -1\n print(infected)\n print(size)\n print(map)\n for i in initial:\n components = map[i]\n s = 0\n for p in components:\n if(infected[p] == 1):\n s += size[p]\n \n if(s > ans_size):\n ans_size = s\n ans_node = i\n elif(s == ans_size):\n ans_node = min(i, ans_node)\n return ans_node\n\n\n def find(self, x, parent):\n if(parent[x] != x):\n parent[x] = self.find(parent[x], parent)\n return parent[x]\n \n def union(self, x, y, parent, size):\n root_x = self.find(x, parent)\n root_y = self.find(y, parent)\n\n if(root_x == root_y):\n return\n \n if(size[root_x] <= size[root_y]):\n parent[root_x] = root_y\n size[root_y] += size[root_x]\n else:\n parent[root_y] = root_x\n size[root_x] += size[root_y]\n\n\n\n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops.
We will remove **exactly one node** from `initial`, **completely removing it and any connections from this node to any other node**.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,1,0\],\[1,1,1\],\[0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Example 3:**
**Input:** graph = \[\[1,1,0,0\],\[1,1,1,0\],\[0,1,1,1\],\[0,0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length < n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Minimize Malware Spread II (Python) | minimize-malware-spread-ii | 0 | 1 | Intuition:\nThe intuition behind the solution is to identify the initially infected node that, when removed, would minimize the spread of malware in the graph. To do this, the code first identifies the connected components in the graph using the Union-Find data structure. It then calculates the number of nodes in each connected component that are infected by each initially infected node. Finally, it selects the initially infected node that infects the largest number of clean nodes in the graph, breaking ties by selecting the node with the smallest index.\n\nApproach:\n1. Initialize the necessary variables and data structures.\n2. Use the Union-Find data structure to find the connected components in the graph.\n3. Iterate over the pairs of clean nodes and merge the connected components if there is an edge between them.\n4. Create a defaultdict `infect_node` to keep track of the nodes infected by each initially infected node.\n5. Create a Counter `infected_by` to count the number of clean nodes infected by each connected component.\n6. Iterate over the initially infected nodes and the clean nodes.\n - If there is an edge between the initially infected node and the clean node, add the connected component of the clean node to the set of infected nodes for the initially infected node.\n - Increment the count of infected nodes by the connected component.\n7. Create a Counter `size` to count the size of each connected component in the graph.\n8. Iterate over the initially infected nodes and their infected nodes.\n - For each infected node, if it infects only one clean node, increment the count by the size of its connected component.\n9. Determine the initially infected node that infects the largest number of clean nodes, breaking ties by selecting the node with the smallest index.\n10. Return the selected initially infected node as the result.\n\nComplexity:\nTime complexity: The time complexity of the solution depends on the size of the graph and the number of initially infected nodes. The Union-Find operations take O(N) time in the worst case, where N is the number of nodes in the graph. The iteration over the initially infected nodes and clean nodes takes O(K * (N - M) + K * M), where K is the number of initially infected nodes and M is the number of clean nodes. Therefore, the overall time complexity is O(N + K * (N - M) + K * M).\nSpace complexity: The space complexity is O(N), where N is the number of nodes in the graph. The Union-Find data structure requires O(N) space, and the additional data structures used in the solution also require O(N) space.\n\n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n N = len(graph)\n uf = UF(N)\n\n clean = set(range(N)) - set(initial)\n\n for u, v in itertools.combinations(clean, 2):\n if graph[u][v]:\n uf.union(u,v)\n\n infect_node = collections.defaultdict(set)\n infected_by = collections.Counter()\n\n ans = min(initial)\n max = -1\n\n for i in initial:\n for c in clean:\n if graph[i][c]==1:\n infect_node[i].add(uf.find(c))\n # infected[uf.find(c)] += [i]\n for idx in infect_node[i]:\n infected_by[idx] += 1\n \n size = collections.Counter(uf.find(i) for i in clean)\n\n for key, nodes in infect_node.items():\n cnt = 0\n for node in nodes:\n if infected_by[node]==1:\n cnt += size[node]\n if cnt > max:\n max = cnt\n ans = key\n elif cnt==max:\n ans = min(ans, key)\n return ans\n \nclass UF:\n def __init__(self, n):\n self.parent = [-1]*n\n self.unique = n\n\n def find(self, a):\n if self.parent[a]>=0:\n self.parent[a] = self.find(self.parent[a])\n return self.parent[a]\n else:\n return a\n \n def union(self, a, b):\n pa = self.find(a)\n pb = self.find(b)\n\n if pa==pb: return False\n\n if pa<pb:\n self.parent[pa] += self.parent[pb]\n self.parent[pb] = pa\n else:\n self.parent[pb] += self.parent[pa]\n self.parent[pa] = pb\n self.unique-=1\n return True\n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops.
We will remove **exactly one node** from `initial`, **completely removing it and any connections from this node to any other node**.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,1,0\],\[1,1,1\],\[0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Example 3:**
**Input:** graph = \[\[1,1,0,0\],\[1,1,1,0\],\[0,1,1,1\],\[0,0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length < n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Solved by using Disjoint set | minimize-malware-spread-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n n=len(graph)\n par=[-1]*n\n size=[1]*n\n \n for i in range(n):\n par[i]=i\n \n def findpar(i):\n if par[i]==i:\n return i\n else:\n par[i]=findpar(par[i])\n return par[i]\n\n def merge(i1,i2):\n if size[i1]>=size[i2]:\n par[i2]=i1\n size[i1]+=size[i2]\n else:\n par[i1]=i2\n size[i2]+=size[i1]\n \n a=set(initial)\n \n for i in range(n):\n for j in range(n):\n if graph[i][j]==1 and (i not in a and j not in a):\n p1=findpar(i)\n p2=findpar(j)\n # print(i,p1,j,p2)\n if p1!=p2:\n merge(p1,p2)\n # print(par[i],size[i],par[j],size[j],56)\n \n inf=[0]*n\n d={}\n for i in initial:\n for j in range(n):\n if graph[i][j]==1 and i!=j and j not in a:\n p=findpar(j)\n if i not in d:\n d[i]=[p]\n inf[p]+=1\n elif p not in d[i]:\n d[i].append(p)\n inf[p]+=1\n \n\n\n \n mini=-1\n ans=-1\n initial.sort()\n for i in initial:\n if i in d:\n b=d[i]\n else:\n mini=max(0,mini)\n ans=min(i,ans)\n continue\n total=0\n for p in b:\n if inf[p]==1 :\n total+=size[p]\n if total>mini:\n mini=total\n ans=i\n \n return initial[0] if ans==-1 else ans\n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops.
We will remove **exactly one node** from `initial`, **completely removing it and any connections from this node to any other node**.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,1,0\],\[1,1,1\],\[0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Example 3:**
**Input:** graph = \[\[1,1,0,0\],\[1,1,1,0\],\[0,1,1,1\],\[0,0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length < n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Brute-force DFS in Python, faster than 70% | minimize-malware-spread-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTry all elements in `initial` and find the best one. This brute-force solution employs depth-first search (DFS) to explore all the inflected nodes in the network where one element from `initial` is removed. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo speed up the performance of DFS, the graph is revised from adjacency matrix to adjacency list. \n\n# Complexity\n- Time complexity: $$O(|U| \\times (|V|+|E|))$$, where $$U$$ is `initial` set and $$|U| \\le |V|, |E| \\le |V|^2$$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n # DFS that isoloates the temporally removed node.\n def dfs(v, removed, visited):\n visited.add(v)\n for u in graph[v]:\n if u != removed and u not in visited:\n dfs(u, removed, visited)\n\n # Reconstruct the graph from adjacency matrix to adjacency list.\n graph = [[u for u, c in enumerate(graph[v]) if c == 1] for v in range(len(graph))]\n ans = (inf, inf)\n for removed in initial:\n visited = set()\n for v in initial:\n if v != removed and v not in visited:\n dfs(v, removed, visited)\n ans = min(ans, (len(visited), removed))\n return ans[1]\n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops.
We will remove **exactly one node** from `initial`, **completely removing it and any connections from this node to any other node**.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,1,0\],\[1,1,1\],\[0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Example 3:**
**Input:** graph = \[\[1,1,0,0\],\[1,1,1,0\],\[0,1,1,1\],\[0,0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length < n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
O(N) Time and Space Union Find Approach | minimize-malware-spread-ii | 0 | 1 | # Intuition\nThe key intuition to this problem besides the realization of Union Find is that we are working with a special type of instance in this problem, namely that \n\nif a node has no infection, we don\'t have to care about it \nif a node has more than one infection, we also don\'t have to care about it \nonly if a node has only one infecting node do we need to care about it \n\nThe other key idea is that \nWe can split initial nodes into clean and infected nodes \n\nWith these, we set up our number of nodes n at start, get the initial infected nodes as set cast of initial, and intial clean nodes as difference of set of all nodes with infected nodes \n\nAfter that, we set up our union find with size n and then process all clean edges in graph as unions of those nodes \n\nWe then process all infected nodes with all clean nodes and if there is a connection we append unique versions of the component keys to the malware on a connection (basically, for each node determine its infection level of either 0, 1, or many)\n\nSet up a malware size dictionary with keys for each initially infected nodes \n\nget the uniquely infected components from our component processing above \n\nloop through uniquely infected components, incrementing the appropriate node in malware size dictionary \n\nGet the max size of the malware values \nGet the item list of the malwave nodes that have a size equal to the max size in O(ni) \n\nset best id as n + 1 as there will never be that node present \n\nloop over the item list and set best id as the min of itself and the id of that item \n\nreturn best item node id \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproach was to solve this in as many of straightforward processes as possible. This was done to reduce the overall looping processions involved into as many flattened components as possible. \n\n# Complexity\n- Time complexity: O(N) where N is total cost of below summation of components \n - O(n) - set up initially infected nodes \n - O(n) - set up initially clean nodes \n - O(n) - set up UF \n - O(ec) - ec is the edges that are clean \n - this is incurred during initial uf set up \n - O(ei) - ei is the edges that are infected \n - this is incurred during set up of components to malware \n - O(ni) - cost of setting up malware size \n - O(p) - cost of setting up uniquely infected components\n - p is the number of parent nodes in the unioned graph \n - O(p) - cost of inputting values to malware size \n - O(p) - cost of finding max value in malware size \n - O(p) - cost of setting up item list \n - O(pm) - cost of finding best id in the item list \n - as these are all linear, we can treat this is a sum of O(N)\n\n- Space complexity: O(N) where N is the total sum of below components \n - O(N) - union find, infected nodes, clean nodes \n - O(P) - components to malware \n - O(UP) - uniquely infected components \n - O(NI) - malware size \n - O(pm) - item list \n - All linear, no stacked amounts, so O(N) \n\n# Code\n```\nclass Solution:\n class UnionFind:\n # initialize based on size \n def __init__(self, size):\n self.size = size\n # set parent as list of range over size \n self.parent = list(range(size))\n # set rank as 1 for i in range size \n self.rank = [1 for i in range(size)]\n \n # find parent recursively \n def find(self, node_id):\n if self.parent[node_id] != node_id : \n self.parent[node_id] = self.find(self.parent[node_id])\n return self.parent[node_id]\n \n # determine if parents match \n def is_connected(self,p,q):\n return self.find(p) == self.find(q)\n \n # combine components of p and q \n def join(self, p, q):\n parent_p = self.find(p)\n parent_q = self.find(q)\n\n # if rank p less than rank q, recall with swap then return \n if self.rank[parent_p] < self.rank[parent_q]:\n self.join(parent_q, parent_p)\n return\n \n # otherwise, if not connected, set q to p and update p rank \n if not self.is_connected(parent_p, parent_q):\n self.parent[parent_q] = parent_p\n self.rank[parent_p] += self.rank[parent_q]\n \n # get the size of the component p is in\n def get_size(self,p):\n return self.rank[self.find(p)]\n \n \n def minMalwareSpread(self, graph: List[List[int]], initial: List[int]) -> int:\n # get length of graph, initially infected and initially clean \n n = len(graph)\n all_nodes = set(range(n))\n initially_infected_nodes = set(initial)\n initially_clean_nodes = all_nodes.difference(initially_infected_nodes)\n\n # set up union find \n uf = Solution.UnionFind(n)\n # process clean nodes originally \n for source in initially_clean_nodes : \n for destination in initially_clean_nodes : \n if graph[source][destination] : \n uf.join(source, destination)\n\n # for each component, get a set of all initially infected nodes that connect directly to it\n components_to_malware = defaultdict(list)\n # loop over initially infected nodes \n for source in initially_infected_nodes :\n # and loop over all initially clean nodes \n for destination in initially_clean_nodes :\n # if they are connected \n if graph[source][destination] == 1 :\n # get the component key \n component_key = uf.find(destination)\n # only add uniques \n if source not in components_to_malware[component_key] : \n components_to_malware[component_key].append(source)\n \n\n # Set up the malware size dictionary for each initially infected node \n malware_size = defaultdict(int)\n # process initial nodes \n for node in initially_infected_nodes :\n # so that they have a value of 0 \n malware_size[node] = 0\n\n # for each component, if it is connected to :\n # 0 malware nodes -> they will never be infected\n # 1 malware nodes -> uniquely infected (only these matter)\n # +2 malware nodes -> never not infected \n # get the uniquely infected components by getting the ones that have a length of 1 in components to malware \n uniquely_infected_components = [component for component in components_to_malware.keys() if len(components_to_malware[component]) == 1]\n\n # go through uniquely infected components only \n for component in uniquely_infected_components :\n # and update malware size for the specific node stored in that list \n malware_size[components_to_malware[component][0]] += uf.get_size(component)\n \n # get the max size of all malware size values \n max_size = max(malware_size.values())\n # get the items that have the max size in the items of the malware size items \n item_list = list(item for item in malware_size.items() if malware_size[item[0]] == max_size)\n # set best id outside of range \n best_id = n + 1 \n # get your best id without sorting \n for item in item_list : \n best_id = min(best_id, item[0])\n # return the best id \n return best_id\n``` | 0 | You are given a network of `n` nodes represented as an `n x n` adjacency matrix `graph`, where the `ith` node is directly connected to the `jth` node if `graph[i][j] == 1`.
Some nodes `initial` are initially infected by malware. Whenever two nodes are directly connected, and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose `M(initial)` is the final number of nodes infected with malware in the entire network after the spread of malware stops.
We will remove **exactly one node** from `initial`, **completely removing it and any connections from this node to any other node**.
Return the node that, if removed, would minimize `M(initial)`. If multiple nodes could be removed to minimize `M(initial)`, return such a node with **the smallest index**.
**Example 1:**
**Input:** graph = \[\[1,1,0\],\[1,1,0\],\[0,0,1\]\], initial = \[0,1\]
**Output:** 0
**Example 2:**
**Input:** graph = \[\[1,1,0\],\[1,1,1\],\[0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Example 3:**
**Input:** graph = \[\[1,1,0,0\],\[1,1,1,0\],\[0,1,1,1\],\[0,0,1,1\]\], initial = \[0,1\]
**Output:** 1
**Constraints:**
* `n == graph.length`
* `n == graph[i].length`
* `2 <= n <= 300`
* `graph[i][j]` is `0` or `1`.
* `graph[i][j] == graph[j][i]`
* `graph[i][i] == 1`
* `1 <= initial.length < n`
* `0 <= initial[i] <= n - 1`
* All the integers in `initial` are **unique**. | null |
Python3 solution | unique-email-addresses | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n myDict = set()\n for e in emails:\n local,domain = e.split(\'@\')\n local = local.split(\'+\')[0]\n local = local.replace(\'.\',\'\')\n myDict.add((local,domain))\n return len(myDict)\n``` | 1 | Every **valid email** consists of a **local name** and a **domain name**, separated by the `'@'` sign. Besides lowercase letters, the email may contain one or more `'.'` or `'+'`.
* For example, in `"[email protected] "`, `"alice "` is the **local name**, and `"leetcode.com "` is the **domain name**.
If you add periods `'.'` between some characters in the **local name** part of an email address, mail sent there will be forwarded to the same address without dots in the local name. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` and `"[email protected] "` forward to the same email address.
If you add a plus `'+'` in the **local name**, everything after the first plus sign **will be ignored**. This allows certain emails to be filtered. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` will be forwarded to `"[email protected] "`.
It is possible to use both of these rules at the same time.
Given an array of strings `emails` where we send one email to each `emails[i]`, return _the number of different addresses that actually receive mails_.
**Example 1:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 2
**Explanation:** "[email protected] " and "[email protected] " actually receive mails.
**Example 2:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 3
**Constraints:**
* `1 <= emails.length <= 100`
* `1 <= emails[i].length <= 100`
* `emails[i]` consist of lowercase English letters, `'+'`, `'.'` and `'@'`.
* Each `emails[i]` contains exactly one `'@'` character.
* All local and domain names are non-empty.
* Local names do not start with a `'+'` character.
* Domain names end with the `".com "` suffix. | null |
Python3 solution | unique-email-addresses | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n myDict = set()\n for e in emails:\n local,domain = e.split(\'@\')\n local = local.split(\'+\')[0]\n local = local.replace(\'.\',\'\')\n myDict.add((local,domain))\n return len(myDict)\n``` | 1 | A binary tree is **uni-valued** if every node in the tree has the same value.
Given the `root` of a binary tree, return `true` _if the given tree is **uni-valued**, or_ `false` _otherwise._
**Example 1:**
**Input:** root = \[1,1,1,1,1,null,1\]
**Output:** true
**Example 2:**
**Input:** root = \[2,2,2,5,2\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val < 100` | null |
📌📌 Easy & Simple || Well-Defined Code || For Beginners 🐍 | unique-email-addresses | 0 | 1 | \'\'\'\n\n\tclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n \n res = set()\n for email in emails:\n local,domain = email.split(\'@\')\n tmp = ""\n for c in local:\n if c==".": continue\n elif c=="+": break\n else: tmp+=c\n res.add(tmp+"@"+domain)\n \n return len(res)\n\n### **If you got the idea please Upvote !!!\uD83E\uDD1E** | 20 | Every **valid email** consists of a **local name** and a **domain name**, separated by the `'@'` sign. Besides lowercase letters, the email may contain one or more `'.'` or `'+'`.
* For example, in `"[email protected] "`, `"alice "` is the **local name**, and `"leetcode.com "` is the **domain name**.
If you add periods `'.'` between some characters in the **local name** part of an email address, mail sent there will be forwarded to the same address without dots in the local name. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` and `"[email protected] "` forward to the same email address.
If you add a plus `'+'` in the **local name**, everything after the first plus sign **will be ignored**. This allows certain emails to be filtered. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` will be forwarded to `"[email protected] "`.
It is possible to use both of these rules at the same time.
Given an array of strings `emails` where we send one email to each `emails[i]`, return _the number of different addresses that actually receive mails_.
**Example 1:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 2
**Explanation:** "[email protected] " and "[email protected] " actually receive mails.
**Example 2:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 3
**Constraints:**
* `1 <= emails.length <= 100`
* `1 <= emails[i].length <= 100`
* `emails[i]` consist of lowercase English letters, `'+'`, `'.'` and `'@'`.
* Each `emails[i]` contains exactly one `'@'` character.
* All local and domain names are non-empty.
* Local names do not start with a `'+'` character.
* Domain names end with the `".com "` suffix. | null |
📌📌 Easy & Simple || Well-Defined Code || For Beginners 🐍 | unique-email-addresses | 0 | 1 | \'\'\'\n\n\tclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n \n res = set()\n for email in emails:\n local,domain = email.split(\'@\')\n tmp = ""\n for c in local:\n if c==".": continue\n elif c=="+": break\n else: tmp+=c\n res.add(tmp+"@"+domain)\n \n return len(res)\n\n### **If you got the idea please Upvote !!!\uD83E\uDD1E** | 20 | A binary tree is **uni-valued** if every node in the tree has the same value.
Given the `root` of a binary tree, return `true` _if the given tree is **uni-valued**, or_ `false` _otherwise._
**Example 1:**
**Input:** root = \[1,1,1,1,1,null,1\]
**Output:** true
**Example 2:**
**Input:** root = \[2,2,2,5,2\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val < 100` | null |
Easy-understanding python solution (44ms, faster than 99.3%) | unique-email-addresses | 0 | 1 | ```\nclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n def parse(email):\n local, domain = email.split(\'@\')\n local = local.split(\'+\')[0].replace(\'.\',"")\n return f"{local}@{domain}"\n \n return len(set(map(parse, emails)))\n``` | 34 | Every **valid email** consists of a **local name** and a **domain name**, separated by the `'@'` sign. Besides lowercase letters, the email may contain one or more `'.'` or `'+'`.
* For example, in `"[email protected] "`, `"alice "` is the **local name**, and `"leetcode.com "` is the **domain name**.
If you add periods `'.'` between some characters in the **local name** part of an email address, mail sent there will be forwarded to the same address without dots in the local name. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` and `"[email protected] "` forward to the same email address.
If you add a plus `'+'` in the **local name**, everything after the first plus sign **will be ignored**. This allows certain emails to be filtered. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` will be forwarded to `"[email protected] "`.
It is possible to use both of these rules at the same time.
Given an array of strings `emails` where we send one email to each `emails[i]`, return _the number of different addresses that actually receive mails_.
**Example 1:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 2
**Explanation:** "[email protected] " and "[email protected] " actually receive mails.
**Example 2:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 3
**Constraints:**
* `1 <= emails.length <= 100`
* `1 <= emails[i].length <= 100`
* `emails[i]` consist of lowercase English letters, `'+'`, `'.'` and `'@'`.
* Each `emails[i]` contains exactly one `'@'` character.
* All local and domain names are non-empty.
* Local names do not start with a `'+'` character.
* Domain names end with the `".com "` suffix. | null |
Easy-understanding python solution (44ms, faster than 99.3%) | unique-email-addresses | 0 | 1 | ```\nclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n def parse(email):\n local, domain = email.split(\'@\')\n local = local.split(\'+\')[0].replace(\'.\',"")\n return f"{local}@{domain}"\n \n return len(set(map(parse, emails)))\n``` | 34 | A binary tree is **uni-valued** if every node in the tree has the same value.
Given the `root` of a binary tree, return `true` _if the given tree is **uni-valued**, or_ `false` _otherwise._
**Example 1:**
**Input:** root = \[1,1,1,1,1,null,1\]
**Output:** true
**Example 2:**
**Input:** root = \[2,2,2,5,2\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val < 100` | null |
simple solution | unique-email-addresses | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n arr=[]\n for i in emails:\n if \'@\' in i:\n at = i.index(\'@\')\n temp=i[:at]\n temp=temp.replace(".","")\n \n if \'+\' in temp:\n plus = temp.index(\'+\')\n temp = temp[0:plus]\n temp+=i[at:]\n if temp not in arr:\n arr.append(temp)\n else:\n continue\n #print(arr)\n return len(arr)\n\n``` | 1 | Every **valid email** consists of a **local name** and a **domain name**, separated by the `'@'` sign. Besides lowercase letters, the email may contain one or more `'.'` or `'+'`.
* For example, in `"[email protected] "`, `"alice "` is the **local name**, and `"leetcode.com "` is the **domain name**.
If you add periods `'.'` between some characters in the **local name** part of an email address, mail sent there will be forwarded to the same address without dots in the local name. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` and `"[email protected] "` forward to the same email address.
If you add a plus `'+'` in the **local name**, everything after the first plus sign **will be ignored**. This allows certain emails to be filtered. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` will be forwarded to `"[email protected] "`.
It is possible to use both of these rules at the same time.
Given an array of strings `emails` where we send one email to each `emails[i]`, return _the number of different addresses that actually receive mails_.
**Example 1:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 2
**Explanation:** "[email protected] " and "[email protected] " actually receive mails.
**Example 2:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 3
**Constraints:**
* `1 <= emails.length <= 100`
* `1 <= emails[i].length <= 100`
* `emails[i]` consist of lowercase English letters, `'+'`, `'.'` and `'@'`.
* Each `emails[i]` contains exactly one `'@'` character.
* All local and domain names are non-empty.
* Local names do not start with a `'+'` character.
* Domain names end with the `".com "` suffix. | null |
simple solution | unique-email-addresses | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n arr=[]\n for i in emails:\n if \'@\' in i:\n at = i.index(\'@\')\n temp=i[:at]\n temp=temp.replace(".","")\n \n if \'+\' in temp:\n plus = temp.index(\'+\')\n temp = temp[0:plus]\n temp+=i[at:]\n if temp not in arr:\n arr.append(temp)\n else:\n continue\n #print(arr)\n return len(arr)\n\n``` | 1 | A binary tree is **uni-valued** if every node in the tree has the same value.
Given the `root` of a binary tree, return `true` _if the given tree is **uni-valued**, or_ `false` _otherwise._
**Example 1:**
**Input:** root = \[1,1,1,1,1,null,1\]
**Output:** true
**Example 2:**
**Input:** root = \[2,2,2,5,2\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val < 100` | null |
Solution | unique-email-addresses | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numUniqueEmails(vector<string>& emails) {\n unordered_set<string> uniqEmails;\n for(string& email: emails) {\n bool inDomain = false;\n string actEmail;\n int i = 0;\n for(int i = 0; i < email.size(); ) {\n char c = email[i];\n if (inDomain) {\n actEmail.push_back(c);\n i++;\n } else {\n if (c == \'@\') {\n actEmail.push_back(c);\n inDomain = true;\n i++;\n } else if (c == \'.\') {\n i++;\n } else if (c == \'+\') {\n while(email[i] != \'@\') {\n i++;\n }\n } else {\n actEmail.push_back(c);\n i++;\n }\n }\n }\n uniqEmails.insert(actEmail);\n }\n return uniqEmails.size();\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n addresses = set()\n\n for email in emails:\n local, domain = email.split(\'@\')\n if \'+\' in local:\n local = local[:local.index(\'+\')]\n local = local.replace(\'.\', \'\')\n addresses.add(local + \'@\' + domain)\n \n return len(addresses)\n```\n\n```Java []\nclass Solution {\n public int numUniqueEmails(String[] emails) {\n Set<String> es = new HashSet<>();\n \n for (String e: emails) {\n es.add(strip(e));\n }\n return es.size();\n }\n public String strip(String e) {\n int i = 0;\n StringBuilder res = new StringBuilder();\n \n while (i < e.length()) {\n char c = e.charAt(i);\n if (c == \'+\') {\n i = e.indexOf(\'@\');\n continue;\n } else if (c == \'@\') {\n res.append(e.substring(i));\n return res.toString();\n } else if (c != \'.\')\n res.append(c);\n i++;\n }\n return res.toString();\n }\n}\n```\n | 2 | Every **valid email** consists of a **local name** and a **domain name**, separated by the `'@'` sign. Besides lowercase letters, the email may contain one or more `'.'` or `'+'`.
* For example, in `"[email protected] "`, `"alice "` is the **local name**, and `"leetcode.com "` is the **domain name**.
If you add periods `'.'` between some characters in the **local name** part of an email address, mail sent there will be forwarded to the same address without dots in the local name. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` and `"[email protected] "` forward to the same email address.
If you add a plus `'+'` in the **local name**, everything after the first plus sign **will be ignored**. This allows certain emails to be filtered. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` will be forwarded to `"[email protected] "`.
It is possible to use both of these rules at the same time.
Given an array of strings `emails` where we send one email to each `emails[i]`, return _the number of different addresses that actually receive mails_.
**Example 1:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 2
**Explanation:** "[email protected] " and "[email protected] " actually receive mails.
**Example 2:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 3
**Constraints:**
* `1 <= emails.length <= 100`
* `1 <= emails[i].length <= 100`
* `emails[i]` consist of lowercase English letters, `'+'`, `'.'` and `'@'`.
* Each `emails[i]` contains exactly one `'@'` character.
* All local and domain names are non-empty.
* Local names do not start with a `'+'` character.
* Domain names end with the `".com "` suffix. | null |
Solution | unique-email-addresses | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numUniqueEmails(vector<string>& emails) {\n unordered_set<string> uniqEmails;\n for(string& email: emails) {\n bool inDomain = false;\n string actEmail;\n int i = 0;\n for(int i = 0; i < email.size(); ) {\n char c = email[i];\n if (inDomain) {\n actEmail.push_back(c);\n i++;\n } else {\n if (c == \'@\') {\n actEmail.push_back(c);\n inDomain = true;\n i++;\n } else if (c == \'.\') {\n i++;\n } else if (c == \'+\') {\n while(email[i] != \'@\') {\n i++;\n }\n } else {\n actEmail.push_back(c);\n i++;\n }\n }\n }\n uniqEmails.insert(actEmail);\n }\n return uniqEmails.size();\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n addresses = set()\n\n for email in emails:\n local, domain = email.split(\'@\')\n if \'+\' in local:\n local = local[:local.index(\'+\')]\n local = local.replace(\'.\', \'\')\n addresses.add(local + \'@\' + domain)\n \n return len(addresses)\n```\n\n```Java []\nclass Solution {\n public int numUniqueEmails(String[] emails) {\n Set<String> es = new HashSet<>();\n \n for (String e: emails) {\n es.add(strip(e));\n }\n return es.size();\n }\n public String strip(String e) {\n int i = 0;\n StringBuilder res = new StringBuilder();\n \n while (i < e.length()) {\n char c = e.charAt(i);\n if (c == \'+\') {\n i = e.indexOf(\'@\');\n continue;\n } else if (c == \'@\') {\n res.append(e.substring(i));\n return res.toString();\n } else if (c != \'.\')\n res.append(c);\n i++;\n }\n return res.toString();\n }\n}\n```\n | 2 | A binary tree is **uni-valued** if every node in the tree has the same value.
Given the `root` of a binary tree, return `true` _if the given tree is **uni-valued**, or_ `false` _otherwise._
**Example 1:**
**Input:** root = \[1,1,1,1,1,null,1\]
**Output:** true
**Example 2:**
**Input:** root = \[2,2,2,5,2\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val < 100` | null |
Python 3 with explanations | unique-email-addresses | 0 | 1 | ```Python 3\nclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n\t\t# Create set which may contain only unique values\n\t\ts = set()\n\t\t# For every entry in the list\n for e in emails:\n\t\t\t# If entry is not empty\n if len(e) > 0:\n\t\t\t\t# Split entry into two parts - before and after @ sign\n a = e.split(\'@\')[0]\n b = e.split(\'@\')[1]\n\t\t\t\t# If first part (local) contains + sign\n if \'+\' in a:\n\t\t\t\t\t# Split this part again into two parts - before and after + sign\n\t\t\t\t\t# and replace dots in the first part with nothing, i.e. remove them\n\t\t\t\t\t# then reconstruct mail address by adding @ and the second part\n s.add(a.split(\'+\')[0].replace(\'.\', \'\') + \'@\' + b)\n else:\n\t\t\t\t\t# If there is no + sign in the first part, then only remove dots\n\t\t\t\t\t# and reconstruct mail address by adding @ and the second part\n s.add(a.replace(\'.\', \'\') + \'@\' + b)\n\t\t# Return length of our set, i.e. number of entries\n return len(s)\n``` | 17 | Every **valid email** consists of a **local name** and a **domain name**, separated by the `'@'` sign. Besides lowercase letters, the email may contain one or more `'.'` or `'+'`.
* For example, in `"[email protected] "`, `"alice "` is the **local name**, and `"leetcode.com "` is the **domain name**.
If you add periods `'.'` between some characters in the **local name** part of an email address, mail sent there will be forwarded to the same address without dots in the local name. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` and `"[email protected] "` forward to the same email address.
If you add a plus `'+'` in the **local name**, everything after the first plus sign **will be ignored**. This allows certain emails to be filtered. Note that this rule **does not apply** to **domain names**.
* For example, `"[email protected] "` will be forwarded to `"[email protected] "`.
It is possible to use both of these rules at the same time.
Given an array of strings `emails` where we send one email to each `emails[i]`, return _the number of different addresses that actually receive mails_.
**Example 1:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 2
**Explanation:** "[email protected] " and "[email protected] " actually receive mails.
**Example 2:**
**Input:** emails = \[ "[email protected] ", "[email protected] ", "[email protected] "\]
**Output:** 3
**Constraints:**
* `1 <= emails.length <= 100`
* `1 <= emails[i].length <= 100`
* `emails[i]` consist of lowercase English letters, `'+'`, `'.'` and `'@'`.
* Each `emails[i]` contains exactly one `'@'` character.
* All local and domain names are non-empty.
* Local names do not start with a `'+'` character.
* Domain names end with the `".com "` suffix. | null |
Python 3 with explanations | unique-email-addresses | 0 | 1 | ```Python 3\nclass Solution:\n def numUniqueEmails(self, emails: List[str]) -> int:\n\t\t# Create set which may contain only unique values\n\t\ts = set()\n\t\t# For every entry in the list\n for e in emails:\n\t\t\t# If entry is not empty\n if len(e) > 0:\n\t\t\t\t# Split entry into two parts - before and after @ sign\n a = e.split(\'@\')[0]\n b = e.split(\'@\')[1]\n\t\t\t\t# If first part (local) contains + sign\n if \'+\' in a:\n\t\t\t\t\t# Split this part again into two parts - before and after + sign\n\t\t\t\t\t# and replace dots in the first part with nothing, i.e. remove them\n\t\t\t\t\t# then reconstruct mail address by adding @ and the second part\n s.add(a.split(\'+\')[0].replace(\'.\', \'\') + \'@\' + b)\n else:\n\t\t\t\t\t# If there is no + sign in the first part, then only remove dots\n\t\t\t\t\t# and reconstruct mail address by adding @ and the second part\n s.add(a.replace(\'.\', \'\') + \'@\' + b)\n\t\t# Return length of our set, i.e. number of entries\n return len(s)\n``` | 17 | A binary tree is **uni-valued** if every node in the tree has the same value.
Given the `root` of a binary tree, return `true` _if the given tree is **uni-valued**, or_ `false` _otherwise._
**Example 1:**
**Input:** root = \[1,1,1,1,1,null,1\]
**Output:** true
**Example 2:**
**Input:** root = \[2,2,2,5,2\]
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val < 100` | null |
Easy python solution beginners friendly. 🔥🔥 | binary-subarrays-with-sum | 0 | 1 | \n# Code\n```\nclass Solution:\n def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:\n //atmost(sum=goal) - atmost(sum=goal-1)\n return self.countSubarrays(nums,goal)-self.countSubarrays(nums,goal-1)\n\n def countSubarrays(self,nums,target):\n l=0\n count=0\n preSum=0\n if target<0:\n return 0\n for r in range(len(nums)):\n preSum+=nums[r]\n while preSum>target:\n preSum-=nums[l]\n l+=1\n count+=(r-l+1)\n return count\n```\n\n | 4 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
Easy python solution beginners friendly. 🔥🔥 | binary-subarrays-with-sum | 0 | 1 | \n# Code\n```\nclass Solution:\n def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:\n //atmost(sum=goal) - atmost(sum=goal-1)\n return self.countSubarrays(nums,goal)-self.countSubarrays(nums,goal-1)\n\n def countSubarrays(self,nums,target):\n l=0\n count=0\n preSum=0\n if target<0:\n return 0\n for r in range(len(nums)):\n preSum+=nums[r]\n while preSum>target:\n preSum-=nums[l]\n l+=1\n count+=(r-l+1)\n return count\n```\n\n | 4 | Given a `wordlist`, we want to implement a spellchecker that converts a query word into a correct word.
For a given `query` word, the spell checker handles two categories of spelling mistakes:
* Capitalization: If the query matches a word in the wordlist (**case-insensitive**), then the query word is returned with the same case as the case in the wordlist.
* Example: `wordlist = [ "yellow "]`, `query = "YellOw "`: `correct = "yellow "`
* Example: `wordlist = [ "Yellow "]`, `query = "yellow "`: `correct = "Yellow "`
* Example: `wordlist = [ "yellow "]`, `query = "yellow "`: `correct = "yellow "`
* Vowel Errors: If after replacing the vowels `('a', 'e', 'i', 'o', 'u')` of the query word with any vowel individually, it matches a word in the wordlist (**case-insensitive**), then the query word is returned with the same case as the match in the wordlist.
* Example: `wordlist = [ "YellOw "]`, `query = "yollow "`: `correct = "YellOw "`
* Example: `wordlist = [ "YellOw "]`, `query = "yeellow "`: `correct = " "` (no match)
* Example: `wordlist = [ "YellOw "]`, `query = "yllw "`: `correct = " "` (no match)
In addition, the spell checker operates under the following precedence rules:
* When the query exactly matches a word in the wordlist (**case-sensitive**), you should return the same word back.
* When the query matches a word up to capitlization, you should return the first such match in the wordlist.
* When the query matches a word up to vowel errors, you should return the first such match in the wordlist.
* If the query has no matches in the wordlist, you should return the empty string.
Given some `queries`, return a list of words `answer`, where `answer[i]` is the correct word for `query = queries[i]`.
**Example 1:**
**Input:** wordlist = \["KiTe","kite","hare","Hare"\], queries = \["kite","Kite","KiTe","Hare","HARE","Hear","hear","keti","keet","keto"\]
**Output:** \["kite","KiTe","KiTe","Hare","hare","","","KiTe","","KiTe"\]
**Example 2:**
**Input:** wordlist = \["yellow"\], queries = \["YellOw"\]
**Output:** \["yellow"\]
**Constraints:**
* `1 <= wordlist.length, queries.length <= 5000`
* `1 <= wordlist[i].length, queries[i].length <= 7`
* `wordlist[i]` and `queries[i]` consist only of only English letters. | null |
Sliding Window Approach | binary-subarrays-with-sum | 0 | 1 | ```\nclass Solution:\n def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:\n res=defaultdict(int)\n res[0]=1\n ans=0\n prefixsum=0\n for i in nums:\n prefixsum+=i\n ans+=res[prefixsum-goal]\n res[prefixsum]+=1\n return ans\n```\n# please upvote me it would encourage me alot\nSpecial Thanks to @lee215\n | 5 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
Sliding Window Approach | binary-subarrays-with-sum | 0 | 1 | ```\nclass Solution:\n def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:\n res=defaultdict(int)\n res[0]=1\n ans=0\n prefixsum=0\n for i in nums:\n prefixsum+=i\n ans+=res[prefixsum-goal]\n res[prefixsum]+=1\n return ans\n```\n# please upvote me it would encourage me alot\nSpecial Thanks to @lee215\n | 5 | Given a `wordlist`, we want to implement a spellchecker that converts a query word into a correct word.
For a given `query` word, the spell checker handles two categories of spelling mistakes:
* Capitalization: If the query matches a word in the wordlist (**case-insensitive**), then the query word is returned with the same case as the case in the wordlist.
* Example: `wordlist = [ "yellow "]`, `query = "YellOw "`: `correct = "yellow "`
* Example: `wordlist = [ "Yellow "]`, `query = "yellow "`: `correct = "Yellow "`
* Example: `wordlist = [ "yellow "]`, `query = "yellow "`: `correct = "yellow "`
* Vowel Errors: If after replacing the vowels `('a', 'e', 'i', 'o', 'u')` of the query word with any vowel individually, it matches a word in the wordlist (**case-insensitive**), then the query word is returned with the same case as the match in the wordlist.
* Example: `wordlist = [ "YellOw "]`, `query = "yollow "`: `correct = "YellOw "`
* Example: `wordlist = [ "YellOw "]`, `query = "yeellow "`: `correct = " "` (no match)
* Example: `wordlist = [ "YellOw "]`, `query = "yllw "`: `correct = " "` (no match)
In addition, the spell checker operates under the following precedence rules:
* When the query exactly matches a word in the wordlist (**case-sensitive**), you should return the same word back.
* When the query matches a word up to capitlization, you should return the first such match in the wordlist.
* When the query matches a word up to vowel errors, you should return the first such match in the wordlist.
* If the query has no matches in the wordlist, you should return the empty string.
Given some `queries`, return a list of words `answer`, where `answer[i]` is the correct word for `query = queries[i]`.
**Example 1:**
**Input:** wordlist = \["KiTe","kite","hare","Hare"\], queries = \["kite","Kite","KiTe","Hare","HARE","Hear","hear","keti","keet","keto"\]
**Output:** \["kite","KiTe","KiTe","Hare","hare","","","KiTe","","KiTe"\]
**Example 2:**
**Input:** wordlist = \["yellow"\], queries = \["YellOw"\]
**Output:** \["yellow"\]
**Constraints:**
* `1 <= wordlist.length, queries.length <= 5000`
* `1 <= wordlist[i].length, queries[i].length <= 7`
* `wordlist[i]` and `queries[i]` consist only of only English letters. | null |
python3 Sloution | binary-subarrays-with-sum | 0 | 1 | \n```\nclass Solution:\n def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:\n sumsMap,s,cnt={0:1},0,0\n for a in nums:\n s+=a\n if s-goal in sumsMap:\n cnt+=sumsMap[s-goal]\n sumsMap[s]=sumsMap.get(s,0)+1\n \n return cnt \n``` | 1 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
python3 Sloution | binary-subarrays-with-sum | 0 | 1 | \n```\nclass Solution:\n def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:\n sumsMap,s,cnt={0:1},0,0\n for a in nums:\n s+=a\n if s-goal in sumsMap:\n cnt+=sumsMap[s-goal]\n sumsMap[s]=sumsMap.get(s,0)+1\n \n return cnt \n``` | 1 | Given a `wordlist`, we want to implement a spellchecker that converts a query word into a correct word.
For a given `query` word, the spell checker handles two categories of spelling mistakes:
* Capitalization: If the query matches a word in the wordlist (**case-insensitive**), then the query word is returned with the same case as the case in the wordlist.
* Example: `wordlist = [ "yellow "]`, `query = "YellOw "`: `correct = "yellow "`
* Example: `wordlist = [ "Yellow "]`, `query = "yellow "`: `correct = "Yellow "`
* Example: `wordlist = [ "yellow "]`, `query = "yellow "`: `correct = "yellow "`
* Vowel Errors: If after replacing the vowels `('a', 'e', 'i', 'o', 'u')` of the query word with any vowel individually, it matches a word in the wordlist (**case-insensitive**), then the query word is returned with the same case as the match in the wordlist.
* Example: `wordlist = [ "YellOw "]`, `query = "yollow "`: `correct = "YellOw "`
* Example: `wordlist = [ "YellOw "]`, `query = "yeellow "`: `correct = " "` (no match)
* Example: `wordlist = [ "YellOw "]`, `query = "yllw "`: `correct = " "` (no match)
In addition, the spell checker operates under the following precedence rules:
* When the query exactly matches a word in the wordlist (**case-sensitive**), you should return the same word back.
* When the query matches a word up to capitlization, you should return the first such match in the wordlist.
* When the query matches a word up to vowel errors, you should return the first such match in the wordlist.
* If the query has no matches in the wordlist, you should return the empty string.
Given some `queries`, return a list of words `answer`, where `answer[i]` is the correct word for `query = queries[i]`.
**Example 1:**
**Input:** wordlist = \["KiTe","kite","hare","Hare"\], queries = \["kite","Kite","KiTe","Hare","HARE","Hear","hear","keti","keet","keto"\]
**Output:** \["kite","KiTe","KiTe","Hare","hare","","","KiTe","","KiTe"\]
**Example 2:**
**Input:** wordlist = \["yellow"\], queries = \["YellOw"\]
**Output:** \["yellow"\]
**Constraints:**
* `1 <= wordlist.length, queries.length <= 5000`
* `1 <= wordlist[i].length, queries[i].length <= 7`
* `wordlist[i]` and `queries[i]` consist only of only English letters. | null |
EASY python sliding window O(1) space EXPLAINED THOROUGHLY | binary-subarrays-with-sum | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n\r\nWe want to use a sliding window approach that keeps sliding the right pointer forward until we have counted the appropriate number of zeros. But it can\'t be solved like a usual sliding window problem because in some cases the right pointer can keep sliding forward to create valid subarrays. Consider going through the example `[000101000100]` to see how the algorithm *should* work. Suppose the `goal` is just $$2$$.\r\n\r\nIn a usual sliding window algorithm, the right pointer slides forward until index $$5$$ at $$1$$. Then the left pointer counts the number of valid subarrays by counting how many times it slides until it finally removes a $$1$$ at index $$3$$ from the window. It should have counted $$4$$ valid subarrays now, each containing the first two $$1$$\'s. But now the problem is each additional $$0$$ after that second $$1$$ should continue increasing the number of valid subarrays by 4. Think about it.\r\n\r\nThis will be the first modification of the usual sliding window algorithm. We keep track of how many valid subarrays the left pointer just counted before the right pointer started moving again. We can call this `lastBucket` and in this case it was $$4$$. Let\'s assume that each time the left pointer slides, it not only updates our current tally of valid subarrays, `ans`, but also this variable `lastBucket` that is initialized to zero. Every time the left pointer has stopped sliding and the right pointer reaches another $$0$$, we wish to add this `lastBucket` to `ans`. We will need to reset `lastBucket` each time the right pointer has created a valid subarray and the left pointer starts counting again.\r\n\r\nWe want this process to recylce `lastBucket`to zero each time the left pointer starts sliding to count valid subarrays again. So, from where we left off, after the right pointer slides to the $$0$$ at index $$8$$ and adds $$`lastBucket` = 4$$ to the `ans`, it will move to the $$1$$ at index $$9$$ to repeat the process. `lastBucket` should reset to zero and the left pointer should start incrementing both `ans` and `lastBucket` each time it slides until it reaches the second $$1$$ at index $$5$$. At this point `ans` has been updated to count the 2 valid subarrays including the second and third $$1$$s, and the `lastBucket` has been updated appropriately to $$2$$. When the right pointer starts sliding again until the end of the array, it will keep incrementing `ans` by $$`lastBucket` = 2$$ needed.\r\n\r\nFinally, consider edge cases. Suppose the array was instead `[000000]` and our `goal` was $$3$$. No valid subarrays will be counted, good.\r\n\r\nSuppose the array was instead `[0001010]` and our `goal` was $$3$$. Still no valid subarrays will be counted, good.\r\n\r\nSuppose the array was instead `[0000000]` and our `goal` was $$0$$. This will likely mess up the algorithm, because the `lastBucket` is reset each time the right pointer creates a valid subarray, which in this case is at every zero. The same is true for something like `[0001010]` when the `goal` is still $$0$$. So let\'s just determine what we do when `goal` is $$0$$.\r\n\r\nIn that case, just keep track of how many $$0$$s there are before each $$1$$. The first $$0$$ creates one valid subarray, so we increment `ans` by one. The next $$0$$ creates two more valid subarrays. The next $$0$$ creates three more. Suppose there are $$m$$ zeros before the first $$1$$. At each $$0$$ we increment `ans` by 1, then 2, then 3, until the $$m$$\'th $$0$$. We can use the `lastBucket` variable to keep track of how much to increment `ans` at each $$0$$. We reset `lastBucket` to zero at every $$1$$ and increment it by 1 at every $$0$$.\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n\r\nIn this implementation, `total` represents the number of $$1$$\'s counted in the window, and `ans` represents the number of valid subarrays counted so far. `left` and `right` are the two pointers of the sliding window. All these variables are initialized to zero.\r\n\r\nThe first modification to the usual sliding window modification is to reset `lastBucket` any time the left pointer is about to start sliding and counting valid subarrays:\r\n```\r\n# NEW\r\nif total == goal:\r\n lastBucket = 0\r\n```\r\nNext, when the left pointer *is* sliding, it should not only increment `ans`, `total`, and `left`, but also `lastBucket`:\r\n```\r\nwhile total == goal:\r\n ans += 1\r\n lastBucket += 1 # NEW\r\n total -= nums[left]\r\n left += 1\r\n```\r\nNow, if the right pointer slides into a $$0$$ while `lastBucket` is nonzero, it means the left pointer has already counted some valid subarrays and the right pointer is creating more. In this instance, we increment `ans` by `lastBucket`:\r\n```\r\n# NEW\r\nif lastBucket != 0 and nums[right] == 0:\r\n ans += lastBucket\r\n```\r\nFinally, take care of the edge case where `goal` is $$0$$:\r\n```\r\n# NEW\r\nif goal == 0:\r\n for num in nums:\r\n if num == 0:\r\n lastBucket += 1\r\n ans += lastBucket\r\n else:\r\n lastBucket = 0\r\n return ans\r\n```\r\n\r\n\r\n\r\n# Complexity\r\n- $$O(n)$$ Time complexity - beats 97.22%:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> Same as the usual sliding window. We are still performing constant time operations on each of the elements of the array.\r\n#\r\n- $$O(1)$$ Space complexity - beats 95.60% :\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> Same as the usual sliding window pattern. We are still not using up any additional space that scaless up with the input size.\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:\r\n\r\n ans = 0\r\n lastBucket = 0 # NEW\r\n \r\n # NEW\r\n if goal == 0:\r\n for num in nums:\r\n if num == 0:\r\n lastBucket += 1\r\n ans += lastBucket\r\n else:\r\n lastBucket = 0\r\n return ans\r\n\r\n\r\n\r\n left = 0\r\n total = 0\r\n\r\n for right in range(len(nums)):\r\n total += nums[right]\r\n\r\n # NEW\r\n if total == goal:\r\n lastBucket = 0\r\n\r\n while total == goal:\r\n ans += 1\r\n lastBucket += 1 # NEW\r\n total -= nums[left]\r\n left += 1\r\n\r\n # NEW\r\n if lastBucket != 0 and nums[right] == 0:\r\n ans += lastBucket\r\n \r\n\r\n return ans\r\n```\r\n\r\n# When to use this pattern\r\n\r\nIt\'s important to recognize how any problem can be reduced to this solution when there is a way to transform the input into 1s and 0s according to a binary criteria.\r\n\r\nFor example, lets say the new task was to tally the number of all subarrays containing exactly `goal` number of **square numbers**. Just iterate through each number and treat it as $$1$$ if it\'s a square and $$0$$ otherwise. Any subarray with a `goal` number of primes is a subarray whose corresponding binary sum is also `goal`. So just use this pattern to tally those subarrays, and the time complexity for this would still be $$O(n)$$. It\'s important to note there is no need to create a copy of the input array just to get the binary list of $$1$$s and $$0$$s. All you need to use is the input array and just reduce each number into a $$1$$ or $$0$$ as you use it. You can modify it directly once it enters your window, or you can leave it in place but treat it as a $$1$$ or $$0$$. So the space complexity is also still $$O(1)$$.\r\n\r\nAnother example would be counting the amount of subarrays with a `goal` number of primes. Here we would just treat the prime numbers as $$1$$ and composite numbers as $$0$$. Unfortunately, we can\'t determine if a number is prime or not in $$O(1)$$ time, so this will affect our new algorithmic time complexity. Suppose we use a naive method to determine which numbers are prime: determine that any number $$k$$ is prime if it is not divisible by any numbers less than or equal to $$\\sqrt{k}$$. Assuming the largest number in the input array is $$k$$, this prime-checking sub-algorithm takes O($$\\sqrt{k}$$) time in its worst-case performance. Since we must use this algorithm on each of the $$n$$ numbers as we loop through them, the time complexity transforms from $$O(n)$$ to $$O(n\\sqrt{k})$$. **Don\'t make the mistake of saying it\'s $$O(n\\sqrt{n})$$ as there are two different relevant input sizes here.** The space complexity stays at $$O(1)$$.\r\n\r\nIn general, the time- and space-cmplexity of the binary function will just be multiplied to those of the original algorithm. For example, let\'s say we were tallying subarrays with `goal` fibonacci numbers. The recursive fibonacci algorithm takes $$O(2^k)$$ time (technically $$O(\\phi{}^k)$$ for bonus points) and $$O(k)$$ space. So incorporating that sub-algorithm into this one transforms the time- and space-complexity into $$O(n) * O(2^k) = O(2^kn)$$ and $$O(1) * O(k) = O(k)$$, respectively, where $$k$$ represents the most number of fibonacci steps we need to take to determine if a number is in the fibonacci sequence.\r\n\r\n# Further practice\r\n\r\n[1248. Count Number of Nice Subarrays](https://leetcode.com/problems/count-number-of-nice-subarrays/description/).\r\n\r\nI\'ll update this as I continue my own practice. Leave a comment if you have some more probems to add too!\r\n\r\n# Upvote, Comment, and Share! | 1 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
EASY python sliding window O(1) space EXPLAINED THOROUGHLY | binary-subarrays-with-sum | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n\r\nWe want to use a sliding window approach that keeps sliding the right pointer forward until we have counted the appropriate number of zeros. But it can\'t be solved like a usual sliding window problem because in some cases the right pointer can keep sliding forward to create valid subarrays. Consider going through the example `[000101000100]` to see how the algorithm *should* work. Suppose the `goal` is just $$2$$.\r\n\r\nIn a usual sliding window algorithm, the right pointer slides forward until index $$5$$ at $$1$$. Then the left pointer counts the number of valid subarrays by counting how many times it slides until it finally removes a $$1$$ at index $$3$$ from the window. It should have counted $$4$$ valid subarrays now, each containing the first two $$1$$\'s. But now the problem is each additional $$0$$ after that second $$1$$ should continue increasing the number of valid subarrays by 4. Think about it.\r\n\r\nThis will be the first modification of the usual sliding window algorithm. We keep track of how many valid subarrays the left pointer just counted before the right pointer started moving again. We can call this `lastBucket` and in this case it was $$4$$. Let\'s assume that each time the left pointer slides, it not only updates our current tally of valid subarrays, `ans`, but also this variable `lastBucket` that is initialized to zero. Every time the left pointer has stopped sliding and the right pointer reaches another $$0$$, we wish to add this `lastBucket` to `ans`. We will need to reset `lastBucket` each time the right pointer has created a valid subarray and the left pointer starts counting again.\r\n\r\nWe want this process to recylce `lastBucket`to zero each time the left pointer starts sliding to count valid subarrays again. So, from where we left off, after the right pointer slides to the $$0$$ at index $$8$$ and adds $$`lastBucket` = 4$$ to the `ans`, it will move to the $$1$$ at index $$9$$ to repeat the process. `lastBucket` should reset to zero and the left pointer should start incrementing both `ans` and `lastBucket` each time it slides until it reaches the second $$1$$ at index $$5$$. At this point `ans` has been updated to count the 2 valid subarrays including the second and third $$1$$s, and the `lastBucket` has been updated appropriately to $$2$$. When the right pointer starts sliding again until the end of the array, it will keep incrementing `ans` by $$`lastBucket` = 2$$ needed.\r\n\r\nFinally, consider edge cases. Suppose the array was instead `[000000]` and our `goal` was $$3$$. No valid subarrays will be counted, good.\r\n\r\nSuppose the array was instead `[0001010]` and our `goal` was $$3$$. Still no valid subarrays will be counted, good.\r\n\r\nSuppose the array was instead `[0000000]` and our `goal` was $$0$$. This will likely mess up the algorithm, because the `lastBucket` is reset each time the right pointer creates a valid subarray, which in this case is at every zero. The same is true for something like `[0001010]` when the `goal` is still $$0$$. So let\'s just determine what we do when `goal` is $$0$$.\r\n\r\nIn that case, just keep track of how many $$0$$s there are before each $$1$$. The first $$0$$ creates one valid subarray, so we increment `ans` by one. The next $$0$$ creates two more valid subarrays. The next $$0$$ creates three more. Suppose there are $$m$$ zeros before the first $$1$$. At each $$0$$ we increment `ans` by 1, then 2, then 3, until the $$m$$\'th $$0$$. We can use the `lastBucket` variable to keep track of how much to increment `ans` at each $$0$$. We reset `lastBucket` to zero at every $$1$$ and increment it by 1 at every $$0$$.\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n\r\nIn this implementation, `total` represents the number of $$1$$\'s counted in the window, and `ans` represents the number of valid subarrays counted so far. `left` and `right` are the two pointers of the sliding window. All these variables are initialized to zero.\r\n\r\nThe first modification to the usual sliding window modification is to reset `lastBucket` any time the left pointer is about to start sliding and counting valid subarrays:\r\n```\r\n# NEW\r\nif total == goal:\r\n lastBucket = 0\r\n```\r\nNext, when the left pointer *is* sliding, it should not only increment `ans`, `total`, and `left`, but also `lastBucket`:\r\n```\r\nwhile total == goal:\r\n ans += 1\r\n lastBucket += 1 # NEW\r\n total -= nums[left]\r\n left += 1\r\n```\r\nNow, if the right pointer slides into a $$0$$ while `lastBucket` is nonzero, it means the left pointer has already counted some valid subarrays and the right pointer is creating more. In this instance, we increment `ans` by `lastBucket`:\r\n```\r\n# NEW\r\nif lastBucket != 0 and nums[right] == 0:\r\n ans += lastBucket\r\n```\r\nFinally, take care of the edge case where `goal` is $$0$$:\r\n```\r\n# NEW\r\nif goal == 0:\r\n for num in nums:\r\n if num == 0:\r\n lastBucket += 1\r\n ans += lastBucket\r\n else:\r\n lastBucket = 0\r\n return ans\r\n```\r\n\r\n\r\n\r\n# Complexity\r\n- $$O(n)$$ Time complexity - beats 97.22%:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> Same as the usual sliding window. We are still performing constant time operations on each of the elements of the array.\r\n#\r\n- $$O(1)$$ Space complexity - beats 95.60% :\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> Same as the usual sliding window pattern. We are still not using up any additional space that scaless up with the input size.\r\n\r\n# Code\r\n```\r\nclass Solution:\r\n def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:\r\n\r\n ans = 0\r\n lastBucket = 0 # NEW\r\n \r\n # NEW\r\n if goal == 0:\r\n for num in nums:\r\n if num == 0:\r\n lastBucket += 1\r\n ans += lastBucket\r\n else:\r\n lastBucket = 0\r\n return ans\r\n\r\n\r\n\r\n left = 0\r\n total = 0\r\n\r\n for right in range(len(nums)):\r\n total += nums[right]\r\n\r\n # NEW\r\n if total == goal:\r\n lastBucket = 0\r\n\r\n while total == goal:\r\n ans += 1\r\n lastBucket += 1 # NEW\r\n total -= nums[left]\r\n left += 1\r\n\r\n # NEW\r\n if lastBucket != 0 and nums[right] == 0:\r\n ans += lastBucket\r\n \r\n\r\n return ans\r\n```\r\n\r\n# When to use this pattern\r\n\r\nIt\'s important to recognize how any problem can be reduced to this solution when there is a way to transform the input into 1s and 0s according to a binary criteria.\r\n\r\nFor example, lets say the new task was to tally the number of all subarrays containing exactly `goal` number of **square numbers**. Just iterate through each number and treat it as $$1$$ if it\'s a square and $$0$$ otherwise. Any subarray with a `goal` number of primes is a subarray whose corresponding binary sum is also `goal`. So just use this pattern to tally those subarrays, and the time complexity for this would still be $$O(n)$$. It\'s important to note there is no need to create a copy of the input array just to get the binary list of $$1$$s and $$0$$s. All you need to use is the input array and just reduce each number into a $$1$$ or $$0$$ as you use it. You can modify it directly once it enters your window, or you can leave it in place but treat it as a $$1$$ or $$0$$. So the space complexity is also still $$O(1)$$.\r\n\r\nAnother example would be counting the amount of subarrays with a `goal` number of primes. Here we would just treat the prime numbers as $$1$$ and composite numbers as $$0$$. Unfortunately, we can\'t determine if a number is prime or not in $$O(1)$$ time, so this will affect our new algorithmic time complexity. Suppose we use a naive method to determine which numbers are prime: determine that any number $$k$$ is prime if it is not divisible by any numbers less than or equal to $$\\sqrt{k}$$. Assuming the largest number in the input array is $$k$$, this prime-checking sub-algorithm takes O($$\\sqrt{k}$$) time in its worst-case performance. Since we must use this algorithm on each of the $$n$$ numbers as we loop through them, the time complexity transforms from $$O(n)$$ to $$O(n\\sqrt{k})$$. **Don\'t make the mistake of saying it\'s $$O(n\\sqrt{n})$$ as there are two different relevant input sizes here.** The space complexity stays at $$O(1)$$.\r\n\r\nIn general, the time- and space-cmplexity of the binary function will just be multiplied to those of the original algorithm. For example, let\'s say we were tallying subarrays with `goal` fibonacci numbers. The recursive fibonacci algorithm takes $$O(2^k)$$ time (technically $$O(\\phi{}^k)$$ for bonus points) and $$O(k)$$ space. So incorporating that sub-algorithm into this one transforms the time- and space-complexity into $$O(n) * O(2^k) = O(2^kn)$$ and $$O(1) * O(k) = O(k)$$, respectively, where $$k$$ represents the most number of fibonacci steps we need to take to determine if a number is in the fibonacci sequence.\r\n\r\n# Further practice\r\n\r\n[1248. Count Number of Nice Subarrays](https://leetcode.com/problems/count-number-of-nice-subarrays/description/).\r\n\r\nI\'ll update this as I continue my own practice. Leave a comment if you have some more probems to add too!\r\n\r\n# Upvote, Comment, and Share! | 1 | Given a `wordlist`, we want to implement a spellchecker that converts a query word into a correct word.
For a given `query` word, the spell checker handles two categories of spelling mistakes:
* Capitalization: If the query matches a word in the wordlist (**case-insensitive**), then the query word is returned with the same case as the case in the wordlist.
* Example: `wordlist = [ "yellow "]`, `query = "YellOw "`: `correct = "yellow "`
* Example: `wordlist = [ "Yellow "]`, `query = "yellow "`: `correct = "Yellow "`
* Example: `wordlist = [ "yellow "]`, `query = "yellow "`: `correct = "yellow "`
* Vowel Errors: If after replacing the vowels `('a', 'e', 'i', 'o', 'u')` of the query word with any vowel individually, it matches a word in the wordlist (**case-insensitive**), then the query word is returned with the same case as the match in the wordlist.
* Example: `wordlist = [ "YellOw "]`, `query = "yollow "`: `correct = "YellOw "`
* Example: `wordlist = [ "YellOw "]`, `query = "yeellow "`: `correct = " "` (no match)
* Example: `wordlist = [ "YellOw "]`, `query = "yllw "`: `correct = " "` (no match)
In addition, the spell checker operates under the following precedence rules:
* When the query exactly matches a word in the wordlist (**case-sensitive**), you should return the same word back.
* When the query matches a word up to capitlization, you should return the first such match in the wordlist.
* When the query matches a word up to vowel errors, you should return the first such match in the wordlist.
* If the query has no matches in the wordlist, you should return the empty string.
Given some `queries`, return a list of words `answer`, where `answer[i]` is the correct word for `query = queries[i]`.
**Example 1:**
**Input:** wordlist = \["KiTe","kite","hare","Hare"\], queries = \["kite","Kite","KiTe","Hare","HARE","Hear","hear","keti","keet","keto"\]
**Output:** \["kite","KiTe","KiTe","Hare","hare","","","KiTe","","KiTe"\]
**Example 2:**
**Input:** wordlist = \["yellow"\], queries = \["YellOw"\]
**Output:** \["yellow"\]
**Constraints:**
* `1 <= wordlist.length, queries.length <= 5000`
* `1 <= wordlist[i].length, queries[i].length <= 7`
* `wordlist[i]` and `queries[i]` consist only of only English letters. | null |
Easy Python Solution | binary-subarrays-with-sum | 0 | 1 | # Intuition\nCounting the subarrays where the sum equals some number is kind of hard and we have to find another way to solve this, may be use some tricks.\nWhat we can do is, we can count number of subarrays with sum greater than goal and also count nuumber of subarrays with sum less than goal, and then substract these from the total number of subarrays. And we can do this using sliding window technique easly.\n\n# Approach\n- count number of subarrays with sum greater than goal\n- count number of subarrays with sum less than goal\n- substract these subarrays from the total number of subarrays we can get from the list.\n - we can find the total number of subarrays of a list with length n by using the formula (n * (n + 1)) // 2\n\n# Complexity\nn = len(nums)\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:\n n = len(nums)\n return (n * (n + 1) // 2) - (self.less_than_goal(nums, goal) + self.greater_than_goal(nums, goal))\n \n def less_than_goal(self, nums, goal):\n n = len(nums)\n count = 0\n left = 0\n curr_sum = 0\n for right in range(n):\n curr_sum += nums[right]\n while left <= right and curr_sum >= goal:\n curr_sum -= nums[left]\n left += 1\n count += right - left + 1\n \n return count\n \n def greater_than_goal(self, nums, goal):\n n = len(nums)\n count = 0\n left = 0\n curr_sum = 0\n for right in range(n):\n curr_sum += nums[right]\n while left <= right and curr_sum > goal:\n count += n - right\n curr_sum -= nums[left]\n left += 1\n \n return count\n \n``` | 1 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
Easy Python Solution | binary-subarrays-with-sum | 0 | 1 | # Intuition\nCounting the subarrays where the sum equals some number is kind of hard and we have to find another way to solve this, may be use some tricks.\nWhat we can do is, we can count number of subarrays with sum greater than goal and also count nuumber of subarrays with sum less than goal, and then substract these from the total number of subarrays. And we can do this using sliding window technique easly.\n\n# Approach\n- count number of subarrays with sum greater than goal\n- count number of subarrays with sum less than goal\n- substract these subarrays from the total number of subarrays we can get from the list.\n - we can find the total number of subarrays of a list with length n by using the formula (n * (n + 1)) // 2\n\n# Complexity\nn = len(nums)\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:\n n = len(nums)\n return (n * (n + 1) // 2) - (self.less_than_goal(nums, goal) + self.greater_than_goal(nums, goal))\n \n def less_than_goal(self, nums, goal):\n n = len(nums)\n count = 0\n left = 0\n curr_sum = 0\n for right in range(n):\n curr_sum += nums[right]\n while left <= right and curr_sum >= goal:\n curr_sum -= nums[left]\n left += 1\n count += right - left + 1\n \n return count\n \n def greater_than_goal(self, nums, goal):\n n = len(nums)\n count = 0\n left = 0\n curr_sum = 0\n for right in range(n):\n curr_sum += nums[right]\n while left <= right and curr_sum > goal:\n count += n - right\n curr_sum -= nums[left]\n left += 1\n \n return count\n \n``` | 1 | Given a `wordlist`, we want to implement a spellchecker that converts a query word into a correct word.
For a given `query` word, the spell checker handles two categories of spelling mistakes:
* Capitalization: If the query matches a word in the wordlist (**case-insensitive**), then the query word is returned with the same case as the case in the wordlist.
* Example: `wordlist = [ "yellow "]`, `query = "YellOw "`: `correct = "yellow "`
* Example: `wordlist = [ "Yellow "]`, `query = "yellow "`: `correct = "Yellow "`
* Example: `wordlist = [ "yellow "]`, `query = "yellow "`: `correct = "yellow "`
* Vowel Errors: If after replacing the vowels `('a', 'e', 'i', 'o', 'u')` of the query word with any vowel individually, it matches a word in the wordlist (**case-insensitive**), then the query word is returned with the same case as the match in the wordlist.
* Example: `wordlist = [ "YellOw "]`, `query = "yollow "`: `correct = "YellOw "`
* Example: `wordlist = [ "YellOw "]`, `query = "yeellow "`: `correct = " "` (no match)
* Example: `wordlist = [ "YellOw "]`, `query = "yllw "`: `correct = " "` (no match)
In addition, the spell checker operates under the following precedence rules:
* When the query exactly matches a word in the wordlist (**case-sensitive**), you should return the same word back.
* When the query matches a word up to capitlization, you should return the first such match in the wordlist.
* When the query matches a word up to vowel errors, you should return the first such match in the wordlist.
* If the query has no matches in the wordlist, you should return the empty string.
Given some `queries`, return a list of words `answer`, where `answer[i]` is the correct word for `query = queries[i]`.
**Example 1:**
**Input:** wordlist = \["KiTe","kite","hare","Hare"\], queries = \["kite","Kite","KiTe","Hare","HARE","Hear","hear","keti","keet","keto"\]
**Output:** \["kite","KiTe","KiTe","Hare","hare","","","KiTe","","KiTe"\]
**Example 2:**
**Input:** wordlist = \["yellow"\], queries = \["YellOw"\]
**Output:** \["yellow"\]
**Constraints:**
* `1 <= wordlist.length, queries.length <= 5000`
* `1 <= wordlist[i].length, queries[i].length <= 7`
* `wordlist[i]` and `queries[i]` consist only of only English letters. | null |
[Handle edge cases by appending maximum at start and end]: Very short & clean python code. | minimum-falling-path-sum | 0 | 1 | # Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n \n maxi = float(\'inf\')\n prev_row = [maxi] + matrix[0][:] + [maxi]\n\n for i in range(1,len(matrix)):\n temp = []\n for j in range(len(matrix[0])):\n temp.append(matrix[i][j] + min(prev_row[j:j+3]))\n\n prev_row = [maxi]+temp+[maxi]\n \n return min(prev_row)\n```\n\n\nEdit: \n\nIn Python: **arr[n] = arr[0] where n = len(arr)**\n\nWith that you can also skip appending maximum at the end of the pre_row. (or you can do other way around by appending it at the end)\n\n\n```\n\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n \n maxi = float(\'inf\')\n prev_row = [maxi] + matrix[0][:]\n\n for i in range(1,len(matrix)):\n temp = []\n for j in range(len(matrix[0])):\n temp.append(matrix[i][j] + min(prev_row[j:j+3]))\n\n prev_row = [maxi]+temp\n \n return min(prev_row)\n\n``` | 1 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
[Handle edge cases by appending maximum at start and end]: Very short & clean python code. | minimum-falling-path-sum | 0 | 1 | # Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n \n maxi = float(\'inf\')\n prev_row = [maxi] + matrix[0][:] + [maxi]\n\n for i in range(1,len(matrix)):\n temp = []\n for j in range(len(matrix[0])):\n temp.append(matrix[i][j] + min(prev_row[j:j+3]))\n\n prev_row = [maxi]+temp+[maxi]\n \n return min(prev_row)\n```\n\n\nEdit: \n\nIn Python: **arr[n] = arr[0] where n = len(arr)**\n\nWith that you can also skip appending maximum at the end of the pre_row. (or you can do other way around by appending it at the end)\n\n\n```\n\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n \n maxi = float(\'inf\')\n prev_row = [maxi] + matrix[0][:]\n\n for i in range(1,len(matrix)):\n temp = []\n for j in range(len(matrix[0])):\n temp.append(matrix[i][j] + min(prev_row[j:j+3]))\n\n prev_row = [maxi]+temp\n \n return min(prev_row)\n\n``` | 1 | Given two integers n and k, return _an array of all the integers of length_ `n` _where the difference between every two consecutive digits is_ `k`. You may return the answer in **any order**.
Note that the integers should not have leading zeros. Integers as `02` and `043` are not allowed.
**Example 1:**
**Input:** n = 3, k = 7
**Output:** \[181,292,707,818,929\]
**Explanation:** Note that 070 is not a valid number, because it has leading zeroes.
**Example 2:**
**Input:** n = 2, k = 1
**Output:** \[10,12,21,23,32,34,43,45,54,56,65,67,76,78,87,89,98\]
**Constraints:**
* `2 <= n <= 9`
* `0 <= k <= 9` | null |
Python Simple 4 Line Solution | minimum-falling-path-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor the first row, we already have the path sum if we pick each column (the value in that one cell).\n\nFor the second row and onward, notice we will just pick the minimum of the three above (above left, abve, and above right, if possible) and add it to the value in the column.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each cell in each row after the first, try to get the three "above" values. \n\nIf any are out of bounds, use a default value of 10001. This is because we will always pick the minimum. Since 1 <= n <= 100 and the value for any 0 <= matrix[i][j] <= 100, we know the max path sum is 10000, so any 10001 will not be chosen ever.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) Used matrix itself for the temp. In an interview they may say "oh that\'s clever" or "hey, that\'s not allowed". In the latter case, just add a temp row list to store your sums and initialize it as row 0.\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n for row in range(1,len(matrix)):\n for col in range(len(matrix)):\n matrix[row][col] = matrix[row][col]+min([matrix[row-1][c+col] if (0<=c+col<len(matrix)) else 10001 for c in range(-1,2)])\n return min(matrix[-1])\n```\n\nThank you friends and happy Leetcoding! | 1 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
Python Simple 4 Line Solution | minimum-falling-path-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor the first row, we already have the path sum if we pick each column (the value in that one cell).\n\nFor the second row and onward, notice we will just pick the minimum of the three above (above left, abve, and above right, if possible) and add it to the value in the column.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each cell in each row after the first, try to get the three "above" values. \n\nIf any are out of bounds, use a default value of 10001. This is because we will always pick the minimum. Since 1 <= n <= 100 and the value for any 0 <= matrix[i][j] <= 100, we know the max path sum is 10000, so any 10001 will not be chosen ever.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) Used matrix itself for the temp. In an interview they may say "oh that\'s clever" or "hey, that\'s not allowed". In the latter case, just add a temp row list to store your sums and initialize it as row 0.\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n for row in range(1,len(matrix)):\n for col in range(len(matrix)):\n matrix[row][col] = matrix[row][col]+min([matrix[row-1][c+col] if (0<=c+col<len(matrix)) else 10001 for c in range(-1,2)])\n return min(matrix[-1])\n```\n\nThank you friends and happy Leetcoding! | 1 | Given two integers n and k, return _an array of all the integers of length_ `n` _where the difference between every two consecutive digits is_ `k`. You may return the answer in **any order**.
Note that the integers should not have leading zeros. Integers as `02` and `043` are not allowed.
**Example 1:**
**Input:** n = 3, k = 7
**Output:** \[181,292,707,818,929\]
**Explanation:** Note that 070 is not a valid number, because it has leading zeroes.
**Example 2:**
**Input:** n = 2, k = 1
**Output:** \[10,12,21,23,32,34,43,45,54,56,65,67,76,78,87,89,98\]
**Constraints:**
* `2 <= n <= 9`
* `0 <= k <= 9` | null |
[Python] Minimum Falling Path Sum | minimum-falling-path-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n m=len(matrix)\n for i in range(1,m):\n for j in range(m):\n matrix[i][j]+=min(matrix[i-1][k] for k in (j-1,j,j+1) if 0<=k and k<m)\n return min(matrix[-1])\n``` | 1 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
[Python] Minimum Falling Path Sum | minimum-falling-path-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n m=len(matrix)\n for i in range(1,m):\n for j in range(m):\n matrix[i][j]+=min(matrix[i-1][k] for k in (j-1,j,j+1) if 0<=k and k<m)\n return min(matrix[-1])\n``` | 1 | Given two integers n and k, return _an array of all the integers of length_ `n` _where the difference between every two consecutive digits is_ `k`. You may return the answer in **any order**.
Note that the integers should not have leading zeros. Integers as `02` and `043` are not allowed.
**Example 1:**
**Input:** n = 3, k = 7
**Output:** \[181,292,707,818,929\]
**Explanation:** Note that 070 is not a valid number, because it has leading zeroes.
**Example 2:**
**Input:** n = 2, k = 1
**Output:** \[10,12,21,23,32,34,43,45,54,56,65,67,76,78,87,89,98\]
**Constraints:**
* `2 <= n <= 9`
* `0 <= k <= 9` | null |
Easy for understand Python | minimum-falling-path-sum | 0 | 1 | \n# Complexity\n- Time complexity: O(n * n)\n\n- Space complexity: O(n * n)\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n n = len(matrix)\n dp = [[0] * n for _ in range(n)]\n for i in range(n):\n dp[0][i] = matrix[0][i]\n \n for i in range(1, n):\n for j in range(n):\n current = dp[i - 1][j]\n if j - 1 >= 0:\n current = min(current, dp[i - 1][j - 1])\n if j + 1 < n:\n current = min(current, dp[i - 1][j + 1])\n dp[i][j] = current + matrix[i][j]\n return min(dp[-1])\n``` | 1 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
Easy for understand Python | minimum-falling-path-sum | 0 | 1 | \n# Complexity\n- Time complexity: O(n * n)\n\n- Space complexity: O(n * n)\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n n = len(matrix)\n dp = [[0] * n for _ in range(n)]\n for i in range(n):\n dp[0][i] = matrix[0][i]\n \n for i in range(1, n):\n for j in range(n):\n current = dp[i - 1][j]\n if j - 1 >= 0:\n current = min(current, dp[i - 1][j - 1])\n if j + 1 < n:\n current = min(current, dp[i - 1][j + 1])\n dp[i][j] = current + matrix[i][j]\n return min(dp[-1])\n``` | 1 | Given two integers n and k, return _an array of all the integers of length_ `n` _where the difference between every two consecutive digits is_ `k`. You may return the answer in **any order**.
Note that the integers should not have leading zeros. Integers as `02` and `043` are not allowed.
**Example 1:**
**Input:** n = 3, k = 7
**Output:** \[181,292,707,818,929\]
**Explanation:** Note that 070 is not a valid number, because it has leading zeroes.
**Example 2:**
**Input:** n = 2, k = 1
**Output:** \[10,12,21,23,32,34,43,45,54,56,65,67,76,78,87,89,98\]
**Constraints:**
* `2 <= n <= 9`
* `0 <= k <= 9` | null |
90% Faster || O(n) Time complexity || Dynamic Programming | minimum-falling-path-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCalculating minimum upto a cell.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDynamic Programming\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n l=len(matrix)\n # Iterating from 2nd row of matrix and creating matrix of minimum sum upto that point.\n for i in range(1,l):\n # For every cell, adding the minimum of three values above it.\n matrix[i][0]+=min(matrix[i-1][0:2])\n for j in range(1,l):\n matrix[i][j]+=min(matrix[i-1][j-1:j+2])\n # Returning minimum of last step.\n return min(matrix[l-1])\n\n```\n | 1 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
90% Faster || O(n) Time complexity || Dynamic Programming | minimum-falling-path-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCalculating minimum upto a cell.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDynamic Programming\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n l=len(matrix)\n # Iterating from 2nd row of matrix and creating matrix of minimum sum upto that point.\n for i in range(1,l):\n # For every cell, adding the minimum of three values above it.\n matrix[i][0]+=min(matrix[i-1][0:2])\n for j in range(1,l):\n matrix[i][j]+=min(matrix[i-1][j-1:j+2])\n # Returning minimum of last step.\n return min(matrix[l-1])\n\n```\n | 1 | Given two integers n and k, return _an array of all the integers of length_ `n` _where the difference between every two consecutive digits is_ `k`. You may return the answer in **any order**.
Note that the integers should not have leading zeros. Integers as `02` and `043` are not allowed.
**Example 1:**
**Input:** n = 3, k = 7
**Output:** \[181,292,707,818,929\]
**Explanation:** Note that 070 is not a valid number, because it has leading zeroes.
**Example 2:**
**Input:** n = 2, k = 1
**Output:** \[10,12,21,23,32,34,43,45,54,56,65,67,76,78,87,89,98\]
**Constraints:**
* `2 <= n <= 9`
* `0 <= k <= 9` | null |
beats 96.9 % | CodeDominar Solution | DP Bottom-up approach | minimum-falling-path-sum | 0 | 1 | \n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n rows,cols = len(matrix),len(matrix[0])\n dp = [[float(\'inf\') for c in range(cols+2)] for r in range(rows+1)]\n \n for c in range(1,cols+1):\n dp[rows][c] = 0\n \n for r in range(rows-1,-1,-1):\n for c in range(cols-1,-1,-1):\n dp[r][c] = matrix[r][c] + min(dp[r+1][c],dp[r+1][c-1],dp[r+1][c+1])\n return min(dp[0])\n\n \n``` | 1 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
beats 96.9 % | CodeDominar Solution | DP Bottom-up approach | minimum-falling-path-sum | 0 | 1 | \n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n rows,cols = len(matrix),len(matrix[0])\n dp = [[float(\'inf\') for c in range(cols+2)] for r in range(rows+1)]\n \n for c in range(1,cols+1):\n dp[rows][c] = 0\n \n for r in range(rows-1,-1,-1):\n for c in range(cols-1,-1,-1):\n dp[r][c] = matrix[r][c] + min(dp[r+1][c],dp[r+1][c-1],dp[r+1][c+1])\n return min(dp[0])\n\n \n``` | 1 | Given two integers n and k, return _an array of all the integers of length_ `n` _where the difference between every two consecutive digits is_ `k`. You may return the answer in **any order**.
Note that the integers should not have leading zeros. Integers as `02` and `043` are not allowed.
**Example 1:**
**Input:** n = 3, k = 7
**Output:** \[181,292,707,818,929\]
**Explanation:** Note that 070 is not a valid number, because it has leading zeroes.
**Example 2:**
**Input:** n = 2, k = 1
**Output:** \[10,12,21,23,32,34,43,45,54,56,65,67,76,78,87,89,98\]
**Constraints:**
* `2 <= n <= 9`
* `0 <= k <= 9` | null |
Python DP | minimum-falling-path-sum | 0 | 1 | # Intuition\nIt\'s a simple DP problem. We need to start with the first row and check row-by-row, and maintaining minimal falling path.\n\n# Approach\nAt each iteration we maintain minimal falling pathes for each item in the row. For a given item it\'s sum will be minimal among pathes from the previous row plus current matrix value. We can come to the current item either from top, top-left or top-right item from the previous row. Among those 3 (or 2, for bound cases) we pick the minimal and record it.\n\n# Complexity\n- Time complexity:\nWe need to traverse the whole matrix of size ``n*m``. Thus time complexity is $$O(n*m)$$\n\n- Space complexity:\nApart from constant-size memory for variables we need to store previous row and current row. It\'s $$O(m)$$\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n n, m = len(matrix), len(matrix[0])\n prev = [matrix[0][j] for j in range(m)]\n for i in range(1, n):\n row = [0] * m\n for j in range(m):\n row[j] = prev[j] + matrix[i][j]\n if j > 0:\n row[j] = min(row[j], prev[j-1] + matrix[i][j])\n if j < m-1:\n row[j] = min(row[j], prev[j+1] + matrix[i][j])\n prev = row\n return min(prev)\n```\n\n\nShall you have any quesations please ask here, and upvote if you like the solution! | 1 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
Python DP | minimum-falling-path-sum | 0 | 1 | # Intuition\nIt\'s a simple DP problem. We need to start with the first row and check row-by-row, and maintaining minimal falling path.\n\n# Approach\nAt each iteration we maintain minimal falling pathes for each item in the row. For a given item it\'s sum will be minimal among pathes from the previous row plus current matrix value. We can come to the current item either from top, top-left or top-right item from the previous row. Among those 3 (or 2, for bound cases) we pick the minimal and record it.\n\n# Complexity\n- Time complexity:\nWe need to traverse the whole matrix of size ``n*m``. Thus time complexity is $$O(n*m)$$\n\n- Space complexity:\nApart from constant-size memory for variables we need to store previous row and current row. It\'s $$O(m)$$\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n n, m = len(matrix), len(matrix[0])\n prev = [matrix[0][j] for j in range(m)]\n for i in range(1, n):\n row = [0] * m\n for j in range(m):\n row[j] = prev[j] + matrix[i][j]\n if j > 0:\n row[j] = min(row[j], prev[j-1] + matrix[i][j])\n if j < m-1:\n row[j] = min(row[j], prev[j+1] + matrix[i][j])\n prev = row\n return min(prev)\n```\n\n\nShall you have any quesations please ask here, and upvote if you like the solution! | 1 | Given two integers n and k, return _an array of all the integers of length_ `n` _where the difference between every two consecutive digits is_ `k`. You may return the answer in **any order**.
Note that the integers should not have leading zeros. Integers as `02` and `043` are not allowed.
**Example 1:**
**Input:** n = 3, k = 7
**Output:** \[181,292,707,818,929\]
**Explanation:** Note that 070 is not a valid number, because it has leading zeroes.
**Example 2:**
**Input:** n = 2, k = 1
**Output:** \[10,12,21,23,32,34,43,45,54,56,65,67,76,78,87,89,98\]
**Constraints:**
* `2 <= n <= 9`
* `0 <= k <= 9` | null |
Solution | minimum-falling-path-sum | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minFallingPathSum(vector<vector<int>>& matrix)\n {\n int ans=matrix[0][0];\n for(int i=1 ; i<matrix.size() ; i++)\n {\n for(int j=0 ; j<matrix.size() ; j++)\n {\n if(j==0)\n {\n matrix[i][j]+=min(matrix[i-1][j] , matrix[i-1][j+1]);\n ans=matrix[i][0];\n }\n else if(j==matrix.size()-1)\n {\n matrix[i][j]+=min(matrix[i-1][j] , matrix[i-1][j-1]);\n }\n else\n {\n int add=min(matrix[i-1][j] , matrix[i-1][j+1]);\n matrix[i][j]+=min(add , matrix[i-1][j-1]);\n }\n if(i==matrix.size()-1)\n {\n ans=min(ans , matrix[i][j]);\n }\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n n = len(matrix)\n res = matrix[n-1]\n for i in range(n-2,-1,-1):\n curr = matrix[i]\n for j in range(n):\n if(j==0):\n curr[j]+=min(res[j],res[j+1])\n elif(j==n-1):\n curr[j]+=min(res[j],res[j-1])\n else:\n curr[j]+=min(res[j],res[j-1],res[j+1])\n res=curr\n return(min(res))\n```\n\n```Java []\nclass Solution {\n int ans = Integer.MAX_VALUE;\n public int minFallingPathSum(int[][] matrix) {\n helper(matrix, matrix.length-2);\n return ans;\n }\n void helper(int[][] matrix, int r) {\n if(r<0) {\n for(int i=0; i<matrix.length; i++) {\n ans = Math.min(ans, matrix[0][i]);\n }\n return;\n }\n for(int i=0; i<matrix.length; i++) {\n int minNextVal = matrix[r+1][i];\n if(i>0) {\n minNextVal = Math.min(minNextVal, matrix[r+1][i-1]);\n }\n if(i<matrix.length-1) {\n minNextVal = Math.min(minNextVal, matrix[r+1][i+1]);\n }\n matrix[r][i] += minNextVal;\n }\n helper(matrix, r-1);\n }\n}\n```\n | 1 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
Solution | minimum-falling-path-sum | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minFallingPathSum(vector<vector<int>>& matrix)\n {\n int ans=matrix[0][0];\n for(int i=1 ; i<matrix.size() ; i++)\n {\n for(int j=0 ; j<matrix.size() ; j++)\n {\n if(j==0)\n {\n matrix[i][j]+=min(matrix[i-1][j] , matrix[i-1][j+1]);\n ans=matrix[i][0];\n }\n else if(j==matrix.size()-1)\n {\n matrix[i][j]+=min(matrix[i-1][j] , matrix[i-1][j-1]);\n }\n else\n {\n int add=min(matrix[i-1][j] , matrix[i-1][j+1]);\n matrix[i][j]+=min(add , matrix[i-1][j-1]);\n }\n if(i==matrix.size()-1)\n {\n ans=min(ans , matrix[i][j]);\n }\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n n = len(matrix)\n res = matrix[n-1]\n for i in range(n-2,-1,-1):\n curr = matrix[i]\n for j in range(n):\n if(j==0):\n curr[j]+=min(res[j],res[j+1])\n elif(j==n-1):\n curr[j]+=min(res[j],res[j-1])\n else:\n curr[j]+=min(res[j],res[j-1],res[j+1])\n res=curr\n return(min(res))\n```\n\n```Java []\nclass Solution {\n int ans = Integer.MAX_VALUE;\n public int minFallingPathSum(int[][] matrix) {\n helper(matrix, matrix.length-2);\n return ans;\n }\n void helper(int[][] matrix, int r) {\n if(r<0) {\n for(int i=0; i<matrix.length; i++) {\n ans = Math.min(ans, matrix[0][i]);\n }\n return;\n }\n for(int i=0; i<matrix.length; i++) {\n int minNextVal = matrix[r+1][i];\n if(i>0) {\n minNextVal = Math.min(minNextVal, matrix[r+1][i-1]);\n }\n if(i<matrix.length-1) {\n minNextVal = Math.min(minNextVal, matrix[r+1][i+1]);\n }\n matrix[r][i] += minNextVal;\n }\n helper(matrix, r-1);\n }\n}\n```\n | 1 | Given two integers n and k, return _an array of all the integers of length_ `n` _where the difference between every two consecutive digits is_ `k`. You may return the answer in **any order**.
Note that the integers should not have leading zeros. Integers as `02` and `043` are not allowed.
**Example 1:**
**Input:** n = 3, k = 7
**Output:** \[181,292,707,818,929\]
**Explanation:** Note that 070 is not a valid number, because it has leading zeroes.
**Example 2:**
**Input:** n = 2, k = 1
**Output:** \[10,12,21,23,32,34,43,45,54,56,65,67,76,78,87,89,98\]
**Constraints:**
* `2 <= n <= 9`
* `0 <= k <= 9` | null |
Simple python solution with memoization | minimum-falling-path-sum | 0 | 1 | # Intuition\nFirst thing that comes to mind is Depth First Search but you can quickly realiza that DFS will lead to Time Limit Exceeded. Becasue we are solving a summation problem at each level again and again that leads to memoization, we can save the computation by only calculating once the minimum sum possible if we select a specific `x, y` in matrix at level `i`. \n\n# Approach\nSince we need to know minimum on the next level, we start with bottom-up approach. Calculate the `memo` array from bottom and then perform simple `min` operation going up.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n^2)$$\n\n---\n\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n m, n = len(matrix), len(matrix[0])\n memo = [[0]*n for _ in range(m)]\n memo[m-1] = matrix[m-1]\n \n\n for i in range(m-2, -1, -1):\n for j in range(n):\n x, y, z = memo[i+1][j], float(\'inf\'), float(\'inf\')\n if j != 0:\n y = memo[i+1][j-1]\n\n if j != n-1:\n z = memo[i+1][j+1] \n\n memo[i][j] = min(x, y, z) + matrix[i][j]\n return min(memo[0])\n\n \n \n``` | 2 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
Simple python solution with memoization | minimum-falling-path-sum | 0 | 1 | # Intuition\nFirst thing that comes to mind is Depth First Search but you can quickly realiza that DFS will lead to Time Limit Exceeded. Becasue we are solving a summation problem at each level again and again that leads to memoization, we can save the computation by only calculating once the minimum sum possible if we select a specific `x, y` in matrix at level `i`. \n\n# Approach\nSince we need to know minimum on the next level, we start with bottom-up approach. Calculate the `memo` array from bottom and then perform simple `min` operation going up.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n^2)$$\n\n---\n\n\n# Code\n```\nclass Solution:\n def minFallingPathSum(self, matrix: List[List[int]]) -> int:\n m, n = len(matrix), len(matrix[0])\n memo = [[0]*n for _ in range(m)]\n memo[m-1] = matrix[m-1]\n \n\n for i in range(m-2, -1, -1):\n for j in range(n):\n x, y, z = memo[i+1][j], float(\'inf\'), float(\'inf\')\n if j != 0:\n y = memo[i+1][j-1]\n\n if j != n-1:\n z = memo[i+1][j+1] \n\n memo[i][j] = min(x, y, z) + matrix[i][j]\n return min(memo[0])\n\n \n \n``` | 2 | Given two integers n and k, return _an array of all the integers of length_ `n` _where the difference between every two consecutive digits is_ `k`. You may return the answer in **any order**.
Note that the integers should not have leading zeros. Integers as `02` and `043` are not allowed.
**Example 1:**
**Input:** n = 3, k = 7
**Output:** \[181,292,707,818,929\]
**Explanation:** Note that 070 is not a valid number, because it has leading zeroes.
**Example 2:**
**Input:** n = 2, k = 1
**Output:** \[10,12,21,23,32,34,43,45,54,56,65,67,76,78,87,89,98\]
**Constraints:**
* `2 <= n <= 9`
* `0 <= k <= 9` | null |
Solution | beautiful-array | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> beautifulArray(int n) {\n vector<int> res = {1};\n while(res.size() != n){\n vector<int> temp;\n for(auto &ele : res) if(ele*2-1<=n) temp.push_back(ele*2-1);\n for(auto &ele : res) if(ele*2<=n) temp.push_back(ele*2);\n res = temp;\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def beautifulArray(self, n: int) -> List[int]:\n res=[1]\n while len(res)<n :\n odd=[2*i-1 for i in res]\n even=[2*i for i in res]\n res=odd+even\n return [i for i in res if i<=n]\n```\n\n```Java []\nclass Solution {\n Map<Integer, int[]> memo;\n public int[] beautifulArray(int N) {\n memo = new HashMap();\n return f(N);\n }\n public int[] f(int N) {\n if (memo.containsKey(N))\n return memo.get(N);\n\n int[] ans = new int[N];\n if (N == 1) {\n ans[0] = 1;\n } else {\n int t = 0;\n for (int x: f((N+1)/2))\n ans[t++] = 2*x - 1;\n for (int x: f(N/2))\n ans[t++] = 2*x;\n }\n memo.put(N, ans);\n return ans;\n }\n}\n```\n | 1 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Solution | beautiful-array | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> beautifulArray(int n) {\n vector<int> res = {1};\n while(res.size() != n){\n vector<int> temp;\n for(auto &ele : res) if(ele*2-1<=n) temp.push_back(ele*2-1);\n for(auto &ele : res) if(ele*2<=n) temp.push_back(ele*2);\n res = temp;\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def beautifulArray(self, n: int) -> List[int]:\n res=[1]\n while len(res)<n :\n odd=[2*i-1 for i in res]\n even=[2*i for i in res]\n res=odd+even\n return [i for i in res if i<=n]\n```\n\n```Java []\nclass Solution {\n Map<Integer, int[]> memo;\n public int[] beautifulArray(int N) {\n memo = new HashMap();\n return f(N);\n }\n public int[] f(int N) {\n if (memo.containsKey(N))\n return memo.get(N);\n\n int[] ans = new int[N];\n if (N == 1) {\n ans[0] = 1;\n } else {\n int t = 0;\n for (int x: f((N+1)/2))\n ans[t++] = 2*x - 1;\n for (int x: f(N/2))\n ans[t++] = 2*x;\n }\n memo.put(N, ans);\n return ans;\n }\n}\n```\n | 1 | You are given the `root` of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return _the minimum number of cameras needed to monitor all nodes of the tree_.
**Example 1:**
**Input:** root = \[0,0,null,0,0\]
**Output:** 1
**Explanation:** One camera is enough to monitor all nodes if placed as shown.
**Example 2:**
**Input:** root = \[0,0,null,0,null,0,null,null,0\]
**Output:** 2
**Explanation:** At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `Node.val == 0` | null |
easy code for beginner with one line | beautiful-array | 0 | 1 | # Intuition\nfirst i done it on 20 lines but now it is one line\n\n# Approach\ndone through simple reccurrsion\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def beautifulArray(self, n: int) -> List[int]:\n return [1] if n<2 else [i*2-1 for i in self.beautifulArray((n+1)//2)]+[i*2 for i in self.beautifulArray(n//2)]\n\n``` | 2 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
easy code for beginner with one line | beautiful-array | 0 | 1 | # Intuition\nfirst i done it on 20 lines but now it is one line\n\n# Approach\ndone through simple reccurrsion\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def beautifulArray(self, n: int) -> List[int]:\n return [1] if n<2 else [i*2-1 for i in self.beautifulArray((n+1)//2)]+[i*2 for i in self.beautifulArray(n//2)]\n\n``` | 2 | You are given the `root` of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return _the minimum number of cameras needed to monitor all nodes of the tree_.
**Example 1:**
**Input:** root = \[0,0,null,0,0\]
**Output:** 1
**Explanation:** One camera is enough to monitor all nodes if placed as shown.
**Example 2:**
**Input:** root = \[0,0,null,0,null,0,null,null,0\]
**Output:** 2
**Explanation:** At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `Node.val == 0` | null |
Detailed Explanation with Diagrams. A Collection of Ideas from Multiple Posts. [Python3] | beautiful-array | 0 | 1 | ## 0. Introduction\nThis post is a collection of all the posts, comments and discussions of the LeetCode community. References mentioned at the bottom! I\'ve attempted to explain things in detail, with diagrams to help understand the intuitions as well.\n\n## 1. Naive Solution\nThe first thing anyone can think of is using `permutations(array)` to enumerate all the permutations in `O(N!)` time. This is bad in itself, but it gets worse. We still need to check the validity of the resultant array. We can do this in `O(N^3)` time, iterative over every possible combination of `i`, `j` and `k`.\n\nBelow is the code for it.\n```\nfrom itertools import permutations\nclass Solution:\n def invalid(self, x):\n n = len(x)\n flag = False\n for i in range(n):\n if flag: break\n for j in range(i+2, n):\n if flag: break\n for k in range(i+1, j):\n if 2*x[k] == x[i]+x[j]: flag = True; break\n return flag\n \n def beautifulArray(self, n: int) -> List[int]:\n for perm in permutations(range(1, n+1)):\n if not self.invalid(perm):\n return perm\n```\n\nThis is clearly a dead end. The time complexity is enormous and impractical. But, what to do?\n\n## 2. Thinking in Terms of Bits\n**Whenever stuck, think in terms of bits.**\n\nIt always helps to think in terms of bits, so let\'s do that. Reformulating the problem, `nums[i]+nums[j] = 2*nums[k]` is not allowed.\n\nIn terms of bits, we can start with thinking what would happen if `nums[i]` or `nums[j]` is odd or even.\n\n\n| nums[i] | nums[j] | nums[k] |\n| ------- | ------- |:------------:|\n| even | even | even/odd |\n| odd | odd | even/odd |\n| even | odd | non-existent |\n| odd | even | non-existent |\n\n**Clearly, it looks like we want to focus on the last two cases. Ensuring that will ensure the validity of the solution.**\n\n## 3. Finding Recursion\nWe know splitting the array into odds and evens is beneficial. The trivial case is `[odd numbers here] [even numbers here]`, or the opposite `[even numbers here] [odd numbers here]`. Both will work. For convenience, I\'ll take the first one.\n\nexample: `n = 7`\n`1 2 3 4 5 6 7` -> `1 3 5 7 | 2 4 6`\n\nThis clearly won\'t work since `1 3 5 7` and `2 4 6` are troublesome in themselves, but if `i` is pointing to `1 3 5 7` and `j` to `2 4 6`, we can stay safe.\n\nNow, what if ... we break the `1 3 5 7` into two again? How? Just do a right-shift operation. (this is one of those problems whose solutions make sense once you know them lmao)\n\nThis makes the problem: `0 1 2 3`. Doesn\'t this look eerily similar to the orignial problem? We can break this down as `1 3 | 0 2`. This will work for `evens` as well (think why). **We have found a recursion!** \n\nThe below diagram should explain it better.\n\n\n\nNote that the right shifting is done for explaination reasons, the goal is to actually just consider alternate elements. \n\n## 4. Code for Recursive Solution\n```\nclass Solution:\n def recurse(self, nums):\n if len(nums) <= 2: return nums\n return self.recurse(nums[::2]) + self.recurse(nums[1::2])\n \n def beautifulArray(self, n: int) -> List[int]:\n return self.recurse([i for i in range(1, n+1)])\n```\n\n## 5. One-liner Solution\nThe final one-liner solution is based on a very interesting observation. Recall how we worked with the trees, where each following height involved right-shifting the binary representation by one. Alternatively, think like this: What happened in the grand scheme? We considered the 0th bit first, then the 1st, then the 2nd and so on.\n\n\n\nIf you note, this is equivalent to a sorting problem! The only difference is that we are considering the number in reverse, in binary. This brings us to the godly one liner solution by lee215.\n\n```\nclass Solution:\n def beautifulArray(self, n: int) -> List[int]:\n return sorted(range(1, n+1), key=lambda x: bin(x)[:1:-1])\n```\n\n## 6. References\n- https://leetcode.com/r0bertz/ \'s post https://leetcode.com/problems/beautiful-array/discuss/644612/Python3-solution-with-detailed-explanation-Beautiful-Array\n- https://leetcode.com/lee215/ \'s post https://leetcode.com/problems/beautiful-array/discuss/186680/Python-Three-1-line-Solutions\n- https://leetcode.com/lee215/ \'s post https://leetcode.com/problems/beautiful-array/discuss/186679/Odd-%2B-Even-Pattern-O(N)\n\n\nIf you want another look at the problem in a different format, here\'s my video explanation.\nhttps://www.youtube.com/watch?v=jHHdiMIJcr0.\n\nFeel free to ask any questions! Criticisms and comments are most welcome. If this helps you, upvote! It gives me motivation to be better :D | 50 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Detailed Explanation with Diagrams. A Collection of Ideas from Multiple Posts. [Python3] | beautiful-array | 0 | 1 | ## 0. Introduction\nThis post is a collection of all the posts, comments and discussions of the LeetCode community. References mentioned at the bottom! I\'ve attempted to explain things in detail, with diagrams to help understand the intuitions as well.\n\n## 1. Naive Solution\nThe first thing anyone can think of is using `permutations(array)` to enumerate all the permutations in `O(N!)` time. This is bad in itself, but it gets worse. We still need to check the validity of the resultant array. We can do this in `O(N^3)` time, iterative over every possible combination of `i`, `j` and `k`.\n\nBelow is the code for it.\n```\nfrom itertools import permutations\nclass Solution:\n def invalid(self, x):\n n = len(x)\n flag = False\n for i in range(n):\n if flag: break\n for j in range(i+2, n):\n if flag: break\n for k in range(i+1, j):\n if 2*x[k] == x[i]+x[j]: flag = True; break\n return flag\n \n def beautifulArray(self, n: int) -> List[int]:\n for perm in permutations(range(1, n+1)):\n if not self.invalid(perm):\n return perm\n```\n\nThis is clearly a dead end. The time complexity is enormous and impractical. But, what to do?\n\n## 2. Thinking in Terms of Bits\n**Whenever stuck, think in terms of bits.**\n\nIt always helps to think in terms of bits, so let\'s do that. Reformulating the problem, `nums[i]+nums[j] = 2*nums[k]` is not allowed.\n\nIn terms of bits, we can start with thinking what would happen if `nums[i]` or `nums[j]` is odd or even.\n\n\n| nums[i] | nums[j] | nums[k] |\n| ------- | ------- |:------------:|\n| even | even | even/odd |\n| odd | odd | even/odd |\n| even | odd | non-existent |\n| odd | even | non-existent |\n\n**Clearly, it looks like we want to focus on the last two cases. Ensuring that will ensure the validity of the solution.**\n\n## 3. Finding Recursion\nWe know splitting the array into odds and evens is beneficial. The trivial case is `[odd numbers here] [even numbers here]`, or the opposite `[even numbers here] [odd numbers here]`. Both will work. For convenience, I\'ll take the first one.\n\nexample: `n = 7`\n`1 2 3 4 5 6 7` -> `1 3 5 7 | 2 4 6`\n\nThis clearly won\'t work since `1 3 5 7` and `2 4 6` are troublesome in themselves, but if `i` is pointing to `1 3 5 7` and `j` to `2 4 6`, we can stay safe.\n\nNow, what if ... we break the `1 3 5 7` into two again? How? Just do a right-shift operation. (this is one of those problems whose solutions make sense once you know them lmao)\n\nThis makes the problem: `0 1 2 3`. Doesn\'t this look eerily similar to the orignial problem? We can break this down as `1 3 | 0 2`. This will work for `evens` as well (think why). **We have found a recursion!** \n\nThe below diagram should explain it better.\n\n\n\nNote that the right shifting is done for explaination reasons, the goal is to actually just consider alternate elements. \n\n## 4. Code for Recursive Solution\n```\nclass Solution:\n def recurse(self, nums):\n if len(nums) <= 2: return nums\n return self.recurse(nums[::2]) + self.recurse(nums[1::2])\n \n def beautifulArray(self, n: int) -> List[int]:\n return self.recurse([i for i in range(1, n+1)])\n```\n\n## 5. One-liner Solution\nThe final one-liner solution is based on a very interesting observation. Recall how we worked with the trees, where each following height involved right-shifting the binary representation by one. Alternatively, think like this: What happened in the grand scheme? We considered the 0th bit first, then the 1st, then the 2nd and so on.\n\n\n\nIf you note, this is equivalent to a sorting problem! The only difference is that we are considering the number in reverse, in binary. This brings us to the godly one liner solution by lee215.\n\n```\nclass Solution:\n def beautifulArray(self, n: int) -> List[int]:\n return sorted(range(1, n+1), key=lambda x: bin(x)[:1:-1])\n```\n\n## 6. References\n- https://leetcode.com/r0bertz/ \'s post https://leetcode.com/problems/beautiful-array/discuss/644612/Python3-solution-with-detailed-explanation-Beautiful-Array\n- https://leetcode.com/lee215/ \'s post https://leetcode.com/problems/beautiful-array/discuss/186680/Python-Three-1-line-Solutions\n- https://leetcode.com/lee215/ \'s post https://leetcode.com/problems/beautiful-array/discuss/186679/Odd-%2B-Even-Pattern-O(N)\n\n\nIf you want another look at the problem in a different format, here\'s my video explanation.\nhttps://www.youtube.com/watch?v=jHHdiMIJcr0.\n\nFeel free to ask any questions! Criticisms and comments are most welcome. If this helps you, upvote! It gives me motivation to be better :D | 50 | You are given the `root` of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return _the minimum number of cameras needed to monitor all nodes of the tree_.
**Example 1:**
**Input:** root = \[0,0,null,0,0\]
**Output:** 1
**Explanation:** One camera is enough to monitor all nodes if placed as shown.
**Example 2:**
**Input:** root = \[0,0,null,0,null,0,null,null,0\]
**Output:** 2
**Explanation:** At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `Node.val == 0` | null |
Python3 solution with detailed explanation - Beautiful Array | beautiful-array | 0 | 1 | First, divide the array into even numbers and odd numbers so that we only need to further arrange numbers within even or odd numbers themselves because nums[i] and nums[j] must be both even or odd and can\'t be one even and one old. \n\nThen, further divide each division into numbers at even indices and odd indices till the division length is either 1 or 2 at which time just return the division. This works the same way as the first step, because if you divide all even numbers by 2, you will have even and odd number again, e.g. `[2,4,6,8,10] -> [1,2,3,4,5]`. If you add odd numbers by 1 and divide by 2, you will also have even and odd numbers, e.g. `[1,3,5,7,9] -> [2,4,6,8,10] -> [1,2,3,4,5]`.\n\n```\nclass Solution:\n def beautifulArray(self, N: int) -> List[int]:\n nums = list(range(1, N+1))\n \n def helper(nums) -> List[int]:\n if len(nums) < 3:\n return nums\n even = nums[::2]\n odd = nums[1::2]\n return helper(even) + helper(old)\n return helper(nums) \n``` | 13 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Python3 solution with detailed explanation - Beautiful Array | beautiful-array | 0 | 1 | First, divide the array into even numbers and odd numbers so that we only need to further arrange numbers within even or odd numbers themselves because nums[i] and nums[j] must be both even or odd and can\'t be one even and one old. \n\nThen, further divide each division into numbers at even indices and odd indices till the division length is either 1 or 2 at which time just return the division. This works the same way as the first step, because if you divide all even numbers by 2, you will have even and odd number again, e.g. `[2,4,6,8,10] -> [1,2,3,4,5]`. If you add odd numbers by 1 and divide by 2, you will also have even and odd numbers, e.g. `[1,3,5,7,9] -> [2,4,6,8,10] -> [1,2,3,4,5]`.\n\n```\nclass Solution:\n def beautifulArray(self, N: int) -> List[int]:\n nums = list(range(1, N+1))\n \n def helper(nums) -> List[int]:\n if len(nums) < 3:\n return nums\n even = nums[::2]\n odd = nums[1::2]\n return helper(even) + helper(old)\n return helper(nums) \n``` | 13 | You are given the `root` of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return _the minimum number of cameras needed to monitor all nodes of the tree_.
**Example 1:**
**Input:** root = \[0,0,null,0,0\]
**Output:** 1
**Explanation:** One camera is enough to monitor all nodes if placed as shown.
**Example 2:**
**Input:** root = \[0,0,null,0,null,0,null,null,0\]
**Output:** 2
**Explanation:** At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `Node.val == 0` | null |
Python easy solution | beautiful-array | 0 | 1 | ```\ndef beautifulArray(self, n: int) -> List[int]:\n\tans = [1]\n\twhile len(ans) < n:\n\t\tres = []\n\t\tfor el in ans:\n\t\t\tif 2 * el - 1 <= n:\n\t\t\t\tres.append(el * 2 - 1)\n\n\t\tfor el in ans: \n\t\t\tif 2 * el <= n:\n\t\t\t\tres.append(el * 2)\n\n\t\tans = res\n\treturn ans\n\n# odd ele -> 2 * el - 1\n# even ele -> 2 * el\n``` | 3 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Python easy solution | beautiful-array | 0 | 1 | ```\ndef beautifulArray(self, n: int) -> List[int]:\n\tans = [1]\n\twhile len(ans) < n:\n\t\tres = []\n\t\tfor el in ans:\n\t\t\tif 2 * el - 1 <= n:\n\t\t\t\tres.append(el * 2 - 1)\n\n\t\tfor el in ans: \n\t\t\tif 2 * el <= n:\n\t\t\t\tres.append(el * 2)\n\n\t\tans = res\n\treturn ans\n\n# odd ele -> 2 * el - 1\n# even ele -> 2 * el\n``` | 3 | You are given the `root` of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return _the minimum number of cameras needed to monitor all nodes of the tree_.
**Example 1:**
**Input:** root = \[0,0,null,0,0\]
**Output:** 1
**Explanation:** One camera is enough to monitor all nodes if placed as shown.
**Example 2:**
**Input:** root = \[0,0,null,0,null,0,null,null,0\]
**Output:** 2
**Explanation:** At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `Node.val == 0` | null |
Python O(n) solution | beautiful-array | 0 | 1 | In this problem we have n = 1000, which is too big to use dfs/backtracking, so we need to find some pattern. We need to avoid structures like i < k < j with nums[i] + nums[j] = 2 * nums[k], which means that nums[i] and nums[j] has the same parity: they are both odd or even. This lead us to the following idea: let us split all numbers into 2 groups: all odd numbers and then all even numbers.\n\n[ odd numbers ] [ even numbers ]\n\nThen if i, j, k lies in two different groups, we are OK, we will hever have forbidden pattern. Also, if we look at odd numbers, imagine n = 12, then we have [1, 3, 5, 7, 9, 11] and if we subtract 1 to each number and divide each number by 2 then we have [0, 1, 2, 3, 4, 5]. Note, that is linear transform: when we did this transformation, if we did not have forbidden pattern, we still do not have it! So, what we need to do is to run function recursively for odd and even numbers and concatenate them.\n\n\n\n# Complexity\nFrom the first sight, time complexity is O(n log n), because we have recursion C(n) = C(n//2) + C((n+1)//2), which lead to O(n log n). However it can be shown that it is O(n). Imagine case n = 105, then we have 105 -> (52, 53) -> (26, 26, 27, 27) -> (13, 13, 13, 13, 14, 14, 14, 14) and if we use memoisation, no need to solve problem each time for 13, we can do it only once. On each level we will have at most two values in our recursion tree. Space complexity is O(n).\n\n\n# Code\n```\nclass Solution:\n def beautifulArray(self, N):\n @lru_cache(None)\n def dfs(N):\n if N == 1: return (1,)\n t1 = dfs((N+1)//2)\n t2 = dfs(N//2)\n return [i*2-1 for i in t1] + [i*2 for i in t2]\n \n return dfs(N)\n``` | 0 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Python O(n) solution | beautiful-array | 0 | 1 | In this problem we have n = 1000, which is too big to use dfs/backtracking, so we need to find some pattern. We need to avoid structures like i < k < j with nums[i] + nums[j] = 2 * nums[k], which means that nums[i] and nums[j] has the same parity: they are both odd or even. This lead us to the following idea: let us split all numbers into 2 groups: all odd numbers and then all even numbers.\n\n[ odd numbers ] [ even numbers ]\n\nThen if i, j, k lies in two different groups, we are OK, we will hever have forbidden pattern. Also, if we look at odd numbers, imagine n = 12, then we have [1, 3, 5, 7, 9, 11] and if we subtract 1 to each number and divide each number by 2 then we have [0, 1, 2, 3, 4, 5]. Note, that is linear transform: when we did this transformation, if we did not have forbidden pattern, we still do not have it! So, what we need to do is to run function recursively for odd and even numbers and concatenate them.\n\n\n\n# Complexity\nFrom the first sight, time complexity is O(n log n), because we have recursion C(n) = C(n//2) + C((n+1)//2), which lead to O(n log n). However it can be shown that it is O(n). Imagine case n = 105, then we have 105 -> (52, 53) -> (26, 26, 27, 27) -> (13, 13, 13, 13, 14, 14, 14, 14) and if we use memoisation, no need to solve problem each time for 13, we can do it only once. On each level we will have at most two values in our recursion tree. Space complexity is O(n).\n\n\n# Code\n```\nclass Solution:\n def beautifulArray(self, N):\n @lru_cache(None)\n def dfs(N):\n if N == 1: return (1,)\n t1 = dfs((N+1)//2)\n t2 = dfs(N//2)\n return [i*2-1 for i in t1] + [i*2 for i in t2]\n \n return dfs(N)\n``` | 0 | You are given the `root` of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return _the minimum number of cameras needed to monitor all nodes of the tree_.
**Example 1:**
**Input:** root = \[0,0,null,0,0\]
**Output:** 1
**Explanation:** One camera is enough to monitor all nodes if placed as shown.
**Example 2:**
**Input:** root = \[0,0,null,0,null,0,null,null,0\]
**Output:** 2
**Explanation:** At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
**Constraints:**
* The number of nodes in the tree is in the range `[1, 1000]`.
* `Node.val == 0` | null |
Easy - 3000 milliseconds | number-of-recent-calls | 0 | 1 | # Intuition\nThe task requires us to count the number of recent requests within a certain time frame. The first intuition is to keep track of the requests as they come in. However, we only care about the requests that happened in the last 3000 milliseconds. This suggests that we should remove old requests that are no longer within this time frame. A queue data structure is ideal for this because it allows us to easily add new requests at the end and remove old requests from the front.\n\n# Approach\nOur approach is to use a deque (double-ended queue) data structure to store the times of the requests. Each time the \'ping\' method is called, we add the new time at the end of the deque. We then remove all times at the front of the deque that are less than \'t - 3000\'. The remaining times in the deque are the requests that happened within the last 3000 milliseconds. To get the number of these requests, we simply return the length of the deque.\n\n# Complexity\n- Time complexity: The time complexity of the \'ping\' operation is \\( O(1) \\). Each \'ping\' call results in a constant number of operations, which does not depend on the size of \'t\' or the number of requests.\n\n- Space complexity: The space complexity is \\( O(N) \\), where \\( N \\) is the maximum number of \'pings\' within a 3000 millisecond time frame. This is because all these \'pings\' could potentially be stored in the deque at the same time.\n\n# Code\n```\nclass RecentCounter:\n def __init__(self):\n self.queue = deque() \n def ping(self, t: int) -> int:\n self.queue.append(t) \n while self.queue[0] < t - 3000: \n self.queue.popleft() \n return len(self.queue) \n``` | 9 | You have a `RecentCounter` class which counts the number of recent requests within a certain time frame.
Implement the `RecentCounter` class:
* `RecentCounter()` Initializes the counter with zero recent requests.
* `int ping(int t)` Adds a new request at time `t`, where `t` represents some time in milliseconds, and returns the number of requests that has happened in the past `3000` milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range `[t - 3000, t]`.
It is **guaranteed** that every call to `ping` uses a strictly larger value of `t` than the previous call.
**Example 1:**
**Input**
\[ "RecentCounter ", "ping ", "ping ", "ping ", "ping "\]
\[\[\], \[1\], \[100\], \[3001\], \[3002\]\]
**Output**
\[null, 1, 2, 3, 3\]
**Explanation**
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = \[1\], range is \[-2999,1\], return 1
recentCounter.ping(100); // requests = \[1, 100\], range is \[-2900,100\], return 2
recentCounter.ping(3001); // requests = \[1, 100, 3001\], range is \[1,3001\], return 3
recentCounter.ping(3002); // requests = \[1, 100, 3001, 3002\], range is \[2,3002\], return 3
**Constraints:**
* `1 <= t <= 109`
* Each test case will call `ping` with **strictly increasing** values of `t`.
* At most `104` calls will be made to `ping`. | null |
Easy - 3000 milliseconds | number-of-recent-calls | 0 | 1 | # Intuition\nThe task requires us to count the number of recent requests within a certain time frame. The first intuition is to keep track of the requests as they come in. However, we only care about the requests that happened in the last 3000 milliseconds. This suggests that we should remove old requests that are no longer within this time frame. A queue data structure is ideal for this because it allows us to easily add new requests at the end and remove old requests from the front.\n\n# Approach\nOur approach is to use a deque (double-ended queue) data structure to store the times of the requests. Each time the \'ping\' method is called, we add the new time at the end of the deque. We then remove all times at the front of the deque that are less than \'t - 3000\'. The remaining times in the deque are the requests that happened within the last 3000 milliseconds. To get the number of these requests, we simply return the length of the deque.\n\n# Complexity\n- Time complexity: The time complexity of the \'ping\' operation is \\( O(1) \\). Each \'ping\' call results in a constant number of operations, which does not depend on the size of \'t\' or the number of requests.\n\n- Space complexity: The space complexity is \\( O(N) \\), where \\( N \\) is the maximum number of \'pings\' within a 3000 millisecond time frame. This is because all these \'pings\' could potentially be stored in the deque at the same time.\n\n# Code\n```\nclass RecentCounter:\n def __init__(self):\n self.queue = deque() \n def ping(self, t: int) -> int:\n self.queue.append(t) \n while self.queue[0] < t - 3000: \n self.queue.popleft() \n return len(self.queue) \n``` | 9 | Given an array of integers `arr`, sort the array by performing a series of **pancake flips**.
In one pancake flip we do the following steps:
* Choose an integer `k` where `1 <= k <= arr.length`.
* Reverse the sub-array `arr[0...k-1]` (**0-indexed**).
For example, if `arr = [3,2,1,4]` and we performed a pancake flip choosing `k = 3`, we reverse the sub-array `[3,2,1]`, so `arr = [1,2,3,4]` after the pancake flip at `k = 3`.
Return _an array of the_ `k`_\-values corresponding to a sequence of pancake flips that sort_ `arr`. Any valid answer that sorts the array within `10 * arr.length` flips will be judged as correct.
**Example 1:**
**Input:** arr = \[3,2,4,1\]
**Output:** \[4,2,4,3\]
**Explanation:**
We perform 4 pancake flips, with k values 4, 2, 4, and 3.
Starting state: arr = \[3, 2, 4, 1\]
After 1st flip (k = 4): arr = \[1, 4, 2, 3\]
After 2nd flip (k = 2): arr = \[4, 1, 2, 3\]
After 3rd flip (k = 4): arr = \[3, 2, 1, 4\]
After 4th flip (k = 3): arr = \[1, 2, 3, 4\], which is sorted.
**Example 2:**
**Input:** arr = \[1,2,3\]
**Output:** \[\]
**Explanation:** The input is already sorted, so there is no need to flip anything.
Note that other answers, such as \[3, 3\], would also be accepted.
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= arr.length`
* All integers in `arr` are unique (i.e. `arr` is a permutation of the integers from `1` to `arr.length`). | null |
Beating 99.34% Python Easiest Solution | number-of-recent-calls | 0 | 1 | \n\n\n# Code\n```\nfrom collections import deque\nclass RecentCounter:\n\n def __init__(self):\n self.q = deque()\n \n def ping(self, t: int) -> int:\n self.q.append(t)\n \n while t - self.q[0] > 3000:\n self.q.popleft()\n \n return len(self.q)\n \n# Your RecentCounter object will be instantiated and called as such:\n# obj = RecentCounter()\n# param_1 = obj.ping(t)\n``` | 10 | You have a `RecentCounter` class which counts the number of recent requests within a certain time frame.
Implement the `RecentCounter` class:
* `RecentCounter()` Initializes the counter with zero recent requests.
* `int ping(int t)` Adds a new request at time `t`, where `t` represents some time in milliseconds, and returns the number of requests that has happened in the past `3000` milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range `[t - 3000, t]`.
It is **guaranteed** that every call to `ping` uses a strictly larger value of `t` than the previous call.
**Example 1:**
**Input**
\[ "RecentCounter ", "ping ", "ping ", "ping ", "ping "\]
\[\[\], \[1\], \[100\], \[3001\], \[3002\]\]
**Output**
\[null, 1, 2, 3, 3\]
**Explanation**
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = \[1\], range is \[-2999,1\], return 1
recentCounter.ping(100); // requests = \[1, 100\], range is \[-2900,100\], return 2
recentCounter.ping(3001); // requests = \[1, 100, 3001\], range is \[1,3001\], return 3
recentCounter.ping(3002); // requests = \[1, 100, 3001, 3002\], range is \[2,3002\], return 3
**Constraints:**
* `1 <= t <= 109`
* Each test case will call `ping` with **strictly increasing** values of `t`.
* At most `104` calls will be made to `ping`. | null |
Beating 99.34% Python Easiest Solution | number-of-recent-calls | 0 | 1 | \n\n\n# Code\n```\nfrom collections import deque\nclass RecentCounter:\n\n def __init__(self):\n self.q = deque()\n \n def ping(self, t: int) -> int:\n self.q.append(t)\n \n while t - self.q[0] > 3000:\n self.q.popleft()\n \n return len(self.q)\n \n# Your RecentCounter object will be instantiated and called as such:\n# obj = RecentCounter()\n# param_1 = obj.ping(t)\n``` | 10 | Given an array of integers `arr`, sort the array by performing a series of **pancake flips**.
In one pancake flip we do the following steps:
* Choose an integer `k` where `1 <= k <= arr.length`.
* Reverse the sub-array `arr[0...k-1]` (**0-indexed**).
For example, if `arr = [3,2,1,4]` and we performed a pancake flip choosing `k = 3`, we reverse the sub-array `[3,2,1]`, so `arr = [1,2,3,4]` after the pancake flip at `k = 3`.
Return _an array of the_ `k`_\-values corresponding to a sequence of pancake flips that sort_ `arr`. Any valid answer that sorts the array within `10 * arr.length` flips will be judged as correct.
**Example 1:**
**Input:** arr = \[3,2,4,1\]
**Output:** \[4,2,4,3\]
**Explanation:**
We perform 4 pancake flips, with k values 4, 2, 4, and 3.
Starting state: arr = \[3, 2, 4, 1\]
After 1st flip (k = 4): arr = \[1, 4, 2, 3\]
After 2nd flip (k = 2): arr = \[4, 1, 2, 3\]
After 3rd flip (k = 4): arr = \[3, 2, 1, 4\]
After 4th flip (k = 3): arr = \[1, 2, 3, 4\], which is sorted.
**Example 2:**
**Input:** arr = \[1,2,3\]
**Output:** \[\]
**Explanation:** The input is already sorted, so there is no need to flip anything.
Note that other answers, such as \[3, 3\], would also be accepted.
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= arr.length`
* All integers in `arr` are unique (i.e. `arr` is a permutation of the integers from `1` to `arr.length`). | null |
Solution | number-of-recent-calls | 1 | 1 | ```C++ []\nclass RecentCounter {\npublic:\nqueue<int>q;\n RecentCounter() { \n }\n int ping(int t) {\n q.push(t);\n while(q.front()<t-3000){\n q.pop();\n }\n return q.size(); \n }\n};\n```\n\n```Python3 []\nfrom collections import deque\n\nclass RecentCounter:\n\n def __init__(self):\n self.queue = deque()\n\n def ping(self, t: int) -> int:\n self.queue.append(t)\n while t - 3000 > self.queue[0]:\n self.queue.popleft()\n return len(self.queue)\n```\n\n```Java []\nclass RecentCounter {\n LinkedList<Integer> swin;\n public RecentCounter() {\n swin = new LinkedList<>();\n }\n public int ping(int t) {\n swin.addLast(t);\n while (swin.getFirst() < t - 3000) swin.removeFirst();\n return swin.size();\n }\n}\n```\n | 2 | You have a `RecentCounter` class which counts the number of recent requests within a certain time frame.
Implement the `RecentCounter` class:
* `RecentCounter()` Initializes the counter with zero recent requests.
* `int ping(int t)` Adds a new request at time `t`, where `t` represents some time in milliseconds, and returns the number of requests that has happened in the past `3000` milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range `[t - 3000, t]`.
It is **guaranteed** that every call to `ping` uses a strictly larger value of `t` than the previous call.
**Example 1:**
**Input**
\[ "RecentCounter ", "ping ", "ping ", "ping ", "ping "\]
\[\[\], \[1\], \[100\], \[3001\], \[3002\]\]
**Output**
\[null, 1, 2, 3, 3\]
**Explanation**
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = \[1\], range is \[-2999,1\], return 1
recentCounter.ping(100); // requests = \[1, 100\], range is \[-2900,100\], return 2
recentCounter.ping(3001); // requests = \[1, 100, 3001\], range is \[1,3001\], return 3
recentCounter.ping(3002); // requests = \[1, 100, 3001, 3002\], range is \[2,3002\], return 3
**Constraints:**
* `1 <= t <= 109`
* Each test case will call `ping` with **strictly increasing** values of `t`.
* At most `104` calls will be made to `ping`. | null |
Solution | number-of-recent-calls | 1 | 1 | ```C++ []\nclass RecentCounter {\npublic:\nqueue<int>q;\n RecentCounter() { \n }\n int ping(int t) {\n q.push(t);\n while(q.front()<t-3000){\n q.pop();\n }\n return q.size(); \n }\n};\n```\n\n```Python3 []\nfrom collections import deque\n\nclass RecentCounter:\n\n def __init__(self):\n self.queue = deque()\n\n def ping(self, t: int) -> int:\n self.queue.append(t)\n while t - 3000 > self.queue[0]:\n self.queue.popleft()\n return len(self.queue)\n```\n\n```Java []\nclass RecentCounter {\n LinkedList<Integer> swin;\n public RecentCounter() {\n swin = new LinkedList<>();\n }\n public int ping(int t) {\n swin.addLast(t);\n while (swin.getFirst() < t - 3000) swin.removeFirst();\n return swin.size();\n }\n}\n```\n | 2 | Given an array of integers `arr`, sort the array by performing a series of **pancake flips**.
In one pancake flip we do the following steps:
* Choose an integer `k` where `1 <= k <= arr.length`.
* Reverse the sub-array `arr[0...k-1]` (**0-indexed**).
For example, if `arr = [3,2,1,4]` and we performed a pancake flip choosing `k = 3`, we reverse the sub-array `[3,2,1]`, so `arr = [1,2,3,4]` after the pancake flip at `k = 3`.
Return _an array of the_ `k`_\-values corresponding to a sequence of pancake flips that sort_ `arr`. Any valid answer that sorts the array within `10 * arr.length` flips will be judged as correct.
**Example 1:**
**Input:** arr = \[3,2,4,1\]
**Output:** \[4,2,4,3\]
**Explanation:**
We perform 4 pancake flips, with k values 4, 2, 4, and 3.
Starting state: arr = \[3, 2, 4, 1\]
After 1st flip (k = 4): arr = \[1, 4, 2, 3\]
After 2nd flip (k = 2): arr = \[4, 1, 2, 3\]
After 3rd flip (k = 4): arr = \[3, 2, 1, 4\]
After 4th flip (k = 3): arr = \[1, 2, 3, 4\], which is sorted.
**Example 2:**
**Input:** arr = \[1,2,3\]
**Output:** \[\]
**Explanation:** The input is already sorted, so there is no need to flip anything.
Note that other answers, such as \[3, 3\], would also be accepted.
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= arr.length`
* All integers in `arr` are unique (i.e. `arr` is a permutation of the integers from `1` to `arr.length`). | null |
Simple Solution But logical, Beats 99.70% | number-of-recent-calls | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen I saw this problem for the first time, I thought problems related to queue in leetcode need to be solved by Node, but it is easier than Nodes here.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIn while statement we check is it empty or not first if it is, we simply append it to queue (composition).\nIn next Input, there is 1 in queue, so we add 1 + 3000 < t, t in this case 100, if it is the case we remove it from queue\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nBig O(n Log (n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nBig O(n)\n# Code\n```\nclass RecentCounter:\n def __init__(self):\n self.queue = deque()\n\n def ping(self, t: int) -> int:\n while self.queue and self.queue[0] + 3000 < t:\n self.queue.popleft()\n self.queue.append(t)\n return len(self.queue)\n``` | 1 | You have a `RecentCounter` class which counts the number of recent requests within a certain time frame.
Implement the `RecentCounter` class:
* `RecentCounter()` Initializes the counter with zero recent requests.
* `int ping(int t)` Adds a new request at time `t`, where `t` represents some time in milliseconds, and returns the number of requests that has happened in the past `3000` milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range `[t - 3000, t]`.
It is **guaranteed** that every call to `ping` uses a strictly larger value of `t` than the previous call.
**Example 1:**
**Input**
\[ "RecentCounter ", "ping ", "ping ", "ping ", "ping "\]
\[\[\], \[1\], \[100\], \[3001\], \[3002\]\]
**Output**
\[null, 1, 2, 3, 3\]
**Explanation**
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = \[1\], range is \[-2999,1\], return 1
recentCounter.ping(100); // requests = \[1, 100\], range is \[-2900,100\], return 2
recentCounter.ping(3001); // requests = \[1, 100, 3001\], range is \[1,3001\], return 3
recentCounter.ping(3002); // requests = \[1, 100, 3001, 3002\], range is \[2,3002\], return 3
**Constraints:**
* `1 <= t <= 109`
* Each test case will call `ping` with **strictly increasing** values of `t`.
* At most `104` calls will be made to `ping`. | null |
Simple Solution But logical, Beats 99.70% | number-of-recent-calls | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen I saw this problem for the first time, I thought problems related to queue in leetcode need to be solved by Node, but it is easier than Nodes here.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIn while statement we check is it empty or not first if it is, we simply append it to queue (composition).\nIn next Input, there is 1 in queue, so we add 1 + 3000 < t, t in this case 100, if it is the case we remove it from queue\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nBig O(n Log (n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nBig O(n)\n# Code\n```\nclass RecentCounter:\n def __init__(self):\n self.queue = deque()\n\n def ping(self, t: int) -> int:\n while self.queue and self.queue[0] + 3000 < t:\n self.queue.popleft()\n self.queue.append(t)\n return len(self.queue)\n``` | 1 | Given an array of integers `arr`, sort the array by performing a series of **pancake flips**.
In one pancake flip we do the following steps:
* Choose an integer `k` where `1 <= k <= arr.length`.
* Reverse the sub-array `arr[0...k-1]` (**0-indexed**).
For example, if `arr = [3,2,1,4]` and we performed a pancake flip choosing `k = 3`, we reverse the sub-array `[3,2,1]`, so `arr = [1,2,3,4]` after the pancake flip at `k = 3`.
Return _an array of the_ `k`_\-values corresponding to a sequence of pancake flips that sort_ `arr`. Any valid answer that sorts the array within `10 * arr.length` flips will be judged as correct.
**Example 1:**
**Input:** arr = \[3,2,4,1\]
**Output:** \[4,2,4,3\]
**Explanation:**
We perform 4 pancake flips, with k values 4, 2, 4, and 3.
Starting state: arr = \[3, 2, 4, 1\]
After 1st flip (k = 4): arr = \[1, 4, 2, 3\]
After 2nd flip (k = 2): arr = \[4, 1, 2, 3\]
After 3rd flip (k = 4): arr = \[3, 2, 1, 4\]
After 4th flip (k = 3): arr = \[1, 2, 3, 4\], which is sorted.
**Example 2:**
**Input:** arr = \[1,2,3\]
**Output:** \[\]
**Explanation:** The input is already sorted, so there is no need to flip anything.
Note that other answers, such as \[3, 3\], would also be accepted.
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= arr.length`
* All integers in `arr` are unique (i.e. `arr` is a permutation of the integers from `1` to `arr.length`). | null |
Python simple queue solution – beats 97% | number-of-recent-calls | 0 | 1 | # Code\n```\nclass RecentCounter:\n\n def __init__(self):\n self.s = []\n\n def ping(self, t: int) -> int:\n while self.s and t - self.s[0] > 3000:\n self.s.pop(0) # remove 1st el if it\'s 3000+ away from t\n self.s.append(t)\n return len(self.s) \n\n```\n\nupdate:\n\n | 4 | You have a `RecentCounter` class which counts the number of recent requests within a certain time frame.
Implement the `RecentCounter` class:
* `RecentCounter()` Initializes the counter with zero recent requests.
* `int ping(int t)` Adds a new request at time `t`, where `t` represents some time in milliseconds, and returns the number of requests that has happened in the past `3000` milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range `[t - 3000, t]`.
It is **guaranteed** that every call to `ping` uses a strictly larger value of `t` than the previous call.
**Example 1:**
**Input**
\[ "RecentCounter ", "ping ", "ping ", "ping ", "ping "\]
\[\[\], \[1\], \[100\], \[3001\], \[3002\]\]
**Output**
\[null, 1, 2, 3, 3\]
**Explanation**
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = \[1\], range is \[-2999,1\], return 1
recentCounter.ping(100); // requests = \[1, 100\], range is \[-2900,100\], return 2
recentCounter.ping(3001); // requests = \[1, 100, 3001\], range is \[1,3001\], return 3
recentCounter.ping(3002); // requests = \[1, 100, 3001, 3002\], range is \[2,3002\], return 3
**Constraints:**
* `1 <= t <= 109`
* Each test case will call `ping` with **strictly increasing** values of `t`.
* At most `104` calls will be made to `ping`. | null |
Python simple queue solution – beats 97% | number-of-recent-calls | 0 | 1 | # Code\n```\nclass RecentCounter:\n\n def __init__(self):\n self.s = []\n\n def ping(self, t: int) -> int:\n while self.s and t - self.s[0] > 3000:\n self.s.pop(0) # remove 1st el if it\'s 3000+ away from t\n self.s.append(t)\n return len(self.s) \n\n```\n\nupdate:\n\n | 4 | Given an array of integers `arr`, sort the array by performing a series of **pancake flips**.
In one pancake flip we do the following steps:
* Choose an integer `k` where `1 <= k <= arr.length`.
* Reverse the sub-array `arr[0...k-1]` (**0-indexed**).
For example, if `arr = [3,2,1,4]` and we performed a pancake flip choosing `k = 3`, we reverse the sub-array `[3,2,1]`, so `arr = [1,2,3,4]` after the pancake flip at `k = 3`.
Return _an array of the_ `k`_\-values corresponding to a sequence of pancake flips that sort_ `arr`. Any valid answer that sorts the array within `10 * arr.length` flips will be judged as correct.
**Example 1:**
**Input:** arr = \[3,2,4,1\]
**Output:** \[4,2,4,3\]
**Explanation:**
We perform 4 pancake flips, with k values 4, 2, 4, and 3.
Starting state: arr = \[3, 2, 4, 1\]
After 1st flip (k = 4): arr = \[1, 4, 2, 3\]
After 2nd flip (k = 2): arr = \[4, 1, 2, 3\]
After 3rd flip (k = 4): arr = \[3, 2, 1, 4\]
After 4th flip (k = 3): arr = \[1, 2, 3, 4\], which is sorted.
**Example 2:**
**Input:** arr = \[1,2,3\]
**Output:** \[\]
**Explanation:** The input is already sorted, so there is no need to flip anything.
Note that other answers, such as \[3, 3\], would also be accepted.
**Constraints:**
* `1 <= arr.length <= 100`
* `1 <= arr[i] <= arr.length`
* All integers in `arr` are unique (i.e. `arr` is a permutation of the integers from `1` to `arr.length`). | null |
Python solution - queue | number-of-recent-calls | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:0(n)\n\n# Code\n```\nclass RecentCounter:\n\n def __init__(self):\n self.all = []\n\n def ping(self, t: int) -> int:\n self.all.append(t)\n min_time = t-3000\n while self.all[0] < min_time:\n self.all.pop(0)\n return len(self.all) \n\n# Your RecentCounter object will be instantiated and called as such:\n# obj = RecentCounter()\n# param_1 = obj.ping(t)\n``` | 2 | You have a `RecentCounter` class which counts the number of recent requests within a certain time frame.
Implement the `RecentCounter` class:
* `RecentCounter()` Initializes the counter with zero recent requests.
* `int ping(int t)` Adds a new request at time `t`, where `t` represents some time in milliseconds, and returns the number of requests that has happened in the past `3000` milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range `[t - 3000, t]`.
It is **guaranteed** that every call to `ping` uses a strictly larger value of `t` than the previous call.
**Example 1:**
**Input**
\[ "RecentCounter ", "ping ", "ping ", "ping ", "ping "\]
\[\[\], \[1\], \[100\], \[3001\], \[3002\]\]
**Output**
\[null, 1, 2, 3, 3\]
**Explanation**
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = \[1\], range is \[-2999,1\], return 1
recentCounter.ping(100); // requests = \[1, 100\], range is \[-2900,100\], return 2
recentCounter.ping(3001); // requests = \[1, 100, 3001\], range is \[1,3001\], return 3
recentCounter.ping(3002); // requests = \[1, 100, 3001, 3002\], range is \[2,3002\], return 3
**Constraints:**
* `1 <= t <= 109`
* Each test case will call `ping` with **strictly increasing** values of `t`.
* At most `104` calls will be made to `ping`. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.