markdown
stringlengths 0
1.02M
| code
stringlengths 0
832k
| output
stringlengths 0
1.02M
| license
stringlengths 3
36
| path
stringlengths 6
265
| repo_name
stringlengths 6
127
|
|---|---|---|---|---|---|
Data cleaning* Filtra horários de aula* remover linhas incompletas (sistema fora do ar)* remover oulier (falhas na coleta de dados).* remover dias não-letivos* remover dias com falhas na medição (sistema fora do ar) | processed = raw.dropna()
processed = processed.set_index(pd.to_datetime (processed['momento'])).drop('momento', axis=1)
(ax1, ax2, ax3) = processed['2019-05-20 00:00:00' : '2019-05-25 00:00:00'].plot(subplots=True, sharex=True)
ax1.legend(loc='upper left')
ax2.legend(loc='upper left')
ax3.legend(loc='upper left')
#ax1.legend(loc="upper right")
processed = processed[processed['pa']<500]
processed = processed[processed['pa']>10]
## Remove fins de semana
# Create an index of just the date portion of your index (this is the slow step)
dfDays = pd.to_datetime(processed.index.date)
# Create a range of business days over that period
dfBdays = pd.bdate_range(start=processed.index[0].date(), end=processed.index[-1].date())
#Filter the series to just those days contained in the business day range.
filtered = processed[dfDays.isin(dfBdays)]
## Removendo dias não-letivos ou com erros
# março
# abril 4, 8, 15, 16,17,18,19, 22, 25, 29
# maio 1, 9, 10, 14, 15, 16, 17
# junho 20, 21
filtered = filtered[~((filtered.index.month == 4) & (filtered.index.day == 4))]
filtered = filtered[~((filtered.index.month == 4) & (filtered.index.day == 8))]
filtered = filtered[~((filtered.index.month == 4) & (filtered.index.day == 15))]
filtered = filtered[~((filtered.index.month == 4) & (filtered.index.day == 16))]
filtered = filtered[~((filtered.index.month == 4) & (filtered.index.day == 17))]
filtered = filtered[~((filtered.index.month == 4) & (filtered.index.day == 18))]
filtered = filtered[~((filtered.index.month == 4) & (filtered.index.day == 19))]
filtered = filtered[~((filtered.index.month == 4) & (filtered.index.day == 22))]
filtered = filtered[~((filtered.index.month == 4) & (filtered.index.day == 25))]
filtered = filtered[~((filtered.index.month == 4) & (filtered.index.day == 29))]
filtered = filtered[~((filtered.index.month == 5) & (filtered.index.day == 1))]
filtered = filtered[~((filtered.index.month == 5) & (filtered.index.day == 9))]
filtered = filtered[~((filtered.index.month == 5) & (filtered.index.day == 10))]
filtered = filtered[~((filtered.index.month == 5) & (filtered.index.day == 14))]
filtered = filtered[~((filtered.index.month == 5) & (filtered.index.day == 15))]
filtered = filtered[~((filtered.index.month == 5) & (filtered.index.day == 16))]
filtered = filtered[~((filtered.index.month == 5) & (filtered.index.day == 17))]
filtered = filtered[~((filtered.index.month == 6) & (filtered.index.day == 20))]
filtered = filtered[~((filtered.index.month == 6) & (filtered.index.day == 21))]
# Selecionando horários de aula
filtered1 = filtered.between_time('08:00:00', '11:00:00')
filtered2 = filtered.between_time('14:00:00', '17:00:00')
filtered = pd.concat([filtered1, filtered2])
filtered = filtered[~((filtered['pa']<50) & (filtered['temp_celsius']>27))]
f, (ax1, ax2) = plt.subplots(1, 2, sharey=True,figsize=(15,6))
ax1.scatter(filtered['temp_celsius'], filtered['pa'], Alpha=0.5)
ax1.set_xlabel("temperatura (ºC)")
ax1.set_ylabel("Potência ativa (KW)")
ax2.scatter(filtered['pressao'], filtered['pa'], Alpha=0.5)
ax2.set_xlabel("Pressão (hPa)")
ax2.set_ylabel("Potência ativa (KW)")
filtered.describe()
filtered['id']=1
filtered
# Cross validation split
from sklearn.model_selection import train_test_split
X = filtered.drop('pa', axis=1)
y = filtered ['pa']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)
X_test
y_test | _____no_output_____ | MIT | artificial_intelligence/01 - ConsumptionRegression/All campus/Fpolis.ipynb | LeonardoSanBenitez/LorisWeb |
Linear Regression | model1 = LinearRegression()
model1.fit (X_train, y_train)
pd.DataFrame(model1.coef_,X.columns,columns=['Coefficient'])
from sklearn import metrics
y_hat1 = model1.predict(X_test)
print ("MAE: ", metrics.mean_absolute_error(y_test, y_hat1))
print ("RMSE: ", np.sqrt(metrics.mean_squared_error(y_test, y_hat1)))
print ("Percentual: ", metrics.mean_absolute_error(y_test,y_hat1)/y_test.mean()*100, "%")
# Previsto vs real
line = np.arange(0, 250, 1)
plt.scatter(y_test,y_hat1, Alpha=0.6)
plt.scatter(line,line)
plt.grid(True)
plt.xlabel("Valores reais")
plt.ylabel("Valores previstos")
plt.scatter(X['temp_celsius'], y,color='g')
plt.scatter(X['temp_celsius'], model1.predict(X),color='k')
plt.show() | _____no_output_____ | MIT | artificial_intelligence/01 - ConsumptionRegression/All campus/Fpolis.ipynb | LeonardoSanBenitez/LorisWeb |
Random Forest | import sklearn.metrics as metrics
import math
from sklearn.ensemble import RandomForestRegressor
mae1 = {}
mae2 = {}
for k in range(1,15, 1):
model2 = RandomForestRegressor(max_depth=k, n_estimators=100, criterion='mae').fit(X_train,y_train)
y_hat = model2.predict(X_train)
mae1[k] = metrics.mean_absolute_error(y_train,y_hat)
y_hat = model2.predict(X_test)
mae2[k] = metrics.mean_absolute_error(y_test,y_hat)
plt.figure()
plt.plot(list(mae1.keys()), list(mae1.values()), label='Erro no conunto de treinamento')
plt.plot(list(mae2.keys()), list(mae2.values()), label='Erro no conunto de teste')
plt.legend(loc='lower left')
plt.xlabel("Altura máxima")
plt.ylabel("MAE")
plt.grid(True)
# Random Forest
model2 = RandomForestRegressor(max_depth=3, n_estimators=100)
model2.fit(X_train,y_train)
# Model Evaluation
y_hat2 = model2.predict(X_test)
print ("MAE: ", metrics.mean_absolute_error(y_test,y_hat2))
print ("RMSE: ", math.sqrt(metrics.mean_squared_error(y_test,y_hat2)))
print ("Percentual: ", metrics.mean_absolute_error(y_test,y_hat2)/y_test.mean()*100, "%")
# Feature analysis
print ("=====================================")
print ("FEATURE IMPORTANCE:")
for i in range(model2.feature_importances_.size):
print (X_train.columns[i], "=", model2.feature_importances_[i])
# Previsto vs real
line = np.arange(0, 250, 1)
plt.scatter(y_test,y_hat, Alpha=0.6)
plt.scatter(line,line)
plt.grid(True)
plt.scatter(X['temp_celsius'], y,color='g')
plt.scatter(X['temp_celsius'], model2.predict(X),color='k')
plt.xlabel("Temperatura (ºC)")
plt.ylabel("Potência Ativa (KW)")
plt.show()
import pickle
with open('fpolis_trained_model.pkl', 'wb') as f:
pickle.dump(model2, f)
with open('fpolis_trained_model.pkl', 'rb') as f:
model2_loaded = pickle.load(f)
model2_loaded | _____no_output_____ | MIT | artificial_intelligence/01 - ConsumptionRegression/All campus/Fpolis.ipynb | LeonardoSanBenitez/LorisWeb |
IntroductionLinear Regression is one of the most famous and widely used machine learning algorithms out there. It assumes that the target variable can be explained as a linear combination of the input features. What does this mean? It means that the target can be viewed as a weighted sum of each feature. Let’s use a practical example to illustrate that.Let’s say that we are opening a restaurant, we make great food but we want to know how much to charge for it. We can be very pragmatic and say that the cost of the meal is directly related to what is in it. We can, for instance, have a rule that each ingredient costs a certain amount, and based on how much there is of each ingredient in the dish, we can calculate its price. There may also be a fixed minimum price for each dish. Mathematically, this is called the intercept. | fixed_price = 5
ingredient_costs = {"meat": 10,
"fish": 13,
"vegetables": 2,
"fries": 3}
def price(**ingredients):
""" returns the price of a dish """
cost = 0
for name, quantity in ingredients.items():
cost += ingredient_costs[name] * quantity
return cost | _____no_output_____ | MIT | notebooks/Learning Units/Linear Regression/Linear Regression - Chapter 1 - Introduction.ipynb | ValentinCalomme/skratch |
The Iris flower data set is a multivariate data set introduced by the British statistician and biologist Ronald Fisher in his 1936 paper The use of multiple measurements in taxonomic problems. The dataset consists of 50 samples from each of three species of Iris (Iris Setosa, Iris virginica, and Iris versicolor). Four features were measured from each sample: the length and the width of the sepals and petals, in centimeters. Import Libraries | import numpy as np
import pandas as pd
from pandas import Series, DataFrame
import seaborn as sns
import matplotlib.pyplot as plt
iris = pd.read_csv("iris.csv")
iris.head() | _____no_output_____ | MIT | Machine Learning Problem-Statements/Iris/Iris_Dataset_Machine_Learning.ipynb | JukMR/Hacktoberfest2020 |
*We can see that we have a column named ID that we donot need , so let's drop it !* | iris.drop("Id", axis=1, inplace = True)
iris.info()
figure = iris[iris.Species == 'Iris-setosa'].plot(kind='scatter', x='SepalLengthCm', y='SepalWidthCm', color='red', label='Setosa')
iris[iris.Species == 'Iris-versicolor'].plot(kind='scatter', x='SepalLengthCm', y='SepalWidthCm', color='blue', label='Versicolor', ax=figure)
iris[iris.Species == 'Iris-virginica'].plot(kind='scatter', x='SepalLengthCm', y='SepalWidthCm', color='green', label='Virginica', ax=figure)
figure.set_xlabel('Sepal Length')
figure.set_ylabel('Sepal Width')
figure.set_title('Sepal Length Vs Width')
figure=plt.gcf()
figure.set_size_inches(7, 4)
plt.show()
figure = iris[iris.Species == 'Iris-setosa'].plot(kind='scatter', x='PetalLengthCm', y='PetalWidthCm', color='red', label='Setosa')
iris[iris.Species == 'Iris-versicolor'].plot(kind='scatter', x='PetalLengthCm', y='PetalWidthCm', color='blue', label='Versicolor', ax=figure)
iris[iris.Species == 'Iris-virginica'].plot(kind='scatter', x='PetalLengthCm', y='PetalWidthCm', color='green', label='Virginica', ax=figure)
figure.set_xlabel('Petal Length')
figure.set_ylabel('Petal Width')
figure.set_title('Petal Length Vs Width')
figure=plt.gcf()
figure.set_size_inches(7, 4)
plt.show()
plt.figure(figsize=(15,10))
plt.subplot(2,2,1)
sns.boxplot(x='Species',y='SepalLengthCm',data=iris)
plt.subplot(2,2,2)
sns.boxplot(x='Species',y='SepalWidthCm',data=iris)
plt.subplot(2,2,3)
sns.boxplot(x='Species',y='PetalLengthCm',data=iris)
plt.subplot(2,2,4)
sns.boxplot(x='Species',y='PetalWidthCm',data=iris)
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn import svm
from sklearn import metrics
from sklearn.tree import DecisionTreeClassifier
import xgboost as xgb | _____no_output_____ | MIT | Machine Learning Problem-Statements/Iris/Iris_Dataset_Machine_Learning.ipynb | JukMR/Hacktoberfest2020 |
Splitting The Data into Training And Testing Dataset | train, test = train_test_split(iris, test_size=0.2)
print(train.shape)
print(test.shape)
train_X = train[['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm']]
train_y = train.Species
test_X = test[['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm']]
test_y = test.Species | _____no_output_____ | MIT | Machine Learning Problem-Statements/Iris/Iris_Dataset_Machine_Learning.ipynb | JukMR/Hacktoberfest2020 |
1. Logistic Regression | model1 = LogisticRegression()
model1.fit(train_X, train_y)
prediction1 = model1.predict(test_X)
print('Accuracy of Logistic Regression is: ', metrics.accuracy_score(prediction1, test_y)) | Accuracy of Logistic Regression is: 0.9333333333333333
| MIT | Machine Learning Problem-Statements/Iris/Iris_Dataset_Machine_Learning.ipynb | JukMR/Hacktoberfest2020 |
2. SVM Classifier | model2 = svm.SVC()
model2.fit(train_X, train_y)
prediction2 = model2.predict(test_X)
print('Accuracy of SVM is: ', metrics.accuracy_score(prediction2, test_y)) | Accuracy of SVM is: 0.9666666666666667
| MIT | Machine Learning Problem-Statements/Iris/Iris_Dataset_Machine_Learning.ipynb | JukMR/Hacktoberfest2020 |
3. K-Nearest Neighbors | model3 = KNeighborsClassifier(n_neighbors=3) # this examines 3 neighbors
model3.fit(train_X, train_y)
prediction3 = model3.predict(test_X)
print('Accuracy of KNN is: ', metrics.accuracy_score(prediction3, test_y)) | Accuracy of KNN is: 0.9666666666666667
| MIT | Machine Learning Problem-Statements/Iris/Iris_Dataset_Machine_Learning.ipynb | JukMR/Hacktoberfest2020 |
4. Decision Tree | model4 = DecisionTreeClassifier()
model4.fit(train_X, train_y)
prediction4 = model4.predict(test_X)
print('Accuracy of Decision Tree is: ', metrics.accuracy_score(prediction4, test_y)) | Accuracy of Decision Tree is: 0.9
| MIT | Machine Learning Problem-Statements/Iris/Iris_Dataset_Machine_Learning.ipynb | JukMR/Hacktoberfest2020 |
5. XGBoost | model5 = xgb.XGBClassifier()
model5.fit(train_X, train_y)
prediction5 = model5.predict(test_X)
print('Accuracy of xgb classifier is: ', metrics.accuracy_score(prediction5, test_y)) | Accuracy of xgb classifier is: 0.9333333333333333
| MIT | Machine Learning Problem-Statements/Iris/Iris_Dataset_Machine_Learning.ipynb | JukMR/Hacktoberfest2020 |
Lagged Price Machine Learning Testing | df1_50 = pd.read_csv(
Path("./Data/QM_50_6month.csv")
)
tickers = list(df1_50["Tickers"])
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
historical = yf.Ticker("idxx").history(period="max")
historical["return"] = historical["Close"].pct_change()
lags = 5
cols = []
for lag in range(1, lags + 1):
col = f'lag_{lag}'
historical[col] = historical['Close'].shift(lag)
cols.append(col)
historical_train = historical.loc[:"2021-01"]
historical_train.dropna(inplace=True)
historical_train
price_3month = historical.loc["2021-02":"2021-04"]
display(price_3month.head())
model = LogisticRegression(C=1e6, solver="lbfgs",
multi_class="auto",
max_iter=1000)
model.fit(historical_train[cols],np.sign(historical_train["return"]))
price_3month["prediction"] = model.predict(price_3month[cols])
price_3month["prediction"].value_counts()
price_3month["prediction"].value_counts()
print(classification_report(price_3month["prediction"],
np.sign(price_3month["return"])))
price_3month["strategy"] = price_3month["prediction"] * price_3month["return"]
price_3month[["strategy","return"]].cumsum().apply(np.exp).plot() | _____no_output_____ | Unlicense | Back Test 2021_02-2021_04.ipynb | tonghuang-uw/Project_2 |
SVC | poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC())
])
poly_kernel_svm_clf.fit(historical_train[cols],np.sign(historical_train["return"]))
price_3month["prediction"] = model.predict(price_3month[cols])
price_3month["prediction"].value_counts()
print(classification_report(price_3month["prediction"],
np.sign(price_3month["return"])))
price_3month["strategy"] = price_3month["prediction"] * price_3month["return"]
price_3month[["strategy","return"]].cumsum().apply(np.exp).plot()
lags = 21
weighting = 1/50
strat = np.zeros(63)
actual = np.zeros(63)
for ticker in tickers:
# Pull the historical data
df_price = yf.Ticker(ticker).history(period="max")
df_price["return"] = df_price["Close"].pct_change()
# Create lags price
cols = []
for lag in range(1, lags + 1):
col = f'lag_{lag}'
df_price[col] = df_price['Close'].shift(lag)
cols.append(col)
df_price.dropna(inplace=True)
# Create train and test data
df_price_train = df_price.loc[:"2020-12"]
df_price_test = df_price.loc["2021-02":"2021-04"]
model = LogisticRegression(C=1e-2, solver="lbfgs",
multi_class="auto",
max_iter=1000)
model.fit(df_price_train[cols], np.sign(df_price_train["return"]))
df_price_test["prediction"] = model.predict(df_price_test[cols])
df_price_test["strategy"] = df_price_test["prediction"] * df_price_test["return"]
cum_ret = df_price_test[["strategy","return"]].cumsum().apply(np.exp)
strat = strat + np.array(cum_ret["strategy"]) * weighting
actual = actual + np.array(cum_ret["return"]) * weighting
print(ticker, cum_ret)
spy = np.array(yf.Ticker("spy").history(period="2y").loc["2021-02":"2021-04"]["Close"].pct_change().cumsum().apply(np.exp))
plt.figure(figsize=(10,8))
plt.plot(strat,'b-', label="Strategy")
plt.plot(actual,'r--', label="Actual")
plt.plot(spy,'g:', label="Spy")
plt.grid()
plt.legend()
spy | _____no_output_____ | Unlicense | Back Test 2021_02-2021_04.ipynb | tonghuang-uw/Project_2 |
SMA | %%time
short_win = 5
long_win = 15
weighting = 1/50
strat = np.zeros(63)
actual = np.zeros(63)
for ticker in tickers:
historical = yf.Ticker(ticker).history(period="max")
historical["return"] = historical["Close"].pct_change()
historical["SMA_short"] = historical["Close"].rolling(window=short_win).mean().shift()
historical["SMA_long"] = historical["Close"].rolling(window=long_win).mean().shift()
historical["distance1"] = (historical["Close"] - historical["SMA_short"]).shift()
historical["distance2"] = (historical["SMA_short"] - historical["SMA_long"]).shift()
historical["distance3"] = (historical["Close"] - historical["SMA_long"]).shift()
historical.dropna(inplace=True)
historical_train = historical.loc["2020-06":"2020"].copy()
historical_test = historical.loc["2021-02":"2021-04"].copy()
scaler = StandardScaler()
X_scaler = scaler.fit(historical_train[["SMA_short","SMA_long","distance1","distance2","distance3"]])
X_train_scaled = X_scaler.transform(historical_train[["SMA_short","SMA_long","distance1","distance2","distance3"]])
X_test_scaled = X_scaler.transform(historical_test[["SMA_short","SMA_long","distance1","distance2","distance3"]])
svm_model = SVC()
svm_model = svm_model.fit(X_train_scaled, np.sign(historical_train[["return"]]))
historical_test["prediction"] = svm_model.predict(X_test_scaled)
historical_test["strategy"] = historical_test["prediction"] * historical_test["return"]
cum_ret = historical_test[["strategy","return"]].cumsum().apply(np.exp)
strat = strat + np.array(cum_ret["strategy"]) * weighting
actual = actual + np.array(cum_ret["return"]) * weighting
print(ticker, cum_ret)
spy = np.array(yf.Ticker("spy").history(period="2y").loc["2021-02":"2021-04"]["Close"].pct_change().cumsum().apply(np.exp))
plt.figure(figsize=(10,8))
plt.plot(strat,'b-', label="Strategy")
plt.plot(actual,'r--', label="Actual")
plt.plot(spy,'g:', label="Spy")
plt.grid()
plt.legend() | _____no_output_____ | Unlicense | Back Test 2021_02-2021_04.ipynb | tonghuang-uw/Project_2 |
EMA | short_win = 12
long_win = 26
strat = np.zeros(63)
actual = np.zeros(63)
for ticker in tickers:
historical = yf.Ticker(ticker).history(period="2y")
historical["return"] = historical["Close"].pct_change()
historical["exp1"] = historical["Close"].ewm(span=short_win, adjust=False).mean().shift()
historical["exp2"] = historical["Close"].ewm(span=long_win, adjust=False).mean().shift()
historical["distance1"] = (historical["Close"] - historical["exp1"]).shift()
historical["distance2"] = (historical["Close"] - historical["exp2"]).shift()
#historical["distance3"] = (historical["exp1"] - historical["exp2"]).shift()
historical.dropna(inplace=True)
historical_train = historical.loc["2020-07":"2020"].copy()
historical_test = historical.loc["2021-02":"2021-04"].copy()
scaler = StandardScaler()
X_scaler = scaler.fit(historical_train[["exp1","exp2","distance1","distance2"]])
X_train_scaled = X_scaler.transform(historical_train[["exp1","exp2","distance1","distance2"]])
X_test_scaled = X_scaler.transform(historical_test[["exp1","exp2","distance1","distance2"]])
svm_model = SVC(C=0.5)
svm_model = svm_model.fit(X_train_scaled, np.sign(historical_train[["return"]]))
historical_test["prediction"] = svm_model.predict(X_test_scaled)
historical_test["strategy"] = historical_test["prediction"] * historical_test["return"]
cum_ret = historical_test[["strategy","return"]].cumsum().apply(np.exp)
strat = strat + np.array(cum_ret["strategy"]) * weighting
actual = actual + np.array(cum_ret["return"]) * weighting
print(ticker, cum_ret)
spy = np.array(yf.Ticker("spy").history(period="2y").loc["2021-02":"2021-04"]["Close"].pct_change().cumsum().apply(np.exp))
plt.figure(figsize=(10,8))
plt.plot(strat,'b-', label="Strategy")
plt.plot(actual,'r--', label="Actual")
plt.plot(spy,'g:', label="Spy")
plt.grid()
plt.legend() | _____no_output_____ | Unlicense | Back Test 2021_02-2021_04.ipynb | tonghuang-uw/Project_2 |
MACD | short_win = 12
long_win = 26
signal_line = 9
strat = np.zeros(63)
actual = np.zeros(63)
for ticker in tickers:
historical = yf.Ticker(ticker).history(period="2y")
historical["return"] = historical["Close"].pct_change()
historical["exp1"] = historical["Close"].ewm(span=short_win, adjust=False).mean().shift()
historical["exp2"] = historical["Close"].ewm(span=long_win, adjust=False).mean().shift()
historical["macd"] = historical["exp1"] - historical["exp2"]
historical["exp3"] = historical["Close"].ewm(span=signal_line, adjust=False).mean().shift()
historical["macd_histogram"] = historical["macd"] - historical["exp3"]
historical["lag_1"] = historical["Close"].shift()
historical["roc"] = ((historical["Close"] - historical["lag_1"])/ historical["lag_1"]).shift()
historical["macd_histogram_lag1"] = historical["macd_histogram"].shift()
historical["roc_macd"] = ((historical["macd_histogram"]-historical["macd_histogram_lag1"])/historical["macd_histogram_lag1"])
historical.dropna(inplace=True)
historical_train = historical.loc[:"2020"].copy()
historical_test = historical.loc["2021-02":"2021-04"].copy()
scaler = StandardScaler()
X_scaler = scaler.fit(historical_train[["roc","roc_macd"]])
X_train_scaled = X_scaler.transform(historical_train[["roc","roc_macd"]])
X_test_scaled = X_scaler.transform(historical_test[["roc","roc_macd"]])
svm_model = SVC(C=0.5)
svm_model = svm_model.fit(X_train_scaled, np.sign(historical_train[["return"]]))
historical_test["prediction"] = svm_model.predict(X_test_scaled)
historical_test["strategy"] = historical_test["prediction"] * historical_test["return"]
cum_ret = historical_test[["strategy","return"]].cumsum().apply(np.exp)
strat = strat + np.array(cum_ret["strategy"]) * weighting
actual = actual + np.array(cum_ret["return"]) * weighting
print(ticker, accuracy_score(historical_test["prediction"],
np.sign(historical_test["return"])))
spy = np.array(yf.Ticker("spy").history(period="2y").loc["2021-02":"2021-04"]["Close"].pct_change().cumsum().apply(np.exp))
plt.figure(figsize=(10,8))
plt.plot(strat,'b-', label="Strategy")
plt.plot(actual,'r--', label="Actual")
plt.plot(spy,'g:', label="Spy")
plt.grid()
plt.legend() | _____no_output_____ | Unlicense | Back Test 2021_02-2021_04.ipynb | tonghuang-uw/Project_2 |
Tutorial 5: Trace - training control and debuggingIn this tutorial, we will talk about another important concept in FastEstimator - Trace.`Trace` is a class contains has 6 event functions below, each event function will be executed on different events of training loop when putting `Trace` inside `Estimator`. If you are a Keras user, you would see that `Trace` is a combination of callbacks and metrics. * on_begin* on_epoch_begin* on_batch_begin* on_batch_end* on_epoch_end* on_end`Trace` differs from keras's callback in the following places:1. Trace has full access to the preprocessing data and prediction data2. Trace can pass data among each other3. Trace is simpler and has fewer event functions than keras callbacks`Trace` can be used for anything that involves training loop, such as changing learning rate, calculating metrics, writing checkpoints and so on. debugging training loop with TraceSince `Trace` can have full access to data used in training loop, one natural usage of `Trace` is debugging training loop, for example, printing network prediction for each batch.Remember in tutorial 3, we customized an operation that scales the prediction score by 10 and write to a new key, let's see whether the operation is working correctly using `Trace`. | import tempfile
import numpy as np
import tensorflow as tf
import fastestimator as fe
from fastestimator.architecture import LeNet
from fastestimator.estimator.trace import Accuracy, ModelSaver
from fastestimator.network.loss import SparseCategoricalCrossentropy
from fastestimator.network.model import FEModel, ModelOp
from fastestimator.pipeline.processing import Minmax
from fastestimator.util.op import TensorOp
class Scale(TensorOp):
def forward(self, data, state):
data = data * 10
return data
(x_train, y_train), (x_eval, y_eval) = tf.keras.datasets.mnist.load_data()
train_data = {"x": np.expand_dims(x_train, -1), "y": y_train}
eval_data = {"x": np.expand_dims(x_eval, -1), "y": y_eval}
data = {"train": train_data, "eval": eval_data}
pipeline = fe.Pipeline(batch_size=32, data=data, ops=Minmax(inputs="x", outputs="x"))
# step 2. prepare model
model = FEModel(model_def=LeNet, model_name="lenet", optimizer="adam")
network = fe.Network(
ops=[ModelOp(inputs="x", model=model, outputs="y_pred"),
SparseCategoricalCrossentropy(inputs=("y", "y_pred")),
Scale(inputs="y_pred", outputs="y_pred_scaled")]) | _____no_output_____ | Apache-2.0 | tutorial/t05_trace_debug_training.ipynb | AriChow/fastestimator |
define trace | from fastestimator.estimator.trace import Trace
class ShowPred(Trace):
def on_batch_end(self, state):
if state["mode"] == "train":
batch_data = state["batch"]
print("step: {}".format(state["batch_idx"]))
print("batch data has following keys: {}".format(list(batch_data.keys())))
print("scaled_prediction is:")
print(batch_data["y_pred_scaled"])
# step 3.prepare estimator
estimator = fe.Estimator(network=network, pipeline=pipeline, epochs=1, traces=ShowPred(), steps_per_epoch=1)
estimator.fit() | ______ __ ______ __ _ __
/ ____/___ ______/ /_/ ____/____/ /_(_)___ ___ ____ _/ /_____ _____
/ /_ / __ `/ ___/ __/ __/ / ___/ __/ / __ `__ \/ __ `/ __/ __ \/ ___/
/ __/ / /_/ (__ ) /_/ /___(__ ) /_/ / / / / / / /_/ / /_/ /_/ / /
/_/ \__,_/____/\__/_____/____/\__/_/_/ /_/ /_/\__,_/\__/\____/_/
FastEstimator-Warn: No ModelSaver Trace detected. Models will not be saved.
FastEstimator-Start: step: 0; lenet_lr: 0.001;
step: 0
batch data has following keys: ['y_pred', 'y', 'x', 'loss', 'y_pred_scaled']
scaled_prediction is:
tf.Tensor(
[[1.0597024 0.88230646 0.9054666 1.0526242 1.0112537 1.1514847
0.9731587 0.9711996 0.84732836 1.1454759 ]
[1.0177196 0.96111745 0.8916435 1.0738678 0.9751328 1.2481465
0.9405147 0.87076896 0.8726471 1.148442 ]
[1.0760062 0.94326234 0.9008551 1.0322686 1.0499443 1.1253775
0.93624175 0.9271722 0.90360963 1.1052628 ]
[1.0469304 0.89323467 0.91441756 1.0751362 0.9745273 1.1652466
0.96247584 0.9406713 0.8315316 1.1958287 ]
[1.0219785 0.929411 0.89820254 1.0585518 0.93793464 1.2132744
0.9584836 0.951019 0.8594369 1.1717079 ]
[1.0567241 0.9066122 0.9052205 1.0659181 1.0157421 1.2072058
0.96398747 0.8855149 0.8579869 1.1350882 ]
[1.0661185 0.91435105 0.89010346 1.0575683 0.9922614 1.2262878
0.93575335 0.91625047 0.86531997 1.135985 ]
[1.0357784 0.8888004 0.8541077 1.0948972 0.98482585 1.283034
0.90922797 0.9051948 0.9000034 1.1441307 ]
[1.0599277 0.90635175 0.89042604 1.0980016 1.0003179 1.2005775
0.97344226 0.904382 0.81406707 1.152506 ]
[1.0498649 0.95371425 0.9321244 1.0166047 1.0222087 1.1368012
0.9753012 0.91623485 0.8738795 1.123267 ]
[1.103452 0.903526 0.9064317 1.0117977 1.0413742 1.1384664
0.96658295 0.93786097 0.8479606 1.1425483 ]
[1.029507 0.92203546 0.9414134 1.023415 1.0161355 1.1061418
0.98370135 0.97101694 0.90548897 1.1011443 ]
[1.0279974 0.95044667 0.93619615 1.0110079 1.0024072 1.1394106
0.9575084 0.8984376 0.89733607 1.1792525 ]
[1.0699053 0.87303096 0.9200075 1.0734357 1.0142893 1.1181858
0.9856108 0.93070036 0.8564811 1.1583531 ]
[1.0348419 0.9044772 0.8707888 1.0723933 1.0153837 1.1527358
0.9473658 0.93430406 0.8998435 1.1678661 ]
[1.0630001 0.8815649 0.8781316 1.080618 0.99296457 1.2163352
0.95687056 0.9228797 0.8936867 1.1139493 ]
[1.0232941 0.8857512 0.8840588 1.092468 0.99615574 1.2249657
0.92473567 0.9100239 0.8655537 1.1929938 ]
[1.0537924 0.88076466 0.8679014 1.1071997 1.006206 1.1429375
0.93528 0.9362229 0.8875452 1.1821507 ]
[1.0308622 0.93516076 0.9209412 1.0852494 1.0089574 1.1817933
0.94350743 0.896239 0.8588871 1.138402 ]
[1.0389919 0.91212773 0.9013858 1.038586 1.0234965 1.1859746
0.95688295 0.9387725 0.84085584 1.1629258 ]
[1.0600939 0.94089186 0.9131027 1.0013218 1.0147965 1.1764416
0.965766 0.95196784 0.870939 1.1046789 ]
[1.1057894 0.8504439 0.83679646 1.1040735 0.9999001 1.2389936
0.9062878 0.9403291 0.8776086 1.1397778 ]
[1.0217856 0.9747643 0.9006238 1.0764693 0.9715878 1.2085975
0.9288042 0.89752984 0.8574368 1.1624014 ]
[1.0469611 0.9568805 0.92177266 1.0700536 0.993606 1.2035027
0.9525442 0.9015994 0.8851406 1.067939 ]
[0.9877974 0.901551 0.93022996 1.0543675 1.0002809 1.1707911
0.94319403 0.971319 0.94477963 1.09569 ]
[0.9924806 0.92723554 0.9150472 1.0373987 1.000831 1.1852853
0.9879187 0.9019555 0.8348947 1.216953 ]
[1.0991246 0.8782563 0.8438319 1.1016914 0.9863124 1.2292806
0.9132333 0.9342602 0.892106 1.1219026 ]
[0.9851291 0.9535258 0.8752247 1.1077297 1.0111363 1.166092
0.969571 0.91310537 0.89379835 1.1246873 ]
[1.0290915 0.88374877 0.84945655 1.0189545 1.0234096 1.2094458
0.88590777 0.9749155 0.9239709 1.2010993 ]
[1.0008084 0.9482253 0.8974297 1.0725788 0.99595183 1.1546551
0.9506333 0.9104537 0.90859526 1.1606691 ]
[1.0367537 0.9001863 0.8841595 1.0721065 0.9803247 1.2551355
0.9427656 0.92319757 0.87253726 1.1328338 ]
[0.9999633 0.9283558 0.8862161 1.0871539 1.0199494 1.1970563
0.9454409 0.9472147 0.92662996 1.0620204 ]], shape=(32, 10), dtype=float32)
FastEstimator-Train: step: 0; loss: 2.3327756;
FastEstimator-Eval: step: 1; epoch: 0; loss: 2.280537; min_loss: 2.280537; since_best_loss: 0;
FastEstimator-Finish: step: 1; total_time: 2.58 sec; lenet_lr: 0.001;
| Apache-2.0 | tutorial/t05_trace_debug_training.ipynb | AriChow/fastestimator |
Flopy MODFLOW Boundary ConditionsFlopy has a new way to enter boundary conditions for some MODFLOW packages. These changes are substantial. Boundary conditions can now be entered as a list of boundaries, as a numpy recarray, or as a dictionary. These different styles are described in this notebook.Flopy also now requires zero-based input. This means that **all boundaries are entered in zero-based layer, row, and column indices**. This means that older Flopy scripts will need to be modified to account for this change. If you are familiar with Python, this should be natural, but if not, then it may take some time to get used to zero-based numbering. Flopy users submit all information in zero-based form, and Flopy converts this to the one-based form required by MODFLOW.The following MODFLOW packages are affected by this change: * Well * Drain * River * General-Head Boundary * Time-Variant Constant Head This notebook explains the different ways to enter these types of boundary conditions. | #begin by importing flopy
import os
import sys
import numpy as np
# run installed version of flopy or add local path
try:
import flopy
except:
fpth = os.path.abspath(os.path.join('..', '..'))
sys.path.append(fpth)
import flopy
workspace = os.path.join('data')
#make sure workspace directory exists
if not os.path.exists(workspace):
os.makedirs(workspace)
print(sys.version)
print('numpy version: {}'.format(np.__version__))
print('flopy version: {}'.format(flopy.__version__)) | flopy is installed in /Users/jdhughes/Documents/Development/flopy_git/flopy_us/flopy
3.7.3 (default, Mar 27 2019, 16:54:48)
[Clang 4.0.1 (tags/RELEASE_401/final)]
numpy version: 1.16.2
flopy version: 3.2.12
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
List of Boundaries Boundary condition information is passed to a package constructor as stress_period_data. In its simplest form, stress_period_data can be a list of individual boundaries, which themselves are lists. The following shows a simple example for a MODFLOW River Package boundary: | stress_period_data = [
[2, 3, 4, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
[2, 3, 5, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
[2, 3, 6, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
]
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data)
m.write_input() | _____no_output_____ | CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
If we look at the River Package created here, you see that the layer, row, and column numbers have been increased by one. | !head -n 10 'data/test.riv' | # RIV package for MODFLOW-2005, generated by Flopy.
3 0
3 0 # stress period 1
3 4 5 10.7 5000.0 -5.7
3 4 6 10.7 5000.0 -5.7
3 4 7 10.7 5000.0 -5.7
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
If this model had more than one stress period, then Flopy will assume that this boundary condition information applies until the end of the simulation | m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
dis = flopy.modflow.ModflowDis(m, nper=3)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data)
m.write_input()
!head -n 10 'data/test.riv' | # RIV package for MODFLOW-2005, generated by Flopy.
3 0
3 0 # stress period 1
3 4 5 10.7 5000.0 -5.7
3 4 6 10.7 5000.0 -5.7
3 4 7 10.7 5000.0 -5.7
-1 0 # stress period 2
-1 0 # stress period 3
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
Recarray of BoundariesNumpy allows the use of recarrays, which are numpy arrays in which each column of the array may be given a different type. Boundary conditions can be entered as recarrays. Information on the structure of the recarray for a boundary condition package can be obtained from that particular package. The structure of the recarray is contained in the dtype. | riv_dtype = flopy.modflow.ModflowRiv.get_default_dtype()
print(riv_dtype) | [('k', '<i8'), ('i', '<i8'), ('j', '<i8'), ('stage', '<f4'), ('cond', '<f4'), ('rbot', '<f4')]
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
Now that we know the structure of the recarray that we want to create, we can create a new one as follows. | stress_period_data = np.zeros((3), dtype=riv_dtype)
stress_period_data = stress_period_data.view(np.recarray)
print('stress_period_data: ', stress_period_data)
print('type is: ', type(stress_period_data)) | stress_period_data: [(0, 0, 0, 0., 0., 0.) (0, 0, 0, 0., 0., 0.) (0, 0, 0, 0., 0., 0.)]
type is: <class 'numpy.recarray'>
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
We can then fill the recarray with our boundary conditions. | stress_period_data[0] = (2, 3, 4, 10.7, 5000., -5.7)
stress_period_data[1] = (2, 3, 5, 10.7, 5000., -5.7)
stress_period_data[2] = (2, 3, 6, 10.7, 5000., -5.7)
print(stress_period_data)
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data)
m.write_input()
!head -n 10 'data/test.riv' | # RIV package for MODFLOW-2005, generated by Flopy.
3 0
3 0 # stress period 1
3 4 5 10.7 5000.0 -5.7
3 4 6 10.7 5000.0 -5.7
3 4 7 10.7 5000.0 -5.7
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
As before, if we have multiple stress periods, then this recarray will apply to all of them. | m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
dis = flopy.modflow.ModflowDis(m, nper=3)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data)
m.write_input()
!head -n 10 'data/test.riv' | # RIV package for MODFLOW-2005, generated by Flopy.
3 0
3 0 # stress period 1
3 4 5 10.7 5000.0 -5.7
3 4 6 10.7 5000.0 -5.7
3 4 7 10.7 5000.0 -5.7
-1 0 # stress period 2
-1 0 # stress period 3
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
Dictionary of BoundariesThe power of the new functionality in Flopy3 is the ability to specify a dictionary for stress_period_data. If specified as a dictionary, the key is the stress period number (**as a zero-based number**), and the value is either a nested list, an integer value of 0 or -1, or a recarray for that stress period.Let's say that we want to use the following schedule for our rivers: 0. No rivers in stress period zero 1. Rivers specified by a list in stress period 1 2. No rivers 3. No rivers 4. No rivers 5. Rivers specified by a recarray 6. Same recarray rivers 7. Same recarray rivers 8. Same recarray rivers | sp1 = [
[2, 3, 4, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
[2, 3, 5, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
[2, 3, 6, 10.7, 5000., -5.7], #layer, row, column, stage, conductance, river bottom
]
print(sp1)
riv_dtype = flopy.modflow.ModflowRiv.get_default_dtype()
sp5 = np.zeros((3), dtype=riv_dtype)
sp5 = sp5.view(np.recarray)
sp5[0] = (2, 3, 4, 20.7, 5000., -5.7)
sp5[1] = (2, 3, 5, 20.7, 5000., -5.7)
sp5[2] = (2, 3, 6, 20.7, 5000., -5.7)
print(sp5)
sp_dict = {0:0, 1:sp1, 2:0, 5:sp5}
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
dis = flopy.modflow.ModflowDis(m, nper=8)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=sp_dict)
m.write_input()
!head -n 10 'data/test.riv' | # RIV package for MODFLOW-2005, generated by Flopy.
3 0
0 0 # stress period 1
3 0 # stress period 2
3 4 5 10.7 5000.0 -5.7
3 4 6 10.7 5000.0 -5.7
3 4 7 10.7 5000.0 -5.7
0 0 # stress period 3
-1 0 # stress period 4
-1 0 # stress period 5
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
MODFLOW Auxiliary VariablesFlopy works with MODFLOW auxiliary variables by allowing the recarray to contain additional columns of information. The auxiliary variables must be specified as package options as shown in the example below.In this example, we also add a string in the last column of the list in order to name each boundary condition. In this case, however, we do not include boundname as an auxiliary variable as MODFLOW would try to read it as a floating point number. | #create an empty array with an iface auxiliary variable at the end
riva_dtype = [('k', '<i8'), ('i', '<i8'), ('j', '<i8'),
('stage', '<f4'), ('cond', '<f4'), ('rbot', '<f4'),
('iface', '<i4'), ('boundname', object)]
riva_dtype = np.dtype(riva_dtype)
stress_period_data = np.zeros((3), dtype=riva_dtype)
stress_period_data = stress_period_data.view(np.recarray)
print('stress_period_data: ', stress_period_data)
print('type is: ', type(stress_period_data))
stress_period_data[0] = (2, 3, 4, 10.7, 5000., -5.7, 1, 'riv1')
stress_period_data[1] = (2, 3, 5, 10.7, 5000., -5.7, 2, 'riv2')
stress_period_data[2] = (2, 3, 6, 10.7, 5000., -5.7, 3, 'riv3')
print(stress_period_data)
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data, dtype=riva_dtype, options=['aux iface'])
m.write_input()
!head -n 10 'data/test.riv' | # RIV package for MODFLOW-2005, generated by Flopy.
3 0 aux iface
3 0 # stress period 1
3 4 5 10.7 5000.0 -5.7 1 riv1
3 4 6 10.7 5000.0 -5.7 2 riv2
3 4 7 10.7 5000.0 -5.7 3 riv3
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
Working with Unstructured GridsFlopy can create an unstructured grid boundary condition package for MODFLOW-USG. This can be done by specifying a custom dtype for the recarray. The following shows an example of how that can be done. | #create an empty array based on nodenumber instead of layer, row, and column
rivu_dtype = [('nodenumber', '<i8'), ('stage', '<f4'), ('cond', '<f4'), ('rbot', '<f4')]
rivu_dtype = np.dtype(rivu_dtype)
stress_period_data = np.zeros((3), dtype=rivu_dtype)
stress_period_data = stress_period_data.view(np.recarray)
print('stress_period_data: ', stress_period_data)
print('type is: ', type(stress_period_data))
stress_period_data[0] = (77, 10.7, 5000., -5.7)
stress_period_data[1] = (245, 10.7, 5000., -5.7)
stress_period_data[2] = (450034, 10.7, 5000., -5.7)
print(stress_period_data)
m = flopy.modflow.Modflow(modelname='test', model_ws=workspace)
riv = flopy.modflow.ModflowRiv(m, stress_period_data=stress_period_data, dtype=rivu_dtype)
m.write_input()
print(workspace)
!head -n 10 'data/test.riv' | data
# RIV package for MODFLOW-2005, generated by Flopy.
3 0
3 0 # stress period 1
77 10.7 5000.0 -5.7
245 10.7 5000.0 -5.7
450034 10.7 5000.0 -5.7
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
Combining two boundary condition packages | ml = flopy.modflow.Modflow(modelname="test",model_ws=workspace)
dis = flopy.modflow.ModflowDis(ml,10,10,10,10)
sp_data1 = {3: [1, 1, 1, 1.0],5:[1,2,4,4.0]}
wel1 = flopy.modflow.ModflowWel(ml, stress_period_data=sp_data1)
ml.write_input()
!head -n 10 'data/test.wel'
sp_data2 = {0: [1, 1, 3, 3.0],8:[9,2,4,4.0]}
wel2 = flopy.modflow.ModflowWel(ml, stress_period_data=sp_data2)
ml.write_input()
!head -n 10 'data/test.wel' | WARNING: unit 20 of package WEL already in use
****Warning -- two packages of the same type: <class 'flopy.modflow.mfwel.ModflowWel'> <class 'flopy.modflow.mfwel.ModflowWel'>
replacing existing Package...
# WEL package for MODFLOW-2005, generated by Flopy.
1 0
1 0 # stress period 1
2 2 4 3.0
-1 0 # stress period 2
-1 0 # stress period 3
-1 0 # stress period 4
-1 0 # stress period 5
-1 0 # stress period 6
-1 0 # stress period 7
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
Now we create a third wel package, using the ```MfList.append()``` method: | wel3 = flopy.modflow.ModflowWel(ml,stress_period_data=\
wel2.stress_period_data.append(
wel1.stress_period_data))
ml.write_input()
!head -n 10 'data/test.wel' | WARNING: unit 20 of package WEL already in use
****Warning -- two packages of the same type: <class 'flopy.modflow.mfwel.ModflowWel'> <class 'flopy.modflow.mfwel.ModflowWel'>
replacing existing Package...
# WEL package for MODFLOW-2005, generated by Flopy.
2 0
1 0 # stress period 1
2 2 4 3.0
-1 0 # stress period 2
-1 0 # stress period 3
2 0 # stress period 4
2 2 4 3.0
2 2 2 1.0
-1 0 # stress period 5
| CC0-1.0 | examples/Notebooks/flopy3_modflow_boundaries.ipynb | briochh/flopy |
!pip install --quiet transformers sentence-transformers nltk pyter3
import json
from pathlib import Path
def read_squad(path):
path = Path(path)
with open(path, 'rb') as f:
squad_dict = json.load(f)
contexts = []
questions = []
answers = []
for group in squad_dict['data']:
for passage in group['paragraphs']:
context = passage['context']
for qa in passage['qas']:
question = qa['question']
for answer in qa['answers']:
contexts.append(context)
questions.append(question)
answers.append(answer)
return contexts, questions, answers
train_contexts, train_questions, train_answers = read_squad('/content/drive/MyDrive/squad/train-v2.0.json')
val_contexts, val_questions, val_answers = read_squad('/content/drive/MyDrive/squad/dev-v2.0.json')
def add_end_idx(answers, contexts):
for answer, context in zip(answers, contexts):
gold_text = answer['text']
start_idx = answer['answer_start']
end_idx = start_idx + len(gold_text)
answer['answer_end'] = end_idx
add_end_idx(train_answers, train_contexts)
add_end_idx(val_answers, val_contexts)
from transformers import AutoTokenizer
tokenizer = AutoTokenizer.from_pretrained('deepset/electra-base-squad2')
train_encodings = tokenizer(train_contexts, train_questions, truncation=True, padding=True)
val_encodings = tokenizer(val_contexts, val_questions, truncation=True, padding=True)
def add_token_positions(encodings, answers):
start_positions = []
end_positions = []
for i in range(len(answers)):
start_positions.append(encodings.char_to_token(i, answers[i]['answer_start']))
end_positions.append(encodings.char_to_token(i, answers[i]['answer_end'] - 1))
# if start position is None, the answer passage has been truncated
if start_positions[-1] is None:
start_positions[-1] = tokenizer.model_max_length
if end_positions[-1] is None:
end_positions[-1] = tokenizer.model_max_length
encodings.update({'start_positions': start_positions, 'end_positions': end_positions})
add_token_positions(train_encodings, train_answers)
add_token_positions(val_encodings, val_answers)
import torch
class SquadDataset(torch.utils.data.Dataset):
def __init__(self, encodings):
self.encodings = encodings
def __getitem__(self, idx):
return {key: torch.tensor(val[idx]) for key, val in self.encodings.items()}
def __len__(self):
return len(self.encodings.input_ids)
train_dataset = SquadDataset(train_encodings)
val_dataset = SquadDataset(val_encodings)
from transformers import AutoModelForQuestionAnswering
model = AutoModelForQuestionAnswering.from_pretrained("deepset/electra-base-squad2")
from torch.utils.data import DataLoader
from transformers import AdamW
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
model.to(device)
model.train()
train_loader = DataLoader(train_dataset, batch_size=16, shuffle=True)
optim = AdamW(model.parameters(), lr=5e-5)
for epoch in range(3):
print("Epoch: ", epoch+1)
for batch in train_loader:
optim.zero_grad()
input_ids = batch['input_ids'].to(device)
attention_mask = batch['attention_mask'].to(device)
start_positions = batch['start_positions'].to(device)
end_positions = batch['end_positions'].to(device)
outputs = model(input_ids, attention_mask=attention_mask, start_positions=start_positions, end_positions=end_positions)
loss = outputs[0]
loss.backward()
optim.step()
model.eval()
def wer_score(hyp, ref, print_matrix=False):
import numpy as np
N = len(hyp)
M = len(ref)
L = np.zeros((N,M))
for i in range(0, N):
for j in range(0, M):
if min(i,j) == 0:
L[i,j] = max(i,j)
else:
deletion = L[i-1,j] + 1
insertion = L[i,j-1] + 1
sub = 1 if hyp[i] != ref[j] else 0
substitution = L[i-1,j-1] + sub
L[i,j] = min(deletion, min(insertion, substitution))
if print_matrix:
print("WER matrix ({}x{}): ".format(N, M))
print(L)
return int(L[N-1, M-1])
def metrics(fname):
# BLEU
from nltk.translate.bleu_score import sentence_bleu, corpus_bleu
scores = []
f = open("/content/drive/MyDrive/squad/poc_english.txt", "r")
f2 = open(fname, "r")
lines = f.readlines()
cand = f2.readlines()
for i in range(len(cand)):
line = lines[i]
candidate = []
l = cand[i].lower().strip('\n')[1:len(cand[i])-2].split(", ")
for item in l:
item = item.strip('.').split(" ")
candidate.append(item)
arr = line.strip('.\n').split(" ")
for i in range(len(arr)):
arr[i] = arr[i].lower()
reference = [arr]
for c in candidate:
# print(reference, c, ': ', sentence_bleu(reference, c, weights=(1,0)))
scores.append(sentence_bleu(reference, c, weights=(1,0)))
print("BLEU: " + str(sum(scores)/(1.0*len(scores))))
# Word2Vec Cosine Similarity
import torch
import torch.nn.functional as F
from sentence_transformers import SentenceTransformer
import nltk
nltk.download('punkt')
from nltk import tokenize
def similarity(par1, par2):
transformer = SentenceTransformer('roberta-base-nli-stsb-mean-tokens')
transformer.eval()
par1 = tokenize.sent_tokenize(par1)
vec1 = torch.Tensor(transformer.encode(par1))
vec1 = vec1.mean(0)
par2 = tokenize.sent_tokenize(par2)
vec2 = torch.Tensor(transformer.encode(par2))
vec2 = vec2.mean(0)
cos_sim = F.cosine_similarity(vec1, vec2, dim=0)
return cos_sim.item()
scores = []
f = open("/content/drive/MyDrive/squad/poc_english.txt", "r")
f2 = open(fname, "r")
lines = f.readlines()
cand = f2.readlines()
for i in range(len(cand)):
line = lines[i]
candidate = []
l = cand[i].lower().strip('\n')[1:len(cand[i])-2].split(", ")
for item in l:
item = item.strip('.').split(" ")
candidate.append(item)
arr = line.strip('.\n').split(" ")
if (len(arr) == 1):
continue
for i in range(len(arr)):
arr[i] = arr[i].lower()
reference = arr
for c in candidate:
scores.append(similarity(" ".join(reference), " ".join(c)))
print("Word2Vec Cosine Similarity: " + str(sum(scores)/(1.0*len(scores))))
# WER
scores = []
f = open("/content/drive/MyDrive/squad/poc_english.txt", "r")
f2 = open(fname, "r")
lines = f.readlines()
cand = f2.readlines()
for i in range(len(cand)):
line = lines[i]
candidate = []
l = cand[i].lower().strip('\n')[1:len(cand[i])-2].split(", ")
for item in l:
item = item.strip('.').split(" ")
candidate.append(item)
arr = line.strip('.\n').split(" ")
if (len(arr) == 1):
continue
for i in range(len(arr)):
arr[i] = arr[i].lower()
reference = arr
for c in candidate:
scores.append(wer_score(c, reference))
print("WER: " + str(sum(scores)/(1.0*len(scores))))
# TER
import pyter
scores = []
f = open("/content/drive/MyDrive/squad/poc_english.txt", "r")
f2 = open(fname, "r")
lines = f.readlines()
cand = f2.readlines()
for i in range(len(cand)):
line = lines[i]
candidate = []
l = cand[i].lower().strip('\n')[1:len(cand[i])-2].split(", ")
for item in l:
item = item.strip('.').split(" ")
candidate.append(item)
arr = line.strip('.\n').split(" ")
if (len(arr) == 1):
continue
for i in range(len(arr)):
arr[i] = arr[i].lower()
reference = arr
for c in candidate:
scores.append(pyter.ter(reference, c))
print("TER: " + str(sum(scores)/(1.0*len(scores))))
def run(modelname, model, tokenizer):
# model = AutoModelForQuestionAnswering.from_pretrained(modelname)
# tokenizer = AutoTokenizer.from_pretrained(modelname)
from transformers import pipeline
nlp = pipeline('question-answering', model=model, tokenizer=tokenizer)
rel_and_food = "A mom is a human. A dad is a human. A mom is a parent. A dad is a parent. A son is a child. A daughter is a child. A son is a human. A daughter is a human. A mom likes cake. A daughter likes cake. A son likes sausage. A dad likes sausage. Cake is a food. Sausage is a food. Mom is a human now. Dad is a human now. Mom is a parent now. Dad is a parent now. Son is a child now. Daughter is a child now. Son is a human now. Daughter is a human now. Mom likes cake now. Daughter likes cake now. Son likes sausage now. Dad likes sausage now. Cake is a food now. Sausage is a food now. Mom was a daughter before. Dad was a son before. Mom was not a parent before. Dad was not a parent before. Mom liked cake before. Dad liked sausage before. Cake was a food before. Sausage was a food before."
prof = "Mom is on the board of directors. Dad is on the board of directors. Son is on the board of directors. Daughter is on the board of directors. Mom writes with chalk on the board. Dad writes with chalk on the board. Son writes with chalk on the board. Daughter writes with chalk on the board. Dad wants Mom to be on the board of directors. Mom wants Dad to be on the board of directors. Dad wants his son to be on the board of directors. Mom wants her daughter to be on the board of directors. Mom writes to Dad with chalk on the board. Dad writes to Mom with chalk on the board. Son writes to Dad with chalk on the board. Daughter writes to Mom with chalk on the board."
tools_and_pos = "Mom has a hammer. Mom has a saw. Dad has a hammer. Dad has a saw. Mom has a telescope. Mom has binoculars. Dad has a telescope. Dad has binoculars. Mom saw Dad with a hammer. Mom saw Dad with a saw. Dad saw Mom with a hammer. Dad saw Mom with a saw. Saw is a tool. Hammer is a tool. Binoculars are a tool. A telescope is a tool. Mom sawed the wood with a saw. Dad sawed the wood with a saw. Son sawed the wood with a saw. Daughter sawed the wood with a saw. Mom knocked the wood with a hammer. Dad knocked the wood with a hammer. Son knocked the wood with a hammer. Daughter knocked the wood with a hammer. Mom saw Dad with binoculars. Mom saw Dad with a telescope. Dad saw Mom with binoculars. Dad saw Mom with a telescope."
f = open("/content/drive/MyDrive/squad/poc_english_queries.txt", "r")
f2name = modelname.split("/")[1] + ".txt"
f2 = open(f2name, "w")
for line in f:
parts = line.split(" ")
context = ""
if "relationships" in parts[0]:
context = rel_and_food
elif "tools" in parts[0]:
context = tools_and_pos
else:
context = prof
question = ""
for i in range(len(parts)-1):
question = question + parts[i+1].rstrip() + " "
question = question[0:len(question)-1] + "?"
f2.write(nlp({'question': question, 'context': context })['answer'].replace(".",",") + "\n")
f2.close()
print(f2name)
metrics(f2name)
print('\n')
run('deepset/electra-base-squad2', model, tokenizer) | electra-base-squad2.txt
| MIT | src/test/resources/Baseline_QA/Baseline_QA_ELECTRA.ipynb | jenka2014/aigents-java-nlp |
|
Machine Translation Inference Pipeline Packages | import os
import shutil
from typing import Dict
from transformers import T5Tokenizer, T5ForConditionalGeneration
from forte import Pipeline
from forte.data import DataPack
from forte.common import Resources, Config
from forte.processors.base import PackProcessor
from forte.data.readers import PlainTextReader | _____no_output_____ | Apache-2.0 | docs/notebook_tutorial/wrap_MT_inference_pipeline.ipynb | Xuezhi-Liang/forte |
BackgroundAfter a Data Scientist is satisfied with the results of a training model, they will have their notebook over to an MLE who has to convert their model into an inference model. Inference Workflow PipelineWe consider `t5-small` as a trained MT model to simplify the example. We should always consider pipeline first when it comes to an inference workflow. As the [glossary](https://asyml-forte.readthedocs.io/en/latest/index_appendices.htmlglossary) suggests, it's an inference system that contains a set of processing components. Therefore, we initialize a `pipeline` below. | pipeline: Pipeline = Pipeline[DataPack]() | _____no_output_____ | Apache-2.0 | docs/notebook_tutorial/wrap_MT_inference_pipeline.ipynb | Xuezhi-Liang/forte |
ReaderAfter observing the dataset, it's a plain `txt` file. Therefore, we can use `PlainTextReader` directly. | pipeline.set_reader(PlainTextReader()) | _____no_output_____ | Apache-2.0 | docs/notebook_tutorial/wrap_MT_inference_pipeline.ipynb | Xuezhi-Liang/forte |
However, it's still beneficial to take a deeper look at how to design this class so that users can customize a reader when needed. ProcessorWe already have an inference model, `t5-small`, and we need a component to make an inference. Therefore, besides the model itself, there are several behaviors needed.1. tokenization that transforms input text into sequences of tokens.2. since T5 has a better performance given a task prompt, we also want to include the prompt in our data.In forte, we have a generic class `PackProcessor` that wraps model and inference-related components and behaviors to process `DataPack`. We need to create a class that inherits the generic method and customizes the behaviors.The generic method to process `DataPack` is `_process(self, input_pack: DataPack)`. It should tokenize the input text, use the model class to make an inference, decode the output token ids, and finally writes the output to a target file.Given what we discussed, we have a processor class below, and we need to add it to the pipeline after defining it. |
class MachineTranslationProcessor(PackProcessor):
"""
Translate the input text and output to a file.
"""
def initialize(self, resources: Resources, configs: Config):
super().initialize(resources, configs)
# Initialize the tokenizer and model
model_name: str = self.configs.pretrained_model
self.tokenizer = T5Tokenizer.from_pretrained(model_name)
self.model = T5ForConditionalGeneration.from_pretrained(model_name)
self.task_prefix = "translate English to German: "
self.tokenizer.padding_side = "left"
self.tokenizer.pad_token = self.tokenizer.eos_token
if not os.path.isdir(self.configs.output_folder):
os.mkdir(self.configs.output_folder)
def _process(self, input_pack: DataPack):
file_name: str = os.path.join(
self.configs.output_folder, os.path.basename(input_pack.pack_name)
)
# en2de machine translation
inputs = self.tokenizer([
self.task_prefix + sentence
for sentence in input_pack.text.split('\n')
], return_tensors="pt", padding=True)
output_sequences = self.model.generate(
input_ids=inputs["input_ids"],
attention_mask=inputs["attention_mask"],
do_sample=False,
)
outputs = self.tokenizer.batch_decode(
output_sequences, skip_special_tokens=True
)
# Write output to the specified file
with open(file=file_name, mode='w') as f:
f.write('\n'.join(outputs))
@classmethod
def default_configs(cls) -> Dict:
return {
"pretrained_model": "t5-small",
"output_folder": "mt_test_output"
}
pipeline.add(MachineTranslationProcessor(), config={
"pretrained_model": "t5-small"
}) | _____no_output_____ | Apache-2.0 | docs/notebook_tutorial/wrap_MT_inference_pipeline.ipynb | Xuezhi-Liang/forte |
ExamplesWe have a working [MT translation pipeline example](https://github.com/asyml/forte/blob/master/docs/notebook_tutorial/wrap_MT_inference_pipeline.ipynb).There are several basic functions of the processor and internal functions defined in this example.* ``initialize()``: Pipeline will call it at the start of processing. The processor will be initialized with ``configs``, and register global resources into ``resource``. The implementation should set up the states of the component. - initialize a pre-trained model - initialize tokenizer - initialize model-specific attributes such as task prefix* ``process()``: using the loaded model to make predictions and write the prediction results out. - we first tokenize the input text - then, we use model to generate output sequence ids - then, we decode output sequence ids into tokens and write the output into a file After setting up the pipeline's components, we can run the pipeline on the input directory as below. | dir_path = os.path.abspath(
os.path.join("data_samples", "machine_translation")
) # notebook should be running from project root folder
pipeline.run(dir_path)
print("Done successfully") | _____no_output_____ | Apache-2.0 | docs/notebook_tutorial/wrap_MT_inference_pipeline.ipynb | Xuezhi-Liang/forte |
One can investigate the machine translation output in folder `mt_test_output` located under the script's directory.Then we remove the output folder below. | shutil.rmtree(MachineTranslationProcessor.default_configs()["output_folder"]) | _____no_output_____ | Apache-2.0 | docs/notebook_tutorial/wrap_MT_inference_pipeline.ipynb | Xuezhi-Liang/forte |
T81-558: Applications of Deep Neural Networks* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), School of Engineering and Applied Science, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).**Module 3 Assignment: Creating Columns in Pandas****Student Name: Your Name** Assignment InstructionsFor this assignment you will use the **reg-30-spring-2018.csv** dataset. This is a dataset that I generated specifically for this semester. You can find the CSV file in the **data** directory of the class GitHub repository here: [reg-30-spring-2018.csv](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/data/reg-30-spring-2018.csv).For this assignment, load and modify the data set. You will submit this modified dataset to the **submit** function. See [Assignment 1](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/assignments/assignment_yourname_class1.ipynb) for details on how to submit an assignment or check that one was submitted.Modify the dataset as follows:* Add a column named *density* that is *weight* divided by *volume*.* Replace the *region* column with dummy variables. * Replace the *item* column with an index encoding value (for example 0 for the first class, 1 for the next, etc. see function *encode_text_index*)* Your submitted dataframe will have these columns: id, distance, height, landings, number, pack, age, usage, weight, item, volume, width, max, power, size, target, density, region-RE-0, region-RE-1, region-RE-10, region-RE-11, region-RE-2, region-RE-3, region-RE-4, region-RE-5, region-RE-6, region-RE-7, region-RE-8, region-RE-9, region-RE-A, region-RE-B, region-RE-C, region-RE-D, region-RE-E, region-RE-F. Helpful FunctionsYou will see these at the top of every module and assignment. These are simply a set of reusable functions that we will make use of. Each of them will be explained as the semester progresses. They are explained in greater detail as the course progresses. Class 4 contains a complete overview of these functions. | from sklearn import preprocessing
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import shutil
import os
import requests
import base64
# Encode text values to dummy variables(i.e. [1,0,0],[0,1,0],[0,0,1] for red,green,blue)
def encode_text_dummy(df, name):
dummies = pd.get_dummies(df[name])
for x in dummies.columns:
dummy_name = "{}-{}".format(name, x)
df[dummy_name] = dummies[x]
df.drop(name, axis=1, inplace=True)
# Encode text values to a single dummy variable. The new columns (which do not replace the old) will have a 1
# at every location where the original column (name) matches each of the target_values. One column is added for
# each target value.
def encode_text_single_dummy(df, name, target_values):
for tv in target_values:
l = list(df[name].astype(str))
l = [1 if str(x) == str(tv) else 0 for x in l]
name2 = "{}-{}".format(name, tv)
df[name2] = l
# Encode text values to indexes(i.e. [1],[2],[3] for red,green,blue).
def encode_text_index(df, name):
le = preprocessing.LabelEncoder()
df[name] = le.fit_transform(df[name])
return le.classes_
# Encode a numeric column as zscores
def encode_numeric_zscore(df, name, mean=None, sd=None):
if mean is None:
mean = df[name].mean()
if sd is None:
sd = df[name].std()
df[name] = (df[name] - mean) / sd
# Convert all missing values in the specified column to the median
def missing_median(df, name):
med = df[name].median()
df[name] = df[name].fillna(med)
# Convert all missing values in the specified column to the default
def missing_default(df, name, default_value):
df[name] = df[name].fillna(default_value)
# Convert a Pandas dataframe to the x,y inputs that TensorFlow needs
def to_xy(df, target):
result = []
for x in df.columns:
if x != target:
result.append(x)
# find out the type of the target column. Is it really this hard? :(
target_type = df[target].dtypes
target_type = target_type[0] if hasattr(target_type, '__iter__') else target_type
# Encode to int for classification, float otherwise. TensorFlow likes 32 bits.
if target_type in (np.int64, np.int32):
# Classification
dummies = pd.get_dummies(df[target])
return df.as_matrix(result).astype(np.float32), dummies.as_matrix().astype(np.float32)
else:
# Regression
return df.as_matrix(result).astype(np.float32), df.as_matrix([target]).astype(np.float32)
# Nicely formatted time string
def hms_string(sec_elapsed):
h = int(sec_elapsed / (60 * 60))
m = int((sec_elapsed % (60 * 60)) / 60)
s = sec_elapsed % 60
return "{}:{:>02}:{:>05.2f}".format(h, m, s)
# Regression chart.
def chart_regression(pred,y,sort=True):
t = pd.DataFrame({'pred' : pred, 'y' : y.flatten()})
if sort:
t.sort_values(by=['y'],inplace=True)
a = plt.plot(t['y'].tolist(),label='expected')
b = plt.plot(t['pred'].tolist(),label='prediction')
plt.ylabel('output')
plt.legend()
plt.show()
# Remove all rows where the specified column is +/- sd standard deviations
def remove_outliers(df, name, sd):
drop_rows = df.index[(np.abs(df[name] - df[name].mean()) >= (sd * df[name].std()))]
df.drop(drop_rows, axis=0, inplace=True)
# Encode a column to a range between normalized_low and normalized_high.
def encode_numeric_range(df, name, normalized_low=-1, normalized_high=1,
data_low=None, data_high=None):
if data_low is None:
data_low = min(df[name])
data_high = max(df[name])
df[name] = ((df[name] - data_low) / (data_high - data_low)) \
* (normalized_high - normalized_low) + normalized_low
# This function submits an assignment. You can submit an assignment as much as you like, only the final
# submission counts. The paramaters are as follows:
# data - Pandas dataframe output.
# key - Your student key that was emailed to you.
# no - The assignment class number, should be 1 through 1.
# source_file - The full path to your Python or IPYNB file. This must have "_class1" as part of its name.
# . The number must match your assignment number. For example "_class2" for class assignment #2.
def submit(data,key,no,source_file=None):
if source_file is None and '__file__' not in globals(): raise Exception('Must specify a filename when a Jupyter notebook.')
if source_file is None: source_file = __file__
suffix = '_class{}'.format(no)
if suffix not in source_file: raise Exception('{} must be part of the filename.'.format(suffix))
with open(source_file, "rb") as image_file:
encoded_python = base64.b64encode(image_file.read()).decode('ascii')
ext = os.path.splitext(source_file)[-1].lower()
if ext not in ['.ipynb','.py']: raise Exception("Source file is {} must be .py or .ipynb".format(ext))
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key':key}, json={'csv':base64.b64encode(data.to_csv(index=False).encode('ascii')).decode("ascii"),
'assignment': no, 'ext':ext, 'py':encoded_python})
if r.status_code == 200:
print("Success: {}".format(r.text))
else: print("Failure: {}".format(r.text)) | _____no_output_____ | Apache-2.0 | assignments/assignment_yourname_class3.ipynb | Chuyi1202/T81-558-Application-of-Deep-Neural-Networks |
Assignment 3 Sample CodeThe following code provides a starting point for this assignment. | import os
import pandas as pd
from scipy.stats import zscore
# This is your student key that I emailed to you at the beginnning of the semester.
key = "qgABjW9GKV1vvFSQNxZW9akByENTpTAo2T9qOjmh" # This is an example key and will not work.
# You must also identify your source file. (modify for your local setup)
# file='/resources/t81_558_deep_learning/assignment_yourname_class1.ipynb' # IBM Data Science Workbench
# file='C:\\Users\\jeffh\\projects\\t81_558_deep_learning\\t81_558_class1_intro_python.ipynb' # Windows
#file='/Users/jeff/projects/t81_558_deep_learning/assignment_yourname_class1.ipynb' # Mac/Linux
file = '...location of your source file...'
# Begin assignment
path = "./data/"
filename_read = os.path.join(path,"reg-30-spring-2018.csv")
df = pd.read_csv(filename_read)
# Calculate density
# Encode dummies
# Save a copy to examine, if you like
df.to_csv('3.csv',index=False)
# Submit
submit(source_file=file,data=df,key=key,no=3) | _____no_output_____ | Apache-2.0 | assignments/assignment_yourname_class3.ipynb | Chuyi1202/T81-558-Application-of-Deep-Neural-Networks |
Checking Your SubmissionYou can always double check to make sure your submission actually happened. The following utility code will help with that. | import requests
import pandas as pd
import base64
import os
def list_submits(key):
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key': key},
json={})
if r.status_code == 200:
print("Success: \n{}".format(r.text))
else:
print("Failure: {}".format(r.text))
def display_submit(key,no):
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key': key},
json={'assignment':no})
if r.status_code == 200:
print("Success: \n{}".format(r.text))
else:
print("Failure: {}".format(r.text))
# Show a listing of all submitted assignments.
key = "qgABjW9GKV1vvFSQNxZW9akByENTpTAo2T9qOjmh"
list_submits(key)
# Show one assignment, by number.
display_submit(key,3) | _____no_output_____ | Apache-2.0 | assignments/assignment_yourname_class3.ipynb | Chuyi1202/T81-558-Application-of-Deep-Neural-Networks |
Variational Autoencoder From book - "Hands-On Machine Learning with Scikit-Learn and TensorFlow" $\bullet$ Perform PCA with an undercomplete linear autoencoder(Undercomplete Autoencode: The internal representation has a lower dimensionality than the input data) | import tensorflow as tf
from tensorflow.contrib.layers import fully_connected
n_inputs = 3 # 3 D input dimension
n_hidden = 2 # 2 D internal representation
n_outputs = n_inputs
learning_rate = 0.01
X = tf.placeholder(tf.float32, shape=[None, n_inputs])
hidden = fully_connected(X, n_hidden, activation_fn = None)
outputs = fully_connected(hidden, n_outputs, activation_fn = None)
reconstruction_loss = tf.reduce_mean(tf.square(outputs - X)) # MSE
optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(reconstruction_loss)
init = tf.global_variables_initializer() | _____no_output_____ | MIT | VAE/VAE.ipynb | DarrenZhang01/Machine-Learning |
Reading and writing fieldsThere are two main file formats to which a `discretisedfield.Field` object can be saved:- [VTK](https://vtk.org/) for visualisation using e.g., [ParaView](https://www.paraview.org/) or [Mayavi](https://docs.enthought.com/mayavi/mayavi/)- OOMMF [Vector Field File Format (OVF)](https://math.nist.gov/oommf/doc/userguide12a5/userguide/Vector_Field_File_Format_OV.html) for exchanging fields with micromagnetic simulators.Let us say we have a nanosphere sample:$$x^2 + y^2 + z^2 <= r^2$$with $r=5\,\text{nm}$. The space is discretised into cells with dimensions $(0.5\,\text{nm}, 0.5\,\text{nm}, 0.5\,\text{nm})$. The value of the field at $(x, y, z)$ point is $(-cy, cx, cz)$, with $c=10^{9}$. The norm of the field inside the cylinder is $10^{6}$.Let us first build that field. | import discretisedfield as df
r = 5e-9
cell = (0.5e-9, 0.5e-9, 0.5e-9)
mesh = df.Mesh(p1=(-r, -r, -r), p2=(r, r, r), cell=cell)
def norm_fun(pos):
x, y, z = pos
if x**2 + y**2 + z**2 <= r**2:
return 1e6
else:
return 0
def value_fun(pos):
x, y, z = pos
c = 1e9
return (-c*y, c*x, c*z)
field = df.Field(mesh, dim=3, value=value_fun, norm=norm_fun) | _____no_output_____ | BSD-3-Clause | docs/field-read-write.ipynb | ubermag/discretisedfield |
Let us have a quick view of the field we created | # NBVAL_IGNORE_OUTPUT
field.plane('z').k3d.vector(color_field=field.z) | _____no_output_____ | BSD-3-Clause | docs/field-read-write.ipynb | ubermag/discretisedfield |
Writing the field to a fileThe main method used for saving field in different files is `discretisedfield.Field.write()`. It takes `filename` as an argument, which is a string with one of the following extensions:- `'.vtk'` for saving in the VTK format- `'.ovf'`, `'.omf'`, `'.ohf'` for saving in the OVF formatLet us firstly save the field in the VTK file. | vtkfilename = 'my_vtk_file.vtk'
field.write(vtkfilename) | _____no_output_____ | BSD-3-Clause | docs/field-read-write.ipynb | ubermag/discretisedfield |
We can check if the file was saved in the current directory. | import os
os.path.isfile(f'./{vtkfilename}') | _____no_output_____ | BSD-3-Clause | docs/field-read-write.ipynb | ubermag/discretisedfield |
Now, we can delete the file: | os.remove(f'./{vtkfilename}') | _____no_output_____ | BSD-3-Clause | docs/field-read-write.ipynb | ubermag/discretisedfield |
Next, we can save the field in the OVF format and check whether it was created in the current directory. | omffilename = 'my_omf_file.omf'
field.write(omffilename)
os.path.isfile(f'./{omffilename}') | _____no_output_____ | BSD-3-Clause | docs/field-read-write.ipynb | ubermag/discretisedfield |
There are three different possible representations of an OVF file: one ASCII (`txt`) and two binary (`bin4` or `bin8`). ASCII `txt` representation is a default representation when `discretisedfield.Field.write()` is called. If any different representation is required, it can be passed via `representation` argument. | field.write(omffilename, representation='bin8')
os.path.isfile(f'./{omffilename}') | _____no_output_____ | BSD-3-Clause | docs/field-read-write.ipynb | ubermag/discretisedfield |
Reading the OVF fileThe method for reading OVF files is a class method `discretisedfield.Field.fromfile()`. By passing a `filename` argument, it reads the file and creates a `discretisedfield.Field` object. It is not required to pass the representation of the OVF file to the `discretisedfield.Field.fromfile()` method, because it can retrieve it from the content of the file. | read_field = df.Field.fromfile(omffilename) | _____no_output_____ | BSD-3-Clause | docs/field-read-write.ipynb | ubermag/discretisedfield |
Like previouly, we can quickly visualise the field | # NBVAL_IGNORE_OUTPUT
read_field.plane('z').k3d.vector(color_field=read_field.z) | _____no_output_____ | BSD-3-Clause | docs/field-read-write.ipynb | ubermag/discretisedfield |
Finally, we can delete the OVF file we created. | os.remove(f'./{omffilename}') | _____no_output_____ | BSD-3-Clause | docs/field-read-write.ipynb | ubermag/discretisedfield |
Now we get the theoretical earth orbital speed: | # Now let's compute the theoretical expectation. First, we load a pck file
# that contain miscellanoeus information, like the G*M values for different
# objects
# First, load the kernel
spiceypy.furnsh('../kernels/pck/gm_de431.tpc')
_, GM_SUN = spiceypy.bodvcd(bodyid=10, item='GM', maxn=1)
# Now compute the orbital speed
V_ORB_FUNC = lambda gm, r: math.sqrt(gm/r)
EARTH_ORB_SPEED_WRT_SUN_THEORY = V_ORB_FUNC(GM_SUN[0], EARTH_SUN_DISTANCE)
# Print the result
print('Theoretical orbital speed of the Earth around the Sun in km/s:', \
EARTH_ORB_SPEED_WRT_SUN_THEORY) | Theoretical orbital speed of the Earth around the Sun in km/s: 29.87838444261713
| MIT | Jorges Notes/Tutorial_1.ipynb | Chuly90/Astroniz-YT-Tutorials |
Lab 05 - "Convolutional Neural Networks (CNNs)" AssignmentsGSERM'21 course "Deep Learning: Fundamentals and Applications", University of St. Gallen In the last lab we learned how to enhance vanilla Artificial Neural Networks (ANNs) using `PyTorch` to classify even more complex images. Therefore, we used a special type of deep neural network referred to **Convolutional Neural Networks (CNNs)**. CNNs encompass the ability to take advantage of the hierarchical pattern in data and assemble more complex patterns using smaller and simpler patterns. In this lab, we aim to leverage that knowledge by applying it to a set of self-coding assignments. But before we do so let's start with another motivational video by NVIDIA: | from IPython.display import YouTubeVideo
# NVIDIA: "Official Intro | GTC 2020 | I AM AI"
YouTubeVideo('e2_hsjpTi4w', width=1000, height=500) | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
As always, pls. don't hesitate to ask all your questions either during the lab, post them in our CANVAS (StudyNet) forum (https://learning.unisg.ch), or send us an email (using the course email). 1. Assignment Objectives: Similar today's lab session, after today's self-coding assignments you should be able to:> 1. Understand the basic concepts, intuitions and major building blocks of **Convolutional Neural Networks (CNNs)**.> 2. Know how to **implement and to train a CNN** to learn a model of tiny image data.> 3. Understand how to apply such a learned model to **classify images** images based on their content into distinct categories.> 4. Know how to **interpret and visualize** the model's classification results. 2. Setup of the Jupyter Notebook Environment Similar to the previous labs, we need to import a couple of Python libraries that allow for data analysis and data visualization. We will mostly use the `PyTorch`, `Numpy`, `Sklearn`, `Matplotlib`, `Seaborn` and a few utility libraries throughout this lab: | # import standard python libraries
import os, urllib, io
from datetime import datetime
import numpy as np | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Import Python machine / deep learning libraries: | # import the PyTorch deep learning library
import torch, torchvision
import torch.nn.functional as F
from torch import nn, optim
from torch.autograd import Variable | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Import the sklearn classification metrics: | # import sklearn classification evaluation library
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Import Python plotting libraries: | # import matplotlib, seaborn, and PIL data visualization libary
import matplotlib.pyplot as plt
import seaborn as sns
from PIL import Image | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Enable notebook matplotlib inline plotting: | %matplotlib inline | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Import Google's GDrive connector and mount your GDrive directories: | # import the Google Colab GDrive connector
from google.colab import drive
# mount GDrive inside the Colab notebook
drive.mount('/content/drive') | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Create a structure of Colab Notebook sub-directories inside of GDrive to store (1) the data as well as (2) the trained neural network models: | # create Colab Notebooks directory
notebook_directory = '/content/drive/MyDrive/Colab Notebooks'
if not os.path.exists(notebook_directory): os.makedirs(notebook_directory)
# create data sub-directory inside the Colab Notebooks directory
data_directory = '/content/drive/MyDrive/Colab Notebooks/data'
if not os.path.exists(data_directory): os.makedirs(data_directory)
# create models sub-directory inside the Colab Notebooks directory
models_directory = '/content/drive/MyDrive/Colab Notebooks/models'
if not os.path.exists(models_directory): os.makedirs(models_directory) | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Set a random `seed` value to obtain reproducable results: | # init deterministic seed
seed_value = 1234
np.random.seed(seed_value) # set numpy seed
torch.manual_seed(seed_value) # set pytorch seed CPU | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Google Colab provides the use of free GPUs for running notebooks. However, if you just execute this notebook as is, it will use your device's CPU. To run the lab on a GPU, got to `Runtime` > `Change runtime type` and set the Runtime type to `GPU` in the drop-down. Running this lab on a CPU is fine, but you will find that GPU computing is faster. *CUDA* indicates that the lab is being run on GPU.Enable GPU computing by setting the `device` flag and init a `CUDA` seed: | # set cpu or gpu enabled device
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu').type
# init deterministic GPU seed
torch.cuda.manual_seed(seed_value)
# log type of device enabled
print('[LOG] notebook with {} computation enabled'.format(str(device))) | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Let's determine if we have access to a GPU provided by e.g. Google's COLab environment: | !nvidia-smi | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
3. Convolutional Neural Networks (CNNs) Assignments 3.1 CIFAR-10 Dataset Download and Data Assessment The **CIFAR-10 database** (**C**anadian **I**nstitute **F**or **A**dvanced **R**esearch) is a collection of images that are commonly used to train machine learning and computer vision algorithms. The database is widely used to conduct computer vision research using machine learning and deep learning methods: (Source: https://www.kaggle.com/c/cifar-10) Further details on the dataset can be obtained via: *Krizhevsky, A., 2009. "Learning Multiple Layers of Features from Tiny Images", ( https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf )."* The CIFAR-10 database contains **60,000 color images** (50,000 training images and 10,000 validation images). The size of each image is 32 by 32 pixels. The collection of images encompasses 10 different classes that represent airplanes, cars, birds, cats, deer, dogs, frogs, horses, ships, and trucks. Let's define the distinct classs for further analytics: | cifar10_classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck'] | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Thereby the dataset contains 6,000 images for each of the ten classes. The CIFAR-10 is a straightforward dataset that can be used to teach a computer how to recognize objects in images.Let's download, transform and inspect the training images of the dataset. Therefore, we first will define the directory we aim to store the training data: | train_path = data_directory + '/train_cifar10' | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Now, let's download the training data accordingly: | # define pytorch transformation into tensor format
transf = torchvision.transforms.Compose([torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# download and transform training images
cifar10_train_data = torchvision.datasets.CIFAR10(root=train_path, train=True, transform=transf, download=True) | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Verify the volume of training images downloaded: | # get the length of the training data
len(cifar10_train_data) | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Let's now decide on where we want to store the evaluation data: | eval_path = data_directory + '/eval_cifar10' | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
And download the evaluation data accordingly: | # define pytorch transformation into tensor format
transf = torchvision.transforms.Compose([torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# download and transform validation images
cifar10_eval_data = torchvision.datasets.CIFAR10(root=eval_path, train=False, transform=transf, download=True) | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Let's also verfify the volume of validation images downloaded: | # get the length of the training data
len(cifar10_eval_data) | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
3.2 Convolutional Neural Network (CNN) Model Training and Evaluation We recommend you to try the following exercises as part of the self-coding session:**Exercise 1: Train the neural network architecture of the lab with increased learning rate.** > Increase the learning rate of the network training to a value of **0.1** (instead of currently 0.001) and re-run the network training for 10 training epochs. Load and evaluate the model exhibiting the lowest training loss. What kind of behavior in terms of loss convergence and prediction accuracy can be observed? | #### Step 1. define and init neural network architecture #############################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 2. define loss, training hyperparameters and dataloader ####################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 3. run model training ######################################################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 4. run model evaluation ####################################################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# *************************************************** | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
**2. Evaluation of "shallow" vs. "deep" neural network architectures.** > In addition to the architecture of the lab notebook, evaluate further (more **shallow** as well as more **deep**) neural network architectures by either **removing or adding convolutional layers** to the network. Train a model (using the architectures you selected) for at least **20 training epochs**. Analyze the prediction performance of the trained models in terms of training time and prediction accuracy. | #### Step 1. define and init neural network architecture #############################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 2. define loss, training hyperparameters and dataloader ####################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 3. run model training ######################################################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# ***************************************************
#### Step 4. run model evaluation ####################################################################################
# ***************************************************
# INSERT YOUR SOLUTION/CODE HERE
# *************************************************** | _____no_output_____ | BSD-3-Clause | lab_05/lab_05_exercises.ipynb | HSG-AIML/LabGSERM |
Data Science Academy - Python Fundamentos - Capítulo 9 Download: http://github.com/dsacademybr Mini-Projeto 2 - Análise Exploratória em Conjunto de Dados do Kaggle Análise 3 | # Imports
import os
import subprocess
import stat
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from datetime import datetime
sns.set(style="white")
%matplotlib inline
# Dataset
clean_data_path = "dataset/autos.csv"
df = pd.read_csv(clean_data_path,encoding="latin-1") | _____no_output_____ | Apache-2.0 | Cap10/Mini-Projeto-Solucao/Mini-Projeto2 - Analise3.ipynb | CezarPoeta/Python-Fundamentos |
Preço médio do veículo por tipo de combustível e tipo de caixa de câmbio | # Crie um Barplot com o Preço médio do veículo por tipo de combustível e tipo de caixa de câmbio
fig, ax = plt.subplots(figsize=(8,5))
colors = ["#00e600", "#ff8c1a","#a180cc"]
sns.barplot(x="fuelType", y="price",hue="gearbox", palette="husl",data=df)
ax.set_title("Preço médio do veículo por tipo de combustível e tipo de caixa de câmbio",fontdict= {'size':12})
ax.xaxis.set_label_text("Tipo de Combustível",fontdict= {'size':14})
ax.yaxis.set_label_text("Preço Médio",fontdict= {'size':14})
plt.show()
# Salvando o plot
fig.savefig("plots/Analise3/fueltype-vehicleType-price.png") | _____no_output_____ | Apache-2.0 | Cap10/Mini-Projeto-Solucao/Mini-Projeto2 - Analise3.ipynb | CezarPoeta/Python-Fundamentos |
Potência média de um veículo por tipo de veículo e tipo de caixa de câmbio | # Crie um Barplot com a Potência média de um veículo por tipo de veículo e tipo de caixa de câmbio
colors = ["windows blue", "amber", "greyish", "faded green", "dusty purple"]
fig, ax = plt.subplots(figsize=(8,5))
sns.set_palette(sns.xkcd_palette(colors))
sns.barplot(x="vehicleType", y="powerPS",hue="gearbox",data=df)
ax.set_title("Potência média de um veículo por tipo de veículo e tipo de caixa de câmbio",fontdict= {'size':12})
ax.xaxis.set_label_text("Tipo de Veículo",fontdict= {'size':14})
ax.yaxis.set_label_text("Potência Média",fontdict= {'size':14})
plt.show()
# Salvando o plot
fig.savefig("plots/Analise3/vehicletype-fueltype-power.png") | _____no_output_____ | Apache-2.0 | Cap10/Mini-Projeto-Solucao/Mini-Projeto2 - Analise3.ipynb | CezarPoeta/Python-Fundamentos |
Calibrate mean and integrated intensity of a fluorescence marker versus concentration Requirements- Images with different concentrations of the fluorescent tag with the concentration clearly specified in the image namePrepare pure solutions of various concentrations of fluorescent tag in imaging media and collect images using parameters that are identical to those used for the experimental data collection (laser power, acquisition time, magnification, etc).We recommend collecting images for 20-30 different concentrations, with 5-10 images per concentration.Clearly mark the concentration in the file or subfolder name in nM or uM. See [example_data/calibration](../../example_data/calibration) for examples of image naming. Note that the example images that we provide are cropped versions of the full images. You should use full images for calibration! Config The following code imports and declares functions used for the processing: | #################################
# Don't modify the code below #
#################################
import intake_io
import os
import re
import numpy as np
import pylab as plt
import seaborn as sns
from skimage import io
import pandas as pd
from tqdm import tqdm
from skimage.measure import regionprops_table
from am_utils.utils import walk_dir, combine_statistics | _____no_output_____ | Apache-2.0 | notebooks/misc/calibrate_intensities.ipynb | stjude/punctatools |
Data & parameters`input_dir`: folder with images to be analyzed`output_dir`: folder to save results`channel_name`: name of the fluorecent tag (e.g. "GFP") Specify data paths and parameters | input_dir = "../../example_data/calibration"
output_dir = "../../test_output/calibration"
channel_name = 'GFP' | _____no_output_____ | Apache-2.0 | notebooks/misc/calibrate_intensities.ipynb | stjude/punctatools |
The following code lists all images in the input directory: | #################################
# Don't modify the code below #
#################################
samples = walk_dir(input_dir)
print(f'{len(samples)} images were found:')
print(np.array(samples)) | 4 images were found:
['../../example_data/calibration/05192021_GFPcalibration_1nM_-_Position_4_XY1621491830.tif'
'../../example_data/calibration/05192021_GFPcalibration_5.62uM_-_Position_5_XY1621485379.tif'
'../../example_data/calibration/05192021_GFPcalibration_31.6nM_-_Position_2_XY1621488646.tif'
'../../example_data/calibration/05192021_GFPcalibration_100uM_-_Position_1_XY1621484495.tif']
| Apache-2.0 | notebooks/misc/calibrate_intensities.ipynb | stjude/punctatools |
The following code loads a random image: | #################################
# Don't modify the code below #
#################################
sample = samples[np.random.randint(len(samples))]
dataset = intake_io.imload(sample)
if 'z' in dataset.dims:
dataset = dataset.max('z')
plt.figure(figsize=(7, 7))
io.imshow(dataset['image'].data) | /research/sharedresources/cbi/public/conda_envs/punctatools/lib/python3.9/site-packages/scikit_image-0.19.0-py3.9-linux-x86_64.egg/skimage/io/_plugins/matplotlib_plugin.py:150: UserWarning: Low image data range; displaying image with stretched contrast.
lo, hi, cmap = _get_display_range(image)
| Apache-2.0 | notebooks/misc/calibrate_intensities.ipynb | stjude/punctatools |
The following code quantifies all input images: | %%time
#################################
# Don't modify the code below #
#################################
def quantify(sample, input_dir, output_dir, channel_name):
dataset = intake_io.imload(sample)
img = np.array(dataset['image'].data)
df = pd.DataFrame(regionprops_table(label_image=np.ones_like(img),
intensity_image=img,
properties=['area', 'mean_intensity']))
df = df.rename(columns={'area': 'image volume pix', 'mean_intensity': rf'{channel_name} mean intensity per image'})
df[rf'{channel_name} integrated intensity per image'] = df[rf'{channel_name} mean intensity per image'] * df['image volume pix']
p_nm = re.compile(rf'([0-9]*\.?[0-9]+)nM')
p_um = re.compile(rf'([0-9]*\.?[0-9]+)uM')
fn = sample[len(input_dir)+1:]
conc_nM = 0
if len(p_nm.findall(fn)) > 0:
conc_nM = float(p_nm.findall(fn)[0])
if len(p_um.findall(fn)) > 0:
conc_nM = float(p_um.findall(fn)[0]) * 1000
df[rf'{channel_name} concentration nM'] = conc_nM
df['Image name'] = fn
fn_out = os.path.join(output_dir, fn.replace('.' + sample.split('.')[-1], '.csv'))
# save the stats
os.makedirs(os.path.dirname(fn_out), exist_ok=True)
df.to_csv(fn_out, index=False)
for sample in tqdm(samples):
quantify(sample, input_dir, output_dir, channel_name)
# combine the cell stats
print('Combining stats...')
combine_statistics(output_dir)
df = pd.read_csv(output_dir.rstrip('/') + '.csv')
df | _____no_output_____ | Apache-2.0 | notebooks/misc/calibrate_intensities.ipynb | stjude/punctatools |
The following code plots intensity versus concentration for sanity check | #################################
# Don't modify the code below #
#################################
for col in [rf'{channel_name} concentration nM', rf'{channel_name} mean intensity per image', rf'{channel_name} integrated intensity per image']:
df['Log ' + col] = np.log10(df[col])
for col in [rf'{channel_name} mean intensity per image', rf'{channel_name} integrated intensity per image']:
plt.figure(figsize=(10, 6))
ax = sns.scatterplot(x = rf'{channel_name} concentration nM', y=col, data=df)
plt.figure(figsize=(10, 6))
ax = sns.scatterplot(x = rf'Log {channel_name} concentration nM', y='Log ' + col, data=df)
| _____no_output_____ | Apache-2.0 | notebooks/misc/calibrate_intensities.ipynb | stjude/punctatools |
Uncomment the following line to install [geemap](https://geemap.org) if needed. | # !pip install geemap
import ee
import geemap
geemap.show_youtube('N7rK2aV1R4c')
Map = geemap.Map()
Map
# Add Earth Engine dataset
image = ee.Image('USGS/SRTMGL1_003')
# Set visualization parameters.
vis_params = {
'min': 0,
'max': 4000,
'palette': ['006633', 'E5FFCC', '662A00', 'D8D8D8', 'F5F5F5'],
}
# Add Earth Engine DEM to map
Map.addLayer(image, vis_params, 'SRTM DEM')
states = ee.FeatureCollection("TIGER/2018/States")
Map.addLayer(states, {}, 'US States')
Map.draw_features
Map.draw_last_feature
roi = ee.FeatureCollection(Map.draw_features)
selected_states = states.filterBounds(roi)
Map.addLayer(selected_states, {}, "Selected states")
clipped_image = image.clip(selected_states)
Map.addLayer(clipped_image, vis_params, 'Clipped image') | _____no_output_____ | MIT | examples/notebooks/05_drawing_tools.ipynb | ppoon23/geemap |
Circuit Quantum Electrodynamics Contents1. [Introduction](intro)2. [The Schrieffer-Wolff Transformation](tswt)3. [Block-diagonalization of the Jaynes-Cummings Hamiltonian](bdotjch)4. [Full Transmon](full-transmon)5. [Qubit Drive with cQED](qdwcqed)6. [The Cross Resonance Entangling Gate](tcreg) 1. Introduction By analogy with Cavity Quantum Electrodynamics (CQED), circuit QED (cQED) exploits the fact that a simple model can be used to both describe the interaction of an atom with an optical cavity and a qubit with a microwave resonator. This model includes the number of photons in the cavity/resonator, the state of the atom/qubit, and the electric dipole interaction between the atom/qubit and cavity/resonator. As we saw in the last section, transmons are actually multi-level systems, but restricting ourselves to the ground $|0\rangle = |g\rangle$ and first excited $|1\rangle = |e\rangle$ states is possible because of the anharmonicity of the transmon. Therefore we can describe the transmon as a qubit desicribed by the Pauli spin matrices$$\sigma^x = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \qquad\sigma^y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \qquad\sigma^z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \qquad$$that generate rotations the respective axes around the Bloch sphere. In that case, the simplest model to describe this interaction is the Jaynes-Cummings Hamiltonian in the rotating wave approximation,$$H_{\rm JC}^{\rm (RWA)}/\hbar = \omega_r a^\dagger a - \frac{1}{2} \omega_q \sigma_z + g(a^\dagger \sigma^- + a \sigma^+).$$where $\omega_r$ and $\omega_r$ are the frequencies of the resonator and "qubit", respectively, $a$ ($a^\dagger$) is the resonator photon annihilation (creation) operator, and $g$ is the electric dipole coupling (half the vacuum Rabi splitting). Note that we are now omitting the hats from the operators. Here, the first term corresponds to the number of photons in the resonator, the second term corresponds to the state of the qubit, and the third is the electric dipole interaction, where $\sigma^\pm = (1/2)(\sigma^x \mp i\sigma^y)$ is the qubit raising/lowering operator. (Note that the signs are inverted from those of *spin* raising/lowering operators, as discussed in the previous chapter).This Hamiltonian can be solved exactly, and the solutions are hybrid qubit/resonator states where an excitation (either a photon in the resonator or excited state of the qubit) swaps between the two at a rate $g$ when they are on-resonance ($\omega_r = \omega_q$). For example, the $a^\dagger \sigma^-$ in the third term creates a photon in the resonator and lowers the qubit from $|1\rangle$ to $|0\rangle$, while the $a\sigma^+$ term destroys a photon in the resonators and excites the qubit from $|0\rangle$ to $|1\rangle$. While interesting, for our quantum computer we want to deal with qubits, and not these hybrid states. This means we want to move to a regimes where the resonator acts as a perturbation to the qubit (and vice-versa), so that their properties merely become "dressed" by the presence of the other. Using a type of perturbation theory, called the Schrieffer-Wolff (S-W) transformation, we can calculate the properties of the qubit and resonator in the regime we wish to operate. Here it should be noted that treating the transmon as a qubit is illustrative for pedagogical reasons, but the same techniques apply when you consider all the levels of the transmon. The higher levels of the transmon have profound effects and must be considered when designing and simulating them. 2. The Schrieffer-Wolff Transformation Schrödinger's Equation (Click here to expand)Problems in quantum mechanics are often that of diagolizing a Hamiltonian eigenvalue equation$$H\psi_m = E_m \psi_m \qquad {\rm for} \quad 1 \le m \le n$$where the $\psi_m$ are the eigenstates with eigenvalue $E_m$. This consists of finding a unitary matrix $U$, such that $H' = U H U^\dagger$ is diagonal. Then the eigenvalue equation$$\hat{H} \psi_m = E_m \psi_m \Longrightarrow U H U^\dagger U \psi_m = E_m U \psi_m \Longrightarrow H' \psi_m' = E_m \psi_m'$$where $\psi_m' = U\psi_m$ are the transformed eigenstates and$$H' = \begin{pmatrix}E_1 & 0 & \cdots & 0 \\0 & E_2 & \cdots & 0 \\\vdots & \vdots & \ddots & 0 \\0 & 0 & \cdots & E_n \end{pmatrix}$$is the diagonalized Hamiltonian.With the S-W transformation, instead of diagolizing the Hamiltonian, we seek to *block-diagonalize* it. Suppose we have a Hamiltonian that can be broken up into a diagonal part and perturbation$$H \quad = \quad \underbrace{\begin{pmatrix}\Box & & & & & & \\ & \Box & & & & & \\ & & \Box & & & & \\ & & & \Box & & & \\ & & & & \Box & & \\ & & & & & \Box & \\ & & & & & & \Box \end{pmatrix}}_\text{diagonal} \quad + \quad \underbrace{\begin{pmatrix}\times & \times & \times & \times & \cdot & \cdot & \cdot \\\times & \times & \times & \times & \cdot & \cdot & \cdot \\\times & \times & \times & \times & \cdot & \cdot & \cdot \\\times & \times & \times & \times & \cdot & \cdot & \cdot \\\cdot & \cdot & \cdot & \cdot & \times & \times & \times \\\cdot & \cdot & \cdot & \cdot & \times & \times & \times \\\cdot & \cdot & \cdot & \cdot & \times & \times & \times \end{pmatrix}}_\text{perturbation}$$and then write the perturbation as $H_1 + H_2$ so that $H = H_0 + H_1 + H_2$, with $H_0$ diagonal, $H_1$ block-diagonal, and $H_2$ non-block diagonal, and we have$$H \quad = \quad \underbrace{\begin{pmatrix}\Box & & & & & & \\ & \Box & & & & & \\ & & \Box & & & & \\ & & & \Box & & & \\ & & & & \Box & & \\ & & & & & \Box & \\ & & & & & & \Box \end{pmatrix}}_\text{diagonal}\quad + \quad\underbrace{\begin{pmatrix}\times & \times & \times & \times & & & \\\times & \times & \times & \times & & & \\\times & \times & \times & \times & & & \\\times & \times & \times & \times & & & \\ & & & & \times & \times & \times \\ & & & & \times & \times & \times \\ & & & & \times & \times & \times \end{pmatrix}}_\text{block diagonal} \quad + \quad\underbrace{\begin{pmatrix} & & & & \cdot & \cdot & \cdot \\ & & & & \cdot & \cdot & \cdot \\ & & & & \cdot & \cdot & \cdot \\ & & & & \cdot & \cdot & \cdot \\\cdot & \cdot & \cdot & \cdot & & & \\\cdot & \cdot & \cdot & \cdot & & & \\\cdot & \cdot & \cdot & \cdot & & & \end{pmatrix}}_\text{block off-diagonal}$$ Block-diagonalizing $H$ consists of finding an operator $S$ such that$$H_{\rm eff} = e^{iS} H e^{-iS} = \sum_{m=0}^\infty \frac{1}{m!} [H, S]^{(m)} = \sum_{m=0}^\infty \lambda^m H^{(m)},$$where $H^{(m)}$ are successive approximations to $H$ (with $H^{(0)} = H_0$) and the generalized commutator is defined resursively as $$[H,S]^{(m)} = [[H,S]^{(m-1)},S] \qquad {\rm with} \qquad [H,S]^{(0)} = H. $$Here we treat $S$ as a Taylor series with$$ S = \sum_{m=1}^\infty \lambda^m S^{(m)} $$to keep track of the order $\lambda$. Then expanding the effective Hamiltonian as a perturbation of $H_1+H_2$ to second order in $\lambda$,$$H_{\rm eff} = H_0 + \lambda (H_1+H_2) + \left[H_0 + \lambda(H_1+H_2), \lambda S^{(1)}\right] + \frac{1}{2} \left[ \left[ H_0 + \lambda(H_1+H_2), \lambda S^{(1)}\right], \lambda S^{(1)}\right] + \left[H_0 + \lambda(H_1+H_2), \lambda^2 S^{(2)}\right] + \ldots \\ \approx H_0 + \lambda \left( H_1 + H_2 + \left[H_0, S^{(1)}\right] \right) + \lambda^2 \left( \left[H_1+H_2, S^{(1)}\right] + \frac{1}{2} \left[ \left[H_0, S^{(1)},\right] S^{(1)}\right] + \left[H_0, S^{(2)}\right]\right)$$Now we know $S$ must be block off-diagonal and anti-hermitian to force the block off-diagonal elements of $H_{\rm eff}$ to vanish, we must have that$$H_{\rm eff}^{\rm off-diag} = \sum_{m=0}^\infty \frac{1}{(2m+1)!} [\underbrace{H_0 + H_1}_\text{block diag}, S]^{(2m+1)} + \sum_{m=0}^\infty \frac{1}{(2m)!} [\underbrace{H_2}_\text{block off-diag}, S]^{(2m)} \equiv 0,$$noting that all the terms in the first series are block off-diagonal and all of those in the second series are block diagonal. This is because the commutator of a block diagonal and block off-diagonal matrix is block off-diagonal and the commutator of two block off-diagonal matrices is block diagonal. Expanding this to the generalized commutator, we can see that $[H^0 + H^1, S]^{(n)}$ with odd $n$ must always be block off-diagonal as well as $[H^2, S]^{(n)}$ with even $n$. Now expanding the off-diagonal part of the Hamiltonain to second order yields$$H_{\rm eff}^{\rm off-diag} = \left[ H_0 + \lambda H_1, \lambda S^{(1)} \right]+\lambda H_2 + \left[H_0 + \lambda H_1, \lambda^2 S^{(2)}\right] + \frac{1}{3!} \left[ H_0+\lambda H_1, \lambda S^{(1)}\right]^{(3)} + \frac{1}{2!} \left[ \lambda H_2, \lambda S^{(1)}\right]^{(2)} \\ = \lambda \left( \left[ H_0, S^{(1)} \right] + H_2 \right) + \lambda^2 \left( \left[H_1, S^{(1)} \right] + \left[H_0, S^{(2)}\right]\right) + \ldots.$$Since each order of $\lambda$ must be identically zero, the following equations determine $S^{(m)}$,$$[H_0, S^{(1)}] = -H_2 \qquad[H_0, S^{(2)}] = -[H_1, S^{(1)}] \qquad[H_0, S^{(3)}] = -[H_1, S^{(2)}] - \frac{1}{3} [[H_2, S^{(1)}], S^{(1)}],$$where our ansatz that satisfied these equations is guaranteed unique by Winkler's work. Then our effective Hamiltonian becomes$$H_{\rm eff} = H_0+H_1+[H_2,S^{(1)}] + \frac{1}{2} [[H_0, S^{(1)}], S^{(1)}] + \ldots = H_0+H_1+\frac{1}{2}[H_2,S^{(1)}] + \ldots$$where the effective Hamiltonian is calculated here to second order and we have taken $\lambda \to 1$. 3. Block-diagonalization of the Jaynes-Cummings Hamiltonian Using the S-W transformation consists of two problems: 1) finding the correct ansatz, and 2) performing the calculations. In most examples, an ansatz of similar form (i.e. anti-hermitian) to the off-diagonal parts is made and confirmed *a postori*. Recently, the manuscript [A Systematic Method for Schrieffer-Wolff Transformation and Its Generalizations](http://www.arxiv.org/abs/2004.06534) has appeared on the arXiv attesting to systematically providing the ansatz and applying it to numerous systems (including the Jaynes-Cumming Hamiltonian below).As such, the *generator* $\eta$ is calculated as $\eta = [H_0, H_2]$. In keeping the scalar coefficients of $\eta$ undetermined, then $S^{(1)}$ can be calculated as the specific $\eta$ that satisfies $[H_0, \eta]=H_2$. Note the hermiticity of $H_0$ and $H_2$ guarantee the anti-hermiticity of $\eta$ and thus $S^{(1)}$. For ease of tedious calculations, we will use the Python package [`sympy`](http://www.sympy.org) for symbolic mathematics. | # import SymPy and define symbols
import sympy as sp
sp.init_printing(use_unicode=True)
wr = sp.Symbol('\omega_r') # resonator frequency
wq = sp.Symbol('\omega_q') # qubit frequency
g = sp.Symbol('g', real=True) # vacuum Rabi coupling
Delta = sp.Symbol('Delta', real=True) # wr - wq; defined later
# import operator relations and define them
from sympy.physics.quantum.boson import BosonOp
a = BosonOp('a') # resonator photon annihilation operator
from sympy.physics.quantum import pauli, Dagger, Commutator
from sympy.physics.quantum.operatorordering import normal_ordered_form
# Pauli matrices
sx = pauli.SigmaX()
sy = pauli.SigmaY()
sz = pauli.SigmaZ()
# qubit raising and lowering operators
splus = pauli.SigmaPlus()
sminus = pauli.SigmaMinus()
# define J-C Hamiltonian in terms of diagonal and non-block diagonal terms
H0 = wr*Dagger(a)*a - (1/2)*wq*sz;
H2 = g*(Dagger(a)*sminus + a*splus);
HJC = H0 + H2; HJC # print
# using the above method for finding the ansatz
eta = Commutator(H0, H2); eta | _____no_output_____ | Apache-2.0 | content/ch-quantum-hardware/cQED-JC-SW.ipynb | muneerqu/qiskit-textbook |
As a note about `sympy`, we will need to used the methods `doit()`, `expand`, `normal_ordered_form`, and `qsimplify_pauli` to proceed with actually taking the commutator, expanding it into terms, normal ordering the bosonic modes (creation before annihilation), and simplify the Pauli algebra. Trying this with $\eta$ yields | pauli.qsimplify_pauli(normal_ordered_form(eta.doit().expand())) | _____no_output_____ | Apache-2.0 | content/ch-quantum-hardware/cQED-JC-SW.ipynb | muneerqu/qiskit-textbook |
Now take $A$ and $B$ as the coefficients of $a^\dagger \sigma_-$ and $a\sigma_+$, respectively. Then the commutator | A = sp.Symbol('A')
B = sp.Symbol('B')
eta = A * Dagger(a) * sminus - B * a * splus;
pauli.qsimplify_pauli(normal_ordered_form(Commutator(H0, eta).doit().expand())) | _____no_output_____ | Apache-2.0 | content/ch-quantum-hardware/cQED-JC-SW.ipynb | muneerqu/qiskit-textbook |
This expression should be equal to $H_2$ | H2 | _____no_output_____ | Apache-2.0 | content/ch-quantum-hardware/cQED-JC-SW.ipynb | muneerqu/qiskit-textbook |
which implies $A = B = g/\Delta$ where $\Delta = \omega_r - \omega_q$ is the frequency detuning between the resonator and qubit. Therefore our $S^{(1)}$ is determined to be | S1 = eta.subs(A, g/Delta)
S1 = S1.subs(B, g/Delta); S1.factor() | _____no_output_____ | Apache-2.0 | content/ch-quantum-hardware/cQED-JC-SW.ipynb | muneerqu/qiskit-textbook |
Then we can calculate the effective second order correction to $H_0$ | Heff = H0 + 0.5*pauli.qsimplify_pauli(normal_ordered_form(Commutator(H2, S1).doit().expand())).simplify(); Heff | _____no_output_____ | Apache-2.0 | content/ch-quantum-hardware/cQED-JC-SW.ipynb | muneerqu/qiskit-textbook |
Tutorial sobre Scala Declaraciones Declaración de variables Existen dos categorias de variables: inmutables y mutables. Las variables mutables son aquellas en las que es posible modificar el contenido de la variable. Las variables inmutables son aquellas en las que no es posible alterar el contenido de las variables, se recomienda el uso de esta ultima. La declaración del tipo de la variable es opcional, Scala es capaz de inferir el tipo del dato. | //Variable inmutable
val a:Int=1
//variable mutable
var b:Int=2 | _____no_output_____ | MIT | Scala-basics.ipynb | FranciscoJavierMartin/Notebooks |
Tipos de datos 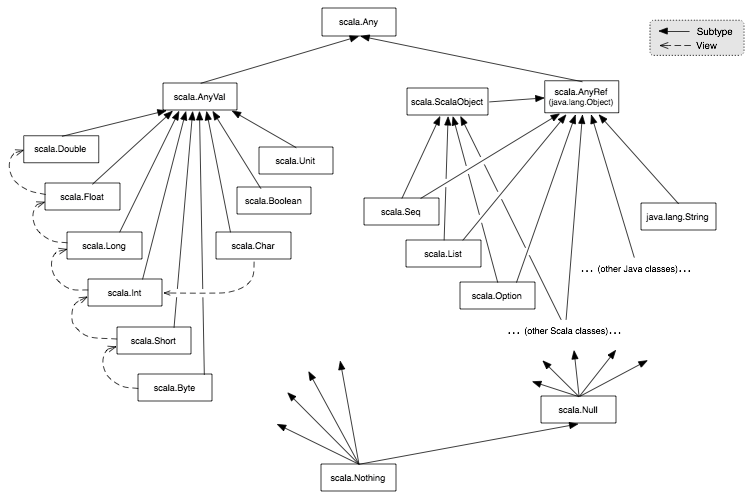 Siempre que se infiere un tipo en Scala, el tipo escogido será siempre el mas bajo posible en la jerarquía.Algunos tipos especiales:- **Any**: Es la clase de la que heredan todas las clases en Scala. Es la clase mas basica.- **AnyVal**: Es la clase padre de todas las clases que representan tipos primitivos.- **AnyRef**: Es la clase padre de todas las clases que no representan tipos primitivos. Todas las subclases de Scala y Java heredan de ella.- **ScalaObject**: Es la clase de la que heredan todas y solo las clases de Scala.- **Unit**: Equivale a `void`. Usar cuando una función no debe retornar ningún valor.- **Nothing**: Es la clase que hereda de todas las clases. Usar solo cuando no acaba la ejecución como en `While(true)`. Declaración de funciones | def funcion1(a:Int,b:Int):Int={
return a+b
}
def funcion2(a:Int,b:Int)={
a+b
}
def funcion3(a:Int,b:Int)=a+b | _____no_output_____ | MIT | Scala-basics.ipynb | FranciscoJavierMartin/Notebooks |
Al igual que con la declaración de variables no es obligatorio declarar el tipo devuelto por la función. Si no se declara una sentencia `return`, el valor de la ultima instrucción es el devuelto por la función. Interpolación de cadenasLa interpolación de cadenas consiste insertar el valor de una variable dentro de una cadena, tambien es posible usar expresiones. | val valor=1
val expresion=2
println(s"El valor de la variable ${valor} y la expresion vale ${expresion+1}") | El valor de la variable 1 y la expresion vale 3
| MIT | Scala-basics.ipynb | FranciscoJavierMartin/Notebooks |
Estructuras de selección If/Else | //Funciona igual que en Java
val verdad:Boolean=true;
if (verdad){
println("Hola")
}else{
println("Adios")
}
| _____no_output_____ | MIT | Scala-basics.ipynb | FranciscoJavierMartin/Notebooks |
En Scala no existe la estructura `switch`, en su lugar existe lo conocido como *pattern matching* Match | val numero:Int=3
val nombre=numero match{ //Puede ir dentro de la llamada a una funcion
case 1=> "Uno"
case 2=> "Dos"
case 3=> "Tres"
case _=> "Ninguno" //Es obligatorio incluir una clausula con _ que se ejecuta cuando no hay coincidencia
}
println(nombre) | _____no_output_____ | MIT | Scala-basics.ipynb | FranciscoJavierMartin/Notebooks |
Estructuras de repetición Bucle *While* | //Igual que en Java
var x=0
while(x<5){
print(x)
x+=1
} | _____no_output_____ | MIT | Scala-basics.ipynb | FranciscoJavierMartin/Notebooks |
Bucle *Do While* | //Igual que en Java
var x=0
do{
print(x)
x+=1
}while(x<5) | _____no_output_____ | MIT | Scala-basics.ipynb | FranciscoJavierMartin/Notebooks |
Bucle *For* | println("For to")
for(i<- 1 to 5){ //Hasta el limite inclusive
print(i)
}
println("\nFor until")
for(i<- 1 until 5){ //Hasta el limite exclusive
print(i)
}
println("\nFor para colecciones")
for(i <- List(1,2,3,4)){ //For para recorrer colecciones
print(i)
} | _____no_output_____ | MIT | Scala-basics.ipynb | FranciscoJavierMartin/Notebooks |
*foreach* | val lista=List(1,2,3,4)
lista.foreach(x=> print(x)) //La funcion no devuelve nada y no modifica el conjunto | _____no_output_____ | MIT | Scala-basics.ipynb | FranciscoJavierMartin/Notebooks |
Clases Indicaciones previasSe deben declarar entre parentesis todos los atributos que vaya a usar la clase. Se pueden declarar otros constructores mediante la definición de this, pero siempre se debe llamar al constructor por defecto que es el que contiene todos los atributos.Los parametros de un constructor constituyen los atributos de la clase y son privados por defecto, si se desea que sean públicos, se debe agregar val (o var) en la declaracion del argumento. Tambien es posible declarar atributos dentro de la propia clase. Estos pueden llevar los modificadores de `public`, `private` o `readonly`. Constructor por defecto | //Declaracion de clases
class Saludo(mensaje: String) { //Estos son los atributos y son accesibles desde cualquier metodo de la clase
def diHola(nombre:String):Unit ={
println(mensaje+" "+nombre);
}
}
val saludo = new Saludo("Hola")
saludo.diHola("Pepe") | _____no_output_____ | MIT | Scala-basics.ipynb | FranciscoJavierMartin/Notebooks |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.