markdown
stringlengths 0
1.02M
| code
stringlengths 0
832k
| output
stringlengths 0
1.02M
| license
stringlengths 3
36
| path
stringlengths 6
265
| repo_name
stringlengths 6
127
|
|---|---|---|---|---|---|
Let's merge the mask and depths | merged = train_mask.merge(depth, how='left')
merged.head()
plt.figure(figsize=(12, 6))
plt.scatter(merged['salt_proportion'], merged['z'])
plt.title('Proportion of salt vs depth')
print("Correlation: ", np.corrcoef(merged['salt_proportion'], merged['z'])[0, 1]) | Correlation: 0.10361580365557428
| MIT | kaggle_tgs_salt_identification.ipynb | JacksonIsaac/colab_notebooks |
Setup Keras and Train | from keras.models import Model, load_model
from keras.layers import Input
from keras.layers.core import Lambda, RepeatVector, Reshape
from keras.layers.convolutional import Conv2D, Conv2DTranspose
from keras.layers.pooling import MaxPooling2D
from keras.layers.merge import concatenate
from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau
from keras import backend as K
im_width = 128
im_height = 128
border = 5
im_chan = 2 # Number of channels: first is original and second cumsum(axis=0)
n_features = 1 # Number of extra features, like depth
#path_train = '../input/train/'
#path_test = '../input/test/'
# Build U-Net model
input_img = Input((im_height, im_width, im_chan), name='img')
input_features = Input((n_features, ), name='feat')
c1 = Conv2D(8, (3, 3), activation='relu', padding='same') (input_img)
c1 = Conv2D(8, (3, 3), activation='relu', padding='same') (c1)
p1 = MaxPooling2D((2, 2)) (c1)
c2 = Conv2D(16, (3, 3), activation='relu', padding='same') (p1)
c2 = Conv2D(16, (3, 3), activation='relu', padding='same') (c2)
p2 = MaxPooling2D((2, 2)) (c2)
c3 = Conv2D(32, (3, 3), activation='relu', padding='same') (p2)
c3 = Conv2D(32, (3, 3), activation='relu', padding='same') (c3)
p3 = MaxPooling2D((2, 2)) (c3)
c4 = Conv2D(64, (3, 3), activation='relu', padding='same') (p3)
c4 = Conv2D(64, (3, 3), activation='relu', padding='same') (c4)
p4 = MaxPooling2D(pool_size=(2, 2)) (c4)
# Join features information in the depthest! layer
f_repeat = RepeatVector(8*8)(input_features)
f_conv = Reshape((8, 8, n_features))(f_repeat)
p4_feat = concatenate([p4, f_conv], -1)
c5 = Conv2D(128, (3, 3), activation='relu', padding='same') (p4_feat)
c5 = Conv2D(128, (3, 3), activation='relu', padding='same') (c5)
u6 = Conv2DTranspose(64, (2, 2), strides=(2, 2), padding='same') (c5)
#check out this skip connection thooooo
u6 = concatenate([u6, c4])
c6 = Conv2D(64, (3, 3), activation='relu', padding='same') (u6)
c6 = Conv2D(64, (3, 3), activation='relu', padding='same') (c6)
u7 = Conv2DTranspose(32, (2, 2), strides=(2, 2), padding='same') (c6)
u7 = concatenate([u7, c3])
c7 = Conv2D(32, (3, 3), activation='relu', padding='same') (u7)
c7 = Conv2D(32, (3, 3), activation='relu', padding='same') (c7)
u8 = Conv2DTranspose(16, (2, 2), strides=(2, 2), padding='same') (c7)
u8 = concatenate([u8, c2])
c8 = Conv2D(16, (3, 3), activation='relu', padding='same') (u8)
c8 = Conv2D(16, (3, 3), activation='relu', padding='same') (c8)
u9 = Conv2DTranspose(8, (2, 2), strides=(2, 2), padding='same') (c8)
u9 = concatenate([u9, c1], axis=3)
c9 = Conv2D(8, (3, 3), activation='relu', padding='same') (u9)
c9 = Conv2D(8, (3, 3), activation='relu', padding='same') (c9)
outputs = Conv2D(1, (1, 1), activation='sigmoid') (c9)
model = Model(inputs=[input_img, input_features], outputs=[outputs])
model.compile(optimizer='adam', loss='binary_crossentropy') #, metrics=[mean_iou]) # The mean_iou metrics seens to leak train and test values...
model.summary()
import sys
from tqdm import tqdm
from keras.preprocessing.image import ImageDataGenerator, array_to_img, img_to_array, load_img
from skimage.transform import resize
train_ids = next(os.walk(train_path+"masks"))[2]
# Get and resize train images and masks
X = np.zeros((len(train_ids), im_height, im_width, im_chan), dtype=np.float32)
y = np.zeros((len(train_ids), im_height, im_width, 1), dtype=np.float32)
X_feat = np.zeros((len(train_ids), n_features), dtype=np.float32)
print('Getting and resizing train images and masks ... ')
sys.stdout.flush()
for n, id_ in tqdm(enumerate(train_ids), total=len(train_ids)):
path = train_path
# Depth
#X_feat[n] = depth.loc[id_.replace('.png', ''), 'z']
# Load X
img = load_img(path + 'images/' + id_, grayscale=True)
x_img = img_to_array(img)
x_img = resize(x_img, (128, 128, 1), mode='constant', preserve_range=True)
# Create cumsum x
x_center_mean = x_img[border:-border, border:-border].mean()
x_csum = (np.float32(x_img)-x_center_mean).cumsum(axis=0)
x_csum -= x_csum[border:-border, border:-border].mean()
x_csum /= max(1e-3, x_csum[border:-border, border:-border].std())
# Load Y
mask = img_to_array(load_img(path + 'masks/' + id_, grayscale=True))
mask = resize(mask, (128, 128, 1), mode='constant', preserve_range=True)
# Save images
X[n, ..., 0] = x_img.squeeze() / 255
X[n, ..., 1] = x_csum.squeeze()
y[n] = mask / 255
print('Done!')
!ls ./masks
!ls ./images
from sklearn.model_selection import train_test_split
X_train, X_valid, X_feat_train, X_feat_valid, y_train, y_valid = train_test_split(X, X_feat, y, test_size=0.15, random_state=42)
callbacks = [
EarlyStopping(patience=5, verbose=1),
ReduceLROnPlateau(patience=3, verbose=1),
ModelCheckpoint('model-tgs-salt-2.h5', verbose=1, save_best_only=True, save_weights_only=False)
]
results = model.fit({'img': X_train, 'feat': X_feat_train}, y_train, batch_size=16, epochs=50, callbacks=callbacks,
validation_data=({'img': X_valid, 'feat': X_feat_valid}, y_valid))
!ls
!unzip -q test.zip -d test | replace test/images/8cf16aa0f5.png? [y]es, [n]o, [A]ll, [N]one, [r]ename: N
| MIT | kaggle_tgs_salt_identification.ipynb | JacksonIsaac/colab_notebooks |
PredictRef: https://www.kaggle.com/jesperdramsch/intro-to-seismic-salt-and-how-to-geophysics | path_test='./test/'
test_ids = next(os.walk(path_test+"images"))[2]
X_test = np.zeros((len(test_ids), im_height, im_width, im_chan), dtype=np.uint8)
X_test_feat = np.zeros((len(test_ids), n_features), dtype=np.float32)
sizes_test = []
print('Getting and resizing test images ... ')
sys.stdout.flush()
for n, id_ in tqdm(enumerate(test_ids), total=len(test_ids)):
path = path_test
img = load_img(path + 'images/' + id_, grayscale=True)
x_img = img_to_array(img)
x_img = resize(x_img, (128, 128, 1), mode='constant', preserve_range=True)
# Create cumsum x
x_center_mean = x_img[border:-border, border:-border].mean()
x_csum = (np.float32(x_img)-x_center_mean).cumsum(axis=0)
x_csum -= x_csum[border:-border, border:-border].mean()
x_csum /= max(1e-3, x_csum[border:-border, border:-border].std())
# Save images
X_test[n, ..., 0] = x_img.squeeze() / 255
X_test[n, ..., 1] = x_csum.squeeze()
#img = load_img(path + '/images/' + id_)
#x = img_to_array(img)[:,:,1]
sizes_test.append([x_img.shape[0], x_img.shape[1]])
#x = resize(x, (128, 128, 1), mode='constant', preserve_range=True)
#X_test[n] = x
print('Done!')
#test_mask = pd.read_csv('test.csv')
#file_list = list(train_mask['id'].values)
#dataset = TGSSaltDataSet(train_path, file_list)
X_train.shape
X_test.shape
!ls -al
preds_test = model.predict([X_test, X_test_feat], verbose=1)
preds_test_t = (preds_test > 0.5).astype(np.uint8)
from tqdm import tnrange
# Create list of upsampled test masks
preds_test_upsampled = []
for i in tnrange(len(preds_test)):
preds_test_upsampled.append(resize(np.squeeze(preds_test[i]),
(sizes_test[i][0], sizes_test[i][1]),
mode='constant', preserve_range=True))
def RLenc(img, order='F', format=True):
"""
img is binary mask image, shape (r,c)
order is down-then-right, i.e. Fortran
format determines if the order needs to be preformatted (according to submission rules) or not
returns run length as an array or string (if format is True)
"""
bytes = img.reshape(img.shape[0] * img.shape[1], order=order)
runs = [] ## list of run lengths
r = 0 ## the current run length
pos = 1 ## count starts from 1 per WK
for c in bytes:
if (c == 0):
if r != 0:
runs.append((pos, r))
pos += r
r = 0
pos += 1
else:
r += 1
# if last run is unsaved (i.e. data ends with 1)
if r != 0:
runs.append((pos, r))
pos += r
r = 0
if format:
z = ''
for rr in runs:
z += '{} {} '.format(rr[0], rr[1])
return z[:-1]
else:
return runs
def rle_encode(im):
'''
im: numpy array, 1 - mask, 0 - background
Returns run length as string formated
'''
pixels = im.flatten(order = 'F')
pixels = np.concatenate([[0], pixels, [0]])
runs = np.where(pixels[1:] != pixels[:-1])[0] + 1
print(runs)
runs = np.unique(runs)
runs = np.sort(runs)
print(runs)
runs[1::2] -= runs[::2]
print(runs)
#print(type(runs))
#runs = sorted(list(set(runs)))
return ' '.join(str(x) for x in runs)
from tqdm import tqdm_notebook
#pred_dict = {fn[:-4]:RLenc(np.round(preds_test_upsampled[i])) for i,fn in tqdm_notebook(enumerate(test_ids))}
def downsample(img):# not used
if img_size_ori == img_size_target:
return img
return resize(img, (img_size_ori, img_size_ori), mode='constant', preserve_range=True)
threshold_best = 0.77
img_size_ori = 101
pred_dict = {idx: rle_encode(np.round(downsample(preds_test[i]) > threshold_best)) for i, idx in enumerate(tqdm_notebook(test_df.index.values))}
sub = pd.DataFrame.from_dict(pred_dict,orient='index')
sub.index.names = ['id']
sub.columns = ['rle_mask']
sub.to_csv('submission.csv')
sub.head()
!ls
!kaggle competitions submit -c tgs-salt-identification-challenge -f submission.csv -m "Re-Submission with sorted rle_mask" | Successfully submitted to TGS Salt Identification Challenge | MIT | kaggle_tgs_salt_identification.ipynb | JacksonIsaac/colab_notebooks |
PredictRef: https://www.kaggle.com/shaojiaxin/u-net-with-simple-resnet-blocks | callbacks = [
EarlyStopping(patience=5, verbose=1),
ReduceLROnPlateau(patience=3, verbose=1),
ModelCheckpoint('model-tgs-salt-new-1.h5', verbose=1, save_best_only=True, save_weights_only=True)
]
#results = model.fit({'img': [X_train, X_train], 'feat': X_feat_train}, y_train, batch_size=16, epochs=50, callbacks=callbacks,
# validation_data=({'img': [X_valid, X_valid], 'feat': X_feat_valid}, y_valid))
epochs = 50
batch_size = 16
history = model.fit(X_train, y_train,
validation_data=[X_valid, y_valid],
epochs=epochs,
batch_size=batch_size,
callbacks=callbacks)
def predict_result(model,x_test,img_size_target): # predict both orginal and reflect x
x_test_reflect = np.array([np.fliplr(x) for x in x_test])
preds_test1 = model.predict(x_test).reshape(-1, img_size_target, img_size_target)
preds_test2_refect = model.predict(x_test_reflect).reshape(-1, img_size_target, img_size_target)
preds_test2 = np.array([ np.fliplr(x) for x in preds_test2_refect] )
preds_avg = (preds_test1 +preds_test2)/2
return preds_avg
train_df = pd.read_csv("train.csv", index_col="id", usecols=[0])
depths_df = pd.read_csv("depths.csv", index_col="id")
train_df = train_df.join(depths_df)
test_df = depths_df[~depths_df.index.isin(train_df.index)]
img_size_target = 101
x_test = np.array([(np.array(load_img("./test/images/{}.png".format(idx), grayscale = True))) / 255 for idx in tqdm(test_df.index)]).reshape(-1, img_size_target, img_size_target, 1)
def rle_encode(im):
'''
im: numpy array, 1 - mask, 0 - background
Returns run length as string formated
'''
pixels = im.flatten(order = 'F')
pixels = np.concatenate([[0], pixels, [0]])
runs = np.where(pixels[1:] != pixels[:-1])[0] + 1
runs[1::2] -= runs[::2]
return ' '.join(str(x) for x in runs)
preds_test = predict_result(model,x_test,img_size_target)
| _____no_output_____ | MIT | kaggle_tgs_salt_identification.ipynb | JacksonIsaac/colab_notebooks |
Save output to drive | from google.colab import drive
drive.mount('/content/gdrive')
!ls /content/gdrive/My\ Drive/kaggle_competitions
!cp model-tgs-salt-1.h5 /content/gdrive/My\ Drive/kaggle_competitions/tgs_salt/
!cp model-tgs-salt-2.h5 /content/gdrive/My\ Drive/kaggle_competitions/tgs_salt/
!cp submission.csv /content/gdrive/My\ Drive/kaggle_competitions/tgs_salt/submission.csv
| _____no_output_____ | MIT | kaggle_tgs_salt_identification.ipynb | JacksonIsaac/colab_notebooks |
Laboratory 18: Linear Regression Full name: R: HEX: Title of the notebook Date:  The human brain is amazing and mysterious in many ways. Have a look at these sequences. You, with the assistance of your brain, can guess the next item in each sequence, right? - A,B,C,D,E, ____ ?- 5,10,15,20,25, ____ ?- 2,4,8,16,32 ____ ?- 0,1,1,2,3, ____ ?- 1, 11, 21, 1211,111221, ____ ?         But how does our brain do this? How do we 'guess | predict' the next step? Is it that there is only one possible option? is it that we have the previous items? or is it the relationship between the items? What if we have more than a single sequence? Maybe two sets of numbers? How can we predict the next "item" in a situation like that?  Blue Points? Red Line? Fit? Does it ring any bells?  --------- Problem 1 (5 pts)The table below contains some experimental observations.|Elapsed Time (s)|Speed (m/s)||---:|---:||0 |0||1.0 |3||2.0 |7||3.0 |12||4.0 |20||5.0 |30||6.0 | 45.6| |7.0 | 60.3 ||8.0 | 77.7 ||9.0 | 97.3 ||10.0| 121.1|1. Plot the speed vs time (speed on y-axis, time on x-axis) using a scatter plot. Use blue markers. 2. Plot a red line on the scatterplot based on the linear model $f(x) = mx + b$ 3. By trial-and-error find values of $m$ and $b$ that provide a good visual fit (i.e. makes the red line explain the blue markers).4. Using this data model estimate the speed at $t = 15~\texttt{sec.}$--------- Let's go over some important terminology: Linear Regression: a basic predictive analytics technique that uses historical data to predict an output variable. The Predictor variable (input): the variable(s) that help predict the value of the output variable. It is commonly referred to as X. The Output variable: the variable that we want to predict. It is commonly referred to as Y. To estimate Y using linear regression, we assume the equation: $Ye = βX + α$*where Yₑ is the estimated or predicted value of Y based on our linear equation.* Our goal is to find statistically significant values of the parameters α and β that minimise the difference between Y and Yₑ. If we are able to determine the optimum values of these two parameters, then we will have the line of best fit that we can use to predict the values of Y, given the value of X. So, how do we estimate α and β?  We can use a method called Ordinary Least Squares (OLS). 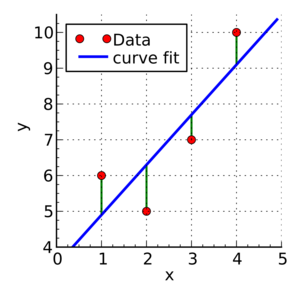 The objective of the least squares method is to find values of α and β that minimise the sum of the squared difference between Y and Yₑ (distance between the linear fit and the observed points). We will not go through the derivation here, but using calculus we can show that the values of the unknown parameters are as follows: 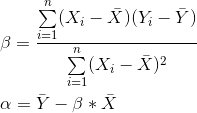 where X̄ is the mean of X values and Ȳ is the mean of Y values. β is simply the covariance of X and Y (Cov(X, Y) devided by the variance of X (Var(X)). Covariance: In probability theory and statistics, covariance is a measure of the joint variability of two random variables. If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values, (i.e., the variables tend to show similar behavior), the covariance is positive. In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other, (i.e., the variables tend to show opposite behavior), the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret because it is not normalized and hence depends on the magnitudes of the variables. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation. 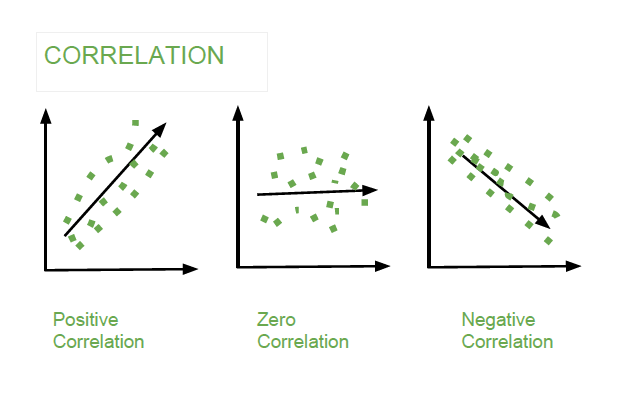 The Correlation Coefficient: Correlation coefficients are used in statistics to measure how strong a relationship is between two variables. There are several types of correlation coefficient, but the most popular is Pearson’s. Pearson’s correlation (also called Pearson’s R) is a correlation coefficient commonly used in linear regression.Correlation coefficient formulas are used to find how strong a relationship is between data. The formulat for Pearson’s R: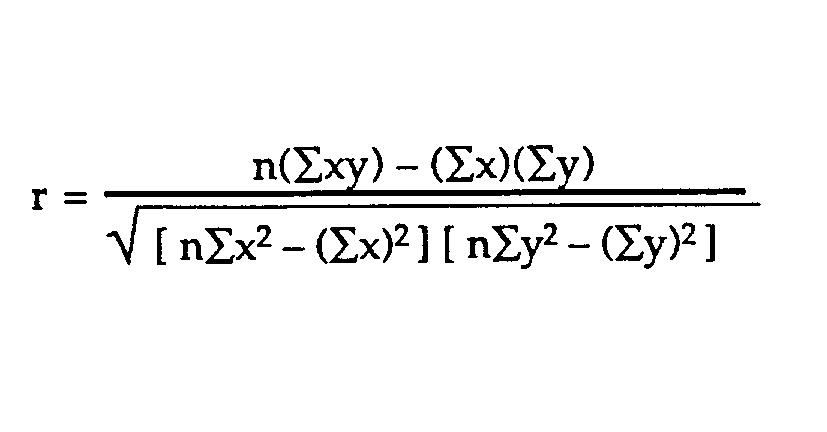 The formulas return a value between -1 and 1, where: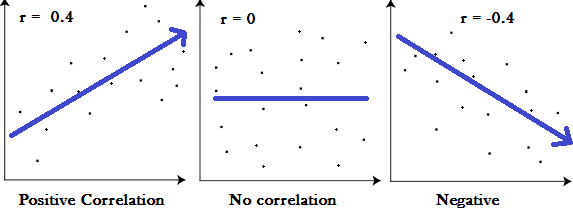 1 : A correlation coefficient of 1 means that for every positive increase in one variable, there is a positive increase of a fixed proportion in the other. For example, shoe sizes go up in (almost) perfect correlation with foot length. -1: A correlation coefficient of -1 means that for every positive increase in one variable, there is a negative decrease of a fixed proportion in the other. For example, the amount of gas in a tank decreases in (almost) perfect correlation with speed. 0 : Zero means that for every increase, there isn’t a positive or negative increase. The two just aren’t related. Example 1: Let's have a look at the Problem 1 from Exam II We had a table of recoded times and speeds from some experimental observations:|Elapsed Time (s)|Speed (m/s)||---:|---:||0 |0||1.0 |3||2.0 |7||3.0 |12||4.0 |20||5.0 |30||6.0 | 45.6| |7.0 | 60.3 ||8.0 | 77.7 ||9.0 | 97.3 ||10.0| 121.1| First let's create a dataframe: | # Load the necessary packages
import numpy as np
import pandas as pd
import statistics
from matplotlib import pyplot as plt
# Create a dataframe:
time = [0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0]
speed = [0, 3, 7, 12, 20, 30, 45.6, 60.3, 77.7, 97.3, 121.2]
data = pd.DataFrame({'Time':time, 'Speed':speed})
data | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
Now, let's explore the data: | data.describe()
time_var = statistics.variance(time)
speed_var = statistics.variance(speed)
print("Variance of recorded times is ",time_var)
print("Variance of recorded times is ",speed_var) | Variance of recorded times is 11.0
Variance of recorded times is 1697.7759999999998
| CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
Is there a relationship ( based on covariance, correlation) between time and speed? | # To find the covariance
data.cov()
# To find the correlation among the columns
# using pearson method
data.corr(method ='pearson') | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
Let's do linear regression with primitive Python: To estimate "y" using the OLS method, we need to calculate "xmean" and "ymean", the covariance of X and y ("xycov"), and the variance of X ("xvar") before we can determine the values for alpha and beta. In our case, X is time and y is Speed. | # Calculate the mean of X and y
xmean = np.mean(time)
ymean = np.mean(speed)
# Calculate the terms needed for the numator and denominator of beta
data['xycov'] = (data['Time'] - xmean) * (data['Speed'] - ymean)
data['xvar'] = (data['Time'] - xmean)**2
# Calculate beta and alpha
beta = data['xycov'].sum() / data['xvar'].sum()
alpha = ymean - (beta * xmean)
print(f'alpha = {alpha}')
print(f'beta = {beta}')
| alpha = -16.78636363636363
beta = 11.977272727272727
| CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
We now have an estimate for alpha and beta! Our model can be written as Yₑ = 11.977 X -16.786, and we can make predictions: | X = np.array(time)
ypred = alpha + beta * X
print(ypred) | [-16.78636364 -4.80909091 7.16818182 19.14545455 31.12272727
43.1 55.07727273 67.05454545 79.03181818 91.00909091
102.98636364]
| CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
Let’s plot our prediction ypred against the actual values of y, to get a better visual understanding of our model: | # Plot regression against actual data
plt.figure(figsize=(12, 6))
plt.plot(X, ypred, color="red") # regression line
plt.plot(time, speed, 'ro', color="blue") # scatter plot showing actual data
plt.title('Actual vs Predicted')
plt.xlabel('Time (s)')
plt.ylabel('Speed (m/s)')
plt.show() | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
The red line is our line of best fit, Yₑ = 11.977 X -16.786. We can see from this graph that there is a positive linear relationship between X and y. Using our model, we can predict y from any values of X! For example, if we had a value X = 20, we can predict that: | ypred_20 = alpha + beta * 20
print(ypred_20) | 222.7590909090909
| CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
Linear Regression with statsmodels: First, we use statsmodels’ ols function to initialise our simple linear regression model. This takes the formula y ~ X, where X is the predictor variable (Time) and y is the output variable (Speed). Then, we fit the model by calling the OLS object’s fit() method. | import statsmodels.formula.api as smf
# Initialise and fit linear regression model using `statsmodels`
model = smf.ols('Speed ~ Time', data=data)
model = model.fit() | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
We no longer have to calculate alpha and beta ourselves as this method does it automatically for us! Calling model.params will show us the model’s parameters: | model.params | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
In the notation that we have been using, α is the intercept and β is the slope i.e. α =-16.786364 and β = 11.977273. | # Predict values
speed_pred = model.predict()
# Plot regression against actual data
plt.figure(figsize=(12, 6))
plt.plot(data['Time'], data['Speed'], 'o') # scatter plot showing actual data
plt.plot(data['Time'], speed_pred, 'r', linewidth=2) # regression line
plt.xlabel('Time (s)')
plt.ylabel('Speed (m/s)')
plt.title('model vs observed')
plt.show() | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
How good do you feel about this predictive model? Will you trust it? Example 2: Advertising and Sells! This is a classic regression problem. we have a dataset of the spendings on TV, Radio, and Newspaper advertisements and number of sales for a specific product. We are interested in exploring the relationship between these parameters and answering the following questions:- Can TV advertising spending predict the number of sales for the product?- Can Radio advertising spending predict the number of sales for the product?- Can Newspaper advertising spending predict the number of sales for the product?- Can we use the three of them to predict the number of sales for the product? | Multiple Linear Regression Model- Which parameter is a better predictor of the number of sales for the product? | # Import and display first rows of the advertising dataset
df = pd.read_csv('advertising.csv')
df.head()
# Describe the df
df.describe()
tv = np.array(df['TV'])
radio = np.array(df['Radio'])
newspaper = np.array(df['Newspaper'])
newspaper = np.array(df['Sales'])
# Get Variance and Covariance - What can we infer?
df.cov()
# Get Correlation Coefficient - What can we infer?
df.corr(method ='pearson')
# Answer the first question: Can TV advertising spending predict the number of sales for the product?
import statsmodels.formula.api as smf
# Initialise and fit linear regression model using `statsmodels`
model = smf.ols('Sales ~ TV', data=df)
model = model.fit()
print(model.params)
# Predict values
TV_pred = model.predict()
# Plot regression against actual data - What do we see?
plt.figure(figsize=(12, 6))
plt.plot(df['TV'], df['Sales'], 'o') # scatter plot showing actual data
plt.plot(df['TV'], TV_pred, 'r', linewidth=2) # regression line
plt.xlabel('TV advertising spending')
plt.ylabel('Sales')
plt.title('Predicting with TV spendings only')
plt.show()
# Answer the second question: Can Radio advertising spending predict the number of sales for the product?
import statsmodels.formula.api as smf
# Initialise and fit linear regression model using `statsmodels`
model = smf.ols('Sales ~ Radio', data=df)
model = model.fit()
print(model.params)
# Predict values
RADIO_pred = model.predict()
# Plot regression against actual data - What do we see?
plt.figure(figsize=(12, 6))
plt.plot(df['Radio'], df['Sales'], 'o') # scatter plot showing actual data
plt.plot(df['Radio'], RADIO_pred, 'r', linewidth=2) # regression line
plt.xlabel('Radio advertising spending')
plt.ylabel('Sales')
plt.title('Predicting with Radio spendings only')
plt.show()
# Answer the third question: Can Newspaper advertising spending predict the number of sales for the product?
import statsmodels.formula.api as smf
# Initialise and fit linear regression model using `statsmodels`
model = smf.ols('Sales ~ Newspaper', data=df)
model = model.fit()
print(model.params)
# Predict values
NP_pred = model.predict()
# Plot regression against actual data - What do we see?
plt.figure(figsize=(12, 6))
plt.plot(df['Newspaper'], df['Sales'], 'o') # scatter plot showing actual data
plt.plot(df['Newspaper'], NP_pred, 'r', linewidth=2) # regression line
plt.xlabel('Newspaper advertising spending')
plt.ylabel('Sales')
plt.title('Predicting with Newspaper spendings only')
plt.show()
# Answer the fourth question: Can we use the three of them to predict the number of sales for the product?
# This is a case of multiple linear regression model. This is simply a linear regression model with more than one predictor:
# and is modelled by: Yₑ = α + β₁X₁ + β₂X₂ + … + βₚXₚ , where p is the number of predictors.
# In this case: Sales = α + β1*TV + β2*Radio + β3*Newspaper
# Multiple Linear Regression with scikit-learn:
from sklearn.linear_model import LinearRegression
# Build linear regression model using TV,Radio and Newspaper as predictors
# Split data into predictors X and output Y
predictors = ['TV', 'Radio', 'Newspaper']
X = df[predictors]
y = df['Sales']
# Initialise and fit model
lm = LinearRegression()
model = lm.fit(X, y)
print(f'alpha = {model.intercept_}')
print(f'betas = {model.coef_}')
# Therefore, our model can be written as:
#Sales = 2.938 + 0.046*TV + 0.1885*Radio -0.001*Newspaper
# we can predict sales from any combination of TV and Radio and Newspaper advertising costs!
#For example, if we wanted to know how many sales we would make if we invested
# $300 in TV advertising and $200 in Radio advertising and $50 in Newspaper advertising
#all we have to do is plug in the values:
new_X = [[300, 200,50]]
print(model.predict(new_X))
# Answer the final question : Which parameter is a better predictor of the number of sales for the product?
# How can we answer that?
# WHAT CAN WE INFER FROM THE BETAs ?
| _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
 *This notebook was inspired by a several blogposts including:* - __"Introduction to Linear Regression in Python"__ by __Lorraine Li__ available at* https://towardsdatascience.com/introduction-to-linear-regression-in-python-c12a072bedf0 - __"In Depth: Linear Regression"__ available at* https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html - __"A friendly introduction to linear regression (using Python)"__ available at* https://www.dataschool.io/linear-regression-in-python/ *Here are some great reads on linear regression:* - __"Linear Regression in Python"__ by __Sadrach Pierre__ available at* https://towardsdatascience.com/linear-regression-in-python-a1d8c13f3242 - __"Introduction to Linear Regression in Python"__ available at* https://cmdlinetips.com/2019/09/introduction-to-linear-regression-in-python/ - __"Linear Regression in Python"__ by __Mirko Stojiljković__ available at* https://realpython.com/linear-regression-in-python/ *Here are some great videos on linear regression:* - __"StatQuest: Fitting a line to data, aka least squares, aka linear regression."__ by __StatQuest with Josh Starmer__ available at* https://www.youtube.com/watch?v=PaFPbb66DxQ&list=PLblh5JKOoLUIzaEkCLIUxQFjPIlapw8nU - __"Statistics 101: Linear Regression, The Very Basics"__ by __Brandon Foltz__ available at* https://www.youtube.com/watch?v=ZkjP5RJLQF4 - __"How to Build a Linear Regression Model in Python | Part 1" and 2,3,4!__ by __Sigma Coding__ available at* https://www.youtube.com/watch?v=MRm5sBfdBBQ Exercise 1: In the "CarsDF.csv" file, you will find a dataset with information about cars and motorcycles including thier age, kilometers driven (mileage), fuel economy, enginer power, engine volume, and selling price. Follow the steps and answer the questions. - Step1: Read the "CarsDF.csv" file as a dataframe. Explore the dataframe and in a markdown cell breifly describe it in your own words. - Step2: Calculate and compare the correlation coefficient of the "selling price" with all the other parameters (execpt for "name", of course!). In a markdown cell, explain the results and state which parameters have the strongest and weakest relationship with "selling price" of a vehicle. - Step3: Use linear regression modeling in primitive python and VISUALLY assess the quality of a linear fit with Age as the predictor, and selling price as outcome. Explain the result of this analysis in a markdown cell.- Step4: Use linear regression modeling with statsmodels and VISUALLY assess the quality of a linear fit with fuel economy as the predictor, and selling price as outcome. Explain the result of this analysis in a markdown cell.- Step5: Use linear regression modeling with statsmodels and VISUALLY assess the quality of a linear fit with engine volume as the predictor, and selling price as outcome. Explain the result of this analysis in a markdown cell.- Step6: In a markdown cell, explain which of the three predictors in steps 3,4, and 5, was a better predictor (resulted in a better fit ) for selling price?- Step7: Use multiple linear regression modeling with scikit-learn and use all the parameters (execpt for "name", of course!) to predict selling price. Then, use this model to predict the selling price of a car that has the following charactristics and decide whether this prediction is reliable in your opinion: - 2 years old - has gone 17000 km - has fuel economy measure of 24.2 kmpl - has an engine power of 74 bhp - has en engine volume of 1260 CC | # Step1:
vdf = pd.read_csv('CarsDF.csv')
vdf.head()
vdf.describe() | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
On Step1: [Double-Click to edit] | # Step2:.
vdf.corr() | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
On Step2: [Double-Click to edit] | #Step3:
# Calculate the mean of X and y
xmean = np.mean(vdf['Age'])
ymean = np.mean(vdf['selling_price'])
# Calculate the terms needed for the numator and denominator of beta
vdf['xycov'] = (vdf['Age'] - xmean) * (vdf['selling_price'] - ymean)
vdf['xvar'] = (vdf['Age'] - xmean)**2
# Calculate beta and alpha
beta = vdf['xycov'].sum() / vdf['xvar'].sum()
alpha = ymean - (beta * xmean)
print(f'alpha = {alpha}')
print(f'beta = {beta}')
X = np.array(vdf['Age'])
Y = np.array(vdf['selling_price'])
ypred = alpha + beta * X
# Plot regression against actual data
plt.figure(figsize=(12, 6))
plt.plot(X, Y, 'ro', color="blue") # scatter plot showing actual data
plt.plot(X, ypred, color="red") # regression line
plt.title('Actual vs Predicted')
plt.xlabel('Age')
plt.ylabel('selling price')
plt.show() | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
On Step3: [Double-Click to edit] | # Step4:
import statsmodels.formula.api as smf
# Initialise and fit linear regression model using `statsmodels`
model = smf.ols('selling_price ~ FuelEconomy_kmpl', data=vdf)
model = model.fit()
model.params
# Predict values
FE_pred = model.predict()
# Plot regression against actual data
plt.figure(figsize=(12, 6))
plt.plot(vdf['FuelEconomy_kmpl'], vdf['selling_price'], 'o') # scatter plot showing actual data
plt.plot(vdf['FuelEconomy_kmpl'], FE_pred, 'r', linewidth=2) # regression line
plt.xlabel('FuelEconomy_kmpl')
plt.ylabel('selling price')
plt.title('model vs observed')
plt.show() | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
On Step4: [Double-Click to edit] | # Step5:
import statsmodels.formula.api as smf
# Initialise and fit linear regression model using `statsmodels`
model = smf.ols('selling_price ~ engine_v', data=vdf)
model = model.fit()
model.params
# Predict values
EV_pred = model.predict()
# Plot regression against actual data
plt.figure(figsize=(12, 6))
plt.plot(vdf['engine_v'], vdf['selling_price'], 'o') # scatter plot showing actual data
plt.plot(vdf['engine_v'], EV_pred, 'r', linewidth=2) # regression line
plt.xlabel('engine_v')
plt.ylabel('selling price')
plt.title('model vs observed')
plt.show() | _____no_output_____ | CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
On Step5: [Double-Click to edit] On Step6: [Double-Click to edit] | #Step7:
# Multiple Linear Regression with scikit-learn:
from sklearn.linear_model import LinearRegression
# Build linear regression model using TV,Radio and Newspaper as predictors
# Split data into predictors X and output Y
predictors = ['Age', 'km_driven', 'FuelEconomy_kmpl','engine_p','engine_v']
X = vdf[predictors]
y = vdf['selling_price']
# Initialise and fit model
lm = LinearRegression()
model = lm.fit(X, y)
print(f'alpha = {model.intercept_}')
print(f'betas = {model.coef_}')
new_X = [[2, 17000,24.2,74,1260]]
print(model.predict(new_X))
| [900102.89014124]
| CC0-1.0 | 1-Lessons/Lesson19/Lab19/.src/Lab19_WS.ipynb | dustykat/engr-1330-psuedo-course |
Import packages | import os
import sys
import time
from datetime import datetime
import GPUtil
import psutil
#######################
# run after two days
# time.sleep(172800)
#######################
os.environ["CUDA_VISIBLE_DEVICES"] = "0,1,2,3"
sys.path.append("../")
def gpu_free(max_gb):
gpu_id = GPUtil.getFirstAvailable(
order="memory"
) # get the fist gpu with the lowest load
GPU = GPUtil.getGPUs()[gpu_id[0]]
GPU_load = GPU.load * 100
GPU_memoryUtil = GPU.memoryUtil / 2.0 ** 10
GPU_memoryTotal = GPU.memoryTotal / 2.0 ** 10
GPU_memoryUsed = GPU.memoryUsed / 2.0 ** 10
GPU_memoryFree = GPU.memoryFree / 2.0 ** 10
print(
"-- total_GPU_memory: %.3fGB;init_GPU_memoryFree:%.3fGB init_GPU_load:%.3f%% GPU_memoryUtil:%d%% GPU_memoryUsed:%.3fGB"
% (GPU_memoryTotal, GPU_memoryFree, GPU_load, GPU_memoryUtil, GPU_memoryUsed)
)
if GPU_memoryFree > max_gb:
return True
return False
def memery_free(max_gb):
available_memory = psutil.virtual_memory().free / 2.0 ** 30
if available_memory > max_gb:
return True
return False
for item_fea_type in [
"random",
"cate",
"cate_word2vec",
"cate_bert",
"cate_one_hot",
"random_word2vec",
"random_bert",
"random_one_hot",
"random_bert_word2vec_one_hot",
"random_cate_word2vec",
"random_cate_bert",
"random_cate_one_hot",
"random_cate_bert_word2vec_one_hot",
]:
while True:
if gpu_free(4) and memery_free(10):
os.environ["CUDA_VISIBLE_DEVICES"] = "0,1,2,3"
gpu_id = GPUtil.getAvailable(order="memory", limit=4)[
0
] # get the fist gpu with the lowest load
print("GPU memery and main memery availale, start a job")
date_time = datetime.now().strftime("%Y_%m_%d_%H_%M_%S")
command = f"CUDA_VISIBLE_DEVICES=0,1,2,3; /home/zm324/anaconda3/envs/beta_rec/bin/python run_tvbr.py --item_fea_type {item_fea_type} --device cuda:{gpu_id} >> ./logs/{date_time}_{item_fea_type}.log &"
os.system(command)
time.sleep(120)
break
else:
print("GPU not availale, sleep for 10 min")
time.sleep(600)
continue | -- total_GPU_memory: 10.761GB;init_GPU_memoryFree:10.760GB init_GPU_load:0.000% GPU_memoryUtil:0% GPU_memoryUsed:0.001GB
GPU memery and main memery availale, start a job
-- total_GPU_memory: 10.761GB;init_GPU_memoryFree:10.757GB init_GPU_load:0.000% GPU_memoryUtil:0% GPU_memoryUsed:0.004GB
GPU memery and main memery availale, start a job
| MIT | demo_control_side_sep_16.ipynb | mengzaiqiao/TVBR |
Checking whether the files are scanned images or true pdfs | def is_image(file_path):
with open(file_path, "rb") as f:
return pdftotext.PDF(f)
print(is_image(filename)) | _____no_output_____ | FTL | tasks/extract_text/notebooks/text_preprocessing_jordi.ipynb | jordiplanascuchi/policy-data-analyzer |
Converting pdf to image files and improving quality | def get_image1(file_path):
"""Get image out of pdf file_path. Splits pdf file into PIL images of each of its pages.
"""
return convert_from_path(file_path, 500)
# Performance tips according to pdf2image:
# Using an output folder is significantly faster if you are using an SSD. Otherwise i/o usually becomes the bottleneck.
# Using multiple threads can give you some gains but avoid more than 4 as this will cause i/o bottleneck (even on my NVMe SSD!).
pages = get_image1(filepaths[0])
display(pages[0]) | _____no_output_____ | FTL | tasks/extract_text/notebooks/text_preprocessing_jordi.ipynb | jordiplanascuchi/policy-data-analyzer |
What can we do here to improve image quality? It already seems pretty good! Evaluating extraction time from each method and saving text to disk | def export_ocr(text, file, extract, out=out_path):
""" Export ocr output text using extract method to file at out
"""
filename = f'{os.path.splitext(os.path.basename(file))[0]}_{extract}.txt'
with open(os.path.join(out, filename), 'w') as the_file:
the_file.write(text)
def wrap_pagenum(page_text, page_num):
""" Wrap page_text with page_num tag
"""
return f"<p n={page_num}>" + page_text + "</p>"
# pytesseract extraction
start_time = time.time()
for file in filepaths:
pages = get_image1(file)
text = ""
for pageNum, imgBlob in enumerate(pages):
page_text = pytesseract.image_to_string(imgBlob, lang="spa")
text += wrap_pagenum(page_text, pageNum)
export_ocr(text, file, "pytesseract") # write extracted text to disk
print("--- %s seconds ---" % (time.time() - start_time))
# tesserocr extraction
start_time = time.time()
for file in filepaths:
pages = get_image1(file)
text = ""
for pageNum, imgBlob in enumerate(pages):
page_text = tesserocr.image_to_text(imgBlob, lang="spa")
text += wrap_pagenum(page_text, pageNum)
export_ocr(text, file, "tesserocr") # write extracted text to disk
print("--- %s seconds ---" % (time.time() - start_time))
# tesserocr extraction using the PyTessBaseAPI
start_time = time.time()
for file in filepaths:
pages = get_image1(file)
text = ""
with tesserocr.PyTessBaseAPI(lang="spa") as api:
for pageNum, imgBlob in enumerate(pages):
api.SetImage(imgBlob)
page_text = api.GetUTF8Text()
text += wrap_pagenum(page_text, pageNum)
export_ocr(text, file, "tesserocr_pytess") # write extracted text to disk
print("--- %s seconds ---" % (time.time() - start_time)) | _____no_output_____ | FTL | tasks/extract_text/notebooks/text_preprocessing_jordi.ipynb | jordiplanascuchi/policy-data-analyzer |
It seems that the pytesseract package provides the fastest extraction and by looking at the extracted text it doesn't seem to exist any difference in the output of all the tested methods. | # comparison between text extracted by the different methods
os.listdir(out_path)
# TODO: perform a more programatical comparison between extracted texts | _____no_output_____ | FTL | tasks/extract_text/notebooks/text_preprocessing_jordi.ipynb | jordiplanascuchi/policy-data-analyzer |
Let's look at the extracted text | with open(os.path.join(out_path, 'Decreto_ejecutivo_57_pytesseract.txt')) as text:
extracted_text = text.read()
extracted_text
# Replace \x0c (page break) by \n
# Match 1 or more occurrences of \n if preceeded by one occurrence of \n OR
# Match 1 or more occurrences of \s (whitespace) if preceeded by one occurrence of \n OR
# Match one occurrence of \n if it isn't followed by \n
print(re.sub("(?<=\n)\n+|(?<=\n)\s+|\n(?!\n)", " ", extracted_text.replace("\x0c", "\n"))) | _____no_output_____ | FTL | tasks/extract_text/notebooks/text_preprocessing_jordi.ipynb | jordiplanascuchi/policy-data-analyzer |
CS109A Introduction to Data Science Standard Section 3: Multiple Linear Regression and Polynomial Regression **Harvard University****Fall 2019****Instructors**: Pavlos Protopapas, Kevin Rader, and Chris Tanner**Section Leaders**: Marios Mattheakis, Abhimanyu (Abhi) Vasishth, Robbert (Rob) Struyven | #RUN THIS CELL
import requests
from IPython.core.display import HTML
styles = requests.get("http://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/cs109.css").text
HTML(styles) | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
For this section, our goal is to get you familiarized with Multiple Linear Regression. We have learned how to model data with kNN Regression and Simple Linear Regression and our goal now is to dive deep into Linear Regression.Specifically, we will: - Load in the titanic dataset from seaborn- Learn a few ways to plot **distributions** of variables using seaborn- Learn about different **kinds of variables** including continuous, categorical and ordinal- Perform single and multiple linear regression- Learn about **interaction** terms- Understand how to **interpret coefficients** in linear regression- Look at **polynomial** regression- Understand the **assumptions** being made in a linear regression model- (Extra): look at some cool plots to raise your EDA game  | # Data and Stats packages
import numpy as np
import pandas as pd
# Visualization packages
import matplotlib.pyplot as plt
import seaborn as sns
sns.set() | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Extending Linear Regression Working with the Titanic Dataset from SeabornFor our dataset, we'll be using the passenger list from the Titanic, which famously sank in 1912. Let's have a look at the data. Some descriptions of the data are at https://www.kaggle.com/c/titanic/data, and here's [how seaborn preprocessed it](https://github.com/mwaskom/seaborn-data/blob/master/process/titanic.py).The task is to build a regression model to **predict the fare**, based on different attributes.Let's keep a subset of the data, which includes the following variables: - age- sex- class- embark_town- alone- **fare** (the response variable) | # Load the dataset from seaborn
titanic = sns.load_dataset("titanic")
titanic.head()
# checking for null values
chosen_vars = ['age', 'sex', 'class', 'embark_town', 'alone', 'fare']
titanic = titanic[chosen_vars]
titanic.info() | <class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 6 columns):
age 714 non-null float64
sex 891 non-null object
class 891 non-null category
embark_town 889 non-null object
alone 891 non-null bool
fare 891 non-null float64
dtypes: bool(1), category(1), float64(2), object(2)
memory usage: 29.8+ KB
| MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
**Exercise**: check the datatypes of each column and display the statistics (min, max, mean and any others) for all the numerical columns of the dataset. | ## your code here
# %load 'solutions/sol1.py'
print(titanic.dtypes)
titanic.describe() | age float64
sex object
class category
embark_town object
alone bool
fare float64
dtype: object
| MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
**Exercise**: drop all the non-null *rows* in the dataset. Is this always a good idea? | ## your code here
# %load 'solutions/sol2.py'
titanic = titanic.dropna(axis=0)
titanic.info() | <class 'pandas.core.frame.DataFrame'>
Int64Index: 712 entries, 0 to 890
Data columns (total 6 columns):
age 712 non-null float64
sex 712 non-null object
class 712 non-null category
embark_town 712 non-null object
alone 712 non-null bool
fare 712 non-null float64
dtypes: bool(1), category(1), float64(2), object(2)
memory usage: 29.3+ KB
| MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Now let us visualize the response variable. A good visualization of the distribution of a variable will enable us to answer three kinds of questions:- What values are central or typical? (e.g., mean, median, modes)- What is the typical spread of values around those central values? (e.g., variance/stdev, skewness)- What are unusual or exceptional values (e.g., outliers) | fig, ax = plt.subplots(1, 3, figsize=(24, 6))
ax = ax.ravel()
sns.distplot(titanic['fare'], ax=ax[0])
# use seaborn to draw distributions
ax[0].set_title('Seaborn distplot')
ax[0].set_ylabel('Normalized frequencies')
sns.violinplot(x='fare', data=titanic, ax=ax[1])
ax[1].set_title('Seaborn violin plot')
ax[1].set_ylabel('Frequencies')
sns.boxplot(x='fare', data=titanic, ax=ax[2])
ax[2].set_title('Seaborn box plot')
ax[2].set_ylabel('Frequencies')
fig.suptitle('Distribution of count'); | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
How do we interpret these plots? Train-Test Split | from sklearn.model_selection import train_test_split
titanic_train, titanic_test = train_test_split(titanic, train_size=0.7, random_state=99)
titanic_train = titanic_train.copy()
titanic_test = titanic_test.copy()
print(titanic_train.shape, titanic_test.shape) | (498, 6) (214, 6)
| MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Simple one-variable OLS **Exercise**: You've done this before: make a simple model using the OLS package from the statsmodels library predicting **fare** using **age** using the training data. Name your model `model_1` and display the summary | from statsmodels.api import OLS
import statsmodels.api as sm
# Your code here
# %load 'solutions/sol3.py'
age_ca = sm.add_constant(titanic_train['age'])
model_1 = OLS(titanic_train['fare'], age_ca).fit()
model_1.summary() | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Dealing with different kinds of variables In general, you should be able to distinguish between three kinds of variables: 1. Continuous variables: such as `fare` or `age`2. Categorical variables: such as `sex` or `alone`. There is no inherent ordering between the different values that these variables can take on. These are sometimes called nominal variables. Read more [here](https://stats.idre.ucla.edu/other/mult-pkg/whatstat/what-is-the-difference-between-categorical-ordinal-and-interval-variables/). 3. Ordinal variables: such as `class` (first > second > third). There is some inherent ordering of the values in the variables, but the values are not continuous either. *Note*: While there is some inherent ordering in `class`, we will be treating it like a categorical variable. | titanic_orig = titanic_train.copy() | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Let us now examine the `sex` column and see the value counts. | titanic_train['sex'].value_counts() | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
**Exercise**: Create a column `sex_male` that is 1 if the passenger is male, 0 if female. The value counts indicate that these are the two options in this particular dataset. Ensure that the datatype is `int`. | # your code here
# %load 'solutions/sol4.py'
# functions that help us create a dummy variable
stratify
titanic_train['sex_male'].value_counts() | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Do we need a `sex_female` column, or a `sex_others` column? Why or why not?Now, let us look at `class` in greater detail. | titanic_train['class_Second'] = (titanic_train['class'] == 'Second').astype(int)
titanic_train['class_Third'] = 1 * (titanic_train['class'] == 'Third') # just another way to do it
titanic_train.info()
# This function automates the above:
titanic_train_copy = pd.get_dummies(titanic_train, columns=['sex', 'class'], drop_first=True)
titanic_train_copy.head() | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Linear Regression with More Variables **Exercise**: Fit a linear regression including the new sex and class variables. Name this model `model_2`. Don't forget the constant! | # your code here
# %load 'solutions/sol5.py'
model_2 = sm.OLS(titanic_train['fare'],
sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third']])).fit()
model_2.summary() | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Interpreting These Results 1. Which of the predictors do you think are important? Why?2. All else equal, what does being male do to the fare? Going back to the example from class3. What is the interpretation of $\beta_0$ and $\beta_1$? Exploring Interactions | sns.lmplot(x="age", y="fare", hue="sex", data=titanic_train, size=6) | /anaconda3/envs/109a/lib/python3.7/site-packages/seaborn/regression.py:546: UserWarning: The `size` paramter has been renamed to `height`; please update your code.
warnings.warn(msg, UserWarning)
| MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
The slopes seem to be different for male and female. What does that indicate?Let us now try to add an interaction effect into our model. | # It seemed like gender interacted with age and class. Can we put that in our model?
titanic_train['sex_male_X_age'] = titanic_train['age'] * titanic_train['sex_male']
model_3 = sm.OLS(
titanic_train['fare'],
sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age']])
).fit()
model_3.summary() | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
**What happened to the `age` and `male` terms?** | # It seemed like gender interacted with age and class. Can we put that in our model?
titanic_train['sex_male_X_class_Second'] = titanic_train['age'] * titanic_train['class_Second']
titanic_train['sex_male_X_class_Third'] = titanic_train['age'] * titanic_train['class_Third']
model_4 = sm.OLS(
titanic_train['fare'],
sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age',
'sex_male_X_class_Second', 'sex_male_X_class_Third']])
).fit()
model_4.summary() | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Polynomial Regression  Perhaps we now believe that the fare also depends on the square of age. How would we include this term in our model? | fig, ax = plt.subplots(figsize=(12,6))
ax.plot(titanic_train['age'], titanic_train['fare'], 'o')
x = np.linspace(0,80,100)
ax.plot(x, x, '-', label=r'$y=x$')
ax.plot(x, 0.04*x**2, '-', label=r'$y=c x^2$')
ax.set_title('Plotting Age (x) vs Fare (y)')
ax.set_xlabel('Age (x)')
ax.set_ylabel('Fare (y)')
ax.legend(); | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
**Exercise**: Create a model that predicts fare from all the predictors in `model_4` + the square of age. Show the summary of this model. Call it `model_5`. Remember to use the training data, `titanic_train`. | # your code here
# %load 'solutions/sol6.py'
titanic_train['age^2'] = titanic_train['age'] **2
model_5 = sm.OLS(
titanic_train['fare'],
sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age',
'sex_male_X_class_Second', 'sex_male_X_class_Third', 'age^2']])
).fit()
model_5.summary() | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Looking at All Our Models: Model Selection What has happened to the $R^2$ as we added more features? Does this mean that the model is better? (What if we kept adding more predictors and interaction terms? **In general, how should we choose a model?** We will spend a lot more time on model selection and learn about ways to do so as the course progresses. | models = [model_1, model_2, model_3, model_4, model_5]
fig, ax = plt.subplots(figsize=(12,6))
ax.plot([model.df_model for model in models], [model.rsquared for model in models], 'x-')
ax.set_xlabel("Model degrees of freedom")
ax.set_title('Model degrees of freedom vs training $R^2$')
ax.set_ylabel("$R^2$"); | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
**What about the test data?**We added a lot of columns to our training data and must add the same to our test data in order to calculate $R^2$ scores. | # Added features for model 1
# Nothing new to be added
# Added features for model 2
titanic_test = pd.get_dummies(titanic_test, columns=['sex', 'class'], drop_first=True)
# Added features for model 3
titanic_test['sex_male_X_age'] = titanic_test['age'] * titanic_test['sex_male']
# Added features for model 4
titanic_test['sex_male_X_class_Second'] = titanic_test['age'] * titanic_test['class_Second']
titanic_test['sex_male_X_class_Third'] = titanic_test['age'] * titanic_test['class_Third']
# Added features for model 5
titanic_test['age^2'] = titanic_test['age'] **2 | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
**Calculating R^2 scores** | from sklearn.metrics import r2_score
r2_scores = []
y_preds = []
y_true = titanic_test['fare']
# model 1
y_preds.append(model_1.predict(sm.add_constant(titanic_test['age'])))
# model 2
y_preds.append(model_2.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second', 'class_Third']])))
# model 3
y_preds.append(model_3.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second', 'class_Third',
'sex_male_X_age']])))
# model 4
y_preds.append(model_4.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second', 'class_Third',
'sex_male_X_age', 'sex_male_X_class_Second',
'sex_male_X_class_Third']])))
# model 5
y_preds.append(model_5.predict(sm.add_constant(titanic_test[['age', 'sex_male', 'class_Second',
'class_Third', 'sex_male_X_age',
'sex_male_X_class_Second',
'sex_male_X_class_Third', 'age^2']])))
for y_pred in y_preds:
r2_scores.append(r2_score(y_true, y_pred))
models = [model_1, model_2, model_3, model_4, model_5]
fig, ax = plt.subplots(figsize=(12,6))
ax.plot([model.df_model for model in models], r2_scores, 'x-')
ax.set_xlabel("Model degrees of freedom")
ax.set_title('Model degrees of freedom vs test $R^2$')
ax.set_ylabel("$R^2$"); | /anaconda3/envs/109a/lib/python3.7/site-packages/numpy/core/fromnumeric.py:2389: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead.
return ptp(axis=axis, out=out, **kwargs)
| MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Regression Assumptions. Should We Even Regress Linearly?  **Question**: What are the assumptions of a linear regression model? We find that the answer to this question can be found on closer examimation of $\epsilon$. What is $\epsilon$? It is assumed that $\epsilon$ is normally distributed with a mean of 0 and variance $\sigma^2$. But what does this tell us?1. Assumption 1: Constant variance of $\epsilon$ errors. This means that if we plot our **residuals**, which are the differences between the true $Y$ and our predicted $\hat{Y}$, they should look like they have constant variance and a mean of 0. We will show this in our plots.2. Assumption 2: Independence of $\epsilon$ errors. This again comes from the distribution of $\epsilon$ that we decide beforehand.3. Assumption 3: Linearity. This is an implicit assumption as we claim that Y can be modeled through a linear combination of the predictors. **Important Note:** Even though our predictors, for instance $X_2$, can be created by squaring or cubing another variable, we still use them in a linear equation as shown above, which is why polynomial regression is still a linear model.4. Assumption 4: Normality. We assume that the $\epsilon$ is normally distributed, and we can show this in a histogram of the residuals.**Exercise**: Calculate the residuals for model 5, our most recent model. Optionally, plot and histogram these residuals and check the assumptions of the model. | # your code here
# %load 'solutions/sol7.py'
# %load 'solutions/sol7.py'
predictors = sm.add_constant(titanic_train[['age', 'sex_male', 'class_Second', 'class_Third', 'sex_male_X_age',
'sex_male_X_class_Second', 'sex_male_X_class_Third', 'age^2']])
y_hat = model_5.predict(predictors)
residuals = titanic_train['fare'] - y_hat
# plotting
fig, ax = plt.subplots(ncols=2, figsize=(16,5))
ax = ax.ravel()
ax[0].set_title('Plot of Residuals')
ax[0].scatter(y_hat, residuals, alpha=0.2)
ax[0].set_xlabel(r'$\hat{y}$')
ax[0].set_xlabel('residuals')
ax[1].set_title('Histogram of Residuals')
ax[1].hist(residuals, alpha=0.7)
ax[1].set_xlabel('residuals')
ax[1].set_ylabel('frequency');
# Mean of residuals
print('Mean of residuals: {}'.format(np.mean(residuals))) | Mean of residuals: 4.784570776163707e-13
| MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
**What can you say about the assumptions of the model?** ---------------- End of Standard Section--------------- Extra: Visual exploration of predictors' correlationsThe dataset for this problem contains 10 simulated predictors and a response variable. | # read in the data
data = pd.read_csv('../data/dataset3.txt')
data.head()
# this effect can be replicated using the scatter_matrix function in pandas plotting
sns.pairplot(data); | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Predictors x1, x2, x3 seem to be perfectly correlated while predictors x4, x5, x6, x7 seem correlated. | data.corr()
sns.heatmap(data.corr()) | _____no_output_____ | MIT | content/sections/section3/notebook/cs109a_section_3.ipynb | lingcog/2019-CS109A |
Count all the words | wordcounter = Counter({})
words_per_video = []
for ann_idx, ann_file in enumerate(all_annotations):
file = open(ann_file, "r")
words = file.read().split()
file.close()
current_wordcounter = Counter(words)
wordcounter += current_wordcounter
words_per_video.append(len(words))
| _____no_output_____ | MIT | Get Stats.ipynb | jrterven/lip_reading_dataset |
Some stats | print("Number of words:", len(wordcounter))
print("10 most common words:")
print(wordcounter.most_common(10))
print("Max words in a video:", max(words_per_video))
print("Min words in a video:", min(words_per_video))
words_per_video_counter = Counter(words_per_video)
print(words_per_video_counter) | Counter({11: 762, 12: 746, 9: 662, 10: 650, 13: 643, 8: 602, 5: 601, 4: 592, 7: 570, 6: 549, 14: 524, 3: 513, 2: 438, 15: 380, 1: 329, 16: 267, 17: 179, 18: 92, 19: 35, 20: 21, 21: 15, 22: 8, 23: 2, 25: 1, 24: 1})
| MIT | Get Stats.ipynb | jrterven/lip_reading_dataset |
hp tuning | # LogisticRegression, L1
logreg = LogisticRegression(penalty='l1',solver='saga',random_state=0,max_iter=10000)
grid = {'C': np.logspace(-5, 5, 11)}
#predefined splits
#gs = GridSearchCV(logreg, grid, cv=ps.split(),scoring='accuracy')
gs = GridSearchCV(logreg, grid, cv=ps.split(),scoring=['roc_auc','average_precision'],refit='roc_auc')
gs.fit(all_cols[0], all_cols[1])
print(gs.best_params_)
print(gs.best_score_) #best cv score
df_gridsearch = pd.DataFrame(gs.cv_results_)
df_gridsearch.to_csv('model_hp_results/guideonly_gene20_075f_classi_LogisticRegression_L1_hp.csv')
# LogisticRegression, L2
logreg = LogisticRegression(penalty='l2',solver='saga',random_state=0,max_iter=10000)
grid = {'C': np.logspace(-5, 5, 11)}
#predefined splits
gs = GridSearchCV(logreg, grid, cv=ps.split(),scoring=['roc_auc','average_precision'],refit='roc_auc')
gs.fit(all_cols[0], all_cols[1])
print(gs.best_params_)
print(gs.best_score_) #best cv score
df_gridsearch = pd.DataFrame(gs.cv_results_)
df_gridsearch.to_csv('model_hp_results/guideonly_gene20_075f_classi_LogisticRegression_L2_hp.csv')
# LogisticRegression, elasticnet
logreg = LogisticRegression(penalty='elasticnet',solver='saga',random_state=0,max_iter=10000)
grid = {'C': np.logspace(-4, 4, 9),'l1_ratio':np.linspace(0.1, 1, num=10)}
gs = GridSearchCV(logreg, grid, cv=ps.split(),scoring=['roc_auc','average_precision'],refit='roc_auc')
gs.fit(all_cols[0], all_cols[1])
print(gs.best_params_)
print(gs.best_score_) #best cv score
df_gridsearch = pd.DataFrame(gs.cv_results_)
df_gridsearch.to_csv('model_hp_results/guideonly_gene20_075f_classi_LogisticRegression_elasticnet_hp.csv')
# https://www.programcreek.com/python/example/91158/sklearn.model_selection.GroupKFold
#random forest
clf = RandomForestClassifier(random_state=0)
grid = {'n_estimators':[100,200,400,800,1000,1200,1500],'max_features':['auto','sqrt','log2']}
gs = GridSearchCV(clf, grid, cv=GroupKFold(n_splits=5))
gs.fit(all_cols[0], all_cols[1], groups=groups)
#GradientBoostingClassifier
gb = ensemble.GradientBoostingClassifier(random_state=0)
grid = {'learning_rate':np.logspace(-2, 0, 3),'n_estimators':[100,200,400,800,1000,1200,1500],'max_depth':[2,3,4,8],'max_features':['auto','sqrt','log2']}
gs = GridSearchCV(gb, grid, cv=GroupKFold(n_splits=5))
gs.fit(all_cols[0], all_cols[1], groups=groups)
print(gs.best_score_) #best cv score
print(gs.best_params_)
df_gridsearch = pd.DataFrame(gs.cv_results_)
df_gridsearch.to_csv('linearmodel_hp_results/classi_gb_hp.csv') | _____no_output_____ | MIT | models/Linear_ensemble/hyperparameter tuning/linear model_new_classification-seq only.ipynb | jingyi7777/CasRx_guide_efficiency |
Test models | def classification_analysis(model_name, split, y_pred,y_true):
test_df = pd.DataFrame(list(zip(list(y_pred), list(y_true))),
columns =['predicted_value', 'true_binary_label'])
thres_list = [0.8, 0.9,0.95]
tp_thres = []
#print('thres_stats')
for thres in thres_list:
df_pre_good = test_df[test_df['predicted_value']>thres]
true_good_label = df_pre_good['true_binary_label'].values
num_real_gg = np.count_nonzero(true_good_label)
if len(true_good_label)>0:
gg_ratio = num_real_gg/len(true_good_label)
tp_thres.append(gg_ratio)
#print('true good guide percent '+str(gg_ratio))
else:
tp_thres.append('na')
outputs = np.array(y_pred)
labels = np.array(y_true)
#plt.clf()
#fig.suptitle('AUC and PRC')
score = roc_auc_score(labels, outputs)
fpr, tpr, _ = roc_curve(labels, outputs)
#print('AUROC '+str(score))
average_precision = average_precision_score(labels, outputs)
precision, recall, thres_prc = precision_recall_curve(labels, outputs)
#print('AUPRC '+str(average_precision))
#plt.savefig(fname='results/linear_models/'+str(model_name)+'precision-recall_'+str(split)+'.png',dpi=600,bbox_inches='tight')
return score,average_precision,tp_thres
#LogisticRegression, little regularization
logreg = LogisticRegression(penalty='l1',solver='saga',random_state=0,max_iter=10000,C=100000000)
auroc_l = []
auprc_l = []
tp_80 = []
tp_90 = []
for s in range(9):
#tr, val, te = create_gene_splits_kfold(dataframe['gene'].values, all_cols, 11, s)
tr, te = create_gene_splits_filter1_kfold_noval(dataframe['gene'].values, all_cols, 9, s)
# training input and output
d_input = tr[0]
d_output = tr[1]
logreg.fit(d_input, d_output) #fit models
#test set
xt = te[0]
#pred = logreg.predict(xt)
pred = logreg.predict_proba(xt)
pred = pred[:,1]
auroc,auprc,tp_thres = classification_analysis('LogisticRegression-L1', s,pred,te[1])
auroc_l.append(auroc)
auprc_l.append(auprc)
if tp_thres[0]!= 'na':
tp_80.append(tp_thres[0])
if tp_thres[1]!= 'na':
tp_90.append(tp_thres[1])
auroc_mean = statistics.mean(auroc_l)
auroc_sd = statistics.stdev(auroc_l)
print('auroc_mean: '+str(auroc_mean))
print('auroc_sd: '+str(auroc_sd))
auprc_mean = statistics.mean(auprc_l)
auprc_sd = statistics.stdev(auprc_l)
print('auprc_mean: '+str(auprc_mean))
print('auprc_sd: '+str(auprc_sd))
tp_80_mean = statistics.mean(tp_80)
tp_80_sd = statistics.stdev(tp_80)
print('tp_80_mean: '+str(tp_80_mean))
print('tp_80_sd: '+str(tp_80_sd))
tp_90_mean = statistics.mean(tp_90)
tp_90_sd = statistics.stdev(tp_90)
print('tp_90_mean: '+str(tp_90_mean))
print('tp_90_sd: '+str(tp_90_sd))
# LogisticRegression, L1
logreg = LogisticRegression(penalty='l1',solver='saga',random_state=0,max_iter=10000,C=0.1)
auroc_l = []
auprc_l = []
tp_80 = []
tp_90 = []
for s in range(9):
#tr, val, te = create_gene_splits_kfold(dataframe['gene'].values, all_cols, 11, s)
tr, te = create_gene_splits_filter1_kfold_noval(dataframe['gene'].values, all_cols, 9, s)
# training input and output
d_input = tr[0]
d_output = tr[1]
logreg.fit(d_input, d_output) #fit models
#test set
xt = te[0]
#pred = logreg.predict(xt)
pred = logreg.predict_proba(xt)
pred = pred[:,1]
auroc,auprc,tp_thres = classification_analysis('LogisticRegression-L1', s,pred,te[1])
auroc_l.append(auroc)
auprc_l.append(auprc)
if tp_thres[0]!= 'na':
tp_80.append(tp_thres[0])
if tp_thres[1]!= 'na':
tp_90.append(tp_thres[1])
auroc_mean = statistics.mean(auroc_l)
auroc_sd = statistics.stdev(auroc_l)
print('auroc_mean: '+str(auroc_mean))
print('auroc_sd: '+str(auroc_sd))
auprc_mean = statistics.mean(auprc_l)
auprc_sd = statistics.stdev(auprc_l)
print('auprc_mean: '+str(auprc_mean))
print('auprc_sd: '+str(auprc_sd))
tp_80_mean = statistics.mean(tp_80)
tp_80_sd = statistics.stdev(tp_80)
print('tp_80_mean: '+str(tp_80_mean))
print('tp_80_sd: '+str(tp_80_sd))
tp_90_mean = statistics.mean(tp_90)
tp_90_sd = statistics.stdev(tp_90)
print('tp_90_mean: '+str(tp_90_mean))
print('tp_90_sd: '+str(tp_90_sd))
# LogisticRegression, L2
logreg = LogisticRegression(penalty='l2',solver='saga',random_state=0,max_iter=10000,C=0.01)
auroc_l = []
auprc_l = []
tp_80 = []
tp_90 = []
for s in range(9):
#tr, val, te = create_gene_splits_kfold(dataframe['gene'].values, all_cols, 11, s)
tr, te = create_gene_splits_filter1_kfold_noval(dataframe['gene'].values, all_cols, 9, s)
# training input and output
d_input = tr[0]
d_output = tr[1]
logreg.fit(d_input, d_output) #fit models
#test set
xt = te[0]
#pred = logreg.predict(xt)
pred = logreg.predict_proba(xt)
pred = pred[:,1]
auroc,auprc,tp_thres = classification_analysis('LogisticRegression-L2', s,pred,te[1])
auroc_l.append(auroc)
auprc_l.append(auprc)
if tp_thres[0]!= 'na':
tp_80.append(tp_thres[0])
if tp_thres[1]!= 'na':
tp_90.append(tp_thres[1])
auroc_mean = statistics.mean(auroc_l)
auroc_sd = statistics.stdev(auroc_l)
print('auroc_mean: '+str(auroc_mean))
print('auroc_sd: '+str(auroc_sd))
auprc_mean = statistics.mean(auprc_l)
auprc_sd = statistics.stdev(auprc_l)
print('auprc_mean: '+str(auprc_mean))
print('auprc_sd: '+str(auprc_sd))
tp_80_mean = statistics.mean(tp_80)
tp_80_sd = statistics.stdev(tp_80)
print('tp_80_mean: '+str(tp_80_mean))
print('tp_80_sd: '+str(tp_80_sd))
tp_90_mean = statistics.mean(tp_90)
tp_90_sd = statistics.stdev(tp_90)
print('tp_90_mean: '+str(tp_90_mean))
print('tp_90_sd: '+str(tp_90_sd))
# LogisticRegression, elasticnet
logreg = LogisticRegression(penalty='elasticnet',solver='saga',random_state=0,max_iter=10000,l1_ratio=0.50,C=0.1)
auroc_l = []
auprc_l = []
tp_80 = []
tp_90 = []
for s in range(9):
#tr, val, te = create_gene_splits_kfold(dataframe['gene'].values, all_cols, 11, s)
tr, te = create_gene_splits_filter1_kfold_noval(dataframe['gene'].values, all_cols, 9, s)
# training input and output
d_input = tr[0]
d_output = tr[1]
logreg.fit(d_input, d_output) #fit models
#test set
xt = te[0]
#pred = logreg.predict(xt)
pred = logreg.predict_proba(xt)
pred = pred[:,1]
auroc,auprc,tp_thres = classification_analysis('LogisticRegression-elasticnet', s,pred,te[1])
auroc_l.append(auroc)
auprc_l.append(auprc)
if tp_thres[0]!= 'na':
tp_80.append(tp_thres[0])
if tp_thres[1]!= 'na':
tp_90.append(tp_thres[1])
auroc_mean = statistics.mean(auroc_l)
auroc_sd = statistics.stdev(auroc_l)
print('auroc_mean: '+str(auroc_mean))
print('auroc_sd: '+str(auroc_sd))
auprc_mean = statistics.mean(auprc_l)
auprc_sd = statistics.stdev(auprc_l)
print('auprc_mean: '+str(auprc_mean))
print('auprc_sd: '+str(auprc_sd))
tp_80_mean = statistics.mean(tp_80)
tp_80_sd = statistics.stdev(tp_80)
print('tp_80_mean: '+str(tp_80_mean))
print('tp_80_sd: '+str(tp_80_sd))
tp_90_mean = statistics.mean(tp_90)
tp_90_sd = statistics.stdev(tp_90)
print('tp_90_mean: '+str(tp_90_mean))
print('tp_90_sd: '+str(tp_90_sd))
#SVM, linear
clf = svm.SVC(kernel='linear',probability=True,random_state=0,C=0.001)
#clf = LinearSVC(dual= False, random_state=0, max_iter=10000,C=1,penalty='l2')
auroc_l = []
auprc_l = []
tp_80 = []
tp_90 = []
for s in range(9):
#tr, val, te = create_gene_splits_kfold(dataframe['gene'].values, all_cols, 11, s)
tr, te = create_gene_splits_filter1_kfold_noval(dataframe['gene'].values, all_cols, 9, s)
# training input and output
d_input = tr[0]
d_output = tr[1]
clf.fit(d_input, d_output) #fit models
#test set
xt = te[0]
pred = clf.predict_proba(xt)
pred = pred[:,1]
#pred = clf.predict(xt)
auroc,auprc,tp_thres = classification_analysis('svm', s,pred,te[1])
auroc_l.append(auroc)
auprc_l.append(auprc)
if tp_thres[0]!= 'na':
tp_80.append(tp_thres[0])
if tp_thres[1]!= 'na':
tp_90.append(tp_thres[1])
auroc_mean = statistics.mean(auroc_l)
auroc_sd = statistics.stdev(auroc_l)
print('auroc_mean: '+str(auroc_mean))
print('auroc_sd: '+str(auroc_sd))
auprc_mean = statistics.mean(auprc_l)
auprc_sd = statistics.stdev(auprc_l)
print('auprc_mean: '+str(auprc_mean))
print('auprc_sd: '+str(auprc_sd))
tp_80_mean = statistics.mean(tp_80)
tp_80_sd = statistics.stdev(tp_80)
#print('tp_80_mean: '+str(tp_80_mean))
#print('tp_80_sd: '+str(tp_80_sd))
tp_90_mean = statistics.mean(tp_90)
tp_90_sd = statistics.stdev(tp_90)
#print('tp_90_mean: '+str(tp_90_mean))
#print('tp_90_sd: '+str(tp_90_sd))
# random forest
#clf = RandomForestClassifier(n_estimators=32,min_samples_split=2, min_samples_leaf=2, max_features='auto',random_state=0)
clf = RandomForestClassifier(n_estimators=1500,max_features='auto',random_state=0)
auroc_l = []
auprc_l = []
tp_80 = []
tp_90 = []
for s in range(9):
#tr, val, te = create_gene_splits_kfold(dataframe['gene'].values, all_cols, 11, s)
#tr, val, te = create_gene_splits_filter1_kfold(dataframe['gene'].values, all_cols, 9, args.split)
tr, te = create_gene_splits_filter1_kfold_noval(dataframe['gene'].values, all_cols, 9, s)
# training input and output
d_input = tr[0]
d_output = tr[1]
clf.fit(d_input, d_output) #fit models
#test set
xt = te[0]
#pred = logreg.predict(xt)
pred = clf.predict_proba(xt)
pred = pred[:,1]
auroc,auprc,tp_thres = classification_analysis('random forest', s,pred,te[1])
auroc_l.append(auroc)
auprc_l.append(auprc)
if tp_thres[0]!= 'na':
tp_80.append(tp_thres[0])
if tp_thres[1]!= 'na':
tp_90.append(tp_thres[1])
auroc_mean = statistics.mean(auroc_l)
auroc_sd = statistics.stdev(auroc_l)
print('auroc_mean: '+str(auroc_mean))
print('auroc_sd: '+str(auroc_sd))
auprc_mean = statistics.mean(auprc_l)
auprc_sd = statistics.stdev(auprc_l)
print('auprc_mean: '+str(auprc_mean))
print('auprc_sd: '+str(auprc_sd))
tp_80_mean = statistics.mean(tp_80)
tp_80_sd = statistics.stdev(tp_80)
print('tp_80_mean: '+str(tp_80_mean))
print('tp_80_sd: '+str(tp_80_sd))
tp_90_mean = statistics.mean(tp_90)
tp_90_sd = statistics.stdev(tp_90)
print('tp_90_mean: '+str(tp_90_mean))
print('tp_90_sd: '+str(tp_90_sd))
#GradientBoostingClassifier
clf = ensemble.GradientBoostingClassifier(random_state=0,max_depth=4,
max_features='auto', n_estimators=1500)
auroc_l = []
auprc_l = []
tp_80 = []
tp_90 = []
#for s in range(11):
for s in range(9):
#tr, val, te = create_gene_splits_kfold(dataframe['gene'].values, all_cols, 11, s)
#tr, val, te = create_gene_splits_filter1_kfold(dataframe['gene'].values, all_cols, 9, args.split)
tr, te = create_gene_splits_filter1_kfold_noval(dataframe['gene'].values, all_cols, 9, s)
# training input and output
d_input = tr[0]
d_output = tr[1]
clf.fit(d_input, d_output) #fit models
#test set
xt = te[0]
pred = clf.predict_proba(xt)
pred = pred[:,1]
auroc,auprc,tp_thres = classification_analysis('GradientBoostingClassifier_hpnew', s,pred,te[1])
auroc_l.append(auroc)
auprc_l.append(auprc)
if tp_thres[0]!= 'na':
tp_80.append(tp_thres[0])
if tp_thres[1]!= 'na':
tp_90.append(tp_thres[1])
auroc_mean = statistics.mean(auroc_l)
auroc_sd = statistics.stdev(auroc_l)
print('auroc_mean: '+str(auroc_mean))
print('auroc_sd: '+str(auroc_sd))
auprc_mean = statistics.mean(auprc_l)
auprc_sd = statistics.stdev(auprc_l)
print('auprc_mean: '+str(auprc_mean))
print('auprc_sd: '+str(auprc_sd))
tp_80_mean = statistics.mean(tp_80)
tp_80_sd = statistics.stdev(tp_80)
print('tp_80_mean: '+str(tp_80_mean))
print('tp_80_sd: '+str(tp_80_sd))
tp_90_mean = statistics.mean(tp_90)
tp_90_sd = statistics.stdev(tp_90)
print('tp_90_mean: '+str(tp_90_mean))
print('tp_90_sd: '+str(tp_90_sd))
print(auroc_l)
print(auprc_l)
print(tp_80)
print(tp_90)
#GradientBoostingClassifier, hp2
clf = ensemble.GradientBoostingClassifier(random_state=0,max_depth=4,
max_features='sqrt', n_estimators=1800)
auroc_l = []
auprc_l = []
tp_80 = []
tp_90 = []
for s in range(9):
tr, te = create_gene_splits_filter1_kfold_noval(dataframe['gene'].values, all_cols, 9, s)
# training input and output
d_input = tr[0]
d_output = tr[1]
clf.fit(d_input, d_output) #fit models
#test set
xt = te[0]
pred = clf.predict_proba(xt)
pred = pred[:,1]
auroc,auprc,tp_thres = classification_analysis('GradientBoostingClassifier_hpnew', s,pred,te[1])
auroc_l.append(auroc)
auprc_l.append(auprc)
if tp_thres[0]!= 'na':
tp_80.append(tp_thres[0])
if tp_thres[1]!= 'na':
tp_90.append(tp_thres[1])
auroc_mean = statistics.mean(auroc_l)
auroc_sd = statistics.stdev(auroc_l)
print('auroc_mean: '+str(auroc_mean))
print('auroc_sd: '+str(auroc_sd))
auprc_mean = statistics.mean(auprc_l)
auprc_sd = statistics.stdev(auprc_l)
print('auprc_mean: '+str(auprc_mean))
print('auprc_sd: '+str(auprc_sd))
tp_80_mean = statistics.mean(tp_80)
tp_80_sd = statistics.stdev(tp_80)
print('tp_80_mean: '+str(tp_80_mean))
print('tp_80_sd: '+str(tp_80_sd))
tp_90_mean = statistics.mean(tp_90)
tp_90_sd = statistics.stdev(tp_90)
print('tp_90_mean: '+str(tp_90_mean))
print('tp_90_sd: '+str(tp_90_sd)) | test: ['RPL31', 'RPS3A', 'CSE1L', 'XAB2', 'PSMD7', 'SUPT6H']
test: ['EEF2', 'RPS11', 'SNRPD2', 'RPL37', 'SF3B3', 'DDX51']
test: ['RPL7', 'RPS9', 'KARS', 'SF3A1', 'RPL32', 'PSMB2']
test: ['RPS7', 'EIF4A3', 'U2AF1', 'PSMA1', 'PHB', 'POLR2D']
test: ['RPSA', 'RPL23A', 'NUP93', 'AQR', 'RPA2', 'SUPT5H']
test: ['RPL6', 'RPS13', 'SF3B2', 'RPS27A', 'PRPF31', 'COPZ1']
test: ['RPS4X', 'PSMD1', 'RPS14', 'NUP98', 'USP39', 'CDC5L']
test: ['RPL5', 'PHB2', 'RPS15A', 'RPS3', 'ARCN1', 'COPS6']
test: ['RPS6', 'PRPF19', 'RPL34', 'Hsp10', 'POLR2I', 'EIF5B']
auroc_mean: 0.8402434698783054
auroc_sd: 0.017096114410535924
auprc_mean: 0.5326705713945947
auprc_sd: 0.029089488378007556
tp_80_mean: 0.8210448665312134
tp_80_sd: 0.08843235627451937
tp_90_mean: 0.8753086419753087
tp_90_sd: 0.19982845866986979
| MIT | models/Linear_ensemble/hyperparameter tuning/linear model_new_classification-seq only.ipynb | jingyi7777/CasRx_guide_efficiency |
Test functions | from utils.sparse import * | _____no_output_____ | Apache-2.0 | jnotebook/test utils sparse functions.ipynb | edervishaj/spotify-recsys-challenge |
Function list 1. inplace_set_rows_zero_where_sum (X, op, cut) 2. inplace_set_cols_zero_where_sum (X, op, cut)3. inplace_set_rows_zero (X, target_rows)4. inplace_set_cols_zero (X, target_cols)5. inplace_row_scale (X, scale)6. inplace_col_scale (X, scale) 7. sum_cols (X)8. sum_rows (X) | m = sp.random(4,5,0.5).tocsr()
m.data = np.ones(m.data.shape[0])
print(m.todense())
inplace_row_scale(m,np.array([1,2,3,4]))
print (m.todense())
m = sp.random(4,5,0.5).tocsc()
m.data = np.ones(m.data.shape[0])
print(m.todense())
inplace_col_scale(m,np.array([1,2,3,4,5]))
print (m.todense())
m = sp.random(4,5,0.5).tocsr()
m.data = np.ones(m.data.shape[0])
print(m.todense())
inplace_set_rows_zero(m,np.array([1,3]))
print (m.todense())
m = sp.random(4,5,0.5).tocsr()
m.data = np.ones(m.data.shape[0])
print(m.todense())
inplace_set_cols_zero(m,np.array([1,3]))
print (m.todense())
m = sp.random(4,5,0.5).tocsr()
print (sum_rows(m))
inplace_set_rows_zero_where_sum(m, '>', 1.5)
print (m.todense())
m = sp.random(4,5,0.5).tocsr()
print (sum_cols(m))
inplace_set_cols_zero_where_sum(m, '>', 1.5)
print (m.todense()) | [1.96108189 1.12923879 0. 1.93997106 0.40970854]
[[0. 0.69020914 0. 0. 0.40970854]
[0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. ]
[0. 0.43902965 0. 0. 0. ]]
| Apache-2.0 | jnotebook/test utils sparse functions.ipynb | edervishaj/spotify-recsys-challenge |
Pivot table- excel에서 보던 것- index축은 groupby와 동일- column에 추가로 labeling값을 추가하여,- Value에 numeric type 값을 aggregation하는 형태 | import dateutil
df_phone = pd.read_csv("code/ch5/data/phone_data.csv")
df_phone['date'] = df_phone['date'].apply(dateutil.parser.parse, dayfirst=True)
df_phone.tail()
df_phone.pivot_table(['duration'], index=['month','item'], columns=['network'], fill_value=0, aggfunc='sum') | _____no_output_____ | MIT | inflearn_machine_learning/pandas/pandas_pivot_crosstab.ipynb | Junhojuno/TIL |
Crosstab- 두 컬럼의 교차 빈도, 비율, 덧셈 등을 구할 때 사용- Pivot table의 특수한 형태- User-Item Rating Matrix 등을 만들 때 사용가능 | df_movie = pd.read_csv("code/ch5/data/movie_rating.csv")
df_movie.tail()
# 평론가의 영화별 평점
pd.crosstab(values=df_movie.rating, index=df_movie.critic, columns=df_movie.title, aggfunc='first').fillna(0)
# 이걸 groupby로 만들어보자.1
df_movie.groupby(['critic','title'])['rating'].first().unstack().fillna(0)
# 이걸 groupby로 만들어보자.2
df_movie.groupby(['critic','title']).agg({'rating' : 'first'}).unstack().fillna(0)
# 이걸 pivot table로 만들어보자
df_movie.pivot_table(values='rating', index='critic', columns='title', aggfunc='first', fill_value=0) | _____no_output_____ | MIT | inflearn_machine_learning/pandas/pandas_pivot_crosstab.ipynb | Junhojuno/TIL |
MNIST Simple DEMO | import argparse
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
class Arguments:
batch = 64
test_batch = 512
epochs = 10
lr = .01
momentum = .5
seed = 42
log_interval = 100
args = Arguments()
class Network(nn.Module):
def __init__(self):
super(Network, self).__init__()
self.conv1 = nn.Conv2d(1, 20, 5, 1)
self.conv2 = nn.Conv2d(20, 50, 5, 1)
self.fc1 = nn.Linear(4*4*50, 500)
self.fc2 = nn.Linear(500, 10)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2, 2)
x = x.view(-1, 4*4*50)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return F.log_softmax(x, dim=1)
def train(args, model, device, train_loader, optimizer, epoch):
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % args.log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
def test(args, model, device, test_loader):
model.eval()
test_loss, correct = 0, 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item()
pred = output.argmax(dim=1, keepdim=True)
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
torch.manual_seed(args.seed)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
kwargs = {
'num_workers': 1,
'pin_memory': True
} if device.type == 'cuda' else {}
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=args.batch, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=args.test_batch, shuffle=True, **kwargs)
model = Network().to(device)
optimizer = optim.SGD(model.parameters(), lr=args.lr, momentum=args.momentum)
for epoch in range(1, args.epochs + 1):
train(args, model, device, train_loader, optimizer, epoch)
test(args, model, device, test_loader)
torch.save(model.state_dict(), "mnist_cnn.pt") | Train Epoch: 1 [0/60000 (0%)] Loss: 2.309220
Train Epoch: 1 [6400/60000 (11%)] Loss: 0.545335
Train Epoch: 1 [12800/60000 (21%)] Loss: 0.417650
Train Epoch: 1 [19200/60000 (32%)] Loss: 0.353491
Train Epoch: 1 [25600/60000 (43%)] Loss: 0.306972
Train Epoch: 1 [32000/60000 (53%)] Loss: 0.133229
Train Epoch: 1 [38400/60000 (64%)] Loss: 0.188936
Train Epoch: 1 [44800/60000 (75%)] Loss: 0.070623
Train Epoch: 1 [51200/60000 (85%)] Loss: 0.258176
Train Epoch: 1 [57600/60000 (96%)] Loss: 0.040762
Test set: Average loss: 0.1040, Accuracy: 9675/10000 (97%)
Train Epoch: 2 [0/60000 (0%)] Loss: 0.235796
Train Epoch: 2 [6400/60000 (11%)] Loss: 0.049525
Train Epoch: 2 [12800/60000 (21%)] Loss: 0.077299
Train Epoch: 2 [19200/60000 (32%)] Loss: 0.058649
Train Epoch: 2 [25600/60000 (43%)] Loss: 0.162579
Train Epoch: 2 [32000/60000 (53%)] Loss: 0.043902
Train Epoch: 2 [38400/60000 (64%)] Loss: 0.037764
Train Epoch: 2 [44800/60000 (75%)] Loss: 0.007759
Train Epoch: 2 [51200/60000 (85%)] Loss: 0.125971
Train Epoch: 2 [57600/60000 (96%)] Loss: 0.033037
Test set: Average loss: 0.0616, Accuracy: 9805/10000 (98%)
Train Epoch: 3 [0/60000 (0%)] Loss: 0.081351
Train Epoch: 3 [6400/60000 (11%)] Loss: 0.088761
Train Epoch: 3 [12800/60000 (21%)] Loss: 0.095073
Train Epoch: 3 [19200/60000 (32%)] Loss: 0.091261
Train Epoch: 3 [25600/60000 (43%)] Loss: 0.160844
Train Epoch: 3 [32000/60000 (53%)] Loss: 0.034395
Train Epoch: 3 [38400/60000 (64%)] Loss: 0.010957
Train Epoch: 3 [44800/60000 (75%)] Loss: 0.033368
Train Epoch: 3 [51200/60000 (85%)] Loss: 0.013109
Train Epoch: 3 [57600/60000 (96%)] Loss: 0.070705
Test set: Average loss: 0.0484, Accuracy: 9847/10000 (98%)
Train Epoch: 4 [0/60000 (0%)] Loss: 0.019743
Train Epoch: 4 [6400/60000 (11%)] Loss: 0.040987
Train Epoch: 4 [12800/60000 (21%)] Loss: 0.061202
Train Epoch: 4 [19200/60000 (32%)] Loss: 0.007646
Train Epoch: 4 [25600/60000 (43%)] Loss: 0.011820
Train Epoch: 4 [32000/60000 (53%)] Loss: 0.022924
Train Epoch: 4 [38400/60000 (64%)] Loss: 0.044619
Train Epoch: 4 [44800/60000 (75%)] Loss: 0.015211
Train Epoch: 4 [51200/60000 (85%)] Loss: 0.016549
Train Epoch: 4 [57600/60000 (96%)] Loss: 0.069062
Test set: Average loss: 0.0358, Accuracy: 9887/10000 (99%)
Train Epoch: 5 [0/60000 (0%)] Loss: 0.036325
Train Epoch: 5 [6400/60000 (11%)] Loss: 0.068640
Train Epoch: 5 [12800/60000 (21%)] Loss: 0.010548
Train Epoch: 5 [19200/60000 (32%)] Loss: 0.029485
Train Epoch: 5 [25600/60000 (43%)] Loss: 0.025582
Train Epoch: 5 [32000/60000 (53%)] Loss: 0.060043
Train Epoch: 5 [38400/60000 (64%)] Loss: 0.013400
Train Epoch: 5 [44800/60000 (75%)] Loss: 0.011863
Train Epoch: 5 [51200/60000 (85%)] Loss: 0.067035
Train Epoch: 5 [57600/60000 (96%)] Loss: 0.056927
Test set: Average loss: 0.0344, Accuracy: 9884/10000 (99%)
Train Epoch: 6 [0/60000 (0%)] Loss: 0.014376
Train Epoch: 6 [6400/60000 (11%)] Loss: 0.006622
Train Epoch: 6 [12800/60000 (21%)] Loss: 0.020543
Train Epoch: 6 [19200/60000 (32%)] Loss: 0.035187
Train Epoch: 6 [25600/60000 (43%)] Loss: 0.038597
Train Epoch: 6 [32000/60000 (53%)] Loss: 0.016477
Train Epoch: 6 [38400/60000 (64%)] Loss: 0.021265
Train Epoch: 6 [44800/60000 (75%)] Loss: 0.034409
Train Epoch: 6 [51200/60000 (85%)] Loss: 0.012662
Train Epoch: 6 [57600/60000 (96%)] Loss: 0.044574
Test set: Average loss: 0.0375, Accuracy: 9879/10000 (99%)
Train Epoch: 7 [0/60000 (0%)] Loss: 0.011418
Train Epoch: 7 [6400/60000 (11%)] Loss: 0.008460
Train Epoch: 7 [12800/60000 (21%)] Loss: 0.024678
Train Epoch: 7 [19200/60000 (32%)] Loss: 0.021109
Train Epoch: 7 [25600/60000 (43%)] Loss: 0.044059
Train Epoch: 7 [32000/60000 (53%)] Loss: 0.012801
Train Epoch: 7 [38400/60000 (64%)] Loss: 0.002572
Train Epoch: 7 [44800/60000 (75%)] Loss: 0.008726
Train Epoch: 7 [51200/60000 (85%)] Loss: 0.032433
Train Epoch: 7 [57600/60000 (96%)] Loss: 0.086093
Test set: Average loss: 0.0300, Accuracy: 9900/10000 (99%)
Train Epoch: 8 [0/60000 (0%)] Loss: 0.005734
Train Epoch: 8 [6400/60000 (11%)] Loss: 0.011664
Train Epoch: 8 [12800/60000 (21%)] Loss: 0.083290
Train Epoch: 8 [19200/60000 (32%)] Loss: 0.014290
Train Epoch: 8 [25600/60000 (43%)] Loss: 0.018174
Train Epoch: 8 [32000/60000 (53%)] Loss: 0.013148
Train Epoch: 8 [38400/60000 (64%)] Loss: 0.010231
Train Epoch: 8 [44800/60000 (75%)] Loss: 0.054055
Train Epoch: 8 [51200/60000 (85%)] Loss: 0.003165
Train Epoch: 8 [57600/60000 (96%)] Loss: 0.023597
Test set: Average loss: 0.0319, Accuracy: 9884/10000 (99%)
Train Epoch: 9 [0/60000 (0%)] Loss: 0.056386
Train Epoch: 9 [6400/60000 (11%)] Loss: 0.022121
Train Epoch: 9 [12800/60000 (21%)] Loss: 0.024276
Train Epoch: 9 [19200/60000 (32%)] Loss: 0.014277
Train Epoch: 9 [25600/60000 (43%)] Loss: 0.027978
Train Epoch: 9 [32000/60000 (53%)] Loss: 0.007992
Train Epoch: 9 [38400/60000 (64%)] Loss: 0.018210
Train Epoch: 9 [44800/60000 (75%)] Loss: 0.023663
Train Epoch: 9 [51200/60000 (85%)] Loss: 0.005544
Train Epoch: 9 [57600/60000 (96%)] Loss: 0.005737
Test set: Average loss: 0.0281, Accuracy: 9906/10000 (99%)
Train Epoch: 10 [0/60000 (0%)] Loss: 0.011280
Train Epoch: 10 [6400/60000 (11%)] Loss: 0.029055
Train Epoch: 10 [12800/60000 (21%)] Loss: 0.007866
Train Epoch: 10 [19200/60000 (32%)] Loss: 0.053182
Train Epoch: 10 [25600/60000 (43%)] Loss: 0.002478
Train Epoch: 10 [32000/60000 (53%)] Loss: 0.001874
Train Epoch: 10 [38400/60000 (64%)] Loss: 0.041121
Train Epoch: 10 [44800/60000 (75%)] Loss: 0.004530
Train Epoch: 10 [51200/60000 (85%)] Loss: 0.038643
Train Epoch: 10 [57600/60000 (96%)] Loss: 0.008336
Test set: Average loss: 0.0264, Accuracy: 9910/10000 (99%)
| MIT | legacy/MNIST/lab.ipynb | MaybeS/mnist |
Project 0: Inaugural project Labor Supply Problem Following labor supply problem is given: $$c^*,l^* = log(c) - v \frac{l^{1+\frac{1}{\epsilon}}}{1+\frac{1}{\epsilon}}\\x = m + wl - [\tau_0wl+\tau_1 \max(wl-\kappa,0)]\\c \in [0,x]\\l \in [0,1]\\$$Where: c is consumption,l is labor supply,m is cash-on-hand, w is the wage rate, $$t_0$$ is the standard labor income tax$$t_1$$ is the top bracket labor income tax,k is the cut-off of top labor income bracketx is total resourcesv scales disutility of labor E is the Frisch elasticity of labor supplyutility is monotonically increasing in consumption, which implies $$c^* = x$$ Question 1 | # All used packages are imported
import numpy as np
import sympy as sm
from scipy import optimize
t0 = sm.symbols('t_0')
t1 = sm.symbols('t_1')
m = 1 #cash-on-hand
v = 10 #disutility of labor
e = 0.3 #elasticity of labor supply
t0 = 0.4 #standard labor income tax
t1 = 0.1 #top bracket labor income tax
k = 0.4 #cut-off for top labor income tax
# Defining utility
def utility(c,v,l,e):
u = np.log(c) - v*(l**(1+1/e)/(1+1/e))
return u
# Defining constraint
def constraint(m,w,l,t0,t1,k):
x = m + w*l - (t0*w*l + t1*np.max(w*l-k,0))
return x
def consumption(l,w,e,v,t0,t1,k):
c = constraint(m,w,l,t0,t1,k)
return -utility(c,v,l,e)
def optimizer(w,e,v,t0,t1,k,m):
res = optimize.minimize_scalar(
consumption, method='bounded',
bounds=(0,1), args=(w,e,v,t0,t1,k))
labor_star = res.x
cons_star = constraint(m,w,labor_star,t0,t1,k)
utility_star = utility(cons_star,v,labor_star,e)
return labor_star,cons_star,utility_star
labor_star = optimizer(0.5,e,v,t0,t1,k,m)[0]
cons_star = optimizer(0.5,e,v,t0,t1,k,m)[1]
u_star = optimizer(0.5,e,v,t0,t1,k,m)[2]
print('labour supply is:' + str(labor_star))
print('consumption is:' + str(cons_star))
print('utility:' + str(u_star)) | labour supply is:0.31961536193545265
consumption is:1.119903840483863
utility:0.09677772523865749
| MIT | Project 1.ipynb | notnasobe666/BlackHatGang |
Question 2 | import matplotlib.pyplot as plt
plt.style.use('grayscale')
# Plot l_star and c_star with w going from 0.5 to 1.5
# The definitions are defined - the used packages is defined above
N = 10000
w_vector = np.linspace(0.5,1.5,num=N)
c_optimal = np.empty(N)
l_optimal = np.empty(N)
# a loop is generated to test the range of W
for i, w in enumerate(w_vector):
optimization = optimizer(w,e,v,t0,t1,k,m)
l_optimal[i]=optimization[0]
c_optimal[i]=optimization[1]
fig = plt.figure(figsize=(10,4))
# Left plot
axis_left = fig.add_subplot(1,2,1)
axis_left.plot(w_vector,l_optimal)
axis_left.set_title('Optimal labor supply given w')
axis_left.set_xlabel('$w$')
axis_left.set_ylabel('$l$')
axis_left.grid(True)
# Right plot
axis_right = fig.add_subplot(1,2,2)
axis_right.plot(w_vector,c_optimal)
axis_right.set_title('Optimal consumption given w')
axis_right.set_xlabel('$w1$')
axis_right.set_ylabel('$c$')
axis_right.grid(True)
plt.show
| _____no_output_____ | MIT | Project 1.ipynb | notnasobe666/BlackHatGang |
Question 3 | # Calculate the tax revenue
tax_revenue = np.sum( t0 * w_vector * l_optimal + t1 * np.max( w_vector * l_optimal - k ,0 ))
print('Total tax revenue is: ' + str(tax_revenue))
| Total tax revenue is: 1775.3896759006836
| MIT | Project 1.ipynb | notnasobe666/BlackHatGang |
Question 4 | # How does the tax revenue change when e = 0.1?
# New epsilon is defined
e_new = 0.1
l_optimal_e_new = np.empty(N)
# Same loop is used as above but only a new labor
# supply is calculated as consumption isn't included
# in the tax revenue formula
for i, w in enumerate(w_vector):
optimization = optimizer(w,e_new,v,t0,t1,k,m)
l_optimal_e_new[i]=optimization[0]
# then the new tax revenue can be calculated
tax_revenue_e_new = np.sum( t0 * w_vector * l_optimal_e_new + t1 * np.max( w_vector * l_optimal_e_new - k ,0))
print('New total tax revenue: '+str(tax_revenue_e_new))
# Thus the difference in tax revenue can be calucalted as
print('The difference in tax revenue is: '+ str(tax_revenue_e_new-tax_revenue)) | New total tax revenue: 3578.900497991557
The difference in tax revenue is: 1803.5108220908735
| MIT | Project 1.ipynb | notnasobe666/BlackHatGang |
Question 5 | # Optimize the tax
# Same optimization formula as above
def tax_optimize(t0,t1,k):
tax_optimal = optimize.minimize_scalar(tax_revenue , method='bounded' , x=[0.1,0.1,0.1])
t0_optimal = tax_optimal.x
t1_optimal = tax_optimal.x
k_optimal = tax_optimal.x
return t0_optimal, t1_optimal, k_optimal
t0_optimal = tax_optimize(t0,t1,k)[0]
t1_optimal = tax_optimize(t0,t1,k)[1]
k_optimal = tax_optimize(t0,t1,k)[2]
print('Optimal t0 is: ' + str(t0_optimal)) | _____no_output_____ | MIT | Project 1.ipynb | notnasobe666/BlackHatGang |
Tic-Tac-Toe AgentIn this notebook, you will learn to build an RL agent (using Q-learning) that learns to play Numerical Tic-Tac-Toe with odd numbers. The environment is playing randomly with the agent, i.e. its strategy is to put an even number randomly in an empty cell. The following is the layout of the notebook: - Defining epsilon-greedy strategy - Tracking state-action pairs for convergence - Define hyperparameters for the Q-learning algorithm - Generating episode and applying Q-update equation - Checking convergence in Q-values Importing librariesWrite the code to import Tic-Tac-Toe class from the environment file | # from <TC_Env> import <TicTacToe> - import your class from environment file
from TCGame_Env import TicTacToe
import collections
import numpy as np
import random
import pickle
import time
from matplotlib import pyplot as plt
from tqdm import tqdm
# Function to convert state array into a string to store it as keys in the dictionary
# states in Q-dictionary will be of form: x-4-5-3-8-x-x-x-x
# x | 4 | 5
# ----------
# 3 | 8 | x
# ----------
# x | x | x
def Q_state(state):
return ('-'.join(str(e) for e in state)).replace('nan','x')
# Defining a function which will return valid (all possible actions) actions corresponding to a state
# Important to avoid errors during deployment.
def valid_actions(state):
valid_Actions = []
valid_Actions = [i for i in env.action_space(state)[0]] ###### -------please call your environment as env
return valid_Actions
# Defining a function which will add new Q-values to the Q-dictionary.
def add_to_dict(state):
state1 = Q_state(state)
valid_act = valid_actions(state)
if state1 not in Q_dict.keys():
for action in valid_act:
Q_dict[state1][action]=0 | _____no_output_____ | MIT | TicTacToe_Agent.ipynb | Chiragchhillar1/ML-TicTacToe |
Epsilon-greedy strategy - Write your code here(you can build your epsilon-decay function similar to the one given at the end of the notebook) | # Defining epsilon-greedy policy. You can choose any function epsilon-decay strategy
def epsilon_greedy(state, time):
max_epsilon = 1.0
min_epsilon = 0.001
epsilon = min_epsilon + (max_epsilon - min_epsilon) * np.exp(-0.000001*time)
z = np.random.random()
if z > epsilon:
action = max(Q_dict[Q_state(state)],key=Q_dict[Q_state(state)].get)
else:
action = random.sample(valid_actions(state),1)[0]
return action | _____no_output_____ | MIT | TicTacToe_Agent.ipynb | Chiragchhillar1/ML-TicTacToe |
Tracking the state-action pairs for checking convergence - write your code here | # Initialise Q_dictionary as 'Q_dict' and States_tracked as 'States_track' (for convergence)
Q_dict = collections.defaultdict(dict)
States_track = collections.defaultdict(dict)
print(len(Q_dict))
print(len(States_track))
# Initialise states to be tracked
def initialise_tracking_states():
sample_q_values = [('x-3-x-x-x-6-x-x-x',(0,1)),
('x-1-x-x-x-x-8-x-x',(2,9)),
('x-x-x-x-6-x-x-x-5',(2,7)),
('x-x-x-x-9-x-6-x-x',(1,7)),
('x-5-x-2-x-x-4-7-x',(0,9)),
('9-x-5-x-x-x-8-x-4',(1,3)),
('2-7-x-x-6-x-x-3-x',(8,5)),
('9-x-x-x-x-2-x-x-x',(2,5)),
('x-x-7-x-x-x-x-x-2',(1,5)),
('5-x-x-x-x-6-x-x-x',(4,9)),
('4-x-x-6-x-x-3-1-x',(8,5)),
('5-x-8-x-x-6-3-x-x',(3,1)),
('x-6-5-x-2-x-x-3-x',(0,7)),
('7-x-5-x-2-x-x-x-6',(1,3))]
for q_values in sample_q_values:
state = q_values[0]
action = q_values[1]
States_track[state][action] = []
#Defining a function to save the Q-dictionary as a pickle file
def save_obj(obj, name ):
with open(name + '.pkl', 'wb') as f:
pickle.dump(obj, f, pickle.HIGHEST_PROTOCOL)
def save_tracking_states():
for state in States_track.keys():
for action in States_track[state].keys():
if state in Q_dict and action in Q_dict[state]:
States_track[state][action].append(Q_dict[state][action])
initialise_tracking_states() | _____no_output_____ | MIT | TicTacToe_Agent.ipynb | Chiragchhillar1/ML-TicTacToe |
Define hyperparameters ---write your code here | EPISODES = 6000000
LR = 0.20
GAMMA = 0.8
threshold = 2540
checkpoint_print_episodes = 600000 | _____no_output_____ | MIT | TicTacToe_Agent.ipynb | Chiragchhillar1/ML-TicTacToe |
Q-update loop ---write your code here | start_time = time.time()
q_track={}
q_track['x-3-x-x-x-6-x-x-x']=[]
q_track['x-1-x-x-x-x-8-x-x']=[]
q_track['x-x-x-x-6-x-x-x-5']=[]
q_track['x-x-x-x-9-x-6-x-x']=[]
q_track['x-5-x-2-x-x-4-7-x']=[]
q_track['9-x-5-x-x-x-8-x-4']=[]
q_track['2-7-x-x-6-x-x-3-x']=[]
q_track['9-x-x-x-x-2-x-x-x']=[]
q_track['x-x-7-x-x-x-x-x-2']=[]
q_track['5-x-x-x-x-6-x-x-x']=[]
q_track['4-x-x-6-x-x-3-1-x']=[]
q_track['5-x-8-x-x-6-3-x-x']=[]
q_track['x-6-5-x-2-x-x-3-x']=[]
q_track['7-x-5-x-2-x-x-x-6']=[]
agent_won_count = 0
env_won_count = 0
tie_count = 0
for episode in range(EPISODES):
##### Start writing your code from the next line
env = TicTacToe()
## Initalizing parameter for the episodes
reward=0
curr_state = env.state
add_to_dict(curr_state)
is_terminal = False
total_reward = 0
while not(is_terminal):
curr_action = epsilon_greedy(curr_state, episode)
if Q_state(curr_state) in q_track.keys():
q_track[Q_state(curr_state)].append(curr_action)
next_state,reward,is_terminal, msg = env.step(curr_state,curr_action)
curr_lookup = Q_state(curr_state)
next_lookup = Q_state(next_state)
if is_terminal:
q_value_max = 0
# Tracking the count of games won by agent and environment
if msg == "Agent Won!":
agent_won_count += 1
elif msg == "Environment Won!":
env_won_count += 1
else:
tie_count += 1
else:
add_to_dict(next_state)
max_next = max(Q_dict[next_lookup],key=Q_dict[next_lookup].get)
q_value_max = Q_dict[next_lookup][max_next]
Q_dict[curr_lookup][curr_action] += LR * ((reward + (GAMMA * (q_value_max))) - Q_dict[curr_lookup][curr_action])
curr_state = next_state
total_reward += reward
if (episode + 1) % checkpoint_print_episodes == 0:
print("After playing %d games, Agent Won : %.4f, Environment Won : %.4f, Tie : %.4f"% (episode + 1,
agent_won_count / (episode + 1), env_won_count /(episode + 1), tie_count / (episode + 1)))
if ((episode + 1) % threshold) == 0:
save_tracking_states()
if ((episode + 1) % 1000000) == 0:
print('Processed %dM episodes'%((episode+1)/1000000))
elapsed_time = time.time() - start_time
save_obj(States_track,'States_tracked')
save_obj(Q_dict,'Policy') | _____no_output_____ | MIT | TicTacToe_Agent.ipynb | Chiragchhillar1/ML-TicTacToe |
Check the Q-dictionary | Q_dict
len(Q_dict)
# try checking for one of the states - that which action your agent thinks is the best -----This will not be evaluated
Q_dict['x-x-5-x-x-x-x-x-4'] | _____no_output_____ | MIT | TicTacToe_Agent.ipynb | Chiragchhillar1/ML-TicTacToe |
Check the states tracked for Q-values convergence(non-evaluative) | # Write the code for plotting the graphs for state-action pairs tracked
plt.figure(0, figsize=(16,7))
plt.subplot(241)
t1=States_track['x-3-x-x-x-6-x-x-x'][(0,1)]
plt.title("(s,a)=('x-3-x-x-x-6-x-x-x',(0,1))")
plt.plot(np.asarray(range(0, len(t1))),np.asarray(t1))
plt.subplot(242)
t2=States_track['x-x-x-x-6-x-x-x-5'][(2,7)]
plt.title("(s,a)=('x-x-x-x-6-x-x-x-5',(2,7))")
plt.plot(np.asarray(range(0, len(t2))),np.asarray(t2))
plt.subplot(243)
t3=States_track['5-x-x-x-x-6-x-x-x'][(4,9)]
plt.title("(s,a)=('5-x-x-x-x-6-x-x-x',(4,9))")
plt.plot(np.asarray(range(0, len(t3))),np.asarray(t3))
plt.subplot(244)
t4=States_track['x-5-x-2-x-x-4-7-x'][(0,9)]
plt.title("(s,a)=('x-5-x-2-x-x-4-7-x',(0,9))")
plt.plot(np.asarray(range(0, len(t4))),np.asarray(t4))
plt.show() | _____no_output_____ | MIT | TicTacToe_Agent.ipynb | Chiragchhillar1/ML-TicTacToe |
Epsilon - decay check | max_epsilon = 1.0
min_epsilon = 0.001
time = np.arange(0,5000000)
epsilon = []
for i in range(0,5000000):
epsilon.append(min_epsilon + (max_epsilon - min_epsilon) * np.exp(-0.000001*i))
plt.plot(time, epsilon)
plt.show() | _____no_output_____ | MIT | TicTacToe_Agent.ipynb | Chiragchhillar1/ML-TicTacToe |
[fnmatch](https://docs.python.org/3/library/fnmatch.html)1. What is fnmatch and why is it useful?1. Why should I use fnmatch and not regex?1. Two examplesFnmatch is part of the python standard library. Allows the use of UNIX style wildcards for string matching. Makes it easy to select a single file type out of a list (e.g. *.csv).While regex is much more powerful, fnmatch offers a simple syntax for using wildcards.If you want to look for a string that starts with 5 characters, then a space and then 3 numbers between 4 and 7 you'll still need to resort to regex though. Simple example | import fnmatch
FILES = ["some_picture.png", "some_data.csv", "another_picture.png"]
# select only the .png files
for file in FILES:
if fnmatch.fnmatch(file, '*.png'):
print(file)
# or using the fnmatch shorthand
print(fnmatch.filter(FILES, '*.png')) | some_picture.png
another_picture.png
['some_picture.png', 'another_picture.png']
| MIT | 2021-06-09-fnmatch.ipynb | phackstock/code-and-tell |
*SIDE NOTE*: The matching is **case insensitive**, if you want to perform a case sensitive match use [`fnmatch.fnmatchcase()`](https://docs.python.org/3/library/fnmatch.htmlfnmatch.fnmatchcase) Match a list of patterns | MODELS = ["MESSAGEix-GLOBIOM 1.0",
"MESSAGEix-GLOBIOM 1.1",
"REMIND-MAgPIE 2.1-4.2",
"REMIND-MAgPIE 1.7-3.2",
"NIGEM",
"POLES GECO2019",
"COFFEE 1.0",
"COFFEE 2.0",
"TEA",
"GCAM5.2",
"GCAM5.3"]
MATCH_MODELS = ["MESSAGEix-GLOBIOM*", "REMIND-MAgPIE*"]
match_any = lambda x, patterns: any(fnmatch.fnmatch(x, pattern) for pattern in patterns)
for m in MODELS:
if match_any(m, MATCH_MODELS):
print(m) | MESSAGEix-GLOBIOM 1.0
MESSAGEix-GLOBIOM 1.1
REMIND-MAgPIE 2.1-4.2
REMIND-MAgPIE 1.7-3.2
| MIT | 2021-06-09-fnmatch.ipynb | phackstock/code-and-tell |
Question 6:Write a code in python to display different functions of python module. | #module required
import time
print("I am Iron Man.")
time.sleep(2.4)#this function delays the time
print("I love you 3000.") #this statement is printed after 2.4 seconds
import time
# seconds passed since epoch
seconds = 1545925769.9618232
local_time = time.ctime(seconds)
print("Local time:", local_time) | _____no_output_____ | MIT | Python/C6.ipynb | pooja-gera/TheWireUsChallenge |
**3.d Formación de vectores****Responsable:**César Zamora Martínez**Infraestructura usada:** Google Colab, para pruebas 0. Importamos librerias necesarias**Fuente:** 3c_formacion_matrices.ipynb, 3c_formacion_abc.ipynb, 3c_formacion_delta.ipynb | !curl https://colab.chainer.org/install | sh -
import cupy as cp
def formar_vectores(mu, Sigma):
'''
Calcula las cantidades u = \Sigma^{-1} \mu y v := \Sigma^{-1} \cdot 1 del problema de Markowitz
Args:
mu (cupy array, vector): valores medios esperados de activos (dimension n)
Sigma (cupy array, matriz): matriz de covarianzas asociada a activos (dimension n x n)
Return:
u (cupy array, escalar): vector dado por \cdot Sigma^-1 \cdot mu (dimension n)
v (cupy array, escalar): vector dado por Sigma^-1 \cdot 1 (dimension n)
'''
# Vector auxiliar con entradas igual a 1
n = Sigma.shape[0]
ones_vector = cp.ones(n)
# Formamos vector \cdot Sigma^-1 mu y Sigm^-1 1
# Nota:
# 1) u= Sigma^-1 \cdot mu se obtiene resolviendo Sigma u = mu
# 2) v= Sigma^-1 \cdot 1 se obtiene resolviendo Sigma v = 1
# Obtiene vectores de interes
u = cp.linalg.solve(Sigma, mu)
u = u.transpose()[0] # correcion de expresion de array
v = cp.linalg.solve(Sigma, ones_vector)
return u , v
def formar_abc(mu, Sigma):
'''
Calcula las cantidades A, B y C del diagrama de flujo del problema de Markowitz
Args:
mu (cupy array, vector): valores medios esperados de activos (dimension n)
Sigma (cupy array, matriz): matriz de covarianzas asociada a activos (dimension n x n)
Return:
A (cupy array, escalar): escalar dado por mu^t \cdot Sigma^-1 \cdot mu
B (cupy array, escalar): escalar dado por 1^t \cdot Sigma^-1 \cdot 1
C (cupy array, escalar): escalar dado por 1^t \cdot Sigma^-1 \cdot mu
'''
# Vector auxiliar con entradas igual a 1
n = Sigma.shape[0]
ones_vector = cp.ones(n)
# Formamos vector \cdot Sigma^-1 mu y Sigm^-1 1
# Nota:
# 1) u= Sigma^-1 \cdot mu se obtiene resolviendo Sigma u = mu
# 2) v= Sigma^-1 \cdot 1 se obtiene resolviendo Sigma v = 1
u, v = formar_vectores(mu, Sigma)
# Obtiene escalares de interes
A = mu.transpose()@u
B = ones_vector.transpose()@v
C = ones_vector.transpose()@u
return A, B, C
def delta(A,B,C):
'''
Calcula las cantidad Delta = AB-C^2 del diagrama de flujo del problema de Markowitz
Args:
A (cupy array, escalar): escalar dado por mu^t \cdot Sigma^-1 \cdot mu
B (cupy array, escalar): escalar dado por 1^t \cdot Sigma^-1 \cdot 1
C (cupy array, escalar): escalar dado por 1^t \cdot Sigma^-1 \cdot mu
Return:
Delta (cupy array, escalar): escalar dado \mu^t \cdot \Sigma^{-1} \cdot \mu
'''
Delta = A*B-C**2
return Delta | _____no_output_____ | RSA-MD | notebooks/Programacion/3d_formacion_vectores.ipynb | izmfc/MNO_finalproject |
1. Implementación**Consideraciones:**. Esta etapa supone que se conocen $\bar{r}$, $\mu$ y $\Sigma$ asociados a los activos, ello con el objeto de es obtener valores escalares que serán relevantes para obtener los pesos del portafolio para el inversionista. Hasta este punto se asume que ya conocemos todos los términos presentes en las expresiones:$$A = \mu^t \cdot \Sigma^{-1} \cdot \mu $$$$B = 1^t \cdot \Sigma^{-1} \cdot 1 $$$$C = 1^t \cdot \Sigma^{-1} \cdot \mu = \mu^t \cdot \Sigma^{-1} \cdot 1 $$Para con ello poder estimar los multiplicadores de Lagrange asociados al problema:$$ w_0 = \frac{1}{\Delta} ( \hat{r} \cdot B - C ) $$$$ w_1 = \frac{1}{\Delta} (A - C \cdot \hat{r}) $$Con los que se forma la solución del sistema dada por$$w = w_0 \cdot (\Sigma^{-1} \mu) + w_1 \cdot (\Sigma^{-1} 1) $$En seguida se presenta el código correspondiente: | def formar_omegas(r, mu, Sigma):
'''
Calcula las cantidades w_o y w_1 del problema de Markowitz
(valores de multiplicadores de Lagrange)
Args:
r (cupy array, escalar): escalar que denota el retorno esperado por el inversionista
mu (cupy array, vector): valores medios esperados de activos (dimension n)
Sigma (cupy array, matriz): matriz de covarianzas asociada a activos (dimension n x n)
Return:
w_0 (cupy array, escalar): escalar dada por
w_0 = \frac{1}{\Delta} (B \Sigma^{-1} \hat{\mu}- C\Sigma^{-1} 1)
w_1 (cupy array, escalar): escalar dado por
w_1 = \frac{1}{\Delta} (C \Sigma^{-1} \hat{\mu}- A\Sigma^{-1} 1)
'''
# Obtenemos u = Sigma^{-1} \hat{\mu}, v = \Sigma^{-1} 1
u, v = formar_vectores(mu, Sigma)
# Escalares relevantes
A, B, C = formar_abc(mu, Sigma)
Delta = delta(A,B,C)
# Formamos w_0 y w_1
w_0 = (1/Delta)*(r*B-C)
w_1 = (1/Delta)*(A-C*r)
return w_0, w_1 | _____no_output_____ | RSA-MD | notebooks/Programacion/3d_formacion_vectores.ipynb | izmfc/MNO_finalproject |
1.1 Valores de prueba | n= 10
# r y mu
r= 10
mu=cp.random.rand(n, 1)
# Sigma
S=cp.random.rand(n, n)
Sigma=S@S
# multiplicadores de lagrande
formar_omegas(r,mu,Sigma) | _____no_output_____ | RSA-MD | notebooks/Programacion/3d_formacion_vectores.ipynb | izmfc/MNO_finalproject |
OverviewThis notebook works on the IEEE-CIS Fraud Detection competition. Here I build a simple XGBoost model based on a balanced dataset. Lessons:. keep the categorical variables as single items. Use a high max_depth for xgboost (maybe 40) Ideas to try:. train divergence of expected value (eg. for TransactionAmt and distance based on the non-fraud subset (not all subset as in the case now). try using a temporal approach to CV | # all imports necessary for this notebook
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import random
import gc
import copy
import missingno as msno
import xgboost
from xgboost import XGBClassifier, XGBRegressor
from sklearn.model_selection import StratifiedKFold, cross_validate, train_test_split
from sklearn.metrics import roc_auc_score, r2_score
import warnings
warnings.filterwarnings('ignore')
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# Helpers
def seed_everything(seed=0):
'''Seed to make all processes deterministic '''
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
def drop_correlated_cols(df, threshold, sample_frac = 1):
'''Drops one of two dataframe's columns whose pairwise pearson's correlation is above the provided threshold'''
if sample_frac != 1:
dataset = df.sample(frac = sample_frac).copy()
else:
dataset = df
col_corr = set() # Set of all the names of deleted columns
corr_matrix = dataset.corr()
for i in range(len(corr_matrix.columns)):
if corr_matrix.columns[i] in col_corr:
continue
for j in range(i):
if (corr_matrix.iloc[i, j] >= threshold) and (corr_matrix.columns[j] not in col_corr):
colname = corr_matrix.columns[i] # getting the name of column
col_corr.add(colname)
del dataset
gc.collect()
df.drop(columns = col_corr, inplace = True)
def calc_feature_difference(df, feature_name, indep_features, min_r2 = 0.1, min_r2_improv = 0, frac1 = 0.1,
max_depth_start = 2, max_depth_step = 4):
from copy import deepcopy
print("Feature name %s" %feature_name)
#print("Indep_features %s" %indep_features)
is_imrpoving = True
curr_max_depth = max_depth_start
best_r2 = float("-inf")
clf_best = np.nan
while is_imrpoving:
clf = XGBRegressor(max_depth = curr_max_depth)
rand_sample_indeces = df[df[feature_name].notnull()].sample(frac = frac1).index
clf.fit(df.loc[rand_sample_indeces, indep_features], df.loc[rand_sample_indeces, feature_name])
rand_sample_indeces = df[df[feature_name].notnull()].sample(frac = frac1).index
pred_y = clf.predict(df.loc[rand_sample_indeces, indep_features])
r2Score = r2_score(df.loc[rand_sample_indeces, feature_name], pred_y)
print("%d, R2 score %.4f" % (curr_max_depth, r2Score))
curr_max_depth = curr_max_depth + max_depth_step
if r2Score > best_r2:
best_r2 = r2Score
clf_best = deepcopy(clf)
if r2Score < best_r2 + (best_r2 * min_r2_improv) or (curr_max_depth > max_depth_start * max_depth_step and best_r2 < min_r2 / 2):
is_imrpoving = False
print("The best R2 score of %.4f" % ( best_r2))
if best_r2 > min_r2:
pred_feature = clf_best.predict(df.loc[:, indep_features])
return (df[feature_name] - pred_feature), best_r2
else:
return df[feature_name], best_r2
seed_everything()
pd.set_option('display.max_columns', 500)
master_df = pd.read_csv('/kaggle/input/ieee-preprocessed/master_df_top_300.csv')
master_df.head()
cols_cat = {'id_12', 'id_13', 'id_14', 'id_15', 'id_16', 'id_17', 'id_18', 'id_19', 'id_20', 'id_21', 'id_22',
'id_23', 'id_24', 'id_25', 'id_26', 'id_27', 'id_28', 'id_29', 'id_30', 'id_31', 'id_32', 'id_33',
'id_34', 'id_35', 'id_36', 'id_37', 'id_38', 'DeviceType', 'DeviceInfo', 'ProductCD', 'card4',
'card6', 'M4','P_emaildomain', 'R_emaildomain', 'card1', 'card2', 'card3', 'card5', 'addr1',
'addr2', 'M1', 'M2', 'M3', 'M5', 'M6', 'M7', 'M8', 'M9'}
%%time
indep_features = ['weekday', 'hours', 'TransactionDT', 'ProductCD', 'card1', 'card2', 'card3', 'card4', 'card5'
, 'card6', 'addr1', 'addr2']
for feature in indep_features:
master_df[feature] = master_df[feature].astype('category').cat.codes
cont_cols_list = list(master_df.select_dtypes(include='number').columns)
cont_features_list = [x for x in cont_cols_list if x not in cols_cat and x not in indep_features and x not in ['TransactionID', 'isFraud', 'TransactionDT', 'is_train_df']]
for cont_feature in cont_features_list:
print(cont_feature)
master_df[cont_feature], best_r2 = calc_feature_difference(master_df, cont_feature, indep_features, frac1= 0.025)
if best_r2 > 0.9:
master_df.drop(columns = [cont_feature], inplace = True)
print(80 * '-')
master_df.to_csv('master_df_time_adjusted_top_300.csv', index=False) | _____no_output_____ | MIT | ieee-preprocess-v2-0-top-300.ipynb | tarekoraby/IEEE-CIS-Fraud-Detection |
Load the iris data | import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_iris
from numpy.linalg import inv
import pandas as pd
import numpy as np
iris = load_iris()
iris['data'][:5,:]
y = np.where(iris['target'] == 2, 1, 0)
X = iris['data']
const = np.ones(shape=y.shape).reshape(-1,1)
mat = np.concatenate( (const, X), axis=1)
mat[:5,:] | _____no_output_____ | MIT | logistic-regression/gradient-descent-logistic-regression.ipynb | appliedecon/data602-lectures |
Recall the algorithm we created for gradient descent for linear regressionUsing the following cost function:$$J(w)=\frac{1}{2}\sum(y^{(i)} - \hat{y}^{(i)})^2$$ | import numpy as np
def gradientDescent(x, y, theta, alpha, m, numIterations):
thetaHistory = list()
xTrans = x.transpose()
costList = list()
for i in range(0, numIterations):
# data x feature weights = y_hat
hypothesis = np.dot(x, theta)
# how far we are off
loss = hypothesis - y
# mse
cost = np.sum(loss ** 2) / (2 * m)
costList.append(cost)
# avg gradient per example
gradient = np.dot(xTrans, loss) / m
# update
theta = theta - alpha * gradient
thetaHistory.append(theta)
return thetaHistory, costList | _____no_output_____ | MIT | logistic-regression/gradient-descent-logistic-regression.ipynb | appliedecon/data602-lectures |
For Logistic regression we replace with our likehihood function:$$J(w)=\sum{[-y^{(i)}log(\theta(z^{(i)}))-(1-y^{(i)})log(1-\theta(z^{(i)})]}$$ And add the sigmoid function to bound $y$ between 0 and 1 | def gradientDescent(x, y, alpha, numIterations):
def mle(y,yhat):
'''
This replaces the mean squared error
'''
return (-y.dot(np.log(yhat)) - ((1-y)).dot(np.log(1-yhat)))
def sigmoid(z):
'''
Transforms values to follow the sigmoid function and bound between 0 and 1
'''
return 1./(1. + np.exp(-np.clip(z, -250, 250)))
# number of examples in the training data
m = x.shape[0]
# initialize weights to small random numbers
theta = np.random.normal(loc=0.0, scale=0.1, size=x.shape[1])
# history of theta values
thetaHistory = list()
xTrans = x.transpose()
# history of cost values
costList = list()
for i in range(0, numIterations):
# predicted value based on feature matrix and current weights
hypothesis = np.dot(x, theta)
# sigmoid transformation so we have bounded values
hypothesis = sigmoid(hypothesis)
# how far we are off from the actual value
loss = hypothesis - y
# determine cost based on the log likehilood function
cost = mle(y, hypothesis)
costList.append(cost)
# avg gradient per example
gradient = np.dot(xTrans, loss) / m
# update the weights
theta = theta - alpha * gradient
thetaHistory.append(theta)
return thetaHistory, costList | _____no_output_____ | MIT | logistic-regression/gradient-descent-logistic-regression.ipynb | appliedecon/data602-lectures |
Let's try it out- Run the algorithm, which gives us the weight and cost history. - Plot the cost to see if it converges. - Make predictions with the last batch of weights. - Apply the sigmoid function to the above predictions. - Plot the actual vs. predicted values. - Plot the evolution of the weights for each iteration. | iters = 500000
import datetime
start_ts = datetime.datetime.now()
betaHistory, costList = gradientDescent(mat, y, alpha=0.01, numIterations=iters)
end_ts = datetime.datetime.now()
print(f'Completed in {end_ts-start_ts}')
# cost history
plt.plot(costList)
plt.title(f'Final cost: {costList[-1]:,.2f}', loc='left')
plt.show()
# predict history
gs_betas = betaHistory[iters-1]
gs_predictions = np.dot(mat, gs_betas)
# we need to apply the sigmoid/activation function to bound the predictions between (0,1)
gs_predictions = 1./(1+np.exp(-gs_predictions))
plt.plot(y, gs_predictions, 'bo', alpha=0.2)
plt.xlabel('Actual')
plt.ylabel('Predicted')
plt.title('Gradient Descent Regression Fit on Training Data')
plt.show()
from collections import defaultdict
thetas = defaultdict(list)
for i in range(len(betaHistory)):
for j in range(len(betaHistory[i])):
thetas[j].append(betaHistory[i][j])
thetasD = pd.DataFrame.from_dict(thetas)
thetasD.plot(legend=False)
plt.title('Beta Estimates')
plt.ylabel('Coefficient')
plt.xlabel('Iteration')
plt.show() | Completed in 0:00:17.566409
| MIT | logistic-regression/gradient-descent-logistic-regression.ipynb | appliedecon/data602-lectures |
셀레니움을 이용한 네이버 블로그(검색창) 크롤러- 네이버 메인 검색 페이지에서 크롤링한다. | import platform
print(platform.architecture())
!python --version
pwd
# 네이버에서 검색어 입력받아 검색 한 후 블로그 메뉴를 선택하고
# 오른쪽에 있는 검색옵션 버튼을 눌러서
# 정렬 방식과 기간을 입력하기
#Step 0. 필요한 모듈과 라이브러리를 로딩하고 검색어를 입력 받습니다.
import sys
import os
import pandas as pd
import numpy as np
import math
from bs4 import BeautifulSoup
import requests
import urllib.request as req
from selenium import webdriver
from selenium.webdriver.common.keys import Keys
import time
import tqdm
from tqdm.notebook import tqdm
query_txt = '성심당여행대전'
start_date= "20190101"
end_date= "20210501"
os.getenv('HOME')
webdriver.__version__
#Step 1. 크롬 웹브라우저 실행
path = os.getenv('HOME')+ '/chromedriver'
driver = webdriver.Chrome(path)
# 사이트 주소는 네이버
c
time.sleep(1)
#Step 2. 네이버 검색창에 "검색어" 검색
element = driver.find_element_by_name("query")
element.send_keys(query_txt)
element.submit()
time.sleep(2)
#Step 3. "블로그" 카테고리 선택
driver.find_element_by_link_text("블로그").click( )
time.sleep(2)
#Step 4. 오른쪽의 검색 옵션 버튼 클릭
driver.find_element_by_class_name("btn_option._search_option_open_btn").click( )
time.sleep(2)
driver.find_element_by_class_name("txt.txt_option._calendar_select_trigger").click() # 관련도순 xpath
# element.find_element_by_css_selector("#header > div.header_common > div > div.area_search > form > fieldset > a.button.button_blog").click() # 관련도순 xpath
# element.clear()
# element.send_keys(query_txt) # query_txt는 위에서 입력한 '이재용'
# element.submit()
#Step 1. 크롬 웹브라우저 실행
path = os.getenv('HOME')+ '/chromedriver'
driver = webdriver.Chrome(path)
# 사이트 주소는 네이버
driver.get('http://www.naver.com')
time.sleep(0.1)
# # login
# login = {
# "id" : "iminu95",
# "pw" : "95bbkmjamy"
# }
# # 아이디와 비밀번호를 입력합니다.
# time.sleep(0.5) ## 0.5초
# driver.find_element_by_class_name('link_login').click( )
# time.sleep(1)
# # driver.find_element_by_name('id').send_keys('아이디') # "아이디라는 값을 보내준다"
# driver.find_element_by_name('id').send_keys(login.get("id"))
# time.sleep(0.5) ## 0.5초
# driver.find_element_by_name('pw').send_keys(login.get("pw"))
# time.sleep(0.5) ## 0.5초
# driver.find_element_by_class_name('btn_global').click( )
# time.sleep(0.5) ## 0.5초
#Step 2. 네이버 검색창에 "검색어" 검색
element = driver.find_element_by_name("query")
element.send_keys(query_txt)
element.submit()
time.sleep(0.1)
#Step 3. "블로그" 카테고리 선택
driver.find_element_by_link_text("블로그").click( )
time.sleep(2)
#Step 4. 오른쪽의 검색 옵션 버튼 클릭
driver.find_element_by_class_name("btn_option._search_option_open_btn").click( )
time.sleep(2)
#Step 6. 날짜 입력
# driver.find_element_by_class_name("txt.txt_option._calendar_select_trigger").click() # 관련도순 xpath
# driver.find_element_by_id("search_start_date").send_keys(start_date)
# driver.find_element_by_id("search_end_date").send_keys(end_date)
# time.sleep(0.1)
# driver.find_element_by_id("periodSearch").click()
# time.sleep(0.1)
# searched_post_num = driver.find_element_by_class_name('search_number').text
# print(searched_post_num)
url_list = []
title_list = []
total_page = 2
# total_page = math.ceil(int(searched_post_num.replace(',', '').strip('건')) / 7)
print('total_page :', total_page)
for i in tqdm(range(0, total_page)): # 페이지 번호
url = f'https://section.blog.naver.com/Search/Post.naver?pageNo={i}&rangeType=sim&orderBy=recentdate&startDate={start_date}&endDate={end_date}&keyword={query_txt}'
driver.get(url)
# response = requests.get(url)
# soup = BeautifulSoup(response.text, 'html.parser')
# print(soup)
time.sleep(0.5)
# area = soup.findAll('div', {'class' : 'list_search_post'}) #.find_all('a', {'class' : 'url'})
# print(area)
# URL 크롤링 시작
titles = "a.sh_blog_title._sp_each_url._sp_each_title" # #content
article_raw = driver.find_elements_by_class_name(titles)
# article_raw = driver.find_elements_by_css_selector('#content > section > div.area_list_search > div:nth-child(1)')
# article_raw = driver.find_elements_by_xpath(f'//*[@id="content"]/section/div[2]/div[{i}]')
# print(article_raw)
# url 크롤링 시작 # 7개
for article in article_raw:
url = article.get_attribute('href')
print(url)
url_list.append(url)
# 제목 크롤링 시작
for article in article_raw:
title = article.get_attribute('title')
title_list.append(title)
print(title)
print('url갯수: ', len(url_list))
print('url갯수: ', len(title_list))
# df = pd.DataFrame({'url':url_list, 'title':title_list})
# # 저장하기
# df.to_csv("./blog_url.csv")
li = [2, 3, 4, 4, 5, 6, 7, 8]
len(li)
for i in range(0, 8, 2):
print(i)
new = []
for i in range(0, len(li)-1, 2):
new.append([li[i], li[i+1]])
new
article_raw = driver.find_elements_by_xpath('//*[@id="content"]/section/div[2]/div[1]')
# article_raw.get_attribute('href')
for i in article_raw:
print(i.get_attribute('href'))
//*[@id="content"]/section/div[2]
//*[@id="content"]/section/div[2]
//*[@id="content"]/section/div[2]
//*[@id="content"]/section/div[2]/div[1]
//*[@id="content"]/section/div[2]/div[2]
//*[@id="content"]/section/div[2]/div[3]
...
//*[@id="content"]/section/div[2]/div[7] | _____no_output_____ | MIT | naversearchCrawlerSelenium.ipynb | JeongCheck/Crawling |
1 page = 7 posts72 page searchsample = https://section.blog.naver.com/Search/Post.naver?pageNo=1&rangeType=PERIOD&orderBy=sim&startDate=2019-01-01&endDate=2021-05-01&keyword=%EC%84%B1%EC%8B%AC%EB%8B%B9%EC%97%AC%ED%96%89%EB%8C%80%EC%A0%84 | ## 제목 눌러서 블로그 페이지 열기
driver.find_element_by_class_name('title').click()
time.sleep(1)
type(searched_post_num), searched_post_num
import re
re.sub('^[0-9]', '', searched_post_num)
searched_post_num
searched_post_num.replace(',', '').replace('건', '')
total_page = math.ceil(int(searched_post_num.replace(',', '').strip('건')) / 7)
total_page | _____no_output_____ | MIT | naversearchCrawlerSelenium.ipynb | JeongCheck/Crawling |
{ 'mean': [axis1, axis2, flattened], 'variance': [axis1, axis2, flattened], 'standard deviation': [axis1, axis2, flattened], 'max': [axis1, axis2, flattened], 'min': [axis1, axis2, flattened], 'sum': [axis1, axis2, flattened]} | calculations['mean']= [a.mean(axis=0).tolist(), a.mean(axis=1).tolist(), a.mean().tolist()]
calculations['mean']
calculations['variance']= [a.var(axis=0).tolist(), a.var(axis=1).tolist(), a.var().tolist()]
calculations
calculations['standard deviation']= [a.std(axis=0).tolist(), a.std(axis=1).tolist(), a.std().tolist()]
calculations
calculations['max']= [a.max(axis=0).tolist(), a.max(axis=1).tolist(), a.max().tolist()]
calculations['min']= [a.min(axis=0).tolist(), a.min(axis=1).tolist(), a.min().tolist()]
calculations['sum']= [a.sum(axis=0).tolist(), a.sum(axis=1).tolist(), a.sum().tolist()]
calculations | _____no_output_____ | MIT | data_analysis/Mean-Variance-Standard Deviation Calculator.ipynb | alanpirotta/freecodecamp_certif |
Torrent To Google Drive Downloader **Important Note:** To get more disk space:> Go to Runtime -> Change Runtime and give GPU as the Hardware Accelerator. You will get around 384GB to download any torrent you want. Install libtorrent and Initialize Session | !apt install python3-libtorrent
import libtorrent as lt
ses = lt.session()
ses.listen_on(6881, 6891)
downloads = [] | _____no_output_____ | MIT | Torrent_To_Google_Drive_Downloader.ipynb | abhibhaw/Torrent-To-Google-Drive-Downloader |
Mount Google DriveTo stream files we need to mount Google Drive. | from google.colab import drive
drive.mount("/content/drive") | _____no_output_____ | MIT | Torrent_To_Google_Drive_Downloader.ipynb | abhibhaw/Torrent-To-Google-Drive-Downloader |
Add From Torrent FileYou can run this cell to add more files as many times as you want | from google.colab import files
source = files.upload()
params = {
"save_path": "/content/drive/My Drive/Torrent",
"ti": lt.torrent_info(list(source.keys())[0]),
}
downloads.append(ses.add_torrent(params)) | _____no_output_____ | MIT | Torrent_To_Google_Drive_Downloader.ipynb | abhibhaw/Torrent-To-Google-Drive-Downloader |
Add From Magnet LinkYou can run this cell to add more files as many times as you want | params = {"save_path": "/content/drive/My Drive/Torrent"}
while True:
magnet_link = input("Enter Magnet Link Or Type Exit: ")
if magnet_link.lower() == "exit":
break
downloads.append(
lt.add_magnet_uri(ses, magnet_link, params)
)
| _____no_output_____ | MIT | Torrent_To_Google_Drive_Downloader.ipynb | abhibhaw/Torrent-To-Google-Drive-Downloader |
Start DownloadSource: https://stackoverflow.com/a/5494823/7957705 and [3 issue](https://github.com/FKLC/Torrent-To-Google-Drive-Downloader/issues/3) which refers to this [stackoverflow question](https://stackoverflow.com/a/6053350/7957705) | import time
from IPython.display import display
import ipywidgets as widgets
state_str = [
"queued",
"checking",
"downloading metadata",
"downloading",
"finished",
"seeding",
"allocating",
"checking fastresume",
]
layout = widgets.Layout(width="auto")
style = {"description_width": "initial"}
download_bars = [
widgets.FloatSlider(
step=0.01, disabled=True, layout=layout, style=style
)
for _ in downloads
]
display(*download_bars)
while downloads:
next_shift = 0
for index, download in enumerate(downloads[:]):
bar = download_bars[index + next_shift]
if not download.is_seed():
s = download.status()
bar.description = " ".join(
[
download.name(),
str(s.download_rate / 1000),
"kB/s",
state_str[s.state],
]
)
bar.value = s.progress * 100
else:
next_shift -= 1
ses.remove_torrent(download)
downloads.remove(download)
bar.close() # Seems to be not working in Colab (see https://github.com/googlecolab/colabtools/issues/726#issue-486731758)
download_bars.remove(bar)
print(download.name(), "complete")
time.sleep(1)
| _____no_output_____ | MIT | Torrent_To_Google_Drive_Downloader.ipynb | abhibhaw/Torrent-To-Google-Drive-Downloader |
Analysis of enrichment | import glob
import json
import math
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from functools import reduce
from collections import OrderedDict, defaultdict
from sklearn.feature_extraction.text import TfidfVectorizer
from scipy.stats import fisher_exact as fisher
from scipy.stats import chi2_contingency as chisq
def ease(n_outliers_path, n_total_path, n_outliers, n_total):
"""
Calculates a contingency table EASE score
[x y]
[z k]
:param n_in_path: number of outliers in the pathway
:param n_total_path: total number of genes in the pathway
:param n_outliers: total number of outliers
:param n_total: total number of genes analysed
:return:
"""
x = max(0, n_outliers_path - 1) # in category, enriched
y = n_total_path # total, enriched
z = n_outliers - n_outliers_path # in category, not enriched
k = n_total - n_total_path # total, not enriched
#if x <= 10:
_, pvalue = fisher(([[x, y], [z, k]]), alternative='greater')
#else:
# _, pvalue, _, _ = chisq(([[x, y], [z, k]]))
return pvalue | _____no_output_____ | MIT | scripts/pathways_3_categorization.ipynb | iganna/evo_epigen |
Collecting all pathway names | pathway_tables = glob.glob("../pathways/*/gp.csv")
dfs = [pd.read_csv(table) for table in pathway_tables]
for i, df in enumerate(dfs):
dfs[i] = df.set_index("SYMBOL")
dfs[i].sort_index(inplace=True)
#print(dfs[i].shape)
dfs[0]
all_entries = list(pd.concat(dfs, axis=1, sort=True).columns)
all_entries[0:10]
structures = pd.read_csv("../extracted/classification_pathways.csv", header=0, index_col="Pathway")
structures = pd.DataFrame(structures, dtype=bool)
del structures["DUPLICATE?"], structures["TRUTHFULNESS"], structures["Garbage"]
structures.head()
all_2 = set(structures.index)
set(all_entries) - all_2
pathway_types = dict()
for pathway in sorted(all_entries):
x = structures.loc[pathway]
pathway_types[pathway] = x[x].index[0]
reverse_counter = defaultdict(int)
for pathway in sorted(all_entries):
category = pathway_types[pathway]
reverse_counter[category] += 1
reverse_counter
ALL_PATHS = sum(reverse_counter.values())
ALL_PATHS | _____no_output_____ | MIT | scripts/pathways_3_categorization.ipynb | iganna/evo_epigen |
By histone tag: | my_tags = ["H3K4me3", "H3K9ac", "H3K27ac", "H3K27me3", "H3K9me3"]
ENR_COUNTERS = dict()
for hg_tag in my_tags:
files_up_human = glob.glob(f"../extracted/Human_{hg_tag}_pathways_up*")
files_down_human = glob.glob(f"../extracted/Human_{hg_tag}_pathways_down*")
files_up_mouse = glob.glob(f"../extracted/Mouse_{hg_tag}_pathways_up*")
files_down_mouse = glob.glob(f"../extracted/Mouse_{hg_tag}_pathways_down*")
files = {"Human+": files_up_human[0],
"Human-": files_down_human[0],
"Mouse+": files_up_mouse[0],
"Mouse-": files_down_mouse[0]}
enriched_counter = defaultdict(lambda: defaultdict(int))
for xtype in files:
with open(files[xtype], "r") as file:
en_pathways = file.read().strip().split("\n")
for pw in en_pathways:
cat = pathway_types[pw]
enriched_counter[xtype][cat] += 1
enriched_counter = pd.DataFrame(enriched_counter).T.fillna(0)
enriched_counter = pd.DataFrame(enriched_counter, dtype=int)
ENR_COUNTERS[hg_tag] = enriched_counter
ENR_COUNTERS[my_tags[0]] | _____no_output_____ | MIT | scripts/pathways_3_categorization.ipynb | iganna/evo_epigen |
Calculates a contingency table EASE score [x y] [z k] :param n_in_path: number of outliers in the pathway :param n_total_path: total number of genes in the pathway :param n_outliers: total number of outliers :param n_total: total number of genes analysed :return: | ksi = defaultdict(dict)
signs = {"+": "positively\u00A0enriched\u00A0(+)",
"-": "negatively\u00A0enriched\u00A0(-)"}
for hg_tag in my_tags:
enriched_counter = ENR_COUNTERS[hg_tag]
for sign in ["+", "-"]:
for org in ["Human", "Mouse"]:
for category in enriched_counter:
n1 = enriched_counter[category][f"{org}{sign}"]
n2 = sum(enriched_counter.loc[f"{org}{sign}"])
n3 = reverse_counter[category]
n4 = ALL_PATHS
#print(n1, n2, n3, n4)
ksi[category][f"{org},\u00A0{hg_tag},\u00A0{signs[sign]}"] = ease(n1, n2, n3, n4)
pd.DataFrame(ksi).to_csv(f"../extracted/pvalues.csv")
pd.DataFrame(ksi)
TAU = pd.DataFrame(ksi)
def get_highlighter_min(color, point):
def highlight_min(s):
'''
highlight the minimums in a Series.
'''
is_max = s <= point
return [f'background-color: {color}' if v else '' for v in is_max]
return highlight_min
data_round = np.round(TAU, 3)
cm = sns.light_palette("green", as_cmap=True, reverse=True)
s = data_round.style.apply(get_highlighter_min("green", 0.05), subset=([i for i in TAU.index if "+" in i], TAU.columns))
cm = sns.light_palette("red", as_cmap=True, reverse=True)
s.apply(get_highlighter_min("red", 0.05), subset=([i for i in TAU.index if "-" in i], TAU.columns))
s | _____no_output_____ | MIT | scripts/pathways_3_categorization.ipynb | iganna/evo_epigen |
Basic usage Thunder offers a variety of analyses and workflows for spatial and temporal data. When run on a cluster, most methods are efficiently and automatically parallelized, but Thunder can also be used on a single machine, especially for testing purposes. We'll walk through a very simple example here as an introduction. The entry point for most workflows is the ``ThunderContext``. If you type ``thunder`` to start the interactive shell, this context is automatically provided as ``tsc``, which is an object that primarily provides functionality for loading and exporting data.We'll start by loading and exploring some toy example data: | data = tsc.loadExample('fish-series') | _____no_output_____ | Apache-2.0 | python/doc/tutorials/src/basic_usage.ipynb | broxtronix/thunder |
``data`` is a ``Series`` object, which is a generic collection of one-dimensional array data sharing a common index. We can inspect it to see metadata: | data | _____no_output_____ | Apache-2.0 | python/doc/tutorials/src/basic_usage.ipynb | broxtronix/thunder |
A ``Series`` object is a collection of key-value records, each containing an identifier as a key and a one-dimensional array as a value. We can look at the first key and value by using ``first()``. | key, value = data.first() | _____no_output_____ | Apache-2.0 | python/doc/tutorials/src/basic_usage.ipynb | broxtronix/thunder |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.