bigcode/jupyter-parsed · Datasets at Hugging Face

cb2d5032b28c8aca852ea69fa05d553a4b1f5596

26,366

ipynb

Jupyter Notebook

assignments/2020/assignment3_colab/assignment3/StyleTransfer-TensorFlow.ipynb

benkmoore/cs231n.github.io

143e8864aed5ebe6b1ffaa407faf58d60de0adb9

[ "MIT" ]

2

2020-10-22T02:10:41.000Z

2021-05-09T11:46:53.000Z

assignments/2020/assignment3_colab/assignment3/StyleTransfer-TensorFlow.ipynb

benkmoore/cs231n.github.io

143e8864aed5ebe6b1ffaa407faf58d60de0adb9

[ "MIT" ]

32

2020-09-17T19:43:53.000Z

2022-03-12T00:55:26.000Z

assignment3/StyleTransfer-TensorFlow.ipynb

BatyrM/Stanford-CS231n-Spring-2020

112ec761589296ae1007165ea7032a3d441b2307

[ "MIT" ]

1

2020-09-24T19:57:47.000Z

43.797342

1,105

0.618372

[ [ [ "empty" ] ] ]

[ "empty" ]

[ [ "empty" ] ]

cb2d521b96bcd767cd775222e2d9e52fed751ae2

228,355

ipynb

Jupyter Notebook

qiskit/basics/getting_started_with_qiskit.ipynb

Chibikuri/qiskit-tutorials

15c121b95249de17e311c869fbc455210b2fcf5e

[ "Apache-2.0" ]

1

2019-03-28T15:23:37.000Z

qiskit/basics/getting_started_with_qiskit.ipynb

Chibikuri/qiskit-tutorials

15c121b95249de17e311c869fbc455210b2fcf5e

[ "Apache-2.0" ]

null

qiskit/basics/getting_started_with_qiskit.ipynb

Chibikuri/qiskit-tutorials

15c121b95249de17e311c869fbc455210b2fcf5e

[ "Apache-2.0" ]

2

2019-03-24T21:00:25.000Z

2019-03-24T21:57:10.000Z

235.417526

152,972

0.915018

[ [ [ "<img src=\"../../images/qiskit-heading.gif\" alt=\"Note: In order for images to show up in this jupyter notebook you need to select File => Trusted Notebook\" width=\"500 px\" align=\"left\">", "_____no_output_____" ], [ "# Getting Started with Qiskit\n\nHere, we provide an overview of working with Qiskit. Qiskit provides the basic building blocks necessary to program quantum computers. The basic concept of Qiskit is an array of quantum circuits. A workflow using Qiskit consists of two stages: **Build** and **Execute**. **Build** allows you to make different quantum circuits that represent the problem you are solving, and **Execute** allows you to run them on different backends. After the jobs have been run, the data is collected. There are methods for putting this data together, depending on the program. This either gives you the answer you wanted, or allows you to make a better program for the next instance.\n\n\n**Contents**\n\n[Circuit basics](#circuit_basics)\n\n[Simulating circuits with Qiskit Aer](#aer_simulation)\n\n[Running circuits using the IBMQ provider](#ibmq_provider)", "_____no_output_____" ], [ "**Code imports**", "_____no_output_____" ] ], [ [ "import numpy as np\nfrom qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister\nfrom qiskit import execute", "_____no_output_____" ] ], [ [ "## Circuit Basics <a id='circuit_basics'></a>\n\n\n### Building the circuit\n\nThe basic elements needed for your first program are the QuantumCircuit, and QuantumRegister.", "_____no_output_____" ] ], [ [ "# Create a Quantum Register with 3 qubits.\nq = QuantumRegister(3, 'q')\n\n# Create a Quantum Circuit acting on the q register\ncirc = QuantumCircuit(q)", "_____no_output_____" ] ], [ [ "<div class=\"alert alert-block alert-info\">\n<b>Note:</b> Naming the QuantumRegister is optional and not required.\n</div>\n\nAfter you create the circuit with its registers, you can add gates (\"operations\") to manipulate the registers. As you proceed through the documentation you will find more gates and circuits; the below is an example of a quantum circuit that makes a three-qubit GHZ state\n\n$$|\\psi\\rangle = \\left(|000\\rangle+|111\\rangle\\right)/\\sqrt{2}.$$\n\nTo create such a state, we start with a 3-qubit quantum register. By default, each qubit in the register is initialized to $|0\\rangle$. To make the GHZ state, we apply the following gates:\n* A Hadamard gate $H$ on qubit 0, which puts it into a superposition state.\n* A controlled-Not operation ($C_{X}$) between qubit 0 and qubit 1.\n* A controlled-Not operation between qubit 0 and qubit 2.\n\nOn an ideal quantum computer, the state produced by running this circuit would be the GHZ state above.\n\nIn Qiskit, operations can be added to the circuit one-by-one, as shown below.", "_____no_output_____" ] ], [ [ "# Add a H gate on qubit 0, putting this qubit in superposition.\ncirc.h(q[0])\n# Add a CX (CNOT) gate on control qubit 0 and target qubit 1, putting\n# the qubits in a Bell state.\ncirc.cx(q[0], q[1])\n# Add a CX (CNOT) gate on control qubit 0 and target qubit 2, putting\n# the qubits in a GHZ state.\ncirc.cx(q[0], q[2])", "_____no_output_____" ] ], [ [ "## Visualize Circuit\n\nYou can visualize your circuit using Qiskit `QuantumCircuit.draw()`, which plots circuit in the form found in many textbooks.", "_____no_output_____" ] ], [ [ "circ.draw()", "_____no_output_____" ] ], [ [ "In this circuit, the qubits are put in order with qubit zero at the top and qubit two at the bottom. The circuit is read left-to-right (meaning that gates which are applied earlier in the circuit show up further to the left).", "_____no_output_____" ], [ "## Simulating circuits using Qiskit Aer <a id='aer_simulation'></a>\n\nQiskit Aer is our package for simulating quantum circuits. It provides many different backends for doing a simulation. Here we use the basic python version.\n\n### Statevector backend\n\nThe most common backend in Qiskit Aer is the `statevector_simulator`. This simulator returns the quantum \nstate which is a complex vector of dimensions $2^n$ where $n$ is the number of qubits \n(so be careful using this as it will quickly get too large to run on your machine).", "_____no_output_____" ], [ "<div class=\"alert alert-block alert-info\">\n\n\nWhen representing the state of a multi-qubit system, the tensor order used in qiskit is different than that use in most physics textbooks. Suppose there are $n$ qubits, and qubit $j$ is labeled as $Q_{j}$. In most textbooks (such as Nielsen and Chuang's \"Quantum Computation and Information\"), the basis vectors for the $n$-qubit state space would be labeled as $Q_{0}\\otimes Q_{1} \\otimes \\cdots \\otimes Q_{n}$. **This is not the ordering used by qiskit!** Instead, qiskit uses an ordering in which the $n^{\\mathrm{th}}$ qubit is on the <em><strong>left</strong></em> side of the tensor product, so that the basis vectors are labeled as $Q_n\\otimes \\cdots \\otimes Q_1\\otimes Q_0$.\n\nFor example, if qubit zero is in state 0, qubit 1 is in state 0, and qubit 2 is in state 1, qiskit would represent this state as $|100\\rangle$, whereas most physics textbooks would represent it as $|001\\rangle$.\n\nThis difference in labeling affects the way multi-qubit operations are represented as matrices. For example, qiskit represents a controlled-X ($C_{X}$) operation with qubit 0 being the control and qubit 1 being the target as\n\n$$C_X = \\begin{pmatrix} 1 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 1 & 0 \\\\ 0 & 1 & 0 & 0 \\\\\\end{pmatrix}.$$\n\n</div>\n\nTo run the above circuit using the statevector simulator, first you need to import Aer and then set the backend to `statevector_simulator`.", "_____no_output_____" ] ], [ [ "# Import Aer\nfrom qiskit import BasicAer\n\n# Run the quantum circuit on a statevector simulator backend\nbackend = BasicAer.get_backend('statevector_simulator')", "_____no_output_____" ] ], [ [ "Now we have chosen the backend it's time to compile and run the quantum circuit. In Qiskit we provide the `execute` function for this. ``execute`` returns a ``job`` object that encapsulates information about the job submitted to the backend.\n\n\n<div class=\"alert alert-block alert-info\">\n<b>Tip:</b> You can obtain the above parameters in Jupyter. Simply place the text cursor on a function and press Shift+Tab.\n</div>", "_____no_output_____" ] ], [ [ "# Create a Quantum Program for execution \njob = execute(circ, backend)", "_____no_output_____" ] ], [ [ "When you run a program, a job object is made that has the following two useful methods: \n`job.status()` and `job.result()` which return the status of the job and a result object respectively.\n\n<div class=\"alert alert-block alert-info\">\n<b>Note:</b> Jobs run asynchronously but when the result method is called it switches to synchronous and waits for it to finish before moving on to another task.\n</div>", "_____no_output_____" ] ], [ [ "result = job.result()", "_____no_output_____" ] ], [ [ "The results object contains the data and Qiskit provides the method \n`result.get_statevector(circ)` to return the state vector for the quantum circuit.", "_____no_output_____" ] ], [ [ "outputstate = result.get_statevector(circ, decimals=3)\nprint(outputstate)", "[0.707+0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j\n 0.707+0.j]\n" ] ], [ [ "Qiskit also provides a visualization toolbox to allow you to view these results.\n\nBelow, we use the visualization function to plot the real and imaginary components of the state vector.", "_____no_output_____" ] ], [ [ "from qiskit.tools.visualization import plot_state_city\nplot_state_city(outputstate)", "_____no_output_____" ] ], [ [ "### Unitary backend", "_____no_output_____" ], [ "Qiskit Aer also includes a `unitary_simulator` that works _provided all the elements in the circuit are unitary operations_. This backend calculates the $2^n \\times 2^n$ matrix representing the gates in the quantum circuit. ", "_____no_output_____" ] ], [ [ "# Run the quantum circuit on a unitary simulator backend\nbackend = BasicAer.get_backend('unitary_simulator')\njob = execute(circ, backend)\nresult = job.result()\n\n# Show the results\nprint(result.get_unitary(circ, decimals=3))", "[[ 0.707+0.j 0.707+0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j\n 0. +0.j 0. +0.j]\n [ 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j\n 0.707+0.j -0.707+0.j]\n [ 0. +0.j 0. +0.j 0.707+0.j 0.707+0.j 0. +0.j 0. +0.j\n 0. +0.j 0. +0.j]\n [ 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0.707+0.j -0.707+0.j\n 0. +0.j 0. +0.j]\n [ 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0.707+0.j 0.707+0.j\n 0. +0.j 0. +0.j]\n [ 0. +0.j 0. +0.j 0.707+0.j -0.707+0.j 0. +0.j 0. +0.j\n 0. +0.j 0. +0.j]\n [ 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j\n 0.707+0.j 0.707+0.j]\n [ 0.707+0.j -0.707+0.j 0. +0.j 0. +0.j 0. +0.j 0. +0.j\n 0. +0.j 0. +0.j]]\n" ] ], [ [ "### OpenQASM backend", "_____no_output_____" ], [ "The simulators above are useful because they provide information about the state output by the ideal circuit and the matrix representation of the circuit. However, a real experiment terminates by _measuring_ each qubit (usually in the computational $|0\\rangle, |1\\rangle$ basis). Without measurement, we cannot gain information about the state. Measurements cause the quantum system to collapse into classical bits. \n\nFor example, suppose we make independent measurements on each qubit of the three-qubit GHZ state\n$$|\\psi\\rangle = |000\\rangle +|111\\rangle)/\\sqrt{2},$$\nand let $xyz$ denote the bitstring that results. Recall that, under the qubit labeling used by Qiskit, $x$ would correspond to the outcome on qubit 2, $y$ to the outcome on qubit 1, and $z$ to the outcome on qubit 0. This representation of the bitstring puts the most significant bit (MSB) on the left, and the least significant bit (LSB) on the right. This is the standard ordering of binary bitstrings. We order the qubits in the same way, which is why Qiskit uses a non-standard tensor product order.\n\nThe probability of obtaining outcome $xyz$ is given by\n$$\\mathrm{Pr}(xyz) = |\\langle xyz | \\psi \\rangle |^{2}.$$\nBy explicit computation, we see there are only two bitstrings that will occur: $000$ and $111$. If the bitstring $000$ is obtained, the state of the qubits is $|000\\rangle$, and if the bitstring is $111$, the qubits are left in the state $|111\\rangle$. The probability of obtaining 000 or 111 is the same; namely, 1/2:\n$$\\begin{align}\n\\mathrm{Pr}(000) &= |\\langle 000 | \\psi \\rangle |^{2} = \\frac{1}{2}\\\\\n\\mathrm{Pr}(111) &= |\\langle 111 | \\psi \\rangle |^{2} = \\frac{1}{2}.\n\\end{align}$$\n\nTo simulate a circuit that includes measurement, we need to add measurements to the original circuit above, and use a different Aer backend.", "_____no_output_____" ] ], [ [ "# Create a Classical Register with 3 bits.\nc = ClassicalRegister(3, 'c')\n# Create a Quantum Circuit\nmeas = QuantumCircuit(q, c)\nmeas.barrier(q)\n# map the quantum measurement to the classical bits\nmeas.measure(q,c)\n\n# The Qiskit circuit object supports composition using\n# the addition operator.\nqc = circ+meas\n\n#drawing the circuit\nqc.draw()", "_____no_output_____" ] ], [ [ "This circuit adds a classical register, and three measurements that are used to map the outcome of qubits to the classical bits. \n\nTo simulate this circuit, we use the ``qasm_simulator`` in Qiskit Aer. Each run of this circuit will yield either the bitstring 000 or 111. To build up statistics about the distribution of the bitstrings (to, e.g., estimate $\\mathrm{Pr}(000)$), we need to repeat the circuit many times. The number of times the circuit is repeated can be specified in the ``execute`` function, via the ``shots`` keyword.", "_____no_output_____" ] ], [ [ "# Use Aer's qasm_simulator\nbackend_sim = BasicAer.get_backend('qasm_simulator')\n\n# Execute the circuit on the qasm simulator.\n# We've set the number of repeats of the circuit\n# to be 1024, which is the default.\njob_sim = execute(qc, backend_sim, shots=1024)\n\n# Grab the results from the job.\nresult_sim = job_sim.result()", "_____no_output_____" ] ], [ [ "Once you have a result object, you can access the counts via the function `get_counts(circuit)`. This gives you the _aggregated_ binary outcomes of the circuit you submitted.", "_____no_output_____" ] ], [ [ "counts = result_sim.get_counts(qc)\nprint(counts)", "{'000': 526, '111': 498}\n" ] ], [ [ "Approximately 50 percent of the time the output bitstring is 000. Qiskit also provides a function `plot_histogram` which allows you to view the outcomes. ", "_____no_output_____" ] ], [ [ "from qiskit.tools.visualization import plot_histogram\nplot_histogram(counts)", "_____no_output_____" ] ], [ [ "The estimated outcome probabilities $\\mathrm{Pr}(000)$ and $\\mathrm{Pr}(111)$ are computed by taking the aggregate counts and dividing by the number of shots (times the circuit was repeated). Try changing the ``shots`` keyword in the ``execute`` function and see how the estimated probabilities change.", "_____no_output_____" ], [ "## Running circuits using the IBMQ provider <a id='ibmq_provider'></a>\n\nTo faciliate access to real quantum computing hardware, we have provided a simple API interface.\nTo access IBMQ devices, you'll need an API token. For the public IBM Q devices, you can generate an API token [here](https://quantumexperience.ng.bluemix.net/qx/account/advanced) (create an account if you don't already have one). For Q Network devices, login to the q-console, click your hub, group, and project, and expand \"Get Access\" to generate your API token and access url.\n\nOur IBMQ provider lets you run your circuit on real devices or on our HPC simulator. Currently, this provider exists within Qiskit, and can be imported as shown below. For details on the provider, see [The IBMQ Provider](the_ibmq_provider.ipynb).", "_____no_output_____" ] ], [ [ "from qiskit import IBMQ", "_____no_output_____" ] ], [ [ "After generating your API token, call: `IBMQ.save_account('MY_TOKEN')`. For Q Network users, you'll also need to include your access url: `IBMQ.save_account('MY_TOKEN', 'URL')`\n\nThis will store your IBMQ credentials in a local file. Unless your registration information has changed, you only need to do this once. You may now load your accounts by calling,", "_____no_output_____" ] ], [ [ "IBMQ.load_accounts()", "_____no_output_____" ] ], [ [ "Once your account has been loaded, you can view the list of backends available to you.", "_____no_output_____" ] ], [ [ "print(\"Available backends:\")\nIBMQ.backends()", "Available backends:\n" ] ], [ [ "### Running circuits on real devices\n\nToday's quantum information processors are small and noisy, but are advancing at a fast pace. They provide a great opportunity to explore what [noisy, intermediate-scale quantum (NISQ)](https://arxiv.org/abs/1801.00862) computers can do.", "_____no_output_____" ], [ "The IBMQ provider uses a queue to allocate the devices to users. We now choose a device with the least busy queue which can support our program (has at least 3 qubits).", "_____no_output_____" ] ], [ [ "from qiskit.providers.ibmq import least_busy\n\nlarge_enough_devices = IBMQ.backends(filters=lambda x: x.configuration().n_qubits > 4 and\n not x.configuration().simulator)\nbackend = least_busy(large_enough_devices)\nprint(\"The best backend is \" + backend.name())", "The best backend is ibmqx4\n" ] ], [ [ "To run the circuit on the backend, we need to specify the number of shots and the number of credits we are willing to spend to run the circuit. Then, we execute the circuit on the backend using the ``execute`` function.", "_____no_output_____" ] ], [ [ "from qiskit.tools.monitor import job_monitor\nshots = 1024 # Number of shots to run the program (experiment); maximum is 8192 shots.\nmax_credits = 3 # Maximum number of credits to spend on executions. \n\njob_exp = execute(qc, backend=backend, shots=shots, max_credits=max_credits)\njob_monitor(job_exp)", "_____no_output_____" ] ], [ [ "``job_exp`` has a ``.result()`` method that lets us get the results from running our circuit.\n\n<div class=\"alert alert-block alert-info\">\n<b>Note:</b> When the .result() method is called, the code block will wait until the job has finished before releasing the cell.\n</div>", "_____no_output_____" ] ], [ [ "result_exp = job_exp.result()", "_____no_output_____" ] ], [ [ "Like before, the counts from the execution can be obtained using ```get_counts(qc)``` ", "_____no_output_____" ] ], [ [ "counts_exp = result_exp.get_counts(qc)\nplot_histogram([counts_exp,counts])", "_____no_output_____" ] ], [ [ "### Simulating circuits using a HPC simulator\n\nThe IBMQ provider also comes with a remote optimized simulator called ``ibmq_qasm_simulator``. This remote simulator is capable of simulating up to 32 qubits. It can be used the \nsame way as the remote real backends. ", "_____no_output_____" ] ], [ [ "backend = IBMQ.get_backend('ibmq_qasm_simulator', hub=None)", "_____no_output_____" ], [ "shots = 1024 # Number of shots to run the program (experiment); maximum is 8192 shots.\nmax_credits = 3 # Maximum number of credits to spend on executions. \n\njob_hpc = execute(qc, backend=backend, shots=shots, max_credits=max_credits)", "_____no_output_____" ], [ "result_hpc = job_hpc.result()", "_____no_output_____" ], [ "counts_hpc = result_hpc.get_counts(qc)\nplot_histogram(counts_hpc)", "_____no_output_____" ] ], [ [ "### Retrieving a previously ran job\n\nIf your experiment takes longer to run then you have time to wait around, or if you simply want to retrieve old jobs back, the IBMQ backends allow you to do that.\nFirst you would need to note your job's ID:", "_____no_output_____" ] ], [ [ "jobID = job_exp.job_id()\n\nprint('JOB ID: {}'.format(jobID)) ", "JOB ID: 5c56667159faae0051bceb52\n" ] ], [ [ "Given a job ID, that job object can be later reconstructed from the backend using retrieve_job:", "_____no_output_____" ] ], [ [ "job_get=backend.retrieve_job(jobID)", "_____no_output_____" ] ], [ [ "and then the results can be obtained from the new job object. ", "_____no_output_____" ] ], [ [ "job_get.result().get_counts(qc)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2d56daccde2bbf813dfb35d6bb6f984d5ca12f

133,149

ipynb

Jupyter Notebook

03_simulacion/casos_codigo/clase02_caso_simulacion_exponencial/simulacion_exponencial.ipynb

juanntripaldi/pyOperativ

8bf58b6221c5344e9d088703782530278cb10ca1

[ "Apache-2.0" ]

1

2021-05-04T12:33:39.000Z

03_simulacion/casos_codigo/clase02_caso_simulacion_exponencial/simulacion_exponencial.ipynb

juanntripaldi/pyOperativ

8bf58b6221c5344e9d088703782530278cb10ca1

[ "Apache-2.0" ]

null

03_simulacion/casos_codigo/clase02_caso_simulacion_exponencial/simulacion_exponencial.ipynb

juanntripaldi/pyOperativ

8bf58b6221c5344e9d088703782530278cb10ca1

[ "Apache-2.0" ]

null

150.791619

31,904

0.879789

[ [ [ "____\n__Universidad Tecnológica Nacional, Buenos Aires__\\\n__Ingeniería Industrial__\\\n__Cátedra de Investigación Operativa__\\\n__Autor: Martín Palazzo__ ([email protected]) y __Rodrigo Maranzana__ ([email protected])\n____", "_____no_output_____" ], [ "# Simulación con distribución Exponencial", "_____no_output_____" ], [ "<h1>Índice<span class=\"tocSkip\"></span></h1>\n<div class=\"toc\"><ul class=\"toc-item\"><li><span><a href=\"#Introducción\" data-toc-modified-id=\"Introducción-1\"><span class=\"toc-item-num\">1  </span>Introducción</a></span></li><li><span><a href=\"#Desarrollo\" data-toc-modified-id=\"Desarrollo-2\"><span class=\"toc-item-num\">2  </span>Desarrollo</a></span><ul class=\"toc-item\"><li><span><a href=\"#Función-de-sampleo-(muestreo)-de-una-variable-aleatoria-con-distribución-exponencial\" data-toc-modified-id=\"Función-de-sampleo-(muestreo)-de-una-variable-aleatoria-con-distribución-exponencial-2.1\"><span class=\"toc-item-num\">2.1  </span>Función de sampleo (muestreo) de una variable aleatoria con distribución exponencial</a></span></li><li><span><a href=\"#Ejemplo-de-sampleo-de-variable-exponencial\" data-toc-modified-id=\"Ejemplo-de-sampleo-de-variable-exponencial-2.2\"><span class=\"toc-item-num\">2.2  </span>Ejemplo de sampleo de variable exponencial</a></span></li><li><span><a href=\"#Ejemplo:-cálculo-de-cantidad-de-autos-que-ingresan-por-hora-en-una-autopista\" data-toc-modified-id=\"Ejemplo:-cálculo-de-cantidad-de-autos-que-ingresan-por-hora-en-una-autopista-2.3\"><span class=\"toc-item-num\">2.3  </span>Ejemplo: cálculo de cantidad de autos que ingresan por hora en una autopista</a></span><ul class=\"toc-item\"><li><span><a href=\"#Simulación-de-tiempos-de-arribo-como-variable-aleatoria-exponencial\" data-toc-modified-id=\"Simulación-de-tiempos-de-arribo-como-variable-aleatoria-exponencial-2.3.1\"><span class=\"toc-item-num\">2.3.1  </span>Simulación de tiempos de arribo como variable aleatoria exponencial</a></span></li><li><span><a href=\"#Tiempos-acumulados\" data-toc-modified-id=\"Tiempos-acumulados-2.3.2\"><span class=\"toc-item-num\">2.3.2  </span>Tiempos acumulados</a></span></li><li><span><a href=\"#Cantidad-de-arribos-por-hora\" data-toc-modified-id=\"Cantidad-de-arribos-por-hora-2.3.3\"><span class=\"toc-item-num\">2.3.3  </span>Cantidad de arribos por hora</a></span></li><li><span><a href=\"#Estadística-sobre-tiempo-entre-arribos\" data-toc-modified-id=\"Estadística-sobre-tiempo-entre-arribos-2.3.4\"><span class=\"toc-item-num\">2.3.4  </span>Estadística sobre tiempo entre arribos</a></span></li><li><span><a href=\"#Estadística-sobre-cantidad-de-arribos\" data-toc-modified-id=\"Estadística-sobre-cantidad-de-arribos-2.3.5\"><span class=\"toc-item-num\">2.3.5  </span>Estadística sobre cantidad de arribos</a></span></li></ul></li></ul></li><li><span><a href=\"#Conclusión\" data-toc-modified-id=\"Conclusión-3\"><span class=\"toc-item-num\">3  </span>Conclusión</a></span></li></ul></div>", "_____no_output_____" ], [ "## Introducción", "_____no_output_____" ], [ "El objetivo de este _Notebook_ es entender cómo se pueden simular valores de una variable aleatoria que sigue distribución exponencial. Ademas, hacer tratamiento de estos resultados obtenidos para obtener información relevante y comprender el uso de distintas librerías de Python.\n\nEsta distribución posee la propiedad de no tener memoria. Es decir, las probabilidades no dependen de la historia que tuvo el proceso.\n\nPor otro lado, esta distribución de probabilidad es sumamente útil para muchos casos que podemos encontrar en la realidad. Algunos ejemplos son: la gestión del mantenimiento industrial, en donde buscamos simular el tiempo entre fallas de una máquina; la teoría de filas de espera, donde el tiempo entre arribos o despachos de personas es la variable aleatoria de interés.", "_____no_output_____" ], [ "## Desarrollo", "_____no_output_____" ], [ "En primer lugar, importamos librerías de utilidad. Por un lado, _Random_ , _Numpy_ y _Math_ para el manejo matemático y de probabilidad; por el otro, _MatPlotLib_ y _Seaborn_ para graficar los resultados.", "_____no_output_____" ] ], [ [ "import random\nimport math\nimport numpy as np\nimport matplotlib.pyplot as plt\nfrom scipy import stats", "_____no_output_____" ] ], [ [ "### Función de sampleo (muestreo) de una variable aleatoria con distribución exponencial", "_____no_output_____" ], [ "Creamos una función para samplear/muestrear un valor de una variable exponencial. Como entrada, en primer lugar, la función nos pedirá el parámetro de tasa $\\lambda$ del proceso. Este parámetro, por ejemplo, podría simbolizar la cantidad de eventos por unidad de tiempo. \n\nAdemás, ingresamos un valor de una variable aleatoria uniforme $u$, entre los valores 0 y 1. Esto se simboliza como:\n\n$u \\sim U(0, 1)$\n\nDentro de la función, calcularemos el valor de la variable aleatoria, que llamamos $t$ a través del método de la transformada inversa de la distribución exponencial, es decir:\n\n$ t = - (1 \\ / \\ \\lambda) \\log{u}$\n\nPor lo tanto t es una variable aleatoria distribuida exponencialmente, es decir:\n\n$t \\sim Exp(\\lambda)$\n\nEn los ejercicios relacionados con investigación operativa, la variable aleatoria a simular con distribución exponencial será t y representará **el tiempo entre arribos** o **el tiempo entre despachos**. A continuación, lo programamos:", "_____no_output_____" ] ], [ [ "# Creamos la función de python llamada \"samplear_exponencial\". \n# Los inputs son \"lam\" y \"r\"\n# El output de la función será la expresión matematica para calcular \"t\"\n# la variable input \"lam\" es el lambda del problema\n# la variable input \"r\" es un número aleatorio muestreado desde una distribución uniforme\n\ndef samplear_exponencial(lam, r):\n return - (1 / lam) * np.log(1-r)", "_____no_output_____" ] ], [ [ "### Ejemplo de sampleo de variable exponencial", "_____no_output_____" ], [ "Buscamos samplear un valor de una variable aleatoria exponencial con una media $\\mu$ de 0.2. Recordemos que la media, o esperanza de la distribución exponencial es:\n\n$\\mathop{\\mathbb{E}}[X] = 1 \\ / \\ \\lambda$\n\nPara entenderlo mejor, este valor de la esperanza podría simbolizar el tiempo medio entre eventos. Por lo tanto, $\\lambda$ sería **la tasa de eventos por unidad de tiempo**.\n", "_____no_output_____" ] ], [ [ "# definimos el valor de la variable mu\nmu = 0.2\n\n# definimos el valor de la variable lamda\nlam = 1 / mu", "_____no_output_____" ] ], [ [ "Para conseguir un valor de la variable aleatoria, simplemente tenemos que llamar a la función __samplear_exponencial__ creada anteriormente. Recordemos primero calcular los valores necesarios para alimentar la función, es decir, el valor del parámetro $\\lambda$, escrito arriba, y un valor de la variable aleatoria uniforme.", "_____no_output_____" ] ], [ [ "# 1) Sampleo de variable aleatoria uniforme:\nu = random.uniform(0.001, 0.999)\nu = 0.41\nlam = 3\n\n# 2) Sampleo de variable aleatoria exponencial utilizando la función \"samplear_exponencial\" que definimos arriba\nvalor_exp = samplear_exponencial(lam, u)\n\n# Imprimir valor:\nprint(f\"Un valor de la variable aleatoria exponencial es t = {valor_exp}\")", "Un valor de la variable aleatoria exponencial es t = 0.1758775806941239\n" ] ], [ [ "En el paso anterior muestreamos aleatoriamente una sola vez una distribución exponencial y obtuvimos un valor de t. Recordemos que _t_ es el tiempo entre eventos, estos eventos pueden ser arribos o despachos por ejemplo. En otras palabras simulamos una variable aleatoria solamente \"en una iteración\". Podriamos repetir el mismo proceso nuevamente para obtener otro numero de _t_ proveniente de la misma distribución exponencial. Repitiendo el proceso vamos a tener otro número de t ya que al inicio cuando muestreamos un valor de la distribución uniforme esta tomará un valor aleatorio que sera distinto al caso anterior. ", "_____no_output_____" ] ], [ [ "# 1) vuelvo a samplear la variable aleatoria uniforme:\nu = random.uniform(0.001, 0.999)\n \n# 2) utilizo el nuevo número aleatorio uniforme U \n# con ese nuevo valor de U lo utilizo como input de la función \"samplear_exponencial\"\n# lambda sigue siendo el mismo ya que la distribución a simular sigue siendo la misma\nvalor_exp = samplear_exponencial(lam, u)\n\n# Imprimir valor:\nprint(f\"Un valor de la variable aleatoria exponencial es t = {valor_exp}\")", "Un valor de la variable aleatoria exponencial es t = 0.02293444529803619\n" ] ], [ [ "### Ejemplo: cálculo de cantidad de autos que ingresan por hora en una autopista", "_____no_output_____" ], [ "Supongamos que buscamos calcular a través de simulación, la cantidad de autos que entran por un ingreso determinado de una autopista por hora. En primer lugar hacemos las siguientes suposiciones:\n\n- Todos los vehículos son iguales.\n- No hay horarios pico, el flujo de autos es siempre igual.\n- El tiempo de arribos de vehículos sigue una distribución exponencial con una media de 0.2 horas.\n\nAdemás sabemos que vamos a trabajar con una simulación de 200 autos ingresados.", "_____no_output_____" ], [ "#### Simulación de tiempos de arribo como variable aleatoria exponencial", "_____no_output_____" ], [ "Vamos a simular 200 tiempos de arribo de vehículos. Cabe aclarar, que cada uno de estos valores simulados son formalmente __\"tiempo de arribo entre vehículos sucesivos\"__. Es decir, representan el tiempo actual en el que ingresa un vehículo desde que ingresó el anterior. Por lo tanto, podemos pensarlos como tiempos relativos al último arribo.\n\nPor ejemplo, si el primer tiempo arrojó 0.7 horas, y el segundo 0.2 horas. El segundo vehículo ingresó 0.2 horas luego del primero. Pensado de manera absoluta, el segundo vehículo ingresó a la suma de los dos tiempos, es decir, a las 0.9 horas.", "_____no_output_____" ] ], [ [ "n = 200\nmu = 0.2\n\nlam = 1 / mu", "_____no_output_____" ] ], [ [ "En primer lugar, creamos un vector de _Numpy_ lleno de ceros y con una longitud igual a la cantidad de sampleos a realizar.", "_____no_output_____" ] ], [ [ "tiempos = np.zeros(n)", "_____no_output_____" ], [ "#visualizamos en pantalla el vector tiempos\ntiempos", "_____no_output_____" ] ], [ [ "Dado que buscamos samplear/muestrear 200 tiempos, vamos a iterar 200 veces la función que creamos anteriormente y guardar su resultado en el vector de nombre __tiempos__ que creamos anteriormente. Podemos pensar a las iteraciones como eventos en donde ingresa un nuevo vehículo.", "_____no_output_____" ] ], [ [ "# hacemos un ciclo \"for\" donde la variable \"i\" iterará y tomará un valor escalonado entre \"0\" y \"n\" de 1 en 1\n# en cada iteración del ciclo \"for\" simularemos distintos valores de tiempo entre arribos\nfor i in range(0, n):\n \n # Sampleo de variable aleatoria uniforme:\n u = random.uniform(0.001, 0.999)\n \n # Sampleo de variable aleatoria exponencial:\n tiempos[i] = samplear_exponencial(lam, u)", "_____no_output_____" ] ], [ [ "A continuación, vamos a imprimir los primeros 20 valores que sampleamos, es decir, acceder al vector __tiempos__. Solamente imprimimos los primeros 20, para evitar visualizar tantos números al mismo tiempo.", "_____no_output_____" ] ], [ [ "tiempos[0:20]\n\n# Nota: recordemos que en Jupyter Notebook podemos visualizar simplemente ejecutando el nombre de un objeto.\n# Esto no sucede en otro contexto, sino que tendremos que escribir print(tiempos[0:20])", "_____no_output_____" ] ], [ [ "Vamos a utilizar el gráfico de barras de la librería _MatPlotLib_ para visualizar los valores obtenidos a través de cada una de las iteraciones en el vector __tiempos__. Es decir, el eje _x_ del gráfico serán las iteraciones y el _y_ el valor de la variable aleatoria correspondiente.", "_____no_output_____" ] ], [ [ "# Creamos una figura y el gráfico de barras:\nplt.figure(figsize=(13,7))\nplt.bar(range(0,n), tiempos)\n\n# Seteamos título y etiquetas de los ejes:\nplt.title(f'Valores simulados de una variable aleatoria Exponencial luego de {n} iteraciones')\nplt.ylabel('Tiempo entre arribos')\nplt.xlabel('Iteración')\n\n# Mostramos el gráfico:\nplt.show()", "_____no_output_____" ] ], [ [ "#### Tiempos acumulados", "_____no_output_____" ], [ "En este punto buscamos calcular los tiempos acumulados en cada iteración. Como dijimos en el título anterior, es lo que más nos interesa a la hora de poder entender las simulaciones. Dado que lo simulado es el \"tiempo entre arribos\", si queremos conocer la hora a la que ingresó un determinado vehículo, necesitamos conocer el acumulado.\n\nCreamos un vector de _Numpy_ lleno de ceros, de longitud de iteraciones, que va a contener los tiempos acumulados en cada iteración. El valor de la primera posición del vector, será el primer valor generado en el vector __tiempos__.", "_____no_output_____" ] ], [ [ "# Creamos un vector de ceros:\nt_acumulado = np.zeros(n)\n\n# Cargamos el primer valor como el primer sampleo de tiempos:\nt_acumulado[0] = tiempos[0]", "_____no_output_____" ] ], [ [ "Luego, comenzamos a llenar el vector con los valores acumulados. \n\nEsto se hace iterando en un ciclo __for__. Dado un índice cualquiera $j$, sumamos el valor del vector __t_acumulado__ en el índice anterior $j-1$ al sampleo hecho en el vector __tiempos__ en el índice $j$ actual.", "_____no_output_____" ] ], [ [ "for j in range(1, n):\n t_acumulado[j] = tiempos[j] + t_acumulado[j-1]", "_____no_output_____" ] ], [ [ "A continuación, vamos a imprimir los primeros 20 valores acumulados de la misma forma que hicimos anteriormente.", "_____no_output_____" ] ], [ [ "t_acumulado[0:20]", "_____no_output_____" ] ], [ [ "De la misma manera que hicimos con las simulaciones, visualizamos los tiempos acumulados por cada iteración con un gráfico de barras.", "_____no_output_____" ] ], [ [ "# Creamos una figura y el gráfico de barras:\nplt.figure(figsize=(13,7))\nplt.bar(range(0, n), t_acumulado)\n\n# Seteamos título y etiquetas de los ejes:\nplt.title(f'Valor acumulado del tiempo entre arribos simulado luego de {n} iteraciones')\nplt.ylabel('Valor acumulado de tiempo entre arribos')\nplt.xlabel('Iteración')\n\n# Mostramos el gráfico:\nplt.show()", "_____no_output_____" ] ], [ [ "#### Cantidad de arribos por hora", "_____no_output_____" ], [ "En este apartado vamos a utilizar el vector de tiempos acumulados __t_acumulado__ para calcular cuantos arribos hubo por hora.\n\nDado que en el vector de tiempos acumulados conocemos para cada vehículo ingresado su tiempo absoluto de arribo, solamente necesitamos clasificarlos según su hora de llegada.\n\nVamos a crear un vector, en el cual cada índice represente una hora de llegada. Por ejemplo, el índice 0, serán los vehículos ingresados desde la hora 0 a la 1.\n\nRevisando el vector __t_acumulado__, sabemos que tenemos acumuladas más de 40 horas absolutas. Al estar ordenados de manera ascendente, podemos revisar la hora de corte en el último valor. Esta hora determina el tamaño del vector de cantidades que queremos armar. En otras palabras, tendremos tantas posiciones como horas enteras registradas y en cada una contaremos la cantidad de vehículos encontrados.", "_____no_output_____" ] ], [ [ "# Creamos un vector donde cada índice representa la hora de llegada.\nult_hora = t_acumulado[-1]\nhoras = int(ult_hora)\narribos_horas = np.zeros(horas + 1).astype(int)", "_____no_output_____" ] ], [ [ "Vamos a iterar para cada vehículo simulado y obtener el valor de tiempo absoluto (acumulado) en el que arribó.\n\nUna manera rápida de poder clasificarlo, es tomar la parte entera del valor de tiempo de arribo. Es decir si el vehículo ingresó a las 3.25, sabemos que pertenece a la clasificación de la hora 3.\n\nA continuación, usamos la hora que encontramos como índice del vector __arribos_horas__ y lo incrementamos en una unidad. Esto quiere decir que un vehículo más ingresó a esa hora.", "_____no_output_____" ] ], [ [ "for i in range(0, n):\n # Extraemos el valor acumulado en el arribo i:\n h = t_acumulado[i]\n \n # Sacamos la parte entera, para saber a qué hora pertenece:\n h_i = int(h)\n \n # Buscamos el índice correspondiente a esa hora y le sumamos 1.\n arribos_horas[h_i] = arribos_horas[h_i] + 1", "_____no_output_____" ] ], [ [ "Imprimimos los primeros 15 valores encontrados por un tema de facilidad de visualización.", "_____no_output_____" ] ], [ [ "arribos_horas[0:15]", "_____no_output_____" ] ], [ [ "Ahora procederemos a graficar el vector __arribos_horas__ en sus primeros 15 valores.", "_____no_output_____" ] ], [ [ "horas_vis = 15\n\n# Creamos una figura y el gráfico de barras:\nplt.figure(figsize=(13,7))\nplt.bar(range(0, horas_vis), arribos_horas[0:horas_vis])\n\n# Seteamos título y etiquetas de los ejes:\nplt.title(f'Cantidad de arribos simulados hora a hora luego de {horas_vis} horas')\nplt.ylabel('Cantidad de arribos')\nplt.xlabel('Hora')\n\n# Mostramos el gráfico:\nplt.show()", "_____no_output_____" ] ], [ [ "#### Estadística sobre tiempo entre arribos", "_____no_output_____" ], [ "En esta sección queremos visualizar que las simulaciones que estamos creando coincidan con la densidad teórica que supusimos al principio.\n\nVamos a graficar un Histograma de los tiempos entre arribos simulados. Luego, graficamos encima la densidad de probabilidad teórica, en este caso la Exponencial con un parámetro $\\lambda$ de 0.2.", "_____no_output_____" ] ], [ [ "# Creamos una figura:\nplt.figure(figsize=(13,7))\n\n# Densidad exponencial teórica:\nxvals = np.linspace(0, np.max(tiempos))\nyvals = stats.expon.pdf(xvals, scale=0.2)\n\nplt.plot(xvals, yvals, c='r', label='Exponencial teórica')\nplt.legend()\n\n# Histograma normalizado de valores de tiempos:\nplt.hist(tiempos, density=True, bins=20, label='Frecuencias de tiempos')\n\n# Formato de gráfico:\nplt.title('Histograma de Horas entre arribos vs. Densidad de probabilidad Exponencial')\nplt.ylabel('Frecuencia de aparición de tiempo entre arribos')\nplt.xlabel('Tiempo entre arribos')\n\n# Visualizamos:\nplt.show()", "_____no_output_____" ] ], [ [ "Además de observar que la función teórica exponencial se ajusta a los valores del histograma, podemos ver cómo se distribuyen alrededor de la media teórica que establecimos al principio.", "_____no_output_____" ], [ "#### Estadística sobre cantidad de arribos", "_____no_output_____" ], [ "En este caso, hacemos lo mismo que antes. Graficamos un histograma de la cantidad de arribos. Luego, construimos la función de masa de probabilidad de Poisson encima.\n\nDebemos usar esta función ya que es la que se relaciona íntimamente con la distribución exponencial. Es sabido, teóricamente que cuando los tiempos entre arribos se distribuyen exponencialmente, las cantidades de arribos lo hacen con la de Poisson.", "_____no_output_____" ] ], [ [ "# Creamos una figura:\nplt.figure(figsize=(13,7))\n\n\n\n# Histograma normalizado de valores de tiempos:\nplt.hist(arribos_horas, density=True, bins=np.max(arribos_horas), label='Frecuencias de cantidad de arribos')\n\n# Función de masa de probabilidad poisson teórica:\nxvals = range(0, np.max(arribos_horas))\nyvals = stats.poisson.pmf(xvals, mu=5)\nplt.plot(xvals, yvals, 'ro', ms=8, mec='r')\nplt.vlines(xvals, 0, yvals, colors='r', linestyles='-', lw=2)\n\n# Formato de gráfico:\nplt.title('Histograma de cantidad de arribos vs. Func. de masa de probabilidad Poisson')\nplt.ylabel('Frecuencia de cantidad de arribos')\nplt.xlabel('Cantidad de arribos')\n\n# Visualizamos:\nplt.show()", "_____no_output_____" ] ], [ [ "Una vez más, en este caso, además de observar que la función de masa se ajusta a los valores del histograma, podemos ver cómo se distribuyen alrededor de la media teórica que establecimos al principio.", "_____no_output_____" ], [ "## Conclusión", "_____no_output_____" ], [ "En este Notebook pudimos observar correctamente cómo simular valores de una variable aleatoria distribuida exponencialmente. Además, comprobamos gráficamente los resultados relacionando los valores obtenidos con sus distribuciones teóricas.\n\nEstos métodos serán útiles en el futuro para poder hacer simulaciones más complejas de filas de espera, procesos industriales conectados o mantenimiento de máquinas.\n\nA modo de discusión, queda preguntarse, \n¿Qué otras distribuciones pueden samplearse con el método de la transformada inversa?\nDado que otra distribución ampliamente utilizada en casos prácticos es la Normal ¿podríamos hacer lo mismo que hicimos en este Notebook?", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ] ]

cb2d5c87c8d585b84fc4f2c82bd7a13bf37cfedc

580,331

ipynb

Jupyter Notebook

_solved/visualization_01_matplotlib.ipynb

jorisvandenbossche/DS-python-data-analysis

b4dd68b9c912c5d5c52c607aa117f5054449c73d

[ "BSD-3-Clause" ]

65

2017-03-21T09:15:40.000Z

2022-02-01T23:43:08.000Z

_solved/visualization_01_matplotlib.ipynb

jorisvandenbossche/DS-python-data-analysis

b4dd68b9c912c5d5c52c607aa117f5054449c73d

[ "BSD-3-Clause" ]

100

2016-12-15T03:44:06.000Z

2022-03-07T08:14:07.000Z

_solved/visualization_01_matplotlib.ipynb

jorisvandenbossche/DS-python-data-analysis

b4dd68b9c912c5d5c52c607aa117f5054449c73d

[ "BSD-3-Clause" ]

52

2016-12-19T07:48:52.000Z

2022-02-19T17:53:48.000Z

455.161569

74,636

0.942104

[ [ [ "<p><font size=\"6\"><b>Visualization - Matplotlib</b></font></p>\n\n> *DS Data manipulation, analysis and visualization in Python* \n> *May/June, 2021*\n>\n> *© 2021, Joris Van den Bossche and Stijn Van Hoey (<mailto:[email protected]>, <mailto:[email protected]>). Licensed under [CC BY 4.0 Creative Commons](http://creativecommons.org/licenses/by/4.0/)*\n\n---\n", "_____no_output_____" ], [ "# Matplotlib", "_____no_output_____" ], [ "[Matplotlib](http://matplotlib.org/) is a Python package used widely throughout the scientific Python community to produce high quality 2D publication graphics. It transparently supports a wide range of output formats including PNG (and other raster formats), PostScript/EPS, PDF and SVG and has interfaces for all of the major desktop GUI (graphical user interface) toolkits. It is a great package with lots of options.\n\nHowever, matplotlib is...\n\n> The 800-pound gorilla — and like most 800-pound gorillas, this one should probably be avoided unless you genuinely need its power, e.g., to make a **custom plot** or produce a **publication-ready** graphic.\n\n> (As we’ll see, when it comes to statistical visualization, the preferred tack might be: “do as much as you easily can in your convenience layer of choice [nvdr e.g. directly from Pandas, or with seaborn], and then use matplotlib for the rest.”)\n\n(quote used from [this](https://dansaber.wordpress.com/2016/10/02/a-dramatic-tour-through-pythons-data-visualization-landscape-including-ggplot-and-altair/) blogpost)\n\nAnd that's we mostly did, just use the `.plot` function of Pandas. So, why do we learn matplotlib? Well, for the *...then use matplotlib for the rest.*; at some point, somehow!\n\nMatplotlib comes with a convenience sub-package called ``pyplot`` which, for consistency with the wider matplotlib community, should always be imported as ``plt``:", "_____no_output_____" ] ], [ [ "import numpy as np\nimport matplotlib.pyplot as plt", "_____no_output_____" ] ], [ [ "## - dry stuff - The matplotlib `Figure`, `axes` and `axis`\n\nAt the heart of **every** plot is the figure object. The \"Figure\" object is the top level concept which can be drawn to one of the many output formats, or simply just to screen. Any object which can be drawn in this way is known as an \"Artist\" in matplotlib.\n\nLets create our first artist using pyplot, and then show it:", "_____no_output_____" ] ], [ [ "fig = plt.figure()\nplt.show()", "_____no_output_____" ] ], [ [ "On its own, drawing the figure artist is uninteresting and will result in an empty piece of paper (that's why we didn't see anything above).\n\nBy far the most useful artist in matplotlib is the **Axes** artist. The Axes artist represents the \"data space\" of a typical plot, a rectangular axes (the most common, but not always the case, e.g. polar plots) will have 2 (confusingly named) **Axis** artists with tick labels and tick marks.\n\n![](../img/matplotlib_fundamentals.png)\n\nThere is no limit on the number of Axes artists which can exist on a Figure artist. Let's go ahead and create a figure with a single Axes artist, and show it using pyplot:", "_____no_output_____" ] ], [ [ "ax = plt.axes()", "_____no_output_____" ], [ "type(ax)", "_____no_output_____" ], [ "type(ax.xaxis), type(ax.yaxis)", "_____no_output_____" ] ], [ [ "Matplotlib's ``pyplot`` module makes the process of creating graphics easier by allowing us to skip some of the tedious Artist construction. For example, we did not need to manually create the Figure artist with ``plt.figure`` because it was implicit that we needed a figure when we created the Axes artist.\n\nUnder the hood matplotlib still had to create a Figure artist, its just we didn't need to capture it into a variable.", "_____no_output_____" ], [ "## - essential stuff - `pyplot` versus Object based", "_____no_output_____" ], [ "Some example data:", "_____no_output_____" ] ], [ [ "x = np.linspace(0, 5, 10)\ny = x ** 2", "_____no_output_____" ] ], [ [ "Observe the following difference:", "_____no_output_____" ], [ "**1. pyplot style: plt...** (you will see this a lot for code online!)", "_____no_output_____" ] ], [ [ "plt.plot(x, y, '-')", "_____no_output_____" ] ], [ [ "**2. creating objects**", "_____no_output_____" ] ], [ [ "fig, ax = plt.subplots()\nax.plot(x, y, '-')", "_____no_output_____" ] ], [ [ "Although a little bit more code is involved, the advantage is that we now have **full control** of where the plot axes are placed, and we can easily add more than one axis to the figure:", "_____no_output_____" ] ], [ [ "fig, ax1 = plt.subplots()\nax1.plot(x, y, '-')\nax1.set_ylabel('y')\n\nax2 = fig.add_axes([0.2, 0.5, 0.4, 0.3]) # inset axes\nax2.set_xlabel('x')\nax2.plot(x, y*2, 'r-')", "_____no_output_____" ] ], [ [ "<div class=\"alert alert-info\" style=\"font-size:18px\">\n\n<b>REMEMBER</b>:\n\n <ul>\n <li>Use the <b>object oriented</b> power of Matplotlib!</li>\n <li>Get yourself used to writing <code>fig, ax = plt.subplots()</code></li>\n</ul>\n</div>", "_____no_output_____" ] ], [ [ "fig, ax = plt.subplots()\nax.plot(x, y, '-')\n# ...", "_____no_output_____" ] ], [ [ "## An small cheat-sheet reference for some common elements", "_____no_output_____" ] ], [ [ "x = np.linspace(-1, 0, 100)\n\nfig, ax = plt.subplots(figsize=(10, 7))\n\n# Adjust the created axes so that its topmost extent is 0.8 of the figure.\nfig.subplots_adjust(top=0.9)\n\nax.plot(x, x**2, color='0.4', label='power 2')\nax.plot(x, x**3, color='0.8', linestyle='--', label='power 3')\n\nax.vlines(x=-0.75, ymin=0., ymax=0.8, color='0.4', linestyle='-.') \nax.axhline(y=0.1, color='0.4', linestyle='-.')\nax.fill_between(x=[-1, 1.1], y1=[0.65], y2=[0.75], color='0.85')\n\nfig.suptitle('Figure title', fontsize=18, \n fontweight='bold')\nax.set_title('Axes title', fontsize=16)\n\nax.set_xlabel('The X axis')\nax.set_ylabel('The Y axis $y=f(x)$', fontsize=16)\n\nax.set_xlim(-1.0, 1.1)\nax.set_ylim(-0.1, 1.)\n\nax.text(0.5, 0.2, 'Text centered at (0.5, 0.2)\\nin data coordinates.',\n horizontalalignment='center', fontsize=14)\n\nax.text(0.5, 0.5, 'Text centered at (0.5, 0.5)\\nin Figure coordinates.',\n horizontalalignment='center', fontsize=14, \n transform=ax.transAxes, color='grey')\n\nax.legend(loc='upper right', frameon=True, ncol=2, fontsize=14)", "_____no_output_____" ] ], [ [ "Adjusting specific parts of a plot is a matter of accessing the correct element of the plot:\n\n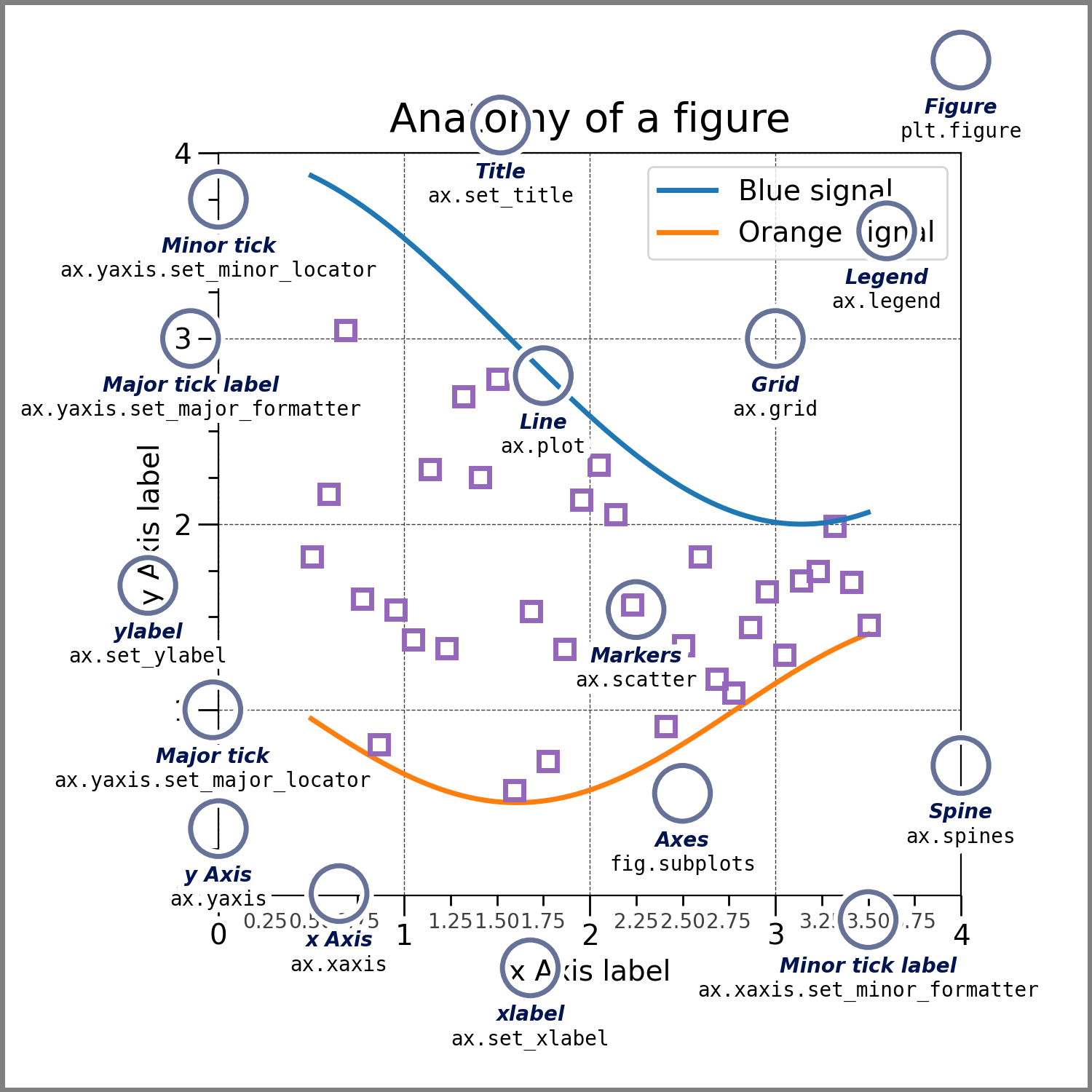![](https://matplotlib.org/stable/_images/anatomy.png)", "_____no_output_____" ], [ "For more information on legend positioning, check [this post](http://stackoverflow.com/questions/4700614/how-to-put-the-legend-out-of-the-plot) on stackoverflow!", "_____no_output_____" ], [ "## I do not like the style...", "_____no_output_____" ], [ "**...understandable**", "_____no_output_____" ], [ "Matplotlib had a bad reputation in terms of its default styling as figures created with earlier versions of Matplotlib were very Matlab-lookalike and mostly not really catchy. \n\nSince Matplotlib 2.0, this has changed: https://matplotlib.org/users/dflt_style_changes.html!\n\nHowever...\n> *Des goûts et des couleurs, on ne discute pas...*\n\n(check [this link](https://fr.wiktionary.org/wiki/des_go%C3%BBts_et_des_couleurs,_on_ne_discute_pas) if you're not french-speaking)\n\nTo account different tastes, Matplotlib provides a number of styles that can be used to quickly change a number of settings:", "_____no_output_____" ] ], [ [ "plt.style.available", "_____no_output_____" ], [ "x = np.linspace(0, 10)\n\nwith plt.style.context('seaborn'): # 'seaborn', ggplot', 'bmh', 'grayscale', 'seaborn-whitegrid', 'seaborn-muted'\n fig, ax = plt.subplots()\n ax.plot(x, np.sin(x) + x + np.random.randn(50))\n ax.plot(x, np.sin(x) + 0.5 * x + np.random.randn(50))\n ax.plot(x, np.sin(x) + 2 * x + np.random.randn(50))", "_____no_output_____" ] ], [ [ "We should not start discussing about colors and styles, just pick **your favorite style**!", "_____no_output_____" ] ], [ [ "plt.style.use('seaborn-whitegrid')", "_____no_output_____" ] ], [ [ "or go all the way and define your own custom style, see the [official documentation](https://matplotlib.org/3.1.1/tutorials/introductory/customizing.html) or [this tutorial](https://colcarroll.github.io/yourplotlib/#/).", "_____no_output_____" ], [ "<div class=\"alert alert-info\">\n\n<b>REMEMBER</b>:\n\n <ul>\n <li>If you just want <b>quickly a good-looking plot</b>, use one of the available styles (<code>plt.style.use('...')</code>)</li>\n <li>Otherwise, the object-oriented way of working makes it possible to change everything!</li>\n</ul>\n</div>", "_____no_output_____" ], [ "## Interaction with Pandas", "_____no_output_____" ], [ "What we have been doing while plotting with Pandas:", "_____no_output_____" ] ], [ [ "import pandas as pd", "_____no_output_____" ], [ "flowdata = pd.read_csv('data/vmm_flowdata.csv', \n index_col='Time', \n parse_dates=True)", "_____no_output_____" ], [ "out = flowdata.plot() # print type()", "_____no_output_____" ] ], [ [ "Under the hood, it creates an Matplotlib Figure with an Axes object.", "_____no_output_____" ], [ "### Pandas versus matplotlib", "_____no_output_____" ], [ "#### Comparison 1: single plot", "_____no_output_____" ] ], [ [ "flowdata.plot(figsize=(16, 6)) # SHIFT + TAB this!", "_____no_output_____" ] ], [ [ "Making this with matplotlib...", "_____no_output_____" ] ], [ [ "fig, ax = plt.subplots(figsize=(16, 6))\nax.plot(flowdata)\nax.legend([\"L06_347\", \"LS06_347\", \"LS06_348\"])", "_____no_output_____" ] ], [ [ "is still ok!", "_____no_output_____" ], [ "#### Comparison 2: with subplots", "_____no_output_____" ] ], [ [ "axs = flowdata.plot(subplots=True, sharex=True,\n figsize=(16, 8), colormap='viridis', # Dark2\n fontsize=15, rot=0)", "_____no_output_____" ] ], [ [ "Mimicking this in matplotlib (just as a reference, it is basically what Pandas is doing under the hood):", "_____no_output_____" ] ], [ [ "from matplotlib import cm\nimport matplotlib.dates as mdates\n\ncolors = [cm.viridis(x) for x in np.linspace(0.0, 1.0, len(flowdata.columns))] # list comprehension to set up the colors\n\nfig, axs = plt.subplots(3, 1, figsize=(16, 8))\n\nfor ax, col, station in zip(axs, colors, flowdata.columns):\n ax.plot(flowdata.index, flowdata[station], label=station, color=col)\n ax.legend()\n if not ax.get_subplotspec().is_last_row():\n ax.xaxis.set_ticklabels([])\n ax.xaxis.set_major_locator(mdates.YearLocator())\n else:\n ax.xaxis.set_major_locator(mdates.YearLocator())\n ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y'))\n ax.set_xlabel('Time')\n ax.tick_params(labelsize=15)", "_____no_output_____" ] ], [ [ "Is already a bit harder ;-)", "_____no_output_____" ], [ "### Best of both worlds...", "_____no_output_____" ] ], [ [ "fig, ax = plt.subplots() #prepare a Matplotlib figure\n\nflowdata.plot(ax=ax) # use Pandas for the plotting", "_____no_output_____" ], [ "fig, ax = plt.subplots(figsize=(15, 5)) #prepare a matplotlib figure\n\nflowdata.plot(ax=ax) # use pandas for the plotting\n\n# Provide further adaptations with matplotlib:\nax.set_xlabel(\"\")\nax.grid(which=\"major\", linewidth='0.5', color='0.8')\nfig.suptitle('Flow station time series', fontsize=15)", "_____no_output_____" ], [ "fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(16, 6)) #provide with matplotlib 2 axis\n\nflowdata[[\"L06_347\", \"LS06_347\"]].plot(ax=ax1) # plot the two timeseries of the same location on the first plot\nflowdata[\"LS06_348\"].plot(ax=ax2, color='0.2') # plot the other station on the second plot\n\n# further adapt with matplotlib\nax1.set_ylabel(\"L06_347\")\nax2.set_ylabel(\"LS06_348\")\nax2.legend()", "_____no_output_____" ] ], [ [ "<div class=\"alert alert-info\">\n\n <b>Remember</b>: \n\n <ul>\n <li>You can do anything with matplotlib, but at a cost... <a href=\"http://stackoverflow.com/questions/tagged/matplotlib\">stackoverflow</a></li>\n \n <li>The preformatting of Pandas provides mostly enough flexibility for quick analysis and draft reporting. It is not for paper-proof figures or customization</li>\n</ul>\n<br>\n\nIf you take the time to make your perfect/spot-on/greatest-ever matplotlib-figure: Make it a <b>reusable function</b>!\n\n</div>", "_____no_output_____" ], [ "An example of such a reusable function to plot data:", "_____no_output_____" ] ], [ [ "%%file plotter.py \n#this writes a file in your directory, check it(!)\n\nimport numpy as np\nimport matplotlib.pyplot as plt\nimport matplotlib.dates as mdates\n\nfrom matplotlib import cm\nfrom matplotlib.ticker import MaxNLocator\n\ndef vmm_station_plotter(flowdata, label=\"flow (m$^3$s$^{-1}$)\"):\n colors = [cm.viridis(x) for x in np.linspace(0.0, 1.0, len(flowdata.columns))] # list comprehension to set up the color sequence\n\n fig, axs = plt.subplots(3, 1, figsize=(16, 8))\n\n for ax, col, station in zip(axs, colors, flowdata.columns):\n ax.plot(flowdata.index, flowdata[station], label=station, color=col) # this plots the data itself\n \n ax.legend(fontsize=15)\n ax.set_ylabel(label, size=15)\n ax.yaxis.set_major_locator(MaxNLocator(4)) # smaller set of y-ticks for clarity\n \n if not ax.get_subplotspec().is_last_row(): # hide the xticklabels from the none-lower row x-axis\n ax.xaxis.set_ticklabels([])\n ax.xaxis.set_major_locator(mdates.YearLocator())\n else: # yearly xticklabels from the lower x-axis in the subplots\n ax.xaxis.set_major_locator(mdates.YearLocator())\n ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y'))\n ax.tick_params(axis='both', labelsize=15, pad=8) # enlarge the ticklabels and increase distance to axis (otherwise overlap)\n return fig, axs", "Overwriting plotter.py\n" ], [ "from plotter import vmm_station_plotter\n# fig, axs = vmm_station_plotter(flowdata)", "_____no_output_____" ], [ "fig, axs = vmm_station_plotter(flowdata, \n label=\"NO$_3$ (mg/l)\")\nfig.suptitle('Ammonium concentrations in the Maarkebeek', fontsize='17')\nfig.savefig('ammonium_concentration.pdf')", "_____no_output_____" ] ], [ [ "<div class=\"alert alert-warning\">\n\n**NOTE**\n\n- Let your hard work pay off, write your own custom functions!\n\n</div>", "_____no_output_____" ], [ "<div class=\"alert alert-info\" style=\"font-size:18px\">\n\n**Remember** \n\n`fig.savefig()` to save your Figure object!\n\n</div>", "_____no_output_____" ], [ "# Need more matplotlib inspiration? ", "_____no_output_____" ], [ "For more in-depth material:\n* http://www.labri.fr/perso/nrougier/teaching/matplotlib/\n* notebooks in matplotlib section: http://nbviewer.jupyter.org/github/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/Index.ipynb#4.-Visualization-with-Matplotlib\n* main reference: [matplotlib homepage](http://matplotlib.org/)", "_____no_output_____" ], [ "<div class=\"alert alert-info\" style=\"font-size:18px\">\n\n**Remember**\n\n- <a href=\"https://matplotlib.org/stable/gallery/index.html\">matplotlib gallery</a> is an important resource to start from\n- Matplotlib has some great [cheat sheets](https://github.com/matplotlib/cheatsheets) available\n\n</div>", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown" ] ]

cb2d601d306ce91b1d28dccad0d8b13ab3bfde70

2,353

ipynb

Jupyter Notebook

code/algorithms/course_udemy_1/Riddles/Interview/Problems - SOLUTIONS/Bridge Crossing - SOLUTION.ipynb

vicb1/miscellaneous

2c9762579abf75ef6cba75d1d1536a693d69e82a

[ "MIT" ]

null

code/algorithms/course_udemy_1/Riddles/Interview/Problems - SOLUTIONS/Bridge Crossing - SOLUTION.ipynb

vicb1/miscellaneous

2c9762579abf75ef6cba75d1d1536a693d69e82a

[ "MIT" ]

null

code/algorithms/course_udemy_1/Riddles/Interview/Problems - SOLUTIONS/Bridge Crossing - SOLUTION.ipynb

vicb1/miscellaneous

2c9762579abf75ef6cba75d1d1536a693d69e82a

[ "MIT" ]

null

31.797297

322

0.586485

[ [ [ "# Bridge Crossing - SOLUTION", "_____no_output_____" ], [ "## Problem Statement\n\nA group of four travelers comes to a bridge at night. The bridge can hold the weight of at most only two of the travelers at a time, and it can- not be crossed without using a flashlight. \n\nThe travelers have one flashlight among them. Each traveler walks at a different speed: The first can cross the bridge in 1 minute, the second in 2 minutes, the third in 5 minutes, and the fourth takes 10 minutes to cross the bridge. If two travelers cross together, they walk at the speed of the slower traveler.\n\nWhat is the least amount of time in which all the travelers can cross from one side of the bridge to the other?\n\n## Solution\n\nThis is part of a common group of [river crossing](https://en.wikipedia.org/wiki/River_crossing_puzzle) puzzles. Its know as the [Bridge and Torch problem](https://en.wikipedia.org/wiki/Bridge_and_torch_problem) (sometimes the times assigned to each person are different).\n\nThe solution to this version is:\n<table class=\"p4table width50\">\n<tr><th>Move</th><th>Time</th>\n</tr>\n<tr><td>(1) & (2) Cross with Torch</td><td>2</td>\n</tr>\n<tr><td>(1) Returns with Torch</td><td>1</td>\n</tr>\n<tr><td>(5) & (10) Cross with Torch</td><td>10</td>\n</tr>\n<tr><td>(2) Returns with Torch</td><td>2</td>\n</tr>\n<tr><td>(1) & (2) Cross with Torch</td><td>2</td>\n</tr>\n<tr><td> </td><th>17</th></tr>\n</table>", "_____no_output_____" ] ] ]

[ "markdown" ]

[ [ "markdown", "markdown" ] ]

cb2d673f07709b525c0f6a2a3509b6940bbe45fc

200,427

ipynb

Jupyter Notebook

Explore_Predictions.ipynb

franklizhou/orientation-specific-chexnet

9b859b8b6eb1d1cf28695cf8f28d8216cb661d89

[ "BSD-3-Clause" ]

null

Explore_Predictions.ipynb

franklizhou/orientation-specific-chexnet

9b859b8b6eb1d1cf28695cf8f28d8216cb661d89

[ "BSD-3-Clause" ]

null

Explore_Predictions.ipynb

franklizhou/orientation-specific-chexnet

9b859b8b6eb1d1cf28695cf8f28d8216cb661d89

[ "BSD-3-Clause" ]

null

564.583099

190,416

0.939739

[ [ [ "# Reproduce CheXNet: Explore Predictions", "_____no_output_____" ], [ "## Import other modules and pandas", "_____no_output_____" ] ], [ [ "import visualize_prediction as V\n\nimport pandas as pd\n\n#suppress pytorch warnings about source code changes\nimport warnings\nwarnings.filterwarnings('ignore')", "0.4.1\n" ] ], [ [ "## Settings for review\nWe can examine individual results in more detail, seeing probabilities of disease for test images. \n\nWe get you started with a small number of the images from the large NIH dataset. \n\nTo explore the full dataset, [download images from NIH (large, ~40gb compressed)](https://nihcc.app.box.com/v/ChestXray-NIHCC), extract all tar.gz files to a single folder, place that path below and set STARTER_IMAGES=False", "_____no_output_____" ] ], [ [ "STARTER_IMAGES=False\nPATH_TO_IMAGES = \"/home/frank_li_zhou/images/images/\"\n\n#STARTER_IMAGES=False\n#PATH_TO_IMAGES = \"your path to NIH data here\"", "_____no_output_____" ] ], [ [ "Load pretrained model (part of cloned repo; should not need to change path unless you want to point to one you retrained)", "_____no_output_____" ] ], [ [ "PATH_TO_MODEL = \"/home/frank_li_zhou/reproduce-chexnet/pretrained/checkpoint\"", "_____no_output_____" ] ], [ [ "Pick the finding you want to see positive examples of:\n\nLABEL can be set to any of:\n- Atelectasis\n- Cardiomegaly\n- Consolidation\n- Edema\n- Effusion\n- Emphysema\n- Fibrosis\n- Hernia\n- Infiltration\n- Mass\n- Nodule\n- Pleural_Thickening\n- Pneumonia\n- Pneumothorax\n", "_____no_output_____" ] ], [ [ "LABEL=\"Cardiomegaly\"", "_____no_output_____" ] ], [ [ "It's more interesting when initially exploring to see cases positive for pathology of interest:", "_____no_output_____" ] ], [ [ "POSITIVE_FINDINGS_ONLY=True", "_____no_output_____" ] ], [ [ "## Load data\n\nThis loads up dataloader and model (note: only test images not used for model training are loaded).", "_____no_output_____" ] ], [ [ "dataloader,model= V.load_data(PATH_TO_IMAGES,LABEL,PATH_TO_MODEL,POSITIVE_FINDINGS_ONLY,STARTER_IMAGES)\nprint(\"Cases for review:\")\nprint(len(dataloader))", "Cases for review:\n582\n" ] ], [ [ "## Examine individual cases\n\nTo explore, run code below to see a random case positive for your selected finding, a heatmap indicating the most influential regions of the image, and the model's estimated probabilities for findings. For many diagnoses, you can see that the model uses features outside the expected region to calibrate its predictions -- [you can read my discussion about this here](https://medium.com/@jrzech/what-are-radiological-deep-learning-models-actually-learning-f97a546c5b98).\n\nPlease note that:\n1) the NIH dataset was noisily labeled by automatically extracting labels from text reports written by radiologists, as described in paper [here](https://arxiv.org/pdf/1705.02315.pdf) and analyzed [here](https://lukeoakdenrayner.wordpress.com/2017/12/18/the-chestxray14-dataset-problems/), so we should not be surprised to see inaccuracies in the provided ground truth labels \n2) high AUCs can be achieved even if many positive cases are assigned absolutely low probabilities of disease, as AUC depends on the relative ranking of probabilities between cases. \n\nYou can run the below cell repeatedly to see different examples:", "_____no_output_____" ] ], [ [ "preds=V.show_next(dataloader,model, LABEL)\npreds", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2d713522731044271a902bc16a2d7d572ac052

12,101

ipynb

Jupyter Notebook

static_files/presentations/DC_Assignment1.ipynb

phonchi/nsysu-math604

b4ccf93c240122735fc7810dcc619cdfb30739d9

[ "MIT" ]

null

static_files/presentations/DC_Assignment1.ipynb

phonchi/nsysu-math604

b4ccf93c240122735fc7810dcc619cdfb30739d9

[ "MIT" ]

null

static_files/presentations/DC_Assignment1.ipynb

phonchi/nsysu-math604

b4ccf93c240122735fc7810dcc619cdfb30739d9

[ "MIT" ]

null

12,101

0.704322

[ [ [ "# Assignment 1", "_____no_output_____" ], [ "#### Student ID: *Double click here to fill the Student ID*\n\n#### Name: *Double click here to fill the name*", "_____no_output_____" ], [ "## Q1: Exploring the TensorFlow playground\n\nhttp://playground.tensorflow.org/\n\n(a) Execute the following steps first:\n1. Change the dataset to exclusive OR dataset (top-right dataset under \"DATA\" panel). \n2. Reduce the hidden layer to only one layer and change the activation function to \"ReLu\". \n3. Run the model five times. Before each trial, hit the \"Reset the network\" button to get a new random initialization. (The \"Reset the network\" button is the circular reset arrow just to the left of the Play button.) \n4. Let each trial run for at least 500 epochs to ensure convergence. \n\nMake some comments about the role of initialization in this non-convex optimization problem. What is the minimum number of neurons required (Keeping all other parameters unchanged) to ensure that it almost always converges to global minima (where the test loss is below 0.02)? Finally, paste the convergence results below.\n\n* Note the convergence results should include all the settings and the model. An example is available [here](https://drive.google.com/file/d/15AXYZLNMNnpZj0kI0CgPdKnyP_KqRncz/view?usp=sharing)", "_____no_output_____" ], [ "<!---Your answer here.---!>", "_____no_output_____" ], [ "(b) Execute the following steps first\n1. Change the dataset to be the spiral (bottom-right dataset under \"DATA\" panel). \n2. Increase the noise level to 50 and leave the training and test set ratio unchanged. \n3. Train the best model you can, using just `X1` and `X2` as input features. Feel free to add or remove layers and neurons. You can also change learning settings like learning rate, regularization rate, activations and batch size. Try to get the test loss below 0.15. \n\nHow many parameters do you have in your models? Describe the model architecture and the training strategy you use. Finally, paste the convergence results below. \n\n* You may need to train the model for enough epochs here and use learning rate scheduling manually", "_____no_output_____" ], [ "<!---Your answer here.---!>", "_____no_output_____" ], [ "(c) Use the same dataset as described above with noise level set to 50. \nThis time, feel free to add additional features or other transformations like `sin(X1)` and `sin(X2)`. Again, try to get the loss below 0.15.\n\nCompare the results with (b) and describe your observation. Describe the model architecture and the training strategy you use. Finally, paste the convergence results below. ", "_____no_output_____" ], [ "<!---Your answer here.---!>", "_____no_output_____" ], [ "## Q2: Takling MNIST with DNN", "_____no_output_____" ], [ "In this question, we will explore the behavior of the vanishing gradient problem (which we have tried to solve using feature engineering in Q1) and try to solve it. The dataset we use is the famous MNIST dataset which contains ten different classes of handwritten digits. The MNIST database contains 60,000 training images and 10,000 testing images. In addition, each grayscale image is fit into a 28x28 pixel bounding box.\n\nhttp://yann.lecun.com/exdb/mnist/", "_____no_output_____" ], [ "(a) Load the MNIST dataset (you may refer to `keras.datasets.mnist.load_data()`), and split it into a training set (48,000 images), a validation set (12,000 images) and a test set (10,000 images). Make sure to standardize the dataset first.", "_____no_output_____" ] ], [ [ "# coding your answer here.", "_____no_output_____" ] ], [ [ "(b) Build a sequential model with 30 hidden dense layers (60 neurons each using ReLU as the activation function) plus an output layer (10 neurons using softmax as the activation function). Train it with SGD optimizer with learning rate 0.001 and momentum 0.9 for 10 epochs on MNIST dataset. \n\nTry to manually calculate how many steps are in one epoch and compare it with the one reported by the program. Finally, plot the learning curves (loss vs epochs) and report the accuracy you get on the test set.", "_____no_output_____" ] ], [ [ "# coding your answer here.", "_____no_output_____" ] ], [ [ "(c) Update the model in (b) to add a BatchNormalization (BN) layer after every hidden layer's activation functions. \n\nHow do the training time and the performance compare with (b)? Try to manually calculate how many non-trainable parameters are in your model and compare it with the one reported by the program. Finally, try moving the BN layers before the hidden layers' activation functions and compare the performance with BN layers after the activation function.", "_____no_output_____" ] ], [ [ "# coding your answer here.", "_____no_output_____" ] ], [ [ "## Q3: High Accuracy CNN for CIFAR-10\nWhen facing problems related to images like Q2, we can consider using CNN instead of DNN. The CIFAR-10 dataset is one of the most widely used datasets for machine learning research. It consists of 60000 32x32 color images in 10 classes, with 6000 images per class. In this problem, we will try to build our own CNN from scratch and achieve the highest possible accuracy on CIFAR-10. \n\nhttps://www.cs.toronto.edu/~kriz/cifar.html", "_____no_output_____" ], [ "(a) Load the CIFAR10 dataset (you may refer to `keras.datasets.cifar10.load_data()`), and split it into a training set (40,000 images), a validation set (10,000 images) and a test set (10,000 images). Make sure the pixel values range from 0 to 1.", "_____no_output_____" ] ], [ [ "# coding your answer here.", "_____no_output_____" ] ], [ [ "(b) Build a Convolutional Neural Network using the following architecture: \n\n| | Type | Maps | Activation |\n|--------|---------------------|---------|------------|\n| Output | Fully connected | 10 | Softmax |\n| S10 | Max Pooling | | |\n| B9 | Batch normalization | | |\n| C8 | Convolution | 64 | ReLu |\n| B7 | Batch normalization | | |\n| C6 | Convolution | 64 | ReLu |\n| S5 | Max Pooling | | |\n| B4 | Batch normalization | | |\n| C3 | Convolution | 32 | ReLu |\n| B2 | Batch normalization | | |\n| C1 | Convolution | 32 | ReLu |\n| In | Input | RGB (3) | |\n\nTrain the model for 20 epochs with NAdam optimizer (Adam with Nesterov momentum). \n\nTry to manually calculate the number of parameters in your model's architecture and compare it with the one reported by `summary()`. Finally, plot the learning curves and report the accuracy on the test set.", "_____no_output_____" ] ], [ [ "# coding your answer here.", "_____no_output_____" ] ], [ [ "(c) Looking at the learning curves, you can see that the model is overfitting. Adding data augmentation layer for the model in (a) as follows.\n\n* Applies random horizontal flipping \n* Rotates the input images by a random value in the range `[–18 degrees, +18 degrees]`)\n* Zooms in or out of the image by a random factor in the range `[-15%, +15%]`\n* Randomly choose a location to crop images down to a target size `[30, 30]`\n* Randomly adjust the contrast of images so that the resulting images are `[0.9, 1.1]` brighter or darker than the original one.\n\nFit your model for enough epochs (60, for instance) and compare its performance and learning curves with the previous model in (b). Finally, report the accuracy on the test set.\n", "_____no_output_____" ] ], [ [ "# coding your answer here.", "_____no_output_____" ] ], [ [ "(d) Replace all the convolution layers in (b) with depthwise separable convolution layers (except the first convolution layer). \n\nTry to manually calculate the number of parameters in your model's architecture and compare it with the one reported by `summary()`. Fit your model and compare its performance with the previous model in (c). Finally, plot the learning curves and report the accuracy on the test set.", "_____no_output_____" ] ], [ [ "# coding your answer here.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2d756c5b8b0f7308306045d85d4239e458e3be

12,703

ipynb

Jupyter Notebook

pydrepr/notebooks/s10_speed_comparison.ipynb

scorpio975/d-repr

1d08024192642233d42d29e1d05f8713ee265bca

[ "MIT" ]

5

2019-10-02T01:04:50.000Z

2022-03-08T09:39:50.000Z

pydrepr/notebooks/s10_speed_comparison.ipynb

scorpio975/d-repr

1d08024192642233d42d29e1d05f8713ee265bca

[ "MIT" ]

3

2020-06-13T22:09:48.000Z

2021-04-23T08:23:49.000Z

pydrepr/notebooks/s10_speed_comparison.ipynb

scorpio975/d-repr

1d08024192642233d42d29e1d05f8713ee265bca

[ "MIT" ]

5

2019-10-02T03:01:27.000Z

2021-02-02T13:34:35.000Z

39.946541

351

0.621113

[ [ [ "#### The purpose of this notebook is to compare D-REPR with other methods such as KR2RML and R2RML in term of performance", "_____no_output_____" ] ], [ [ "import re, numpy as np\nimport matplotlib.pyplot as plt\nfrom tqdm import tqdm_notebook as tqdm\n\n%matplotlib inline\nplt.rcParams[\"figure.figsize\"] = (10.0, 8.0) # set default size of plots\nplt.rcParams[\"image.interpolation\"] = \"nearest\"\nplt.rcParams[\"image.cmap\"] = \"gray\"\n\n%load_ext autoreload\n%autoreload 2", "The autoreload extension is already loaded. To reload it, use:\n %reload_ext autoreload\n" ], [ "%reload_ext autoreload", "_____no_output_____" ], [ "def read_exec_time(log_file: str, tag_str: str='>>> [DREPR]', print_exec_time: bool=True):\n \"\"\"Read the executing time of the program\"\"\"\n with open(log_file, \"r\") as f:\n for line in f:\n if line.startswith(\">>> [DREPR]\"):\n m = re.search(\"((?:\\d+\\.)?\\d+) ?ms\", line)\n exec_time = m.group(1)\n if print_exec_time:\n print(line.strip(), \"-- extract exec_time:\", exec_time)\n return float(exec_time)\n raise Exception(\"Doesn't found any output message\")", "_____no_output_____" ] ], [ [ "#### KR2RML\n\nTo setup KR2RML, we need to first download Web-Karma-2.2 from the web, modify the file: `karma-offline/src/main/java/edu/isi/karma/rdf/OfficeRDFGenerator` to add this code to line 184: `System.out.println(\">>> [DREPR] Finish converting RDF after \" + String.valueOf(System.currentTimeMillis() - l) + \"ms\");` to print the runtime to stdout.\n\nThen run `mvn install -Dmaven.test.skip=true` at the root directory to install dependencies before actually converting data to RDF", "_____no_output_____" ] ], [ [ "%cd /workspace/tools-evaluation/Web-Karma-2.2/karma-offline\n\nDATA_FILE = \"/workspace/drepr/drepr/rdrepr/data/insurance.csv\"\nMODEL_FILE = \"/workspace/drepr/drepr/rdrepr/data/insurance.level-0.model.ttl\"\nOUTPUT_FILE = \"/tmp/kr2rml_output.ttl\"\n\nkarma_exec_times = []\n\nfor i in tqdm(range(3)):\n !mvn exec:java -Dexec.mainClass=\"edu.isi.karma.rdf.OfflineRdfGenerator\" -Dexec.args=\" \\\n --sourcetype CSV \\\n --filepath \\\"{DATA_FILE}\\\" \\\n --modelfilepath \\\"{MODEL_FILE}\\\" \\\n --sourcename test \\\n --outputfile {OUTPUT_FILE}\" -Dexec.classpathScope=compile > /tmp/karma_speed_comparison.log\n \n karma_exec_times.append(read_exec_time(\"/tmp/karma_speed_comparison.log\"))\n !rm /tmp/karma_speed_comparison.log\n \nprint(f\"run 3 times, average: {np.mean(karma_exec_times)}ms\")", "/workspace/Web-Karma-2.2/karma-offline\n" ] ], [ [ "<hr />\n\nReport information about the output and input", "_____no_output_____" ] ], [ [ "with open(DATA_FILE, \"r\") as f:\n n_records = sum(1 for _ in f) - 1\n print(\"#records:\", n_records, f\"({round(n_records * 1000 / np.mean(karma_exec_times), 2)} records/s)\")\nwith open(OUTPUT_FILE, \"r\") as f:\n n_triples = sum(1 for line in f if line.strip().endswith(\".\"))\n print(\"#triples:\", n_triples, f\"({round(n_triples * 1000 / np.mean(karma_exec_times), 2)} triples/s)\")", "#records: 36634 (6147.68 records/s)\n#triples: 256438 (43033.73 triples/s)\n" ] ], [ [ "#### MorphRDB\n\nAssuming that you have followed their installation guides at [this](https://github.com/oeg-upm/morph-rdb/wiki/Installation) and [usages](https://github.com/oeg-upm/morph-rdb/wiki/Usage#csv-files). We are going to create r2rml mappings and invoke their program to map data into RDF", "_____no_output_____" ] ], [ [ "%cd /workspace/tools-evaluation/morph-rdb/morph-examples\n\n!java -cp .:morph-rdb-dist-3.9.17.jar:dependency/\\* es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner /workspace/drepr/drepr/rdrepr/data insurance.level-0.morph.properties", "/workspace/tools-evaluation/morph-rdb/morph-examples\n[main] INFO es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVProperties - reading configuration file : /workspace/drepr/drepr/rdrepr/data/insurance.level-0.morph.properties\n[main] ERROR es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVProperties - Configuration file not found: /workspace/drepr/drepr/rdrepr/data/insurance.level-0.morph.properties\njava.io.FileNotFoundException: /workspace/drepr/drepr/rdrepr/data/insurance.level-0.morph.properties (No such file or directory)\n\tat java.io.FileInputStream.open0(Native Method)\n\tat java.io.FileInputStream.open(FileInputStream.java:195)\n\tat java.io.FileInputStream.<init>(FileInputStream.java:138)\n\tat java.io.FileInputStream.<init>(FileInputStream.java:93)\n\tat es.upm.fi.dia.oeg.morph.base.MorphProperties.readConfigurationFile(MorphProperties.scala:91)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphRDBProperties.readConfigurationFile(MorphRDBProperties.scala:18)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVProperties.readConfigurationFile(MorphCSVProperties.scala:23)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVProperties$.apply(MorphCSVProperties.scala:67)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner$.apply(MorphCSVRunner.scala:41)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner$.main(MorphCSVRunner.scala:60)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner.main(MorphCSVRunner.scala)\njava.io.FileNotFoundException: /workspace/drepr/drepr/rdrepr/data/insurance.level-0.morph.properties (No such file or directory)\n\tat java.io.FileInputStream.open0(Native Method)\n\tat java.io.FileInputStream.open(FileInputStream.java:195)\n\tat java.io.FileInputStream.<init>(FileInputStream.java:138)\n\tat java.io.FileInputStream.<init>(FileInputStream.java:93)\n\tat es.upm.fi.dia.oeg.morph.base.MorphProperties.readConfigurationFile(MorphProperties.scala:91)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphRDBProperties.readConfigurationFile(MorphRDBProperties.scala:18)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVProperties.readConfigurationFile(MorphCSVProperties.scala:23)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVProperties$.apply(MorphCSVProperties.scala:67)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner$.apply(MorphCSVRunner.scala:41)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner$.main(MorphCSVRunner.scala:60)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner.main(MorphCSVRunner.scala)\n[main] ERROR es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner$ - Exception occured: /workspace/drepr/drepr/rdrepr/data/insurance.level-0.morph.properties (No such file or directory)\nException in thread \"main\" java.io.FileNotFoundException: /workspace/drepr/drepr/rdrepr/data/insurance.level-0.morph.properties (No such file or directory)\n\tat java.io.FileInputStream.open0(Native Method)\n\tat java.io.FileInputStream.open(FileInputStream.java:195)\n\tat java.io.FileInputStream.<init>(FileInputStream.java:138)\n\tat java.io.FileInputStream.<init>(FileInputStream.java:93)\n\tat es.upm.fi.dia.oeg.morph.base.MorphProperties.readConfigurationFile(MorphProperties.scala:91)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphRDBProperties.readConfigurationFile(MorphRDBProperties.scala:18)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVProperties.readConfigurationFile(MorphCSVProperties.scala:23)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVProperties$.apply(MorphCSVProperties.scala:67)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner$.apply(MorphCSVRunner.scala:41)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner$.main(MorphCSVRunner.scala:60)\n\tat es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner.main(MorphCSVRunner.scala)\n" ] ], [ [ "#### DREPR", "_____no_output_____" ] ], [ [ "%cd /workspace/drepr/drepr/rdrepr\n\nDREPR_EXEC_LOG = \"/tmp/drepr_exec_log.log\"\n\n!cargo run --release > {DREPR_EXEC_LOG}\ndrepr_exec_times = read_exec_time(DREPR_EXEC_LOG)\n!rm {DREPR_EXEC_LOG}", "/workspace/drepr/drepr/rdrepr\n\u001b[0m\u001b[0m\u001b[1m\u001b[32m Finished\u001b[0m release [optimized] target(s) in 0.18s\n\u001b[0m\u001b[0m\u001b[1m\u001b[32m Running\u001b[0m `target/release/drepr`\n>>> [DREPR] runtime: 146.171066ms -- extract exec_time: 146.171066\n" ], [ "with open(\"/tmp/drepr_output.ttl\", \"r\") as f:\n n_triples = sum(1 for line in f if line.strip().endswith(\".\"))\n print(\"#triples:\", n_triples, f\"({round(n_triples * 1000 / np.mean(drepr_exec_times), 2)} triples/s)\")", "#triples: 256438 (1754369.09 triples/s)\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ] ]

cb2d9551539142a452626e8ae4aa661f61700ffa

56,082

ipynb

Jupyter Notebook

Results/exp2_c1.ipynb

sachinsharma9780/Collaborativ_Intelligence

8fad4874c6b2759cc83a002effb87b446f431a1f

[ "MIT" ]

1

2019-06-07T21:41:00.000Z

Results/exp2_c1.ipynb

sachinsharma9780/Collaborativ_Intelligence

8fad4874c6b2759cc83a002effb87b446f431a1f

[ "MIT" ]

null

Results/exp2_c1.ipynb

sachinsharma9780/Collaborativ_Intelligence

8fad4874c6b2759cc83a002effb87b446f431a1f

[ "MIT" ]

1

2018-12-11T14:56:19.000Z

74.676431

18,356

0.782533

[ [ [ "#Importing necessary libraries \nimport keras\nimport numpy as np\nimport pandas as pd\nfrom keras.applications import VGG16, inception_v3, resnet50, mobilenet\nfrom keras import models\nfrom keras import layers\nfrom keras import optimizers\nfrom sklearn.metrics import classification_report, confusion_matrix\nimport matplotlib.pyplot as plt\nimport os \nimport glob\nimport tifffile as tif\nfrom sklearn.preprocessing import OneHotEncoder, LabelEncoder\nfrom tempfile import TemporaryFile\nfrom sklearn import model_selection\nfrom keras.models import Sequential\nfrom keras.layers import Dense, Dropout, Flatten\nfrom keras.layers import Conv2D, MaxPooling2D\nfrom keras.layers.normalization import BatchNormalization\nfrom keras.preprocessing.image import ImageDataGenerator\nfrom keras.regularizers import l1", "Using TensorFlow backend.\n" ], [ "# dataset\ndataset = []\npaths = []\nlabels = []\ninput_size = 64\ninput_size = 64\nnum_channel = 13\n# getting paths of stored images \ndef read_files(path):\n for dirpath, dirnames, filenames in os.walk(path):\n #print('Current path: ', dirpath)\n #print('Directories: ', dirnames)\n #print('Files: ', filenames)\n #print(dirpath)\n #os.chdir(dirpath)\n paths.append(dirpath)\n \n \nread_files('/home/sachin_sharma/Desktop/exp2_tif')\npaths.sort()\npaths = paths[1:]\nfile_names = []", "_____no_output_____" ], [ "print(paths)", "['/home/sachin_sharma/Desktop/exp2_tif/Else', '/home/sachin_sharma/Desktop/exp2_tif/Industrial', '/home/sachin_sharma/Desktop/exp2_tif/Residential']\n" ], [ "# Converting 13 channel images to np array\ndef img_array(paths):\n print('{}'.format(paths))\n os.chdir('{}'.format(paths))\n for file in glob.glob(\"*.tif\"):\n #print('name of file: '+ file)\n file_names.append(file)\n x = tif.imread('{}'.format(file))\n basename, ext = os.path.splitext(file)\n labels.append(basename)\n x = np.resize(x, (64, 64, 13))\n dataset.append(x)\n\n#calling\nfor pths in paths:\n img_array(pths)\n", "/home/sachin_sharma/Desktop/exp2_tif/Else\n/home/sachin_sharma/Desktop/exp2_tif/Industrial\n/home/sachin_sharma/Desktop/exp2_tif/Residential\n" ], [ "# lets see the shape of random element in a dataset\nprint(dataset[400].shape)", "(64, 64, 13)\n" ], [ "# Getting the list of max pixel value in each image\n\"\"\"\"max_pixel_val = []\ndef max_pixel(data):\n max_pixel_val.append(np.amax(data))\n \n# calling \nfor data in dataset:\n max_pixel(data)\"\"\"", "_____no_output_____" ], [ "\"\"\"# max of all pixel values\nmax_all_pixel_value = max(max_pixel_val) \nprint('max pixel value from all 13 band images: ',max_all_pixel_value)\"\"\"", "max pixel value from all 13 band images: 28002\n" ], [ "# Normalizing\n\"\"\"X_nparray = np.array(dataset).astype(np.float64)\nX_mean = np.mean(X_nparray, axis=(0,1,2))\nX_std = np.std(X_nparray, axis=(0,1,2))\n\nX_nparray -= X_mean\nX_nparray /= X_std\n\nprint(X_nparray.shape)\nprint(X_mean.shape)\"\"\"", "(28988, 64, 64, 13)\n(13,)\n" ], [ "X_nparray = np.array(dataset)\n", "_____no_output_____" ], [ "\n\n#print(type(X_mean))\nprint(X_mean)\n#print(X_std)", "_____no_output_____" ], [ "print(np.mean(X_nparray, axis=(0,1,2)))\n#print(np.std(X_nparray, axis=(0,1,2)))", "[-9.46398206e-13 7.74425898e-13 2.95134115e-14 -4.64246698e-13\n -3.94404213e-12 -6.04875067e-12 -2.91569061e-11 1.90276346e-11\n 7.92099959e-12 -3.30594483e-10 4.43646169e-12 7.26433773e-12\n 6.84944891e-12]\n" ], [ "# label encoding\nlbl_encoder = LabelEncoder()\nohe = OneHotEncoder()\n ", "_____no_output_____" ], [ "# assigning labels to each image\nlabels_1 = []\nfor l in labels:\n labels_1.append(l.split(\"_\")[0])\n\nlbl_list = lbl_encoder.fit_transform(labels_1)\nY = ohe.fit_transform(lbl_list.reshape(-1,1)).toarray().astype(int)\n", "/home/sachin_sharma/.conda/envs/tf18/lib/python3.6/site-packages/sklearn/preprocessing/_encoders.py:368: FutureWarning: The handling of integer data will change in version 0.22. Currently, the categories are determined based on the range [0, max(values)], while in the future they will be determined based on the unique values.\nIf you want the future behaviour and silence this warning, you can specify \"categories='auto'\".\nIn case you used a LabelEncoder before this OneHotEncoder to convert the categories to integers, then you can now use the OneHotEncoder directly.\n warnings.warn(msg, FutureWarning)\n" ], [ "# labels\nprint(Y[21500])", "[0 1 0]\n" ], [ "# splitting the dataset into training set test set\ntrain_data, test_data, train_labels, test_labels = model_selection.train_test_split(X_nparray, Y, test_size = 0.4, random_state = 0)\n", "_____no_output_____" ], [ "# Trained data shape\nprint(train_data.shape)\n", "(17392, 64, 64, 13)\n" ], [ "# test data shape\nprint(test_data.shape)", "(11596, 64, 64, 13)\n" ], [ "# train labels shape\nprint(train_labels.shape)\n# some first 10 hot encodings\nprint(train_labels[:10])", "(17392, 3)\n[[1 0 0]\n [1 0 0]\n [0 0 1]\n [1 0 0]\n [1 0 0]\n [1 0 0]\n [1 0 0]\n [1 0 0]\n [0 1 0]\n [1 0 0]]\n" ], [ "# test label shape\nprint(test_labels.shape)", "(11596, 3)\n" ], [ "# hyperparameters\nbatch_size = 50\nnum_classes = 3\nepochs = 20\ninput_shape = (input_size, input_size, num_channel)\nl1_lambda = 0.00003", "_____no_output_____" ], [ "# model\nmodel = Sequential()\nmodel.add(BatchNormalization(input_shape=input_shape)) \nmodel.add(Conv2D(64, (2,2), W_regularizer=l1(l1_lambda), activation='relu')) \nmodel.add(Conv2D(64, (2,2), W_regularizer=l1(l1_lambda), activation='relu'))\nmodel.add(MaxPooling2D(pool_size=(2,2)))\nmodel.add(Dropout(0.3))\nmodel.add(Flatten())\nmodel.add(Dense(512, activation='relu'))\nmodel.add(Dropout(0.5))\nmodel.add(Dense(num_classes, activation='softmax'))\nmodel.summary()\n\nopt = keras.optimizers.Adam()\nmodel.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])", "/home/sachin_sharma/.conda/envs/tf18/lib/python3.6/site-packages/ipykernel_launcher.py:4: UserWarning: Update your `Conv2D` call to the Keras 2 API: `Conv2D(64, (2, 2), activation=\"relu\", kernel_regularizer=<keras.reg...)`\n after removing the cwd from sys.path.\n/home/sachin_sharma/.conda/envs/tf18/lib/python3.6/site-packages/ipykernel_launcher.py:5: UserWarning: Update your `Conv2D` call to the Keras 2 API: `Conv2D(64, (2, 2), activation=\"relu\", kernel_regularizer=<keras.reg...)`\n \"\"\"\n" ], [ "# fitting model\nhistory = model.fit(train_data, train_labels,\n batch_size=batch_size,\n epochs=epochs,\n verbose=1,\n validation_data=(test_data, test_labels),\n )\n ", "Train on 17392 samples, validate on 11596 samples\nEpoch 1/20\n 350/17392 [..............................] - ETA: 17:25 - loss: 3.6945 - acc: 0.6686" ], [ "# saving the model\nos.chdir('/home/sachin_sharma/Desktop')\nmodel.save('exp2_c1.h5')", "_____no_output_____" ], [ "# scores\nscore = model.evaluate(test_data, test_labels, verbose=0)\nprint('Test loss:', score[0])\nprint('Test accuracy:', score[1])", "Test loss: 0.20147273086831255\nTest accuracy: 0.8750431183166609\n" ], [ "# Confusion Matrix and Classification report\nY_pred = model.predict(test_data)\ny_pred = np.argmax(Y_pred, axis=1) # predictions\nprint('Confusion Matrix')\ncm = confusion_matrix(test_labels.argmax(axis=1), y_pred)\n#print(cm)\n\ndef cm2df(cm, labels):\n df = pd.DataFrame()\n # rows\n for i, row_label in enumerate(labels):\n rowdata={}\n # columns\n for j, col_label in enumerate(labels): \n rowdata[col_label]=cm[i,j]\n df = df.append(pd.DataFrame.from_dict({row_label:rowdata}, orient='index'))\n return df[labels]\n\ndf = cm2df(cm, [\"Else\", \"Industrial\", \"Residential\"])\nprint(df)", "Confusion Matrix\n Else Industrial Residential\nElse 8559 0 0\nIndustrial 8 1587 2\nResidential 4 1435 1\n" ], [ "# Classification Report\nprint('Classification Report')\ntarget_names = ['Else','Industrial','Residential']\nclassificn_report = classification_report(test_labels.argmax(axis=1), y_pred, target_names=target_names)\nprint(classificn_report)\n", "Classification Report\n precision recall f1-score support\n\n Else 1.00 1.00 1.00 8559\n Industrial 0.53 0.99 0.69 1597\n Residential 0.33 0.00 0.00 1440\n\n micro avg 0.88 0.88 0.88 11596\n macro avg 0.62 0.66 0.56 11596\nweighted avg 0.85 0.88 0.83 11596\n\n" ], [ "# Plotting the Loss and Classification Accuracy\nmodel.metrics_names\nprint(history.history.keys())\n# \"Accuracy\"\nplt.plot(history.history['acc'])\nplt.plot(history.history['val_acc'])\nplt.title('Model Accuracy')\nplt.ylabel('Accuracy')\nplt.xlabel('Epoch')\nplt.legend(['train', 'test'], loc='upper left')\nplt.show()\nplt.savefig('classifcn.png')\n\n# \"Loss\"\nplt.plot(history.history['loss'])\nplt.plot(history.history['val_loss'])\nplt.title('Model loss')\nplt.ylabel('Loss')\nplt.xlabel('Epoch')\nplt.legend(['train', 'test'], loc='upper left')\nplt.show()", "dict_keys(['val_loss', 'val_acc', 'loss', 'acc'])\n" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2dae0da89b9055e2d545cf61ef174c532c92f1

45,897

ipynb

Jupyter Notebook

Chapter01/c1-code.ipynb

FarhadManiCodes/Pandas-Cookbook-Second-Edition

afbe9d4aa962677b35829c135093fc81cf2a718e

[ "MIT" ]

null

Chapter01/c1-code.ipynb

FarhadManiCodes/Pandas-Cookbook-Second-Edition

afbe9d4aa962677b35829c135093fc81cf2a718e

[ "MIT" ]

null

Chapter01/c1-code.ipynb

FarhadManiCodes/Pandas-Cookbook-Second-Edition

afbe9d4aa962677b35829c135093fc81cf2a718e

[ "MIT" ]

null

23.29797

1,432

0.525677

[ [ [ "# Chapter 1: Pandas Foundations", "_____no_output_____" ] ], [ [ "import pandas as pd\nimport numpy as np", "_____no_output_____" ] ], [ [ "## Introduction", "_____no_output_____" ], [ "## Dissecting the anatomy of a DataFrame", "_____no_output_____" ] ], [ [ "pd.set_option('max_columns', 4, 'max_rows', 10)", "_____no_output_____" ], [ "movies = pd.read_csv('../data/movie.csv')\nmovies.head()", "_____no_output_____" ] ], [ [ "### How it works...", "_____no_output_____" ], [ "## DataFrame Attributes", "_____no_output_____" ], [ "### How to do it... {#how-to-do-it-1}", "_____no_output_____" ] ], [ [ "movies = pd.read_csv('../data/movie.csv')\ncolumns = movies.columns\nindex = movies.index\ndata = movies.values", "_____no_output_____" ], [ "columns", "_____no_output_____" ], [ "index", "_____no_output_____" ], [ "data", "_____no_output_____" ], [ "type(index)", "_____no_output_____" ], [ "type(columns)", "_____no_output_____" ], [ "type(data)", "_____no_output_____" ], [ "issubclass(pd.RangeIndex, pd.Index)", "_____no_output_____" ] ], [ [ "### How it works...", "_____no_output_____" ], [ "### There's more", "_____no_output_____" ] ], [ [ "index.values", "_____no_output_____" ], [ "columns.values", "_____no_output_____" ] ], [ [ "## Understanding data types", "_____no_output_____" ], [ "### How to do it... {#how-to-do-it-2}", "_____no_output_____" ] ], [ [ "movies = pd.read_csv('data/movie.csv')", "_____no_output_____" ], [ "movies.dtypes", "_____no_output_____" ], [ "movies.get_dtype_counts()", "_____no_output_____" ], [ "movies.info()", "_____no_output_____" ] ], [ [ "### How it works...", "_____no_output_____" ] ], [ [ "pd.Series(['Paul', np.nan, 'George']).dtype", "_____no_output_____" ] ], [ [ "### There's more...", "_____no_output_____" ], [ "### See also", "_____no_output_____" ], [ "## Selecting a Column", "_____no_output_____" ], [ "### How to do it... {#how-to-do-it-3}", "_____no_output_____" ] ], [ [ "movies = pd.read_csv('data/movie.csv')\nmovies['director_name']", "_____no_output_____" ], [ "movies.director_name", "_____no_output_____" ], [ "movies.loc[:, 'director_name']", "_____no_output_____" ], [ "movies.iloc[:, 1]", "_____no_output_____" ], [ "movies['director_name'].index", "_____no_output_____" ], [ "movies['director_name'].dtype", "_____no_output_____" ], [ "movies['director_name'].size", "_____no_output_____" ], [ "movies['director_name'].name", "_____no_output_____" ], [ "type(movies['director_name'])", "_____no_output_____" ], [ "movies['director_name'].apply(type).unique()", "_____no_output_____" ] ], [ [ "### How it works...", "_____no_output_____" ], [ "### There's more", "_____no_output_____" ], [ "### See also", "_____no_output_____" ], [ "## Calling Series Methods", "_____no_output_____" ] ], [ [ "s_attr_methods = set(dir(pd.Series))\nlen(s_attr_methods)", "_____no_output_____" ], [ "df_attr_methods = set(dir(pd.DataFrame))\nlen(df_attr_methods)", "_____no_output_____" ], [ "len(s_attr_methods & df_attr_methods)", "_____no_output_____" ] ], [ [ "### How to do it... {#how-to-do-it-4}", "_____no_output_____" ] ], [ [ "movies = pd.read_csv('data/movie.csv')\ndirector = movies['director_name']\nfb_likes = movies['actor_1_facebook_likes']", "_____no_output_____" ], [ "director.dtype", "_____no_output_____" ], [ "fb_likes.dtype", "_____no_output_____" ], [ "director.head()", "_____no_output_____" ], [ "director.sample(n=5, random_state=42)", "_____no_output_____" ], [ "fb_likes.head()", "_____no_output_____" ], [ "director.value_counts()", "_____no_output_____" ], [ "fb_likes.value_counts()", "_____no_output_____" ], [ "director.size", "_____no_output_____" ], [ "director.shape", "_____no_output_____" ], [ "len(director)", "_____no_output_____" ], [ "director.unique()", "_____no_output_____" ], [ "director.count()", "_____no_output_____" ], [ "fb_likes.count()", "_____no_output_____" ], [ "fb_likes.quantile()", "_____no_output_____" ], [ "fb_likes.min()", "_____no_output_____" ], [ "fb_likes.max()", "_____no_output_____" ], [ "fb_likes.mean()", "_____no_output_____" ], [ "fb_likes.median()", "_____no_output_____" ], [ "fb_likes.std()", "_____no_output_____" ], [ "fb_likes.describe()", "_____no_output_____" ], [ "director.describe()", "_____no_output_____" ], [ "fb_likes.quantile(.2)", "_____no_output_____" ], [ "fb_likes.quantile([.1, .2, .3, .4, .5, .6, .7, .8, .9])", "_____no_output_____" ], [ "director.isna()", "_____no_output_____" ], [ "fb_likes_filled = fb_likes.fillna(0)\nfb_likes_filled.count()", "_____no_output_____" ], [ "fb_likes_dropped = fb_likes.dropna()\nfb_likes_dropped.size", "_____no_output_____" ] ], [ [ "### How it works...", "_____no_output_____" ], [ "### There's more...", "_____no_output_____" ] ], [ [ "director.value_counts(normalize=True)", "_____no_output_____" ], [ "director.hasnans", "_____no_output_____" ], [ "director.notna()", "_____no_output_____" ] ], [ [ "### See also", "_____no_output_____" ], [ "## Series Operations", "_____no_output_____" ] ], [ [ "5 + 9 # plus operator example. Adds 5 and 9", "_____no_output_____" ] ], [ [ "### How to do it... {#how-to-do-it-5}", "_____no_output_____" ] ], [ [ "movies = pd.read_csv('data/movie.csv')\nimdb_score = movies['imdb_score']\nimdb_score", "_____no_output_____" ], [ "imdb_score + 1", "_____no_output_____" ], [ "imdb_score * 2.5", "_____no_output_____" ], [ "imdb_score // 7", "_____no_output_____" ], [ "imdb_score > 7", "_____no_output_____" ], [ "director = movies['director_name']\ndirector == 'James Cameron'", "_____no_output_____" ] ], [ [ "### How it works...", "_____no_output_____" ], [ "### There's more...", "_____no_output_____" ] ], [ [ "imdb_score.add(1) # imdb_score + 1", "_____no_output_____" ], [ "imdb_score.gt(7) # imdb_score > 7", "_____no_output_____" ] ], [ [ "### See also", "_____no_output_____" ], [ "## Chaining Series Methods", "_____no_output_____" ], [ "### How to do it... {#how-to-do-it-6}", "_____no_output_____" ] ], [ [ "movies = pd.read_csv('data/movie.csv')\nfb_likes = movies['actor_1_facebook_likes']\ndirector = movies['director_name']", "_____no_output_____" ], [ "director.value_counts().head(3)", "_____no_output_____" ], [ "fb_likes.isna().sum()", "_____no_output_____" ], [ "fb_likes.dtype", "_____no_output_____" ], [ "(fb_likes.fillna(0)\n .astype(int)\n .head()\n)", "_____no_output_____" ] ], [ [ "### How it works...", "_____no_output_____" ], [ "### There's more...", "_____no_output_____" ] ], [ [ "(fb_likes.fillna(0)\n #.astype(int)\n #.head()\n)", "_____no_output_____" ], [ "(fb_likes.fillna(0)\n .astype(int)\n #.head()\n)", "_____no_output_____" ], [ "fb_likes.isna().mean()", "_____no_output_____" ], [ "fb_likes.fillna(0) \\\n .astype(int) \\\n .head()", "_____no_output_____" ], [ "def debug_df(df):\n print(\"BEFORE\")\n print(df)\n print(\"AFTER\")\n return df", "_____no_output_____" ], [ "(fb_likes.fillna(0)\n .pipe(debug_df)\n .astype(int) \n .head()\n)", "_____no_output_____" ], [ "intermediate = None\ndef get_intermediate(df):\n global intermediate\n intermediate = df\n return df", "_____no_output_____" ], [ "res = (fb_likes.fillna(0)\n .pipe(get_intermediate)\n .astype(int) \n .head()\n)", "_____no_output_____" ], [ "intermediate", "_____no_output_____" ] ], [ [ "## Renaming Column Names", "_____no_output_____" ], [ "### How to do it...", "_____no_output_____" ] ], [ [ "movies = pd.read_csv('data/movie.csv')", "_____no_output_____" ], [ "col_map = {'director_name':'Director Name', \n 'num_critic_for_reviews': 'Critical Reviews'} ", "_____no_output_____" ], [ "movies.rename(columns=col_map).head()", "_____no_output_____" ] ], [ [ "### How it works... {#how-it-works-8}", "_____no_output_____" ], [ "### There's more {#theres-more-7}", "_____no_output_____" ] ], [ [ "idx_map = {'Avatar':'Ratava', 'Spectre': 'Ertceps',\n \"Pirates of the Caribbean: At World's End\": 'POC'}\ncol_map = {'aspect_ratio': 'aspect',\n \"movie_facebook_likes\": 'fblikes'}\n(movies\n .set_index('movie_title')\n .rename(index=idx_map, columns=col_map)\n .head(3)\n)", "_____no_output_____" ], [ "movies = pd.read_csv('data/movie.csv', index_col='movie_title')\nids = movies.index.tolist()\ncolumns = movies.columns.tolist()", "_____no_output_____" ] ], [ [ "# rename the row and column labels with list assignments", "_____no_output_____" ] ], [ [ "ids[0] = 'Ratava'\nids[1] = 'POC'\nids[2] = 'Ertceps'\ncolumns[1] = 'director'\ncolumns[-2] = 'aspect'\ncolumns[-1] = 'fblikes'\nmovies.index = ids\nmovies.columns = columns", "_____no_output_____" ], [ "movies.head(3)", "_____no_output_____" ], [ "def to_clean(val):\n return val.strip().lower().replace(' ', '_')", "_____no_output_____" ], [ "movies.rename(columns=to_clean).head(3)", "_____no_output_____" ], [ "cols = [col.strip().lower().replace(' ', '_')\n for col in movies.columns]\nmovies.columns = cols\nmovies.head(3)", "_____no_output_____" ] ], [ [ "## Creating and Deleting columns", "_____no_output_____" ], [ "### How to do it... {#how-to-do-it-9}", "_____no_output_____" ] ], [ [ "movies = pd.read_csv('data/movie.csv')\nmovies['has_seen'] = 0", "_____no_output_____" ], [ "idx_map = {'Avatar':'Ratava', 'Spectre': 'Ertceps',\n \"Pirates of the Caribbean: At World's End\": 'POC'}\ncol_map = {'aspect_ratio': 'aspect',\n \"movie_facebook_likes\": 'fblikes'}\n(movies\n .rename(index=idx_map, columns=col_map)\n .assign(has_seen=0)\n)", "_____no_output_____" ], [ "total = (movies['actor_1_facebook_likes'] +\n movies['actor_2_facebook_likes'] + \n movies['actor_3_facebook_likes'] + \n movies['director_facebook_likes'])", "_____no_output_____" ], [ "total.head(5)", "_____no_output_____" ], [ "cols = ['actor_1_facebook_likes','actor_2_facebook_likes',\n 'actor_3_facebook_likes','director_facebook_likes']\nsum_col = movies[cols].sum(axis='columns')\nsum_col.head(5)", "_____no_output_____" ], [ "movies.assign(total_likes=sum_col).head(5)", "_____no_output_____" ], [ "def sum_likes(df):\n return df[[c for c in df.columns\n if 'like' in c]].sum(axis=1)", "_____no_output_____" ], [ "movies.assign(total_likes=sum_likes).head(5)", "_____no_output_____" ], [ "(movies\n .assign(total_likes=sum_col)\n ['total_likes']\n .isna()\n .sum()\n)", "_____no_output_____" ], [ "(movies\n .assign(total_likes=total)\n ['total_likes']\n .isna()\n .sum()\n)", "_____no_output_____" ], [ "(movies\n .assign(total_likes=total.fillna(0))\n ['total_likes']\n .isna()\n .sum()\n)", "_____no_output_____" ], [ "def cast_like_gt_actor_director(df):\n return df['cast_total_facebook_likes'] >= \\\n df['total_likes']", "_____no_output_____" ], [ "df2 = (movies\n .assign(total_likes=total,\n is_cast_likes_more = cast_like_gt_actor_director)\n)", "_____no_output_____" ], [ "df2['is_cast_likes_more'].all()", "_____no_output_____" ], [ "df2 = df2.drop(columns='total_likes')", "_____no_output_____" ], [ "actor_sum = (movies\n [[c for c in movies.columns if 'actor_' in c and '_likes' in c]]\n .sum(axis='columns')\n)", "_____no_output_____" ], [ "actor_sum.head(5)", "_____no_output_____" ], [ "movies['cast_total_facebook_likes'] >= actor_sum", "_____no_output_____" ], [ "movies['cast_total_facebook_likes'].ge(actor_sum)", "_____no_output_____" ], [ "movies['cast_total_facebook_likes'].ge(actor_sum).all()", "_____no_output_____" ], [ "pct_like = (actor_sum\n .div(movies['cast_total_facebook_likes'])\n)", "_____no_output_____" ], [ "pct_like.describe()", "_____no_output_____" ], [ "pd.Series(pct_like.values,\n index=movies['movie_title'].values).head()", "_____no_output_____" ] ], [ [ "### How it works... {#how-it-works-9}", "_____no_output_____" ], [ "### There's more... {#theres-more-8}", "_____no_output_____" ] ], [ [ "profit_index = movies.columns.get_loc('gross') + 1\nprofit_index", "_____no_output_____" ], [ "movies.insert(loc=profit_index,\n column='profit',\n value=movies['gross'] - movies['budget'])", "_____no_output_____" ], [ "del movies['director_name']", "_____no_output_____" ] ], [ [ "### See also", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ] ]

cb2daf1eaf8d8fcbe17946ed4cdb311e02788100

6,139

ipynb

Jupyter Notebook

0.8/_downloads/659de5944f8dc1f0424c48f86a240d84/hyperparameter-optimization.ipynb

scikit-optimize/scikit-optimize.github.io

209d20f8603b7b6663f27f058560f3e15a546d76

[ "BSD-3-Clause" ]

15

2016-07-27T13:17:06.000Z

2021-08-31T14:18:07.000Z

0.8/_downloads/659de5944f8dc1f0424c48f86a240d84/hyperparameter-optimization.ipynb

scikit-optimize/scikit-optimize.github.io

209d20f8603b7b6663f27f058560f3e15a546d76

[ "BSD-3-Clause" ]

2

2018-05-09T15:01:09.000Z

2020-10-22T00:56:21.000Z

0.8/_downloads/659de5944f8dc1f0424c48f86a240d84/hyperparameter-optimization.ipynb

scikit-optimize/scikit-optimize.github.io

209d20f8603b7b6663f27f058560f3e15a546d76

[ "BSD-3-Clause" ]

6

2017-08-19T12:05:57.000Z

2021-02-16T20:54:58.000Z

44.810219

1,312

0.620296

[ [ [ "%matplotlib inline", "_____no_output_____" ] ], [ [ "\n# Tuning a scikit-learn estimator with `skopt`\n\nGilles Louppe, July 2016\nKatie Malone, August 2016\nReformatted by Holger Nahrstaedt 2020\n\n.. currentmodule:: skopt\n\nIf you are looking for a :obj:`sklearn.model_selection.GridSearchCV` replacement checkout\n`sphx_glr_auto_examples_sklearn-gridsearchcv-replacement.py` instead.\n\n## Problem statement\n\nTuning the hyper-parameters of a machine learning model is often carried out\nusing an exhaustive exploration of (a subset of) the space all hyper-parameter\nconfigurations (e.g., using :obj:`sklearn.model_selection.GridSearchCV`), which\noften results in a very time consuming operation.\n\nIn this notebook, we illustrate how to couple :class:`gp_minimize` with sklearn's\nestimators to tune hyper-parameters using sequential model-based optimisation,\nhopefully resulting in equivalent or better solutions, but within less\nevaluations.\n\nNote: scikit-optimize provides a dedicated interface for estimator tuning via\n:class:`BayesSearchCV` class which has a similar interface to those of\n:obj:`sklearn.model_selection.GridSearchCV`. This class uses functions of skopt to perform hyperparameter\nsearch efficiently. For example usage of this class, see\n`sphx_glr_auto_examples_sklearn-gridsearchcv-replacement.py`\nexample notebook.\n", "_____no_output_____" ] ], [ [ "print(__doc__)\nimport numpy as np", "_____no_output_____" ] ], [ [ "## Objective\nTo tune the hyper-parameters of our model we need to define a model,\ndecide which parameters to optimize, and define the objective function\nwe want to minimize.\n\n", "_____no_output_____" ] ], [ [ "from sklearn.datasets import load_boston\nfrom sklearn.ensemble import GradientBoostingRegressor\nfrom sklearn.model_selection import cross_val_score\n\nboston = load_boston()\nX, y = boston.data, boston.target\nn_features = X.shape[1]\n\n# gradient boosted trees tend to do well on problems like this\nreg = GradientBoostingRegressor(n_estimators=50, random_state=0)", "_____no_output_____" ] ], [ [ "Next, we need to define the bounds of the dimensions of the search space\nwe want to explore and pick the objective. In this case the cross-validation\nmean absolute error of a gradient boosting regressor over the Boston\ndataset, as a function of its hyper-parameters.\n\n", "_____no_output_____" ] ], [ [ "from skopt.space import Real, Integer\nfrom skopt.utils import use_named_args\n\n\n# The list of hyper-parameters we want to optimize. For each one we define the\n# bounds, the corresponding scikit-learn parameter name, as well as how to\n# sample values from that dimension (`'log-uniform'` for the learning rate)\nspace = [Integer(1, 5, name='max_depth'),\n Real(10**-5, 10**0, \"log-uniform\", name='learning_rate'),\n Integer(1, n_features, name='max_features'),\n Integer(2, 100, name='min_samples_split'),\n Integer(1, 100, name='min_samples_leaf')]\n\n# this decorator allows your objective function to receive a the parameters as\n# keyword arguments. This is particularly convenient when you want to set\n# scikit-learn estimator parameters\n@use_named_args(space)\ndef objective(**params):\n reg.set_params(**params)\n\n return -np.mean(cross_val_score(reg, X, y, cv=5, n_jobs=-1,\n scoring=\"neg_mean_absolute_error\"))", "_____no_output_____" ] ], [ [ "## Optimize all the things!\nWith these two pieces, we are now ready for sequential model-based\noptimisation. Here we use gaussian process-based optimisation.\n\n", "_____no_output_____" ] ], [ [ "from skopt import gp_minimize\nres_gp = gp_minimize(objective, space, n_calls=50, random_state=0)\n\n\"Best score=%.4f\" % res_gp.fun", "_____no_output_____" ], [ "print(\"\"\"Best parameters:\n- max_depth=%d\n- learning_rate=%.6f\n- max_features=%d\n- min_samples_split=%d\n- min_samples_leaf=%d\"\"\" % (res_gp.x[0], res_gp.x[1],\n res_gp.x[2], res_gp.x[3],\n res_gp.x[4]))", "_____no_output_____" ] ], [ [ "## Convergence plot\n\n", "_____no_output_____" ] ], [ [ "from skopt.plots import plot_convergence\n\nplot_convergence(res_gp)", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ] ]

cb2dc2ac277c50b44251235f798cd33b0ebcadc3

682,240

ipynb

Jupyter Notebook

deeplearning1/nbs/lesson1-work_through_lecture.ipynb

ibuder/fastai_courses

16f222509edc424a32efffb8cef34c6780f8e2b5

[ "Apache-2.0" ]

null

deeplearning1/nbs/lesson1-work_through_lecture.ipynb

ibuder/fastai_courses

16f222509edc424a32efffb8cef34c6780f8e2b5

[ "Apache-2.0" ]

null

deeplearning1/nbs/lesson1-work_through_lecture.ipynb

ibuder/fastai_courses

16f222509edc424a32efffb8cef34c6780f8e2b5

[ "Apache-2.0" ]

null

682.24

430,632

0.936911

[ [ [ "# Using Convolutional Neural Networks", "_____no_output_____" ], [ "Welcome to the first week of the first deep learning certificate! We're going to use convolutional neural networks (CNNs) to allow our computer to see - something that is only possible thanks to deep learning.", "_____no_output_____" ], [ "## Introduction to this week's task: 'Dogs vs Cats'", "_____no_output_____" ], [ "We're going to try to create a model to enter the [Dogs vs Cats](https://www.kaggle.com/c/dogs-vs-cats) competition at Kaggle. There are 25,000 labelled dog and cat photos available for training, and 12,500 in the test set that we have to try to label for this competition. According to the Kaggle web-site, when this competition was launched (end of 2013): *\"**State of the art**: The current literature suggests machine classifiers can score above 80% accuracy on this task\"*. So if we can beat 80%, then we will be at the cutting edge as of 2013!", "_____no_output_____" ], [ "## Basic setup", "_____no_output_____" ], [ "There isn't too much to do to get started - just a few simple configuration steps.\n\nThis shows plots in the web page itself - we always wants to use this when using jupyter notebook:", "_____no_output_____" ] ], [ [ "%matplotlib inline", "_____no_output_____" ] ], [ [ "Define path to data: (It's a good idea to put it in a subdirectory of your notebooks folder, and then exclude that directory from git control by adding it to .gitignore.)", "_____no_output_____" ] ], [ [ "pwd", "_____no_output_____" ] ], [ [ "You need to download the data to this path...see below for the download link.", "_____no_output_____" ] ], [ [ "#path = \"data/dogscats/\"\n# For testing code, not enough data for anything serious\npath = \"data/dogscats/sample/\" ", "_____no_output_____" ] ], [ [ "A few basic libraries that we'll need for the initial exercises:", "_____no_output_____" ] ], [ [ "from __future__ import division, print_function\n\nimport os, json\nfrom glob import glob\nimport numpy as np\nnp.set_printoptions(precision=4, linewidth=100)\nfrom matplotlib import pyplot as plt", "_____no_output_____" ] ], [ [ "We have created a file most imaginatively called 'utils.py' to store any little convenience functions we'll want to use. We will discuss these as we use them.", "_____no_output_____" ] ], [ [ "import utils\nfrom utils import plots", "Using TensorFlow backend.\n" ] ], [ [ "# Use a pretrained VGG model with our **Vgg16** class", "_____no_output_____" ], [ "Our first step is simply to use a model that has been fully created for us, which can recognise a wide variety (1,000 categories) of images. We will use 'VGG', which won the 2014 Imagenet competition, and is a very simple model to create and understand. The VGG Imagenet team created both a larger, slower, slightly more accurate model (*VGG 19*) and a smaller, faster model (*VGG 16*). We will be using VGG 16 since the much slower performance of VGG19 is generally not worth the very minor improvement in accuracy.\n\nWe have created a python class, *Vgg16*, which makes using the VGG 16 model very straightforward. ", "_____no_output_____" ], [ "## The punchline: state of the art custom model in 7 lines of code\n\nHere's everything you need to do to get >97% accuracy on the Dogs vs Cats dataset - we won't analyze how it works behind the scenes yet, since at this stage we're just going to focus on the minimum necessary to actually do useful work.", "_____no_output_____" ] ], [ [ "# As large as you can, but no larger than 64 is recommended. \n# If you have an older or cheaper GPU, you'll run out of memory, so will have to decrease this.\nbatch_size=32", "_____no_output_____" ], [ "# Import our class, and instantiate\nimport vgg16\nimport imp\nimp.reload(vgg16)\nfrom vgg16 import Vgg16", "_____no_output_____" ] ], [ [ "Download data from http://files.fast.ai/data/ (`dogscats.zip` is the relevant file for this.)", "_____no_output_____" ] ], [ [ "vgg = Vgg16()\n# Grab a few images at a time for training and validation.\n# NB: They must be in subdirectories named based on their category\nbatches = vgg.get_batches(path+'train', batch_size=batch_size)\nval_batches = vgg.get_batches(path+'valid', batch_size=batch_size*2)\nvgg.finetune(batches)\nvgg.fit(batches, val_batches, nb_epoch=1)", "Found 23000 images belonging to 2 classes.\nFound 2000 images belonging to 2 classes.\nEpoch 1/1\n718/718 [==============================] - 224s 312ms/step - loss: 0.4727 - acc: 0.8701 - val_loss: 0.2377 - val_acc: 0.9183\n" ] ], [ [ "I think the low performance compared to official lesson1 notebook is due to remaining Theano vs. Tensorflow incompatible stuff (i.e. it's not using VGG16 exactly). I propose to sidestep this by building a \"new\" model in Keras+TF using pretrained VGG16 now available in Keras.", "_____no_output_____" ], [ "The code above will work for any image recognition task, with any number of categories! All you have to do is to put your images into one folder per category, and run the code above.\n\nLet's take a look at how this works, step by step...", "_____no_output_____" ], [ "## Use Vgg16 for basic image recognition\n\nLet's start off by using the *Vgg16* class to recognise the main imagenet category for each image.\n\nWe won't be able to enter the Cats vs Dogs competition with an Imagenet model alone, since 'cat' and 'dog' are not categories in Imagenet - instead each individual breed is a separate category. However, we can use it to see how well it can recognise the images, which is a good first step.\n\nFirst, create a Vgg16 object:", "_____no_output_____" ] ], [ [ "vgg = Vgg16()", "_____no_output_____" ] ], [ [ "Vgg16 is built on top of *Keras* (which we will be learning much more about shortly!), a flexible, easy to use deep learning library that sits on top of Theano or Tensorflow. Keras reads groups of images and labels in *batches*, using a fixed directory structure, where images from each category for training must be placed in a separate folder.\n\nLet's grab batches of data from our training folder:", "_____no_output_____" ] ], [ [ "batches = vgg.get_batches(path+'train', batch_size=4)", "Found 16 images belonging to 2 classes.\n" ] ], [ [ "(BTW, when Keras refers to 'classes', it doesn't mean python classes - but rather it refers to the categories of the labels, such as 'pug', or 'tabby'.)\n\n*Batches* is just a regular python iterator. Each iteration returns both the images themselves, as well as the labels.", "_____no_output_____" ] ], [ [ "imgs,labels = next(batches)", "_____no_output_____" ] ], [ [ "As you can see, the labels for each image are an array, containing a 1 in the first position if it's a cat, and in the second position if it's a dog. This approach to encoding categorical variables, where an array containing just a single 1 in the position corresponding to the category, is very common in deep learning. It is called *one hot encoding*. \n\nThe arrays contain two elements, because we have two categories (cat, and dog). If we had three categories (e.g. cats, dogs, and kangaroos), then the arrays would each contain two 0's, and one 1.", "_____no_output_____" ] ], [ [ "plots(imgs, titles=labels)", "_____no_output_____" ] ], [ [ "We can now pass the images to Vgg16's predict() function to get back probabilities, category indexes, and category names for each image's VGG prediction.", "_____no_output_____" ] ], [ [ "vgg.predict(imgs, True)", "_____no_output_____" ] ], [ [ "The category indexes are based on the ordering of categories used in the VGG model - e.g here are the first four:", "_____no_output_____" ] ], [ [ "vgg.classes[:4]", "_____no_output_____" ] ], [ [ "(Note that, other than creating the Vgg16 object, none of these steps are necessary to build a model; they are just showing how to use the class to view imagenet predictions.)", "_____no_output_____" ], [ "## Use our Vgg16 class to finetune a Dogs vs Cats model\n\nTo change our model so that it outputs \"cat\" vs \"dog\", instead of one of 1,000 very specific categories, we need to use a process called \"finetuning\". Finetuning looks from the outside to be identical to normal machine learning training - we provide a training set with data and labels to learn from, and a validation set to test against. The model learns a set of parameters based on the data provided.\n\nHowever, the difference is that we start with a model that is already trained to solve a similar problem. The idea is that many of the parameters should be very similar, or the same, between the existing model, and the model we wish to create. Therefore, we only select a subset of parameters to train, and leave the rest untouched. This happens automatically when we call *fit()* after calling *finetune()*.\n\nWe create our batches just like before, and making the validation set available as well. A 'batch' (or *mini-batch* as it is commonly known) is simply a subset of the training data - we use a subset at a time when training or predicting, in order to speed up training, and to avoid running out of memory.", "_____no_output_____" ] ], [ [ "batch_size=32", "_____no_output_____" ], [ "batches = vgg.get_batches(path+'train', batch_size=batch_size)\nval_batches = vgg.get_batches(path+'valid', batch_size=batch_size)", "Found 16 images belonging to 2 classes.\nFound 8 images belonging to 2 classes.\n" ] ], [ [ "Calling *finetune()* modifies the model such that it will be trained based on the data in the batches provided - in this case, to predict either 'dog' or 'cat'.", "_____no_output_____" ] ], [ [ "vgg.finetune(batches)", "_____no_output_____" ] ], [ [ "Finally, we *fit()* the parameters of the model using the training data, reporting the accuracy on the validation set after every epoch. (An *epoch* is one full pass through the training data.)", "_____no_output_____" ] ], [ [ "vgg.fit(batches, val_batches, nb_epoch=10)", "Epoch 1/10\n1/1 [==============================] - 1s 627ms/step - loss: 1.4330 - acc: 0.5625 - val_loss: 0.6651 - val_acc: 0.7500\nEpoch 2/10\n1/1 [==============================] - 0s 473ms/step - loss: 0.8482 - acc: 0.6875 - val_loss: 0.6438 - val_acc: 0.8750\nEpoch 3/10\n1/1 [==============================] - 0s 461ms/step - loss: 0.3983 - acc: 0.7500 - val_loss: 0.6467 - val_acc: 0.8750\nEpoch 4/10\n1/1 [==============================] - 0s 350ms/step - loss: 0.1895 - acc: 0.8750 - val_loss: 0.5969 - val_acc: 0.8750\nEpoch 5/10\n1/1 [==============================] - 0s 358ms/step - loss: 0.5256 - acc: 0.8125 - val_loss: 0.5668 - val_acc: 0.8750\nEpoch 6/10\n1/1 [==============================] - 0s 455ms/step - loss: 0.2721 - acc: 0.8125 - val_loss: 0.5602 - val_acc: 0.8750\nEpoch 7/10\n1/1 [==============================] - 0s 357ms/step - loss: 0.0431 - acc: 1.0000 - val_loss: 0.5541 - val_acc: 0.8750\nEpoch 8/10\n1/1 [==============================] - 0s 450ms/step - loss: 0.2385 - acc: 0.8750 - val_loss: 0.5797 - val_acc: 0.8750\nEpoch 9/10\n1/1 [==============================] - 0s 348ms/step - loss: 0.0344 - acc: 1.0000 - val_loss: 0.5926 - val_acc: 0.8750\nEpoch 10/10\n1/1 [==============================] - 0s 457ms/step - loss: 0.1247 - acc: 0.9375 - val_loss: 0.6244 - val_acc: 0.8750\n" ] ], [ [ "That shows all of the steps involved in using the Vgg16 class to create an image recognition model using whatever labels you are interested in. For instance, this process could classify paintings by style, or leaves by type of disease, or satellite photos by type of crop, and so forth.\n\nNext up, we'll dig one level deeper to see what's going on in the Vgg16 class.", "_____no_output_____" ], [ "# Create a VGG model from scratch in Keras\n\nFor the rest of this tutorial, we will not be using the Vgg16 class at all. Instead, we will recreate from scratch the functionality we just used. This is not necessary if all you want to do is use the existing model - but if you want to create your own models, you'll need to understand these details. It will also help you in the future when you debug any problems with your models, since you'll understand what's going on behind the scenes.", "_____no_output_____" ], [ "## Model setup\n\nWe need to import all the modules we'll be using from numpy, scipy, and keras:", "_____no_output_____" ] ], [ [ "from numpy.random import random, permutation\nfrom scipy import misc, ndimage\nfrom scipy.ndimage.interpolation import zoom\n\nimport keras\nfrom keras import backend as K\nfrom keras.utils.data_utils import get_file\nfrom keras.models import Sequential, Model\nfrom keras.layers.core import Flatten, Dense, Dropout, Lambda\nfrom keras.layers import Input\nfrom keras.layers.convolutional import Convolution2D, MaxPooling2D, ZeroPadding2D\nfrom keras.optimizers import SGD, RMSprop\nfrom keras.preprocessing import image", "_____no_output_____" ] ], [ [ "Let's import the mappings from VGG ids to imagenet category ids and descriptions, for display purposes later.", "_____no_output_____" ] ], [ [ "FILES_PATH = 'http://files.fast.ai/models/'; CLASS_FILE='imagenet_class_index.json'\n# Keras' get_file() is a handy function that downloads files, and caches them for re-use later\nfpath = get_file(CLASS_FILE, FILES_PATH+CLASS_FILE, cache_subdir='models')\nwith open(fpath) as f: class_dict = json.load(f)\n# Convert dictionary with string indexes into an array\nclasses = [class_dict[str(i)][1] for i in range(len(class_dict))]", "_____no_output_____" ] ], [ [ "Here's a few examples of the categories we just imported:", "_____no_output_____" ] ], [ [ "classes[:5]", "_____no_output_____" ] ], [ [ "## Model creation\n\nCreating the model involves creating the model architecture, and then loading the model weights into that architecture. We will start by defining the basic pieces of the VGG architecture.\n\nVGG has just one type of convolutional block, and one type of fully connected ('dense') block. Here's the convolutional block definition:", "_____no_output_____" ] ], [ [ "def ConvBlock(layers, model, filters):\n for i in range(layers): \n model.add(ZeroPadding2D((1,1)))\n model.add(Convolution2D(filters, 3, 3, activation='relu'))\n model.add(MaxPooling2D((2,2), strides=(2,2)))", "_____no_output_____" ] ], [ [ "...and here's the fully-connected definition.", "_____no_output_____" ] ], [ [ "def FCBlock(model):\n model.add(Dense(4096, activation='relu'))\n model.add(Dropout(0.5))", "_____no_output_____" ] ], [ [ "When the VGG model was trained in 2014, the creators subtracted the average of each of the three (R,G,B) channels first, so that the data for each channel had a mean of zero. Furthermore, their software that expected the channels to be in B,G,R order, whereas Python by default uses R,G,B. We need to preprocess our data to make these two changes, so that it is compatible with the VGG model:", "_____no_output_____" ] ], [ [ "# Mean of each channel as provided by VGG researchers\nvgg_mean = np.array([123.68, 116.779, 103.939]).reshape((3,1,1))\n\ndef vgg_preprocess(x):\n x = x - vgg_mean # subtract mean\n return x[:, ::-1] # reverse axis bgr->rgb", "_____no_output_____" ] ], [ [ "Now we're ready to define the VGG model architecture - look at how simple it is, now that we have the basic blocks defined!", "_____no_output_____" ] ], [ [ "def VGG_16():\n model = Sequential()\n model.add(Lambda(vgg_preprocess, input_shape=(3,224,224)))\n\n ConvBlock(2, model, 64)\n ConvBlock(2, model, 128)\n ConvBlock(3, model, 256)\n ConvBlock(3, model, 512)\n ConvBlock(3, model, 512)\n\n model.add(Flatten())\n FCBlock(model)\n FCBlock(model)\n model.add(Dense(1000, activation='softmax'))\n return model", "_____no_output_____" ] ], [ [ "We'll learn about what these different blocks do later in the course. For now, it's enough to know that:\n\n- Convolution layers are for finding patterns in images\n- Dense (fully connected) layers are for combining patterns across an image\n\nNow that we've defined the architecture, we can create the model like any python object:", "_____no_output_____" ] ], [ [ "model = VGG_16()", "_____no_output_____" ] ], [ [ "As well as the architecture, we need the weights that the VGG creators trained. The weights are the part of the model that is learnt from the data, whereas the architecture is pre-defined based on the nature of the problem. \n\nDownloading pre-trained weights is much preferred to training the model ourselves, since otherwise we would have to download the entire Imagenet archive, and train the model for many days! It's very helpful when researchers release their weights, as they did here.", "_____no_output_____" ] ], [ [ "fpath = get_file('vgg16.h5', FILES_PATH+'vgg16.h5', cache_subdir='models')\nmodel.load_weights(fpath)", "_____no_output_____" ] ], [ [ "## Getting imagenet predictions\n\nThe setup of the imagenet model is now complete, so all we have to do is grab a batch of images and call *predict()* on them.", "_____no_output_____" ] ], [ [ "batch_size = 4", "_____no_output_____" ] ], [ [ "Keras provides functionality to create batches of data from directories containing images; all we have to do is to define the size to resize the images to, what type of labels to create, whether to randomly shuffle the images, and how many images to include in each batch. We use this little wrapper to define some helpful defaults appropriate for imagenet data:", "_____no_output_____" ] ], [ [ "def get_batches(dirname, gen=image.ImageDataGenerator(), shuffle=True, \n batch_size=batch_size, class_mode='categorical'):\n return gen.flow_from_directory(path+dirname, target_size=(224,224), \n class_mode=class_mode, shuffle=shuffle, batch_size=batch_size)", "_____no_output_____" ] ], [ [ "From here we can use exactly the same steps as before to look at predictions from the model.", "_____no_output_____" ] ], [ [ "batches = get_batches('train', batch_size=batch_size)\nval_batches = get_batches('valid', batch_size=batch_size)\nimgs,labels = next(batches)\n\n# This shows the 'ground truth'\nplots(imgs, titles=labels)", "Found 23000 images belonging to 2 classes.\nFound 2000 images belonging to 2 classes.\n" ] ], [ [ "The VGG model returns 1,000 probabilities for each image, representing the probability that the model assigns to each possible imagenet category for each image. By finding the index with the largest probability (with *np.argmax()*) we can find the predicted label.", "_____no_output_____" ] ], [ [ "def pred_batch(imgs):\n preds = model.predict(imgs)\n idxs = np.argmax(preds, axis=1)\n\n print('Shape: {}'.format(preds.shape))\n print('First 5 classes: {}'.format(classes[:5]))\n print('First 5 probabilities: {}\\n'.format(preds[0, :5]))\n print('Predictions prob/class: ')\n \n for i in range(len(idxs)):\n idx = idxs[i]\n print (' {:.4f}/{}'.format(preds[i, idx], classes[idx]))", "_____no_output_____" ], [ "pred_batch(imgs)", "Shape: (4, 1000)\nFirst 5 classes: [u'tench', u'goldfish', u'great_white_shark', u'tiger_shark', u'hammerhead']\nFirst 5 probabilities: [ 1.1169e-08 1.7160e-07 2.2501e-06 2.3426e-08 5.9417e-08]\n\nPredictions prob/class: \n 0.2285/papillon\n 0.2947/lynx\n 0.6434/Egyptian_cat\n 0.4845/Australian_terrier\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ] ]

cb2dc5f9be62ddbc08dadc8eb9d742a54601d73d

13,934

ipynb

Jupyter Notebook

step2.ipynb

tyburam/wit-dataworkshop

337130b687d355b73db3fab429171155bca9908d

[ "MIT" ]

null

step2.ipynb

tyburam/wit-dataworkshop

337130b687d355b73db3fab429171155bca9908d

[ "MIT" ]

null

step2.ipynb

tyburam/wit-dataworkshop

337130b687d355b73db3fab429171155bca9908d

[ "MIT" ]

null

41.347181

396

0.629252

[ [ [ "import pandas as pd\nimport numpy as np\nimport xgboost as xgb\n\nfrom sklearn import preprocessing\nfrom sklearn.cross_validation import KFold\n\nfrom sklearn.metrics import mean_absolute_error\n\n%matplotlib inline", "/Users/mateusztybura/anaconda3/lib/python3.6/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also note that the interface of the new CV iterators are different from that of this module. This module will be removed in 0.20.\n \"This module will be removed in 0.20.\", DeprecationWarning)\n" ], [ "train = pd.read_csv('train.csv')", "_____no_output_____" ], [ "cat_feats = train.select_dtypes(include=[\"object\"]).columns\n\nfor feat in cat_feats:\n train[feat + '_id'] = preprocessing.LabelEncoder().fit_transform(train[feat].values)", "_____no_output_____" ], [ "num_feats = [feat for feat in train.columns if 'cont' in feat]\nid_feats = [feat for feat in train.columns if '_id' in feat]\n\nX = train[num_feats + id_feats].values\ny = train['loss'].values", "_____no_output_____" ], [ "model = xgb.XGBRegressor(\n max_depth = 12,\n learning_rate = 0.2,\n n_estimators = 20,\n silent = 0,\n objective = 'reg:linear',\n nthread = -1,\n # gamma = 5290.,\n # min_child_weight = 4.2922,\n subsample = 0.7,\n colsample_bytree = 0.6,\n seed = 2017\n)", "_____no_output_____" ], [ "nfolds = 3\nfolds = KFold(len(y), n_folds=nfolds, shuffle = True, random_state = 2017)\n\n\nfor num_iter, (train_index, test_index) in enumerate(folds):\n X_train, y_train = X[train_index], y[train_index]\n X_test, y_test = X[test_index], y[test_index]\n \n model.fit(X_train, y_train,\n eval_metric='mae',\n eval_set=[(X[train_index], y[train_index]), (X[test_index], y[test_index])],\n verbose=True)\n \n y_pred = model.predict(X_test)\n y_pred[y_pred<0] = 0\n \n score = mean_absolute_error(y_test, y_pred)\n print(\"Fold{0}, score={1}\".format(num_iter+1, score))", "[0]\tvalidation_0-mae:2444.59\tvalidation_1-mae:2456.73\n[1]\tvalidation_0-mae:1994.44\tvalidation_1-mae:2015.5\n[2]\tvalidation_0-mae:1679.35\tvalidation_1-mae:1714.77\n[3]\tvalidation_0-mae:1467.29\tvalidation_1-mae:1519.74\n[4]\tvalidation_0-mae:1331.48\tvalidation_1-mae:1401.69\n[5]\tvalidation_0-mae:1238.07\tvalidation_1-mae:1327.88\n[6]\tvalidation_0-mae:1179.27\tvalidation_1-mae:1282.38\n[7]\tvalidation_0-mae:1137.55\tvalidation_1-mae:1256.62\n[8]\tvalidation_0-mae:1104.23\tvalidation_1-mae:1238.52\n[9]\tvalidation_0-mae:1085.17\tvalidation_1-mae:1231.48\n[10]\tvalidation_0-mae:1070.75\tvalidation_1-mae:1227.66\n[11]\tvalidation_0-mae:1058.24\tvalidation_1-mae:1226.64\n[12]\tvalidation_0-mae:1050.15\tvalidation_1-mae:1225.68\n[13]\tvalidation_0-mae:1040.02\tvalidation_1-mae:1225.85\n[14]\tvalidation_0-mae:1029.32\tvalidation_1-mae:1224.26\n[15]\tvalidation_0-mae:1021.08\tvalidation_1-mae:1223.43\n[16]\tvalidation_0-mae:1013.28\tvalidation_1-mae:1223.66\n[17]\tvalidation_0-mae:1004.45\tvalidation_1-mae:1223.76\n[18]\tvalidation_0-mae:998.408\tvalidation_1-mae:1223.95\n[19]\tvalidation_0-mae:989.761\tvalidation_1-mae:1224.11\nFold1, score=1224.1078371375197\n[0]\tvalidation_0-mae:2453.79\tvalidation_1-mae:2425.29\n[1]\tvalidation_0-mae:2002.32\tvalidation_1-mae:1985.29\n[2]\tvalidation_0-mae:1688.14\tvalidation_1-mae:1687.45\n[3]\tvalidation_0-mae:1475.56\tvalidation_1-mae:1496.06\n[4]\tvalidation_0-mae:1337.74\tvalidation_1-mae:1380.47\n[5]\tvalidation_0-mae:1242.45\tvalidation_1-mae:1310.64\n[6]\tvalidation_0-mae:1182.54\tvalidation_1-mae:1270.56\n[7]\tvalidation_0-mae:1140.19\tvalidation_1-mae:1246.18\n[8]\tvalidation_0-mae:1105.65\tvalidation_1-mae:1230.63\n[9]\tvalidation_0-mae:1085.32\tvalidation_1-mae:1223.83\n[10]\tvalidation_0-mae:1070.09\tvalidation_1-mae:1221.12\n[11]\tvalidation_0-mae:1055.65\tvalidation_1-mae:1221.63\n[12]\tvalidation_0-mae:1048.61\tvalidation_1-mae:1222.62\n[13]\tvalidation_0-mae:1037.73\tvalidation_1-mae:1223.7\n[14]\tvalidation_0-mae:1026.7\tvalidation_1-mae:1223.91\n[15]\tvalidation_0-mae:1017.04\tvalidation_1-mae:1224.06\n[16]\tvalidation_0-mae:1010.43\tvalidation_1-mae:1224.49\n[17]\tvalidation_0-mae:1000.18\tvalidation_1-mae:1224.82\n[18]\tvalidation_0-mae:991.844\tvalidation_1-mae:1225.37\n[19]\tvalidation_0-mae:984.471\tvalidation_1-mae:1225.06\nFold2, score=1225.0567140658316\n[0]\tvalidation_0-mae:2438.91\tvalidation_1-mae:2462.18\n[1]\tvalidation_0-mae:1990.33\tvalidation_1-mae:2021.27\n[2]\tvalidation_0-mae:1675.13\tvalidation_1-mae:1719.31\n[3]\tvalidation_0-mae:1464.25\tvalidation_1-mae:1525.29\n[4]\tvalidation_0-mae:1323.12\tvalidation_1-mae:1402.33\n[5]\tvalidation_0-mae:1229.86\tvalidation_1-mae:1329.2\n[6]\tvalidation_0-mae:1169.32\tvalidation_1-mae:1285.26\n[7]\tvalidation_0-mae:1128.45\tvalidation_1-mae:1259.78\n[8]\tvalidation_0-mae:1096.68\tvalidation_1-mae:1245.34\n[9]\tvalidation_0-mae:1075.07\tvalidation_1-mae:1236.78\n[10]\tvalidation_0-mae:1061.35\tvalidation_1-mae:1233.31\n[11]\tvalidation_0-mae:1048.73\tvalidation_1-mae:1231.54\n[12]\tvalidation_0-mae:1040.74\tvalidation_1-mae:1230.17\n[13]\tvalidation_0-mae:1030.07\tvalidation_1-mae:1229.64\n[14]\tvalidation_0-mae:1024.49\tvalidation_1-mae:1229.59\n[15]\tvalidation_0-mae:1013.17\tvalidation_1-mae:1228.62\n[16]\tvalidation_0-mae:1005.18\tvalidation_1-mae:1228.77\n[17]\tvalidation_0-mae:993.365\tvalidation_1-mae:1228.67\n[18]\tvalidation_0-mae:982.065\tvalidation_1-mae:1229.4\n[19]\tvalidation_0-mae:975.589\tvalidation_1-mae:1229.36\nFold3, score=1229.3648513041749\n" ] ], [ [ "## Task\n\nOne cell above there's a model wich use y like a target variable.\nModeify the code in order to use transformed targert variable by logarithm...\n\n\nsome TIPS:\n1. y_log_train = np.log(y_train)\n2. model.fit(X_train, y_log_train, ...\n3. y_log_pred = model.predict(X_test)\n4. y_pred = np.exp(y_log_pred)\n", "_____no_output_____" ] ], [ [ "nfolds = 3\nfolds = KFold(len(y), n_folds=nfolds, shuffle = True, random_state = 2017)\n\nfor num_iter, (train_index, test_index) in enumerate(folds):\n X_train, y_train = X[train_index], y[train_index]\n X_test, y_test = X[test_index], y[test_index]\n \n y_log_train = np.log(y_train + 1)\n y_log_test = np.log(y_test + 1)\n \n model.fit(X_train, y_log_train,\n eval_metric='mae',\n eval_set=[(X_train, y_log_train), (X_test, y_log_test)],\n verbose=True)\n \n y_log_pred = model.predict(X_test)\n y_pred = np.exp(y_log_pred) - 1\n y_pred[y_pred<0] = 0\n \n score = mean_absolute_error(y_test, y_pred)\n print(\"Fold{0}, score={1}\".format(num_iter+1, score))", "[0]\tvalidation_0-mae:5.74862\tvalidation_1-mae:5.75208\n[1]\tvalidation_0-mae:4.5996\tvalidation_1-mae:4.60274\n[2]\tvalidation_0-mae:3.68053\tvalidation_1-mae:3.68353\n[3]\tvalidation_0-mae:2.94528\tvalidation_1-mae:2.94818\n[4]\tvalidation_0-mae:2.35766\tvalidation_1-mae:2.36079\n[5]\tvalidation_0-mae:1.88847\tvalidation_1-mae:1.89223\n[6]\tvalidation_0-mae:1.51523\tvalidation_1-mae:1.51957\n[7]\tvalidation_0-mae:1.22132\tvalidation_1-mae:1.22775\n[8]\tvalidation_0-mae:0.992724\tvalidation_1-mae:1.00206\n[9]\tvalidation_0-mae:0.818921\tvalidation_1-mae:0.832099\n[10]\tvalidation_0-mae:0.691232\tvalidation_1-mae:0.7083\n[11]\tvalidation_0-mae:0.599814\tvalidation_1-mae:0.621182\n[12]\tvalidation_0-mae:0.535346\tvalidation_1-mae:0.560397\n[13]\tvalidation_0-mae:0.490003\tvalidation_1-mae:0.518635\n[14]\tvalidation_0-mae:0.45736\tvalidation_1-mae:0.490402\n[15]\tvalidation_0-mae:0.434806\tvalidation_1-mae:0.471185\n[16]\tvalidation_0-mae:0.418197\tvalidation_1-mae:0.458144\n[17]\tvalidation_0-mae:0.406375\tvalidation_1-mae:0.449303\n[18]\tvalidation_0-mae:0.398181\tvalidation_1-mae:0.443457\n[19]\tvalidation_0-mae:0.39176\tvalidation_1-mae:0.439218\nFold1, score=1228.1140482185338\n[0]\tvalidation_0-mae:5.75187\tvalidation_1-mae:5.743\n[1]\tvalidation_0-mae:4.60209\tvalidation_1-mae:4.59355\n[2]\tvalidation_0-mae:3.68295\tvalidation_1-mae:3.67477\n[3]\tvalidation_0-mae:2.94734\tvalidation_1-mae:2.93958\n[4]\tvalidation_0-mae:2.35891\tvalidation_1-mae:2.35153\n[5]\tvalidation_0-mae:1.88957\tvalidation_1-mae:1.88278\n[6]\tvalidation_0-mae:1.51665\tvalidation_1-mae:1.51072\n[7]\tvalidation_0-mae:1.2222\tvalidation_1-mae:1.21753\n[8]\tvalidation_0-mae:0.99368\tvalidation_1-mae:0.991831\n[9]\tvalidation_0-mae:0.820644\tvalidation_1-mae:0.822592\n[10]\tvalidation_0-mae:0.693184\tvalidation_1-mae:0.699732\n[11]\tvalidation_0-mae:0.601681\tvalidation_1-mae:0.613379\n[12]\tvalidation_0-mae:0.536664\tvalidation_1-mae:0.553382\n[13]\tvalidation_0-mae:0.491134\tvalidation_1-mae:0.512989\n[14]\tvalidation_0-mae:0.458686\tvalidation_1-mae:0.485186\n[15]\tvalidation_0-mae:0.436219\tvalidation_1-mae:0.466631\n[16]\tvalidation_0-mae:0.419857\tvalidation_1-mae:0.453692\n[17]\tvalidation_0-mae:0.407911\tvalidation_1-mae:0.445641\n[18]\tvalidation_0-mae:0.399662\tvalidation_1-mae:0.44021\n[19]\tvalidation_0-mae:0.392809\tvalidation_1-mae:0.436425\nFold2, score=1209.683919529437\n[0]\tvalidation_0-mae:5.74774\tvalidation_1-mae:5.75295\n[1]\tvalidation_0-mae:4.59923\tvalidation_1-mae:4.60468\n[2]\tvalidation_0-mae:3.68026\tvalidation_1-mae:3.68582\n[3]\tvalidation_0-mae:2.94517\tvalidation_1-mae:2.95056\n[4]\tvalidation_0-mae:2.3577\tvalidation_1-mae:2.36281\n[5]\tvalidation_0-mae:1.88882\tvalidation_1-mae:1.8936\n[6]\tvalidation_0-mae:1.51575\tvalidation_1-mae:1.52097\n[7]\tvalidation_0-mae:1.22153\tvalidation_1-mae:1.22859\n[8]\tvalidation_0-mae:0.993454\tvalidation_1-mae:1.00273\n[9]\tvalidation_0-mae:0.820226\tvalidation_1-mae:0.833088\n[10]\tvalidation_0-mae:0.692717\tvalidation_1-mae:0.709321\n[11]\tvalidation_0-mae:0.60124\tvalidation_1-mae:0.621681\n[12]\tvalidation_0-mae:0.537368\tvalidation_1-mae:0.560741\n[13]\tvalidation_0-mae:0.492133\tvalidation_1-mae:0.518769\n[14]\tvalidation_0-mae:0.460617\tvalidation_1-mae:0.490358\n[15]\tvalidation_0-mae:0.437108\tvalidation_1-mae:0.471197\n[16]\tvalidation_0-mae:0.42017\tvalidation_1-mae:0.45838\n[17]\tvalidation_0-mae:0.407\tvalidation_1-mae:0.449699\n[18]\tvalidation_0-mae:0.397082\tvalidation_1-mae:0.443846\n[19]\tvalidation_0-mae:0.390565\tvalidation_1-mae:0.439323\nFold3, score=1234.1922054663805\n" ] ] ]

[ "code", "markdown", "code" ]

[ [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ] ]

cb2dd19b2fd8c0504b5f1b32fae88611e417c545

452,932

ipynb

Jupyter Notebook

M_accelerate_7lastlayer-8fold_90.73-Copy1.ipynb

JYJatBUPT/More_Compact_MobileNet

70f6d7de93ce3206bfd3c90eab9ebe2e4b6cd4d8

[ "Apache-2.0" ]

2

2019-03-19T04:26:31.000Z

2020-11-30T00:43:36.000Z

M_accelerate_7lastlayer-8fold_90.73-Copy1.ipynb

JYJatBUPT/More_Compact_MobileNet

70f6d7de93ce3206bfd3c90eab9ebe2e4b6cd4d8

[ "Apache-2.0" ]

null

M_accelerate_7lastlayer-8fold_90.73-Copy1.ipynb

JYJatBUPT/More_Compact_MobileNet

70f6d7de93ce3206bfd3c90eab9ebe2e4b6cd4d8

[ "Apache-2.0" ]

null

60.102442

22,064

0.604517

[ [ [ "# <center>MobileNet - Pytorch", "_____no_output_____" ], [ "# Step 1: Prepare data", "_____no_output_____" ] ], [ [ "# MobileNet-Pytorch\nimport argparse \nimport torch\nimport numpy as np\nimport torch.nn as nn\nimport torch.nn.functional as F\nimport torch.optim as optim\nfrom torch.optim.lr_scheduler import StepLR\nfrom torchvision import datasets, transforms\nfrom torch.autograd import Variable\nfrom torch.utils.data.sampler import SubsetRandomSampler\nfrom sklearn.metrics import accuracy_score\n#from mobilenets import mobilenet\n\nuse_cuda = torch.cuda.is_available()\nuse_cudause_cud = torch.cuda.is_available()\ndtype = torch.cuda.FloatTensor if use_cuda else torch.FloatTensor", "_____no_output_____" ], [ "# Train, Validate, Test. Heavily inspired by Kevinzakka https://github.com/kevinzakka/DenseNet/blob/master/data_loader.py\n\nnormalize = transforms.Normalize(mean=[0.485, 0.456, 0.406],\n std=[0.229, 0.224, 0.225])\n\nvalid_size=0.1\n\n# define transforms\nvalid_transform = transforms.Compose([\n transforms.ToTensor(),\n normalize\n])\n\ntrain_transform = transforms.Compose([\n transforms.RandomCrop(32, padding=4),\n transforms.RandomHorizontalFlip(),\n transforms.ToTensor(),\n normalize\n])\n\n\n# load the dataset\ntrain_dataset = datasets.CIFAR10(root=\"data\", train=True, \n download=True, transform=train_transform)\n\nvalid_dataset = datasets.CIFAR10(root=\"data\", train=True, \n download=True, transform=valid_transform)\n\nnum_train = len(train_dataset)\nindices = list(range(num_train))\nsplit = int(np.floor(valid_size * num_train)) #5w张图片的10%用来当做验证集\n\n\nnp.random.seed(42)# 42\nnp.random.shuffle(indices) # 随机乱序[0,1,...,49999]\n\ntrain_idx, valid_idx = indices[split:], indices[:split]\n\n\ntrain_sampler = SubsetRandomSampler(train_idx) # 这个很有意思\nvalid_sampler = SubsetRandomSampler(valid_idx)\n\n###################################################################################\n# ------------------------- 使用不同的批次大小 ------------------------------------\n###################################################################################\n\nshow_step=2 # 批次大，show_step就小点\nmax_epoch=80 # 训练最大epoch数目\n\ntrain_loader = torch.utils.data.DataLoader(train_dataset, \n batch_size=256, sampler=train_sampler)\n\nvalid_loader = torch.utils.data.DataLoader(valid_dataset, \n batch_size=256, sampler=valid_sampler)\n\n\ntest_transform = transforms.Compose([\n transforms.ToTensor(), normalize\n])\n\ntest_dataset = datasets.CIFAR10(root=\"data\", \n train=False, \n download=True,transform=test_transform)\n\ntest_loader = torch.utils.data.DataLoader(test_dataset, \n batch_size=256, \n shuffle=True)", "Files already downloaded and verified\nFiles already downloaded and verified\nFiles already downloaded and verified\n" ] ], [ [ "# Step 2: Model Config", "_____no_output_____" ], [ "# 32 缩放5次到 1x1@1024 \n# From https://github.com/kuangliu/pytorch-cifar \nimport torch\nimport torch.nn as nn\nimport torch.nn.functional as F\n\n\nclass Block(nn.Module):\n '''Depthwise conv + Pointwise conv'''\n def __init__(self, in_planes, out_planes, stride=1):\n super(Block, self).__init__()\n \n # 分组卷积数=输入通道数\n self.conv1 = nn.Conv2d(in_planes, in_planes, kernel_size=3, stride=stride, padding=1, groups=in_planes, bias=False)\n \n self.bn1 = nn.BatchNorm2d(in_planes)\n \n \n #self.conv2 = nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=1, padding=0, bias=False)\n \n one_conv_kernel_size = 3\n self.conv1D= nn.Conv1d(1, out_planes, one_conv_kernel_size, stride=1,padding=1,groups=1,dilation=1,bias=False) # 在__init__初始化 \n \n self.bn2 = nn.BatchNorm2d(out_planes)\n\n def forward(self, x):\n \n out = F.relu(self.bn1(self.conv1(x)))\n \n # -------------------------- Attention -----------------------\n w = F.avg_pool2d(x,x.shape[-1]) #最好在初始化层定义好\n #print(w.shape)\n # [bs,in_Channel,1,1]\n w = w.view(w.shape[0],1,w.shape[1])\n # [bs,1,in_Channel]\n # one_conv_filter = nn.Conv1d(1, out_channel, one_conv_kernel_size, stride=1,padding=1,groups=1,dilation=1) # 在__init__初始化\n # [bs,out_channel,in_Channel]\n w = self.conv1D(w)\n w = 0.5*F.tanh(w) # [-0.5,+0.5]\n # -------------- softmax ---------------------------\n #print(w.shape)\n w = w.view(w.shape[0],w.shape[1],w.shape[2],1,1)\n #print(w.shape)\n \n # ------------------------- fusion --------------------------\n out=out.view(out.shape[0],1,out.shape[1],out.shape[2],out.shape[3])\n #print(\"x size:\",out.shape)\n \n out=out*w\n #print(\"after fusion x size:\",out.shape)\n out=out.sum(dim=2)\n \n out = F.relu(self.bn2(out))\n \n return out\n\n\nclass MobileNet(nn.Module):\n # (128,2) means conv planes=128, conv stride=2, by default conv stride=1\n cfg = [64, (128,2), 128, (256,2), 256, (512,2), 512, 512, 512, 512, 512, (1024,2), 1024]\n\n def __init__(self, num_classes=10):\n super(MobileNet, self).__init__()\n self.conv1 = nn.Conv2d(3, 32, kernel_size=3, stride=1, padding=1, bias=False)\n \n self.bn1 = nn.BatchNorm2d(32)\n self.layers = self._make_layers(in_planes=32) # 自动化构建层\n self.linear = nn.Linear(1024, num_classes)\n\n def _make_layers(self, in_planes):\n layers = []\n for x in self.cfg:\n out_planes = x if isinstance(x, int) else x[0]\n stride = 1 if isinstance(x, int) else x[1]\n layers.append(Block(in_planes, out_planes, stride))\n in_planes = out_planes\n return nn.Sequential(*layers)\n\n def forward(self, x):\n out = F.relu(self.bn1(self.conv1(x)))\n out = self.layers(out)\n out = F.avg_pool2d(out, 2)\n out = out.view(out.size(0), -1)\n out = self.linear(out)\n return out", "_____no_output_____" ] ], [ [ "# 32 缩放5次到 1x1@1024 \n# From https://github.com/kuangliu/pytorch-cifar \nimport torch\nimport torch.nn as nn\nimport torch.nn.functional as F\n\nclass Block_Attention_HALF(nn.Module):\n '''Depthwise conv + Pointwise conv'''\n def __init__(self, in_planes, out_planes, stride=1):\n super(Block_Attention_HALF, self).__init__()\n \n # 分组卷积数=输入通道数\n self.conv1 = nn.Conv2d(in_planes, in_planes, kernel_size=3, stride=stride, padding=1, groups=in_planes, bias=False)\n \n self.bn1 = nn.BatchNorm2d(in_planes)\n \n #------------------------ 一半 ------------------------------\n self.conv2 = nn.Conv2d(in_planes, int(out_planes*0.125), kernel_size=1, stride=1, padding=0, bias=False)\n \n #------------------------ 另一半 ----------------------------\n one_conv_kernel_size = 17 # [3,7,9]\n self.conv1D= nn.Conv1d(1, int(out_planes*0.875), one_conv_kernel_size, stride=1,padding=8,groups=1,dilation=1,bias=False) # 在__init__初始化 \n \n #------------------------------------------------------------\n self.bn2 = nn.BatchNorm2d(out_planes)\n\n def forward(self, x):\n \n out = F.relu6(self.bn1(self.conv1(x)))\n \n # -------------------------- Attention -----------------------\n w = F.avg_pool2d(x,x.shape[-1]) #最好在初始化层定义好\n #print(w.shape)\n # [bs,in_Channel,1,1]\n in_channel=w.shape[1]\n #w = w.view(w.shape[0],1,w.shape[1])\n # [bs,1,in_Channel]\n # 对这批数据取平均且保留第0维\n \n #w= w.mean(dim=0,keepdim=True)\n \n \n# MAX=w.shape[0]\n# NUM=torch.floor(MAX*torch.rand(1)).long()\n# if NUM>=0 and NUM<MAX:\n# w=w[NUM]\n# else:\n# w=w[0]\n # w=w[0]\n w=torch.randn(w[0].shape).cuda()*0.1\n a=torch.randn(1).cuda()*0.1\n if a>0.39:\n print(w.shape)\n print(w)\n \n w=w.view(1,1,in_channel)\n # [bs=1,1,in_Channel]\n # one_conv_filter = nn.Conv1d(1, out_channel, one_conv_kernel_size, stride=1,padding=1,groups=1,dilation=1) # 在__init__初始化\n # [bs=1,out_channel//2,in_Channel]\n w = self.conv1D(w)\n # [bs=1,out_channel//2,in_Channel]\n \n #-------------------------------------\n w = 0.5*F.tanh(w) # [-0.5,+0.5]\n \n if a>0.39:\n print(w.shape)\n print(w)\n \n # [bs=1,out_channel//2,in_Channel]\n w=w.view(w.shape[1],w.shape[2],1,1)\n # [out_channel//2,in_Channel,1,1]\n \n # -------------- softmax ---------------------------\n #print(w.shape)\n \n # ------------------------- fusion --------------------------\n \n # conv 1x1\n out_1=self.conv2(out)\n out_2=F.conv2d(out,w,bias=None,stride=1,groups=1,dilation=1)\n out=torch.cat([out_1,out_2],1)\n \n # ----------------------- 试一试不要用relu -------------------------------\n out = F.relu6(self.bn2(out))\n \n return out\n\nclass Block_Attention(nn.Module):\n '''Depthwise conv + Pointwise conv'''\n def __init__(self, in_planes, out_planes, stride=1):\n super(Block_Attention, self).__init__()\n \n # 分组卷积数=输入通道数\n self.conv1 = nn.Conv2d(in_planes, in_planes, kernel_size=3, stride=stride, padding=1, groups=in_planes, bias=False)\n \n self.bn1 = nn.BatchNorm2d(in_planes)\n \n \n #self.conv2 = nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=1, padding=0, bias=False)\n \n one_conv_kernel_size = 17 # [3,7,9]\n self.conv1D= nn.Conv1d(1, out_planes, one_conv_kernel_size, stride=1,padding=8,groups=1,dilation=1,bias=False) # 在__init__初始化 \n \n \n self.bn2 = nn.BatchNorm2d(out_planes)\n\n def forward(self, x):\n \n out = F.relu(self.bn1(self.conv1(x)))\n \n # -------------------------- Attention -----------------------\n w = F.avg_pool2d(x,x.shape[-1]) #最好在初始化层定义好\n #print(w.shape)\n # [bs,in_Channel,1,1]\n in_channel=w.shape[1]\n #w = w.view(w.shape[0],1,w.shape[1])\n # [bs,1,in_Channel]\n # 对这批数据取平均且保留第0维\n \n #w= w.mean(dim=0,keepdim=True)\n \n \n# MAX=w.shape[0]\n# NUM=torch.floor(MAX*torch.rand(1)).long()\n# if NUM>=0 and NUM<MAX:\n# w=w[NUM]\n# else:\n# w=w[0]\n \n w=w[0]\n \n w=w.view(1,1,in_channel)\n # [bs=1,1,in_Channel]\n # one_conv_filter = nn.Conv1d(1, out_channel, one_conv_kernel_size, stride=1,padding=1,groups=1,dilation=1) # 在__init__初始化\n # [bs=1,out_channel,in_Channel]\n w = self.conv1D(w)\n # [bs=1,out_channel,in_Channel]\n w = 0.5*F.tanh(w) # [-0.5,+0.5]\n # [bs=1,out_channel,in_Channel]\n w=w.view(w.shape[1],w.shape[2],1,1)\n # [out_channel,in_Channel,1,1]\n \n # -------------- softmax ---------------------------\n #print(w.shape)\n \n # ------------------------- fusion --------------------------\n \n # conv 1x1\n out=F.conv2d(out,w,bias=None,stride=1,groups=1,dilation=1)\n\n out = F.relu(self.bn2(out))\n \n return out\n\n\nclass Block(nn.Module):\n '''Depthwise conv + Pointwise conv'''\n def __init__(self, in_planes, out_planes, stride=1):\n super(Block, self).__init__()\n \n # 分组卷积数=输入通道数\n self.conv1 = nn.Conv2d(in_planes, in_planes, kernel_size=3, stride=stride, padding=1, groups=in_planes, bias=False)\n \n self.bn1 = nn.BatchNorm2d(in_planes)\n \n self.conv2 = nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=1, padding=0, bias=False)\n \n self.bn2 = nn.BatchNorm2d(out_planes)\n\n def forward(self, x):\n out = F.relu(self.bn1(self.conv1(x)))\n out = F.relu(self.bn2(self.conv2(out)))\n return out\n\n\nclass MobileNet(nn.Module):\n # (128,2) means conv planes=128, conv stride=2, by default conv stride=1\n #cfg = [64, (128,2), 128, (256,2), 256, (512,2), 512, 512, 512, 512, 512, (1024,2), 1024]\n \n #cfg = [64, (128,2), 128, (256,2), 256, (512,2), 512, 512, 512, 512, 512, (1024,2), [1024,1]]\n cfg = [64, (128,2), 128, 256, 256, (512,2), [512,1], [512,1], [512,1],[512,1], [512,1], [1024,1], [1024,1]]\n \n def __init__(self, num_classes=10):\n super(MobileNet, self).__init__()\n self.conv1 = nn.Conv2d(3, 32, kernel_size=3, stride=1, padding=1, bias=False)\n \n self.bn1 = nn.BatchNorm2d(32)\n self.layers = self._make_layers(in_planes=32) # 自动化构建层\n self.linear = nn.Linear(1024, num_classes)\n\n def _make_layers(self, in_planes):\n layers = []\n for x in self.cfg:\n if isinstance(x, int):\n out_planes = x\n stride = 1 \n layers.append(Block(in_planes, out_planes, stride))\n elif isinstance(x, tuple):\n out_planes = x[0]\n stride = x[1]\n layers.append(Block(in_planes, out_planes, stride))\n # AC层通过list存放设置参数\n elif isinstance(x, list):\n out_planes= x[0]\n stride = x[1] if len(x)==2 else 1\n layers.append(Block_Attention_HALF(in_planes, out_planes, stride)) \n else:\n pass\n \n in_planes = out_planes\n \n return nn.Sequential(*layers)\n\n def forward(self, x):\n out = F.relu(self.bn1(self.conv1(x)))\n out = self.layers(out)\n out = F.avg_pool2d(out, 8)\n out = out.view(out.size(0), -1)\n out = self.linear(out)\n return out", "_____no_output_____" ], [ "# From https://github.com/Z0m6ie/CIFAR-10_PyTorch\n#model = mobilenet(num_classes=10, large_img=False)\n\n# From https://github.com/kuangliu/pytorch-cifar \nif torch.cuda.is_available():\n model=MobileNet(10).cuda()\nelse:\n model=MobileNet(10)\n\noptimizer = optim.SGD(model.parameters(), lr=0.1, momentum=0.9, weight_decay=5e-4)\n#scheduler = StepLR(optimizer, step_size=70, gamma=0.1)\nscheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[50,70,75,80], gamma=0.1)\ncriterion = nn.CrossEntropyLoss()", "_____no_output_____" ], [ "# Implement validation\ndef train(epoch):\n model.train()\n #writer = SummaryWriter()\n for batch_idx, (data, target) in enumerate(train_loader):\n if use_cuda:\n data, target = data.cuda(), target.cuda()\n data, target = Variable(data), Variable(target)\n optimizer.zero_grad()\n output = model(data)\n correct = 0\n pred = output.data.max(1, keepdim=True)[1] # get the index of the max log-probability\n correct += pred.eq(target.data.view_as(pred)).sum()\n \n loss = criterion(output, target)\n loss.backward()\n accuracy = 100. * (correct.cpu().numpy()/ len(output))\n optimizer.step()\n if batch_idx % 5*show_step == 0:\n# if batch_idx % 2*show_step == 0:\n# print(model.layers[1].conv1D.weight.shape)\n# print(model.layers[1].conv1D.weight[0:2][0:2])\n \n print('Train Epoch: {} [{}/{} ({:.0f}%)]\\tLoss: {:.6f}, Accuracy: {:.2f}'.format(\n epoch, batch_idx * len(data), len(train_loader.dataset),\n 100. * batch_idx / len(train_loader), loss.item(), accuracy))\n# f1=open(\"Cifar10_INFO.txt\",\"a+\")\n# f1.write(\"\\n\"+'Train Epoch: {} [{}/{} ({:.0f}%)]\\tLoss: {:.6f}, Accuracy: {:.2f}'.format(\n# epoch, batch_idx * len(data), len(train_loader.dataset),\n# 100. * batch_idx / len(train_loader), loss.item(), accuracy))\n# f1.close()\n \n #writer.add_scalar('Loss/Loss', loss.item(), epoch)\n #writer.add_scalar('Accuracy/Accuracy', accuracy, epoch)\n scheduler.step()", "_____no_output_____" ], [ "def validate(epoch):\n model.eval()\n #writer = SummaryWriter()\n valid_loss = 0\n correct = 0\n for data, target in valid_loader:\n if use_cuda:\n data, target = data.cuda(), target.cuda()\n data, target = Variable(data), Variable(target)\n output = model(data)\n valid_loss += F.cross_entropy(output, target, size_average=False).item() # sum up batch loss\n pred = output.data.max(1, keepdim=True)[1] # get the index of the max log-probability\n correct += pred.eq(target.data.view_as(pred)).sum()\n\n valid_loss /= len(valid_idx)\n accuracy = 100. * correct.cpu().numpy() / len(valid_idx)\n print('\\nValidation set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\\n'.format(\n valid_loss, correct, len(valid_idx),\n 100. * correct / len(valid_idx)))\n \n# f1=open(\"Cifar10_INFO.txt\",\"a+\")\n# f1.write('\\nValidation set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\\n'.format(\n# valid_loss, correct, len(valid_idx),\n# 100. * correct / len(valid_idx)))\n# f1.close()\n #writer.add_scalar('Loss/Validation_Loss', valid_loss, epoch)\n #writer.add_scalar('Accuracy/Validation_Accuracy', accuracy, epoch)\n return valid_loss, accuracy", "_____no_output_____" ], [ "# Fix best model\n\ndef test(epoch):\n model.eval()\n test_loss = 0\n correct = 0\n for data, target in test_loader:\n if use_cuda:\n data, target = data.cuda(), target.cuda()\n data, target = Variable(data), Variable(target)\n output = model(data)\n test_loss += F.cross_entropy(output, target, size_average=False).item() # sum up batch loss\n pred = output.data.max(1, keepdim=True)[1] # get the index of the max log-probability\n correct += pred.eq(target.data.view_as(pred)).cpu().sum()\n\n test_loss /= len(test_loader.dataset)\n print('\\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\\n'.format(\n test_loss, correct, len(test_loader.dataset),\n 100. * correct.cpu().numpy() / len(test_loader.dataset)))\n \n# f1=open(\"Cifar10_INFO.txt\",\"a+\")\n# f1.write('\\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\\n'.format(\n# test_loss, correct, len(test_loader.dataset),\n# 100. * correct.cpu().numpy() / len(test_loader.dataset)))\n# f1.close()", "_____no_output_____" ], [ "def save_best(loss, accuracy, best_loss, best_acc):\n if best_loss == None:\n best_loss = loss\n best_acc = accuracy\n file = 'saved_models/best_save_model.p'\n torch.save(model.state_dict(), file)\n \n elif loss < best_loss and accuracy > best_acc:\n best_loss = loss\n best_acc = accuracy\n file = 'saved_models/best_save_model.p'\n torch.save(model.state_dict(), file)\n return best_loss, best_acc", "_____no_output_____" ], [ "# Fantastic logger for tensorboard and pytorch, \n# run tensorboard by opening a new terminal and run \"tensorboard --logdir runs\"\n# open tensorboard at http://localhost:6006/\nfrom tensorboardX import SummaryWriter\nbest_loss = None\nbest_acc = None\n\nimport time \nSINCE=time.time()\n\nfor epoch in range(max_epoch):\n train(epoch)\n \n loss, accuracy = validate(epoch)\n best_loss, best_acc = save_best(loss, accuracy, best_loss, best_acc)\n \n NOW=time.time() \n DURINGS=NOW-SINCE\n SINCE=NOW\n print(\"the time of this epoch:[{} s]\".format(DURINGS))\n \n if epoch>=10 and (epoch-10)%2==0:\n test(epoch)\n \n# writer = SummaryWriter() \n# writer.export_scalars_to_json(\"./all_scalars.json\")\n\n# writer.close()\n\n#---------------------------- Test ------------------------------\ntest(epoch)", "Train Epoch: 0 [0/50000 (0%)]\tLoss: 2.312560, Accuracy: 7.42\nTrain Epoch: 0 [1280/50000 (3%)]\tLoss: 2.300102, Accuracy: 15.23\nTrain Epoch: 0 [2560/50000 (6%)]\tLoss: 2.335298, Accuracy: 11.72\nTrain Epoch: 0 [3840/50000 (9%)]\tLoss: 2.307236, Accuracy: 13.28\nTrain Epoch: 0 [5120/50000 (11%)]\tLoss: 2.253827, Accuracy: 14.84\nTrain Epoch: 0 [6400/50000 (14%)]\tLoss: 2.313224, Accuracy: 12.89\nTrain Epoch: 0 [7680/50000 (17%)]\tLoss: 2.237643, Accuracy: 14.84\nTrain Epoch: 0 [8960/50000 (20%)]\tLoss: 2.262410, Accuracy: 16.80\nTrain Epoch: 0 [10240/50000 (23%)]\tLoss: 2.265726, Accuracy: 19.14\nTrain Epoch: 0 [11520/50000 (26%)]\tLoss: 2.362818, Accuracy: 12.50\nTrain Epoch: 0 [12800/50000 (28%)]\tLoss: 2.321834, Accuracy: 11.72\nTrain Epoch: 0 [14080/50000 (31%)]\tLoss: 2.252849, Accuracy: 14.06\nTrain Epoch: 0 [15360/50000 (34%)]\tLoss: 2.206976, Accuracy: 14.84\nTrain Epoch: 0 [16640/50000 (37%)]\tLoss: 2.146763, Accuracy: 17.19\nTrain Epoch: 0 [17920/50000 (40%)]\tLoss: 2.320033, Accuracy: 14.06\nTrain Epoch: 0 [19200/50000 (43%)]\tLoss: 2.185206, Accuracy: 19.92\nTrain Epoch: 0 [20480/50000 (45%)]\tLoss: 2.101847, Accuracy: 22.66\nTrain Epoch: 0 [21760/50000 (48%)]\tLoss: 2.162167, Accuracy: 15.62\nTrain Epoch: 0 [23040/50000 (51%)]\tLoss: 2.207897, Accuracy: 17.19\nTrain Epoch: 0 [24320/50000 (54%)]\tLoss: 2.104957, Accuracy: 14.45\nTrain Epoch: 0 [25600/50000 (57%)]\tLoss: 2.197385, Accuracy: 15.62\nTrain Epoch: 0 [26880/50000 (60%)]\tLoss: 2.157121, Accuracy: 16.80\nTrain Epoch: 0 [28160/50000 (62%)]\tLoss: 2.165185, Accuracy: 16.41\nTrain Epoch: 0 [29440/50000 (65%)]\tLoss: 2.137403, Accuracy: 18.36\nTrain Epoch: 0 [30720/50000 (68%)]\tLoss: 2.189405, Accuracy: 17.58\nTrain Epoch: 0 [32000/50000 (71%)]\tLoss: 2.155578, Accuracy: 20.31\nTrain Epoch: 0 [33280/50000 (74%)]\tLoss: 2.073215, Accuracy: 16.80\nTrain Epoch: 0 [34560/50000 (77%)]\tLoss: 2.159607, Accuracy: 15.23\nTrain Epoch: 0 [35840/50000 (80%)]\tLoss: 2.100454, Accuracy: 17.97\nTrain Epoch: 0 [37120/50000 (82%)]\tLoss: 2.058793, Accuracy: 20.31\nTrain Epoch: 0 [38400/50000 (85%)]\tLoss: 2.066559, Accuracy: 18.36\nTrain Epoch: 0 [39680/50000 (88%)]\tLoss: 2.063380, Accuracy: 21.88\nTrain Epoch: 0 [40960/50000 (91%)]\tLoss: 2.154810, Accuracy: 21.88\nTrain Epoch: 0 [42240/50000 (94%)]\tLoss: 2.173177, Accuracy: 14.45\nTrain Epoch: 0 [43520/50000 (97%)]\tLoss: 2.123212, Accuracy: 21.48\nTrain Epoch: 0 [35000/50000 (99%)]\tLoss: 2.008989, Accuracy: 26.50\n\nValidation set: Average loss: 3.4260, Accuracy: 836/5000 (16.00%)\n\nthe time of this epoch:[36.32422876358032 s]\nTrain Epoch: 1 [0/50000 (0%)]\tLoss: 2.048492, Accuracy: 16.80\nTrain Epoch: 1 [1280/50000 (3%)]\tLoss: 2.130375, Accuracy: 17.19\nTrain Epoch: 1 [2560/50000 (6%)]\tLoss: 2.067176, Accuracy: 23.05\nTrain Epoch: 1 [3840/50000 (9%)]\tLoss: 2.072017, Accuracy: 17.19\nTrain Epoch: 1 [5120/50000 (11%)]\tLoss: 1.940232, Accuracy: 18.75\nTrain Epoch: 1 [6400/50000 (14%)]\tLoss: 2.092479, Accuracy: 18.75\nTrain Epoch: 1 [7680/50000 (17%)]\tLoss: 2.001548, Accuracy: 21.09\nTrain Epoch: 1 [8960/50000 (20%)]\tLoss: 2.118967, Accuracy: 22.27\nTrain Epoch: 1 [10240/50000 (23%)]\tLoss: 1.917855, Accuracy: 22.66\nTrain Epoch: 1 [11520/50000 (26%)]\tLoss: 2.040094, Accuracy: 20.70\nTrain Epoch: 1 [12800/50000 (28%)]\tLoss: 2.060454, Accuracy: 17.58\nTrain Epoch: 1 [14080/50000 (31%)]\tLoss: 2.199717, Accuracy: 18.36\nTrain Epoch: 1 [15360/50000 (34%)]\tLoss: 2.154625, Accuracy: 21.09\nTrain Epoch: 1 [16640/50000 (37%)]\tLoss: 2.021475, Accuracy: 21.09\nTrain Epoch: 1 [17920/50000 (40%)]\tLoss: 2.049151, Accuracy: 25.39\nTrain Epoch: 1 [19200/50000 (43%)]\tLoss: 2.017867, Accuracy: 17.58\nTrain Epoch: 1 [20480/50000 (45%)]\tLoss: 1.947752, Accuracy: 22.66\nTrain Epoch: 1 [21760/50000 (48%)]\tLoss: 1.971291, Accuracy: 19.53\nTrain Epoch: 1 [23040/50000 (51%)]\tLoss: 1.909628, Accuracy: 22.27\nTrain Epoch: 1 [24320/50000 (54%)]\tLoss: 1.902658, Accuracy: 23.05\nTrain Epoch: 1 [25600/50000 (57%)]\tLoss: 1.911438, Accuracy: 20.70\nTrain Epoch: 1 [26880/50000 (60%)]\tLoss: 1.954872, Accuracy: 21.88\nTrain Epoch: 1 [28160/50000 (62%)]\tLoss: 1.950485, Accuracy: 21.88\nTrain Epoch: 1 [29440/50000 (65%)]\tLoss: 1.913121, Accuracy: 24.22\nTrain Epoch: 1 [30720/50000 (68%)]\tLoss: 1.895135, Accuracy: 23.83\nTrain Epoch: 1 [32000/50000 (71%)]\tLoss: 1.879922, Accuracy: 23.83\nTrain Epoch: 1 [33280/50000 (74%)]\tLoss: 1.984703, Accuracy: 20.70\nTrain Epoch: 1 [34560/50000 (77%)]\tLoss: 1.927495, Accuracy: 17.58\nTrain Epoch: 1 [35840/50000 (80%)]\tLoss: 1.946153, Accuracy: 20.70\nTrain Epoch: 1 [37120/50000 (82%)]\tLoss: 1.913933, Accuracy: 28.12\nTrain Epoch: 1 [38400/50000 (85%)]\tLoss: 1.861745, Accuracy: 24.22\nTrain Epoch: 1 [39680/50000 (88%)]\tLoss: 1.901368, Accuracy: 22.27\nTrain Epoch: 1 [40960/50000 (91%)]\tLoss: 1.911890, Accuracy: 25.78\nTrain Epoch: 1 [42240/50000 (94%)]\tLoss: 1.935811, Accuracy: 25.00\nTrain Epoch: 1 [43520/50000 (97%)]\tLoss: 1.798017, Accuracy: 27.34\nTrain Epoch: 1 [35000/50000 (99%)]\tLoss: 1.849900, Accuracy: 26.00\n\nValidation set: Average loss: 2.4787, Accuracy: 964/5000 (19.00%)\n\nthe time of this epoch:[36.06772446632385 s]\nTrain Epoch: 2 [0/50000 (0%)]\tLoss: 1.851610, Accuracy: 28.91\nTrain Epoch: 2 [1280/50000 (3%)]\tLoss: 1.797981, Accuracy: 25.39\nTrain Epoch: 2 [2560/50000 (6%)]\tLoss: 1.841409, Accuracy: 26.17\nTrain Epoch: 2 [3840/50000 (9%)]\tLoss: 1.818565, Accuracy: 25.39\nTrain Epoch: 2 [5120/50000 (11%)]\tLoss: 1.799491, Accuracy: 28.12\nTrain Epoch: 2 [6400/50000 (14%)]\tLoss: 1.903175, Accuracy: 26.56\nTrain Epoch: 2 [7680/50000 (17%)]\tLoss: 1.888515, Accuracy: 23.83\nTrain Epoch: 2 [8960/50000 (20%)]\tLoss: 1.854425, Accuracy: 19.92\nTrain Epoch: 2 [10240/50000 (23%)]\tLoss: 1.902104, Accuracy: 26.95\nTrain Epoch: 2 [11520/50000 (26%)]\tLoss: 1.831596, Accuracy: 25.39\nTrain Epoch: 2 [12800/50000 (28%)]\tLoss: 1.854480, Accuracy: 26.56\nTrain Epoch: 2 [14080/50000 (31%)]\tLoss: 1.981502, Accuracy: 25.78\nTrain Epoch: 2 [15360/50000 (34%)]\tLoss: 1.727607, Accuracy: 31.25\nTrain Epoch: 2 [16640/50000 (37%)]\tLoss: 1.826833, Accuracy: 25.39\nTrain Epoch: 2 [17920/50000 (40%)]\tLoss: 1.706803, Accuracy: 30.47\nTrain Epoch: 2 [19200/50000 (43%)]\tLoss: 1.715549, Accuracy: 26.95\nTrain Epoch: 2 [20480/50000 (45%)]\tLoss: 1.806748, Accuracy: 27.73\nTrain Epoch: 2 [21760/50000 (48%)]\tLoss: 1.776164, Accuracy: 27.34\nTrain Epoch: 2 [23040/50000 (51%)]\tLoss: 1.715230, Accuracy: 31.25\nTrain Epoch: 2 [24320/50000 (54%)]\tLoss: 1.824515, Accuracy: 26.56\nTrain Epoch: 2 [25600/50000 (57%)]\tLoss: 1.791737, Accuracy: 28.91\nTrain Epoch: 2 [26880/50000 (60%)]\tLoss: 1.739356, Accuracy: 32.03\nTrain Epoch: 2 [28160/50000 (62%)]\tLoss: 1.796457, Accuracy: 27.73\nTrain Epoch: 2 [29440/50000 (65%)]\tLoss: 1.719077, Accuracy: 30.86\nTrain Epoch: 2 [30720/50000 (68%)]\tLoss: 1.781397, Accuracy: 26.56\nTrain Epoch: 2 [32000/50000 (71%)]\tLoss: 1.780506, Accuracy: 24.61\nTrain Epoch: 2 [33280/50000 (74%)]\tLoss: 1.794382, Accuracy: 23.44\nTrain Epoch: 2 [34560/50000 (77%)]\tLoss: 1.768749, Accuracy: 35.55\nTrain Epoch: 2 [35840/50000 (80%)]\tLoss: 1.739653, Accuracy: 27.73\nTrain Epoch: 2 [37120/50000 (82%)]\tLoss: 1.727915, Accuracy: 27.73\nTrain Epoch: 2 [38400/50000 (85%)]\tLoss: 1.721376, Accuracy: 31.64\nTrain Epoch: 2 [39680/50000 (88%)]\tLoss: 1.668226, Accuracy: 30.47\nTrain Epoch: 2 [40960/50000 (91%)]\tLoss: 1.719538, Accuracy: 31.25\nTrain Epoch: 2 [42240/50000 (94%)]\tLoss: 1.695486, Accuracy: 37.11\nTrain Epoch: 2 [43520/50000 (97%)]\tLoss: 1.709754, Accuracy: 31.25\nTrain Epoch: 2 [35000/50000 (99%)]\tLoss: 1.783534, Accuracy: 28.50\n\nValidation set: Average loss: 2.1852, Accuracy: 1087/5000 (21.00%)\n\nthe time of this epoch:[36.05256795883179 s]\nTrain Epoch: 3 [0/50000 (0%)]\tLoss: 1.793518, Accuracy: 30.08\nTrain Epoch: 3 [1280/50000 (3%)]\tLoss: 1.747078, Accuracy: 31.25\nTrain Epoch: 3 [2560/50000 (6%)]\tLoss: 1.629845, Accuracy: 35.16\nTrain Epoch: 3 [3840/50000 (9%)]\tLoss: 1.755058, Accuracy: 30.47\nTrain Epoch: 3 [5120/50000 (11%)]\tLoss: 1.720590, Accuracy: 30.08\nTrain Epoch: 3 [6400/50000 (14%)]\tLoss: 1.658480, Accuracy: 32.42\nTrain Epoch: 3 [7680/50000 (17%)]\tLoss: 1.733943, Accuracy: 32.81\nTrain Epoch: 3 [8960/50000 (20%)]\tLoss: 1.702329, Accuracy: 32.81\nTrain Epoch: 3 [10240/50000 (23%)]\tLoss: 1.756698, Accuracy: 28.12\nTrain Epoch: 3 [11520/50000 (26%)]\tLoss: 1.792281, Accuracy: 33.98\nTrain Epoch: 3 [12800/50000 (28%)]\tLoss: 1.702533, Accuracy: 30.08\n" ] ], [ [ "# Step 3: Test", "_____no_output_____" ] ], [ [ "test(epoch)", "\nTest set: Average loss: 0.6902, Accuracy: 8877/10000 (88.77%)\n\n" ] ], [ [ "## 第一次 scale 位于[0,1]", "_____no_output_____" ], [ "![](http://op4a94iq8.bkt.clouddn.com/18-7-14/70206949.jpg)", "_____no_output_____" ] ], [ [ "# 查看训练过程的信息\nimport matplotlib.pyplot as plt\n\ndef parse(in_file,flag):\n num=-1\n ys=list()\n xs=list()\n losses=list()\n with open(in_file,\"r\") as reader:\n for aLine in reader:\n #print(aLine)\n\n res=[e for e in aLine.strip('\\n').split(\" \")]\n if res[0]==\"Train\" and flag==\"Train\":\n num=num+1\n ys.append(float(res[-1]))\n xs.append(int(num))\n losses.append(float(res[-3].split(',')[0]))\n if res[0]==\"Validation\" and flag==\"Validation\":\n num=num+1\n xs.append(int(num))\n tmp=[float(e) for e in res[-2].split('/')]\n ys.append(100*float(tmp[0]/tmp[1]))\n losses.append(float(res[-4].split(',')[0]))\n\n plt.figure(1)\n plt.plot(xs,ys,'ro')\n\n\n plt.figure(2)\n plt.plot(xs, losses, 'ro')\n plt.show()\n\ndef main():\n in_file=\"D://INFO.txt\"\n # 显示训练阶段的正确率和Loss信息\n parse(in_file,\"Train\") # \"Validation\"\n # 显示验证阶段的正确率和Loss信息\n #parse(in_file,\"Validation\") # \"Validation\"\n\n\nif __name__==\"__main__\":\n main()", "_____no_output_____" ], [ "# 查看训练过程的信息\nimport matplotlib.pyplot as plt\n\ndef parse(in_file,flag):\n num=-1\n ys=list()\n xs=list()\n losses=list()\n with open(in_file,\"r\") as reader:\n for aLine in reader:\n #print(aLine)\n\n res=[e for e in aLine.strip('\\n').split(\" \")]\n if res[0]==\"Train\" and flag==\"Train\":\n num=num+1\n ys.append(float(res[-1]))\n xs.append(int(num))\n losses.append(float(res[-3].split(',')[0]))\n if res[0]==\"Validation\" and flag==\"Validation\":\n num=num+1\n xs.append(int(num))\n tmp=[float(e) for e in res[-2].split('/')]\n ys.append(100*float(tmp[0]/tmp[1]))\n losses.append(float(res[-4].split(',')[0]))\n\n plt.figure(1)\n plt.plot(xs,ys,'r-')\n\n\n plt.figure(2)\n plt.plot(xs, losses, 'r-')\n plt.show()\n\ndef main():\n in_file=\"D://INFO.txt\"\n # 显示训练阶段的正确率和Loss信息\n parse(in_file,\"Train\") # \"Validation\"\n # 显示验证阶段的正确率和Loss信息\n parse(in_file,\"Validation\") # \"Validation\"\n\n\nif __name__==\"__main__\":\n main()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ] ]

cb2de94dbce93ce25c20dab6c094df5f9c94ebb8

26,257

ipynb

Jupyter Notebook

Lesson-01_Tensor_Manipulation.ipynb

Tony-Khor/PyTorch-From-Zero-to-All

d8f9b6d81fe390dee93a887f342dc818553e61b3

[ "MIT" ]

null

Lesson-01_Tensor_Manipulation.ipynb

Tony-Khor/PyTorch-From-Zero-to-All

d8f9b6d81fe390dee93a887f342dc818553e61b3

[ "MIT" ]

null

Lesson-01_Tensor_Manipulation.ipynb

Tony-Khor/PyTorch-From-Zero-to-All

d8f9b6d81fe390dee93a887f342dc818553e61b3

[ "MIT" ]

null

19.306618

213

0.405568

[ [ [ "# Lab 1: Tensor Manipulation", "_____no_output_____" ], [ "First Author: Seungjae Ryan Lee (seungjaeryanlee at gmail dot com)\nSecond Author: Ki Hyun Kim (nlp.with.deep.learning at gmail dot com)", "_____no_output_____" ], [ "<div class=\"alert alert-warning\">\n NOTE: This corresponds to <a href=\"https://www.youtube.com/watch?v=ZYX0FaqUeN4&t=23s&list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm&index=25\">Lab 8 of Deep Learning Zero to All Season 1 for TensorFlow</a>.\n</div>", "_____no_output_____" ], [ "## Imports", "_____no_output_____" ], [ "Run `pip install -r requirements.txt` in terminal to install all required Python packages.", "_____no_output_____" ] ], [ [ "import numpy as np\nimport torch", "_____no_output_____" ] ], [ [ "## NumPy Review", "_____no_output_____" ], [ "We hope that you are familiar with `numpy` and basic linear algebra.", "_____no_output_____" ], [ "### 1D Array with NumPy", "_____no_output_____" ] ], [ [ "t = np.array([0., 1., 2., 3., 4., 5., 6.])\nprint(t)", "[ 0. 1. 2. 3. 4. 5. 6.]\n" ], [ "print('Rank of t: ', t.ndim)\nprint('Shape of t: ', t.shape)", "Rank of t: 1\nShape of t: (7,)\n" ], [ "print('t[0] t[1] t[-1] = ', t[0], t[1], t[-1]) # Element\nprint('t[2:5] t[4:-1] = ', t[2:5], t[4:-1]) # Slicing\nprint('t[:2] t[3:] = ', t[:2], t[3:]) # Slicing", "t[0] t[1] t[-1] = 0.0 1.0 6.0\nt[2:5] t[4:-1] = [ 2. 3. 4.] [ 4. 5.]\nt[:2] t[3:] = [ 0. 1.] [ 3. 4. 5. 6.]\n" ] ], [ [ "### 2D Array with NumPy", "_____no_output_____" ] ], [ [ "t = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.], [10., 11., 12.]])\nprint(t)", "[[ 1. 2. 3.]\n [ 4. 5. 6.]\n [ 7. 8. 9.]\n [ 10. 11. 12.]]\n" ], [ "print('Rank of t: ', t.ndim)\nprint('Shape of t: ', t.shape)", "Rank of t: 2\nShape of t: (4, 3)\n" ] ], [ [ "## PyTorch is like NumPy (but better)", "_____no_output_____" ], [ "### 1D Array with PyTorch", "_____no_output_____" ] ], [ [ "t = torch.FloatTensor([0., 1., 2., 3., 4., 5., 6.])\nprint(t)", "tensor([0., 1., 2., 3., 4., 5., 6.])\n" ], [ "print(t.dim()) # rank\nprint(t.shape) # shape\nprint(t.size()) # shape\nprint(t[0], t[1], t[-1]) # Element\nprint(t[2:5], t[4:-1]) # Slicing\nprint(t[:2], t[3:]) # Slicing", "1\ntorch.Size([7])\ntorch.Size([7])\ntensor(0.) tensor(1.) tensor(6.)\ntensor([2., 3., 4.]) tensor([4., 5.])\ntensor([0., 1.]) tensor([3., 4., 5., 6.])\n" ] ], [ [ "### 2D Array with PyTorch", "_____no_output_____" ] ], [ [ "t = torch.FloatTensor([[1., 2., 3.],\n [4., 5., 6.],\n [7., 8., 9.],\n [10., 11., 12.]\n ])\nprint(t)", "tensor([[ 1., 2., 3.],\n [ 4., 5., 6.],\n [ 7., 8., 9.],\n [10., 11., 12.]])\n" ], [ "print(t.dim()) # rank\nprint(t.size()) # shape\nprint(t[:, 1])\nprint(t[:, 1].size())\nprint(t[:, :-1])", "2\ntorch.Size([4, 3])\ntensor([ 2., 5., 8., 11.])\ntorch.Size([4])\ntensor([[ 1., 2.],\n [ 4., 5.],\n [ 7., 8.],\n [10., 11.]])\n" ] ], [ [ "### Shape, Rank, Axis", "_____no_output_____" ] ], [ [ "t = torch.FloatTensor([[[[1, 2, 3, 4],\n [5, 6, 7, 8],\n [9, 10, 11, 12]],\n [[13, 14, 15, 16],\n [17, 18, 19, 20],\n [21, 22, 23, 24]]\n ]])", "_____no_output_____" ], [ "print(t.dim()) # rank = 4\nprint(t.size()) # shape = (1, 2, 3, 4)", "4\ntorch.Size([1, 2, 3, 4])\n" ] ], [ [ "## Frequently Used Operations in PyTorch", "_____no_output_____" ], [ "### Mul vs. Matmul", "_____no_output_____" ] ], [ [ "print()\nprint('-------------')\nprint('Mul vs Matmul')\nprint('-------------')\nm1 = torch.FloatTensor([[1, 2], [3, 4]])\nm2 = torch.FloatTensor([[1], [2]])\nprint('Shape of Matrix 1: ', m1.shape) # 2 x 2\nprint('Shape of Matrix 2: ', m2.shape) # 2 x 1\nprint(m1.matmul(m2)) # 2 x 1\n\nm1 = torch.FloatTensor([[1, 2], [3, 4]])\nm2 = torch.FloatTensor([[1], [2]])\nprint('Shape of Matrix 1: ', m1.shape) # 2 x 2\nprint('Shape of Matrix 2: ', m2.shape) # 2 x 1\nprint(m1 * m2) # 2 x 2\nprint(m1.mul(m2))", "\n-------------\nMul vs Matmul\n-------------\nShape of Matrix 1: torch.Size([2, 2])\nShape of Matrix 2: torch.Size([2, 1])\ntensor([[ 5.],\n [11.]])\nShape of Matrix 1: torch.Size([2, 2])\nShape of Matrix 2: torch.Size([2, 1])\ntensor([[1., 2.],\n [6., 8.]])\ntensor([[1., 2.],\n [6., 8.]])\n" ] ], [ [ "### Broadcasting", "_____no_output_____" ], [ "<div class=\"alert alert-warning\">\n Carelessly using broadcasting can lead to code hard to debug.\n</div>", "_____no_output_____" ] ], [ [ "# Same shape\nm1 = torch.FloatTensor([[3, 3]])\nm2 = torch.FloatTensor([[2, 2]])\nprint(m1 + m2)", "tensor([[5., 5.]])\n" ], [ "# Vector + scalar\nm1 = torch.FloatTensor([[1, 2]])\nm2 = torch.FloatTensor([3]) # 3 -> [[3, 3]]\nprint(m1 + m2)", "tensor([[4., 5.]])\n" ], [ "# 2 x 1 Vector + 1 x 2 Vector\nm1 = torch.FloatTensor([[1, 2]])\nm2 = torch.FloatTensor([[3], [4]])\nprint(m1 + m2)", "tensor([[4., 5.],\n [5., 6.]])\n" ] ], [ [ "### Mean", "_____no_output_____" ] ], [ [ "t = torch.FloatTensor([1, 2])\nprint(t.mean())", "tensor(1.5000)\n" ], [ "# Can't use mean() on integers\nt = torch.LongTensor([1, 2])\ntry:\n print(t.mean())\nexcept Exception as exc:\n print(exc)", "Can only calculate the mean of floating types. Got Long instead.\n" ] ], [ [ "You can also use `t.mean` for higher rank tensors to get mean of all elements, or mean by particular dimension.", "_____no_output_____" ] ], [ [ "t = torch.FloatTensor([[1, 2], [3, 4]])\nprint(t)", "tensor([[1., 2.],\n [3., 4.]])\n" ], [ "print(t.mean())\nprint(t.mean(dim=0))\nprint(t.mean(dim=1))\nprint(t.mean(dim=-1))", "tensor(2.5000)\ntensor([2., 3.])\ntensor([1.5000, 3.5000])\ntensor([1.5000, 3.5000])\n" ] ], [ [ "### Sum", "_____no_output_____" ] ], [ [ "t = torch.FloatTensor([[1, 2], [3, 4]])\nprint(t)", "tensor([[1., 2.],\n [3., 4.]])\n" ], [ "print(t.sum())\nprint(t.sum(dim=0))\nprint(t.sum(dim=1))\nprint(t.sum(dim=-1))", "tensor(10.)\ntensor([4., 6.])\ntensor([3., 7.])\ntensor([3., 7.])\n" ] ], [ [ "### Max and Argmax", "_____no_output_____" ] ], [ [ "t = torch.FloatTensor([[1, 2], [3, 4]])\nprint(t)", "tensor([[1., 2.],\n [3., 4.]])\n" ] ], [ [ "The `max` operator returns one value if it is called without an argument.", "_____no_output_____" ] ], [ [ "print(t.max()) # Returns one value: max", "tensor(4.)\n" ] ], [ [ "The `max` operator returns 2 values when called with dimension specified. The first value is the maximum value, and the second value is the argmax: the index of the element with maximum value.", "_____no_output_____" ] ], [ [ "print(t.max(dim=0)) # Returns two values: max and argmax\nprint('Max: ', t.max(dim=0)[0])\nprint('Argmax: ', t.max(dim=0)[1])", "(tensor([3., 4.]), tensor([1, 1]))\nMax: tensor([3., 4.])\nArgmax: tensor([1, 1])\n" ], [ "print(t.max(dim=1))\nprint(t.max(dim=-1))", "(tensor([2., 4.]), tensor([1, 1]))\n(tensor([2., 4.]), tensor([1, 1]))\n" ] ], [ [ "### View", "_____no_output_____" ], [ "<div class=\"alert alert-warning\">\n This is a function hard to master, but is very useful!\n</div>", "_____no_output_____" ] ], [ [ "t = np.array([[[0, 1, 2],\n [3, 4, 5]],\n\n [[6, 7, 8],\n [9, 10, 11]]])\nft = torch.FloatTensor(t)\nprint(ft.shape)", "torch.Size([2, 2, 3])\n" ], [ "print(ft.view([-1, 3]))\nprint(ft.view([-1, 3]).shape)", "tensor([[ 0., 1., 2.],\n [ 3., 4., 5.],\n [ 6., 7., 8.],\n [ 9., 10., 11.]])\ntorch.Size([4, 3])\n" ], [ "print(ft.view([-1, 1, 3]))\nprint(ft.view([-1, 1, 3]).shape)", "tensor([[[ 0., 1., 2.]],\n\n [[ 3., 4., 5.]],\n\n [[ 6., 7., 8.]],\n\n [[ 9., 10., 11.]]])\ntorch.Size([4, 1, 3])\n" ] ], [ [ "### Squeeze", "_____no_output_____" ] ], [ [ "ft = torch.FloatTensor([[0], [1], [2]])\nprint(ft)\nprint(ft.shape)", "tensor([[0.],\n [1.],\n [2.]])\ntorch.Size([3, 1])\n" ], [ "print(ft.squeeze())\nprint(ft.squeeze().shape)", "tensor([0., 1., 2.])\ntorch.Size([3])\n" ] ], [ [ "### Unsqueeze", "_____no_output_____" ] ], [ [ "ft = torch.Tensor([0, 1, 2])\nprint(ft.shape)", "torch.Size([3])\n" ], [ "print(ft.unsqueeze(0))\nprint(ft.unsqueeze(0).shape)", "tensor([[0., 1., 2.]])\ntorch.Size([1, 3])\n" ], [ "print(ft.view(1, -1))\nprint(ft.view(1, -1).shape)", "tensor([[0., 1., 2.]])\ntorch.Size([1, 3])\n" ], [ "print(ft.unsqueeze(1))\nprint(ft.unsqueeze(1).shape)", "tensor([[0.],\n [1.],\n [2.]])\ntorch.Size([3, 1])\n" ], [ "print(ft.unsqueeze(-1))\nprint(ft.unsqueeze(-1).shape)", "tensor([[0.],\n [1.],\n [2.]])\ntorch.Size([3, 1])\n" ] ], [ [ "### Scatter (for one-hot encoding)", "_____no_output_____" ], [ "<div class=\"alert alert-warning\">\n Scatter is a very flexible function. We only discuss how to use it to get a one-hot encoding of indices.\n</div>", "_____no_output_____" ] ], [ [ "lt = torch.LongTensor([[0], [1], [2], [0]])\nprint(lt)", "tensor([[0],\n [1],\n [2],\n [0]])\n" ], [ "one_hot = torch.zeros(4, 3) # batch_size = 4, classes = 3\none_hot.scatter_(1, lt, 1)\nprint(one_hot)", "tensor([[1., 0., 0.],\n [0., 1., 0.],\n [0., 0., 1.],\n [1., 0., 0.]])\n" ] ], [ [ "### Casting", "_____no_output_____" ] ], [ [ "lt = torch.LongTensor([1, 2, 3, 4])\nprint(lt)", "tensor([1, 2, 3, 4])\n" ], [ "print(lt.float())", "tensor([1., 2., 3., 4.])\n" ], [ "bt = torch.ByteTensor([True, False, False, True])\nprint(bt)", "tensor([1, 0, 0, 1], dtype=torch.uint8)\n" ], [ "print(bt.long())\nprint(bt.float())", "tensor([1, 0, 0, 1])\ntensor([1., 0., 0., 1.])\n" ] ], [ [ "### Concatenation", "_____no_output_____" ] ], [ [ "x = torch.FloatTensor([[1, 2], [3, 4]])\ny = torch.FloatTensor([[5, 6], [7, 8]])", "_____no_output_____" ], [ "print(torch.cat([x, y], dim=0))\nprint(torch.cat([x, y], dim=1))", "tensor([[1., 2.],\n [3., 4.],\n [5., 6.],\n [7., 8.]])\ntensor([[1., 2., 5., 6.],\n [3., 4., 7., 8.]])\n" ] ], [ [ "### Stacking", "_____no_output_____" ] ], [ [ "x = torch.FloatTensor([1, 4])\ny = torch.FloatTensor([2, 5])\nz = torch.FloatTensor([3, 6])", "_____no_output_____" ], [ "print(torch.stack([x, y, z]))\nprint(torch.stack([x, y, z], dim=1))", "tensor([[1., 4.],\n [2., 5.],\n [3., 6.]])\ntensor([[1., 2., 3.],\n [4., 5., 6.]])\n" ], [ "print(torch.cat([x.unsqueeze(0), y.unsqueeze(0), z.unsqueeze(0)], dim=0))", "tensor([[1., 4.],\n [2., 5.],\n [3., 6.]])\n" ] ], [ [ "### Ones and Zeros Like", "_____no_output_____" ] ], [ [ "x = torch.FloatTensor([[0, 1, 2], [2, 1, 0]])\nprint(x)", "tensor([[0., 1., 2.],\n [2., 1., 0.]])\n" ], [ "print(torch.ones_like(x))\nprint(torch.zeros_like(x))", "tensor([[1., 1., 1.],\n [1., 1., 1.]])\ntensor([[0., 0., 0.],\n [0., 0., 0.]])\n" ] ], [ [ "### In-place Operation", "_____no_output_____" ] ], [ [ "x = torch.FloatTensor([[1, 2], [3, 4]])", "_____no_output_____" ], [ "print(x.mul(2.))\nprint(x)\nprint(x.mul_(2.))\nprint(x)", "tensor([[2., 4.],\n [6., 8.]])\ntensor([[1., 2.],\n [3., 4.]])\ntensor([[2., 4.],\n [6., 8.]])\ntensor([[2., 4.],\n [6., 8.]])\n" ] ], [ [ "## Miscellaneous", "_____no_output_____" ], [ "### Zip", "_____no_output_____" ] ], [ [ "for x, y in zip([1, 2, 3], [4, 5, 6]):\n print(x, y)", "1 4\n2 5\n3 6\n" ], [ "for x, y, z in zip([1, 2, 3], [4, 5, 6], [7, 8, 9]):\n print(x, y, z)", "1 4 7\n2 5 8\n3 6 9\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ] ]

cb2dec69459629e8b5dffa487e7f10f2ae266ce2

140,028

ipynb

Jupyter Notebook

parcels/parcels/examples/tutorial_Argofloats.ipynb

pdnooteboom/NA_forams

789b45d8cc14225f31242c9c648f4f36c76d2fc4

[ "MIT" ]

null

parcels/parcels/examples/tutorial_Argofloats.ipynb

pdnooteboom/NA_forams

789b45d8cc14225f31242c9c648f4f36c76d2fc4

[ "MIT" ]

null

parcels/parcels/examples/tutorial_Argofloats.ipynb

pdnooteboom/NA_forams

789b45d8cc14225f31242c9c648f4f36c76d2fc4

[ "MIT" ]

1

2020-04-04T03:55:41.000Z

679.747573

132,300

0.946432

[ [ [ "## Tutorial on how to simulate an Argo float in Parcels", "_____no_output_____" ], [ "This tutorial shows how simple it is to construct a Kernel in Parcels that mimics the [vertical movement of Argo floats](http://www.argo.ucsd.edu/operation_park_profile.jpg).", "_____no_output_____" ] ], [ [ "# Define the new Kernel that mimics Argo vertical movement\ndef ArgoVerticalMovement(particle, fieldset, time):\n driftdepth = 1000 # maximum depth in m\n maxdepth = 2000 # maximum depth in m\n vertical_speed = 0.10 # sink and rise speed in m/s\n cycletime = 10 * 86400 # total time of cycle in seconds\n drifttime = 9 * 86400 # time of deep drift in seconds\n\n if particle.cycle_phase == 0:\n # Phase 0: Sinking with vertical_speed until depth is driftdepth\n particle.depth += vertical_speed * particle.dt\n if particle.depth >= driftdepth:\n particle.cycle_phase = 1\n\n elif particle.cycle_phase == 1:\n # Phase 1: Drifting at depth for drifttime seconds\n particle.drift_age += particle.dt\n if particle.drift_age >= drifttime:\n particle.drift_age = 0 # reset drift_age for next cycle\n particle.cycle_phase = 2\n\n elif particle.cycle_phase == 2:\n # Phase 2: Sinking further to maxdepth\n particle.depth += vertical_speed * particle.dt\n if particle.depth >= maxdepth:\n particle.cycle_phase = 3\n\n elif particle.cycle_phase == 3:\n # Phase 3: Rising with vertical_speed until at surface\n particle.depth -= vertical_speed * particle.dt\n #particle.temp = fieldset.temp[time, particle.depth, particle.lat, particle.lon] # if fieldset has temperature\n if particle.depth <= fieldset.mindepth:\n particle.depth = fieldset.mindepth\n #particle.temp = 0./0. # reset temperature to NaN at end of sampling cycle\n particle.cycle_phase = 4\n\n elif particle.cycle_phase == 4:\n # Phase 4: Transmitting at surface until cycletime is reached\n if particle.cycle_age > cycletime:\n particle.cycle_phase = 0\n particle.cycle_age = 0\n\n particle.cycle_age += particle.dt # update cycle_age", "_____no_output_____" ] ], [ [ "And then we can run Parcels with this 'custom kernel'. \n\nNote that below we use the two-dimensional velocity fields of GlobCurrent, as these are provided as example_data with Parcels. \n\nWe therefore assume that the horizontal velocities are the same throughout the entire water column. However, the `ArgoVerticalMovement` kernel will work on any `FieldSet`, including from full three-dimensional hydrodynamic data. \n\nIf the hydrodynamic data also has a Temperature Field, then uncommenting the lines about temperature will also simulate the sampling of temperature.", "_____no_output_____" ] ], [ [ "from parcels import FieldSet, ParticleSet, JITParticle, AdvectionRK4, ErrorCode, Variable\nfrom datetime import timedelta\nimport numpy as np\n\n# Load the GlobCurrent data in the Agulhas region from the example_data\nfilenames = {'U': \"GlobCurrent_example_data/20*.nc\",\n 'V': \"GlobCurrent_example_data/20*.nc\"}\nvariables = {'U': 'eastward_eulerian_current_velocity',\n 'V': 'northward_eulerian_current_velocity'}\ndimensions = {'lat': 'lat', 'lon': 'lon', 'time': 'time'}\nfieldset = FieldSet.from_netcdf(filenames, variables, dimensions)\nfieldset.mindepth = fieldset.U.depth[0] # uppermost layer in the hydrodynamic data\n\n# Define a new Particle type including extra Variables\nclass ArgoParticle(JITParticle):\n # Phase of cycle: init_descend=0, drift=1, profile_descend=2, profile_ascend=3, transmit=4\n cycle_phase = Variable('cycle_phase', dtype=np.int32, initial=0.)\n cycle_age = Variable('cycle_age', dtype=np.float32, initial=0.)\n drift_age = Variable('drift_age', dtype=np.float32, initial=0.)\n #temp = Variable('temp', dtype=np.float32, initial=np.nan) # if fieldset has temperature\n\n# Initiate one Argo float in the Agulhas Current\npset = ParticleSet(fieldset=fieldset, pclass=ArgoParticle, lon=[32], lat=[-31], depth=[0])\n\n# combine Argo vertical movement kernel with built-in Advection kernel\nkernels = ArgoVerticalMovement + pset.Kernel(AdvectionRK4)\n\n# Now execute the kernels for 30 days, saving data every 30 minutes\npset.execute(kernels, runtime=timedelta(days=30), dt=timedelta(minutes=5), \n output_file=pset.ParticleFile(name=\"argo_float\", outputdt=timedelta(minutes=30)))", "WARNING: Casting lon data to np.float32\nWARNING: Casting lat data to np.float32\nWARNING: Casting depth data to np.float32\nINFO: Compiled ArgoParticleArgoVerticalMovementAdvectionRK4 ==> /var/folders/r2/8593q8z93kd7t4j9kbb_f7p00000gr/T/parcels-504/9b8a821c179c51426159d7b7efb2e070.so\n100% (2592000.0 of 2592000.0) |##########| Elapsed Time: 0:00:10 Time: 0:00:10\n" ] ], [ [ "Now we can plot the trajectory of the Argo float with some simple calls to netCDF4 and matplotlib", "_____no_output_____" ] ], [ [ "%matplotlib inline\nimport netCDF4\nfrom mpl_toolkits.mplot3d import Axes3D\nimport matplotlib.pyplot as plt\n\nnc = netCDF4.Dataset(\"argo_float.nc\")\nx = nc.variables[\"lon\"][:].squeeze()\ny = nc.variables[\"lat\"][:].squeeze()\nz = nc.variables[\"z\"][:].squeeze()\nnc.close()\n\nfig = plt.figure(figsize=(13,10))\nax = plt.axes(projection='3d')\ncb = ax.scatter(x, y, z, c=z, s=20, marker=\"o\")\nax.set_xlabel(\"Longitude\")\nax.set_ylabel(\"Latitude\")\nax.set_zlabel(\"Depth (m)\")\nax.set_zlim(np.max(z),0)\nplt.show()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2df1493e5f775c9b8070d63bc2580fdda4514e

69,554

ipynb

Jupyter Notebook

[분석실무]3.고객행동분석.ipynb

kamzzang/ADPStudy

5676be538c44050bdc3221b6d1eec35cbf95f4c1

[ "MIT" ]

null

[분석실무]3.고객행동분석.ipynb

kamzzang/ADPStudy

5676be538c44050bdc3221b6d1eec35cbf95f4c1

[ "MIT" ]

null

[분석실무]3.고객행동분석.ipynb

kamzzang/ADPStudy

5676be538c44050bdc3221b6d1eec35cbf95f4c1

[ "MIT" ]

1

2022-02-10T15:59:54.000Z

32.126559

6,320

0.419832

[ [ [ "# 고객의 행동 분석/파악\n* use_log.csv : 선테 이용 이력(2018년 4월 ~ 2019년 3월)\n* customer_master.csv : 2019년 3월 말 회원 데이터(이전 탈퇴 회원 포함)\n* class_master.csv : 회원 구분(종일, 주간, 야간)\n* campaign_master.csv : 행사 구분(입회비 유무)", "_____no_output_____" ], [ "## 1. 데이터 확인", "_____no_output_____" ] ], [ [ "import pandas as pd\nuselog = pd.read_csv('use_log.csv')\nprint(len(uselog))\nuselog.head()", "197428\n" ], [ "customer = pd.read_csv('customer_master.csv')\nprint(len(customer))\ncustomer.head()", "4192\n" ], [ "class_master = pd.read_csv('class_master.csv')\nprint(len(class_master))\nclass_master.head()", "3\n" ], [ "campaign_master = pd.read_csv('campaign_master.csv')\nprint(len(campaign_master))\ncampaign_master.head()", "3\n" ] ], [ [ "## 2. 고객 데이터 가공", "_____no_output_____" ] ], [ [ "customer_join = pd.merge(customer, class_master, on='class', how='left')\ncustomer_join = pd.merge(customer_join, campaign_master, on='campaign_id', how='left')\ncustomer_join.head()", "_____no_output_____" ], [ "customer_join.isnull().sum()", "_____no_output_____" ] ], [ [ "## 3. 고객 데이터 집계", "_____no_output_____" ] ], [ [ "customer_join.groupby('class_name').count()['customer_id']", "_____no_output_____" ], [ "customer_join.groupby('campaign_name').count()['customer_id']", "_____no_output_____" ], [ "customer_join.groupby('gender').count()['customer_id']", "_____no_output_____" ], [ "customer_join.groupby('is_deleted').count()['customer_id'] # 1 : 탈퇴", "_____no_output_____" ], [ "customer_join['start_date'] = pd.to_datetime(customer_join['start_date'])\ncustomer_start = customer_join.loc[customer_join['start_date'] > pd.to_datetime('20180401')]\nprint(len(customer_start))", "1361\n" ] ], [ [ "## 4. 최신 고객 데이터 집계\n* 가장 최근 월의 고객만 추출", "_____no_output_____" ] ], [ [ "customer_join['end_date'] = pd.to_datetime(customer_join['end_date'])\ncustomer_newer = customer_join.loc[(customer_join['end_date'] >= pd.to_datetime('20190331')) | \\\n (customer_join['end_date'].isna())]\nprint(len(customer_newer))\ncustomer_newer['end_date'].unique()", "2953\n" ], [ "customer_newer.groupby('class_name').count()['customer_id']", "_____no_output_____" ], [ "customer_newer.groupby('campaign_name').count()['customer_id']", "_____no_output_____" ], [ "customer_newer.groupby('gender').count()['customer_id']", "_____no_output_____" ] ], [ [ "## 5. 이용 이력 데이터 집계\n* 월 이용 횟수의 평균값, 중앙값, 최댓값, 최솟값과 정기적 이용 여부를 고객 데이터에 추가", "_____no_output_____" ] ], [ [ "uselog['usedate'] = pd.to_datetime(uselog['usedate'])\nuselog['연월'] = uselog['usedate'].dt.strftime('%Y%m')\nuselog_months = uselog.groupby(['연월', 'customer_id'], as_index=False).count()\nuselog_months.rename(columns={'log_id':'count'}, inplace=True)\ndel uselog_months['usedate']\nuselog_months.head()", "_____no_output_____" ], [ "uselog_customer = uselog_months.groupby('customer_id').agg(['mean', 'median', 'max', 'min'])['count']\nuselog_customer = uselog_customer.reset_index(drop=False)\nuselog_customer.head()", "_____no_output_____" ] ], [ [ "## 6. 이용 이력 데이터로부터 정기 이용 여부 체크\n* 월별 정기적 이용 여부는 고객마다 월/요일별 집계, 최대값이 4이상인 요일이 하나라도 있을 경우 1", "_____no_output_____" ] ], [ [ "uselog['weekday'] = uselog['usedate'].dt.weekday # 0 ~ 6 : 월요일 ~ 일요일\nuselog_weekday = uselog.groupby(['customer_id', '연월', 'weekday'], as_index=False).count()[['customer_id',\n '연월', 'weekday', 'log_id']]\nuselog_weekday.rename(columns={'log_id':'count'}, inplace=True)\nuselog_weekday.head()", "_____no_output_____" ], [ "uselog_weekday = uselog_weekday.groupby('customer_id', as_index=False).max()[['customer_id', 'count']]\nuselog_weekday['routine_flg'] = 0\nuselog_weekday['routine_flg'] = uselog_weekday['routine_flg'].where(uselog_weekday['count']<4, 1)\nuselog_weekday.head()", "_____no_output_____" ] ], [ [ "## 7. 고객 데이터와 이용 애력 데이터를 결합", "_____no_output_____" ] ], [ [ "customer_join = pd.merge(customer_join, uselog_customer, on='customer_id', how='left')\ncustomer_join = pd.merge(customer_join, uselog_weekday[['customer_id', 'routine_flg']], on='customer_id', how='left')\ncustomer_join.head()", "_____no_output_____" ], [ "customer_join.isnull().sum()", "_____no_output_____" ] ], [ [ "## 8. 회원 기간 계산\n* 기본 계산 : start_date와 end_date의 차이\n* 탈퇴하지 않은 회원은 end_date가 결측치이므로 임의로 2019년 4월 30일로 해서 3월 31일에 탈퇴한 사람과 차이를 둔다.", "_____no_output_____" ] ], [ [ "from dateutil.relativedelta import relativedelta\n\ncustomer_join['calc_date'] = customer_join['end_date']\ncustomer_join['calc_date'] = customer_join['calc_date'].fillna(pd.to_datetime('20190430'))\ncustomer_join['membership_period'] = 0\n\nfor i in range(len(customer_join)):\n delta = relativedelta(customer_join['calc_date'].iloc[i], customer_join['start_date'].iloc[i])\n customer_join['membership_period'].iloc[i] = delta.years*12 + delta.months\n \ncustomer_join.head()", "C:\\Anaconda3\\lib\\site-packages\\pandas\\core\\indexing.py:670: SettingWithCopyWarning: \nA value is trying to be set on a copy of a slice from a DataFrame\n\nSee the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy\n self._setitem_with_indexer(indexer, value)\n" ] ], [ [ "## 9. 통계량 파악", "_____no_output_____" ] ], [ [ "customer_join[['mean', 'median', 'max', 'min']].describe()", "_____no_output_____" ], [ "customer_join.groupby('routine_flg').count()['customer_id']", "_____no_output_____" ], [ "import matplotlib.pyplot as plt\n%matplotlib inline\n\nplt.hist(customer_join['membership_period'])", "_____no_output_____" ] ], [ [ "## 10. 탈퇴 회원과 지속 회의의 차이 파악", "_____no_output_____" ] ], [ [ "customer_end = customer_join.loc[customer_join['is_deleted']==1]\ncustomer_end.describe()", "_____no_output_____" ], [ "customer_stay = customer_join.loc[customer_join['is_deleted']==0]\ncustomer_stay.describe()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ] ]

cb2df72b417fe036bde259c18f0f978f435021c1

93,876

ipynb

Jupyter Notebook

boiler/TensorFlow.ipynb

dev-ejc/automated_financial_analysis

d68f842a5cbd54509e6f0df3ae7cc52d520f76eb

[ "MIT" ]

2

2021-08-12T03:56:34.000Z

2021-08-14T18:18:28.000Z

boiler/TensorFlow.ipynb

dev-ejc/automated_financial_analysis

d68f842a5cbd54509e6f0df3ae7cc52d520f76eb

[ "MIT" ]

null

boiler/TensorFlow.ipynb

dev-ejc/automated_financial_analysis

d68f842a5cbd54509e6f0df3ae7cc52d520f76eb

[ "MIT" ]

null

58.6725

22,292

0.585783

[ [ [ "from database.market import Market\nfrom database.strategy import Strategy\nfrom extractor.tiingo_extractor import TiingoExtractor\nfrom preprocessor.model_preprocessor import ModelPreprocessor\nfrom preprocessor.predictor_preprocessor import PredictorPreprocessor\nfrom modeler.modeler import Modeler\nfrom datetime import datetime, timedelta\nfrom tqdm import tqdm\nimport pandas as pd\nimport pickle\nimport tensorflow as tf\nimport warnings\nwarnings.simplefilter(action='ignore', category=Warning)\nfrom modeler.modeler import Modeler", "_____no_output_____" ], [ "market = Market()\nstrat= Strategy(\"aggregate\")\n## Loading Constants", "_____no_output_____" ], [ "market.connect()\ntickers = market.retrieve_data(\"sp500\")\nmarket.close()\nyears = 10\nend = datetime.now()\nstart = datetime.now() - timedelta(days=365.25*years)", "_____no_output_____" ], [ "market.connect()\ntest = market.retrieve_data(\"dataset_regression\")\nmarket.close()", "_____no_output_____" ], [ "test", "_____no_output_____" ], [ "ticker = \"AAPL\"\nm = Modeler(ticker)\ndata = test.copy()\ndata[\"y\"] = data[ticker]\nfeatures = data.drop([\"date\",\"y\",\"_id\"],axis=1)", "_____no_output_____" ], [ "for column in tqdm(features.columns):\n for i in range(14):\n features[\"ticker_{}_{}\".format(column,i)] = features[column].shift(i)\nfeatures = features[14:]", "100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████| 436/436 [00:08<00:00, 54.08it/s]\n" ], [ "for i in range(14):\n data[\"y_{}\".format(i)] = data[\"y\"].shift(i)\ndata = data[14:]", "_____no_output_____" ], [ "new_labels = []\nfor i in range(len(data[\"y\"])):\n row = data.iloc[i]\n new_labels.append(row[[x for x in data.columns if \"y_\" in x]].values)", "_____no_output_____" ], [ "# new = []\n# for column in tqdm([x for x in features.columns if \"_\" not in x]):\n# new_row = []\n# for i in range(1,360):\n# row = features.iloc[i]\n# new_row.append(row[[x for x in features.columns if (\"ticker_\" + column + \"_\") in x]].values)\n# new.append(new_row)", "_____no_output_____" ], [ "features", "_____no_output_____" ], [ "predictions = []\nfor i in tqdm(range(14)):\n results = pd.DataFrame(m.sk_model({\"X\":features[i:],\"y\":data[\"y\"].shift(i)[i:]}))\n prediction = results.sort_values(\"score\",ascending=False).iloc[0][\"model\"].predict(features[-14:])\n predictions.append(prediction[len(prediction)-1])", "100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 14/14 [03:34<00:00, 15.29s/it]\n" ], [ "import matplotlib.pyplot as plt\nstuff = data[-14:]\nstuff[\"predict\"] = predictions\nplt.plot(stuff[\"y\"])\nplt.plot(stuff[\"predict\"])\nplt.show()", "_____no_output_____" ], [ "features[-14:]", "_____no_output_____" ], [ "stuff", "_____no_output_____" ], [ "m = tf.keras.models.Sequential([\n tf.keras.layers.Dense(units=64,activation=\"relu\"),\n tf.keras.layers.Dense(units=64,activation=\"relu\"),\n tf.keras.layers.Dense(units=1)\n])\nm.compile(loss=tf.losses.MeanSquaredError(),metrics=[tf.metrics.mean_squared_error])", "_____no_output_____" ], [ "predictions = []\nfor i in range(14):\n m.fit(tf.stack(features[i:]),tf.stack(data[\"y\"].shift(i)[i:]))\n prediction = m.predict(tf.stack(features))\n predictions.append(prediction[0])", "99/99 [==============================] - 1s 6ms/step - loss: 123474.1484 - mean_squared_error: 123474.1484\n99/99 [==============================] - 1s 5ms/step - loss: 775.6915 - mean_squared_error: 775.6915\n99/99 [==============================] - 0s 5ms/step - loss: 559.5361 - mean_squared_error: 559.5361\n98/98 [==============================] - 1s 5ms/step - loss: 476.2378 - mean_squared_error: 476.2378\n98/98 [==============================] - 1s 6ms/step - loss: 448.9850 - mean_squared_error: 448.9850\n98/98 [==============================] - 1s 6ms/step - loss: 471.0747 - mean_squared_error: 471.0747\n98/98 [==============================] - 1s 5ms/step - loss: 431.9784 - mean_squared_error: 431.9784\n98/98 [==============================] - 0s 5ms/step - loss: 417.2934 - mean_squared_error: 417.2934\n98/98 [==============================] - 1s 5ms/step - loss: 390.7068 - mean_squared_error: 390.7068\n98/98 [==============================] - 1s 6ms/step - loss: 401.5533 - mean_squared_error: 401.5533\n98/98 [==============================] - 0s 5ms/step - loss: 416.8732 - mean_squared_error: 416.8732\n98/98 [==============================] - 1s 6ms/step - loss: 383.3142 - mean_squared_error: 383.3142\n98/98 [==============================] - 1s 6ms/step - loss: 416.5927 - mean_squared_error: 416.5927\n98/98 [==============================] - 1s 5ms/step - loss: 381.3717 - mean_squared_error: 381.3717\n" ], [ "import matplotlib.pyplot as plt\nstuff = data[-14:]\nstuff[\"predict\"] = predictions\nplt.plot(stuff[\"y\"])\nplt.plot(stuff[\"predict\"])\nplt.show()", "_____no_output_____" ], [ "days = 100\nend = datetime(2020,7,1)\nstart = end - timedelta(days=days)\nbase = pd.date_range(start,end)\ngap = 2\nrows = []\ntraining_days = 100\nstrat.connect()\nfor date in tqdm(base):\n if date.weekday() < 5:\n training_start = date - timedelta(days=training_days)\n training_end = date\n if date.weekday() == 4:\n prediction_date = date + timedelta(days=3)\n else:\n prediction_date = date + timedelta(days=1)\n classification = strat.retrieve_training_data(\"dataset_classification\",training_start,prediction_date)\n classification_prediction = pd.DataFrame([classification.drop([\"Date\",\"_id\"],axis=1).iloc[len(classification[\"Date\"])-1]])\n if len(classification) > 60 and len(classification_prediction) > 0:\n for i in range(46,47):\n try:\n ticker = tickers.iloc[i][\"Symbol\"]\n if ticker in classification.columns:\n sector = tickers.iloc[i][\"GICS Sector\"]\n sub_sector = tickers.iloc[i][\"GICS Sub Industry\"]\n cik = int(tickers.iloc[i][\"CIK\"].item())\n classification_data = classification.copy()\n classification_data[\"y\"] = classification_data[ticker]\n classification_data[\"y\"] = classification_data[\"y\"].shift(-gap)\n classification_data = classification_data[:-gap]\n mt = ModelPreprocessor(ticker)\n rc = mt.day_trade_preprocess_classify(classification_data.copy(),ticker)\n sp = Modeler(ticker)\n results_rc = sp.classify_tf(rc)\n results = pd.DataFrame([results_rc])\n model = results.sort_values(\"accuracy\",ascending=False).iloc[0]\n m = model[\"model\"]\n mr = PredictorPreprocessor(ticker)\n refined = mr.preprocess_classify(classification_prediction.copy())\n cleaned = classification_prediction\n factors = refined[\"X\"]\n prediction = [x[0] for x in m.predict(factors)]\n product = market.retrieve_price_data(\"prices\",ticker)\n product[\"Date\"] = [datetime.strptime(x,\"%Y-%m-%d\") for x in product[\"Date\"]]\n product = product[(product[\"Date\"] > training_end) & (product[\"Date\"] <= prediction_date)]\n product[\"predicted\"] = prediction\n product[\"predicted\"] = [1 if x > 0 else 0 for x in product[\"predicted\"]]\n product[\"accuracy\"] = model[\"accuracy\"]\n product.sort_values(\"Date\",inplace=True)\n product = product[[\"Date\",\"Adj_Close\",\"predicted\",\"accuracy\",\"ticker\"]].dropna()\n strat.store_data(\"sim_tf\",product)\n except Exception as e:\n print(str(e))\nstrat.close()", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2df7c4945894b5353dadd6f6e872c1d0d0f947

2,767

ipynb

Jupyter Notebook

ch17/TF Datasets and LibriSpeech.ipynb

fneitzel/MLwithTensorFlow2ed

479f74e54c42a231b058472407e82b37c61dac88

[ "Apache-2.0" ]

96

2020-02-02T22:56:24.000Z

2022-03-20T22:39:54.000Z

ch17/TF Datasets and LibriSpeech.ipynb

fneitzel/MLwithTensorFlow2ed

479f74e54c42a231b058472407e82b37c61dac88

[ "Apache-2.0" ]

11

2020-07-30T04:11:10.000Z

2022-01-13T03:14:35.000Z

ch17/TF Datasets and LibriSpeech.ipynb

fneitzel/MLwithTensorFlow2ed

479f74e54c42a231b058472407e82b37c61dac88

[ "Apache-2.0" ]

43

2019-12-04T15:02:34.000Z

2022-03-12T22:06:12.000Z

24.27193

91

0.527647

[ [ [ "import tensorflow as tf\nimport glob\nfrom tensorflow.data.experimental import AUTOTUNE ", "_____no_output_____" ], [ "speech_data_path = \"../data/LibriSpeech\"\ntrain_path = speech_data_path + \"/train-clean-100\"\ndev_path = speech_data_path + \"/dev-clean\"\ntest_path = speech_data_path + \"/test-clean\"\n", "_____no_output_____" ], [ "train_audio_wav = [file for file in glob.glob(train_path + \"/*/*/*.wav\")]", "_____no_output_____" ], [ "print(len(train_audio_wav))", "_____no_output_____" ], [ "BATCH_SIZE=10\ntrain_size=100\ntrain_audio_ds = tf.data.Dataset.from_tensor_slices(train_audio_wav[0:train_size])\ntrain_audio_ds = train_audio_ds.batch(25)\ntrain_audio_ds = train_audio_ds.shuffle(buffer_size=train_size)\ntrain_audio_ds = train_audio_ds.prefetch(buffer_size=AUTOTUNE)\nnum_epochs = 2", "_____no_output_____" ], [ "with tf.Session() as sess:\n sess.run(tf.global_variables_initializer())\n \n for epoch in range(0, num_epochs):\n iter = train_audio_ds.make_one_shot_iterator()\n batch_num = 0\n iter_op = iter.get_next()\n\n while True:\n try:\n train_batch = sess.run(iter_op)\n print(train_batch)\n batch_num += 1\n print('Batch Num %d ' % (batch_num))\n except tf.errors.OutOfRangeError:\n print('Epoch %d ' % (epoch))\n break", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code" ] ]

cb2df875c883c0737650790a2ef2fe59217d715e

26,160

ipynb

Jupyter Notebook

cloud/notebooks/python_sdk/deployments/keras/Use Keras to recognize hand-written digits.ipynb

muthukumarbala07/watson-machine-learning-samples

ecc66faf7a7c60ca168b9c7ef0bca3c766babb94

[ "Apache-2.0" ]

null

cloud/notebooks/python_sdk/deployments/keras/Use Keras to recognize hand-written digits.ipynb

muthukumarbala07/watson-machine-learning-samples

ecc66faf7a7c60ca168b9c7ef0bca3c766babb94

[ "Apache-2.0" ]

null

cloud/notebooks/python_sdk/deployments/keras/Use Keras to recognize hand-written digits.ipynb

muthukumarbala07/watson-machine-learning-samples

ecc66faf7a7c60ca168b9c7ef0bca3c766babb94

[ "Apache-2.0" ]

null

29.761092

2,640

0.564755

[ [ [ "\n# Use Keras to recognize hand-written digits with `ibm-watson-machine-learning`\n\nThis notebook uses the Keras machine learning framework with the Watson Machine Learning service. It contains steps and code to work with [ibm-watson-machine-learning](https://pypi.python.org/pypi/ibm-watson-machine-learning) library available in PyPI repository. It also introduces commands for getting model and training data, persisting model, deploying model and scoring it.\n\nSome familiarity with Python is helpful. This notebook uses Python 3.8.", "_____no_output_____" ], [ "## Learning goals\n\nThe learning goals of this notebook are:\n\n- Download an externally trained Keras model with dataset.\n- Persist an external model in Watson Machine Learning repository.\n- Deploy model for online scoring using client library.\n- Score sample records using client library.\n\n\n## Contents\n\nThis notebook contains the following parts:\n\n1.\t[Setup](#setup)\n2.\t[Download externally created Keras model and data](#download)\n3.\t[Persist externally created Keras model](#upload)\n4.\t[Deploy and score in a Cloud](#deploy)\n5. [Clean up](#cleanup)\n6.\t[Summary and next steps](#summary)", "_____no_output_____" ], [ "<a id=\"setup\"></a>\n## 1. Set up the environment\n\nBefore you use the sample code in this notebook, you must perform the following setup tasks:\n\n- Create a <a href=\"https://console.ng.bluemix.net/catalog/services/ibm-watson-machine-learning/\" target=\"_blank\" rel=\"noopener no referrer\">Watson Machine Learning (WML) Service</a> instance (a free plan is offered and information about how to create the instance can be found <a href=\"https://dataplatform.cloud.ibm.com/docs/content/wsj/analyze-data/ml-service-instance.html?context=analytics\" target=\"_blank\" rel=\"noopener no referrer\">here</a>).", "_____no_output_____" ], [ "### Connection to WML\n\nAuthenticate the Watson Machine Learning service on IBM Cloud. You need to provide platform `api_key` and instance `location`.\n\nYou can use [IBM Cloud CLI](https://cloud.ibm.com/docs/cli/index.html) to retrieve platform API Key and instance location.\n\nAPI Key can be generated in the following way:\n```\nibmcloud login\nibmcloud iam api-key-create API_KEY_NAME\n```\n\nIn result, get the value of `api_key` from the output.\n\n\nLocation of your WML instance can be retrieved in the following way:\n```\nibmcloud login --apikey API_KEY -a https://cloud.ibm.com\nibmcloud resource service-instance WML_INSTANCE_NAME\n```\n\nIn result, get the value of `location` from the output.", "_____no_output_____" ], [ "**Tip**: Your `Cloud API key` can be generated by going to the [**Users** section of the Cloud console](https://cloud.ibm.com/iam#/users). From that page, click your name, scroll down to the **API Keys** section, and click **Create an IBM Cloud API key**. Give your key a name and click **Create**, then copy the created key and paste it below. You can also get a service specific url by going to the [**Endpoint URLs** section of the Watson Machine Learning docs](https://cloud.ibm.com/apidocs/machine-learning). You can check your instance location in your <a href=\"https://console.ng.bluemix.net/catalog/services/ibm-watson-machine-learning/\" target=\"_blank\" rel=\"noopener no referrer\">Watson Machine Learning (WML) Service</a> instance details.\n\nYou can also get service specific apikey by going to the [**Service IDs** section of the Cloud Console](https://cloud.ibm.com/iam/serviceids). From that page, click **Create**, then copy the created key and paste it below.\n\n**Action**: Enter your `api_key` and `location` in the following cell.", "_____no_output_____" ] ], [ [ "api_key = 'PASTE YOUR PLATFORM API KEY HERE'\nlocation = 'PASTE YOUR INSTANCE LOCATION HERE'", "_____no_output_____" ], [ "wml_credentials = {\n \"apikey\": api_key,\n \"url\": 'https://' + location + '.ml.cloud.ibm.com'\n}", "_____no_output_____" ] ], [ [ "### Install and import the `ibm-watson-machine-learning` package\n**Note:** `ibm-watson-machine-learning` documentation can be found <a href=\"http://ibm-wml-api-pyclient.mybluemix.net/\" target=\"_blank\" rel=\"noopener no referrer\">here</a>.", "_____no_output_____" ] ], [ [ "!pip install -U ibm-watson-machine-learning", "_____no_output_____" ], [ "from ibm_watson_machine_learning import APIClient\n\nclient = APIClient(wml_credentials)", "_____no_output_____" ] ], [ [ "### Working with spaces\n\nFirst of all, you need to create a space that will be used for your work. If you do not have space already created, you can use [Deployment Spaces Dashboard](https://dataplatform.cloud.ibm.com/ml-runtime/spaces?context=cpdaas) to create one.\n\n- Click New Deployment Space\n- Create an empty space\n- Select Cloud Object Storage\n- Select Watson Machine Learning instance and press Create\n- Copy `space_id` and paste it below\n\n**Tip**: You can also use SDK to prepare the space for your work. More information can be found [here](https://github.com/IBM/watson-machine-learning-samples/blob/master/cloud/notebooks/python_sdk/instance-management/Space%20management.ipynb).\n\n**Action**: Assign space ID below", "_____no_output_____" ] ], [ [ "space_id = 'PASTE YOUR SPACE ID HERE'", "_____no_output_____" ] ], [ [ "You can use `list` method to print all existing spaces.", "_____no_output_____" ] ], [ [ "client.spaces.list(limit=10)", "_____no_output_____" ] ], [ [ "To be able to interact with all resources available in Watson Machine Learning, you need to set **space** which you will be using.", "_____no_output_____" ] ], [ [ "client.set.default_space(space_id)", "_____no_output_____" ] ], [ [ "<a id=\"download\"></a>\n## 2. Download externally created Keras model and data\nIn this section, you will download externally created Keras models and data used for training it.", "_____no_output_____" ] ], [ [ "import os\nimport wget\n\ndata_dir = 'MNIST_DATA'\nif not os.path.isdir(data_dir):\n os.mkdir(data_dir)\n \nmodel_path = os.path.join(data_dir, 'mnist_keras.h5.tgz')\nif not os.path.isfile(model_path):\n wget.download(\"https://github.com/IBM/watson-machine-learning-samples/raw/master/cloud/models/keras/mnist_keras.h5.tgz\", out=data_dir)", "_____no_output_____" ], [ "import os\nimport wget\n\ndata_dir = 'MNIST_DATA'\nif not os.path.isdir(data_dir):\n os.mkdir(data_dir)\n \nfilename = os.path.join(data_dir, 'mnist.npz')\nif not os.path.isfile(filename):\n wget.download('https://s3.amazonaws.com/img-datasets/mnist.npz', out=data_dir) ", "_____no_output_____" ], [ "import numpy as np\n\ndataset = np.load(filename)\nx_test = dataset['x_test']", "_____no_output_____" ] ], [ [ "<a id=\"upload\"></a>\n## 3. Persist externally created Keras model", "_____no_output_____" ], [ "In this section, you will learn how to store your model in Watson Machine Learning repository by using the Watson Machine Learning Client.", "_____no_output_____" ], [ "### 3.1: Publish model", "_____no_output_____" ], [ "#### Publish model in Watson Machine Learning repository on Cloud.", "_____no_output_____" ], [ "Define model name, type and software specification needed to deploy model later.", "_____no_output_____" ] ], [ [ "sofware_spec_uid = client.software_specifications.get_id_by_name(\"default_py3.8\")", "_____no_output_____" ], [ "metadata = {\n client.repository.ModelMetaNames.NAME: 'External Keras model',\n client.repository.ModelMetaNames.TYPE: 'tensorflow_2.4',\n client.repository.ModelMetaNames.SOFTWARE_SPEC_UID: sofware_spec_uid\n}\n\npublished_model = client.repository.store_model(\n model=model_path,\n meta_props=metadata)", "_____no_output_____" ] ], [ [ "### 3.2: Get model details", "_____no_output_____" ] ], [ [ "import json\n\npublished_model_uid = client.repository.get_model_uid(published_model)\nmodel_details = client.repository.get_details(published_model_uid)\nprint(json.dumps(model_details, indent=2))", "{\n \"entity\": {\n \"software_spec\": {\n \"id\": \"2b73a275-7cbf-420b-a912-eae7f436e0bc\"\n },\n \"type\": \"keras_2.2.5\"\n },\n \"metadata\": {\n \"created_at\": \"2020-08-11T09:14:37.258Z\",\n \"id\": \"2b5a3f9e-2c20-4e25-8586-dff0309d512a\",\n \"modified_at\": \"2020-08-11T09:14:42.535Z\",\n \"name\": \"External Keras model\",\n \"owner\": \"IBMid-310002AFR6\",\n \"space_id\": \"968d9b1a-3cb4-4029-bc57-f53ec5e8743b\"\n }\n}\n" ] ], [ [ "### 3.3 Get all models", "_____no_output_____" ] ], [ [ "models_details = client.repository.list_models()", "_____no_output_____" ] ], [ [ "<a id=\"deploy\"></a>\n## 4. Deploy and score in a Cloud", "_____no_output_____" ], [ "In this section you will learn how to create online scoring and to score a new data record by using the Watson Machine Learning Client.", "_____no_output_____" ], [ "### 4.1: Create model deployment", "_____no_output_____" ], [ "#### Create online deployment for published model", "_____no_output_____" ] ], [ [ "metadata = {\n client.deployments.ConfigurationMetaNames.NAME: \"Deployment of external Keras model\",\n client.deployments.ConfigurationMetaNames.ONLINE: {}\n}\n\ncreated_deployment = client.deployments.create(published_model_uid, meta_props=metadata)", "\n\n#######################################################################################\n\nSynchronous deployment creation for uid: '2b5a3f9e-2c20-4e25-8586-dff0309d512a' started\n\n#######################################################################################\n\n\ninitializing.\nready\n\n\n------------------------------------------------------------------------------------------------\nSuccessfully finished deployment creation, deployment_uid='1a11f778-d430-4c41-bbba-9d116205f906'\n------------------------------------------------------------------------------------------------\n\n\n" ] ], [ [ "**Note**: Here we use deployment url saved in published_model object. In next section, we show how to retrive deployment url from Watson Machine Learning instance.", "_____no_output_____" ] ], [ [ "deployment_uid = client.deployments.get_uid(created_deployment)", "_____no_output_____" ] ], [ [ "Now you can print an online scoring endpoint. ", "_____no_output_____" ] ], [ [ "scoring_endpoint = client.deployments.get_scoring_href(created_deployment)\nprint(scoring_endpoint)", "https://yp-qa.ml.cloud.ibm.com/ml/v4/deployments/1a11f778-d430-4c41-bbba-9d116205f906/predictions\n" ] ], [ [ "You can also list existing deployments.", "_____no_output_____" ] ], [ [ "client.deployments.list()", "_____no_output_____" ] ], [ [ "### 4.2: Get deployment details", "_____no_output_____" ] ], [ [ "client.deployments.get_details(deployment_uid)", "_____no_output_____" ] ], [ [ "<a id=\"score\"></a>\n### 4.3: Score", "_____no_output_____" ], [ "You can use below method to do test scoring request against deployed model.", "_____no_output_____" ], [ "Let's first visualize two samples from dataset, we'll use for scoring.", "_____no_output_____" ] ], [ [ "%matplotlib inline\nimport matplotlib.pyplot as plt", "_____no_output_____" ], [ "for i, image in enumerate([x_test[0], x_test[1]]):\n plt.subplot(2, 2, i + 1)\n plt.axis('off')\n plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')", "_____no_output_____" ] ], [ [ "Prepare scoring payload with records to score.", "_____no_output_____" ] ], [ [ "score_0 = (x_test[0].ravel() / 255).tolist()\nscore_1 = (x_test[1].ravel() / 255).tolist()", "_____no_output_____" ], [ "scoring_payload = {\"input_data\": [{\"values\": [score_0, score_1]}]}", "_____no_output_____" ] ], [ [ "Use ``client.deployments.score()`` method to run scoring.", "_____no_output_____" ] ], [ [ "predictions = client.deployments.score(deployment_uid, scoring_payload)", "_____no_output_____" ], [ "print(json.dumps(predictions, indent=2))", "{\n \"predictions\": [\n {\n \"fields\": [\n \"prediction\",\n \"prediction_classes\",\n \"probability\"\n ],\n \"values\": [\n [\n [\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 1.0,\n 0.0,\n 0.0\n ],\n 7,\n [\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 1.0,\n 0.0,\n 0.0\n ]\n ],\n [\n [\n 0.0,\n 0.0,\n 1.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0\n ],\n 2,\n [\n 0.0,\n 0.0,\n 1.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0,\n 0.0\n ]\n ]\n ]\n }\n ]\n}\n" ] ], [ [ "<a id=\"cleanup\"></a>\n## 5. Clean up", "_____no_output_____" ], [ "If you want to clean up all created assets:\n- experiments\n- trainings\n- pipelines\n- model definitions\n- models\n- functions\n- deployments\n\nplease follow up this sample [notebook](https://github.com/IBM/watson-machine-learning-samples/blob/master/cloud/notebooks/python_sdk/instance-management/Machine%20Learning%20artifacts%20management.ipynb).", "_____no_output_____" ], [ "<a id=\"summary\"></a>\n## 6. Summary and next steps", "_____no_output_____" ], [ " You successfully completed this notebook! You learned how to use Keras machine learning library as well as Watson Machine Learning for model creation and deployment. Check out our _[Online Documentation](https://dataplatform.cloud.ibm.com/docs/content/wsj/getting-started/welcome-main.html?context=analytics?pos=2)_ for more samples, tutorials, documentation, how-tos, and blog posts. ", "_____no_output_____" ], [ "### Authors\n\n**Daniel Ryszka**, Software Engineer", "_____no_output_____" ], [ "Copyright © 2020, 2021 IBM. This notebook and its source code are released under the terms of the MIT License.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ] ]

cb2dfc3d12af30d45c47f9be585dd8d60dfc729c

44,344

ipynb

Jupyter Notebook

Copy_of_Welcome_To_Colaboratory.ipynb

katie-chiang/ARMultiDoodle

2d1426e273676d0097099453a3ea7fb10ab5f9c4

[ "MIT" ]

1

2018-07-16T07:20:17.000Z

Copy_of_Welcome_To_Colaboratory.ipynb

katie-chiang/ARMultiDoodle

2d1426e273676d0097099453a3ea7fb10ab5f9c4

[ "MIT" ]

null

Copy_of_Welcome_To_Colaboratory.ipynb

katie-chiang/ARMultiDoodle

2d1426e273676d0097099453a3ea7fb10ab5f9c4

[ "MIT" ]

null

137.287926

31,886

0.846563

[ [ [ "<a href=\"https://colab.research.google.com/github/katie-chiang/ARMultiDoodle/blob/master/Copy_of_Welcome_To_Colaboratory.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>", "_____no_output_____" ], [ "<p><img alt=\"Colaboratory logo\" height=\"45px\" src=\"/img/colab_favicon.ico\" align=\"left\" hspace=\"10px\" vspace=\"0px\"></p>\n\n<h1>What is Colaboratory?</h1>\n\nColaboratory, or \"Colab\" for short, allows you to write and execute Python in your browser, with \n- Zero configuration required\n- Free access to GPUs\n- Easy sharing\n\nWhether you're a **student**, a **data scientist** or an **AI researcher**, Colab can make your work easier. Watch [Introduction to Colab](https://www.youtube.com/watch?v=inN8seMm7UI) to learn more, or just get started below!", "_____no_output_____" ], [ "## **Getting started**\n\nThe document you are reading is not a static web page, but an interactive environment called a **Colab notebook** that lets you write and execute code.\n\nFor example, here is a **code cell** with a short Python script that computes a value, stores it in a variable, and prints the result:", "_____no_output_____" ] ], [ [ "seconds_in_a_day = 24 * 60 * 60\nseconds_in_a_day\n\nhello", "_____no_output_____" ], [ "# test screeeeem", "_____no_output_____" ] ], [ [ "To execute the code in the above cell, select it with a click and then either press the play button to the left of the code, or use the keyboard shortcut \"Command/Ctrl+Enter\". To edit the code, just click the cell and start editing.\n\nVariables that you define in one cell can later be used in other cells:", "_____no_output_____" ] ], [ [ "seconds_in_a_week = 7 * seconds_in_a_day\nseconds_in_a_week\n\n🤣🤣🤣😂😎😎🙄😫😫\n\nug\n\nkatie\n\nmax", "_____no_output_____" ] ], [ [ "Colab notebooks allow you to combine **executable code** and **rich text** in a single document, along with **images**, **HTML**, **LaTeX** and more. When you create your own Colab notebooks, they are stored in your Google Drive account. You can easily share your Colab notebooks with co-workers or friends, allowing them to comment on your notebooks or even edit them. To learn more, see [Overview of Colab](/notebooks/basic_features_overview.ipynb). To create a new Colab notebook you can use the File menu above, or use the following link: [create a new Colab notebook](http://colab.research.google.com#create=true).\n\nColab notebooks are Jupyter notebooks that are hosted by Colab. To learn more about the Jupyter project, see [jupyter.org](https://www.jupyter.org).", "_____no_output_____" ], [ "## Data science\n\nWith Colab you can harness the full power of popular Python libraries to analyze and visualize data. The code cell below uses **numpy** to generate some random data, and uses **matplotlib** to visualize it. To edit the code, just click the cell and start editing.", "_____no_output_____" ] ], [ [ "import numpy as np\nfrom matplotlib import pyplot as plt\n\nys = 200 + np.random.randn(100)\nx = [x for x in range(len(ys))]\n\nplt.plot(x, ys, '-')\nplt.fill_between(x, ys, 195, where=(ys > 195), facecolor='g', alpha=0.6)\n\nplt.title(\"Sample Visualization\")\nplt.show()", "_____no_output_____" ] ], [ [ "You can import your own data into Colab notebooks from your Google Drive account, including from spreadsheets, as well as from Github and many other sources. To learn more about importing data, and how Colab can be used for data science, see the links below under [Working with Data](#working-with-data).", "_____no_output_____" ], [ "## Machine learning\n\nWith Colab you can import an image dataset, train an image classifier on it, and evaluate the model, all in just [a few lines of code](https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/quickstart/beginner.ipynb). Colab notebooks execute code on Google's cloud servers, meaning you can leverage the power of Google hardware, including [GPUs and TPUs](#using-accelerated-hardware), regardless of the power of your machine. All you need is a browser.", "_____no_output_____" ], [ "Colab is used extensively in the machine learning community with applications including:\n- Getting started with TensorFlow\n- Developing and training neural networks\n- Experimenting with TPUs\n- Disseminating AI research\n- Creating tutorials\n\nTo see sample Colab notebooks that demonstrate machine learning applications, see the [machine learning examples](#machine-learning-examples) below.", "_____no_output_____" ], [ "## More Resources\n\n### Working with Notebooks in Colab\n- [Overview of Colaboratory](/notebooks/basic_features_overview.ipynb)\n- [Guide to Markdown](/notebooks/markdown_guide.ipynb)\n- [Importing libraries and installing dependencies](/notebooks/snippets/importing_libraries.ipynb)\n- [Saving and loading notebooks in GitHub](https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb)\n- [Interactive forms](/notebooks/forms.ipynb)\n- [Interactive widgets](/notebooks/widgets.ipynb)\n- <img src=\"/img/new.png\" height=\"20px\" align=\"left\" hspace=\"4px\" alt=\"New\"></img>\n [TensorFlow 2 in Colab](/notebooks/tensorflow_version.ipynb)\n\n<a name=\"working-with-data\"></a>\n### Working with Data\n- [Loading data: Drive, Sheets, and Google Cloud Storage](/notebooks/io.ipynb) \n- [Charts: visualizing data](/notebooks/charts.ipynb)\n- [Getting started with BigQuery](/notebooks/bigquery.ipynb)\n\n### Machine Learning Crash Course\nThese are a few of the notebooks from Google's online Machine Learning course. See the [full course website](https://developers.google.com/machine-learning/crash-course/) for more.\n- [Intro to Pandas](/notebooks/mlcc/intro_to_pandas.ipynb)\n- [Tensorflow concepts](/notebooks/mlcc/tensorflow_programming_concepts.ipynb)\n- [First steps with TensorFlow](/notebooks/mlcc/first_steps_with_tensor_flow.ipynb)\n- [Intro to neural nets](/notebooks/mlcc/intro_to_neural_nets.ipynb)\n- [Intro to sparse data and embeddings](/notebooks/mlcc/intro_to_sparse_data_and_embeddings.ipynb)\n\n<a name=\"using-accelerated-hardware\"></a>\n### Using Accelerated Hardware\n- [TensorFlow with GPUs](/notebooks/gpu.ipynb)\n- [TensorFlow with TPUs](/notebooks/tpu.ipynb)", "_____no_output_____" ], [ "<a name=\"machine-learning-examples\"></a>\n\n## Machine Learning Examples\n\nTo see end-to-end examples of the interactive machine learning analyses that Colaboratory makes possible, check out these tutorials using models from [TensorFlow Hub](https://tfhub.dev).\n\nA few featured examples:\n\n- [Retraining an Image Classifier](https://tensorflow.org/hub/tutorials/tf2_image_retraining): Build a Keras model on top of a pre-trained image classifier to distinguish flowers.\n- [Text Classification](https://tensorflow.org/hub/tutorials/tf2_text_classification): Classify IMDB movie reviews as either *positive* or *negative*.\n- [Style Transfer](https://tensorflow.org/hub/tutorials/tf2_arbitrary_image_stylization): Use deep learning to transfer style between images.\n- [Multilingual Universal Sentence Encoder Q&A](https://tensorflow.org/hub/tutorials/retrieval_with_tf_hub_universal_encoder_qa): Use a machine learning model to answer questions from the SQuAD dataset.\n- [Video Interpolation](https://tensorflow.org/hub/tutorials/tweening_conv3d): Predict what happened in a video between the first and the last frame.\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown" ] ]

cb2e13f060ce5196ff5efddd81c5245ac7eac111

202,898

ipynb

Jupyter Notebook

analysis/dimensionalty_sim/plot_210413_across_masked_noise_small_signal.ipynb

htem/cb2_project_analysis

a677cbadc7e3bf0074975a94ed1d06b4801899c0

[ "MIT" ]

null

analysis/dimensionalty_sim/plot_210413_across_masked_noise_small_signal.ipynb

htem/cb2_project_analysis

a677cbadc7e3bf0074975a94ed1d06b4801899c0

[ "MIT" ]

null

analysis/dimensionalty_sim/plot_210413_across_masked_noise_small_signal.ipynb

htem/cb2_project_analysis

a677cbadc7e3bf0074975a94ed1d06b4801899c0

[ "MIT" ]

null

380.67167

71,736

0.930507

[ [ [ "import random\nimport copy\nimport logging\nimport sys\n\nfrom run_tests_201204 import *\n\nimport os\nimport sys\nimport importlib\nfrom collections import defaultdict\nsys.path.insert(0, '/n/groups/htem/Segmentation/shared-nondev/cb2_segmentation/analysis_mf_grc')\nfrom tools_pattern import get_eucledean_dist\nimport compress_pickle\nimport my_plot\nfrom my_plot import MyPlotData, my_box_plot\nimport seaborn as sns\n\nscript_n = 'plot_210413_across_masked_noise'\n\ndata_script = 'batch_210414_across_masked_noise'\ndb_path = '/n/groups/htem/Segmentation/shared-nondev/cb2_segmentation/analysis_mf_grc/dimensionality_sim/' \\\n f'{data_script}/'\n\n\nscaled_noise = 1\ncore_noise = 0\nn_mfs = 400\nn_grcs = 2400\n\nsignal_ratio = .5\nsignal_type = 'random'\n\ndb = {}\nmodel = 'scaleup4'\ndb[model] = compress_pickle.load(\n db_path+f'{data_script}_{model}_{n_grcs}_{n_mfs}_signal_ratio_{signal_ratio}_signal_type_{signal_type}_0.3_512_10.gz')\nmodel = 'random'\ndb[model] = compress_pickle.load(\n db_path+f'{data_script}_{model}_{n_grcs}_{n_mfs}_signal_ratio_{signal_ratio}_signal_type_{signal_type}_0.3_512_10.gz')\nmodel = 'naive_random4'\ndb[model] = compress_pickle.load(\n db_path+f'{data_script}_{model}_{n_grcs}_{n_mfs}_signal_ratio_{signal_ratio}_signal_type_{signal_type}_0.3_512_10.gz')\n\navg_grc_dim_list = defaultdict(list)\nfor ress in db['random']:\n ress_tries = ress\n for ress in ress_tries:\n# print(ress)\n for noise in ress:\n res = ress[noise]\n grc_dim = res['grc_dim']\n avg_grc_dim_list[noise].append(grc_dim)\n\navg_grc_dim = {}\nfor noise in avg_grc_dim_list:\n avg_grc_dim[noise] = sum(avg_grc_dim_list[noise])/len(avg_grc_dim_list[noise])\n\navg_grc_dim_list = defaultdict(list)\nfor ress in db['naive_random4']:\n ress_tries = ress\n for ress in ress_tries:\n# print(ress)\n for noise in ress:\n res = ress[noise]\n grc_dim = res['grc_dim']\n avg_grc_dim_list[noise].append(grc_dim)\n\navg_grc_dim2 = {}\nfor noise in avg_grc_dim_list:\n avg_grc_dim2[noise] = sum(avg_grc_dim_list[noise])/len(avg_grc_dim_list[noise])", "_____no_output_____" ], [ "\nname_map = {\n 'scaleup4': \"Observed\",\n 'global_random': \"Global Random\",\n 'random': \"Global Random\",\n# 'naive_random_17': \"Local Random\",\n 'naive_random4': \"Local Random\",\n}\n\npalette = {\n name_map['scaleup4']: sns.color_palette()[0],\n name_map['global_random']: sns.color_palette()[1],\n name_map['random']: sns.color_palette()[1],\n name_map['naive_random4']: sns.color_palette()[2],\n# name_map['naive_random_21']: sns.color_palette()[2],\n}\n\n\nmpd = MyPlotData()\nress_ref = db['naive_random4'][0][0]\nresss_ref2 = db['naive_random4'][0]\nfor model_name in [\n# 'global_random',\n# 'naive_random_17',\n 'random',\n 'naive_random4',\n 'scaleup4',\n ]:\n ress = db[model_name]\n# print(ress)\n ress_tries = ress[0] # get the first element in tuple\n# ress = ress[0] # get the first try\n for n_try, ress in enumerate(ress_tries):\n# print(resss_ref2[0])\n# print(resss_ref2.keys())\n if n_try >= len(resss_ref2):\n print(n_try)\n continue\n ress_ref2 = resss_ref2[n_try]\n for noise in ress:\n # print(noise)\n res = ress[noise]\n# res_ref = ress_ref[noise]\n res_ref2 = ress_ref2[noise]\n # hamming_distance_norm = res['hamming_distance']/res['num_grcs']\n mpd.add_data_point(\n model=name_map[model_name],\n noise=noise*100,\n grc_dim=res['grc_dim'],\n grc_dim_norm=res['grc_dim']/res_ref2['grc_dim'],\n grc_dim_norm2=res['grc_dim']/avg_grc_dim[noise],\n grc_dim_norm3=res['grc_dim']/avg_grc_dim2[noise],\n grc_by_mf_dim=res['grc_dim']/res['mf_dim'],\n# grc_by_mf_dim_ref=res['grc_dim']/res_ref['mf_dim'],\n num_grcs=res['num_grcs'],\n num_mfs=res['num_mfs'],\n voi=res['voi'],\n grc_pop_corr=res['grc_pop_corr'],\n grc_pop_corr_norm=res['grc_pop_corr']/res_ref2['grc_pop_corr'],\n binary_similarity=res['binary_similarity'],\n hamming_distance=res['hamming_distance'],\n normalized_mse=res['normalized_mse'],\n )\n\n# importlib.reload(my_plot); my_plot.my_relplot(\n# mpd,\n# x='noise',\n# y='grc_dim',\n# hue='model',\n# context='paper',\n# palette=palette,\n# linewidth=1,\n# log_scale_y=True,\n# width=10,\n# # ylim=[0, None],\n# y_axis_label='Dim. Expansion ($x$)',\n# x_axis_label='MF Input Variation (%)',\n# title='noise',\n# save_filename=f'{script_n}_act_30.svg',\n# show=True,\n# )\n", "_____no_output_____" ], [ "\nimportlib.reload(my_plot); my_plot.my_relplot(\n mpd,\n x='noise',\n y='grc_dim',\n hue='model',\n context='paper',\n palette=palette,\n linewidth=1,\n# log_scale_y=True,\n width=10,\n# ylim=[.9, 1.1],\n y_axis_label='Dim. Expansion ($x$)',\n x_axis_label='MF Input Variation (%)',\n title='noise',\n save_filename=f'{script_n}.svg',\n show=True,\n )\n", "Height: 7.518796992481203, Aspect: 1.33\n" ], [ "\nimportlib.reload(my_plot); my_plot.my_relplot(\n mpd,\n x='noise',\n y='grc_dim_norm2',\n hue='model',\n context='paper',\n palette=palette,\n linewidth=2,\n# log_scale_y=True,\n# ci='sd',\n ci=68,\n width=3.5,\n height=2.5,\n ylim=[0, 1.05],\n y_axis_label='Rel. Noise ($x$)',\n x_axis_label='Stochastic Noise (%)',\n# title='noise',\n save_filename=f'{script_n}_rel_noise_reduction.svg',\n show=True,\n )\n", "Height: 2.5, Aspect: 1.4\n" ], [ "\nimportlib.reload(my_plot); my_plot.my_relplot(\n mpd,\n x='noise',\n y='grc_dim_norm3',\n hue='model',\n context='paper',\n palette=palette,\n linewidth=2,\n# log_scale_y=True,\n# ci='sd',\n ci=68,\n width=3.5,\n height=2.5,\n ylim=[.5, 1.8],\n y_axis_label='Rel. Noise ($x$)',\n x_axis_label='Stochastic Noise (%)',\n# title='noise',\n save_filename=f'{script_n}_rel_noise_reduction2.svg',\n show=True,\n )\n", "Height: 2.5, Aspect: 1.4\n" ], [ "\nimportlib.reload(my_plot); my_plot.my_relplot(\n mpd,\n x='noise',\n y='grc_pop_corr_norm',\n hue='model',\n context='paper',\n palette=palette,\n linewidth=2,\n# log_scale_y=True,\n# ci='sd',\n ci=68,\n width=3.5,\n height=2.5,\n# ylim=[0, 1.05],\n y_axis_label='Rel. Noise ($x$)',\n x_axis_label='Stochastic Noise (%)',\n# title='noise',\n save_filename=f'{script_n}_popcorr.svg',\n show=True,\n )\n", "Height: 2.5, Aspect: 1.4\n" ], [ "\nimportlib.reload(my_plot); my_plot.my_relplot(\n mpd,\n x='noise',\n y='grc_dim',\n hue='model',\n context='paper',\n palette=palette,\n linewidth=2,\n# log_scale_y=True,\n# ci='sd',\n ci=68,\n width=3.5,\n height=2.5,\n# ylim=[0, 1.05],\n y_axis_label='Noise ($x$)',\n x_axis_label='Stochastic Noise (%)',\n# title='noise',\n save_filename=f'{script_n}_noise_reduction.svg',\n show=True,\n )\n", "Height: 2.5, Aspect: 1.4\n" ], [ "\nimportlib.reload(my_plot); my_plot.my_relplot(\n mpd,\n x='noise',\n y='grc_by_mf_dim',\n hue='model',\n context='paper',\n palette=palette,\n linewidth=2,\n# log_scale_y=True,\n# ci='sd',\n# ci=68,\n width=3.5,\n height=3,\n# ylim=[.9, 1.1],\n y_axis_label='Dim. Expansion ($x$)',\n x_axis_label='Graded Variation (%)',\n# title='noise',\n save_filename=f'{script_n}_dim_expansion.svg',\n show=True,\n )\n", "Height: 3, Aspect: 1.1666666666666667\n" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2e1a51d161710439ce6f3fe40c400e4b773877

70,886

ipynb

Jupyter Notebook

MNist_with_Pytorch.ipynb

RoisulIslamRumi/MNIST-PyTorch

f87ab06785efb07a87f35770365885a285ec8694

[ "MIT" ]

null

MNist_with_Pytorch.ipynb

RoisulIslamRumi/MNIST-PyTorch

f87ab06785efb07a87f35770365885a285ec8694

[ "MIT" ]

null

MNist_with_Pytorch.ipynb

RoisulIslamRumi/MNIST-PyTorch

f87ab06785efb07a87f35770365885a285ec8694

[ "MIT" ]

null

39.734305

7,294

0.542336

[ [ [ "<a href=\"https://colab.research.google.com/github/RoisulIslamRumi/MNIST-PyTorch/blob/main/MNist_with_Pytorch.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>", "_____no_output_____" ] ], [ [ "#Import required libraries\nimport torch #imports all essential modules to build NN\nimport torchvision #to preprocess and transforma the data\nimport torch.nn as nn\nfrom torchvision import datasets, transforms \nimport matplotlib.pyplot as plt\nfrom torch import optim\nimport numpy as np\n%matplotlib inline", "_____no_output_____" ] ], [ [ "Normalize does the following for each channel: \n**image = (image - mean) / std**\n\nThe parameters **mean**, **std** are passed as 0.5, 0.5 which will normalize the image in the range [-1,1]. For example, the minimum value 0 will be converted to (0-0.5)/0.5=-1, the maximum value of 1 will be converted to (1-0.5)/0.5=1.\n\nTo get your image back in [0,1] range the equation would be:\n\nimage = ((image * std) + mean) ", "_____no_output_____" ] ], [ [ "mean = 0.5\nstd = 0.5\n#'Transforms' converts the images to tensor and preprocess them to normalize \n# with a SD of 1\ntransform = transforms.Compose([\n transforms.ToTensor(),\n transforms.Normalize(mean, std)])\ntrainset = torchvision.datasets.MNIST('~/.pytorch/MNIST_data/', train=True,\n transform=transform, download=True)\ntrainloader = torch.utils.data.DataLoader(trainset,batch_size=64, shuffle=True)\n\n", "Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz\nDownloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz to /root/.pytorch/MNIST_data/MNIST/raw/train-images-idx3-ubyte.gz\n" ], [ "num_of_images = trainloader.dataset.data.shape[0]\nheight = trainloader.dataset.data.shape[1]\nwidth = trainloader.dataset.data.shape[2]", "_____no_output_____" ], [ "input_size = height * width\nhidden_layers = [128,64]\noutput_size = 10\n", "_____no_output_____" ], [ "from torch.nn.modules.linear import Linear\nmodel = nn.Sequential(nn.Linear(input_size,hidden_layers[0]),\n nn.ReLU(),\n nn.Linear(hidden_layers[0],hidden_layers[1]),\n nn.ReLU(),\n nn.Linear(hidden_layers[1], output_size),\n nn.LogSoftmax(dim=1)\n )\nprint(model)\ncriterion = nn.NLLLoss()\noptimizer = optim.SGD(model.parameters(), lr = 0.003)", "Sequential(\n (0): Linear(in_features=784, out_features=128, bias=True)\n (1): ReLU()\n (2): Linear(in_features=128, out_features=64, bias=True)\n (3): ReLU()\n (4): Linear(in_features=64, out_features=10, bias=True)\n (5): LogSoftmax(dim=1)\n)\n" ], [ "epochs = 5\nloss = 0\nfor e in range(epochs):\n running_loss = 0\n for images, labels in trainloader:\n #Flatten the image from 28*28 to 784*1 column vector\n images = images.view(images.shape[0], -1)\n\n #set grad to 0\n optimizer.zero_grad()\n output = model(images)\n loss = criterion(output,labels)\n\n #backprop\n loss.backward()\n\n #update the grads\n optimizer.step()\n running_loss += loss.item()\n loss = running_loss\nprint(\"Training loss:\",(loss/len(trainloader)))\n", "Training loss: 0.37707768968427613\n" ], [ "def view_classify(img, ps):\n ps = ps.data.numpy().squeeze()\n fig, (ax1, ax2) = plt.subplots(figsize=(6,9), ncols=2)\n ax1.imshow(img.resize_(1, 28, 28).numpy().squeeze())\n ax1.axis('off')\n ax2.barh(np.arange(10), ps)\n ax2.set_aspect(0.1)\n ax2.set_yticks(np.arange(10))\n ax2.set_yticklabels(np.arange(10))\n ax2.set_title('Class Probability')\n ax2.set_xlim(0, 1.1)\n plt.tight_layout()", "_____no_output_____" ], [ "# Getting the image to test\nimages, labels = next(iter(trainloader))\n\nimg = images[0].view(1,784)\n\nwith torch.no_grad():\n logps = model(img)\n\nps = torch.exp(logps)\nview_classify(img,ps)\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ] ]

cb2e1dc98f59f4656c41572bf803955ada3d1579

85,454

ipynb

Jupyter Notebook

analysis/cospar/working_001_makeobsvisc.ipynb

rsbyrne/thesis

44689b1d06c5b08fd44054313d7a6148b0e44a24

[ "MIT" ]

null

analysis/cospar/working_001_makeobsvisc.ipynb

rsbyrne/thesis

44689b1d06c5b08fd44054313d7a6148b0e44a24

[ "MIT" ]

null

analysis/cospar/working_001_makeobsvisc.ipynb

rsbyrne/thesis

44689b1d06c5b08fd44054313d7a6148b0e44a24

[ "MIT" ]

1

2021-06-10T14:35:54.000Z

37.121633

177

0.608702

[ [ [ "import sys, os\neverestPath = os.path.abspath('everest')\nif not everestPath in sys.path:\n sys.path.insert(0, everestPath)", "_____no_output_____" ], [ "from everest.h5anchor.reader import Reader\nfrom everest.h5anchor.writer import Writer\nfrom everest.h5anchor.fetch import Fetch\nfrom everest.h5anchor.scope import Scope", "_____no_output_____" ], [ "reader = Reader('merged', '.')", "_____no_output_____" ], [ "observers = reader[Fetch('*/supertype') == 'Observer']\nthermos = reader[Fetch('*/type') == 'Thermo']\nvelviscs = reader[Fetch('*/type') == 'VelVisc']\nsystems = reader[Fetch('*/supertype') == 'System']\nisos = reader[Fetch('*/type') == 'Isovisc']\narrs = reader[Fetch('*/type') == 'Arrhenius']\nvps = reader[Fetch('*/type') == 'Viscoplastic']\n\nvpObs = reader[Fetch('*/observee/type') == 'Viscoplastic']\nvpThermos = vpObs & thermos", "_____no_output_____" ], [ "writer = Writer('obsvisc', '.')", "_____no_output_____" ], [ "for key, indices in vpObs:\n print(key)\n observeeKey = reader[f\"{key}/inputs/observee\"][len('_built_'):]\n writer.add_dict(reader[f\"{observeeKey}/inputs\"], observeeKey)\n writer.add_dict(reader[f\"{key}/outputs\"], observeeKey)", "iastuoaosfie-phoutrthoogr\nyeitssteadr-gluodroaps\nciirhxoox-tziocheadwiu\nuosneasmue-eyeeesfui\nweuvfaarh-iiproobliasc\ndrouzuuploi-plauscsluub\neviabuep-oopluotweudr\nautiagreath-espeeieghae\nuzoesmoesc-eokruispasc\nsougoshui-froengzheesc\nwreaghxiurh-aaplaeoongoe\nkiescxuts-tsoechicoi\nskuedwsfitr-pleuklthuzh\nxufspaosk-oabroisce\nsnungbekw-auzhuuuusmau\nyeodwgigl-eisweovutz\nswiozoituu-easnaouatha\nawioaprei-dwoifldauj\nwaarhtwaang-sneoslkeop\niesciurhuez-chuehpraar\nzhaublstez-psuukwdriesk\nklaislstiutz-iekoitouc\nouzaubleisp-stitreutwo\naotoireigl-oxeeegroo\nchuavokriu-oesnoeduorh\noxaanu-dweostplagr\nslienkwoesk-iachayoakw\nfretzgebl-oawiheitr\nthaurhsoesf-spiblauglei\nbliatwaofuo-obraiouchua\naileiiewau-chiaspwoish\nuiscooaghoi-esuoiosnoe\nskovsciuh-waisfiusmoa\nuuchooplutr-bruukrpiusp\nphourhpliosc-pleuthuisnuo\nxoowxoigr-ietzocook\naicaaouboi-uajautuug\neidroaoograa-pleojbruesh\nstiglohoi-thoirstuaph\nzezhhusn-fluohoadwoe\n" ], [ "ts = reader['*/t']\ndts = {\n key: type(val)((*np.diff(val), 0.), extendable = True)\n for key, val in ts.items()\n }\nfor key, data in dts.items():\n writer.add(data, 'dt', key)", "_____no_output_____" ], [ "obsReader = Reader('obsvisc', '.')", "_____no_output_____" ], [ "mydata = obsReader['*/f']", "_____no_output_____" ], [ "mydata", "_____no_output_____" ], [ "with reader.open():\n for key in reader.h5file:\n print(key)\n grp = reader.h5file[key]\n grp['t'] = grp['chron'][:len(grp['Nu'])]", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2e285b1428255ebfec6cbe365b246e4f8adbaa

592,291

ipynb

Jupyter Notebook

eda/Exploratory_Data_Analysis.ipynb

not-a-hot-dog/spotify_project

b928fecb136cffdd62c650b054ca543047800f11

[ "MIT" ]

null

eda/Exploratory_Data_Analysis.ipynb

not-a-hot-dog/spotify_project

b928fecb136cffdd62c650b054ca543047800f11

[ "MIT" ]

1

2019-12-08T17:23:49.000Z

eda/Exploratory_Data_Analysis.ipynb

not-a-hot-dog/spotify_project

b928fecb136cffdd62c650b054ca543047800f11

[ "MIT" ]

null

744.084171

109,068

0.950435

[ [ [ "# Exploratory Data Analysis", "_____no_output_____" ] ], [ [ "# Import libraries\n%matplotlib inline\nimport pandas as pd\nimport numpy as np\nimport matplotlib.pyplot as plt\nimport seaborn as sns \nfrom sklearn.preprocessing import StandardScaler, MinMaxScaler\nfrom sklearn import neighbors\nfrom matplotlib.colors import ListedColormap", "_____no_output_____" ] ], [ [ "## Description of the Data", "_____no_output_____" ], [ "### Data Cleaning Process", "_____no_output_____" ], [ "### Data Structure", "_____no_output_____" ] ], [ [ "# Import the dataframe\nplaylist_df = pd.read_csv(\"data/playlists.csv\", index_col = 0)\nsongs_df = pd.read_csv(\"data/songs_100000_feat_cleaned.csv\", index_col = 0)\ncombined_df = pd.read_csv(\"data/subset100playlists.csv\", index_col = 0)", "/home/kaivalya/.anaconda3/lib/python3.7/site-packages/numpy/lib/arraysetops.py:569: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison\n mask |= (ar1 == a)\n" ], [ "combined_df.dtypes", "_____no_output_____" ] ], [ [ "## Exploratory Data Analysis", "_____no_output_____" ], [ "### What is the composition of playlists in the cleaned dataset?", "_____no_output_____" ], [ "First, we investigate the high level composition of the playlists in our cleaned dataset. How many playlists and songs do we have? What is the distribution of the number of songs per playlist? Are certain songs used significantly more than others?", "_____no_output_____" ] ], [ [ "n_tracks = playlist_df.track_uri.nunique()\nn_playlists = playlist_df.pid.nunique()\n\nsummary_stats = pd.DataFrame([{'Statistic': 'Unique Tracks', 'Value': n_tracks},\n {'Statistic': 'Unique Playlists', 'Value': n_playlists}])", "_____no_output_____" ], [ "track_uri_stats = playlist_df.groupby('track_uri')['pid'].count().sort_values(ascending = False).cumsum()\nweights = 1/track_uri_stats.max()\nweighted_track_uri_stats = track_uri_stats * weights\ncum_px = weighted_track_uri_stats[weighted_track_uri_stats.gt(0.9)].index[0]\ncum_px = round(weighted_track_uri_stats.index.get_loc(cum_px)/n_tracks, 2)*100", "_____no_output_____" ], [ "pid_stats = playlist_df.groupby('pid')['track_uri'].count()", "_____no_output_____" ], [ "fig, ax = plt.subplots(1,3, figsize = (18,5))\n\nax[0].set_title('Magnitude of the Data', fontsize=15)\nax[0].set_ylabel('Frequency', fontsize=15)\nsummary_stats.plot.bar(x = 'Statistic', y='Value', color=['k','g'], rot=0, legend = False, ax = ax[0], fontsize=15)\n\nax[1].set_title('Number of Tracks per Playlist', fontsize=15)\nax[1].hist(pid_stats, color = 'k', alpha = 0.9)\nax[1].axvline(pid_stats.mean(), ls = '--', label = 'Mean # of songs')\nax[1].set_ylabel('Number of Tracks', fontsize=15)\nax[1].set_xlabel('Playlists', fontsize=15)\nax[1].legend()\n\nax[2].set_title(f'{cum_px} % of the tracks are on 90% of the playlists', fontsize=15)\nax[2].plot(np.arange(n_tracks), weighted_track_uri_stats, c = 'k', label='?')\nax[2].set_ylabel('Proportion of Playlists', fontsize=15)\nax[2].set_xlabel('Tracks', fontsize=15)\nax[2].axhline(0.9, ls = '--', label = '90% of Playlists')\nax[2].legend()\nplt.suptitle('High-Level Playlist Features\\n\\n', fontsize=20)\nplt.show()", "_____no_output_____" ] ], [ [ "The plots above show immediately the impact of our playlist selection criteria on the dataset that will be used for training, testing, and validating our models.\n* The number of songs per playlist is not normally distributed, and we only have playlists that include more than 100 songs.\n* 18% of songs are on 90% of playlists. So we can expect overlap of songs between playlists.", "_____no_output_____" ], [ "### What do songs sound like?", "_____no_output_____" ] ], [ [ "song_feature_cols = ['acousticness', 'danceability', 'duration_ms',\n 'energy', 'instrumentalness', 'key', 'liveness', 'loudness', 'speechiness',\n 'tempo', 'time_signature', 'valence']\n\nsong_subset_df = songs_df[song_feature_cols]", "_____no_output_____" ], [ "columns = song_subset_df.columns\nfig = song_subset_df.hist(figsize=(21,14), column = columns)\nplt.suptitle('How does the distribution of song features look?', fontsize=40)\n[x.title.set_size(32) for x in fig.ravel()]\nplt.show()", "_____no_output_____" ], [ "fig = song_subset_df.hist(figsize=(21,14), column=['acousticness','loudness','danceability','energy'])\nplt.suptitle('How does the distribution of song features look?', fontsize=40)\n[x.title.set_size(32) for x in fig.ravel()]\nplt.show()", "_____no_output_____" ], [ "scaler = MinMaxScaler().fit(song_subset_df)\nscaled_songs_df = pd.DataFrame(scaler.transform(song_subset_df), columns = columns)\nplt.figure(figsize=(8,5))\nscaled_songs_df.boxplot(figsize=(21,7))\nplt.xticks(rotation=90)\nplt.title('Is there significant variation in song features?', fontsize=20)\nplt.show()", "/home/kaivalya/.anaconda3/lib/python3.7/site-packages/sklearn/preprocessing/data.py:334: DataConversionWarning: Data with input dtype int64, float64 were all converted to float64 by MinMaxScaler.\n return self.partial_fit(X, y)\n" ], [ "corr_mat = song_subset_df.corr()\nmask = np.zeros_like(corr_mat)\nmask[np.triu_indices_from(mask)] = True\n \nplt.figure(figsize=(15,10))\nplt.title('Track Feature Correlations', fontsize=35)\nsns.heatmap(corr_mat, cmap='Spectral', annot=True, mask=mask)\nplt.xticks(fontsize=20)\nplt.yticks(fontsize=20)\n\n", "_____no_output_____" ] ], [ [ "### Do playlists tend to have very similar songs, or very different songs?", "_____no_output_____" ], [ "We wanted to know whether playlists in our training set tend to be built from songs that are similar to each other or songs that are different from each other. If the same songs appear in many playlists, we could perhaps identify these and recommend them. Alternatively, if playlists tend to be composed of songs that all have similar features, we could use information about the distribution of feature scores in a stub playlist to recommend additional songs for the playlist.", "_____no_output_____" ] ], [ [ "len(np.unique(playlist_df.pid))", "_____no_output_____" ], [ "playlists_per_track = playlist_df.groupby('track_uri').count()\nplaylists_per_track = playlists_per_track.sort_values('pid', ascending=False)\nl = [1,2,3,4,5,10,20,50,100,500]\nll = []\nfor i in l:\n ll.append(len(playlists_per_track[playlists_per_track['pid'] >= i]))\nfor i in range(1, len(l)):\n l[i] = 'Songs in ' + str(l[i]) + '+ playlists '\nl[0] = 'Total Songs (one or more)'\nbarp = sns.barplot(ll,l, orient='h')\nplt.title('Number of Playlists that Tracks Appear In', fontsize=15)\n", "_____no_output_____" ], [ "subset_cols = ['pid', 'acousticness', 'danceability', 'duration_ms', 'count',\n 'energy', 'instrumentalness', 'key', 'liveness', 'loudness', 'speechiness',\n 'tempo', 'time_signature', 'valence']\n\nsubset_df = combined_df[subset_cols]", "_____no_output_____" ], [ "def process_playlists(df, fun, along):\n index = df.eval(along).unique()\n columns = df.columns[df.columns != along]\n n_rows = len(index)\n n_columns = len(columns)\n \n # Construct output df\n output = pd.DataFrame(np.zeros((n_rows, n_columns)), index = index, columns = columns)\n\n # Loop through playslists and apply function\n for playlist in index:\n subset = df.loc[df['pid'] == playlist, columns]\n output.loc[playlist,:] = fun(subset)\n return output", "_____no_output_____" ], [ "def gini(x):\n # Mean absolute difference\n mad = x.mad()\n mean = x.mean()\n \n # Relative mean absolute difference\n rmad = abs(mad/mean)\n \n # Gini coefficient\n g = 0.5 * rmad\n return g", "_____no_output_____" ], [ "playlist_ginis = process_playlists(subset_df, gini, 'pid')", "_____no_output_____" ], [ "systemwide_playlist_ginis = gini(subset_df.groupby(['pid']).mean())\nsystemwide_playlist_ginis", "_____no_output_____" ], [ "ax = playlist_ginis.mean().plot.barh()\nax.set_ylabel('Track Feature')\nax.set_xlabel('Gini Coefficient (0 = Perfect Equality)')\nplt.title('Do playlists tend to have songs with similar features?')\nplt.show()", "_____no_output_____" ], [ "fig, ax = plt.subplots(figsize =(5, 8)) \nsns.violinplot(ax = ax, data = playlist_ginis, orient = 'h' )\nax.set_ylabel('Track Feature', fontsize=15)\nax.set_xlabel('Gini Coefficient (0 = Perfect Equality)', fontsize=15)\nplt.title('Do playlists tend to have songs with similar features?', fontsize=15)\nplt.show()", "_____no_output_____" ], [ "\nsong_feature_cols = ['acousticness', 'danceability', 'duration_ms', 'count',\n 'energy', 'instrumentalness', 'key', 'liveness', 'loudness', 'speechiness',\n 'tempo', 'time_signature', 'valence']", "_____no_output_____" ], [ "fig, ax = plt.subplots(figsize = (9,4.5))\nax = sns.scatterplot(playlist_ginis.mean(), systemwide_playlist_ginis, s = 75, hue = song_feature_cols)\nax.set_ylabel('Similarity Across Playlists (0 = Perfect Equality)')\nax.set_xlabel('Similarity Within Playlists (0 = Perfect Equality)')\nax.legend(title = 'Track Feature')\nplt.title('Do track features differentiate playlists?', fontsize=14)\nplt.show()", "_____no_output_____" ] ], [ [ "### Do natural clusters of songs emerge as playlists?", "_____no_output_____" ], [ "It seems from our exploratory analysis so far, that using song feature based methods to recommend songs that are \"similar\" to those already in a playlist is exceedingly difficult. To motivate this visually, we show a scatterplot of two arbitrary feature values, for songs in a few playlists.", "_____no_output_____" ] ], [ [ "combined_df = combined_df[combined_df.pos < 50]\nplt.figure(figsize=(8,6))\nfor playlist_id, mark in zip(np.unique(combined_df.pid)[30:34], ['4', '3', '2', '1']):\n plt.scatter(x=combined_df[combined_df.pid == playlist_id].valence, y=combined_df[combined_df.pid == playlist_id].danceability, marker=mark, label='playlist #'+mark)\nplt.legend()\nplt.xlabel('Song - Valence', fontsize=13)\nplt.ylabel('Song - Danceability', fontsize=13)\nplt.title('Playlists do not Separate in Song feature-space', fontsize=15)\n", "_____no_output_____" ] ], [ [ "Visualising with decision boundaries:", "_____no_output_____" ] ], [ [ "combined_df2 = combined_df[['danceability','valence','pid']]\ncombined_df2 = combined_df2[(combined_df2.pid == np.unique(combined_df.pid)[30]) | (combined_df2.pid == np.unique(combined_df.pid)[31]) | (combined_df2.pid == np.unique(combined_df.pid)[32]) | (combined_df2.pid == np.unique(combined_df.pid)[33])]\n\ncombined_df2.pid = combined_df2.pid.replace(np.unique(combined_df.pid)[30], 1)\ncombined_df2.pid = combined_df2.pid.replace(np.unique(combined_df.pid)[31], 2)\ncombined_df2.pid = combined_df2.pid.replace(np.unique(combined_df.pid)[32], 3)\ncombined_df2.pid = combined_df2.pid.replace(np.unique(combined_df.pid)[33], 4)", "_____no_output_____" ], [ "plt.figure(figsize=(10,8))\n\ncmap_light = ListedColormap(['#5fb7f4', '#ffbf4e', '#6ce06c', '#f66768'])\n\nclf = neighbors.KNeighborsClassifier(1)\nclf.fit(combined_df2[['valence','danceability']], combined_df2['pid'])\nxx, yy = np.meshgrid(np.arange(-0.01, 1.01, 0.001), np.arange(0.19, 1.01, 0.001))\nZ = clf.predict(np.c_[xx.ravel(), yy.ravel()])\nZ = Z.reshape(xx.shape)\nplt.pcolormesh(xx, yy, Z, cmap=cmap_light)\n\n\n\nfor playlist_id, mark in zip(np.unique(combined_df.pid)[30:34], ['4', '3', '2', '1']):\n plt.scatter(x=combined_df[combined_df.pid == playlist_id].valence, y=combined_df[combined_df.pid == playlist_id].danceability, marker=mark, label='playlist #'+mark)\nplt.legend()\nplt.xlabel('Track valence', fontsize=20)\nplt.ylabel('Track danceability', fontsize=20)\nplt.title('Separating Playlists in valence-danceability Feature Space', fontsize=23)", "_____no_output_____" ] ], [ [ "Note that most of the points are in the center, where there is extremely high variance in colors. It seems like regios on the plot edges are acceptable, but this is actually due to dearth of data (large region, defined by single point), and is thus not likely to have good accuracy", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ] ]

cb2e2a410f5396f2d463a69b681877554ba0c8f2

190,787

ipynb

Jupyter Notebook

solutions/2 Data exploration Exercises Solution.ipynb

joelrivas/Keras

f8a8bd3de43ca5db0c5b13f5b2ff0bfb352b0830

[ "MIT" ]

null

solutions/2 Data exploration Exercises Solution.ipynb

joelrivas/Keras

f8a8bd3de43ca5db0c5b13f5b2ff0bfb352b0830

[ "MIT" ]

null

solutions/2 Data exploration Exercises Solution.ipynb

joelrivas/Keras

f8a8bd3de43ca5db0c5b13f5b2ff0bfb352b0830

[ "MIT" ]

null

220.818287

44,576

0.910838

[ [ [ "import numpy as np\n\n%matplotlib inline\nimport matplotlib.pyplot as plt\n\nimport pandas as pd", "_____no_output_____" ] ], [ [ "## Exercise 1\n- load the dataset: `../data/international-airline-passengers.csv`\n- inspect it using the `.info()` and `.head()` commands\n- use the function `pd.to_datetime()` to change the column type of 'Month' to a datatime type\n- set the index of df to be a datetime index using the column 'Month' and the `df.set_index()` method\n- choose the appropriate plot and display the data\n- choose appropriate scale\n- label the axes", "_____no_output_____" ] ], [ [ "# - load the dataset: ../data/international-airline-passengers.csv\ndf = pd.read_csv('../data/international-airline-passengers.csv')", "_____no_output_____" ], [ "# - inspect it using the .info() and .head() commands\ndf.info()", "_____no_output_____" ], [ "df.head()", "_____no_output_____" ], [ "# - use the function to_datetime() to change the column type of 'Month' to a datatime type\n# - set the index of df to be a datetime index using the column 'Month' and tthe set_index() method\n\ndf['Month'] = pd.to_datetime(df['Month'])\ndf = df.set_index('Month')", "_____no_output_____" ], [ "df.head()", "_____no_output_____" ], [ "# - choose the appropriate plot and display the data\n# - choose appropriate scale\n# - label the axes\n\ndf.plot()", "_____no_output_____" ] ], [ [ "## Exercise 2\n- load the dataset: `../data/weight-height.csv`\n- inspect it\n- plot it using a scatter plot with Weight as a function of Height\n- plot the male and female populations with 2 different colors on a new scatter plot\n- remember to label the axes", "_____no_output_____" ] ], [ [ "# - load the dataset: ../data/weight-height.csv\n# - inspect it\ndf = pd.read_csv('../data/weight-height.csv')\ndf.head()", "_____no_output_____" ], [ "df.info()", "<class 'pandas.core.frame.DataFrame'>\nRangeIndex: 10000 entries, 0 to 9999\nData columns (total 3 columns):\nGender 10000 non-null object\nHeight 10000 non-null float64\nWeight 10000 non-null float64\ndtypes: float64(2), object(1)\nmemory usage: 234.5+ KB\n" ], [ "df.describe()", "_____no_output_____" ], [ "df['Gender'].value_counts()", "_____no_output_____" ], [ "# - plot it using a scatter plot with Weight as a function of Height\n_ = df.plot(kind='scatter', x='Height', y='Weight')", "_____no_output_____" ], [ "# - plot the male and female populations with 2 different colors on a new scatter plot\n# - remember to label the axes\n\n# this can be done in several ways, showing 2 here:\nmales = df[df['Gender'] == 'Male']\nfemales = df.query('Gender == \"Female\"')\nfig, ax = plt.subplots()\n\nmales.plot(kind='scatter', x='Height', y='Weight',\n ax=ax, color='blue', alpha=0.3,\n title='Male & Female Populations')\n\nfemales.plot(kind='scatter', x='Height', y='Weight',\n ax=ax, color='red', alpha=0.3)", "_____no_output_____" ], [ "df['Gendercolor'] = df['Gender'].map({'Male': 'blue', 'Female': 'red'})\ndf.head()", "_____no_output_____" ], [ "df.plot(kind='scatter', \n x='Height',\n y='Weight',\n c=df['Gendercolor'],\n alpha=0.3,\n title='Male & Female Populations')", "_____no_output_____" ], [ "fig, ax = plt.subplots()\nax.plot(males['Height'], males['Weight'], 'ob', \n females['Height'], females['Weight'], 'or', alpha=0.3)\nplt.xlabel('Height')\nplt.ylabel('Weight')\nplt.title('Male & Female Populations')", "_____no_output_____" ] ], [ [ "## Exercise 3\n- plot the histogram of the heights for males and for females on the same plot\n- use alpha to control transparency in the plot comand\n- plot a vertical line at the mean of each population using `plt.axvline()`", "_____no_output_____" ] ], [ [ "males['Height'].plot(kind='hist',\n bins=50,\n range=(50, 80),\n alpha=0.3,\n color='blue')\n\nfemales['Height'].plot(kind='hist',\n bins=50,\n range=(50, 80),\n alpha=0.3,\n color='red')\n\nplt.title('Height distribution')\nplt.legend([\"Males\", \"Females\"])\nplt.xlabel(\"Heigth (in)\")\n\n\nplt.axvline(males['Height'].mean(), color='blue', linewidth=2)\nplt.axvline(females['Height'].mean(), color='red', linewidth=2)\n", "_____no_output_____" ], [ "males['Height'].plot(kind='hist',\n bins=200,\n range=(50, 80),\n alpha=0.3,\n color='blue',\n cumulative=True,\n normed=True)\n\nfemales['Height'].plot(kind='hist',\n bins=200,\n range=(50, 80),\n alpha=0.3,\n color='red',\n cumulative=True,\n normed=True)\n\nplt.title('Height distribution')\nplt.legend([\"Males\", \"Females\"])\nplt.xlabel(\"Heigth (in)\")\n\nplt.axhline(0.8)\nplt.axhline(0.5)\nplt.axhline(0.2)", "_____no_output_____" ] ], [ [ "## Exercise 4\n- plot the weights of the males and females using a box plot\n- which one is easier to read?\n- (remember to put in titles, axes and legends)", "_____no_output_____" ] ], [ [ "dfpvt = df.pivot(columns = 'Gender', values = 'Weight')", "_____no_output_____" ], [ "dfpvt.head()", "_____no_output_____" ], [ "dfpvt.info()", "<class 'pandas.core.frame.DataFrame'>\nInt64Index: 10000 entries, 0 to 9999\nData columns (total 2 columns):\nFemale 5000 non-null float64\nMale 5000 non-null float64\ndtypes: float64(2)\nmemory usage: 234.4 KB\n" ], [ "dfpvt.plot(kind='box')\nplt.title('Weight Box Plot')\nplt.ylabel(\"Weight (lbs)\")", "_____no_output_____" ] ], [ [ "## Exercise 5\n- load the dataset: `../data/titanic-train.csv`\n- learn about scattermatrix here: http://pandas.pydata.org/pandas-docs/stable/visualization.html\n- display the data using a scattermatrix", "_____no_output_____" ] ], [ [ "df = pd.read_csv('../data/titanic-train.csv')\ndf.head()", "_____no_output_____" ], [ "from pandas.tools.plotting import scatter_matrix", "_____no_output_____" ], [ "_ = scatter_matrix(df.drop('PassengerId', axis=1), figsize=(10, 10))", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ] ]

cb2e2ce4ace99b9c067d4eb068de64acddd04d4b

37,499

ipynb

Jupyter Notebook

Untitled2.ipynb

bad-wolf69/NetTruder

ad7bd30bcb984548aa6f3898edb5930735eff4ec

[ "Apache-2.0" ]

null

Untitled2.ipynb

bad-wolf69/NetTruder

ad7bd30bcb984548aa6f3898edb5930735eff4ec

[ "Apache-2.0" ]

null

Untitled2.ipynb

bad-wolf69/NetTruder

ad7bd30bcb984548aa6f3898edb5930735eff4ec

[ "Apache-2.0" ]

null

44.325059

1,413

0.524761

[ [ [ "from datetime import datetime\nimport mysql.connector\nfrom sys import exit\n\nHOST = \"localhost\"\nUSER = \"root\"\nPASSWORD = \"root\"\nDATABASE = \"hotel\"", "_____no_output_____" ], [ "database = mysql.connector.connect(\n host=\"localhost\",\n user=\"noel\",\n password=\"root\",\n auth_plugin='mysql_native_password'\n \n )\n\n\nmycursor = database.cursor()", "_____no_output_____" ], [ "!pip uninstall mysql-connector", "_____no_output_____" ], [ "def get_database():\n try:\n database = mysql.connector.connect(\n host=\"localhost\",\n user=\"noel\",\n password=\"root\",\n database=DATABASE\n )\n cursor = database.cursor(dictionary=True)\n return database, cursor\n except mysql.connector.Error:\n return None, None\n", "_____no_output_____" ], [ "SCREEN_WIDTH = 50", "_____no_output_____" ], [ "def print_center(s):\n x_pos = SCREEN_WIDTH // 2\n print((\" \" * x_pos), s)\n\n\ndef print_bar():\n print(\"=\" * 100)\n\n\ndef print_bar_ln():\n print_bar()\n print()\n\n\ndef input_center(s):\n x_pos = SCREEN_WIDTH // 2\n print((\" \" * x_pos), s, end='')\n return input()", "_____no_output_____" ], [ "ROOMS_TABLE_NAME = \"rooms\"\n", "_____no_output_____" ], [ "class Room:\n def __init__(self):\n self.room_id = 0\n self.room_no = 0\n self.floor = \"\"\n self.beds = \"\"\n self.available = \"\"\n\n def create(self, room_id, room_no, floor, beds, available):\n self.room_id = room_id\n self.room_no = room_no\n self.floor = floor\n self.beds = beds\n self.available = available\n return self\n\n def create_from_record(self, record):\n self.room_id = record['id']\n self.room_no = record['room_no']\n self.floor = record['floor']\n self.beds = record['beds']\n self.available = record['available']\n return self\n\n def print_all(self):\n print(str(self.room_id).ljust(3),\n str(self.room_no).ljust(15),\n self.floor.ljust(15),\n str(self.beds).ljust(15),\n str(self.available).ljust(15))\n\n def print_full(self):\n print_bar()\n print(\"Record #\", self.room_id)\n print(\"Room No: \", self.room_no)\n print(\"Floor: \", self.floor)\n print(\"Beds: \", self.beds)\n print(\"available: \", self.available)\n print_bar()", "_____no_output_____" ], [ "def create_room():\n room_id = None\n room_no = int(input(\"Enter the room no: \"))\n floor = input(\"Enter the floor (Ex. ground, first etc.): \")\n beds = int(input(\"Enter number of beds: \"))\n available = True\n return Room().create(room_id, room_no, floor, beds, available)\n", "_____no_output_____" ], [ "def print_room_header():\n print(\"=\"*100)\n print(\"id\".ljust(3),\n \"room no\".ljust(15),\n \"floor\".ljust(15),\n \"beds\".ljust(15),\n \"available\".ljust(15)\n )\n print(\"=\"*100)", "_____no_output_____" ], [ "def create_rooms_table(database):\n cursor = database.cursor()\n cursor.execute(\"DROP table if exists {0}\".format(ROOMS_TABLE_NAME))\n cursor.execute(\"create table {0} (\"\n \"id int primary key auto_increment,\"\n \"room_no int,\"\n \"floor varchar(50),\"\n \"beds int,\"\n \"available bool)\".format(ROOMS_TABLE_NAME))", "_____no_output_____" ], [ "def add_room(database, cursor):\n room = create_room()\n query = \"insert into {0}(room_no,floor,beds,available) values({1},'{2}',{3},{4})\".\\\n format(ROOMS_TABLE_NAME, room.room_no, room.floor, room.beds, room.available)\n try:\n cursor.execute(query)\n database.commit()\n except mysql.connector.Error as err:\n create_rooms_table(database)\n cursor.execute(query)\n database.commit()\n print(\"Operation Successful\")\n", "_____no_output_____" ], [ "def show_room_record(cursor, query):\n try:\n cursor.execute(query)\n records = cursor.fetchall()\n if cursor.rowcount == 0:\n print(\"No Matching Records\")\n return\n record = records[0]\n room = Room().create_from_record(record)\n room.print_full()\n return room\n except mysql.connector.Error as err:\n print(err)", "_____no_output_____" ], [ "def show_room_records(cursor, query):\n try:\n cursor.execute(query)\n records = cursor.fetchall()\n if cursor.rowcount == 0:\n print(\"No Matching Records\")\n return\n print_room_header()\n for record in records:\n room = Room().create_from_record(record)\n room.print_all()\n return records\n except mysql.connector.Error as err:\n print(err)", "_____no_output_____" ], [ "def get_and_print_room_by_no(cursor):\n room_no = int(input(\"Enter the room no: \"))\n query = \"select * from {0} where room_no={1}\".format(ROOMS_TABLE_NAME, room_no)\n room = show_room_record(cursor, query)\n return room\n", "_____no_output_____" ], [ "def edit_room_by_room_no(database, cursor):\n room = get_and_print_room_by_no(cursor)\n if room is not None:\n query = \"update {0} set\".format(ROOMS_TABLE_NAME)\n print(\"Input new values (leave blank to keep previous value)\")\n room_no = input(\"Enter new room no: \")\n if len(room_no) > 0:\n query += \" room_no={0},\".format(room_no)\n floor = input(\"Enter new floor: \")\n if len(floor) > 0:\n query += \" floor='{0}',\".format(floor)\n beds = input(\"Enter number of beds: \")\n if len(beds) > 0:\n query += \" beds={0},\".format(beds)\n query = query[0:-1] + \" where id={0}\".format(room.room_id)\n confirm = input(\"Confirm Update (Y/N): \").lower()\n if confirm == 'y':\n cursor.execute(query)\n database.commit()\n print(\"Operation Successful\")\n else:\n print(\"Operation Cancelled\")\n\n", "_____no_output_____" ], [ "def change_room_status(database, cursor, room_id, available):\n query = \"update {0} set available={1} where id={2}\".format(ROOMS_TABLE_NAME, available, room_id)\n cursor.execute(query)\n database.commit()\n", "_____no_output_____" ], [ "def delete_room_by_room_no(database, cursor):\n room = get_and_print_room_by_no(cursor)\n if room is not None:\n confirm = input(\"Confirm Deletion (Y/N): \").lower()\n if confirm == 'y':\n query = \"delete from {0} where id={1}\".format(ROOMS_TABLE_NAME, room.room_id)\n cursor.execute(query)\n database.commit()\n print(\"Operation Successful\")\n else:\n print(\"Operation Cancelled\")\n", "_____no_output_____" ], [ "def room_menu(database, cursor):\n while True:\n print()\n print(\"============================\")\n print(\"==========Room Menu=========\")\n print(\"============================\")\n print()\n\n print(\"1. Add new room\")\n print(\"2. Get room details by room no\")\n print(\"3. Find available rooms by number of beds\")\n print(\"4. Edit Room details\")\n print(\"5. Delete room\")\n print(\"6. View all rooms\")\n print(\"0. Go Back\")\n choice = int(input(\"Enter your choice: \"))\n if choice == 1:\n add_room(database, cursor)\n elif choice == 2:\n room_no = int(input(\"Enter the room no: \"))\n query = \"select * from {0} where room_no={1}\".format(ROOMS_TABLE_NAME, room_no)\n show_room_records(cursor, query)\n elif choice == 3:\n beds = int(input(\"Enter number of beds required: \"))\n query = \"select * from {0} where beds={1}\".format(ROOMS_TABLE_NAME, beds)\n show_room_records(cursor, query)\n elif choice == 4:\n edit_room_by_room_no(database, cursor)\n elif choice == 5:\n delete_room_by_room_no(database, cursor)\n elif choice == 6:\n query = \"select * from {0}\".format(ROOMS_TABLE_NAME)\n show_room_records(cursor, query)\n elif choice == 0:\n break\n else:\n print(\"Invalid choice (Press 0 to go back)\")\n", "_____no_output_____" ], [ "CUSTOMER_TABLE_NAME = \"customers\"", "_____no_output_____" ], [ "class Customer:\n def __init__(self):\n self.customer_id = 0\n self.name = \"\"\n self.address = \"\"\n self.phone = \"\"\n self.room_no = \"0\"\n self.entry_date = \"\"\n self.checkout_date = \"\"\n\n def create(self, customer_id, name, address, phone, room_no, entry_date, checkout_date):\n self.customer_id = customer_id\n self.name = name\n self.address = address\n self.phone = phone\n self.room_no = room_no\n self.entry_date = entry_date\n self.checkout_date = checkout_date\n return self\n\n def create_from_record(self, record):\n self.customer_id = record['id']\n self.name = record['name']\n self.address = record['address']\n self.phone = record['phone']\n self.room_no = record['room_no']\n self.entry_date = record['entry']\n self.checkout_date = record['checkout']\n return self\n\n def print_all(self):\n print(str(self.customer_id).ljust(3),\n self.name[0:15].ljust(15),\n self.address[0:15].ljust(15),\n self.phone.ljust(15),\n str(self.room_no).ljust(10),\n self.entry_date.strftime(\"%d-%b-%y\").ljust(15),\n (self.checkout_date.strftime(\"%d %b %y\") if self.checkout_date is not None else \"None\").ljust(15))\n\n def print_full(self):\n print_bar()\n print(\"Customer #\", self.customer_id)\n print(\"Name: \", self.name)\n print(\"Address: \", self.address)\n print(\"Phone: \", self.phone)\n print(\"Checked in to room #\", self.room_no, \" on \", self.entry_date.strftime(\"%d %b %y\"))\n print(\"Checkout: \", self.checkout_date.strftime(\"%d %b %y\") if self.checkout_date is not None else None)\n print_bar()\n", "_____no_output_____" ], [ "def create_customer(room_no):\n customer_id = None\n name = input(\"Enter the name: \")\n address = input(\"Enter the address: \")\n phone = input(\"Enter the phone: \")\n entry_date = datetime.now()\n return Customer().create(customer_id, name, address, phone, room_no, entry_date, None)\n", "_____no_output_____" ], [ "def print_customer_header():\n print(\"=\"*100)\n print(\"id\".ljust(3),\n \"name\".ljust(15),\n \"address\".ljust(15),\n \"phone\".ljust(15),\n \"room no\".ljust(10),\n \"entry\".ljust(15),\n \"check out\".ljust(15))\n print(\"=\"*100)", "_____no_output_____" ], [ "def create_customer_table(database):\n cursor = database.cursor()\n cursor.execute(\"DROP table if exists {0}\".format(CUSTOMER_TABLE_NAME))\n cursor.execute(\"create table {0} (\"\n \"id int primary key auto_increment,\"\n \"name varchar(20),\"\n \"address varchar(50),\"\n \"phone varchar(10),\"\n \"room_no int,\"\n \"entry datetime,\"\n \"checkout datetime)\".format(CUSTOMER_TABLE_NAME))\n", "_____no_output_____" ], [ "NUMBER_OF_RECORDS_PER_PAGE = 10\n", "_____no_output_____" ], [ "def add_customer(database, cursor):\n room = get_and_print_room_by_no(cursor)\n if room is not None:\n customer = create_customer(room.room_no)\n confirm = input(\"Complete the operation? (Y/N) \").lower()\n if confirm == 'y':\n query = \"insert into {0}(name, address, phone, room_no, entry) values('{1}','{2}','{3}',{4},'{5}')\". \\\n format(CUSTOMER_TABLE_NAME, customer.name, customer.address, customer.phone,\n customer.room_no, customer.entry_date.strftime(\"%Y-%m-%d %H:%M:%S\"))\n try:\n cursor.execute(query)\n database.commit()\n except mysql.connector.Error:\n create_customer_table(database)\n cursor.execute(query)\n database.commit()\n change_room_status(database, cursor, room.room_id, False)\n print(\"Operation Successful\")\n else:\n print(\"Operation Canceled\")\n", "_____no_output_____" ], [ "def show_customer_records(cursor, query):\n try:\n cursor.execute(query)\n records = cursor.fetchall()\n if cursor.rowcount == 0:\n print(\"No Matching Records\")\n return\n print_customer_header()\n for record in records:\n customer = Customer().create_from_record(record)\n customer.print_all()\n return records\n except mysql.connector.Error as err:\n print(err)\n", "_____no_output_____" ], [ "def show_customer_record(cursor, query):\n try:\n cursor.execute(query)\n records = cursor.fetchall()\n if cursor.rowcount == 0:\n print(\"No Matching Records\")\n return\n record = records[0]\n customer = Customer().create_from_record(record)\n customer.print_full()\n return customer\n except mysql.connector.Error as err:\n print(err)", "_____no_output_____" ], [ "def get_and_print_customer_by_room_no(cursor):\n room = get_and_print_room_by_no(cursor)\n if room is not None:\n query = \"select * from {0} where room_no={1} order by id desc limit 1\".format(CUSTOMER_TABLE_NAME, room.room_no)\n customer = show_customer_record(cursor, query)\n return room, customer\n return None, None\n", "_____no_output_____" ], [ "def check_out(database, cursor):\n room, customer = get_and_print_customer_by_room_no(cursor)\n if room is not None and customer is not None:\n confirm = input(\"Confirm checkout? (Y/N): \")\n if confirm == 'y':\n checkout = datetime.now()\n query = \"update {0} set checkout='{1}' where id={2}\".\\\n format(CUSTOMER_TABLE_NAME, checkout.strftime(\"%Y-%m-%d %H:%M:%S\"), customer.customer_id)\n cursor.execute(query)\n database.commit()\n change_room_status(database, cursor,room.room_id, True)\n print(\"Operation Successful\")\n else:\n print(\"Operation Cancelled\")", "_____no_output_____" ], [ "def edit_customer_by_room_no(database, cursor):\n room, customer = get_and_print_customer_by_room_no(cursor)\n if room is not None and customer is not None:\n query = \"update {0} set\".format(CUSTOMER_TABLE_NAME)\n print(\"Input new values (leave blank to keep previous value)\")\n name = input(\"Enter new name: \")\n if len(name) > 0:\n query += \" name='{0}',\".format(name)\n address = input(\"Enter new address: \")\n if len(address) > 0:\n query += \" address='{0}',\".format(address)\n phone = input(\"Enter number of phone: \")\n if len(phone) > 0:\n query += \" phone='{0}',\".format(phone)\n query = query[0:-1] + \" where id={0}\".format(customer.customer_id)\n confirm = input(\"Confirm Update (Y/N): \").lower()\n if confirm == 'y':\n cursor.execute(query)\n database.commit()\n print(\"Operation Successful\")\n else:\n print(\"Operation Cancelled\")", "_____no_output_____" ], [ "def delete_customer_by_room_no(database, cursor):\n room, customer = get_and_print_customer_by_room_no(cursor)\n if room is not None and customer is not None:\n confirm = input(\"Confirm Deletion (Y/N): \").lower()\n if confirm == 'y':\n query = \"delete from {0} where id={1}\".format(CUSTOMER_TABLE_NAME, customer.customer_id)\n cursor.execute(query)\n database.commit()\n print(\"Operation Successful\")\n else:\n print(\"Operation Cancelled\")\n", "_____no_output_____" ], [ "def customer_menu(database, cursor):\n while True:\n print()\n print(\"==============================\")\n print(\"==========Customer Menu=========\")\n print(\"==============================\")\n print()\n print(\"1. New Customer\")\n print(\"2. Show Customer Details by name\")\n print(\"3. Show customer details by customer_id\")\n print(\"4. Show customer details by address\")\n print(\"5. Show customer details by phone number\")\n print(\"6. Show customer details by room no\")\n print(\"7. Show customer details by check in date\")\n print(\"8. Show current list of customers\")\n print(\"9. Check out\")\n print(\"10. Edit customer Details\")\n print(\"11. Delete Customer record\")\n print(\"12. View all customers\")\n print(\"0. Go Back\")\n choice = int(input(\"Enter your choice: \"))\n if choice == 1:\n add_customer(database, cursor)\n elif choice == 2:\n name = input(\"Enter the name: \").lower()\n query = \"select * from {0} where name like '%{1}%'\".format(CUSTOMER_TABLE_NAME, name)\n show_customer_records(cursor, query)\n elif choice == 3:\n customer_id = input(\"Enter the customer id: \")\n query = \"select * from {0} where id = {1}\".format(CUSTOMER_TABLE_NAME, customer_id)\n show_customer_record(cursor, query)\n elif choice == 4:\n address = input(\"Enter the address: \").lower()\n query = \"select * from {0} where address like '%{1}%'\".format(CUSTOMER_TABLE_NAME, address)\n show_customer_records(cursor, query)\n elif choice == 5:\n phone = input(\"Enter the phone number: \")\n query = \"select * from {0} where phone like '%{1}%'\".format(CUSTOMER_TABLE_NAME, phone)\n show_customer_records(cursor, query)\n elif choice == 6:\n room_no = input(\"Enter the room_no: \")\n query = \"select * from {0} where room_no = {1}\".format(CUSTOMER_TABLE_NAME, room_no)\n show_customer_record(cursor, query)\n elif choice == 7:\n print(\"Enter the check in date: \")\n day = int(input(\"day of month: \"))\n month = int(input(\"month: \"))\n year = int(input(\"year: \"))\n query = \"select * from {0} where date(entry) = '{1}-{2}-{3}'\".format(CUSTOMER_TABLE_NAME, year, month, day)\n show_customer_records(cursor, query)\n elif choice == 8:\n query = \"select * from {0} where checkout is null\".format(CUSTOMER_TABLE_NAME)\n show_customer_records(cursor, query)\n elif choice == 9:\n check_out(database, cursor)\n elif choice == 10:\n edit_customer_by_room_no(database, cursor)\n elif choice == 11:\n delete_customer_by_room_no(database, cursor)\n elif choice == 12:\n query = \"select * from {0}\".format(CUSTOMER_TABLE_NAME)\n show_customer_records(cursor, query)\n elif choice == 0:\n break\n else:\n print(\"Invalid choice (Press 0 to go back)\")", "_____no_output_____" ], [ "if __name__ == '__main__':\n database, cursor = get_database()\n if database is None:\n print(\"The Database does not exist or not accessible.\")\n exit(1)\n while True:\n print()\n print_center(\"==============================\")\n print_center(\"=====xyz Hotels=====\")\n print_center(\"==============================\")\n print_center(\"1. Manage Rooms\")\n print_center(\"2. Manage Customers\")\n print_center(\"0. Exit\")\n print()\n choice = int(input_center(\"Enter your choice: \"))\n if choice == 1:\n room_menu(database, cursor)\n elif choice == 2:\n customer_menu(database, cursor)\n elif choice == 0:\n break\n else:\n print(\"Invalid choice (Press 0 to exit)\")\n print_center(\"GoodBye\")", "The Database does not exist or not accessible.\n" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2e3a9432d08118738c26024d1ddf565e96a62a

7,031

ipynb

Jupyter Notebook

HW/2/temperature_sensor.ipynb

sulaimanbehzad/Classifying-Images

28794a126ae069a7613ac4e94642d52e592c04f8

[ "MIT" ]

1

2021-02-06T15:14:01.000Z

HW/2/temperature_sensor.ipynb

sulaimanbehzad/Classifying-Images

28794a126ae069a7613ac4e94642d52e592c04f8

[ "MIT" ]

null

HW/2/temperature_sensor.ipynb

sulaimanbehzad/Classifying-Images

28794a126ae069a7613ac4e94642d52e592c04f8

[ "MIT" ]

null

31.671171

748

0.479733

[ [ [ "<a href=\"https://colab.research.google.com/github/sulaimanbehzad/Classifying-Images/blob/main/HW/2/temperature_sensor.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>", "_____no_output_____" ], [ "# Checking temperature status of the sensor", "_____no_output_____" ] ], [ [ "## install the python MQTT library", "_____no_output_____" ], [ "! pip install paho.mqtt", "Collecting paho.mqtt\n\u001b[?25l Downloading https://files.pythonhosted.org/packages/32/d3/6dcb8fd14746fcde6a556f932b5de8bea8fedcb85b3a092e0e986372c0e7/paho-mqtt-1.5.1.tar.gz (101kB)\n\r\u001b[K |███▏ | 10kB 12.3MB/s eta 0:00:01\r\u001b[K |██████▍ | 20kB 5.0MB/s eta 0:00:01\r\u001b[K |█████████▋ | 30kB 3.9MB/s eta 0:00:01\r\u001b[K |████████████▉ | 40kB 1.7MB/s eta 0:00:01\r\u001b[K |████████████████ | 51kB 2.0MB/s eta 0:00:01\r\u001b[K |███████████████████▎ | 61kB 2.2MB/s eta 0:00:01\r\u001b[K |██████████████████████▌ | 71kB 2.3MB/s eta 0:00:01\r\u001b[K |█████████████████████████▊ | 81kB 2.5MB/s eta 0:00:01\r\u001b[K |█████████████████████████████ | 92kB 2.7MB/s eta 0:00:01\r\u001b[K |████████████████████████████████| 102kB 2.3MB/s \n\u001b[?25hBuilding wheels for collected packages: paho.mqtt\n Building wheel for paho.mqtt (setup.py) ... \u001b[?25l\u001b[?25hdone\n Created wheel for paho.mqtt: filename=paho_mqtt-1.5.1-cp37-none-any.whl size=61565 sha256=5e5ebe418d6a3628a1ba67184b1a050de0903a38dd670d1515dc85ad05c6e887\n Stored in directory: /root/.cache/pip/wheels/75/e2/f5/78942b19b4d135605e58dfe85fba52253b14d636aabf76904b\nSuccessfully built paho.mqtt\nInstalling collected packages: paho.mqtt\nSuccessfully installed paho.mqtt\n" ], [ "pip --version", "pip 19.3.1 from /usr/local/lib/python3.7/dist-packages/pip (python 3.7)\n" ] ], [ [ "## Import the libraries needed ", "_____no_output_____" ] ], [ [ "import paho.mqtt.client as mqtt\nimport paho.mqtt.subscribe as subscribe\nimport time\nimport requests", "_____no_output_____" ], [ "def telegram_bot_sendtext(bot_message):\n bot_token = '1861332067:AAFxb0opR3GSSMBW2U-4YqJoz0JmjpxAlQI'\n bot_chatID = '409409462' #must be updated\n send_text = 'https://api.telegram.org/bot' + bot_token + '/sendMessage?chat_id=' + bot_chatID + '&parse_mode=Markdown&text=' + bot_message\n response = requests.get(send_text)\n return response.json()\n\n", "_____no_output_____" ], [ "def check_payload(payload):\n if payload >=35:\n telegram_bot_sendtext(\"Room temperature exceeds 35 celcius degress\")\n elif payload <= 5:\n telegram_bot_sendtext(\"Room temperature dropped lower than 5 celcius degress\")\n\n", "_____no_output_____" ], [ "def on_message(client, userdata, message):\n payload = int(message.payload.decode(\"utf-8\")) \n payload = 40\n topic = str(message.topic)\n check_payload(payload)\n print(\"%s : %d\" % (topic, payload))\n print(\"message qos=\",message.qos)\n print(\"message retain flag=\",message.retain)", "_____no_output_____" ], [ "def on_log(client, userdata, level, buf):\n print(\"log: \",buf)", "_____no_output_____" ], [ "subscribe.callback(on_message, \"iot9902/temp\", hostname=\"broker.hivemq.com\")", "iot9902/temp : 40\nmessage qos= 0\nmessage retain flag= 0\niot9902/temp : 40\nmessage qos= 0\nmessage retain flag= 0\n" ] ] ]

[ "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ] ]

cb2e3b7d3ee27f9c8482f463fe71ef93a93479a1

2,145

ipynb

Jupyter Notebook

hpc/openacc/English/openacc_start.ipynb

Anish-Saxena/gpubootcamp

469ed5ed1fbfdaee780cec90e2fb59e5bba089b5

[ "Apache-2.0" ]

1

2022-02-20T12:33:03.000Z

hpc/openacc/English/openacc_start.ipynb

hiter-joe/gpubootcamp

bc358e6af3a06f5f554ec93cbf402da82c56e93d

[ "Apache-2.0" ]

null

hpc/openacc/English/openacc_start.ipynb

hiter-joe/gpubootcamp

bc358e6af3a06f5f554ec93cbf402da82c56e93d

[ "Apache-2.0" ]

1

2021-03-02T17:24:29.000Z

30.211268

157

0.586946

[ [ [ "## Introduction to OpenACC Tutorial\n\n### Learning Objectives\n\nLearn how to program GPUs with OpenACC though hands on experience.\n\n### Tutorial Outline\n- Lab 1: Introduction to OpenACC ([Lab 1](./Lab1.ipynb))\n - What is OpenACC and Why Should You Care?\n - Profile-driven Development\n - First Steps with OpenACC\n - Introduction to Parallel directive\n - How to compile a serial application with PGI compiler\n- Lab 2: OpenACC Data Management ([Lab 2](./Lab2.ipynb))\n * OpenACC Data Management\n * OpenACC data directive/clauses\n * OpenACC update directive\n- Lab 3 : Loop Optimizations with OpenACC ([Lab 3](./Lab3.ipynb))\n * Collapse clause\n * Tile clause\n * Gang Worker Vector\n\n\n### Tutorial Duration\nThe lab material will be presented in a 3hr session. Link to material is available for download at the end of the lab.\n\n### Content Level\nBeginner, Intermediate\n\n### Target Audience and Prerequisites\nThe target audience for this lab is researchers/graduate students and developers who are interested in learning about programming GPUs with OpenACC.\n\nProgramming experience with C/C++ or Fortran is desirable.\n\n--- \n\n## Licensing \n\nThis material is released by NVIDIA Corporation under the Creative Commons Attribution 4.0 International (CC BY 4.0). ", "_____no_output_____" ] ] ]

[ "markdown" ]

[ [ "markdown" ] ]

cb2e3bcfebfd37a7613ee3f8fe3228cc06db1444

59,485

ipynb

Jupyter Notebook

examples/notebooks/Macaulay_resultant.ipynb

Michal-Gagala/sympy

3cc756c2af73b5506102abaeefd1b654e286e2c8

[ "MIT" ]

null

examples/notebooks/Macaulay_resultant.ipynb

Michal-Gagala/sympy

3cc756c2af73b5506102abaeefd1b654e286e2c8

[ "MIT" ]

null

examples/notebooks/Macaulay_resultant.ipynb

Michal-Gagala/sympy

3cc756c2af73b5506102abaeefd1b654e286e2c8

[ "MIT" ]

null

78.892573

14,917

0.752593

[ [ [ "import sympy as sym\nfrom sympy.polys.multivariate_resultants import MacaulayResultant\n\nsym.init_printing()", "_____no_output_____" ] ], [ [ "Macaulay Resultant\n------------------", "_____no_output_____" ], [ "The Macauly resultant is a multivariate resultant. It is used for calculating the resultant of $n$ polynomials\nin $n$ variables. The Macaulay resultant is calculated as the determinant of two matrices,\n\n$$R = \\frac{\\text{det}(A)}{\\text{det}(M)}.$$", "_____no_output_____" ], [ "Matrix $A$\n-----------", "_____no_output_____" ], [ "There are a number of steps needed to construct matrix $A$. Let us consider an example from https://dl.acm.org/citation.cfm?id=550525 to \nshow the construction.", "_____no_output_____" ] ], [ [ "x, y, z = sym.symbols('x, y, z')", "_____no_output_____" ], [ "a_1_1, a_1_2, a_1_3, a_2_2, a_2_3, a_3_3 = sym.symbols('a_1_1, a_1_2, a_1_3, a_2_2, a_2_3, a_3_3')\nb_1_1, b_1_2, b_1_3, b_2_2, b_2_3, b_3_3 = sym.symbols('b_1_1, b_1_2, b_1_3, b_2_2, b_2_3, b_3_3')\nc_1, c_2, c_3 = sym.symbols('c_1, c_2, c_3')", "_____no_output_____" ], [ "variables = [x, y, z]", "_____no_output_____" ], [ "f_1 = a_1_1 * x ** 2 + a_1_2 * x * y + a_1_3 * x * z + a_2_2 * y ** 2 + a_2_3 * y * z + a_3_3 * z ** 2", "_____no_output_____" ], [ "f_2 = b_1_1 * x ** 2 + b_1_2 * x * y + b_1_3 * x * z + b_2_2 * y ** 2 + b_2_3 * y * z + b_3_3 * z ** 2", "_____no_output_____" ], [ "f_3 = c_1 * x + c_2 * y + c_3 * z", "_____no_output_____" ], [ "polynomials = [f_1, f_2, f_3]\nmac = MacaulayResultant(polynomials, variables)", "_____no_output_____" ] ], [ [ "**Step 1** Calculated $d_i$ for $i \\in n$. ", "_____no_output_____" ] ], [ [ "mac.degrees", "_____no_output_____" ] ], [ [ "**Step 2.** Get $d_M$.", "_____no_output_____" ] ], [ [ "mac.degree_m", "_____no_output_____" ] ], [ [ "**Step 3.** All monomials of degree $d_M$ and size of set.", "_____no_output_____" ] ], [ [ "mac.get_monomials_set()", "_____no_output_____" ], [ "mac.monomial_set", "_____no_output_____" ], [ "mac.monomials_size", "_____no_output_____" ] ], [ [ "These are the columns of matrix $A$.", "_____no_output_____" ], [ "**Step 4** Get rows and fill matrix.", "_____no_output_____" ] ], [ [ "mac.get_row_coefficients()", "_____no_output_____" ] ], [ [ "Each list is being multiplied by polynomials $f_1$, $f_2$ and $f_3$ equivalently. Then we fill the matrix\nbased on the coefficient of the monomials in the columns.", "_____no_output_____" ] ], [ [ "matrix = mac.get_matrix()\nmatrix", "_____no_output_____" ] ], [ [ "Matrix $M$\n-----------", "_____no_output_____" ], [ "Columns that are non reduced are kept. The rows which contain one if the $a_i$s is dropoed.\n$a_i$s are the coefficients of $x_i ^ {d_i}$.", "_____no_output_____" ] ], [ [ "mac.get_submatrix(matrix)", "_____no_output_____" ] ], [ [ "Second example\n-----------------\nThis is from: http://isc.tamu.edu/resources/preprints/1996/1996-02.pdf", "_____no_output_____" ] ], [ [ "x, y, z = sym.symbols('x, y, z')", "_____no_output_____" ], [ "a_0, a_1, a_2 = sym.symbols('a_0, a_1, a_2')\nb_0, b_1, b_2 = sym.symbols('b_0, b_1, b_2')\nc_0, c_1, c_2,c_3, c_4 = sym.symbols('c_0, c_1, c_2, c_3, c_4')", "_____no_output_____" ], [ "f = a_0 * y - a_1 * x + a_2 * z\ng = b_1 * x ** 2 + b_0 * y ** 2 - b_2 * z ** 2\nh = c_0 * y - c_1 * x ** 3 + c_2 * x ** 2 * z - c_3 * x * z ** 2 + c_4 * z ** 3", "_____no_output_____" ], [ "polynomials = [f, g, h]", "_____no_output_____" ], [ "mac = MacaulayResultant(polynomials, variables=[x, y, z])", "_____no_output_____" ], [ "mac.degrees", "_____no_output_____" ], [ "mac.degree_m", "_____no_output_____" ], [ "mac.get_monomials_set()", "_____no_output_____" ], [ "mac.get_size()", "_____no_output_____" ], [ "mac.monomial_set", "_____no_output_____" ], [ "mac.get_row_coefficients()", "_____no_output_____" ], [ "matrix = mac.get_matrix()\nmatrix", "_____no_output_____" ], [ "matrix.shape", "_____no_output_____" ], [ "mac.get_submatrix(mac.get_matrix())", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2e3f663ddbaeab3d6b7fe0d130b567f40d2726

5,272

ipynb

Jupyter Notebook

_posts/pandas/insets/insets.ipynb

bmb804/documentation

57826d25e0afea7fff6a8da9abab8be2f7a4b48c

[ "CC-BY-3.0" ]

2

2019-06-24T23:55:53.000Z

2019-07-08T12:22:56.000Z

_posts/pandas/insets/insets.ipynb

bmb804/documentation

57826d25e0afea7fff6a8da9abab8be2f7a4b48c

[ "CC-BY-3.0" ]

15

2020-06-30T21:21:30.000Z

2021-08-02T21:16:33.000Z

_posts/pandas/insets/insets.ipynb

bmb804/documentation

57826d25e0afea7fff6a8da9abab8be2f7a4b48c

[ "CC-BY-3.0" ]

1

2019-11-10T04:01:48.000Z

29.954545

210

0.556715

[ [ [ "### Simple Inset Graph", "_____no_output_____" ] ], [ [ "import plotly.plotly as py\nimport plotly.graph_objs as go\n\ntrace1 = go.Scatter(\n x=[1, 2, 3],\n y=[4, 3, 2]\n)\ntrace2 = go.Scatter(\n x=[20, 30, 40],\n y=[30, 40, 50],\n xaxis='x2',\n yaxis='y2'\n)\ndata = [trace1, trace2]\nlayout = go.Layout(\n xaxis2=dict(\n domain=[0.6, 0.95],\n anchor='y2'\n ),\n yaxis2=dict(\n domain=[0.6, 0.95],\n anchor='x2'\n )\n)\nfig = go.Figure(data=data, layout=layout)\npy.iplot(fig, filename='simple-inset')", "_____no_output_____" ] ], [ [ "##### See more examples of [insets with Plotly's native Python syntax](https://plot.ly/python/insets/)", "_____no_output_____" ] ], [ [ "from IPython.display import display, HTML\n\ndisplay(HTML('<link href=\"//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700\" rel=\"stylesheet\" type=\"text/css\" />'))\ndisplay(HTML('<link rel=\"stylesheet\" type=\"text/css\" href=\"http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css\">'))\n\n! pip install git+https://github.com/plotly/publisher.git --upgrade\nimport publisher\npublisher.publish(\n 'insets.ipynb', 'pandas/insets/', 'Inset Plots | plotly',\n 'How to create inset plots with Pandas in Plotly.', \n title = \"Inset Plots | plotly\",\n name = \"Inset Plots\",\n has_thumbnail='true', thumbnail='thumbnail/insets.jpg', \n language='pandas', page_type='example_index',\n display_as='multiple_axes', order=3)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2e3fb4b714e98e3bb9899a22abb6c39dd6f55c

850,367

ipynb

Jupyter Notebook

source/examples/cookbook/map_california_housing.ipynb

JetBrains/lets-plot-docs

73583bce5308d34b341d9f8a7249ccb34a95f504

[ "MIT" ]

2

2021-06-02T10:24:24.000Z

2021-11-08T09:50:22.000Z

source/examples/cookbook/map_california_housing.ipynb

JetBrains/lets-plot-docs

73583bce5308d34b341d9f8a7249ccb34a95f504

[ "MIT" ]

13

2021-05-25T19:49:50.000Z

2022-03-22T12:30:29.000Z

source/examples/cookbook/map_california_housing.ipynb

JetBrains/lets-plot-docs

73583bce5308d34b341d9f8a7249ccb34a95f504

[ "MIT" ]

4

2021-01-19T12:26:21.000Z

2022-03-19T07:47:52.000Z

1,117.43364

246,523

0.748474

[ [ [ "# Visulizing spatial information - California Housing\n\nThis demo shows a simple workflow when working with geospatial data:\n\n * Obtaining a dataset which includes geospatial references.\n * Obtaining a desired geometries (boundaries etc.)\n * Visualisation \n \nIn this example we will make a simple **proportional symbols map** using the `California Housing` dataset in `sklearn` package.", "_____no_output_____" ] ], [ [ "import numpy as np\nimport pandas as pd\nimport geopandas as gpd\nfrom lets_plot import *\n\nLetsPlot.setup_html()", "_____no_output_____" ] ], [ [ "## Prepare the dataset", "_____no_output_____" ] ], [ [ "from sklearn.datasets import fetch_california_housing\n\ncalifornia_housing_bunch = fetch_california_housing()\ndata = pd.DataFrame(california_housing_bunch.data, columns=california_housing_bunch.feature_names)\n\n# Add $-value field to the dataframe.\n# dataset.target: numpy array of shape (20640,)\n# Each value corresponds to the average house value in units of 100,000.\ndata['Value($)'] = california_housing_bunch.target * 100000\ndata.head()", "_____no_output_____" ], [ "# Draw a random sample from the data set.\ndata = data.sample(n=1000)", "_____no_output_____" ] ], [ [ "## Static map\n\nLet's create a static map using regular `ggplot2` geometries.\n\nVarious shape files related to the state of California are available at https://data.ca.gov web site.\n\nFor the purpose of this demo the Calofornia State Boundaty zip was downloaded from \nhttps://data.ca.gov/dataset/ca-geographic-boundaries and unpacked to `ca-state-boundary` subdirectory.", "_____no_output_____" ], [ "### Use `geopandas` to read a shape file to GeoDataFrame", "_____no_output_____" ] ], [ [ "#CA = gpd.read_file(\"./ca-state-boundary/CA_State_TIGER2016.shp\")\n\nfrom lets_plot.geo_data import *\n\nCA = geocode_states('CA').scope('US').inc_res(2).get_boundaries()\nCA.head()", "The geodata is provided by © OpenStreetMap contributors and is made available here under the Open Database License (ODbL).\n" ] ], [ [ "Keeping in mind that our target is the housing value, fill the choropleth over the state contours using `geom_map()`function", "_____no_output_____" ], [ "### Make a plot out of polygon and points\n\nThe color of the points will reflect the house age and\nthe size of the points will reflect the value of the house.", "_____no_output_____" ] ], [ [ "# The plot base \np = ggplot() + scale_color_gradient(name='House Age', low='red', high='green')\n\n# The points layer\npoints = geom_point(aes(x='Longitude',\n y='Latitude',\n size='Value($)',\n color='HouseAge'), \n data=data,\n alpha=0.8)\n\n# The map\np + geom_polygon(data=CA, fill='#F8F4F0', color='#B71234')\\\n + points\\\n + theme_classic() + theme(axis='blank')\\\n + ggsize(600, 500)", "_____no_output_____" ] ], [ [ "## Interactive map\n\nThe `geom_livemap()` function creates an interactive base-map super-layer to which other geometry layers are added.", "_____no_output_____" ], [ "### Configuring map tiles\n\nBy default *Lets-PLot* offers high quality vector map tiles but also can fetch raster tiles from a 3d-party Z-X-Y [tile servers](https://wiki.openstreetmap.org/wiki/Tile_servers).\n\nFor the sake of the demo lets use *CARTO Antique* tiles by [CARTO](https://carto.com/attribution/) as our basemap.", "_____no_output_____" ] ], [ [ "LetsPlot.set(\n maptiles_zxy(\n url='https://cartocdn_c.global.ssl.fastly.net/base-antique/{z}/{x}/{y}@2x.png',\n attribution='<a href=\"https://www.openstreetmap.org/copyright\">© OpenStreetMap contributors</a> <a href=\"https://carto.com/attributions#basemaps\">© CARTO</a>, <a href=\"https://carto.com/attributions\">© CARTO</a>'\n )\n)", "_____no_output_____" ] ], [ [ "### Make a plot similar to the one above but interactive", "_____no_output_____" ] ], [ [ "p + geom_livemap()\\\n + geom_polygon(data=CA, fill='white', color='#B71234', alpha=0.5)\\\n + points", "_____no_output_____" ] ], [ [ "### Adjust the initial viewport\n\nUse parameters `location` and `zoom` to define the initial viewport.", "_____no_output_____" ] ], [ [ "# Pass `[lon,lat]` value to the `location` (near Los Angeles)\np + geom_livemap(location=[-118.15, 33.96], zoom=7)\\\n + geom_polygon(data=CA, fill='white', color='#B71234', alpha=0.5, size=1)\\\n + points", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2e44068476ef5e6870feee80b351436bc51dea

17,236

ipynb

Jupyter Notebook

model/pairwise_similarity.ipynb

byukan/movie-rec

1ad6cc7fd7fae1b45790cdd30c28c753fb314cf2

[ "BSD-3-Clause" ]

1

2022-02-16T03:22:33.000Z

model/pairwise_similarity.ipynb

byukan/movie-rec

1ad6cc7fd7fae1b45790cdd30c28c753fb314cf2

[ "BSD-3-Clause" ]

null

model/pairwise_similarity.ipynb

byukan/movie-rec

1ad6cc7fd7fae1b45790cdd30c28c753fb314cf2

[ "BSD-3-Clause" ]

null

42.039024

259

0.51288

[ [ [ "# Calculating Similarity\n\ncreate some transformer embedded vectors, then use a cosine similarity", "_____no_output_____" ] ], [ [ "# # imdb_top_10 = pd.read_csv('../data/imdb_top_1000.csv').head(10)\n\n# # p.dump(imdb_top_10, open('imdb_top_10.p', 'wb'))\n\n# # df = p.load(open('/Users/b/movie-rec/model/imdb_top_10.p', 'rb'))\n\n# sentences = df['Overview']\n# [x for x, y in h.compute_similarity(0, sentences)]", "_____no_output_____" ], [ "import h\nimport pandas as pd\npd.set_option('display.max_colwidth', None)\n# use movies dataset\ndf = pd.read_csv('../data/imdb_top_1000.csv').head(10)\ndf['title_overview'] = df['Series_Title'] + ' ' + df['Overview']\ndf[['Series_Title', 'Overview']].head(10)", "_____no_output_____" ], [ "h.compute_similarity(0, sentences)", "_____no_output_____" ], [ "sentences = df['Overview']\nh.compute_similarity(0, sentences)\n\ndf['similar_movies'] = pd.Series(df.index).apply(lambda x: h.compute_similarity(x, df['Overview']))\ndf['similar_movies']", "_____no_output_____" ], [ "sentence_embeddings = h.sentence_transformer_similarity(df['title_overview'])\nsentence_embeddings", "_____no_output_____" ], [ "from sklearn.metrics.pairwise import cosine_similarity\ndef list_similarity_scores(main_index, embeddings):\n similarity_scores = cosine_similarity(\n [sentence_embeddings[main_index]],\n sentence_embeddings)\n ranked_list = sorted([(i, x) for i, x in enumerate(similarity_scores[0])], key=lambda x: x[1], reverse=True)\n return ranked_list[:10]", "_____no_output_____" ], [ "df['similarity_scores'] = pd.Series(df.index).apply(lambda x: list_similarity_scores(x, df['Overview']))\ndf['similarity_scores'][0]", "_____no_output_____" ], [ "df['similar_movies'] = pd.Series(df.index).apply(lambda y: [(df['Series_Title'][int(x)], df['Overview'][int(x)]) for x in [x[0] for x in df['similarity_scores'][y]]])\ndf['similar_movies'][0]", "_____no_output_____" ], [ "df[['similar_movies', 'similarity_scores', 'Series_Title',\n 'Released_Year',\n 'Certificate',\n 'Runtime',\n 'Genre',\n 'IMDB_Rating',\n 'Overview',\n 'Meta_score',\n 'Director',\n 'Star1',\n 'Star2',\n 'Star3',\n 'Star4',\n 'No_of_Votes',\n 'Gross',\n 'Poster_Link']].to_csv('similar_movies_df.csv')", "_____no_output_____" ] ] ]

[ "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2e459cd2d4e23cc7473be96cc8b27076aa3af6

3,421

ipynb

Jupyter Notebook

notebooks/sts/evaluate-sts-performance-on-bootstraps.ipynb

mit-ccrg/ml4c3-mirror

ea23e26eeb9814bb057f2c86c62c923dd347aa95

[ "BSD-3-Clause" ]

null

notebooks/sts/evaluate-sts-performance-on-bootstraps.ipynb

mit-ccrg/ml4c3-mirror

ea23e26eeb9814bb057f2c86c62c923dd347aa95

[ "BSD-3-Clause" ]

null

notebooks/sts/evaluate-sts-performance-on-bootstraps.ipynb

mit-ccrg/ml4c3-mirror

ea23e26eeb9814bb057f2c86c62c923dd347aa95

[ "BSD-3-Clause" ]

null

24.262411

141

0.505992

[ [ [ "# Calculate AUCs for bootstraps using STS model scores", "_____no_output_____" ] ], [ [ "import os\nimport numpy as np\nimport pandas as pd\nfrom sklearn.metrics import roc_auc_score", "_____no_output_____" ] ], [ [ "## Load y and y_hat for entire STS DataFrame", "_____no_output_____" ] ], [ [ "root = os.path.expanduser(\"~/dropbox/sts-data\")\nfpath = os.path.join(root, \"sts-mgh.csv\")\ndf = pd.read_csv(fpath, low_memory=False)", "_____no_output_____" ] ], [ [ "## Iterate over bootstrap test sets", "_____no_output_____" ] ], [ [ "path_to_bootstraps = os.path.expanduser(\"~/dropbox/sts-data\")\ncohorts = [\n# \"cabg\",\n# \"valve\",\n# \"cabg-valve\",\n \"major\",\n# \"other\",\n# \"all-elective\",\n \"major-elective\",\n# \"other-elective\",\n]", "_____no_output_____" ], [ "aucs = {}\nfor cohort in cohorts:\n aucs[cohort] = []\n for bootstrap in range(10):\n fpath = os.path.join(path_to_bootstraps, f\"bootstraps-ecg-{cohort}\", str(bootstrap), \"test.csv\")\n test = pd.read_csv(fpath, low_memory=False, usecols=[\"mrn\", \"death\", \"predmort\"])\n\n y = test.death.to_numpy()\n y_hat = test.predmort.to_numpy()\n n_tot = len(y)\n\n n_scores = sum(~np.isnan(y_hat))\n frac_scores = n_scores / len(y) * 100\n\n not_nan = ~np.isnan(y_hat)\n y = y[not_nan]\n y_hat = y_hat[not_nan]\n\n auc = roc_auc_score(y_true=y, y_score=y_hat)\n aucs[cohort].append(auc)\n\n print(f\"{cohort}: bootstrap {bootstrap+1}, {n_scores}/{n_tot} patients have STS scores ({frac_scores:.1f}%), AUC={auc:0.3f}\")", "_____no_output_____" ], [ "df_aucs = pd.DataFrame(aucs)\ndf_aucs.index.name = \"bootstrap\"\ndf_aucs", "_____no_output_____" ], [ "fpath = os.path.expanduser(\"~/dropbox/sts-net/figures-and-tables/sts.csv\")\ndf_aucs.to_csv(fpath)\nprint(f\"Saved AUCs of STS risk score predictions to {fpath}\")", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ] ]

cb2e48511a8cb609cb6bcf1ae46a657dd80ed960

31,108

ipynb

Jupyter Notebook

docs/sphinx/source/use_cases/qa/semantic-retrieval-for-question-answering-applications.ipynb

vespa-engine/pyvespa

86f5dbe346d922c21ad2f45ca86ba04f86e343bc

[ "Apache-2.0" ]

18

2020-11-27T09:30:10.000Z

2022-03-27T14:07:01.000Z

docs/sphinx/source/use_cases/qa/semantic-retrieval-for-question-answering-applications.ipynb

vespa-engine/pyvespa

86f5dbe346d922c21ad2f45ca86ba04f86e343bc

[ "Apache-2.0" ]

49

2020-10-02T07:35:33.000Z

2022-03-29T13:39:34.000Z

docs/sphinx/source/use_cases/qa/semantic-retrieval-for-question-answering-applications.ipynb

vespa-engine/pyvespa

86f5dbe346d922c21ad2f45ca86ba04f86e343bc

[ "Apache-2.0" ]

3

2021-02-16T22:22:28.000Z

2021-05-24T13:57:49.000Z

33.164179

723

0.557252

[ [ [ "# Build sentence/paragraph level QA application from python with Vespa\n\n> Retrieve paragraph and sentence level information with sparse and dense ranking features", "_____no_output_____" ], [ "We will walk through the steps necessary to create a question answering (QA) application that can retrieve sentence or paragraph level answers based on a combination of semantic and/or term-based search. We start by discussing the dataset used and the question and sentence embeddings generated for semantic search. We then include the steps necessary to create and deploy a Vespa application to serve the answers. We make all the required data available to feed the application and show how to query for sentence and paragraph level answers based on a combination of semantic and term-based search.\n\nThis tutorial is based on [earlier work](https://docs.vespa.ai/en/semantic-qa-retrieval.html) by the Vespa team to reproduce the results of the paper [ReQA: An Evaluation for End-to-End Answer Retrieval Models](https://arxiv.org/abs/1907.04780) by Ahmad Et al. using the Stanford Question Answering Dataset (SQuAD) v1.1 dataset.", "_____no_output_____" ], [ "## About the data", "_____no_output_____" ], [ "We are going to use the Stanford Question Answering Dataset (SQuAD) v1.1 dataset. The data contains paragraphs (denoted here as context), and each paragraph has questions that have answers in the associated paragraph. We have parsed the dataset and organized the data that we will use in this tutorial to make it easier to follow along.", "_____no_output_____" ], [ "### Paragraph", "_____no_output_____" ] ], [ [ "import requests, json\n\ncontext_data = json.loads(\n requests.get(\"https://data.vespa.oath.cloud/blog/qa/sample_context_data.json\").text\n)", "_____no_output_____" ] ], [ [ "Each `context` data point contains a `context_id` that uniquely identifies a paragraph, a `text` field holding the paragraph string, and a `questions` field holding a list of question ids that can be answered from the paragraph text. We also include a `dataset` field to identify the data source if we want to index more than one dataset in our application.", "_____no_output_____" ] ], [ [ "context_data[0]", "_____no_output_____" ] ], [ [ "### Questions", "_____no_output_____" ], [ "According to the data point above, `context_id = 0` can be used to answer the questions with `id = [0, 1, 2, 3, 4]`. We can load the file containing the questions and display those first five questions.", "_____no_output_____" ] ], [ [ "from pandas import read_csv\n\nquestions = read_csv(\n filepath_or_buffer=\"https://data.vespa.oath.cloud/blog/qa/sample_questions.csv\", sep=\"\\t\", \n)", "_____no_output_____" ], [ "questions[[\"question_id\", \"question\"]].head()", "_____no_output_____" ] ], [ [ "### Paragraph sentences", "_____no_output_____" ], [ "To build a more accurate application, we can break the paragraphs down into sentences. For example, the first sentence below comes from the paragraph with `context_id = 0` and can answer the question with `question_id = 4`.", "_____no_output_____" ] ], [ [ "sentence_data = json.loads(\n requests.get(\"https://data.vespa.oath.cloud/blog/qa/sample_sentence_data.json\").text\n)", "_____no_output_____" ], [ "{k:sentence_data[0][k] for k in [\"text\", \"dataset\", \"questions\", \"context_id\"]}", "_____no_output_____" ] ], [ [ "### Embeddings", "_____no_output_____" ], [ "We want to combine semantic (dense) and term-based (sparse) signals to answer the questions sent to our application. We have generated embeddings for both the questions and the sentences to implement the semantic search, each having size equal to 512.", "_____no_output_____" ] ], [ [ "questions[[\"question_id\", \"embedding\"]].head(1)", "_____no_output_____" ], [ "sentence_data[0][\"sentence_embedding\"][\"values\"][0:5] # display the first five elements", "_____no_output_____" ] ], [ [ "Here is [the script](https://github.com/vespa-engine/sample-apps/blob/master/semantic-qa-retrieval/bin/convert-to-vespa-squad.py) containing the code that we used to generate the sentence and questions embeddings. We used [Google's Universal Sentence Encoder](https://tfhub.dev/google/universal-sentence-encoder) at the time but feel free to replace it with embeddings generated by your preferred model.", "_____no_output_____" ], [ "## Create and deploy the application", "_____no_output_____" ], [ "We can now build a sentence-level Question answering application based on the data described above.", "_____no_output_____" ], [ "### Schema to hold context information", "_____no_output_____" ], [ "The `context` schema will have a document containing the four relevant fields described in the data section. We create an index for the `text` field and use `enable-bm25` to pre-compute data required to speed up the use of BM25 for ranking. The `summary` indexing indicates that all the fields will be included in the requested context documents. The `attribute` indexing store the fields in memory as an attribute for sorting, querying, and grouping.", "_____no_output_____" ] ], [ [ "from vespa.package import Document, Field\n\ncontext_document = Document(\n fields=[\n Field(name=\"questions\", type=\"array<int>\", indexing=[\"summary\", \"attribute\"]),\n Field(name=\"dataset\", type=\"string\", indexing=[\"summary\", \"attribute\"]),\n Field(name=\"context_id\", type=\"int\", indexing=[\"summary\", \"attribute\"]), \n Field(name=\"text\", type=\"string\", indexing=[\"summary\", \"index\"], index=\"enable-bm25\"), \n ]\n)", "_____no_output_____" ] ], [ [ "The default fieldset means query tokens will be matched against the `text` field by default. We defined two rank-profiles (`bm25` and `nativeRank`) to illustrate that we can define and experiment with as many rank-profiles as we want. You can create different ones using [the ranking expressions and features](https://docs.vespa.ai/en/ranking-expressions-features.html) available.", "_____no_output_____" ] ], [ [ "from vespa.package import Schema, FieldSet, RankProfile\n\ncontext_schema = Schema(\n name=\"context\",\n document=context_document, \n fieldsets=[FieldSet(name=\"default\", fields=[\"text\"])], \n rank_profiles=[\n RankProfile(name=\"bm25\", inherits=\"default\", first_phase=\"bm25(text)\"), \n RankProfile(name=\"nativeRank\", inherits=\"default\", first_phase=\"nativeRank(text)\")]\n)", "_____no_output_____" ] ], [ [ "### Schema to hold sentence information", "_____no_output_____" ], [ "The document of the `sentence` schema will inherit the fields defined in the `context` document to avoid unnecessary duplication of the same field types. Besides, we add the `sentence_embedding` field defined to hold a one-dimensional tensor of floats of size 512. We will store the field as an attribute in memory and build an ANN `index` using the `HNSW` (hierarchical navigable small world) algorithm. Read [this blog post](https://blog.vespa.ai/approximate-nearest-neighbor-search-in-vespa-part-1/) to know more about Vespa’s journey to implement ANN search and the [documentation](https://docs.vespa.ai/documentation/approximate-nn-hnsw.html) for more information about the HNSW parameters.", "_____no_output_____" ] ], [ [ "from vespa.package import HNSW\n\nsentence_document = Document(\n inherits=\"context\", \n fields=[\n Field(\n name=\"sentence_embedding\", \n type=\"tensor<float>(x[512])\", \n indexing=[\"attribute\", \"index\"], \n ann=HNSW(\n distance_metric=\"euclidean\", \n max_links_per_node=16, \n neighbors_to_explore_at_insert=500\n )\n )\n ]\n)", "_____no_output_____" ] ], [ [ "For the `sentence` schema, we define three rank profiles. The `semantic-similarity` uses the Vespa `closeness` ranking feature, which is defined as `1/(1 + distance)` so that sentences with embeddings closer to the question embedding will be ranked higher than sentences that are far apart. The `bm25` is an example of a term-based rank profile, and `bm25-semantic-similarity` combines both term-based and semantic-based signals as an example of a hybrid approach.", "_____no_output_____" ] ], [ [ "sentence_schema = Schema(\n name=\"sentence\", \n document=sentence_document, \n fieldsets=[FieldSet(name=\"default\", fields=[\"text\"])], \n rank_profiles=[\n RankProfile(\n name=\"semantic-similarity\", \n inherits=\"default\", \n first_phase=\"closeness(sentence_embedding)\"\n ),\n RankProfile(\n name=\"bm25\", \n inherits=\"default\", \n first_phase=\"bm25(text)\"\n ),\n RankProfile(\n name=\"bm25-semantic-similarity\", \n inherits=\"default\", \n first_phase=\"bm25(text) + closeness(sentence_embedding)\"\n )\n ]\n)", "_____no_output_____" ] ], [ [ "### Build the application package", "_____no_output_____" ], [ "We can now define our `qa` application by creating an application package with both the `context_schema` and the `sentence_schema` that we defined above. In addition, we need to inform Vespa that we plan to send a query ranking feature named `query_embedding` with the same type that we used to define the `sentence_embedding` field.", "_____no_output_____" ] ], [ [ "from vespa.package import ApplicationPackage, QueryProfile, QueryProfileType, QueryTypeField\n\napp_package = ApplicationPackage(\n name=\"qa\", \n schema=[context_schema, sentence_schema], \n query_profile=QueryProfile(),\n query_profile_type=QueryProfileType(\n fields=[\n QueryTypeField(\n name=\"ranking.features.query(query_embedding)\", \n type=\"tensor<float>(x[512])\"\n )\n ]\n )\n)", "_____no_output_____" ] ], [ [ "### Deploy the application", "_____no_output_____" ], [ "We can deploy the `app_package` in a Docker container (or to [Vespa Cloud](https://cloud.vespa.ai/)):", "_____no_output_____" ] ], [ [ "import os\nfrom vespa.deployment import VespaDocker\n\ndisk_folder = os.path.join(os.getenv(\"WORK_DIR\"), \"sample_application\")\nvespa_docker = VespaDocker(\n port=8081, \n disk_folder=disk_folder # requires absolute path\n)\napp = vespa_docker.deploy(application_package=app_package)", "Waiting for configuration server.\nWaiting for configuration server.\nWaiting for configuration server.\nWaiting for configuration server.\nWaiting for configuration server.\nWaiting for configuration server.\nWaiting for application status.\nWaiting for application status.\nFinished deployment.\n" ] ], [ [ "## Feed the data", "_____no_output_____" ], [ "Once deployed, we can use the `Vespa` instance `app` to interact with the application. We can start by feeding context and sentence data.", "_____no_output_____" ] ], [ [ "for idx, sentence in enumerate(sentence_data):\n app.feed_data_point(schema=\"sentence\", data_id=idx, fields=sentence)", "_____no_output_____" ], [ "for context in context_data:\n app.feed_data_point(schema=\"context\", data_id=context[\"context_id\"], fields=context)", "_____no_output_____" ] ], [ [ "## Sentence level retrieval", "_____no_output_____" ], [ "The query below sends the first question embedding (`questions.loc[0, \"embedding\"]`) through the `ranking.features.query(query_embedding)` parameter and use the `nearestNeighbor` search operator to retrieve the closest 100 sentences in embedding space using Euclidean distance as configured in the `HNSW` settings. The sentences returned will be ranked by the `semantic-similarity` rank profile defined in the `sentence` schema.", "_____no_output_____" ] ], [ [ "result = app.query(body={\n 'yql': 'select * from sources sentence where ([{\"targetNumHits\":100}]nearestNeighbor(sentence_embedding,query_embedding));',\n 'hits': 100,\n 'ranking.features.query(query_embedding)': questions.loc[0, \"embedding\"],\n 'ranking.profile': 'semantic-similarity' \n})", "_____no_output_____" ], [ "result.hits[0]", "_____no_output_____" ] ], [ [ "## Sentence level hybrid retrieval", "_____no_output_____" ], [ "In addition to sending the query embedding, we can send the question string (`questions.loc[0, \"question\"]`) via the `query` parameter and use the `or` operator to retrieve documents that satisfy either the semantic operator `nearestNeighbor` or the term-based operator `userQuery`. Choosing `type` equal `any` means that the term-based operator will retrieve all the documents that match at least one query token. The retrieved documents will be ranked by the hybrid rank-profile `bm25-semantic-similarity`.", "_____no_output_____" ] ], [ [ "result = app.query(body={\n 'yql': 'select * from sources sentence where ([{\"targetNumHits\":100}]nearestNeighbor(sentence_embedding,query_embedding)) or userQuery();',\n 'query': questions.loc[0, \"question\"],\n 'type': 'any',\n 'hits': 100,\n 'ranking.features.query(query_embedding)': questions.loc[0, \"embedding\"],\n 'ranking.profile': 'bm25-semantic-similarity' \n})", "_____no_output_____" ], [ "result.hits[0]", "_____no_output_____" ] ], [ [ "## Paragraph level retrieval", "_____no_output_____" ], [ "For paragraph-level retrieval, we use Vespa's [grouping](https://docs.vespa.ai/en/grouping.html) feature to retrieve paragraphs instead of sentences. In the sample query below, we group by `context_id` and use the paragraph’s max sentence score to represent the paragraph level score. We limit the number of paragraphs returned by 3, and each paragraph contains at most two sentences. We return all the summary features for each sentence. All those configurations can be changed to fit different use cases.", "_____no_output_____" ] ], [ [ "result = app.query(body={\n 'yql': ('select * from sources sentence where ([{\"targetNumHits\":10000}]nearestNeighbor(sentence_embedding,query_embedding)) |' \n 'all(group(context_id) max(3) order(-max(relevance())) each( max(2) each(output(summary())) as(sentences)) as(paragraphs));'),\n 'hits': 0,\n 'ranking.features.query(query_embedding)': questions.loc[0, \"embedding\"],\n 'ranking.profile': 'bm25-semantic-similarity' \n})", "_____no_output_____" ], [ "paragraphs = result.json[\"root\"][\"children\"][0][\"children\"][0]", "_____no_output_____" ], [ "paragraphs[\"children\"][0] # top-ranked paragraph", "_____no_output_____" ], [ "paragraphs[\"children\"][1] # second-ranked paragraph", "_____no_output_____" ] ], [ [ "### Clean up environment", "_____no_output_____" ] ], [ [ "from shutil import rmtree\n\nrmtree(disk_folder, ignore_errors=True)\nvespa_docker.container.stop()\nvespa_docker.container.remove()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ] ]

cb2e4a5e401145a6fd03a209ed59f82b8e51c6ee

64,273

ipynb

Jupyter Notebook

_docs/nbs/2022-02-01-mlops-optimus.ipynb

sparsh-ai/recohut

4121f665761ffe38c9b6337eaa9293b26bee2376

[ "Apache-2.0" ]

null

_docs/nbs/2022-02-01-mlops-optimus.ipynb

sparsh-ai/recohut

4121f665761ffe38c9b6337eaa9293b26bee2376

[ "Apache-2.0" ]

1

2022-01-12T05:40:57.000Z

_docs/nbs/2022-02-01-mlops-optimus.ipynb

RecoHut-Projects/recohut

4121f665761ffe38c9b6337eaa9293b26bee2376

[ "Apache-2.0" ]

null

32,136.5

64,272

0.459695

[ [ [ "!pip install pyoptimus", "_____no_output_____" ], [ "!pip install py-dateinfer url_parser\n!pip install -U pandas\n!pip install python-libmagic", "_____no_output_____" ], [ "!mkdir /content/x\n!git clone https://github.com/PacktPublishing/Data-Processing-with-Optimus.git /content/x\n%cd /content", "_____no_output_____" ], [ "!mv /content/x/Chapter01/foo.txt .\n!mv /content/x/Chapter01/path/to/file.csv .", "_____no_output_____" ], [ "import pandas as pd\n\npd.read_csv('file.csv')", "_____no_output_____" ], [ "from optimus import Optimus", "_____no_output_____" ], [ "op = Optimus('pandas')", "_____no_output_____" ] ], [ [ "### Basics", "_____no_output_____" ] ], [ [ "# df = op.load.file('file.csv')\ndf = op.load.csv('file.csv')\ndf", "_____no_output_____" ], [ "df = df.cols.rename(\"function\", \"job\")\ndf", "_____no_output_____" ], [ "df = df.cols.upper(\"name\").cols.lower(\"job\")\ndf", "_____no_output_____" ], [ "df.cols.drop(\"name\") ", "_____no_output_____" ], [ "df.rows.drop(df[\"name\"]==\"MEGATRON\") ", "_____no_output_____" ], [ "df.display()", "_____no_output_____" ], [ "df.cols.capitalize(\"name\", output_cols=\"cap_name\") ", "_____no_output_____" ], [ "df.profile(bins=10) ", "_____no_output_____" ], [ "dfn = op.create.dataframe({\"A\":[\"1\",2,\"4\",\"!\",None]})\ndfn", "_____no_output_____" ], [ "dfn.cols.min(\"A\"), dfn.cols.max(\"A\")", "_____no_output_____" ], [ "df = op.create.dataframe({\n \"A\":[\"1\",2,\"4\",\"!\",None],\n \"B\":[\"Optimus\",\"Bumblebee\", \"Eject\", None, None]\n}) \n\ndf.profile(bins=10) ", "_____no_output_____" ], [ "df.columns_sample(\"*\") ", "_____no_output_____" ], [ "df.execute()", "_____no_output_____" ], [ "df = op.load.csv(\"foo.txt\", sep=\",\") \ntype(df.data)", "_____no_output_____" ], [ "df", "_____no_output_____" ], [ "df = df.cols.upper(\"*\") \ndf.meta[\"transformations\"] ", "_____no_output_____" ] ], [ [ "### Read some rows from parquet", "_____no_output_____" ], [ "Pandas still doesn't support reading few of the rows, instead of full. So we can use Optimus in this case.", "_____no_output_____" ] ], [ [ "import pandas as pd\n\ndf = pd.read_csv('file.csv')\ndf.to_parquet('file.parquet.snappy', compression='snappy')\ndf", "_____no_output_____" ], [ "pd.read_parquet('file.parquet.snappy', nrows=2)", "_____no_output_____" ], [ "df = op.load.parquet('file.parquet.snappy', n_rows=2)\ndf", "'load.parquet' on Pandas loads the whole dataset and then truncates it\n" ] ], [ [ "### Optimize memory", "_____no_output_____" ] ], [ [ "df = op.create.dataframe({ \n \"a\": [1000,2000,3000,4000,5000]*10000, \n \"b\": [1,2,3,4,5]*10000 \n}) \ndf.size() ", "_____no_output_____" ], [ "df = df.optimize()\ndf.size() ", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ] ]

cb2e67dc3628775cddba69e9369bb10128ae9071

31,347

ipynb

Jupyter Notebook

debug/manual_graph.ipynb

sergeivolodin/causality-disentanglement-rl

5a41b4a2e3d85fa7e9c8450215fdc6cf954df867

[ "CC0-1.0" ]

2

2020-12-11T05:26:24.000Z

2021-04-21T06:12:58.000Z

debug/manual_graph.ipynb

sergeivolodin/causality-disentanglement-rl

5a41b4a2e3d85fa7e9c8450215fdc6cf954df867

[ "CC0-1.0" ]

9

2020-04-30T16:29:50.000Z

2021-03-26T07:32:18.000Z

debug/manual_graph.ipynb

sergeivolodin/causality-disentanglement-rl

5a41b4a2e3d85fa7e9c8450215fdc6cf954df867

[ "CC0-1.0" ]

null

49.995215

268

0.502855

[ [ [ "from graphviz import Digraph", "_____no_output_____" ], [ "g = Digraph(engine='dot')\n\ng.node('a01', color='red')\ng.node('a02', color='red')\ng.node('a03', color='red')\ng.node('a04', color='red')\ng.node('a05', color='red')\n\ng.node('rew')\ng.node('done')\n\ng.node('s01', color='green')\ng.node('s02', color='green')\ng.node('s03', color='green')\ng.node('s04', color='green')\ng.node('s05', color='green')\n\ng.edge('a01', 's01')\ng.edge('a02', 's02')\ng.edge('a03', 's03')\ng.edge('a04', 's04')\ng.edge('a05', 's05')\n\ng.edge('a01', 'rew')\ng.edge('a02', 'rew')\ng.edge('a03', 'rew')\ng.edge('a04', 'rew')\ng.edge('a05', 'rew')\n\ng.edge('s01', 'rew')\ng.edge('s02', 'rew')\ng.edge('s03', 'rew')\ng.edge('s04', 'rew')\ng.edge('s05', 'rew')\n\ng.edge('s01', 'done')\ng.edge('s02', 'done')\ng.edge('s03', 'done')\ng.edge('s04', 'done')\ng.edge('s05', 'done')", "_____no_output_____" ], [ "g.view()", "_____no_output_____" ], [ "g.unflatten(stagger=3)", "_____no_output_____" ], [ "g.view()", "_____no_output_____" ], [ "g.engine", "_____no_output_____" ], [ "g", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code" ] ]

cb2e856f5e019cfe07dd1d696a22e4b10090c30c

43,473

ipynb

Jupyter Notebook

examples/notebooks/protein_ligand_complex_notebook.ipynb

weiwang2330/deepchem

facf18b32587140962f874be3a652c04f4cf8f58

[ "MIT" ]

null

examples/notebooks/protein_ligand_complex_notebook.ipynb

weiwang2330/deepchem

facf18b32587140962f874be3a652c04f4cf8f58

[ "MIT" ]

null

examples/notebooks/protein_ligand_complex_notebook.ipynb

weiwang2330/deepchem

facf18b32587140962f874be3a652c04f4cf8f58

[ "MIT" ]

null

69.114467

19,814

0.764267

[ [ [ "# Basic Protein-Ligand Affinity Models\n#Tutorial: Use machine learning to model protein-ligand affinity.", "_____no_output_____" ], [ "Written by Evan Feinberg and Bharath Ramsundar\n\nCopyright 2016, Stanford University\n\nThis DeepChem tutorial demonstrates how to use mach.ine learning for modeling protein-ligand binding affinity", "_____no_output_____" ], [ "Overview:\n\nIn this tutorial, you will trace an arc from loading a raw dataset to fitting a cutting edge ML technique for predicting binding affinities. This will be accomplished by writing simple commands to access the deepchem Python API, encompassing the following broad steps:\n\n1. Loading a chemical dataset, consisting of a series of protein-ligand complexes.\n2. Featurizing each protein-ligand complexes with various featurization schemes. \n3. Fitting a series of models with these featurized protein-ligand complexes.\n4. Visualizing the results.", "_____no_output_____" ], [ "First, let's point to a \"dataset\" file. This can come in the format of a CSV file or Pandas DataFrame. Regardless\nof file format, it must be columnar data, where each row is a molecular system, and each column represents\na different piece of information about that system. For instance, in this example, every row reflects a \nprotein-ligand complex, and the following columns are present: a unique complex identifier; the SMILES string\nof the ligand; the binding affinity (Ki) of the ligand to the protein in the complex; a Python `list` of all lines\nin a PDB file for the protein alone; and a Python `list` of all lines in a ligand file for the ligand alone.\n\nThis should become clearer with the example. (Make sure to set `DISPLAY = True`)\n", "_____no_output_____" ] ], [ [ "%load_ext autoreload\n%autoreload 2\n%pdb off\n# set DISPLAY = True when running tutorial\nDISPLAY = False\n# set PARALLELIZE to true if you want to use ipyparallel\nPARALLELIZE = False\nimport warnings\nwarnings.filterwarnings('ignore')", "Automatic pdb calling has been turned OFF\n" ], [ "import deepchem as dc\n\ndataset_file= \"../../datasets/pdbbind_core_df.pkl.gz\"\nraw_dataset = dc.utils.save.load_from_disk(dataset_file)", "Warning: No xgboost installed on your system\nAttempting to run %s will throw runtime errors\n" ] ], [ [ "Let's see what `dataset` looks like:", "_____no_output_____" ] ], [ [ "print(\"Type of dataset is: %s\" % str(type(raw_dataset)))\nprint(raw_dataset[:5])\nprint(\"Shape of dataset is: %s\" % str(raw_dataset.shape))", "Type of dataset is: <class 'pandas.core.frame.DataFrame'>\n pdb_id smiles \\\n0 2d3u CC1CCCCC1S(O)(O)NC1CC(C2CCC(CN)CC2)SC1C(O)O \n1 3cyx CC(C)(C)NC(O)C1CC2CCCCC2C[NH+]1CC(O)C(CC1CCCCC... \n2 3uo4 OC(O)C1CCC(NC2NCCC(NC3CCCCC3C3CCCCC3)N2)CC1 \n3 1p1q CC1ONC(O)C1CC([NH3+])C(O)O \n4 3ag9 NC(O)C(CCC[NH2+]C([NH3+])[NH3+])NC(O)C(CCC[NH2... \n\n complex_id \\\n0 2d3uCC1CCCCC1S(O)(O)NC1CC(C2CCC(CN)CC2)SC1C(O)O \n1 3cyxCC(C)(C)NC(O)C1CC2CCCCC2C[NH+]1CC(O)C(CC1C... \n2 3uo4OC(O)C1CCC(NC2NCCC(NC3CCCCC3C3CCCCC3)N2)CC1 \n3 1p1qCC1ONC(O)C1CC([NH3+])C(O)O \n4 3ag9NC(O)C(CCC[NH2+]C([NH3+])[NH3+])NC(O)C(CCC... \n\n protein_pdb \\\n0 [HEADER 2D3U PROTEIN\\n, COMPND 2D3U PROT... \n1 [HEADER 3CYX PROTEIN\\n, COMPND 3CYX PROT... \n2 [HEADER 3UO4 PROTEIN\\n, COMPND 3UO4 PROT... \n3 [HEADER 1P1Q PROTEIN\\n, COMPND 1P1Q PROT... \n4 [HEADER 3AG9 PROTEIN\\n, COMPND 3AG9 PROT... \n\n ligand_pdb \\\n0 [COMPND 2d3u ligand \\n, AUTHOR GENERATED... \n1 [COMPND 3cyx ligand \\n, AUTHOR GENERATED... \n2 [COMPND 3uo4 ligand \\n, AUTHOR GENERATED... \n3 [COMPND 1p1q ligand \\n, AUTHOR GENERATED... \n4 [COMPND 3ag9 ligand \\n, AUTHOR GENERATED... \n\n ligand_mol2 label \n0 [### \\n, ### Created by X-TOOL on Thu Aug 28 2... 6.92 \n1 [### \\n, ### Created by X-TOOL on Thu Aug 28 2... 8.00 \n2 [### \\n, ### Created by X-TOOL on Fri Aug 29 0... 6.52 \n3 [### \\n, ### Created by X-TOOL on Thu Aug 28 2... 4.89 \n4 [### \\n, ### Created by X-TOOL on Thu Aug 28 2... 8.05 \nShape of dataset is: (193, 7)\n" ] ], [ [ "One of the missions of ```deepchem``` is to form a synapse between the chemical and the algorithmic worlds: to be able to leverage the powerful and diverse array of tools available in Python to analyze molecules. This ethos applies to visual as much as quantitative examination:", "_____no_output_____" ] ], [ [ "import nglview\nimport tempfile\nimport os\nimport mdtraj as md\nimport numpy as np\nimport deepchem.utils.visualization\n#from deepchem.utils.visualization import combine_mdtraj, visualize_complex, convert_lines_to_mdtraj\n\ndef combine_mdtraj(protein, ligand):\n chain = protein.topology.add_chain()\n residue = protein.topology.add_residue(\"LIG\", chain, resSeq=1)\n for atom in ligand.topology.atoms:\n protein.topology.add_atom(atom.name, atom.element, residue)\n protein.xyz = np.hstack([protein.xyz, ligand.xyz])\n protein.topology.create_standard_bonds()\n return protein\n\ndef visualize_complex(complex_mdtraj):\n ligand_atoms = [a.index for a in complex_mdtraj.topology.atoms if \"LIG\" in str(a.residue)]\n binding_pocket_atoms = md.compute_neighbors(complex_mdtraj, 0.5, ligand_atoms)[0]\n binding_pocket_residues = list(set([complex_mdtraj.topology.atom(a).residue.resSeq for a in binding_pocket_atoms]))\n binding_pocket_residues = [str(r) for r in binding_pocket_residues]\n binding_pocket_residues = \" or \".join(binding_pocket_residues)\n\n traj = nglview.MDTrajTrajectory( complex_mdtraj ) # load file from RCSB PDB\n ngltraj = nglview.NGLWidget( traj )\n ngltraj.representations = [\n { \"type\": \"cartoon\", \"params\": {\n \"sele\": \"protein\", \"color\": \"residueindex\"\n } },\n { \"type\": \"licorice\", \"params\": {\n \"sele\": \"(not hydrogen) and (%s)\" % binding_pocket_residues\n } },\n { \"type\": \"ball+stick\", \"params\": {\n \"sele\": \"LIG\"\n } }\n ]\n return ngltraj\n\ndef visualize_ligand(ligand_mdtraj):\n traj = nglview.MDTrajTrajectory( ligand_mdtraj ) # load file from RCSB PDB\n ngltraj = nglview.NGLWidget( traj )\n ngltraj.representations = [\n { \"type\": \"ball+stick\", \"params\": {\"sele\": \"all\" } } ]\n return ngltraj\n\ndef convert_lines_to_mdtraj(molecule_lines):\n tempdir = tempfile.mkdtemp()\n molecule_file = os.path.join(tempdir, \"molecule.pdb\")\n with open(molecule_file, \"wb\") as f:\n f.writelines(molecule_lines)\n molecule_mdtraj = md.load(molecule_file)\n return molecule_mdtraj\n\nfirst_protein, first_ligand = raw_dataset.iloc[0][\"protein_pdb\"], raw_dataset.iloc[0][\"ligand_pdb\"]\n\nprotein_mdtraj = convert_lines_to_mdtraj(first_protein)\nligand_mdtraj = convert_lines_to_mdtraj(first_ligand)\ncomplex_mdtraj = combine_mdtraj(protein_mdtraj, ligand_mdtraj)", "_____no_output_____" ], [ "ngltraj = visualize_complex(complex_mdtraj)\nngltraj", "_____no_output_____" ] ], [ [ "Now that we're oriented, let's use ML to do some chemistry. \n\nSo, step (2) will entail featurizing the dataset.\n\nThe available featurizations that come standard with deepchem are ECFP4 fingerprints, RDKit descriptors, NNScore-style bdescriptors, and hybrid binding pocket descriptors. Details can be found on ```deepchem.io```.", "_____no_output_____" ] ], [ [ "grid_featurizer = dc.feat.RdkitGridFeaturizer(\n voxel_width=16.0, feature_types=\"voxel_combined\", \n voxel_feature_types=[\"ecfp\", \"splif\", \"hbond\", \"pi_stack\", \"cation_pi\", \"salt_bridge\"], \n ecfp_power=5, splif_power=5, parallel=True, flatten=True)\ncompound_featurizer = dc.feat.CircularFingerprint(size=128)", "_____no_output_____" ] ], [ [ "Note how we separate our featurizers into those that featurize individual chemical compounds, compound_featurizers, and those that featurize molecular complexes, complex_featurizers.\n\nNow, let's perform the actual featurization. Calling ```loader.featurize()``` will return an instance of class ```Dataset```. Internally, ```loader.featurize()``` (a) computes the specified features on the data, (b) transforms the inputs into ```X``` and ```y``` NumPy arrays suitable for ML algorithms, and (c) constructs a ```Dataset()``` instance that has useful methods, such as an iterator, over the featurized data. This is a little complicated, so we will use MoleculeNet to featurize the PDBBind core set for us.", "_____no_output_____" ] ], [ [ "PDBBIND_tasks, (train_dataset, valid_dataset, test_dataset), transformers = dc.molnet.load_pdbbind_grid()", "Loading dataset from disk.\nTIMING: dataset construction took 0.024 s\nLoading dataset from disk.\nTIMING: dataset construction took 0.010 s\nLoading dataset from disk.\nTIMING: dataset construction took 0.010 s\nLoading dataset from disk.\n" ] ], [ [ "Now, we conduct a train-test split. If you'd like, you can choose `splittype=\"scaffold\"` instead to perform a train-test split based on Bemis-Murcko scaffolds.", "_____no_output_____" ], [ "We generate separate instances of the Dataset() object to hermetically seal the train dataset from the test dataset. This style lends itself easily to validation-set type hyperparameter searches, which we will illustate in a separate section of this tutorial. ", "_____no_output_____" ], [ "The performance of many ML algorithms hinges greatly on careful data preprocessing. Deepchem comes standard with a few options for such preprocessing.", "_____no_output_____" ], [ "Now, we're ready to do some learning! \n\nTo fit a deepchem model, first we instantiate one of the provided (or user-written) model classes. In this case, we have a created a convenience class to wrap around any ML model available in Sci-Kit Learn that can in turn be used to interoperate with deepchem. To instantiate an ```SklearnModel```, you will need (a) task_types, (b) model_params, another ```dict``` as illustrated below, and (c) a ```model_instance``` defining the type of model you would like to fit, in this case a ```RandomForestRegressor```.", "_____no_output_____" ] ], [ [ "from sklearn.ensemble import RandomForestRegressor\n\nsklearn_model = RandomForestRegressor(n_estimators=100)\nmodel = dc.models.SklearnModel(sklearn_model)\nmodel.fit(train_dataset)", "_____no_output_____" ], [ "from deepchem.utils.evaluate import Evaluator\nimport pandas as pd\n\nmetric = dc.metrics.Metric(dc.metrics.r2_score)\n\nevaluator = Evaluator(model, train_dataset, transformers)\ntrain_r2score = evaluator.compute_model_performance([metric])\nprint(\"RF Train set R^2 %f\" % (train_r2score[\"r2_score\"]))\n\nevaluator = Evaluator(model, valid_dataset, transformers)\nvalid_r2score = evaluator.compute_model_performance([metric])\nprint(\"RF Valid set R^2 %f\" % (valid_r2score[\"r2_score\"]))", "computed_metrics: [0.87165637813866481]\nRF Train set R^2 0.871656\ncomputed_metrics: [0.1561422855082335]\nRF Valid set R^2 0.156142\n" ] ], [ [ "In this simple example, in few yet intuitive lines of code, we traced the machine learning arc from featurizing a raw dataset to fitting and evaluating a model. \n\nHere, we featurized only the ligand. The signal we observed in R^2 reflects the ability of circular fingerprints and random forests to learn general features that make ligands \"drug-like.\"", "_____no_output_____" ] ], [ [ "predictions = model.predict(test_dataset)\nprint(predictions)", "[ 5.0557 5.716 6.1845 7.9055 5.9617 6.3135 5.3563 7.0066 5.6421\n 6.334 6.5798 6.5744 4.9209 6.9901 7.2046 6.5845 6.9427 6.9793\n 6.9515 5.9193]\n" ], [ "# TODO(rbharath): This cell visualizes the ligand with highest predicted activity. Commenting it out for now. Fix this later\n#from deepchem.utils.visualization import visualize_ligand\n\n#top_ligand = predictions.iloc[0]['ids']\n#ligand1 = convert_lines_to_mdtraj(dataset.loc[dataset['complex_id']==top_ligand]['ligand_pdb'].values[0])\n#if DISPLAY:\n# ngltraj = visualize_ligand(ligand1)\n# ngltraj", "_____no_output_____" ], [ "# TODO(rbharath): This cell visualizes the ligand with lowest predicted activity. Commenting it out for now. Fix this later\n#worst_ligand = predictions.iloc[predictions.shape[0]-2]['ids']\n#ligand1 = convert_lines_to_mdtraj(dataset.loc[dataset['complex_id']==worst_ligand]['ligand_pdb'].values[0])\n#if DISPLAY:\n# ngltraj = visualize_ligand(ligand1)\n# ngltraj", "_____no_output_____" ] ], [ [ "# The protein-ligand complex view.", "_____no_output_____" ], [ "The preceding simple example, in few yet intuitive lines of code, traces the machine learning arc from featurizing a raw dataset to fitting and evaluating a model. \n\nIn this next section, we illustrate ```deepchem```'s modularity, and thereby the ease with which one can explore different featurization schemes, different models, and combinations thereof, to achieve the best performance on a given dataset. We will demonstrate this by examining protein-ligand interactions. ", "_____no_output_____" ], [ "In the previous section, we featurized only the ligand. The signal we observed in R^2 reflects the ability of grid fingerprints and random forests to learn general features that make ligands \"drug-like.\" In this section, we demonstrate how to use hyperparameter searching to find a higher scoring ligands.", "_____no_output_____" ] ], [ [ "def rf_model_builder(model_params, model_dir):\n sklearn_model = RandomForestRegressor(**model_params)\n return dc.models.SklearnModel(sklearn_model, model_dir)\n\nparams_dict = {\n \"n_estimators\": [10, 50, 100],\n \"max_features\": [\"auto\", \"sqrt\", \"log2\", None],\n}\n\nmetric = dc.metrics.Metric(dc.metrics.r2_score)\noptimizer = dc.hyper.HyperparamOpt(rf_model_builder)\nbest_rf, best_rf_hyperparams, all_rf_results = optimizer.hyperparam_search(\n params_dict, train_dataset, valid_dataset, transformers,\n metric=metric)", "Fitting model 1/12\nhyperparameters: {'n_estimators': 10, 'max_features': 'auto'}\ncomputed_metrics: [0.11307395856711755]\nModel 1/12, Metric r2_score, Validation set 0: 0.113074\n\tbest_validation_score so far: 0.113074\nFitting model 2/12\nhyperparameters: {'n_estimators': 10, 'max_features': 'sqrt'}\ncomputed_metrics: [0.099148571900583904]\nModel 2/12, Metric r2_score, Validation set 1: 0.099149\n\tbest_validation_score so far: 0.113074\nFitting model 3/12\nhyperparameters: {'n_estimators': 10, 'max_features': 'log2'}\ncomputed_metrics: [0.011951380345950557]\nModel 3/12, Metric r2_score, Validation set 2: 0.011951\n\tbest_validation_score so far: 0.113074\nFitting model 4/12\nhyperparameters: {'n_estimators': 10, 'max_features': None}\ncomputed_metrics: [0.088399300891687682]\nModel 4/12, Metric r2_score, Validation set 3: 0.088399\n\tbest_validation_score so far: 0.113074\nFitting model 5/12\nhyperparameters: {'n_estimators': 50, 'max_features': 'auto'}\ncomputed_metrics: [0.15902254520297032]\nModel 5/12, Metric r2_score, Validation set 4: 0.159023\n\tbest_validation_score so far: 0.159023\nFitting model 6/12\nhyperparameters: {'n_estimators': 50, 'max_features': 'sqrt'}\ncomputed_metrics: [0.11169781065527806]\nModel 6/12, Metric r2_score, Validation set 5: 0.111698\n\tbest_validation_score so far: 0.159023\nFitting model 7/12\nhyperparameters: {'n_estimators': 50, 'max_features': 'log2'}\ncomputed_metrics: [0.059318984812613107]\nModel 7/12, Metric r2_score, Validation set 6: 0.059319\n\tbest_validation_score so far: 0.159023\nFitting model 8/12\nhyperparameters: {'n_estimators': 50, 'max_features': None}\ncomputed_metrics: [0.19599469907033895]\nModel 8/12, Metric r2_score, Validation set 7: 0.195995\n\tbest_validation_score so far: 0.195995\nFitting model 9/12\nhyperparameters: {'n_estimators': 100, 'max_features': 'auto'}\ncomputed_metrics: [0.13128321736117132]\nModel 9/12, Metric r2_score, Validation set 8: 0.131283\n\tbest_validation_score so far: 0.195995\nFitting model 10/12\nhyperparameters: {'n_estimators': 100, 'max_features': 'sqrt'}\ncomputed_metrics: [0.18386751402403434]\nModel 10/12, Metric r2_score, Validation set 9: 0.183868\n\tbest_validation_score so far: 0.195995\nFitting model 11/12\nhyperparameters: {'n_estimators': 100, 'max_features': 'log2'}\ncomputed_metrics: [0.079031671201846287]\nModel 11/12, Metric r2_score, Validation set 10: 0.079032\n\tbest_validation_score so far: 0.195995\nFitting model 12/12\nhyperparameters: {'n_estimators': 100, 'max_features': None}\ncomputed_metrics: [0.16382517016852427]\nModel 12/12, Metric r2_score, Validation set 11: 0.163825\n\tbest_validation_score so far: 0.195995\ncomputed_metrics: [0.86969508698615849]\nBest hyperparameters: (50, None)\ntrain_score: 0.869695\nvalidation_score: 0.195995\n" ], [ "%matplotlib inline\n\nimport matplotlib\nimport numpy as np\nimport matplotlib.pyplot as plt\n\nrf_predicted_test = best_rf.predict(test_dataset)\nrf_true_test = test_dataset.y\nplt.scatter(rf_predicted_test, rf_true_test)\nplt.xlabel('Predicted pIC50s')\nplt.ylabel('True IC50')\nplt.title(r'RF predicted IC50 vs. True pIC50')\nplt.xlim([2, 11])\nplt.ylim([2, 11])\nplt.plot([2, 11], [2, 11], color='k')\nplt.show()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ] ]

cb2e8858a6e6704a7cf51c903dee5cda6f5b6d67

191,153

ipynb

Jupyter Notebook

content/ch-algorithms/shor.ipynb

nogayama/qiskit-textbook

f766964c7d78037eeb2a6e94d13252a7587b0383

[ "Apache-2.0" ]

null

content/ch-algorithms/shor.ipynb

nogayama/qiskit-textbook

f766964c7d78037eeb2a6e94d13252a7587b0383

[ "Apache-2.0" ]

null

content/ch-algorithms/shor.ipynb

nogayama/qiskit-textbook

f766964c7d78037eeb2a6e94d13252a7587b0383

[ "Apache-2.0" ]

1

2020-04-01T04:00:12.000Z

44.423193

578

0.455468

[ [ [ "empty" ] ] ]

[ "empty" ]

[ [ "empty" ] ]

cb2eb0e2dc0b14c78dc289813cf297e3bed87f78

837

ipynb

Jupyter Notebook

HelloGithub.ipynb

annadutki/dw_matrix1

6c6dfe64b5b77cbab655a7d292f294e0545c4ddc

[ "MIT" ]

null

HelloGithub.ipynb

annadutki/dw_matrix1

6c6dfe64b5b77cbab655a7d292f294e0545c4ddc

[ "MIT" ]

null

HelloGithub.ipynb

annadutki/dw_matrix1

6c6dfe64b5b77cbab655a7d292f294e0545c4ddc

[ "MIT" ]

null

837

0.689367

[ [ [ "print('Hello Github')", "Hello Github\n" ], [ "", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code" ] ]

cb2ec09c1e08fc33897d79c4a8f620149c6f9f1e

50,818

ipynb

Jupyter Notebook

tutorial.ipynb

fossabot/quadtree

2ddcf534e187025df070a6d8c83afbc68569b6bf

[ "MIT" ]

1

2021-05-19T06:19:59.000Z

tutorial.ipynb

fossabot/quadtree

2ddcf534e187025df070a6d8c83afbc68569b6bf

[ "MIT" ]

1

2021-05-18T08:03:20.000Z

tutorial.ipynb

fossabot/quadtree

2ddcf534e187025df070a6d8c83afbc68569b6bf

[ "MIT" ]

1

2021-05-18T07:59:46.000Z

89.943363

21,940

0.834035

[ [ [ "# Quadtrees iterating on pairs of neighbouring items", "_____no_output_____" ], [ "A quadtree is a tree data structure in which each node has exactly four children. It is a particularly efficient way to store elements when you need to quickly find them according to their x-y coordinates.\n\nA common problem with elements in quadtrees is to detect pairs of elements which are closer than a definite threshold.\n\nThe proposed implementation efficiently addresses this problem.", "_____no_output_____" ] ], [ [ "from smartquadtree import Quadtree", "_____no_output_____" ] ], [ [ "## Creation & insertion of elements", "_____no_output_____" ], [ "As you instantiate your quadtree, you must specify the center of your space then the height and width.", "_____no_output_____" ] ], [ [ "q = Quadtree(0, 0, 10, 10)", "_____no_output_____" ] ], [ [ "The output of a quadtree on the console is pretty explicit. (You can refer to next section for the meaning of \"No mask set\")", "_____no_output_____" ] ], [ [ "q", "_____no_output_____" ] ], [ [ "You can easily insert elements from which you can naturally infer x-y coordinates (e.g. tuples or lists)", "_____no_output_____" ] ], [ [ "q.insert((1, 2))\nq.insert((-3, 4))\nq", "_____no_output_____" ] ], [ [ "No error is raised if the element you are trying to insert is outside the scope of the quadtree. But it won't be stored anyway!", "_____no_output_____" ] ], [ [ "q.insert((-20, 0))\nq", "_____no_output_____" ] ], [ [ "If you want to insert other Python objects, be sure to provide `get_x()` and `get_y()` methods to your class!", "_____no_output_____" ] ], [ [ "class Point(object):\n\n def __init__(self, x, y, color):\n self.x = x\n self.y = y\n self.color = color\n\n def __repr__(self):\n return \"(%.2f, %.2f) %s\" % (self.x, self.y, self.color)\n\n def get_x(self):\n return self.x\n\n def get_y(self):\n return self.y\n", "_____no_output_____" ] ], [ [ "You cannot insert elements of a different type from the first element inserted.", "_____no_output_____" ] ], [ [ "q.insert(Point(2, -7, \"red\"))", "_____no_output_____" ] ], [ [ "But feel free to create a new one and play with it:", "_____no_output_____" ] ], [ [ "point_quadtree = Quadtree(5, 5, 5, 5)\npoint_quadtree.insert(Point(2, 7, \"red\"))\npoint_quadtree", "_____no_output_____" ] ], [ [ "## Simple iteration", "_____no_output_____" ] ], [ [ "from random import random\nq = Quadtree(0, 0, 10, 10, 16)\nfor a in range(50):\n q.insert([random()*20-10, random()*20-10])", "_____no_output_____" ] ], [ [ "The `print` function does not display all elements and uses the `__repr__()` method of each element.", "_____no_output_____" ] ], [ [ "print(q)", "<smartquadtree.Quadtree at 0x7fc28b94c0b0>\nTotal number of elements: 50\nNo mask set\nFirst elements:\n [5.576253335483335, 2.9926458306078647],\n [2.956289387002718, 3.792134207741281],\n [3.9903269308895766, 5.492168007874362],\n ...\n" ] ], [ [ "We can write our own iterator and print each element we encounter the way we like.", "_____no_output_____" ] ], [ [ "from __future__ import print_function\nfor p in q.elements():\n print (\"[%.2f, %.2f]\" % (p[0], p[1]), end=\" \")", "[5.58, 2.99] [2.96, 3.79] [3.99, 5.49] [3.43, 1.10] [7.73, 4.09] [9.67, 6.81] [2.95, 4.12] [0.14, 5.80] [2.77, 7.87] [0.05, 1.61] [-8.74, 7.64] [-1.22, 1.90] [-0.95, 3.91] [-3.17, 1.09] [-7.41, 4.26] [-8.25, 6.47] [-6.91, 3.80] [-3.73, 3.10] [-5.74, 8.80] [8.50, -9.31] [2.49, -9.10] [6.64, -8.61] [0.40, -2.93] [7.99, -4.08] [4.71, -6.75] [0.12, -1.84] [0.72, -2.94] [9.62, -9.90] [0.15, -9.75] [8.67, -7.19] [2.44, -3.60] [5.08, -8.63] [8.86, -1.87] [1.07, -9.43] [-7.96, -5.53] [-2.53, -5.75] [-1.31, -5.81] [-7.24, -3.55] [-8.76, -9.37] [-8.48, -1.33] [-1.28, -0.69] [-6.60, -4.65] [-4.28, -0.89] [-7.56, -7.31] [-4.72, -7.02] [-1.98, -2.33] [-3.43, -5.74] [-3.71, -1.13] [-1.01, -7.29] [-2.04, -5.90] " ] ], [ [ "It is easy to filter the iteration process and apply the function only on elements inside a given polygon. Use the `set_mask()` method and pass a list of x-y coordinates. The polygon will be automatically closed.", "_____no_output_____" ] ], [ [ "q.set_mask([(-3, -7), (-3, 7), (3, 7), (3, -7)])\nprint(q)", "<smartquadtree.Quadtree at 0x7fc28b94c0b0>\nTotal number of elements: 50\nTotal number of elements inside mask: 15\nFirst elements inside the mask:\n [2.956289387002718, 3.792134207741281],\n [2.945472950394006, 4.1166899654293765],\n [0.14379102547949074, 5.797490949080599],\n ...\n" ] ], [ [ "The same approach can be used to count the number of elements inside the quadtree.", "_____no_output_____" ] ], [ [ "print (sum (1 for x in q.elements()))\nprint (sum (1 for x in q.elements(ignore_mask=True)))\n", "15\n50\n" ] ], [ [ "As a mask is set on the quadtree, we only counted the elements inside the mask. You can use the `size()` method to count elements and ignore the mask by default. Disabling the mask with `set_mask(None)` is also a possibility.", "_____no_output_____" ] ], [ [ "print (\"%d elements (size method)\" % q.size())\nprint (\"%d elements (don't ignore the mask)\" % q.size(False))\n\nq.set_mask(None)\nprint (\"%d elements (disable the mask)\" % q.size())", "50 elements (size method)\n15 elements (don't ignore the mask)\n50 elements (disable the mask)\n" ] ], [ [ "## Playing with plots", "_____no_output_____" ] ], [ [ "%matplotlib inline\nfrom matplotlib import pyplot as plt\n \nq = Quadtree(5, 5, 5, 5, 10)\n\nfor a in range(200):\n q.insert([random()*10, random()*10])\n \nfig = plt.figure()\nplt.axis([0, 10, 0, 10])\n\nq.set_mask(None)\nfor p in q.elements():\n plt.plot([p[0]], [p[1]], 'o', color='lightgrey')\n\nq.set_mask([(3, 3), (3, 7), (7, 7), (7, 3)])\n\nfor p in q.elements():\n plt.plot([p[0]], [p[1]], 'ro')\n\n_ = plt.plot([3, 3, 7, 7, 3], [3, 7, 7, 3, 3], 'r')\n", "_____no_output_____" ] ], [ [ "## Iteration on pairs of neighbouring elements", "_____no_output_____" ], [ "Iterating on pairs of neighbouring elements is possible through the `neighbour_elements()` function. It works as a generator and yields pair of elements, the first one being inside the mask (if specified), the second one being in the same cell or in any neighbouring cell, also in the mask.\n\nNote that if `(a, b)` is yielded by `neighbour_elements()`, `(b, a)` will be omitted from future yields.", "_____no_output_____" ] ], [ [ "q = Quadtree(5, 5, 5, 5, 10)\nq.set_limitation(2) # do not create a new subdivision if one side of the cell is below 2\n\nfor a in range(200):\n q.insert([random()*10, random()*10])\n\nfig = plt.figure()\nplt.axis([0, 10, 0, 10])\n\nfor p in q.elements():\n plt.plot([p[0]], [p[1]], 'o', color='lightgrey')\n\nq.set_mask([(1, 1), (4, 1), (5, 4), (2, 5), (1, 1)])\n \nfor p in q.elements():\n plt.plot([p[0]], [p[1]], 'o', color='green')\n \nfor p1, p2 in q.neighbour_elements():\n if ((p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2 < 1):\n plt.plot([p1[0]], [p1[1]], 'o', color='red')\n plt.plot([p2[0]], [p2[1]], 'o', color='red')\n plt.plot([p1[0], p2[0]], [p1[1], p2[1]], 'red')\n\n_ = plt.plot([1, 4, 5, 2, 1], [1, 1, 4, 5, 1], 'r')\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ] ]

cb2ec148bc9f9887cb69465b0296d54c3fcc318e

13,528

ipynb

Jupyter Notebook

tensorflow/day4/practice/.ipynb_checkpoints/P_04_02_NN_TEST-checkpoint.ipynb

daludaluking/LG_AI_all_in_one-

e0855af811deb1e5cf1695430bd52a8eb3d48827

[ "Apache-2.0" ]

null

tensorflow/day4/practice/.ipynb_checkpoints/P_04_02_NN_TEST-checkpoint.ipynb

daludaluking/LG_AI_all_in_one-

e0855af811deb1e5cf1695430bd52a8eb3d48827

[ "Apache-2.0" ]

null

tensorflow/day4/practice/.ipynb_checkpoints/P_04_02_NN_TEST-checkpoint.ipynb

daludaluking/LG_AI_all_in_one-

e0855af811deb1e5cf1695430bd52a8eb3d48827

[ "Apache-2.0" ]

null

98.744526

1,557

0.678149

[ [ [ "#-*- coding: utf-8 -*-\n\nimport tensorflow as tf\nimport matplotlib.pyplot as plt\nimport numpy as np\nimport cv2\n\n\n", "_____no_output_____" ], [ "# MNIST 데이터 불러오기\n(X_train, Y_train), (X_test, Y_test) = tf.keras.datasets.mnist.load_data()\n\n", "_____no_output_____" ], [ "## TEST할 이미지 선택\ntest_image = X_test[0] ## image에 matrix 곱\n\n\n", "_____no_output_____" ], [ "## NN 이미로 이차원으로 데이터를 넣어주어야 해서 1x784 형태로 reshape하고 노말라이제이션\ntest_image_reshape = test_image.reshape(1,784).astype('float64') ## 이미지가 2-d이므로 1-d로 변환하여 nn으로 전달\n### (28x28)이미지 를 784 개로 reshape 앞에 1이라는 숫자는 데이터 1개다. batch size의미.\n\n", "_____no_output_____" ], [ "## 모델 불러오기\nmodel = tf.keras.models.load_model('./MNIST_model\\\\30-0.4827.hdf5') # 모델을 새로 불러옴\n\n", "_____no_output_____" ], [ "# 불러온 모델로 값 예측하기.\nY_prediction = model.predict(test_image_reshape)\n## Y_prediction = [[ 0.1 0.1 .... 0.7 0.1 ]] 1개의 이미지의 결과를 10개의 값 으로 예측\n# 10개는 각 perceptron의 예측 값.\n\n", "_____no_output_____" ], [ "## 10개의 class가 각 확률 값으로 나오기 때문에 가장 높은값을 출력하는 인덱스를 추출. 그럼 이것이 결국 class임.\n### np.argmax는 들어온 행렬에서 가장 높은값이 있는 index를 반환해주는 함수.\nindex=np.argmax(Y_prediction)\nvlaue=Y_prediction[:, index]\nplt.imshow(test_image, cmap='Greys')\nplt.xlabel(str(index)+\" \" +str(vlaue))\nplt.show()", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code" ] ]

cb2ecad01bdf2613f92a0020fac3f30344cfce1b

398,935

ipynb

Jupyter Notebook

examples/pycut_example.ipynb

vlukes/imcut

63bde3b233cc19500fa554cdb998217af12d614a

[ "BSD-3-Clause" ]

57

2018-07-18T08:32:23.000Z

2022-02-11T02:39:56.000Z

examples/pycut_example.ipynb

mjirik/pyseg_base

f9e6c0592b1d5ba10dbef8f774f3c7e6822ba698

[ "BSD-3-Clause" ]

13

2019-06-01T05:03:41.000Z

2022-03-28T07:27:19.000Z

examples/pycut_example.ipynb

mjirik/pyseg_base

f9e6c0592b1d5ba10dbef8f774f3c7e6822ba698

[ "BSD-3-Clause" ]

23

2018-09-06T05:05:09.000Z

2022-02-09T13:41:42.000Z

1,201.611446

224,592

0.95876

[ [ [ "import sys\nimport os\n# path_to_script = os.path.dirname(os.path.abspath(__file__))\npath_to_imcut = os.path.abspath(\"..\")\nsys.path.insert(0, path_to_imcut)\n\n\npath_to_imcut \nimport imcut\n\nimcut.__file__", "_____no_output_____" ], [ "import numpy as np\nimport scipy\nimport scipy.ndimage\n# import sed3\nimport matplotlib.pyplot as plt\n", "_____no_output_____" ] ], [ [ "## Input data", "_____no_output_____" ] ], [ [ "sz = [10, 300, 300]\ndist = 30\nnoise_intensity = 25\nnoise_std = 20\nsignal_intensity = 50\n\nsegmentation = np.zeros(sz)\nsegmentation[5, 100, 100] = 1\nsegmentation[5, 150, 120] = 1\nsegmentation = scipy.ndimage.morphology.distance_transform_edt(1 - segmentation)\nsegmentation = (segmentation < dist).astype(np.int8)\n\nseeds = np.zeros_like(segmentation)\nseeds[5, 90:100, 90:100] = 1\nseeds[5, 190:200, 190:200] = 2\n# np.random.random(sz) * 100\nplt.figure(figsize=(15,5))\nplt.subplot(121)\nplt.imshow(segmentation[5, :, :])\nplt.colorbar()\n\ndata3d = np.random.normal(size=sz, loc=noise_intensity, scale=noise_std) \ndata3d += segmentation * signal_intensity\ndata3d = data3d.astype(np.int16)\n\nplt.subplot(122)\nplt.imshow(data3d[5, :, :], cmap=\"gray\")\nplt.colorbar()", "_____no_output_____" ] ], [ [ "## Graph-Cut segmentation", "_____no_output_____" ] ], [ [ "from imcut import pycut", "_____no_output_____" ], [ "segparams = {\n 'method':'graphcut',\n# 'method': 'multiscale_graphcut',\n 'use_boundary_penalties': False,\n 'boundary_dilatation_distance': 2,\n 'boundary_penalties_weight': 1,\n 'block_size': 8,\n 'tile_zoom_constant': 1\n}\ngc = pycut.ImageGraphCut(data3d, segparams=segparams)\ngc.set_seeds(seeds)\ngc.run()\noutput_segmentation = gc.segmentation", "_____no_output_____" ], [ "plt.figure(figsize=(15,5))\nplt.subplot(121)\nplt.imshow(output_segmentation[5, :, :])\nplt.colorbar()", "_____no_output_____" ] ], [ [ "## Model debug", "_____no_output_____" ] ], [ [ "segparams = {\n 'method':'graphcut',\n# 'method': 'multiscale_graphcut',\n 'use_boundary_penalties': False,\n 'boundary_dilatation_distance': 2,\n 'boundary_penalties_weight': 1,\n 'block_size': 8,\n 'tile_zoom_constant': 1\n}\ngc = pycut.ImageGraphCut(data3d, segparams=segparams)\ngc.set_seeds(seeds)\ngc.run()\noutput_segmentation = gc.segmentation", "_____no_output_____" ], [ "a=gc.debug_show_model(start=-100, stop=200)", "_____no_output_____" ], [ "gc.debug_show_reconstructed_similarity()", "tdata1 max 399 min 0 dtype int32\ntdata2 max 272 min 0 dtype int32\n" ] ], [ [ "## Other parameters", "_____no_output_____" ] ], [ [ "segparams_ssgc = {\n \"method\": \"graphcut\",\n# \"use_boundary_penalties\": False,\n# 'boundary_penalties_weight': 30,\n# 'boundary_penalties_sigma': 200, \n# 'boundary_dilatation_distance': 2,\n# 'use_apriori_if_available': True, \n# 'use_extra_features_for_training': False,\n# 'apriori_gamma': 0.1,\n \"modelparams\": {\n \"type\": \"gmmsame\",\n \"params\": {\"n_components\": 2},\n \"return_only_object_with_seeds\": True,\n \"fv_type\": \"intensity\",\n# \"fv_type\": \"intensity_and_blur\",\n# \"fv_type\": \"fv_extern\",\n# \"fv_extern\": fv_fcn()\n \n }\n \n}", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ] ]

cb2ece2df72d467e3294d71bb73a8d83a5181514

512,176

ipynb

Jupyter Notebook

tp5/notebook.ipynb

alexis-thual/audio-signal-analysis

226e654d7482869c0976199babebac1c67c3803a

[ "MIT" ]

null

tp5/notebook.ipynb

alexis-thual/audio-signal-analysis

226e654d7482869c0976199babebac1c67c3803a

[ "MIT" ]

null

tp5/notebook.ipynb

alexis-thual/audio-signal-analysis

226e654d7482869c0976199babebac1c67c3803a

[ "MIT" ]

null

1,078.265263

113,068

0.953165

[ [ [ "import numpy as np\nimport matplotlib.pyplot as plt\n\nimport IPython\nimport scipy.io.wavfile as wav\nimport scipy.signal as ss", "_____no_output_____" ], [ "def plotSound(signal, frameRate):\n plt.plot(signal)\n plt.show()", "_____no_output_____" ], [ "soundStrings = ['aeiou.wav', 'an_in_on.wav']\nselectedSoundString = soundStrings[1]\nframeRate, frames = wav.read(selectedSoundString)\nplotSound(frames, frameRate)\nIPython.display.Audio(frames, rate=frameRate)", "_____no_output_____" ], [ "from math import floor, ceil", "_____no_output_____" ], [ "def nextPower(n, p):\n m = 1\n while m <= n:\n m *= p\n return m\n\ndef periode(signal, frameRate, pmin=1/300, pmax=1/80, seuil=0.7):\n signal = signal - np.mean(signal)\n N = len(signal)\n\n Nmin = 1 + ceil(pmin * frameRate)\n Nmax = min(1 + floor(pmax * frameRate), N)\n\n Nfft = nextPower(2 * N - 1, 2)\n fourierSignal = np.fft.fft(signal, n=Nfft)\n S = fourierSignal * np.conjugate(fourierSignal) / N\n r = np.real(np.fft.ifft(S))\n \n i = np.argmax(r[Nmin:Nmax])\n rmax = r[Nmin:Nmax][i]\n P = i + Nmin - 2\n corr = rmax / r[0] * N / (N-P)\n voise = corr > seuil\n if not voise:\n P = round(10e-3 * frameRate)\n\n return P, voise", "_____no_output_____" ], [ "def analysisPitchMarks(signal, frameRate):\n tArray = [1]\n vArray = [0]\n PArray = [10e-3 * frameRate]\n\n while True:\n t = tArray[-1]\n P = PArray[-1]\n duration = floor(2.5 * P)\n\n if t + duration > len(signal):\n break\n\n x = signal[t:t + duration]\n newP, voise = periode(x, frameRate)\n vArray.append(voise)\n PArray.append(newP)\n tArray.append(t + newP)\n \n A = np.zeros((3, len(tArray)))\n A[0,:] = tArray\n A[1,:] = vArray\n A[2,:] = PArray\n\n return A", "_____no_output_____" ], [ "A = analysisPitchMarks(frames, frameRate)\nB = np.zeros((2, A.shape[1]))\nB[0,:] = A[0,:]\nB[1,:] = np.arange(A.shape[1])", "_____no_output_____" ] ], [ [ "```\nA[0] = time marks (in frames)\nA[1] = 0/1 voise\nA[2] = pitch duration (in frames)\n```\n\n```\nB[0, i] = time mark in frames for the ith synthese mark\nB[1, i] = synthese mark id\n```", "_____no_output_____" ] ], [ [ "plt.figure(figsize=(15, 4))\nplt.plot(frames, zorder=0)\nplt.scatter(A[0, np.nonzero(A[1])[0]], [0] * len(np.nonzero(A[1])[0]), c=\"r\", s=50)\nplt.show()", "_____no_output_____" ], [ "def sythesis(signal, frameRate, A, B):\n n = int(B[0,-1]) + floor(A[2, int(B[1,-1])]) + 1\n y = np.zeros(n)\n\n for k in range(1, B.shape[1]):\n ta = int(A[0,int(B[1,k])])\n P = int(A[2,int(B[1,k])])\n ts = int(B[0,k])\n x = signal[ta-P:ta+P+1]\n x = x * np.hanning(2*P+1)\n y[ts-P:ts+P+1] += x\n \n return y", "_____no_output_____" ], [ "y = sythesis(frames, frameRate, A, B)\nplotSound(y, frameRate)\nIPython.display.Audio(y, rate=frameRate)", "_____no_output_____" ], [ "def changeTimeScale(alpha, A, frameRate):\n t = [1]\n n = [0,1]\n\n while int(n[-1]) < A.shape[1]:\n t.append(t[-1] + A[2,int(n[-1])])\n n.append(n[-1] + 1 / alpha)\n\n B = np.zeros((2, len(t)))\n B[0,:] = np.array(t, dtype=int)\n B[1,:] = np.array(n[:-1], dtype=int)\n return B", "_____no_output_____" ], [ "# Test\nA = analysisPitchMarks(frames, frameRate)\nB = changeTimeScale(1.5, A, frameRate)\ny = sythesis(frames, frameRate, A, B)\nplotSound(y, frameRate)\nIPython.display.Audio(y, rate=frameRate)", "_____no_output_____" ], [ "def changePitchScale(beta, A, frameRate):\n t = [1]\n scale = [1 / beta if A[1, 0] else 1]\n n = [0, scale[0]]\n\n while int(n[-1]) < A.shape[1]:\n scale.append(1 / beta if A[1, int(n[-1])] else 1)\n t.append(t[-1] + scale[-1] * A[2, int(n[-1])])\n n.append(n[-1] + scale[-1])\n\n B = np.zeros((2, len(t)))\n B[0,:] = np.array(t, dtype=int)\n B[1,:] = np.array(n[:-1], dtype=int)\n return B", "_____no_output_____" ], [ "# Test\nA = analysisPitchMarks(frames, frameRate)\nB = changePitchScale(0.7, A, frameRate)\ny = sythesis(frames, frameRate, A, B)\nplotSound(y, frameRate)\nIPython.display.Audio(y, rate=frameRate)", "_____no_output_____" ], [ "def changeBothScales(alpha, beta, A, frameRate):\n t = [1]\n scale = [1 / beta if A[1, 0] else 1]\n n = [0, scale[0]]\n\n while int(n[-1]) < A.shape[1]:\n scale.append(1 / beta if A[1, int(n[-1])] else 1)\n t.append(t[-1] + scale[-1] * A[2, int(n[-1])])\n n.append(n[-1] + scale[-1] + 1 / alpha)\n \n B = np.zeros((2, len(t)))\n B[0,:] = np.array(t, dtype=int)\n B[1,:] = np.array(n[:-1], dtype=int)\n return B", "_____no_output_____" ], [ "# Test\nA = analysisPitchMarks(frames, frameRate)\nB = changeBothScales(0.7, 0.7, A, frameRate)\ny = sythesis(frames, frameRate, A, B)\nplotSound(y, frameRate)\nIPython.display.Audio(y, rate=frameRate)", "_____no_output_____" ] ] ]

[ "code", "markdown", "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2eddb6a0d6e938f434264021b58aac194e8d71

152,221

ipynb

Jupyter Notebook

Sandbox/Notebooks/Clustering/NLP Jason's edits.ipynb

LorenzoNajt/ErdosInstitute-SIG_Project

7dc82434eb20c6ed673a365a67ea8f3653997f64

[ "MIT" ]

2

2021-05-06T22:18:38.000Z

2021-05-07T19:53:17.000Z

Sandbox/Notebooks/Clustering/NLP Jason's edits.ipynb

LorenzoNajt/ErdosInstitute-SIG_Project

7dc82434eb20c6ed673a365a67ea8f3653997f64

[ "MIT" ]

null

Sandbox/Notebooks/Clustering/NLP Jason's edits.ipynb

LorenzoNajt/ErdosInstitute-SIG_Project

7dc82434eb20c6ed673a365a67ea8f3653997f64

[ "MIT" ]

null

102.230356

26,452

0.805388

[ [ [ "from edahelper import *\nimport sklearn.naive_bayes as NB\nimport sklearn.linear_model\nfrom sklearn.model_selection import train_test_split\nfrom sklearn.feature_extraction.text import CountVectorizer\nfrom sklearn.feature_extraction.text import TfidfTransformer\nfrom sklearn.pipeline import Pipeline\nfrom sklearn.linear_model import LinearRegression\nfrom sklearn.metrics import mean_squared_error, r2_score, accuracy_score\n# Resources:\n\n#https://scikit-learn.org/stable/tutorial/text_analytics/working_with_text_data.html\n", "_____no_output_____" ], [ "wsb = pd.read_csv('../Data/wsb_cleaned.csv')", "_____no_output_____" ], [ "#set up appropriate subset, removing comment outliers\n#also chose to look at only self posts\ndfog=wsb.loc[(wsb.is_self==True) & (wsb.ups>=10) & (wsb.num_comments<=10000) & ~(wsb[\"title\"].str.contains(\"Thread|thread|Sunday Live Chat|consolidation zone|Containment Zone|Daily Discussion|Daily discussion|Saturday Chat|What Are Your Moves Tomorrow|What Are Your Moves Today|MEGATHREAD\",na=False))]", "_____no_output_____" ] ], [ [ " ## Preprocessing\n \n Removing characters that are not alphanumeric or spaces:", "_____no_output_____" ] ], [ [ "def RegexCols(df,cols):\n newdf=df\n regex = re.compile('[^a-zA-Z ]')\n for col in cols:\n newdf=newdf.assign(**{col: df.loc[:,col].apply(lambda x : regex.sub('', str(x) ))})\n return newdf\ndf=RegexCols(dfog,['title', 'author', 'selftext'])\n#df=pd.DataFrame()\n#regex = re.compile('[^a-zA-Z ]')\n#for col in ['title', 'author', 'selftext']:\n# df.loc[:,col] = dfog.loc[:,col].apply(lambda x : regex.sub('', str(x) ))", "_____no_output_____" ] ], [ [ "Filtering the data frame, count vectorizing titles.", "_____no_output_____" ], [ "# Can we predict the number of upvotes using the self text?", "_____no_output_____" ] ], [ [ "#create the train test split\n#try to predict ups using the self text\nX_train, X_test, y_train, y_test = train_test_split(df['selftext'], df['ups'], test_size=0.2, random_state=46)\n\n#make a pipeline to do bag of words and linear regression\ntext_clf = Pipeline([\n ('vect', CountVectorizer()),\n ('tfidf', TfidfTransformer()),\n ('clf', LinearRegression(copy_X=True)),\n])", "_____no_output_____" ], [ "text_clf.fit(X_train,y_train)", "_____no_output_____" ], [ "#text_clf.predict(X_train)\nprint(r2_score(y_train,text_clf.predict(X_train)))\nprint(r2_score(y_test,text_clf.predict(X_test)))", "0.6221427821443792\n-1.01242558018135\n" ], [ "#wow, that is terrible. we do worse than if we just guessed the mean all the time. ", "_____no_output_____" ] ], [ [ "# Can we predict the number of upvotes using the words in the title?", "_____no_output_____" ], [ "## NLP on words in the title\n", "_____no_output_____" ] ], [ [ "#this time we don't need only self posts\ndf2og=wsb.loc[(wsb.ups>=10) & (wsb.num_comments<=10000) & ~(wsb[\"title\"].str.contains(\"Thread|thread|Sunday Live Chat|consolidation zone|Containment Zone|Daily Discussion|Daily discussion|Saturday Chat|What Are Your Moves Tomorrow|What Are Your Moves Today|MEGATHREAD\",na=False))]\ndf2=RegexCols(df2og,['title', 'author', 'selftext'])", "_____no_output_____" ], [ "X_train, X_test, y_train, y_test = train_test_split(df2['title'], df2['ups'], test_size=0.2, random_state=46)\n\ntext_clf = Pipeline([\n ('vect', CountVectorizer()),\n ('tfidf', TfidfTransformer()),\n ('clf', LinearRegression(copy_X=True)),\n])\n\ntext_clf.fit(X_train,y_train)\n\nprint(r2_score(y_train,text_clf.predict(X_train)))\nprint(r2_score(y_test,text_clf.predict(X_test)))\n\nresults = pd.DataFrame()\nresults[\"predicted\"] = text_clf.predict(X_test)\nresults[\"true\"] = list(y_test)\nsns.scatterplot(data = results, x = \"predicted\", y = \"true\")\n", "0.2698255652620519\n-0.19033973194092324\n" ] ], [ [ "Doesn't look particularly useful... neither does using lasso...", "_____no_output_____" ] ], [ [ "X_train, X_test, y_train, y_test = train_test_split(df2['title'], df2['ups'], test_size=0.2, random_state=46)\n\ntext_clf = Pipeline([\n ('vect', CountVectorizer()),\n ('tfidf', TfidfTransformer()),\n ('clf', sklearn.linear_model.Lasso()),\n])\n\ntext_clf.fit(X_train,y_train)\n\nprint(r2_score(y_train,text_clf.predict(X_train)))\nprint(r2_score(y_test,text_clf.predict(X_test)))\n\nresults = pd.DataFrame()\nresults[\"predicted\"] = text_clf.predict(X_test)\nresults[\"true\"] = list(y_test)\nsns.scatterplot(data = results, x = \"predicted\", y = \"true\")\n", "0.019312400789961992\n0.005437116554178001\n" ] ], [ [ "# Can we predict if a post will be ignored?", "_____no_output_____" ] ], [ [ "def PopClassify(ups):\n if ups <100:\n return 0\n elif ups<100000:\n return 1\n else:\n return 2\n\n#df2['popularity']=PopClassify(df2['ups'])\n\ndf2['popularity'] = df2['ups'].map(lambda score: PopClassify(score))\n\n#df['ignored'] = df['ups'] <= 100 # What is a good cutoff for being ignored?\n#df = wsb[ wsb['ups'] >= 20]\ndf2.head()", "_____no_output_____" ], [ "X_train, X_test, y_train, y_test = train_test_split(df2['title'], df2['popularity'], test_size=0.2, random_state=46)", "_____no_output_____" ], [ "from sklearn.naive_bayes import MultinomialNB\n\ntext_clf = Pipeline([('vect', CountVectorizer()),\n ('tfidf', TfidfTransformer()),\n ('clf', MultinomialNB()),\n])\n\ntext_clf.fit(X_train,y_train)", "_____no_output_____" ], [ "p=text_clf.predict(X_train)\nprint(np.where(p==1))\nprint(np.where(p==2))", "(array([ 65, 78, 99, ..., 116695, 116713, 116730], dtype=int64),)\n(array([], dtype=int64),)\n" ], [ "np.mean(p==y_train)", "_____no_output_____" ], [ "p2=text_clf.predict(X_test)\nnp.mean(p2==y_test)", "_____no_output_____" ], [ "#what if we just predict 0 all the time?\nprint(np.mean(y_train==0))\nprint(np.mean(y_test==0))", "0.7193350576386153\n0.7167962728238155\n" ], [ "def PopClassifyn(ups,n):\n if ups <n:\n return 0\n else:\n return 1", "_____no_output_____" ], [ "#the above shows that the 0 category is too big. maybe cut it down to 50? Also throw out the top category\n\n\n\ndf2['popularity'] = df2['ups'].map(lambda score: PopClassifyn(score,50))\n\nX_train, X_test, y_train, y_test = train_test_split(df2['title'], df2['popularity'], test_size=0.2, random_state=46)", "_____no_output_____" ], [ "text_clf = Pipeline([('vect', CountVectorizer()),\n ('tfidf', TfidfTransformer()),\n ('clf', MultinomialNB()),\n])\n\ntext_clf.fit(X_train,y_train)", "_____no_output_____" ], [ "print(\"accuracy on training data:\")\np=text_clf.predict(X_train)\nprint(np.mean(p==y_train))\nprint(np.mean(y_train==0))\nprint(\"accuracy on testing data:\")\nprint(np.mean(text_clf.predict(X_test)==y_test))\nprint(np.mean(y_test==0))", "accuracy on training data:\n0.6819170620578613\n0.5839571093335161\naccuracy on testing data:\n0.597478674934055\n0.5830906786338255\n" ], [ "#slight improvement on the testing data, but lost on the training data...\n#what about something more extreme? Let's keep all the posts with a score of 1. Let's try to predict ups>1\ndf3og=wsb.loc[(wsb.num_comments<=10000) & ~(wsb[\"title\"].str.contains(\"Thread|thread|Sunday Live Chat|consolidation zone|Containment Zone|Daily Discussion|Daily discussion|Saturday Chat|What Are Your Moves Tomorrow|What Are Your Moves Today|MEGATHREAD\",na=False))]", "_____no_output_____" ], [ "df3=RegexCols(df3og,['title', 'author', 'selftext'])", "_____no_output_____" ], [ "df3['popularity'] = df3['ups'].map(lambda score: PopClassifyn(score,2))\n\nX_train, X_test, y_train, y_test = train_test_split(df3['title'], df3['popularity'], test_size=0.2, random_state=46,stratify=df3['popularity'])", "_____no_output_____" ], [ "text_clf = Pipeline([('vect', CountVectorizer()),\n ('tfidf', TfidfTransformer()),\n ('clf', MultinomialNB()),\n])\n\ntext_clf.fit(X_train,y_train)", "_____no_output_____" ], [ "print(\"accuracy on training data:\")\np=text_clf.predict(X_train)\nprint(np.mean(p==y_train))\nprint(np.mean(y_train==0))\nprint(\"accuracy on testing data:\")\nprint(np.mean(text_clf.predict(X_test)==y_test))\nprint(np.mean(y_test==0))", "accuracy on training data:\n0.7778754969417438\n0.7723380039556363\naccuracy on testing data:\n0.7715679681002201\n0.7723360141989041\n" ], [ "#nothing!! what if we try using the selftext?\n#back to df\ndf4og=wsb.loc[(wsb.is_self==True) & (wsb.num_comments<=10000) & ~(wsb[\"title\"].str.contains(\"Thread|thread|Sunday Live Chat|consolidation zone|Containment Zone|Daily Discussion|Daily discussion|Saturday Chat|What Are Your Moves Tomorrow|What Are Your Moves Today|MEGATHREAD\",na=False))]\n\ndf4=RegexCols(df4og,['title', 'author', 'selftext'])\n\ndf4['popularity'] = df4['ups'].map(lambda score: PopClassifyn(score,2))\n\nX_train, X_test, y_train, y_test = train_test_split(df4['selftext'], df4['popularity'], test_size=0.2, random_state=46,stratify=df4['popularity'])", "_____no_output_____" ], [ "text_clf = Pipeline([('vect', CountVectorizer()),\n ('tfidf', TfidfTransformer()),\n ('clf', MultinomialNB()),\n])\n\ntext_clf.fit(X_train,y_train)", "_____no_output_____" ], [ "print(\"accuracy on training data:\")\np=text_clf.predict(X_train)\nprint(np.mean(p==y_train))\nprint(np.mean(y_train==0))\nprint(\"accuracy on testing data:\")\nprint(np.mean(text_clf.predict(X_test)==y_test))\nprint(np.mean(y_test==0))", "accuracy on training data:\n0.8448670002451768\n0.7857120658040588\naccuracy on testing data:\n0.8437849634653369\n0.7857093525974833\n" ], [ "#okay, this is not too bad!\n#other ways to measure how well this is doing?\n#let's try the ROC AUC score\nfrom sklearn.metrics import roc_curve\n\n#text_clf.predict_proba(X_train)[:,1]\nprobs=text_clf.predict_proba(X_train)[:,1]\n\nroc_curve(y_train,probs)", "_____no_output_____" ], [ "fpr,tpr,cutoffs = roc_curve(y_train,probs)\nplt.figure(figsize=(12,8))\n\nplt.plot(fpr,tpr)\n\nplt.xlabel(\"False Positive Rate\",fontsize=16)\nplt.ylabel(\"True Positive Rate\",fontsize=16)\n\nplt.xticks(fontsize=12)\nplt.yticks(fontsize=12)\n\nplt.show()", "_____no_output_____" ], [ "from sklearn.metrics import roc_auc_score\nroc_auc_score(y_train,probs)", "_____no_output_____" ], [ "#now let's try logistic regression rather than naive Bayes?\nfrom sklearn.linear_model import LogisticRegression\nfrom sklearn.preprocessing import StandardScaler\ntext_clf = Pipeline([('vect', CountVectorizer()),\n ('tfidf', TfidfTransformer()),\n #('standardscaler', StandardScaler()),\n ('clf', LogisticRegression(max_iter=1000)),\n])\n\ntext_clf.fit(X_train,y_train)", "_____no_output_____" ], [ "print(\"accuracy on training data:\")\np=text_clf.predict(X_train)\n#print(np.mean(p==y_train))\nprint(accuracy_score(y_train,p))\nprint(np.mean(y_train==0))\nprint(\"accuracy on testing data:\")\nprint(np.mean(text_clf.predict(X_test)==y_test))\nprint(np.mean(y_test==0))", "accuracy on training data:\n0.8566113119718772\n0.8566113119718772\n0.7857120658040588\naccuracy on testing data:\n0.8554359987292292\n0.7857093525974833\n" ], [ "#added later, for ROC curve and AUC score\nprobs=text_clf.predict_proba(X_train)[:,1]\nfpr,tpr,cutoffs = roc_curve(y_train,probs)\nplt.figure(figsize=(12,8))\n\nplt.plot(fpr,tpr)\n\nplt.xlabel(\"False Positive Rate\",fontsize=16)\nplt.ylabel(\"True Positive Rate\",fontsize=16)\n\nplt.xticks(fontsize=12)\nplt.yticks(fontsize=12)\n\nplt.show()\n\nprint(roc_auc_score(y_train,probs))", "_____no_output_____" ], [ "from sklearn.model_selection import cross_validate as cv\nfrom sklearn.metrics import SCORERS as sc\nfrom sklearn.metrics import make_scorer as ms\nfrom sklearn.metrics import balanced_accuracy_score as bas", "_____no_output_____" ], [ "scorer_dict={\n 'accuracy_scorer' : ms(accuracy_score),\n 'auc_scorer' : ms(roc_auc_score),\n 'bas_scorer' : ms(bas)\n}\n\n\n", "_____no_output_____" ], [ "#scores = cross_validate(lasso, X, y, cv=3,\n#... scoring=('r2', 'neg_mean_squared_error'),\n#... return_train_score=True)\n\n#X_train, X_test, y_train, y_test = train_test_split(df4['selftext'], df4['popularity'], test_size=0.2, random_state=46,stratify=df4['popularity'])\n\nscores=cv(text_clf,df4['selftext'],df4['popularity'],cv=5,scoring=scorer_dict, return_train_score=True)", "_____no_output_____" ], [ "print(scores)", "{'fit_time': array([40.94248843, 38.55260706, 52.81538129, 53.88970828, 45.90364528]), 'score_time': array([3.83659148, 3.69096971, 1.59402537, 1.73765063, 2.72420716]), 'test_accuracy_scorer': array([0.84263851, 0.88653535, 0.86513944, 0.83763027, 0.82727066]), 'train_accuracy_scorer': array([0.85876956, 0.8485412 , 0.85103095, 0.86105754, 0.86371304]), 'test_auc_scorer': array([0.75561674, 0.78339892, 0.68621156, 0.63678264, 0.61136783]), 'train_auc_scorer': array([0.69011388, 0.68260579, 0.6941842 , 0.72016217, 0.72657212]), 'test_bas_scorer': array([0.75561674, 0.78339892, 0.68621156, 0.63678264, 0.61136783]), 'train_bas_scorer': array([0.69011388, 0.68260579, 0.6941842 , 0.72016217, 0.72657212])}\n" ], [ "print(np.mean(scores['test_accuracy_scorer']))\nprint(np.mean(scores['test_bas_scorer']))\nprint(np.mean(scores['test_auc_scorer']))", "0.8518428455611801\n0.6946755403441747\n0.6946755403441747\n" ], [ "#this is very slightly better than the other one. Might be even better if we can scale the data", "_____no_output_____" ], [ "text_clf = Pipeline([('vect', CountVectorizer()),\n ('tfidf', TfidfTransformer()),\n ('standardscaler', StandardScaler(with_mean=False)),\n ('clf', LogisticRegression(max_iter=10000)),\n])\n\ntext_clf.fit(X_train,y_train)", "_____no_output_____" ], [ "print(\"accuracy on training data:\")\np=text_clf.predict(X_train)\nprint(np.mean(p==y_train))\nprint(np.mean(y_train==0))\nprint(\"accuracy on testing data:\")\nprint(np.mean(text_clf.predict(X_test)==y_test))\nprint(np.mean(y_test==0))", "_____no_output_____" ], [ "#scaling somehow made it worse on the testing data??", "_____no_output_____" ] ], [ [ "# Can we cluster similar posts?", "_____no_output_____" ] ], [ [ "df3.sort_values(by=\"ups\")", "_____no_output_____" ], [ "\n", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ] ]

cb2ee916cd2858b79ec63bb33fe937167408c5e8

959,312

ipynb

Jupyter Notebook

IPython_Notebooks/Fig2_EEGvsPIR_plusFig3.ipynb

LozRiviera/COMPASS_paper

73d3cd7fd8f0ce4349ff7c7e4b66d57f329a76c4

[ "MIT" ]

1

2021-03-17T19:50:37.000Z

IPython_Notebooks/Fig2_EEGvsPIR_plusFig3.ipynb

LozRiviera/COMPASS_paper

73d3cd7fd8f0ce4349ff7c7e4b66d57f329a76c4

[ "MIT" ]

null

IPython_Notebooks/Fig2_EEGvsPIR_plusFig3.ipynb

LozRiviera/COMPASS_paper

73d3cd7fd8f0ce4349ff7c7e4b66d57f329a76c4

[ "MIT" ]

null

658.415923

343,314

0.928244

[ [ [ "## Sleep analysis, using Passive Infrared (PIR) data, in 10sec bins from a single central PIR, at 200-220mm above the cage floor. Previously EEG-telemetered animals allow direct comparison of sleep scored by direct and non-invasive methods. ", "_____no_output_____" ], [ "### 1st setup analysis environment:", "_____no_output_____" ] ], [ [ "import numpy as np # calculations\nimport pandas as pd # dataframes and IO\nimport matplotlib.pyplot as plt # plotting\n# show graphs/figures in notebooks\n%matplotlib inline\n\nimport seaborn as sns # statistical plots and analysis\nsns.set(style=\"ticks\") # styling\nsns.set_context(\"poster\")", "_____no_output_____" ] ], [ [ "### Then import .CSV text file from activity monitoring (with ISO-8601 encoding for the timepoints)", "_____no_output_____" ] ], [ [ "PIR = pd.read_csv('../PIRdata/1sensorPIRvsEEGdata.csv',parse_dates=True,index_col=0)", "_____no_output_____" ], [ "PIR.head()", "_____no_output_____" ], [ "PIR.pop('PIR4') # remove channels with no Telemetered mice / no sensor\nPIR.pop('PIR6')\nPIR.columns=('Act_A', 'Act_B','Act_C', 'Act_D', 'Light') # and rename the remaining columns with activity data\n#PIR.plot(subplots=True, figsize=(16,12))", "_____no_output_____" ] ], [ [ "### next identify time of lights ON (to match start of scored EEG data)", "_____no_output_____" ] ], [ [ "PIR['Light']['2014-03-18 08:59:30': '2014-03-18 09:00:40'].plot(figsize =(16,4))", "_____no_output_____" ] ], [ [ "### Define period to match EEG data", "_____no_output_____" ] ], [ [ "PIR_24 = PIR.truncate(before='2014-03-18 09:00:00', after='2014-03-19 09:00:00')\nPIR_24shift = PIR_24.tshift(-9, freq='H') # move data on timescale so 0 represents 'lights on'\nPIR_24shift.plot(subplots=True,figsize=(20,10))\n", "_____no_output_____" ] ], [ [ "### Define sleepscan function and run with selected data ", "_____no_output_____" ] ], [ [ "# run through trace looking for bouts of sleep (defined as 4 or more sequential '0' values) variable 'a' is dataframe of PIR data\n\ndef sleepscan(a,bins):\n ss = a.rolling(bins).sum()\n y = ss==0\n return y.astype(int) # if numerical output is required", "_____no_output_____" ], [ "# for each column of activity data define PIR-derived sleep as a new column\nss =PIR_24shift.assign(PIR_A =sleepscan(PIR_24shift['Act_A'],4), \n PIR_B =sleepscan(PIR_24shift['Act_B'],4),\n PIR_C =sleepscan(PIR_24shift['Act_C'],4),\n PIR_D =sleepscan(PIR_24shift['Act_D'],4)).resample('10S').mean()\n \nss.head() # show top of new dataframe", "_____no_output_____" ] ], [ [ "### Importing EEG data scored by Sibah Hasan (follow correction for channels A and B on EEG recordings)\n\n#### Scored as 10 second bins starting at 9am (lights on) , for clarity we will only import the columns for total sleep, although REM and NREM sleep were scored)", "_____no_output_____" ] ], [ [ "eeg10S = pd.read_csv('../PIRdata/EEG_4mice10sec.csv',index_col=False, \n usecols=['MouseA Total sleep ','MouseB Total sleep ','MouseC Total sleep ','MouseD Total sleep '])\neeg10S.columns=('EEG_A', 'EEG_B', 'EEG_C','EEG_D') # rename columns\neeg10S.head()", "_____no_output_____" ], [ "ss.reset_index(inplace=True) # use sequential numbered index to allow concatination (joining) of data\nss_all = pd.concat([ss,eeg10S], axis=1) # join data\nss_all.set_index('Time',inplace=True) # Time as index\n\nss_all.head()", "_____no_output_____" ], [ "#ss_all.pop('index') # and drop old index\nss_all.head()", "_____no_output_____" ] ], [ [ "### Then resample as an average of 30min to get proportion sleep (scored from immobility) ", "_____no_output_____" ] ], [ [ "EEG30 = ss_all.resample('30T').mean() \nEEG30.tail()", "_____no_output_____" ], [ "EEG30.loc[:,['PIR_A','EEG_A']].plot(figsize=(18,4)) # show data for one mouse ", "_____no_output_____" ], [ "# red #A10000 and blue #011C4E colour pallette for figure2\n\nEEGred = [\"#A10000\", \"#011C4E\"] \n\nsns.palplot(sns.color_palette(EEGred)) # show colours\n", "_____no_output_____" ], [ "sns.set_palette(EEGred)\nsns.set_context('poster')\n\nfig, (ax1,ax2, ax3, ax4) = plt.subplots(nrows=4, ncols=1)\nfig.text(1, 0.87,'A',fontsize=24, horizontalalignment='center',verticalalignment='center')\nfig.text(1, 0.635,'B',fontsize=24, horizontalalignment='center',verticalalignment='center')\nfig.text(1, 0.4,'C',fontsize=24, horizontalalignment='center',verticalalignment='center')\nfig.text(1, 0.162,'D',fontsize=24, horizontalalignment='center',verticalalignment='center')\nfig.text(0,0.7, 'Proportion of time asleep', fontsize=18, rotation='vertical')\nfig.text(0.5,0,'Time', fontsize=18)\nfig.text(0.08,0.14,'PIR', fontsize=21, color=\"#011C4E\", fontweight='semibold')\nfig.text(0.08,0.11,'EEG', fontsize=21, color=\"#A10000\", fontweight='semibold')\n\nplt.subplot(411)\nplt.plot(EEG30.index, EEG30['EEG_A'], label= \"EEG total sleep\",lw=2)\nplt.fill_between(EEG30.index, 0, 1, where=EEG30.index>='2014-03-18 12:00:00',lw=0, alpha=0.6, facecolor='#aaaaaa')\nplt.plot(EEG30.index, EEG30['PIR_A'],label= \"PIR sleep\", lw=2)\nplt.xticks(horizontalalignment='left',fontsize=12)\nplt.yticks([0,0.5,1],fontsize=12)\n\n\nplt.subplot(412)\nplt.plot(EEG30.index, EEG30['EEG_B'], lw=2)\nplt.plot(EEG30.index, EEG30['PIR_B'], lw=2)\nplt.fill_between(EEG30.index, 0, 1, where=EEG30.index>='2014-03-18 12:00:00',lw=0, alpha=0.6, facecolor='#aaaaaa')\nplt.xticks(horizontalalignment='left',fontsize=12)\nplt.yticks([0,0.5,1],fontsize=12)\n\nplt.subplot(413)\nplt.plot(EEG30.index, EEG30['EEG_C'], lw=2)\nplt.plot(EEG30.index, EEG30['PIR_C'], lw=2)\nplt.fill_between(EEG30.index, 0, 1, where=EEG30.index>='2014-03-18 12:00:00',lw=0, alpha=0.6, facecolor='#aaaaaa')\nplt.xticks(horizontalalignment='left',fontsize=12)\nplt.yticks([0,0.5,1],fontsize=12)\n\nplt.subplot(414)\nplt.plot(EEG30.index, EEG30['EEG_D'], lw=2)\nplt.plot(EEG30.index, EEG30['PIR_D'], lw=2)\nplt.fill_between(EEG30.index, 0, 1, where=EEG30.index>='2014-03-18 12:00:00',lw=0, alpha=0.6, facecolor='#aaaaaa')\nplt.xticks(horizontalalignment='left',fontsize=12)\nplt.yticks([0,0.5,1],fontsize=12)\n\n\nplt.tight_layout(h_pad=0.2,pad=2)\n\n# options for saving figures\n#plt.savefig('correlations_BlueRed.eps',format='eps', dpi=1200, bbox_inches='tight', pad_inches=0.5) \n#plt.savefig('correlations_BlueRed.jpg',format='jpg', dpi=600,frameon=2, bbox_inches='tight', pad_inches=0.5)\n\nplt.show()", "_____no_output_____" ], [ "sns.set_style(\"white\")\nsns.set_context(\"talk\", font_scale=0.6)\ncorr30 = EEG30\ncorr30.pop('Light')\nsns.corrplot(corr30, sig_stars=False) # show correlation plot for all values \n#plt.savefig('../../Figures/CorrFig3left.eps',format='eps', dpi=600,pad_inches=0.2, frameon=2)", "C:\\Users\\labrown\\Anaconda2\\envs\\COMPASS\\lib\\site-packages\\seaborn\\linearmodels.py:1285: UserWarning: The `corrplot` function has been deprecated in favor of `heatmap` and will be removed in a forthcoming release. Please update your code.\n warnings.warn((\"The `corrplot` function has been deprecated in favor \"\nC:\\Users\\labrown\\Anaconda2\\envs\\COMPASS\\lib\\site-packages\\seaborn\\linearmodels.py:1351: UserWarning: The `symmatplot` function has been deprecated in favor of `heatmap` and will be removed in a forthcoming release. Please update your code.\n warnings.warn((\"The `symmatplot` function has been deprecated in favor \"\n" ] ], [ [ "# Bland-Altman as an alternative to correlation plots?", "_____no_output_____" ], [ "### Combined data from all 4 mice (paired estimates of sleep by PIR and EEG aligned in Excel)", "_____no_output_____" ] ], [ [ "df = pd.read_csv('../PIRdata/blandAltLandD.csv')", "_____no_output_____" ], [ "def bland_altman_plot(data1, data2, *args, **kwargs):\n data1 = np.asarray(data1)\n data2 = np.asarray(data2)\n mean = np.mean([data1, data2], axis=0)\n diff = data1 - data2 # Difference between data1 and data2\n md = np.mean(diff) # Mean of the difference\n sd = np.std(diff, axis=0) # Standard deviation of the difference\n\n plt.scatter(mean, diff, *args, **kwargs)\n plt.axis([0, 30, -30, 30])\n plt.axhline(md, linestyle='-', *args, **kwargs)\n plt.axhline(md + 1.96*sd, linestyle='--', *args, **kwargs)\n plt.axhline(md - 1.96*sd, linestyle='--', *args, **kwargs)\n ", "_____no_output_____" ], [ "def bland_altman_output(data1, data2, *args, **kwargs):\n data1 = np.asarray(data1)\n data2 = np.asarray(data2)\n mean = np.mean([data1, data2], axis=0)\n diff = data1 - data2 # Difference between data1 and data2\n md = np.mean(diff) # Mean of the difference\n sd = np.std(diff, axis=0) # Standard deviation of the difference\n return md , md-(1.96*sd), md+(1.96*sd)", "_____no_output_____" ], [ "sns.set_context('talk')\nc1, c2, c3 = sns.blend_palette([\"#002147\",\"gold\",\"grey\"], 3)\nplt.subplot(111, axisbg=c3)\n\nbland_altman_plot(df.PIR_Light, df.EEG_Light,color=c2, linewidth=3)\nbland_altman_plot(df.PIR_dark, df.EEG_dark,color=c1, linewidth=3)\nplt.xlabel('Average score from both methods (min)', fontsize=14)\nplt.ylabel('PIR score - EEG score (min)', fontsize=14)\n\nplt.title('Bland-Altman comparison of PIR-derived sleep and EEG-scored sleep', fontsize=16)\n\n#plt.savefig('../../Figures/blandAltman4mice.eps',format='eps', dpi=1200,pad_inches=1,\n# frameon=0)\nplt.show()", "_____no_output_____" ], [ "bland_altman_output(df.PIR_Light, df.EEG_Light)", "_____no_output_____" ], [ "bland_altman_output(df.PIR_dark, df.EEG_dark)", "_____no_output_____" ], [ "# Combine (concatenate) these data to get overall comparison of measurements\n\ndf.PIR = pd.concat([df.PIR_dark, df.PIR_Light],axis=0)\ndf.EEG = pd.concat([df.EEG_dark, df.EEG_Light],axis=0)\ndfall =pd.concat([df.PIR, df.EEG], axis=1, keys=['PIR', 'EEG'])\ndfall.head()", "_____no_output_____" ], [ "bland_altman_output(dfall.PIR, dfall.EEG) # mean and 95% CIs for overall comparison", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2ee96c9e7a982526c83579c317146f5a294f43

959,533

ipynb

Jupyter Notebook

notebooks/SMELTresults.ipynb

SalishSeaCast/analysis-susan

52633f4fe82af6d7c69dff58f69f0da4f7933f48

[ "Apache-2.0" ]

null

notebooks/SMELTresults.ipynb

SalishSeaCast/analysis-susan

52633f4fe82af6d7c69dff58f69f0da4f7933f48

[ "Apache-2.0" ]

null

notebooks/SMELTresults.ipynb

SalishSeaCast/analysis-susan

52633f4fe82af6d7c69dff58f69f0da4f7933f48

[ "Apache-2.0" ]

null

1,680.443082

243,022

0.94844

[ [ [ "# Notebook to Look at SMELT results \n", "_____no_output_____" ] ], [ [ "import netCDF4 as nc\nimport matplotlib.pyplot as plt\nimport matplotlib.colors\nfrom matplotlib.colors import LogNorm\nimport datetime\nimport os\nimport numpy as np\n\nfrom salishsea_tools import visualisations as vis\nfrom salishsea_tools import (teos_tools, tidetools, viz_tools)\n\n%matplotlib inline", "_____no_output_____" ], [ "def results_dataset(results_dir, date, ndays, period, grid_type):\n datestr = date.strftime('%Y%m%d')\n dateend = date + datetime.timedelta(days=ndays-1)\n dateendstr = dateend.strftime('%Y%m%d')\n fname = os.path.join(results_dir,\n 'SalishSea_{}_{}_{}_{}.nc'.format(period, datestr, dateendstr, grid_type))\n print (fname)\n grid = nc.Dataset(fname)\n return grid", "_____no_output_____" ], [ "mesh_mask = nc.Dataset('/ocean/sallen/allen/research/MEOPAR/NEMO-forcing/grid/mesh_mask_downbyone2.nc')\ntmask = mesh_mask.variables['tmask'][:]\n\ngrid_B = nc.Dataset('/ocean/sallen/allen/research/MEOPAR/NEMO-forcing/grid/bathy_downonegrid2.nc')\nbathy, lons, lats = tidetools.get_bathy_data(grid_B)\n\nfinal = '/results/SalishSea/nowcast-green/14aug16/'\ndate = datetime.datetime(2016, 8, 14)\nptrc_T = results_dataset(final, date, 1, '1h', 'ptrc_T')\nnitrateF = ptrc_T.variables['NO3'][0,:,:,:]\nprint (nitrateF.shape)\n\ninitial = '/results/SalishSea/nowcast-green/14jan16/'\nni = results_dataset(initial, datetime.datetime(2016, 1, 14), 1, '1h', 'ptrc_T')\n#print (ni.variables.keys())\n#nitrate0 = ni.variables['TRNNO3'][0,:]\nnitrate0 = ni.variables['NO3'][0,:,:,:]", "/results/SalishSea/nowcast-green/14aug16/SalishSea_1h_20160814_20160814_ptrc_T.nc\n(40, 898, 398)\n/results/SalishSea/nowcast-green/14jan16/SalishSea_1h_20160114_20160114_ptrc_T.nc\n" ], [ "fig,ax = plt.subplots(1,1,figsize=(15,5))\nclevels = np.arange(0., 31., 1)\ncbar = vis.contour_thalweg(ax, nitrate0, bathy, lons, lats, mesh_mask, 'gdept_0', clevels, cmap='viridis')\nax.set_ylim([450,0])\ncbar.set_label('Nitrate [uM]')\nax.set_title('Initial Nitrate')", "_____no_output_____" ], [ "fig,ax = plt.subplots(1,1,figsize=(15,5))\ncbar = vis.contour_thalweg(ax, nitrateF, bathy, lons, lats, mesh_mask, 'gdept_0', clevels, cmap='viridis')\nax.set_ylim([450,0])\ncbar.set_label('Nitrate [uM]')\nax.set_title('Nitrate')", "_____no_output_____" ], [ "phyto0 = ni.variables['PHY'][0,:] + ni.variables['PHY2'][0,:]\nclevels = np.arange(0, 12, 1.)\nfig,ax = plt.subplots(1,1,figsize=(15,5))\ncbar = vis.contour_thalweg(ax, phyto0, bathy, lons, lats, mesh_mask, 'gdept_0', clevels, cmap='viridis')\nax.set_ylim([50,0])\ncbar.set_label('Log Initial Phyto [uM]')\nax.set_title('Initial Diatoms + Flag');", "_____no_output_____" ], [ "diatoms = ptrc_T.variables['PHY2'][0,:,:,:] \nfig,ax = plt.subplots(1,1,figsize=(15,5))\ncbar = vis.contour_thalweg(ax, diatoms, bathy, lons, lats, mesh_mask, 'gdept_0', clevels, cmap='viridis')\nax.set_ylim([50,0])\ncbar.set_label('Diatoms [uM]')\nax.set_title('Diatoms');", "_____no_output_____" ], [ "diatoms_masked = np.ma.array(diatoms[0:20], mask=np.logical_not(tmask[0, 0:20]))\nsum_diatoms = np.sum(diatoms_masked, axis=0)\nfig, ax = plt.subplots(1, 3, figsize=(15,10))\ncmap = plt.get_cmap('plasma')\ncmap.set_bad('black')\nmesh = ax[0].pcolormesh(sum_diatoms, cmap=cmap, vmax = 100)\nfig.colorbar(mesh, ax=ax[0])\nax[0].set_title('Top 20 m Diatoms (uM/m$^2$)')\nmesh = ax[1].pcolormesh(diatoms_masked[0], cmap=cmap, vmax = 10)\nfig.colorbar(mesh, ax=ax[1])\nax[1].set_title('Surface Diatoms (uM/m$^3$)')\nmesh = ax[2].pcolormesh(diatoms_masked[11], cmap=cmap, vmax= 10)\nax[2].set_title('10.5 m Depth Diatoms (uM/m$^3$)')\nfig.colorbar(mesh, ax=ax[2])", "_____no_output_____" ], [ "flag = ptrc_T.variables['PHY'][0,:,:,:]\nfig,ax = plt.subplots(1,1,figsize=(15,5))\ncbar = vis.contour_thalweg(ax, flag, bathy, lons, lats, mesh_mask, 'gdept_0', clevels, cmap='viridis')\nax.set_ylim([450,0])\ncbar.set_label('Flagellates [uM]')\nax.set_title('Flagellates');", "_____no_output_____" ], [ "fig,ax = plt.subplots(1,2,figsize=(15,5))\nclevels = [-0.55, -0.3, -0.05, 0.05, 0.3, 0.55]\n\ncbar = vis.contour_thalweg(ax[0], nitrateF-nitrate0, bathy, lons, lats, mesh_mask, 'gdept_0', clevels, cmap='bwr')\nax[0].set_ylim([450,0])\nax[0].set_xlim([0,400])\ncbar.set_label('Nitrate [uM]')\nax[0].set_title('Difference in Nitrate')\n\ncbar = vis.contour_thalweg(ax[1], nitrateF-nitrate0, bathy, lons, lats, mesh_mask, 'gdept_0', clevels, cmap='bwr')\nax[1].set_ylim([450,0])\nax[1].set_xlim([400, 724])\ncbar.set_label('Nitrate [uM]')\nax[1].set_title('Difference in Nitrate')", "_____no_output_____" ], [ "print (ptrc_T.variables.keys())\n#nitrateF = ptrc_T.variables['NO3'][:,:,:,:]\n", "_____no_output_____" ], [ "for v in ptrc_T.variables.keys():\n print (v, np.max(ptrc_T.variables[v][:]))", "DOC 17.9814\nMICZ 3.33046\nMYRI 2.08737\nNH4 7.2663\nNO3 45.2287\nO2 4506.66\nPHY 3.80859\nPHY2 14.1644\nPOC 2.28843\nSi 102.265\narea 239355.0\nbSi 11.9662\nbounds_lat 51.1048\nbounds_lon -121.318\ndeptht 441.466\ndeptht_bounds 454.932\nnav_lat 51.1048\nnav_lon -121.318\ntime_centered 3679300800.0\ntime_centered_bounds 3679344000.0\ntime_counter 3679300800.0\ntime_counter_bounds 3679344000.0\n" ], [ "oxy = ptrc_T.variables['O2'][0, :]\nclevels = np.arange(150, 300, 10)\nfig,ax = plt.subplots(1,1,figsize=(15,5))\ncbar = vis.contour_thalweg(ax, oxy, bathy, lons, lats, mesh_mask, 'gdept_0', clevels, cmap='viridis')\nax.set_ylim([450,0]);\n", "_____no_output_____" ], [ "oxy_in = ni.variables['O2'][0, :]\nclevels = np.arange(150, 300, 10)\nfig,ax = plt.subplots(1,1,figsize=(15,5))\ncbar = vis.contour_thalweg(ax, oxy_in, bathy, lons, lats, mesh_mask, 'gdept_0', clevels, cmap='viridis')\nax.set_ylim([450,0]);", "_____no_output_____" ], [ "oxy_masked = np.ma.array(oxy, mask=np.logical_not(tmask[0]))\nsum_oxy = np.sum(oxy_masked, axis=0)\nfig, ax = plt.subplots(1, 2, figsize=(10,10))\ncmap = plt.get_cmap('plasma')\ncmap.set_bad('black')\nmesh = ax[0].pcolormesh(sum_oxy, cmap=cmap)\nfig.colorbar(mesh, ax=ax[0])\nax[0].set_title('Integrated Oxygen')\nmesh = ax[1].pcolormesh(oxy_masked[0], cmap=cmap)\nfig.colorbar(mesh, ax=ax[1])\nax[1].set_title('Surface Oxygen')", "_____no_output_____" ], [ "imax=750; imin = 470; jmin=100; jmax=250\ndiatoms_masked = np.ma.array(diatoms[0:20], mask=np.logical_not(tmask[0, 0:20]))\nnitrate_masked = np.ma.array(nitrateF[0:20], mask=np.logical_not(tmask[0, 0:20]))\nsum_diatoms = np.sum(diatoms_masked, axis=0)\nfig, ax = plt.subplots(1, 3, figsize=(15, 7))\ncmap = plt.get_cmap('plasma')\ncmap.set_bad('burlywood')\nmesh = ax[2].pcolormesh(sum_diatoms[imin:imax, jmin:jmax], cmap=cmap, norm=matplotlib.colors.LogNorm(), vmin=3)\nfig.colorbar(mesh, ax=ax[2])\nax[2].set_title('Top 20 m Diatoms (uM N/m$^2$)')\n\nmesh = ax[1].pcolormesh(diatoms_masked[0, imin:imax, jmin:jmax], cmap=cmap, norm=matplotlib.colors.LogNorm() ,vmin=0.03)\nfig.colorbar(mesh, ax=ax[1])\nax[1].set_title('Surface Diatoms (uM N/m$^3$)')\nmesh = ax[0].pcolormesh(nitrate_masked[0, imin:imax, jmin:jmax], cmap=cmap, norm=matplotlib.colors.LogNorm(), vmin=0.003)\nax[0].set_title('Surface Nitrate (uM N/m$^3$)')\nfig.colorbar(mesh, ax=ax[0])\nfor axi in ax:\n viz_tools.set_aspect(axi)\n axi.set_xlim((0,150))\n axi.set_ylim((0,280))\n axi.text(10, 20, 'Vancouver Island')\n axi.text(100, 245, 'Jervis Inlet')\n axi.text(8, 190, 'Comox')\nax[0].text(0, -20, 'Model Results for Aug 14, 2016: all are logscale')\nax[0].text(0, -30, 'Note surface nitrate source from north, and surface diatom bloom in response')\nax[0].text(0, -40, 'However, depth-integrated diatoms are much more widespread due to sub-surface growth')", "_____no_output_____" ] ] ]

[ "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2eeeb1a3d96dd95c32780f8008a311ffb0f32b

208,534

ipynb

Jupyter Notebook

.ipynb_checkpoints/Matplotlib implementation-checkpoint.ipynb

nishantml/Data-Science-Notebooks

4a468b8492341e56894d064177f79ba7ae4dc1b0

[ "MIT" ]

1

2020-05-19T17:48:34.000Z

Matplotlib implementation.ipynb

nishantml/Data-Science-Notebooks

4a468b8492341e56894d064177f79ba7ae4dc1b0

[ "MIT" ]

null

Matplotlib implementation.ipynb

nishantml/Data-Science-Notebooks

4a468b8492341e56894d064177f79ba7ae4dc1b0

[ "MIT" ]

null

283.719728

33,180

0.927647

[ [ [ "### What is Matplotlib?\nMatplotlib is a plotting library for the Python, Pyplot is a matplotlib module which provides a MATLAB-like interface. Matplotlib is designed to be as usable as MATLAB, with the ability to use Python, and the advantage of being free and open-source.\n\n#### What does Matplotlib Pyplot do?\nMatplotlib is a collection of command style functions that make matplotlib work like MATLAB. Each pyplot function makes some change to a figure: e.g., creates a figure, creates a plotting area in a figure, plots some lines in a plotting area, decorates the plot with labels, etc.", "_____no_output_____" ] ], [ [ "# import matplotlib\nimport matplotlib.pyplot as plt\nimport numpy as np\nimport pandas as pd", "_____no_output_____" ] ], [ [ "### Line chart\nIt is a chart in which series of data are plotted by straight lines, in which we can use line chart (straight lines) to compare related features i.e (x and y). We can explicitly define the grid, the x and y axis scale and labels, title and display options.", "_____no_output_____" ] ], [ [ "a= range(1,16)\nb = np.array(a)**2\n#Now by just appliying plot command and the below chart will appear\nplt.plot(a,b)", "_____no_output_____" ], [ "# we can change the line color by following code ", "_____no_output_____" ], [ "plt.plot(a,b,color='red')", "_____no_output_____" ], [ "#we can change the type of line and its width by ls and lw variable \nplt.plot(a,b,color='red', ls='--',lw=2)", "_____no_output_____" ], [ "# OR WE CAN DEFINE THE MARKER \nplt.plot(a,b,color='green', marker='4',mew=10)", "_____no_output_____" ], [ "# we can enable grid view \nplt.grid()\nplt.plot(a,b,color='orange', ls='--',lw=2)", "_____no_output_____" ] ], [ [ "Plotting the line chart from panda DataFrame ", "_____no_output_____" ] ], [ [ "delhi_sale = [45,34,76,65,73,40]\nbangalore_sale = [51,14,36,95,33,45]\npune_sale = [39,85,34,12,55,8]\nsales = pd.DataFrame({'Delhi':delhi_sale,'Bangalore':bangalore_sale,'Pune':pune_sale})\nsales", "_____no_output_____" ], [ "## Lets plot line chart and xtricks and ytricks are used to specify significant range of axis\nsales.plot(xticks=range(1,6),yticks=range(0,100,20))", "_____no_output_____" ], [ "# we can define color for different lines", "_____no_output_____" ], [ "color = ['Red','Yellow','Black']\nsales.plot(xticks=range(1,6),yticks=range(0,100,20),color = color)", "_____no_output_____" ] ], [ [ "### Bar Chart\nBar Chart is used to analyse the group of data,A bar chart or bar graph is a chart or graph that presents categorical data with rectangular bars with heights or lengths proportional to the values that they represent. The bars can be plotted vertically or horizontally.\n", "_____no_output_____" ] ], [ [ "plt.bar(a,b)", "_____no_output_____" ] ], [ [ "Plotting the Bar chart from panda DataFrame", "_____no_output_____" ] ], [ [ "#we can generate bar chart from pandas DataFrame \nsales.plot(kind='bar')", "_____no_output_____" ] ], [ [ "### Pie Chart\nPie chart represents whole data as a circle. Different categories makes slice along the circle based on their propertion \n", "_____no_output_____" ] ], [ [ "a = [3,4,5,8,15]\nplt.pie(a,labels=['A','B','C','D','E'])", "_____no_output_____" ], [ "# we can define color for each categories \ncolor_list = ['Red','Blue','Green','black','orange']\nplt.pie(a,labels=['A','B','C','D','E'],colors=color_list)", "_____no_output_____" ] ], [ [ "### Histograms \nHistogram allows us to determine the shape of continuous data. It is one of the plot which is used in statistics. Using this we can detect the distribution of data,outliers in the data and other useful properties \nto construct histogram from continuous data, we need to create bins and put data in the appropriate bin,The bins parameter tells you the number of bins that your data will be divided into.", "_____no_output_____" ] ], [ [ "# For example, here we ask for 20 bins:\nx = np.random.randn(100)\nplt.hist(x, bins=20)", "_____no_output_____" ], [ "# And here we ask for bin edges at the locations [-4, -3, -2... 3, 4].\nplt.hist(x, bins=range(-4, 5))", "_____no_output_____" ] ], [ [ "### Scatter Plot\nIt is used to show the relationship between two set of data points. For example, any person weight and height.\n", "_____no_output_____" ] ], [ [ "N = 50\nx = np.random.rand(N)\ny = np.random.rand(N)\ncolors = np.random.rand(N)\narea = (30 * np.random.rand(N))**2 # 0 to 15 point radii\n\nplt.scatter(x, y, s=area, c=colors, alpha=0.5)\nplt.show()", "_____no_output_____" ] ], [ [ "### Bow Plot\nBow plot is used to understand the variable spread. In Box plot , rectangle top boundary represents third quantile, bottom boundary represents first quantile and line in the box indicates medium\nverticle line at the top indicates max value and vertical line at the bottom indicates the min value ", "_____no_output_____" ] ], [ [ "box_data = np.random.normal(56,10,50).astype(int)\nplt.boxplot(box_data)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2ef1d12c04955bb21a42e666c9bb7773a19e81

35,191

ipynb

Jupyter Notebook

site/zh-cn/tutorials/load_data/images.ipynb

phoenix-fork-tensorflow/docs-l10n

2287738c22e3e67177555e8a41a0904edfcf1544

[ "Apache-2.0" ]

491

2020-01-27T19:05:32.000Z

2022-03-31T08:50:44.000Z

site/zh-cn/tutorials/load_data/images.ipynb

phoenix-fork-tensorflow/docs-l10n

2287738c22e3e67177555e8a41a0904edfcf1544

[ "Apache-2.0" ]

511

2020-01-27T22:40:05.000Z

2022-03-21T08:40:55.000Z

site/zh-cn/tutorials/load_data/images.ipynb

phoenix-fork-tensorflow/docs-l10n

2287738c22e3e67177555e8a41a0904edfcf1544

[ "Apache-2.0" ]

627

2020-01-27T21:49:52.000Z

2022-03-28T18:11:50.000Z

23.906929

257

0.465005

[ [ [ "##### Copyright 2019 The TensorFlow Authors.", "_____no_output_____" ] ], [ [ "#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n# you may not use this file except in compliance with the License.\n# You may obtain a copy of the License at\n#\n# https://www.apache.org/licenses/LICENSE-2.0\n#\n# Unless required by applicable law or agreed to in writing, software\n# distributed under the License is distributed on an \"AS IS\" BASIS,\n# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n# See the License for the specific language governing permissions and\n# limitations under the License.\n", "_____no_output_____" ] ], [ [ "# 用 tf.data 加载图片", "_____no_output_____" ], [ "<table class=\"tfo-notebook-buttons\" align=\"left\">\n <td>\n <a target=\"_blank\" href=\"https://tensorflow.google.cn/tutorials/load_data/images\"><img src=\"https://tensorflow.google.cn/images/tf_logo_32px.png\" />在 tensorflow.google.cn 上查看</a>\n </td>\n <td>\n <a target=\"_blank\" href=\"https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/load_data/images.ipynb\"><img src=\"https://tensorflow.google.cn/images/colab_logo_32px.png\" />在 Google Colab 运行</a>\n </td>\n <td>\n <a target=\"_blank\" href=\"https://github.com/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/load_data/images.ipynb\"><img src=\"https://tensorflow.google.cn/images/GitHub-Mark-32px.png\" />在 Github 上查看源代码</a>\n </td>\n <td>\n <a href=\"https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/zh-cn/tutorials/load_data/images.ipynb\"><img src=\"https://tensorflow.google.cn/images/download_logo_32px.png\" />下载此 notebook</a>\n </td>\n</table>", "_____no_output_____" ], [ "Note: 我们的 TensorFlow 社区翻译了这些文档。因为社区翻译是尽力而为，所以无法保证它们是最准确的，并且反映了最新的\n[官方英文文档](https://tensorflow.google.cn/?hl=en)。如果您有改进此翻译的建议，请提交 pull request 到\n[tensorflow/docs](https://github.com/tensorflow/docs) GitHub 仓库。要志愿地撰写或者审核译文，请加入\n[[email protected] Google Group](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-zh-cn)。", "_____no_output_____" ], [ "本教程提供一个如何使用 `tf.data` 加载图片的简单例子。\n\n本例中使用的数据集分布在图片文件夹中，一个文件夹含有一类图片。", "_____no_output_____" ], [ "## 配置", "_____no_output_____" ] ], [ [ "import tensorflow as tf", "_____no_output_____" ], [ "AUTOTUNE = tf.data.experimental.AUTOTUNE", "_____no_output_____" ] ], [ [ "## 下载并检查数据集", "_____no_output_____" ], [ "### 检索图片\n\n在你开始任何训练之前，你将需要一组图片来教会网络你想要训练的新类别。你已经创建了一个文件夹，存储了最初使用的拥有创作共用许可的花卉照片。", "_____no_output_____" ] ], [ [ "import pathlib\ndata_root_orig = tf.keras.utils.get_file(origin='https://storage.googleapis.com/download.tensorflow.org/example_images/flower_photos.tgz',\n fname='flower_photos', untar=True)\ndata_root = pathlib.Path(data_root_orig)\nprint(data_root)", "_____no_output_____" ] ], [ [ "下载了 218 MB 之后，你现在应该有花卉照片副本：", "_____no_output_____" ] ], [ [ "for item in data_root.iterdir():\n print(item)", "_____no_output_____" ], [ "import random\nall_image_paths = list(data_root.glob('*/*'))\nall_image_paths = [str(path) for path in all_image_paths]\nrandom.shuffle(all_image_paths)\n\nimage_count = len(all_image_paths)\nimage_count", "_____no_output_____" ], [ "all_image_paths[:10]", "_____no_output_____" ] ], [ [ "### 检查图片\n现在让我们快速浏览几张图片，这样你知道你在处理什么：", "_____no_output_____" ] ], [ [ "import os\nattributions = (data_root/\"LICENSE.txt\").open(encoding='utf-8').readlines()[4:]\nattributions = [line.split(' CC-BY') for line in attributions]\nattributions = dict(attributions)", "_____no_output_____" ], [ "import IPython.display as display\n\ndef caption_image(image_path):\n image_rel = pathlib.Path(image_path).relative_to(data_root)\n return \"Image (CC BY 2.0) \" + ' - '.join(attributions[str(image_rel)].split(' - ')[:-1])\n", "_____no_output_____" ], [ "for n in range(3):\n image_path = random.choice(all_image_paths)\n display.display(display.Image(image_path))\n print(caption_image(image_path))\n print()", "_____no_output_____" ] ], [ [ "### 确定每张图片的标签", "_____no_output_____" ], [ "列出可用的标签：", "_____no_output_____" ] ], [ [ "label_names = sorted(item.name for item in data_root.glob('*/') if item.is_dir())\nlabel_names", "_____no_output_____" ] ], [ [ "为每个标签分配索引：", "_____no_output_____" ] ], [ [ "label_to_index = dict((name, index) for index, name in enumerate(label_names))\nlabel_to_index", "_____no_output_____" ] ], [ [ "创建一个列表，包含每个文件的标签索引：", "_____no_output_____" ] ], [ [ "all_image_labels = [label_to_index[pathlib.Path(path).parent.name]\n for path in all_image_paths]\n\nprint(\"First 10 labels indices: \", all_image_labels[:10])", "_____no_output_____" ] ], [ [ "### 加载和格式化图片", "_____no_output_____" ], [ "TensorFlow 包含加载和处理图片时你需要的所有工具：", "_____no_output_____" ] ], [ [ "img_path = all_image_paths[0]\nimg_path", "_____no_output_____" ] ], [ [ "以下是原始数据：", "_____no_output_____" ] ], [ [ "img_raw = tf.io.read_file(img_path)\nprint(repr(img_raw)[:100]+\"...\")", "_____no_output_____" ] ], [ [ "将它解码为图像 tensor（张量）：", "_____no_output_____" ] ], [ [ "img_tensor = tf.image.decode_image(img_raw)\n\nprint(img_tensor.shape)\nprint(img_tensor.dtype)", "_____no_output_____" ] ], [ [ "根据你的模型调整其大小：", "_____no_output_____" ] ], [ [ "img_final = tf.image.resize(img_tensor, [192, 192])\nimg_final = img_final/255.0\nprint(img_final.shape)\nprint(img_final.numpy().min())\nprint(img_final.numpy().max())\n", "_____no_output_____" ] ], [ [ "将这些包装在一个简单的函数里，以备后用。", "_____no_output_____" ] ], [ [ "def preprocess_image(image):\n image = tf.image.decode_jpeg(image, channels=3)\n image = tf.image.resize(image, [192, 192])\n image /= 255.0 # normalize to [0,1] range\n\n return image", "_____no_output_____" ], [ "def load_and_preprocess_image(path):\n image = tf.io.read_file(path)\n return preprocess_image(image)", "_____no_output_____" ], [ "import matplotlib.pyplot as plt\n\nimage_path = all_image_paths[0]\nlabel = all_image_labels[0]\n\nplt.imshow(load_and_preprocess_image(img_path))\nplt.grid(False)\nplt.xlabel(caption_image(img_path))\nplt.title(label_names[label].title())\nprint()", "_____no_output_____" ] ], [ [ "## 构建一个 `tf.data.Dataset`", "_____no_output_____" ], [ "### 一个图片数据集", "_____no_output_____" ], [ "构建 `tf.data.Dataset` 最简单的方法就是使用 `from_tensor_slices` 方法。\n\n将字符串数组切片，得到一个字符串数据集：", "_____no_output_____" ] ], [ [ "path_ds = tf.data.Dataset.from_tensor_slices(all_image_paths)", "_____no_output_____" ] ], [ [ "`shapes（维数）` 和 `types（类型）` 描述数据集里每个数据项的内容。在这里是一组标量二进制字符串。", "_____no_output_____" ] ], [ [ "print(path_ds)", "_____no_output_____" ] ], [ [ "现在创建一个新的数据集，通过在路径数据集上映射 `preprocess_image` 来动态加载和格式化图片。", "_____no_output_____" ] ], [ [ "image_ds = path_ds.map(load_and_preprocess_image, num_parallel_calls=AUTOTUNE)", "_____no_output_____" ], [ "import matplotlib.pyplot as plt\n\nplt.figure(figsize=(8,8))\nfor n, image in enumerate(image_ds.take(4)):\n plt.subplot(2,2,n+1)\n plt.imshow(image)\n plt.grid(False)\n plt.xticks([])\n plt.yticks([])\n plt.xlabel(caption_image(all_image_paths[n]))\n plt.show()", "_____no_output_____" ] ], [ [ "### 一个`(图片, 标签)`对数据集", "_____no_output_____" ], [ "使用同样的 `from_tensor_slices` 方法你可以创建一个标签数据集：", "_____no_output_____" ] ], [ [ "label_ds = tf.data.Dataset.from_tensor_slices(tf.cast(all_image_labels, tf.int64))", "_____no_output_____" ], [ "for label in label_ds.take(10):\n print(label_names[label.numpy()])", "_____no_output_____" ] ], [ [ "由于这些数据集顺序相同，你可以将他们打包在一起得到一个`(图片, 标签)`对数据集：", "_____no_output_____" ] ], [ [ "image_label_ds = tf.data.Dataset.zip((image_ds, label_ds))", "_____no_output_____" ] ], [ [ "这个新数据集的 `shapes（维数）` 和 `types（类型）` 也是维数和类型的元组，用来描述每个字段：", "_____no_output_____" ] ], [ [ "print(image_label_ds)", "_____no_output_____" ] ], [ [ "注意：当你拥有形似 `all_image_labels` 和 `all_image_paths` 的数组，`tf.data.dataset.Dataset.zip` 的替代方法是将这对数组切片。", "_____no_output_____" ] ], [ [ "ds = tf.data.Dataset.from_tensor_slices((all_image_paths, all_image_labels))\n\n# 元组被解压缩到映射函数的位置参数中\ndef load_and_preprocess_from_path_label(path, label):\n return load_and_preprocess_image(path), label\n\nimage_label_ds = ds.map(load_and_preprocess_from_path_label)\nimage_label_ds", "_____no_output_____" ] ], [ [ "### 训练的基本方法", "_____no_output_____" ], [ "要使用此数据集训练模型，你将会想要数据：\n\n* 被充分打乱。\n* 被分割为 batch。\n* 永远重复。\n* 尽快提供 batch。\n\n使用 `tf.data` api 可以轻松添加这些功能。", "_____no_output_____" ] ], [ [ "BATCH_SIZE = 32\n\n# 设置一个和数据集大小一致的 shuffle buffer size（随机缓冲区大小）以保证数据\n# 被充分打乱。\nds = image_label_ds.shuffle(buffer_size=image_count)\nds = ds.repeat()\nds = ds.batch(BATCH_SIZE)\n# 当模型在训练的时候，`prefetch` 使数据集在后台取得 batch。\nds = ds.prefetch(buffer_size=AUTOTUNE)\nds", "_____no_output_____" ] ], [ [ "这里有一些注意事项：\n\n1. 顺序很重要。\n\n * 在 `.repeat` 之后 `.shuffle`，会在 epoch 之间打乱数据（当有些数据出现两次的时候，其他数据还没有出现过）。\n \n * 在 `.batch` 之后 `.shuffle`，会打乱 batch 的顺序，但是不会在 batch 之间打乱数据。\n\n1. 你在完全打乱中使用和数据集大小一样的 `buffer_size（缓冲区大小）`。较大的缓冲区大小提供更好的随机化，但使用更多的内存，直到超过数据集大小。\n\n1. 在从随机缓冲区中拉取任何元素前，要先填满它。所以当你的 `Dataset（数据集）`启动的时候一个大的 `buffer_size（缓冲区大小）`可能会引起延迟。\n\n1. 在随机缓冲区完全为空之前，被打乱的数据集不会报告数据集的结尾。`Dataset（数据集）`由 `.repeat` 重新启动，导致需要再次等待随机缓冲区被填满。\n\n\n最后一点可以通过使用 `tf.data.Dataset.apply` 方法和融合过的 `tf.data.experimental.shuffle_and_repeat` 函数来解决:", "_____no_output_____" ] ], [ [ "ds = image_label_ds.apply(\n tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))\nds = ds.batch(BATCH_SIZE)\nds = ds.prefetch(buffer_size=AUTOTUNE)\nds", "_____no_output_____" ] ], [ [ "### 传递数据集至模型\n\n从 `tf.keras.applications` 取得 MobileNet v2 副本。\n\n该模型副本会被用于一个简单的迁移学习例子。\n\n设置 MobileNet 的权重为不可训练：", "_____no_output_____" ] ], [ [ "mobile_net = tf.keras.applications.MobileNetV2(input_shape=(192, 192, 3), include_top=False)\nmobile_net.trainable=False", "_____no_output_____" ] ], [ [ "该模型期望它的输出被标准化至 `[-1,1]` 范围内：\n\n```\nhelp(keras_applications.mobilenet_v2.preprocess_input)\n```\n\n<pre>\n……\n该函数使用“Inception”预处理，将\nRGB 值从 [0, 255] 转化为 [-1, 1]\n……\n</pre>", "_____no_output_____" ], [ "在你将输出传递给 MobilNet 模型之前，你需要将其范围从 `[0,1]` 转化为 `[-1,1]`：", "_____no_output_____" ] ], [ [ "def change_range(image,label):\n return 2*image-1, label\n\nkeras_ds = ds.map(change_range)", "_____no_output_____" ] ], [ [ "MobileNet 为每张图片的特征返回一个 `6x6` 的空间网格。\n\n传递一个 batch 的图片给它，查看结果：", "_____no_output_____" ] ], [ [ "# 数据集可能需要几秒来启动，因为要填满其随机缓冲区。\nimage_batch, label_batch = next(iter(keras_ds))", "_____no_output_____" ], [ "feature_map_batch = mobile_net(image_batch)\nprint(feature_map_batch.shape)", "_____no_output_____" ] ], [ [ "构建一个包装了 MobileNet 的模型并在 `tf.keras.layers.Dense` 输出层之前使用 `tf.keras.layers.GlobalAveragePooling2D` 来平均那些空间向量：", "_____no_output_____" ] ], [ [ "model = tf.keras.Sequential([\n mobile_net,\n tf.keras.layers.GlobalAveragePooling2D(),\n tf.keras.layers.Dense(len(label_names), activation = 'softmax')])", "_____no_output_____" ] ], [ [ "现在它产出符合预期 shape(维数)的输出：", "_____no_output_____" ] ], [ [ "logit_batch = model(image_batch).numpy()\n\nprint(\"min logit:\", logit_batch.min())\nprint(\"max logit:\", logit_batch.max())\nprint()\n\nprint(\"Shape:\", logit_batch.shape)", "_____no_output_____" ] ], [ [ "编译模型以描述训练过程：", "_____no_output_____" ] ], [ [ "model.compile(optimizer=tf.keras.optimizers.Adam(),\n loss='sparse_categorical_crossentropy',\n metrics=[\"accuracy\"])", "_____no_output_____" ] ], [ [ "此处有两个可训练的变量 —— Dense 层中的 `weights（权重）` 和 `bias（偏差）`：", "_____no_output_____" ] ], [ [ "len(model.trainable_variables)", "_____no_output_____" ], [ "model.summary()", "_____no_output_____" ] ], [ [ "你已经准备好来训练模型了。\n\n注意，出于演示目的每一个 epoch 中你将只运行 3 step，但一般来说在传递给 `model.fit()` 之前你会指定 step 的真实数量，如下所示：", "_____no_output_____" ] ], [ [ "steps_per_epoch=tf.math.ceil(len(all_image_paths)/BATCH_SIZE).numpy()\nsteps_per_epoch", "_____no_output_____" ], [ "model.fit(ds, epochs=1, steps_per_epoch=3)", "_____no_output_____" ] ], [ [ "## 性能\n\n注意：这部分只是展示一些可能帮助提升性能的简单技巧。深入指南，请看：[输入 pipeline（管道）的性能](https://tensorflow.google.cn/guide/performance/datasets)。\n\n上面使用的简单 pipeline（管道）在每个 epoch 中单独读取每个文件。在本地使用 CPU 训练时这个方法是可行的，但是可能不足以进行 GPU 训练并且完全不适合任何形式的分布式训练。", "_____no_output_____" ], [ "要研究这点，首先构建一个简单的函数来检查数据集的性能：", "_____no_output_____" ] ], [ [ "import time\ndefault_timeit_steps = 2*steps_per_epoch+1\n\ndef timeit(ds, steps=default_timeit_steps):\n overall_start = time.time()\n # 在开始计时之前\n # 取得单个 batch 来填充 pipeline（管道）（填充随机缓冲区）\n it = iter(ds.take(steps+1))\n next(it)\n\n start = time.time()\n for i,(images,labels) in enumerate(it):\n if i%10 == 0:\n print('.',end='')\n print()\n end = time.time()\n\n duration = end-start\n print(\"{} batches: {} s\".format(steps, duration))\n print(\"{:0.5f} Images/s\".format(BATCH_SIZE*steps/duration))\n print(\"Total time: {}s\".format(end-overall_start))", "_____no_output_____" ] ], [ [ "当前数据集的性能是：", "_____no_output_____" ] ], [ [ "ds = image_label_ds.apply(\n tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))\nds = ds.batch(BATCH_SIZE).prefetch(buffer_size=AUTOTUNE)\nds", "_____no_output_____" ], [ "timeit(ds)", "_____no_output_____" ] ], [ [ "### 缓存", "_____no_output_____" ], [ "使用 `tf.data.Dataset.cache` 在 epoch 之间轻松缓存计算结果。这是非常高效的，特别是当内存能容纳全部数据时。\n\n在被预处理之后（解码和调整大小），图片在此被缓存了：", "_____no_output_____" ] ], [ [ "ds = image_label_ds.cache()\nds = ds.apply(\n tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))\nds = ds.batch(BATCH_SIZE).prefetch(buffer_size=AUTOTUNE)\nds", "_____no_output_____" ], [ "timeit(ds)", "_____no_output_____" ] ], [ [ "使用内存缓存的一个缺点是必须在每次运行时重建缓存，这使得每次启动数据集时有相同的启动延迟：", "_____no_output_____" ] ], [ [ "timeit(ds)", "_____no_output_____" ] ], [ [ "如果内存不够容纳数据，使用一个缓存文件：", "_____no_output_____" ] ], [ [ "ds = image_label_ds.cache(filename='./cache.tf-data')\nds = ds.apply(\n tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))\nds = ds.batch(BATCH_SIZE).prefetch(1)\nds", "_____no_output_____" ], [ "timeit(ds)", "_____no_output_____" ] ], [ [ "这个缓存文件也有可快速重启数据集而无需重建缓存的优点。注意第二次快了多少：", "_____no_output_____" ] ], [ [ "timeit(ds)", "_____no_output_____" ] ], [ [ "### TFRecord 文件", "_____no_output_____" ], [ "#### 原始图片数据\n\nTFRecord 文件是一种用来存储一串二进制 blob 的简单格式。通过将多个示例打包进同一个文件内，TensorFlow 能够一次性读取多个示例，当使用一个远程存储服务，如 GCS 时，这对性能来说尤其重要。\n\n首先，从原始图片数据中构建出一个 TFRecord 文件：", "_____no_output_____" ] ], [ [ "image_ds = tf.data.Dataset.from_tensor_slices(all_image_paths).map(tf.io.read_file)\ntfrec = tf.data.experimental.TFRecordWriter('images.tfrec')\ntfrec.write(image_ds)", "_____no_output_____" ] ], [ [ "接着，构建一个从 TFRecord 文件读取的数据集，并使用你之前定义的 `preprocess_image` 函数对图像进行解码/重新格式化：", "_____no_output_____" ] ], [ [ "image_ds = tf.data.TFRecordDataset('images.tfrec').map(preprocess_image)", "_____no_output_____" ] ], [ [ "压缩该数据集和你之前定义的标签数据集以得到期望的 `(图片,标签)` 对：", "_____no_output_____" ] ], [ [ "ds = tf.data.Dataset.zip((image_ds, label_ds))\nds = ds.apply(\n tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))\nds=ds.batch(BATCH_SIZE).prefetch(AUTOTUNE)\nds", "_____no_output_____" ], [ "timeit(ds)", "_____no_output_____" ] ], [ [ "这比 `缓存` 版本慢，因为你还没有缓存预处理。", "_____no_output_____" ], [ "#### 序列化的 Tensor（张量）", "_____no_output_____" ], [ "要为 TFRecord 文件省去一些预处理过程，首先像之前一样制作一个处理过的图片数据集：", "_____no_output_____" ] ], [ [ "paths_ds = tf.data.Dataset.from_tensor_slices(all_image_paths)\nimage_ds = paths_ds.map(load_and_preprocess_image)\nimage_ds", "_____no_output_____" ] ], [ [ "现在你有一个 tensor（张量）数据集，而不是一个 `.jpeg` 字符串数据集。\n\n要将此序列化至一个 TFRecord 文件你首先将该 tensor（张量）数据集转化为一个字符串数据集：", "_____no_output_____" ] ], [ [ "ds = image_ds.map(tf.io.serialize_tensor)\nds", "_____no_output_____" ], [ "tfrec = tf.data.experimental.TFRecordWriter('images.tfrec')\ntfrec.write(ds)", "_____no_output_____" ] ], [ [ "有了被缓存的预处理，就能从 TFrecord 文件高效地加载数据——只需记得在使用它之前反序列化：", "_____no_output_____" ] ], [ [ "ds = tf.data.TFRecordDataset('images.tfrec')\n\ndef parse(x):\n result = tf.io.parse_tensor(x, out_type=tf.float32)\n result = tf.reshape(result, [192, 192, 3])\n return result\n\nds = ds.map(parse, num_parallel_calls=AUTOTUNE)\nds", "_____no_output_____" ] ], [ [ "现在，像之前一样添加标签和进行相同的标准操作：", "_____no_output_____" ] ], [ [ "ds = tf.data.Dataset.zip((ds, label_ds))\nds = ds.apply(\n tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))\nds=ds.batch(BATCH_SIZE).prefetch(AUTOTUNE)\nds", "_____no_output_____" ], [ "timeit(ds)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ] ]

cb2f13d87e4ba68658a4bee175fa7a80035ea503

90,332

ipynb

Jupyter Notebook

Transfer Learning VGG-16.ipynb

mullazeeshan/Cat-Dog-Transfer-Learning

e037ab1852eb2cb0c41df3bae176aedc003f9f0c

[ "MIT" ]

null

Transfer Learning VGG-16.ipynb

mullazeeshan/Cat-Dog-Transfer-Learning

e037ab1852eb2cb0c41df3bae176aedc003f9f0c

[ "MIT" ]

null

Transfer Learning VGG-16.ipynb

mullazeeshan/Cat-Dog-Transfer-Learning

e037ab1852eb2cb0c41df3bae176aedc003f9f0c

[ "MIT" ]

null

92.743326

54,134

0.786167

[ [ [ "!wget https://download.microsoft.com/download/3/E/1/3E1C3F21-ECDB-4869-8368-6DEBA77B919F/kagglecatsanddogs_3367a.zip\n!unzip -q kagglecatsanddogs_3367a.zip", "--2019-05-11 21:04:13-- https://download.microsoft.com/download/3/E/1/3E1C3F21-ECDB-4869-8368-6DEBA77B919F/kagglecatsanddogs_3367a.zip\nResolving download.microsoft.com (download.microsoft.com)... 184.26.80.188, 2600:1406:e800:48f::e59, 2600:1406:e800:48e::e59\nConnecting to download.microsoft.com (download.microsoft.com)|184.26.80.188|:443... connected.\nHTTP request sent, awaiting response... 200 OK\nLength: 824894548 (787M) [application/octet-stream]\nSaving to: ‘kagglecatsanddogs_3367a.zip’\n\nkagglecatsanddogs_3 100%[===================>] 786.68M 141MB/s in 5.6s \n\n2019-05-11 21:04:19 (140 MB/s) - ‘kagglecatsanddogs_3367a.zip’ saved [824894548/824894548]\n\n" ], [ "import os\nimport numpy as np\nimport shutil\nimport glob\nimport warnings\nwarnings.filterwarnings('ignore')\n\ncat_files = os.listdir('PetImages/Cat')\ndog_files = os.listdir('PetImages/Dog')\n\nfor cat in cat_files:\n src = os.path.join('PetImages/Cat',cat)\n dst = os.path.join('PetImages/Cat','cat_'+cat)\n os.rename( src,dst )\n\nfor dog in dog_files:\n src = os.path.join('PetImages/Dog',dog)\n dst = os.path.join('PetImages/Dog','dog_'+dog)\n os.rename( src , dst )\n \n\ncat_files = glob.glob('PetImages/Cat/*')\ndog_files = glob.glob('PetImages/Dog/*')\n\nprint(len(cat_files),len(dog_files))\n\ncat_train = np.random.choice(cat_files, size=3000, replace=False)\ndog_train = np.random.choice(dog_files, size=3000, replace=False)\ncat_files = list(set(cat_files) - set(cat_train))\ndog_files = list(set(dog_files) - set(dog_train))\n\ncat_val = np.random.choice(cat_files, size=1000, replace=False)\ndog_val = np.random.choice(dog_files, size=1000, replace=False)\ncat_files = list(set(cat_files) - set(cat_val))\ndog_files = list(set(dog_files) - set(dog_val))\n\ncat_test = np.random.choice(cat_files, size=1000, replace=False)\ndog_test = np.random.choice(dog_files, size=1000, replace=False)\n\nprint('Cat datasets:', cat_train.shape, cat_val.shape, cat_test.shape)\nprint('Dog datasets:', dog_train.shape, dog_val.shape, dog_test.shape)\n#rm -r PetImages/ kagglecatsanddogs_3367a.zip readme\\[1\\].txt MSR-LA\\ -\\ 3467.docx", "12501 12501\nCat datasets: (3000,) (1000,) (1000,)\nDog datasets: (3000,) (1000,) (1000,)\n" ] ], [ [ "### Splitting Train, Validation, Test Data", "_____no_output_____" ] ], [ [ "train_dir = 'training_data'\nval_dir = 'validation_data'\ntest_dir = 'test_data'\n\ntrain_files = np.concatenate([cat_train, dog_train])\nvalidate_files = np.concatenate([cat_val, dog_val])\ntest_files = np.concatenate([cat_test, dog_test])\n\nos.mkdir(train_dir) if not os.path.isdir(train_dir) else None\nos.mkdir(val_dir) if not os.path.isdir(val_dir) else None\nos.mkdir(test_dir) if not os.path.isdir(test_dir) else None\n\nfor fn in train_files:\n shutil.copy(fn, train_dir)\n\nfor fn in validate_files:\n shutil.copy(fn, val_dir)\n \nfor fn in test_files:\n shutil.copy(fn, test_dir)\n#!rm -r test_data/ training_data/ validation_data/", "_____no_output_____" ], [ "from keras.preprocessing.image import ImageDataGenerator, load_img, img_to_array, array_to_img\n\nIMG_DIM = (150,150)\n\n\ntrain_files = glob.glob('training_data/*')\ntrain_imgs = [];train_labels = []\nfor file in train_files:\n try:\n train_imgs.append( img_to_array(load_img( file,target_size=IMG_DIM )) )\n train_labels.append(file.split('/')[1].split('_')[0])\n except:\n pass\ntrain_imgs = np.array(train_imgs)\n\nvalidation_files = glob.glob('validation_data/*')\nvalidation_imgs = [];validation_labels = []\nfor file in validation_files:\n try:\n validation_imgs.append( img_to_array(load_img( file,target_size=IMG_DIM )) )\n validation_labels.append(file.split('/')[1].split('_')[0])\n except:\n pass\ntrain_imgs = np.array(train_imgs)\nvalidation_imgs = np.array(validation_imgs)\n\n\nprint('Train dataset shape:', train_imgs.shape, \n '\\tValidation dataset shape:', validation_imgs.shape)", "Using TensorFlow backend.\n" ], [ "# encode text category labels\nfrom sklearn.preprocessing import LabelEncoder\n\nle = LabelEncoder()\nle.fit(train_labels)\ntrain_labels_enc = le.transform(train_labels)\nvalidation_labels_enc = le.transform(validation_labels)", "_____no_output_____" ] ], [ [ "### Image Augmentation", "_____no_output_____" ] ], [ [ "train_datagen = ImageDataGenerator(rescale=1./255, \n zoom_range=0.3, \n rotation_range=50,\n width_shift_range=0.2, \n height_shift_range=0.2, \n shear_range=0.2, \n horizontal_flip=True, \n fill_mode='nearest')\nval_datagen = ImageDataGenerator(rescale=1./255)\ntrain_generator = train_datagen.flow(train_imgs, train_labels_enc, batch_size=30)\nval_generator = val_datagen.flow(validation_imgs, validation_labels_enc, batch_size=20)", "_____no_output_____" ] ], [ [ "### Keras Model", "_____no_output_____" ] ], [ [ "from keras.layers import Flatten, Dense, Dropout\nfrom keras.applications import VGG16\nfrom keras.models import Model\nfrom keras import optimizers\n\ninput_shape = (150, 150, 3)\n\nvgg = VGG16(include_top=False, weights='imagenet',input_shape=input_shape)\n\nvgg.trainable = False\nfor layer in vgg.layers[:-8]:\n layer.trainable = False\n\nvgg_output = vgg.layers[-1].output\n\nfc1 = Flatten()(vgg_output)\nfc1 = Dense(512, activation='relu')(fc1)\nfc1_dropout = Dropout(0.3)(fc1)\n\nfc2 = Dense(512, activation='relu')(fc1_dropout)\nfc2_dropout = Dropout(0.3)(fc2)\n\noutput = Dense(1, activation='sigmoid')(fc2_dropout)\nmodel = Model(vgg.input, output)\n\n\nmodel.compile(loss='binary_crossentropy',\n optimizer=optimizers.RMSprop(lr=1e-4),\n metrics=['accuracy'])\n\n\nmodel.summary()", "WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.\nInstructions for updating:\nColocations handled automatically by placer.\nWARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/keras/backend/tensorflow_backend.py:3445: calling dropout (from tensorflow.python.ops.nn_ops) with keep_prob is deprecated and will be removed in a future version.\nInstructions for updating:\nPlease use `rate` instead of `keep_prob`. Rate should be set to `rate = 1 - keep_prob`.\n_________________________________________________________________\nLayer (type) Output Shape Param # \n=================================================================\ninput_1 (InputLayer) (None, 150, 150, 3) 0 \n_________________________________________________________________\nblock1_conv1 (Conv2D) (None, 150, 150, 64) 1792 \n_________________________________________________________________\nblock1_conv2 (Conv2D) (None, 150, 150, 64) 36928 \n_________________________________________________________________\nblock1_pool (MaxPooling2D) (None, 75, 75, 64) 0 \n_________________________________________________________________\nblock2_conv1 (Conv2D) (None, 75, 75, 128) 73856 \n_________________________________________________________________\nblock2_conv2 (Conv2D) (None, 75, 75, 128) 147584 \n_________________________________________________________________\nblock2_pool (MaxPooling2D) (None, 37, 37, 128) 0 \n_________________________________________________________________\nblock3_conv1 (Conv2D) (None, 37, 37, 256) 295168 \n_________________________________________________________________\nblock3_conv2 (Conv2D) (None, 37, 37, 256) 590080 \n_________________________________________________________________\nblock3_conv3 (Conv2D) (None, 37, 37, 256) 590080 \n_________________________________________________________________\nblock3_pool (MaxPooling2D) (None, 18, 18, 256) 0 \n_________________________________________________________________\nblock4_conv1 (Conv2D) (None, 18, 18, 512) 1180160 \n_________________________________________________________________\nblock4_conv2 (Conv2D) (None, 18, 18, 512) 2359808 \n_________________________________________________________________\nblock4_conv3 (Conv2D) (None, 18, 18, 512) 2359808 \n_________________________________________________________________\nblock4_pool (MaxPooling2D) (None, 9, 9, 512) 0 \n_________________________________________________________________\nblock5_conv1 (Conv2D) (None, 9, 9, 512) 2359808 \n_________________________________________________________________\nblock5_conv2 (Conv2D) (None, 9, 9, 512) 2359808 \n_________________________________________________________________\nblock5_conv3 (Conv2D) (None, 9, 9, 512) 2359808 \n_________________________________________________________________\nblock5_pool (MaxPooling2D) (None, 4, 4, 512) 0 \n_________________________________________________________________\nflatten_1 (Flatten) (None, 8192) 0 \n_________________________________________________________________\ndense_1 (Dense) (None, 512) 4194816 \n_________________________________________________________________\ndropout_1 (Dropout) (None, 512) 0 \n_________________________________________________________________\ndense_2 (Dense) (None, 512) 262656 \n_________________________________________________________________\ndropout_2 (Dropout) (None, 512) 0 \n_________________________________________________________________\ndense_3 (Dense) (None, 1) 513 \n=================================================================\nTotal params: 19,172,673\nTrainable params: 17,437,185\nNon-trainable params: 1,735,488\n_________________________________________________________________\n" ], [ "import pandas as pd\nlayers = [(layer, layer.name, layer.trainable) for layer in model.layers]\npd.DataFrame(layers, columns=['Layer Type', 'Layer Name', 'Layer Trainable']) ", "_____no_output_____" ], [ "from keras.callbacks import EarlyStopping, ModelCheckpoint\n\nfilepath=\"saved_models/vgg_transfer_learn_dogvscat.h5\"\n\nsave_model_cb = ModelCheckpoint(filepath, monitor='val_acc', verbose=2, save_best_only=True, mode='max')\n# callback to stop the training if no improvement\nearly_stopping_cb = EarlyStopping(monitor='val_loss', patience=7, mode='min')\n\ncallbacks_list = [save_model_cb,early_stopping_cb]\n\nhistory = model.fit_generator(train_generator, steps_per_epoch=100, epochs=100,\n validation_data=val_generator, validation_steps=50, \n verbose=2,callbacks=callbacks_list) ", "WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.\nInstructions for updating:\nUse tf.cast instead.\nEpoch 1/100\n - 24s - loss: 0.6913 - acc: 0.5683 - val_loss: 0.5941 - val_acc: 0.7670\n\nEpoch 00001: val_acc improved from -inf to 0.76700, saving model to saved_models/vgg_transfer_learn_dogvscat.h5\nEpoch 2/100\n - 21s - loss: 0.5215 - acc: 0.7513 - val_loss: 0.4317 - val_acc: 0.8000\n\nEpoch 00002: val_acc improved from 0.76700 to 0.80000, saving model to saved_models/vgg_transfer_learn_dogvscat.h5\nEpoch 3/100\n - 18s - loss: 0.4392 - acc: 0.8050 - val_loss: 0.2326 - val_acc: 0.9060\n\nEpoch 00003: val_acc improved from 0.80000 to 0.90600, saving model to saved_models/vgg_transfer_learn_dogvscat.h5\nEpoch 4/100\n - 18s - loss: 0.3877 - acc: 0.8360 - val_loss: 0.2522 - val_acc: 0.9080\n\nEpoch 00004: val_acc improved from 0.90600 to 0.90800, saving model to saved_models/vgg_transfer_learn_dogvscat.h5\nEpoch 5/100\n - 18s - loss: 0.4047 - acc: 0.8420 - val_loss: 0.1939 - val_acc: 0.9210\n\nEpoch 00005: val_acc improved from 0.90800 to 0.92100, saving model to saved_models/vgg_transfer_learn_dogvscat.h5\nEpoch 6/100\n - 20s - loss: 0.3546 - acc: 0.8580 - val_loss: 0.3172 - val_acc: 0.8950\n\nEpoch 00006: val_acc did not improve from 0.92100\nEpoch 7/100\n - 19s - loss: 0.3495 - acc: 0.8640 - val_loss: 0.2710 - val_acc: 0.9080\n\nEpoch 00007: val_acc did not improve from 0.92100\nEpoch 8/100\n - 18s - loss: 0.3236 - acc: 0.8613 - val_loss: 0.1848 - val_acc: 0.9270\n\nEpoch 00008: val_acc improved from 0.92100 to 0.92700, saving model to saved_models/vgg_transfer_learn_dogvscat.h5\nEpoch 9/100\n - 18s - loss: 0.3220 - acc: 0.8723 - val_loss: 0.2740 - val_acc: 0.9320\n\nEpoch 00009: val_acc improved from 0.92700 to 0.93200, saving model to saved_models/vgg_transfer_learn_dogvscat.h5\nEpoch 10/100\n - 19s - loss: 0.3034 - acc: 0.8746 - val_loss: 0.1948 - val_acc: 0.9310\n\nEpoch 00010: val_acc did not improve from 0.93200\nEpoch 11/100\n - 18s - loss: 0.2919 - acc: 0.8820 - val_loss: 0.1839 - val_acc: 0.9400\n\nEpoch 00011: val_acc improved from 0.93200 to 0.94000, saving model to saved_models/vgg_transfer_learn_dogvscat.h5\nEpoch 12/100\n - 18s - loss: 0.2987 - acc: 0.8816 - val_loss: 0.2716 - val_acc: 0.9030\n\nEpoch 00012: val_acc did not improve from 0.94000\nEpoch 13/100\n - 18s - loss: 0.2879 - acc: 0.8870 - val_loss: 0.1975 - val_acc: 0.9200\n\nEpoch 00013: val_acc did not improve from 0.94000\nEpoch 14/100\n - 18s - loss: 0.3175 - acc: 0.8716 - val_loss: 0.2850 - val_acc: 0.9240\n\nEpoch 00014: val_acc did not improve from 0.94000\nEpoch 15/100\n - 19s - loss: 0.3048 - acc: 0.8863 - val_loss: 0.2069 - val_acc: 0.9200\n\nEpoch 00015: val_acc did not improve from 0.94000\nEpoch 16/100\n - 19s - loss: 0.3155 - acc: 0.8766 - val_loss: 0.1515 - val_acc: 0.9390\n\nEpoch 00016: val_acc did not improve from 0.94000\nEpoch 17/100\n - 18s - loss: 0.2923 - acc: 0.8963 - val_loss: 0.2877 - val_acc: 0.8920\n\nEpoch 00017: val_acc did not improve from 0.94000\nEpoch 18/100\n - 18s - loss: 0.2936 - acc: 0.8880 - val_loss: 0.1676 - val_acc: 0.9330\n\nEpoch 00018: val_acc did not improve from 0.94000\nEpoch 19/100\n - 19s - loss: 0.3047 - acc: 0.8813 - val_loss: 0.2313 - val_acc: 0.9230\n\nEpoch 00019: val_acc did not improve from 0.94000\nEpoch 20/100\n - 18s - loss: 0.3235 - acc: 0.8896 - val_loss: 0.2459 - val_acc: 0.9170\n\nEpoch 00020: val_acc did not improve from 0.94000\nEpoch 21/100\n - 18s - loss: 0.2898 - acc: 0.8893 - val_loss: 0.2059 - val_acc: 0.9380\n\nEpoch 00021: val_acc did not improve from 0.94000\nEpoch 22/100\n - 18s - loss: 0.2759 - acc: 0.8943 - val_loss: 0.2351 - val_acc: 0.9220\n\nEpoch 00022: val_acc did not improve from 0.94000\nEpoch 23/100\n - 18s - loss: 0.2981 - acc: 0.8783 - val_loss: 0.1400 - val_acc: 0.9450\n\nEpoch 00023: val_acc improved from 0.94000 to 0.94500, saving model to saved_models/vgg_transfer_learn_dogvscat.h5\nEpoch 24/100\n - 19s - loss: 0.3097 - acc: 0.8903 - val_loss: 0.2690 - val_acc: 0.9260\n\nEpoch 00024: val_acc did not improve from 0.94500\nEpoch 25/100\n - 18s - loss: 0.3076 - acc: 0.8913 - val_loss: 0.1940 - val_acc: 0.9110\n\nEpoch 00025: val_acc did not improve from 0.94500\nEpoch 26/100\n - 18s - loss: 0.2969 - acc: 0.8953 - val_loss: 0.2101 - val_acc: 0.9300\n\nEpoch 00026: val_acc did not improve from 0.94500\nEpoch 27/100\n - 18s - loss: 0.2720 - acc: 0.8883 - val_loss: 0.2825 - val_acc: 0.8800\n\nEpoch 00027: val_acc did not improve from 0.94500\nEpoch 28/100\n - 19s - loss: 0.3663 - acc: 0.8792 - val_loss: 0.2281 - val_acc: 0.9450\n\nEpoch 00028: val_acc did not improve from 0.94500\nEpoch 29/100\n - 18s - loss: 0.2987 - acc: 0.8820 - val_loss: 0.1870 - val_acc: 0.9220\n\nEpoch 00029: val_acc did not improve from 0.94500\nEpoch 30/100\n - 18s - loss: 0.3263 - acc: 0.8983 - val_loss: 0.2469 - val_acc: 0.9280\n\nEpoch 00030: val_acc did not improve from 0.94500\n" ] ], [ [ "### Model Performance", "_____no_output_____" ] ], [ [ "%matplotlib inline\nimport matplotlib.pyplot as plt\n\nf, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))\nt = f.suptitle('Basic CNN Performance', fontsize=12)\nf.subplots_adjust(top=0.85, wspace=0.3)\n\n\nepoch_list = history.epoch\nax1.plot(epoch_list, history.history['acc'], label='Train Accuracy')\nax1.plot(epoch_list, history.history['val_acc'], label='Validation Accuracy')\nax1.set_xticks(np.arange(0, epoch_list[-1], 3))\nax1.set_ylabel('Accuracy Value')\nax1.set_xlabel('Epoch')\nax1.set_title('Accuracy')\nl1 = ax1.legend(loc=\"best\")\n\nax2.plot(epoch_list, history.history['loss'], label='Train Loss')\nax2.plot(epoch_list, history.history['val_loss'], label='Validation Loss')\nax2.set_xticks(np.arange(0, epoch_list[-1], 3))\nax2.set_ylabel('Loss Value')\nax2.set_xlabel('Epoch')\nax2.set_title('Loss')\nl2 = ax2.legend(loc=\"best\")", "_____no_output_____" ], [ "if not os.path.exists('saved_models'): os.mkdir('saved_models')\nmodel.save('saved_models/vgg transfer learning.h5')", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ] ]

cb2f1f5e5b6ed1eba72fe25aaa3f1f8e4b90f9e4

5,519

ipynb

Jupyter Notebook

211112/RGBG sparse.ipynb

igor-morawski/notebooks

444fcaff99b7a5d30022a105d3d55a611b6fa4ce

[ "MIT" ]

null

211112/RGBG sparse.ipynb

igor-morawski/notebooks

444fcaff99b7a5d30022a105d3d55a611b6fa4ce

[ "MIT" ]

null

211112/RGBG sparse.ipynb

igor-morawski/notebooks

444fcaff99b7a5d30022a105d3d55a611b6fa4ce

[ "MIT" ]

null

23.58547

158

0.431962

[ [ [ "import ipyplot\n%matplotlib notebook\nimport matplotlib.pyplot as plt\n\nimport rawpy \nimport cv2\nimport numpy as np\n\n\nimport os\nimport os.path as op\n\n\ndata_dir = op.join(\"..\", \"data\")\nimg_name = \"DSC01088\"\nraw_fp = op.join(data_dir, img_name+\".ARW\")\n\nassert op.exists(raw_fp)", "_____no_output_____" ], [ "raw = rawpy.imread(raw_fp)\n\nmono = raw.postprocess(half_size=True, no_auto_bright=True, no_auto_scale=True, output_color=rawpy.ColorSpace.raw, output_bps=16)[:,:,1].copy()/2**16\nprint(mono.shape)", "(1836, 2748)\n" ], [ "image = np.expand_dims(mono, -1)\nH, W = image.shape[:2]\npacked = np.concatenate((image[0:H:2, 0:W:2, :], # R\n image[0:H:2, 1:W:2, :], # GR\n image[1:H:2, 0:W:2, :], # GB\n image[1:H:2, 1:W:2, :]), axis=2) # B", "_____no_output_____" ], [ "print(packed.shape)", "(918, 1374, 4)\n" ], [ "def mono2sparse_rgbg(image):\n H, W = image.shape[:2]\n sparse = np.zeros([H,W,3], dtype=image.dtype)\n sparse[0:H:2, 0:W:2, 0] = image[0:H:2, 0:W:2, 0] # R\n sparse[0:H:2, 1:W:2, 1] = image[0:H:2, 1:W:2, 0] # GR\n sparse[1:H:2, 0:W:2, 1] = image[1:H:2, 0:W:2, 0] # GB\n sparse[1:H:2, 1:W:2, 2] = image[1:H:2, 1:W:2, 0] # B\n return sparse\nsparse = mono2sparse_rgbg(image)\nprint(sparse.shape)", "(1836, 2748, 3)\n" ], [ "print(image[0:3, 0:3])\nprint(sparse[0:3, 0:3, 0])\nprint(sparse[0:3, 0:3, 1])\nprint(sparse[0:3, 0:3, 2])", "[[[0.00494385]\n [0.01222229]\n [0.00727844]]\n\n [[0.01963806]\n [0.00054932]\n [0.00343323]]\n\n [[0.00590515]\n [0.00549316]\n [0.01812744]]]\n[[0.00494385 0. 0.00727844]\n [0. 0. 0. ]\n [0.00590515 0. 0.01812744]]\n[[0. 0.01222229 0. ]\n [0.01963806 0. 0.00343323]\n [0. 0.00549316 0. ]]\n[[0. 0. 0. ]\n [0. 0.00054932 0. ]\n [0. 0. 0. ]]\n" ], [ "def packed2sparse_rgbg(image):\n _H, _W, C = image.shape\n H, W = 2*_H, 2*_W\n sparse = np.zeros([H,W,3], dtype=image.dtype)\n print(sparse[0:H:2, 0:W:2, 0].shape, image[:, :, 0].shape)\n sparse[0:H:2, 0:W:2, 0] = image[:, :, 0] # R\n sparse[0:H:2, 1:W:2, 1] = image[:, :, 1] # GR\n sparse[1:H:2, 0:W:2, 1] = image[:, :, 2] # GB\n sparse[1:H:2, 1:W:2, 2] = image[:, :, 3] # B\n return sparse\nsparse = packed2sparse_rgbg(packed)\nprint(sparse.shape)", "(918, 1374) (918, 1374)\n(1836, 2748, 3)\n" ], [ "print((sparse[0:7, 0:7, 0] > 0).sum())\nprint((sparse[0:7, 0:7, 1] > 0).sum())\nprint((sparse[0:7, 0:7, 1] > float(\"-INF\")).sum())\n", "16\n20\n49\n" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2f209395bf04e758d81a9e9c49f5fd547f5c4e

19,233

ipynb

Jupyter Notebook

EHR_Claims/Lasso/EHR_C_Death_SMOTE.ipynb

shreyaskar123/EHR-Discontinuity

8d2becfd784b9cbe697f8308d60023701971ef5d

[ "MIT" ]

null

EHR_Claims/Lasso/EHR_C_Death_SMOTE.ipynb

shreyaskar123/EHR-Discontinuity

8d2becfd784b9cbe697f8308d60023701971ef5d

[ "MIT" ]

null

EHR_Claims/Lasso/EHR_C_Death_SMOTE.ipynb

shreyaskar123/EHR-Discontinuity

8d2becfd784b9cbe697f8308d60023701971ef5d

[ "MIT" ]

null

36.704198

276

0.625019

[ [ [ "import pandas as pd \nmedicare = pd.read_csv(\"/netapp2/home/se197/data/CMS/Data/medicare.csv\")", "_____no_output_____" ], [ "train_set = medicare[medicare.Hospital != 'BWH'] # MGH; n = 204014\nvalidation_set = medicare[medicare.Hospital == 'BWH'] # BWH and Neither; n = 115726\nimport numpy as np\n\nfifty_perc_EHR_cont = np.percentile(medicare['Cal_MPEC_R0'],50)\ntrain_set_high = train_set[train_set.Cal_MPEC_R0 >= fifty_perc_EHR_cont]\ntrain_set_low= train_set[train_set.Cal_MPEC_R0 < fifty_perc_EHR_cont]\n\nvalidation_set_high = validation_set[validation_set.Cal_MPEC_R0 >= fifty_perc_EHR_cont]\nvalidation_set_low = validation_set[validation_set.Cal_MPEC_R0 < fifty_perc_EHR_cont]\n", "_____no_output_____" ], [ "predictor_variable_claims = [\n 'Co_CAD_RC0', 'Co_Embolism_RC0', 'Co_DVT_RC0', 'Co_PE_RC0', 'Co_AFib_RC0',\n 'Co_Hypertension_RC0', 'Co_Hyperlipidemia_RC0', 'Co_Atherosclerosis_RC0',\n 'Co_HF_RC0', 'Co_HemoStroke_RC0', 'Co_IscheStroke_RC0', 'Co_OthStroke_RC0',\n 'Co_TIA_RC0', 'Co_COPD_RC0', 'Co_Asthma_RC0', 'Co_Pneumonia_RC0', 'Co_Alcoholabuse_RC0',\n 'Co_Drugabuse_RC0', 'Co_Epilepsy_RC0', 'Co_Cancer_RC0', 'Co_MorbidObesity_RC0',\n 'Co_Dementia_RC0', 'Co_Depression_RC0', 'Co_Bipolar_RC0', 'Co_Psychosis_RC0',\n 'Co_Personalitydisorder_RC0', 'Co_Adjustmentdisorder_RC0', 'Co_Anxiety_RC0',\n 'Co_Generalizedanxiety_RC0', 'Co_OldMI_RC0', 'Co_AcuteMI_RC0', 'Co_PUD_RC0',\n 'Co_UpperGIbleed_RC0', 'Co_LowerGIbleed_RC0', 'Co_Urogenitalbleed_RC0',\n 'Co_Othbleed_RC0', 'Co_PVD_RC0', 'Co_LiverDisease_RC0', 'Co_MRI_RC0',\n 'Co_ESRD_RC0', 'Co_Obesity_RC0', 'Co_Sepsis_RC0', 'Co_Osteoarthritis_RC0',\n 'Co_RA_RC0', 'Co_NeuroPain_RC0', 'Co_NeckPain_RC0', 'Co_OthArthritis_RC0',\n 'Co_Osteoporosis_RC0', 'Co_Fibromyalgia_RC0', 'Co_Migraine_RC0', 'Co_Headache_RC0',\n 'Co_OthPain_RC0', 'Co_GeneralizedPain_RC0', 'Co_PainDisorder_RC0',\n 'Co_Falls_RC0', 'Co_CoagulationDisorder_RC0', 'Co_WhiteBloodCell_RC0', 'Co_Parkinson_RC0',\n 'Co_Anemia_RC0', 'Co_UrinaryIncontinence_RC0', 'Co_DecubitusUlcer_RC0',\n 'Co_Oxygen_RC0', 'Co_Mammography_RC0', 'Co_PapTest_RC0', 'Co_PSATest_RC0',\n 'Co_Colonoscopy_RC0', 'Co_FecalOccultTest_RC0', 'Co_FluShot_RC0', 'Co_PneumococcalVaccine_RC0' , 'Co_RenalDysfunction_RC0', 'Co_Valvular_RC0', 'Co_Hosp_Prior30Days_RC0',\n 'Co_RX_Antibiotic_RC0', 'Co_RX_Corticosteroid_RC0', 'Co_RX_Aspirin_RC0', 'Co_RX_Dipyridamole_RC0',\n 'Co_RX_Clopidogrel_RC0', 'Co_RX_Prasugrel_RC0', 'Co_RX_Cilostazol_RC0', 'Co_RX_Ticlopidine_RC0',\n 'Co_RX_Ticagrelor_RC0', 'Co_RX_OthAntiplatelet_RC0', 'Co_RX_NSAIDs_RC0',\n 'Co_RX_Opioid_RC0', 'Co_RX_Antidepressant_RC0', 'Co_RX_AAntipsychotic_RC0', 'Co_RX_TAntipsychotic_RC0',\n 'Co_RX_Anticonvulsant_RC0', 'Co_RX_PPI_RC0', 'Co_RX_H2Receptor_RC0', 'Co_RX_OthGastro_RC0',\n 'Co_RX_ACE_RC0', 'Co_RX_ARB_RC0', 'Co_RX_BBlocker_RC0', 'Co_RX_CCB_RC0', 'Co_RX_Thiazide_RC0',\n 'Co_RX_Loop_RC0', 'Co_RX_Potassium_RC0', 'Co_RX_Nitrates_RC0', 'Co_RX_Aliskiren_RC0',\n 'Co_RX_OthAntihypertensive_RC0', 'Co_RX_Antiarrhythmic_RC0', 'Co_RX_OthAnticoagulant_RC0',\n 'Co_RX_Insulin_RC0', 'Co_RX_Noninsulin_RC0', 'Co_RX_Digoxin_RC0', 'Co_RX_Statin_RC0',\n 'Co_RX_Lipid_RC0', 'Co_RX_Lithium_RC0', 'Co_RX_Benzo_RC0', 'Co_RX_ZDrugs_RC0',\n 'Co_RX_OthAnxiolytic_RC0', 'Co_RX_Barbiturate_RC0', 'Co_RX_Dementia_RC0', 'Co_RX_Hormone_RC0',\n 'Co_RX_Osteoporosis_RC0', 'Co_N_Drugs_RC0', 'Co_N_Hosp_RC0', 'Co_Total_HospLOS_RC0',\n 'Co_N_MDVisit_RC0', 'Co_RX_AnyAspirin_RC0', 'Co_RX_AspirinMono_RC0', 'Co_RX_ClopidogrelMono_RC0',\n 'Co_RX_AspirinClopidogrel_RC0', 'Co_RX_DM_RC0', 'Co_RX_Antipsychotic_RC0'\n]\n\n\nco_train_gpop = train_set[predictor_variable_claims]\nco_train_high = train_set_high[predictor_variable_claims]\nco_train_low = train_set_low[predictor_variable_claims]\n\nco_validation_gpop = validation_set[predictor_variable_claims]\nco_validation_high = validation_set_high[predictor_variable_claims]\nco_validation_low = validation_set_low[predictor_variable_claims]", "_____no_output_____" ], [ "out_train_death_gpop = train_set['ehr_claims_death']\nout_train_death_high = train_set_high['ehr_claims_death']\nout_train_death_low = train_set_low['ehr_claims_death']\n\nout_validation_death_gpop = validation_set['ehr_claims_death']\nout_validation_death_high = validation_set_high['ehr_claims_death']\nout_validation_death_low = validation_set_low['ehr_claims_death']", "_____no_output_____" ] ], [ [ "# Template LR ", "_____no_output_____" ] ], [ [ "def lasso(X,y):\n from sklearn.linear_model import Lasso\n from sklearn.model_selection import GridSearchCV\n model = Lasso()\n param_grid = [\n {'alpha' : np.logspace(-4, 4, 20)}\n ]\n clf = GridSearchCV(model, param_grid, cv = 5, verbose = True, n_jobs = 1)\n best_clf = clf.fit(X, y)\n return best_clf", "_____no_output_____" ], [ "def scores(X_train,y_train, best_clf):\n from sklearn.metrics import accuracy_score\n from sklearn.metrics import f1_score\n from sklearn.metrics import fbeta_score\n from sklearn.metrics import roc_auc_score \n from sklearn.metrics import log_loss\n import numpy as np\n pred = np.round(best_clf.predict(X_train))\n actual = y_train\n prob = best_clf.predict(X_train)\n print(accuracy_score(actual,pred))\n print(f1_score(actual,pred, average = 'macro'))\n print(fbeta_score(actual,pred, average = 'macro', beta = 2))\n print(roc_auc_score(actual, prob))\n print(log_loss(actual,prob))", "_____no_output_____" ], [ "def cross_val(X,y):\n from sklearn.model_selection import KFold\n from sklearn.model_selection import cross_validate\n from sklearn.metrics import log_loss\n from sklearn.metrics import roc_auc_score\n from sklearn.metrics import fbeta_score\n import sklearn\n import numpy as np\n cv = KFold(n_splits=5, random_state=1, shuffle=True)\n log_loss = [] \n auc = [] \n accuracy = []\n f1 = []\n f2 = [] \n for train_index, test_index in cv.split(X):\n X_train, X_test, y_train, y_test = X.iloc[train_index], X.iloc[test_index], y.iloc[train_index], y.iloc[test_index]\n model = lasso(X_train, y_train)\n prob = model.predict(X_test) # prob is a vector of probabilities \n pred = np.round(model.predict(X_test)) # pred is the rounded predictions \n log_loss.append(sklearn.metrics.log_loss(y_test, prob))\n auc.append(sklearn.metrics.roc_auc_score(y_test, prob))\n accuracy.append(sklearn.metrics.accuracy_score(y_test, pred))\n f1.append(sklearn.metrics.f1_score(y_test, pred, average = 'macro'))\n f2.append(fbeta_score(y_test,pred, average = 'macro', beta = 2))\n print(np.mean(accuracy))\n print(np.mean(f1))\n print(np.mean(f2))\n print(np.mean(auc))\n print(np.mean(log_loss))", "_____no_output_____" ] ], [ [ "# General Population", "_____no_output_____" ] ], [ [ "from imblearn.over_sampling import SMOTE\nsm = SMOTE(random_state = 42)\nco_train_gpop_sm,out_train_death_gpop_sm = sm.fit_resample(co_train_gpop,out_train_death_gpop)\n\nbest_clf = lasso(co_train_gpop_sm, out_train_death_gpop_sm)\n\ncross_val(co_train_gpop_sm, out_train_death_gpop_sm)\n\nprint()\n\nscores(co_train_gpop, out_train_death_gpop, best_clf)\n\nprint()\n\nscores(co_validation_gpop, out_validation_death_gpop, best_clf)\n\n#comb = [] \n#for i in range(len(predictor_variable_claims)):\n #comb.append(predictor_variable_claims[i] + str(best_clf.best_estimator_.coef_[:,i:i+1]))\n#comb", "Fitting 5 folds for each of 20 candidates, totalling 100 fits\n" ] ], [ [ "# High Continuity ", "_____no_output_____" ] ], [ [ "from imblearn.over_sampling import SMOTE\nsm = SMOTE(random_state = 42)\nco_train_high_sm,out_train_death_high_sm = sm.fit_resample(co_train_high, out_train_death_high)\n\nbest_clf = lasso(co_train_high_sm, out_train_death_high_sm)\n\ncross_val(co_train_high_sm, out_train_death_high_sm)\n\nprint()\n\nscores(co_train_high, out_train_death_high, best_clf)\n\nprint()\n\nscores(co_validation_high, out_validation_death_high, best_clf)\n\n#comb = [] \n#for i in range(len(predictor_variable_claims)):\n #comb.append(predictor_variable_claims[i] + str(best_clf.best_estimator_.coef_[:,i:i+1]))\n#comb", "Fitting 5 folds for each of 20 candidates, totalling 100 fits\nFitting 5 folds for each of 20 candidates, totalling 100 fits\nFitting 5 folds for each of 20 candidates, totalling 100 fits\nFitting 5 folds for each of 20 candidates, totalling 100 fits\n" ] ], [ [ "# Low Continuity", "_____no_output_____" ] ], [ [ "from imblearn.over_sampling import SMOTE\nsm = SMOTE(random_state = 42)\nco_train_low_sm,out_train_death_low_sm = sm.fit_resample(co_train_low,out_train_death_low)\n\nbest_clf = lasso(co_train_low_sm, out_train_death_low_sm)\n\ncross_val(co_train_low_sm, out_train_death_low_sm)\n\nprint()\n\nscores(co_train_low, out_train_death_low, best_clf)\n\nprint()\n\nscores(co_validation_low, out_validation_death_low, best_clf)\n\n#comb = [] \n#for i in range(len(predictor_variable_claims)):\n #comb.append(predictor_variable_claims[i] + str(best_clf.best_estimator_.coef_[:,i:i+1]))\n#comb", "Fitting 5 folds for each of 20 candidates, totalling 100 fits\nFitting 5 folds for each of 20 candidates, totalling 100 fits\nFitting 5 folds for each of 20 candidates, totalling 100 fits\nFitting 5 folds for each of 20 candidates, totalling 100 fits\nFitting 5 folds for each of 20 candidates, totalling 100 fits\nFitting 5 folds for each of 20 candidates, totalling 100 fits\n0.7754689223979404\n0.7754165504612924\n0.7754359801843529\n0.8508869492109585\n0.6347038745337287\n\n0.7701365077311251\n0.6486935454987156\n0.6960906194289609\n0.8412130257340931\n0.729983338237978\n\n0.7424126741744608\n0.6345209735011402\n0.6775516646090722\n0.8142679642181803\n0.8065143731277347\n" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2f29ee6d2c7f2cb14b98dd1683d85b29c7758d

882,619

ipynb

Jupyter Notebook

Nikhil/IA - Hugo.ipynb

HugoLeBoennec/A4_Intelligence_Artificielle

f169be9895c4a191232febd786d941ff52eacf2e

[ "MIT" ]

null

Nikhil/IA - Hugo.ipynb

HugoLeBoennec/A4_Intelligence_Artificielle

f169be9895c4a191232febd786d941ff52eacf2e

[ "MIT" ]

null

Nikhil/IA - Hugo.ipynb

HugoLeBoennec/A4_Intelligence_Artificielle

f169be9895c4a191232febd786d941ff52eacf2e

[ "MIT" ]

null

565.418962

379,500

0.930961

[ [ [ "Import des données\n", "_____no_output_____" ] ], [ [ "from __future__ import division, print_function, unicode_literals\n\n# imports\nimport numpy as np\nimport os\nimport pandas as pd\n\n# stabilité du notebook d'une exécution à l'autre\nnp.random.seed(42)\n\n# ignorer les warnings inutiles (voir SciPy issue #5998)\nimport warnings\nwarnings.filterwarnings(action=\"ignore\", message=\"^internal gelsd\")\n\nurl = 'https://raw.githubusercontent.com/HugoLeBoennec/A4_Intelligence_Artificielle/main/Projet/'\n\ngeneral_data = pd.read_csv(url + \"dataset/general_data.csv\", error_bad_lines=False)\nemployee_survey_data = pd.read_csv(url + \"dataset/employee_survey_data.csv\", error_bad_lines=False)\nmanager_survey_data = pd.read_csv(url + \"dataset/manager_survey_data.csv\", error_bad_lines=False)\nout_time = pd.read_csv(url + \"dataset/out_time.csv\", error_bad_lines=False)\nin_time = pd.read_csv(url + \"dataset/in_time.csv\", error_bad_lines=False)\nemployee_survey_data", "_____no_output_____" ] ], [ [ "Fusion des tableaux", "_____no_output_____" ] ], [ [ "alldata = pd.merge(general_data, employee_survey_data)\nalldata", "_____no_output_____" ] ], [ [ "Affichage des données", "_____no_output_____" ] ], [ [ "import seaborn as sns\nimport matplotlib.pyplot as plt\n\nsns.countplot(x=alldata.Attrition, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.BusinessTravel, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.Department, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.DistanceFromHome, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.Education, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.EducationField, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.EmployeeCount, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.EducationField, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.Gender, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.JobLevel, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.JobRole, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.MaritalStatus, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.MonthlyIncome, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.NumCompaniesWorked, data= alldata, palette='hls')\nplt.show()\nsns.countplot(x=alldata.Over18, data= alldata, palette='hls')\nplt.show()", "_____no_output_____" ], [ "pd.crosstab(alldata.WorkLifeBalance,alldata.MaritalStatus).plot(kind='bar')\nplt.title('MaritalStatus par WorkLifeBalance')\nplt.xlabel('MaritalStatus')\nplt.ylabel('WorkLifeBalance')\nplt.show()", "_____no_output_____" ], [ "table1 = pd.crosstab(alldata.WorkLifeBalance, alldata.MaritalStatus)\ntable1.div(table1.sum(1).astype(float), axis=0).plot(kind='bar', stacked = True)\nplt.title('MaritalStatus par WorkLifeBalance')\nplt.xlabel('MaritalStatus')\nplt.ylabel('WorkLifeBalance')\nplt.show()", "_____no_output_____" ], [ "table2 = pd.crosstab(alldata.JobSatisfaction, alldata.Attrition)\ntable2.div(table2.sum(1).astype(float), axis=0).plot(kind=\"bar\", stacked=True)\nplt.title(\"Attrition en fonction de la satisfation au travail\")\nplt.xlabel(\"Satisfaction au travail\")\nplt.ylabel(\"Proportion d'employés\")\nplt.show()", "_____no_output_____" ] ], [ [ "suppression des nan", "_____no_output_____" ] ], [ [ "copy_alldata = alldata\ncopy_alldata.dropna(inplace = True)\ncopy_alldata.isnull().sum().sort_values(ascending=False).head()", "_____no_output_____" ] ], [ [ "remplacement des variables qualitatives en quantitative", "_____no_output_____" ] ], [ [ "#Change Attrition column values to numeric values\nattrition={'Yes':1, 'No':0}\nGender={'Female':1, 'Male':0}\nMaritalStatus={'Divorced':2, 'Married':1, 'Single':0 }\nDepartment={ 'Research & Development':2, 'Human Resources':1, 'Sales':0 }\nBusinessTravel={ 'Travel_Rarely':0, 'Travel_Frequently':1, 'Non-Travel':2}\nEducationField={ 'Life Sciences':0, 'Other':1, 'Medical':2, 'Marketing':3, 'Technical Degree':4, 'Human Resources':5}\nJobRole={ 'Healthcare Representative':0, 'Research Scientist':1, 'Sales Executive':2, 'Human Resources':3, 'Research Director':4, 'Laboratory Technician':5, 'Manufacturing Director':6, 'Sales Representative': 7, 'Manager':8}\n#raw_data.Attrition=[attrition[item] for item in raw_data.Attrition]\ncopy_alldata.Attrition=copy_alldata.Attrition.map(lambda x:attrition[x])\ncopy_alldata.EducationField=copy_alldata.EducationField.map(lambda x:EducationField[x])\ncopy_alldata.Gender=copy_alldata.Gender.map(lambda x:Gender[x])\ncopy_alldata.MaritalStatus=copy_alldata.MaritalStatus.map(lambda x:MaritalStatus[x])\ncopy_alldata.Department=copy_alldata.Department.map(lambda x:Department[x])\ncopy_alldata.BusinessTravel=copy_alldata.BusinessTravel.map(lambda x:BusinessTravel[x])\ncopy_alldata.JobRole=copy_alldata.JobRole.map(lambda x:JobRole[x])\n\nprint(copy_alldata)", " Age Attrition BusinessTravel Department DistanceFromHome Education \\\n0 51 0 0 0 6 2 \n1 31 1 1 2 10 1 \n2 32 0 1 2 17 4 \n3 38 0 2 2 2 5 \n4 32 0 0 2 10 1 \n... ... ... ... ... ... ... \n4404 29 0 0 0 4 3 \n4405 42 0 0 2 5 4 \n4406 29 0 0 2 2 4 \n4407 25 0 0 2 25 2 \n4408 42 0 0 0 18 2 \n\n EducationField EmployeeCount EmployeeID Gender ... StandardHours \\\n0 0 1 1 1 ... 8 \n1 0 1 2 1 ... 8 \n2 1 1 3 0 ... 8 \n3 0 1 4 0 ... 8 \n4 2 1 5 0 ... 8 \n... ... ... ... ... ... ... \n4404 1 1 4405 1 ... 8 \n4405 2 1 4406 1 ... 8 \n4406 2 1 4407 0 ... 8 \n4407 0 1 4408 0 ... 8 \n4408 2 1 4409 0 ... 8 \n\n StockOptionLevel TotalWorkingYears TrainingTimesLastYear \\\n0 0 1.0 6 \n1 1 6.0 3 \n2 3 5.0 2 \n3 3 13.0 5 \n4 2 9.0 2 \n... ... ... ... \n4404 0 6.0 2 \n4405 1 10.0 5 \n4406 0 10.0 2 \n4407 0 5.0 4 \n4408 1 10.0 2 \n\n YearsAtCompany YearsSinceLastPromotion YearsWithCurrManager \\\n0 1 0 0 \n1 5 1 4 \n2 5 0 3 \n3 8 7 5 \n4 6 0 4 \n... ... ... ... \n4404 6 1 5 \n4405 3 0 2 \n4406 3 0 2 \n4407 4 1 2 \n4408 9 7 8 \n\n EnvironmentSatisfaction JobSatisfaction WorkLifeBalance \n0 3.0 4.0 2.0 \n1 3.0 2.0 4.0 \n2 2.0 2.0 1.0 \n3 4.0 4.0 3.0 \n4 4.0 1.0 3.0 \n... ... ... ... \n4404 3.0 4.0 3.0 \n4405 4.0 1.0 3.0 \n4406 4.0 4.0 3.0 \n4407 1.0 3.0 3.0 \n4408 4.0 1.0 3.0 \n\n[4300 rows x 27 columns]\n" ] ], [ [ "calcule des corélations", "_____no_output_____" ] ], [ [ "corr_features=copy_alldata.corr()\ncorr_features.iloc[:,1]", "_____no_output_____" ], [ " def Heat_map(data, features):\n plt.figure(figsize=(20, 10))\n sns.heatmap(data[features].corr(), cmap='RdBu', annot=True)\n plt.xticks(rotation=45) \n plt.title('Heatmap of Correlation Matrix')\n\nHeat_map(copy_alldata,list(copy_alldata.columns))", "_____no_output_____" ] ], [ [ "application d'un model", "_____no_output_____" ] ], [ [ "\n# X = copy_alldata.loc[:, copy_alldata.columns != 'quit']\nX, y = copy_alldata.loc[:, copy_alldata.columns !=\"Attrition\"], copy_alldata.loc[:, \"Attrition\"]\nX = pd.get_dummies(X, drop_first= True)\nX.head()\ny = pd.get_dummies(y, drop_first= True)\ny.head()\n\nfrom sklearn.model_selection import train_test_split\ny = np.ravel(y)\nX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)", "_____no_output_____" ], [ "!pip install graphviz; yellowbrick", "Requirement already satisfied: graphviz in c:\\users\\hugo\\anaconda3\\lib\\site-packages (0.16)\nCollecting yellowbrick\n Downloading yellowbrick-1.3.post1-py3-none-any.whl (271 kB)\nRequirement already satisfied: scipy>=1.0.0 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from yellowbrick) (1.5.2)\nRequirement already satisfied: matplotlib!=3.0.0,>=2.0.2 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from yellowbrick) (3.3.2)\nRequirement already satisfied: numpy<1.20,>=1.16.0 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from yellowbrick) (1.19.2)\nRequirement already satisfied: cycler>=0.10.0 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from yellowbrick) (0.10.0)\nRequirement already satisfied: scikit-learn>=0.20 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from yellowbrick) (0.23.2)\nRequirement already satisfied: pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.3 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from matplotlib!=3.0.0,>=2.0.2->yellowbrick) (2.4.7)\nRequirement already satisfied: python-dateutil>=2.1 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from matplotlib!=3.0.0,>=2.0.2->yellowbrick) (2.8.1)\nRequirement already satisfied: certifi>=2020.06.20 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from matplotlib!=3.0.0,>=2.0.2->yellowbrick) (2020.6.20)\nRequirement already satisfied: kiwisolver>=1.0.1 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from matplotlib!=3.0.0,>=2.0.2->yellowbrick) (1.3.0)\nRequirement already satisfied: pillow>=6.2.0 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from matplotlib!=3.0.0,>=2.0.2->yellowbrick) (8.0.1)\nRequirement already satisfied: six in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from cycler>=0.10.0->yellowbrick) (1.15.0)\nRequirement already satisfied: threadpoolctl>=2.0.0 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from scikit-learn>=0.20->yellowbrick) (2.1.0)\nRequirement already satisfied: joblib>=0.11 in c:\\users\\hugo\\anaconda3\\lib\\site-packages (from scikit-learn>=0.20->yellowbrick) (0.17.0)\nInstalling collected packages: yellowbrick\nSuccessfully installed yellowbrick-1.3.post1\n" ], [ "from sklearn import tree\nfrom sklearn.tree import DecisionTreeClassifier\nfrom sklearn.ensemble import RandomForestClassifier\nfrom sklearn.metrics import accuracy_score\nfrom sklearn.tree import export_graphviz # display the tree within a Jupyter notebook\nfrom IPython.display import SVG\nfrom graphviz import Source\nfrom IPython.display import display\nfrom ipywidgets import interactive, IntSlider, FloatSlider, interact\nimport ipywidgets\nfrom IPython.display import Image\nfrom subprocess import call\nimport matplotlib.image as mpimg", "_____no_output_____" ], [ "@interact\ndef plot_tree(crit=[\"gini\", \"entropy\"],\n split=[\"best\", \"random\"],\n depth=IntSlider(min=1,max=30,value=2, continuous_update=False),\n min_split=IntSlider(min=2,max=5,value=2, continuous_update=False),\n min_leaf=IntSlider(min=1,max=5,value=1, continuous_update=False)):\n \n estimator = DecisionTreeClassifier(random_state=0,\n criterion=crit,\n splitter = split,\n max_depth = depth,\n min_samples_split=min_split,\n min_samples_leaf=min_leaf)\n estimator.fit(X_train, y_train)\n print('Decision Tree Training Accuracy: {:.3f}'.format(accuracy_score(y_train, estimator.predict(X_train))))\n print('Decision Tree Test Accuracy: {:.3f}'.format(accuracy_score(y_test, estimator.predict(X_test))))\n\n# graph = Source(tree.export_graphviz(estimator,\n# out_file=None,\n# feature_names=X_train.columns,\n# class_names=['0', '1'],\n# filled = True))\n \n# display(Image(data=graph.pipe(format='png')))\n \n return estimator", "_____no_output_____" ], [ "@interact\ndef plot_tree_rf(crit=[\"gini\", \"entropy\"],\n bootstrap=[\"True\", \"False\"],\n depth=IntSlider(min=1,max=30,value=3, continuous_update=False),\n forests=IntSlider(min=1,max=200,value=100,continuous_update=False),\n min_split=IntSlider(min=2,max=5,value=2, continuous_update=False),\n min_leaf=IntSlider(min=1,max=5,value=1, continuous_update=False)):\n \n estimator = RandomForestClassifier(random_state=1,\n criterion=crit,\n bootstrap=bootstrap,\n n_estimators=forests,\n max_depth=depth,\n min_samples_split=min_split,\n min_samples_leaf=min_leaf,\n n_jobs=-1,\n verbose=False).fit(X_train, y_train)\n\n print('Random Forest Training Accuracy: {:.3f}'.format(accuracy_score(y_train, estimator.predict(X_train))))\n print('Random Forest Test Accuracy: {:.3f}'.format(accuracy_score(y_test, estimator.predict(X_test))))\n num_tree = estimator.estimators_[0]\n print('\\nVisualizing Decision Tree:', 0)\n \n# graph = Source(tree.export_graphviz(num_tree,\n# out_file=None,\n# feature_names=X_train.columns,\n# class_names=['0', '1'],\n# filled = True))\n \n# display(Image(data=graph.pipe(format='png')))\n \n return estimator", "_____no_output_____" ], [ "from yellowbrick.model_selection import FeatureImportances\nplt.rcParams['figure.figsize'] = (12,8)\nplt.style.use(\"ggplot\")\n\nrf = RandomForestClassifier(bootstrap='True', class_weight=None, criterion='gini',\n max_depth=3, max_features='auto', max_leaf_nodes=None,\n min_impurity_decrease=0.0, min_impurity_split=None,\n min_samples_leaf=1, min_samples_split=2,\n min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=-1,\n oob_score=False, random_state=1, verbose=False,\n warm_start=False)\n\nviz = FeatureImportances(rf)\nviz.fit(X_train, y_train)\nviz.show();", "_____no_output_____" ], [ "from yellowbrick.classifier import ROCAUC\n\nvisualizer = ROCAUC(rf, classes=[\"stayed\", \"quit\"])\n\nvisualizer.fit(X_train, y_train) # Fit the training data to the visualizer\nvisualizer.score(X_test, y_test) # Evaluate the model on the test data\nvisualizer.poof();\n", "_____no_output_____" ], [ "dt = DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=2,\n max_features=None, max_leaf_nodes=None,\n min_impurity_decrease=0.0, min_impurity_split=None,\n min_samples_leaf=1, min_samples_split=2,\n min_weight_fraction_leaf=0.0, presort=False, random_state=0,\n splitter='best')\n\nvisualizer = ROCAUC(dt, classes=[\"stayed\", \"quit\"])\n\nvisualizer.fit(X_train, y_train) # Fit the training data to the visualizer\nvisualizer.score(X_test, y_test) # Evaluate the model on the test data\nvisualizer.poof();", "C:\\Users\\Hugo\\anaconda3\\lib\\site-packages\\sklearn\\tree\\_classes.py:323: FutureWarning: The parameter 'presort' is deprecated and has no effect. It will be removed in v0.24. You can suppress this warning by not passing any value to the 'presort' parameter.\n warnings.warn(\"The parameter 'presort' is deprecated and has no \"\n" ], [ "from sklearn.linear_model import LogisticRegressionCV\n\nlogit = LogisticRegressionCV(random_state=1, n_jobs=-1,max_iter=500,\n cv=10)\n\nlr = logit.fit(X_train, y_train)\n\nprint('Logistic Regression Accuracy: {:.3f}'.format(accuracy_score(y_test, lr.predict(X_test))))\n\nvisualizer = ROCAUC(lr, classes=[\"stayed\", \"quit\"])\n\nvisualizer.fit(X_train, y_train) # Fit the training data to the visualizer\nvisualizer.score(X_test, y_test) # Evaluate the model on the test data\nvisualizer.poof();", "Logistic Regression Accuracy: 0.838\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2f2ce0aef0caa31aa0785cba631ffa1ad2d408

11,555

ipynb

Jupyter Notebook

code/api/python/flickr-download-theatre.ipynb

HeardLibrary/digital-scholarship

c2a791376ecea4efff4ff57c7a93b291b605d956

[ "CC0-1.0" ]

25

2018-09-27T03:46:38.000Z

2022-03-13T00:08:22.000Z

code/api/python/flickr-download-theatre.ipynb

HeardLibrary/digital-scholarship

c2a791376ecea4efff4ff57c7a93b291b605d956

[ "CC0-1.0" ]

22

2019-07-23T15:30:14.000Z

2022-03-29T22:04:37.000Z

code/api/python/flickr-download-theatre.ipynb

HeardLibrary/digital-scholarship

c2a791376ecea4efff4ff57c7a93b291b605d956

[ "CC0-1.0" ]

18

2019-01-28T16:40:28.000Z

2022-01-13T01:59:00.000Z

43.115672

508

0.60926

[ [ [ "This script is based on instructions given in [this lesson](https://github.com/HeardLibrary/digital-scholarship/blob/master/code/scrape/pylesson/lesson2-api.ipynb). \n\n## Import libraries and load API key from file\n\nThe API key should be the only item in a text file called `flickr_api_key.txt` located in the user's home directory. No trailing newline and don't include the \"secret\".", "_____no_output_____" ] ], [ [ "from pathlib import Path\nimport requests\nimport json\nimport csv\nfrom time import sleep\nimport webbrowser\n\n# define some canned functions we need to use\n\n# write a list of dictionaries to a CSV file\ndef write_dicts_to_csv(table, filename, fieldnames):\n with open(filename, 'w', newline='', encoding='utf-8') as csv_file_object:\n writer = csv.DictWriter(csv_file_object, fieldnames=fieldnames)\n writer.writeheader()\n for row in table:\n writer.writerow(row)\n\nhome = str(Path.home()) #gets path to home directory; supposed to work for Win and Mac\nkey_filename = 'flickr_api_key.txt'\napi_key_path = home + '/' + key_filename\n\ntry:\n with open(api_key_path, 'rt', encoding='utf-8') as file_object:\n api_key = file_object.read()\n # print(api_key) # delete this line once the script is working; don't want the key as part of the notebook\nexcept:\n print(key_filename + ' file not found - is it in your home directory?')", "_____no_output_____" ] ], [ [ "## Make a test API call to the account\n\nWe need to know the user ID. Go to flickr.com, and search for vutheatre. The result is https://www.flickr.com/photos/123262983@N05 which tells us that the ID is 123262983@N05 . There are a lot of kinds of searches we can do. A list is [here](https://www.flickr.com/services/api/). Let's try `flickr.people.getPhotos` (described [here](https://www.flickr.com/services/api/flickr.people.getPhotos.html)). This method doesn't actually get the photos; it gets metadata about the photos for an account.\n\nThe main purpose of this query is to find out the number of photos that are available so that we can know how to set up the next part. The number of photos is in `['photos']['total']`, so we can extract that from the response data.", "_____no_output_____" ] ], [ [ "user_id = '123262983@N05' # vutheatre's ID\nendpoint_url = 'https://www.flickr.com/services/rest'\nmethod = 'flickr.people.getPhotos'\nfilename = 'theatre-metadata.csv'\n\nparam_dict = {\n 'method' : method,\n# 'tags' : 'kangaroo',\n# 'extras' : 'url_o',\n 'per_page' : '1', # default is 100, maximum is 500. Use paging to retrieve more than 500.\n 'page' : '1',\n 'user_id' : user_id,\n 'oauth_consumer_key' : api_key,\n 'nojsoncallback' : '1', # this parameter causes the API to return actual JSON instead of its weird default string\n 'format' : 'json' # overrides the default XML serialization for the search results\n }\n\nmetadata_response = requests.get(endpoint_url, params = param_dict)\n\n# print(metadata_response.url) # uncomment this if testing is needed, again don't reveal key in notebook\ndata = metadata_response.json()\nprint(json.dumps(data, indent=4))\nprint()\n\nnumber_photos = int(data['photos']['total']) # need to convert string to number\nprint('Number of photos: ', number_photos)", "_____no_output_____" ] ], [ [ "## Test to see what kinds of useful metadata we can get\n\nThe instructions for the [method](https://www.flickr.com/services/api/flickr.people.getPhotos.html) says what kinds of \"extras\" you can request metadata about. Let's ask for everything that we care about and don't already know: \n\n`description,license,original_format,date_taken,original_format,geo,tags,machine_tags,media,url_t,url_o`\n\n`url_t` is the URL for a thumbnail of the image and `url_o` is the URL to retrieve the original photo. The dimensions of these images will be given automatically when we request the URLs, so we don't need `o_dims`. There isn't any place to request the title, since it's automatically returned.", "_____no_output_____" ] ], [ [ "param_dict = {\n 'method' : method,\n 'extras' : 'description,license,original_format,date_taken,original_format,geo,tags,machine_tags,media,url_t,url_o',\n 'per_page' : '1', # default is 100, maximum is 500. Use paging to retrieve more than 500.\n 'page' : '1',\n 'user_id' : user_id,\n 'oauth_consumer_key' : api_key,\n 'nojsoncallback' : '1', # this parameter causes the API to return actual JSON instead of its weird default string\n 'format' : 'json' # overrides the default XML serialization for the search results\n }\n\nmetadata_response = requests.get(endpoint_url, params = param_dict)\n# print(metadata_response.url) # uncomment this if testing is needed, again don't reveal key in notebook\n\ndata = metadata_response.json()\nprint(json.dumps(data, indent=4))\nprint()", "_____no_output_____" ] ], [ [ "## Create and test the function to extract the data we want\n\n", "_____no_output_____" ] ], [ [ "def extract_data(photo_number, data):\n dictionary = {} # create an empty dictionary\n\n # load the response data into a dictionary\n dictionary['id'] = data['photos']['photo'][photo_number]['id']\n dictionary['title'] = data['photos']['photo'][photo_number]['title']\n dictionary['license'] = data['photos']['photo'][photo_number]['license']\n dictionary['description'] = data['photos']['photo'][photo_number]['description']['_content']\n\n # convert the stupid date format to ISO 8601 dateTime; don't know the time zone - maybe add later?\n temp_time = data['photos']['photo'][photo_number]['datetaken']\n dictionary['date_taken'] = temp_time.replace(' ', 'T')\n\n dictionary['tags'] = data['photos']['photo'][photo_number]['tags']\n dictionary['machine_tags'] = data['photos']['photo'][photo_number]['machine_tags']\n dictionary['original_format'] = data['photos']['photo'][photo_number]['originalformat']\n dictionary['latitude'] = data['photos']['photo'][photo_number]['latitude']\n dictionary['longitude'] = data['photos']['photo'][photo_number]['longitude']\n dictionary['thumbnail_url'] = data['photos']['photo'][photo_number]['url_t']\n dictionary['original_url'] = data['photos']['photo'][photo_number]['url_o']\n dictionary['original_height'] = data['photos']['photo'][photo_number]['height_o']\n dictionary['original_width'] = data['photos']['photo'][photo_number]['width_o']\n \n return dictionary\n\n# test the function with a single row\ntable = []\n\nphoto_number = 0\nphoto_dictionary = extract_data(photo_number, data)\ntable.append(photo_dictionary)\n\n# write the data to a file\nfieldnames = photo_dictionary.keys() # use the keys from the last dictionary for column headers; assume all are the same\nwrite_dicts_to_csv(table, filename, fieldnames)\n\nprint('Done')", "_____no_output_____" ] ], [ [ "## Create the loops to do the paging\n\nFlickr limits the number of photos that can be requested to 500. Since we have more than that, we need to request the data 500 photos at a time.", "_____no_output_____" ] ], [ [ "per_page = 5 # use 500 for full download, use smaller number like 5 for testing\npages = number_photos // per_page # the // operator returns the integer part of the division (\"floor\")\ntable = []\n\n#for page_number in range(0, pages + 1): # need to add one to get the final partial page\nfor page_number in range(0, 1): # use this to do only one page for testing\n print('retrieving page ', page_number + 1)\n page_string = str(page_number + 1)\n param_dict = {\n 'method' : method,\n 'extras' : 'description,license,original_format,date_taken,original_format,geo,tags,machine_tags,media,url_t,url_o',\n 'per_page' : str(per_page), # default is 100, maximum is 500.\n 'page' : page_string,\n 'user_id' : user_id,\n 'oauth_consumer_key' : api_key,\n 'nojsoncallback' : '1', # this parameter causes the API to return actual JSON instead of its weird default string\n 'format' : 'json' # overrides the default XML serialization for the search results\n }\n metadata_response = requests.get(endpoint_url, params = param_dict)\n data = metadata_response.json()\n# print(json.dumps(data, indent=4)) # uncomment this line for testing\n \n # data['photos']['photo'] is the number of photos for which data was returned\n for image_number in range(0, len(data['photos']['photo'])):\n photo_dictionary = extract_data(image_number, data)\n table.append(photo_dictionary)\n\n # write the data to a file\n # We could just do this for all the data at the end.\n # But if the search fails in the middle, we will at least get partial results\n fieldnames = photo_dictionary.keys() # use the keys from the last dictionary for column headers; assume all are the same\n write_dicts_to_csv(table, filename, fieldnames)\n\n sleep(1) # wait a second to avoid getting blocked for hitting the API to rapidly\n\nprint('Done')", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2f3a820ca259c9446d702f640c6f176221f90b

30,931

ipynb

Jupyter Notebook

finite_ntk/notebooks/ntk_fisher_speed_test_gp.ipynb

adamian/xfer

c4c6fe6dc785f5dee99fef699d1fa4f12dd80849

[ "Apache-2.0" ]

244

2018-08-31T18:35:29.000Z

2022-03-20T01:12:50.000Z

finite_ntk/notebooks/ntk_fisher_speed_test_gp.ipynb

wjmaddox/xfer

b6e1c88bfc5e8b4a7077032ab84c5b8bced9f5cd

[ "Apache-2.0" ]

26

2018-08-29T15:31:21.000Z

2021-06-24T08:05:53.000Z

finite_ntk/notebooks/ntk_fisher_speed_test_gp.ipynb

wjmaddox/xfer

b6e1c88bfc5e8b4a7077032ab84c5b8bced9f5cd

[ "Apache-2.0" ]

57

2018-09-11T13:40:35.000Z

2022-02-22T14:43:34.000Z

85.444751

20,436

0.823413

[ [ [ "import matplotlib.pyplot as plt\nimport torch\nimport gpytorch\nimport time\nimport numpy as np\n\n%matplotlib inline", "_____no_output_____" ], [ "import pickle", "_____no_output_____" ], [ "import finite_ntk\n%pdb", "Automatic pdb calling has been turned ON\n" ], [ "class ExactGPModel(gpytorch.models.ExactGP):\n # exact RBF Gaussian process class\n def __init__(self, train_x, train_y, likelihood, model, use_linearstrategy=False):\n super(ExactGPModel, self).__init__(train_x, train_y, likelihood)\n self.mean_module = gpytorch.means.ConstantMean()\n self.covar_module = finite_ntk.lazy.NTK(\n model=model, use_linearstrategy=use_linearstrategy\n )\n\n def forward(self, x):\n mean_x = self.mean_module(x)\n covar_x = self.covar_module(x)\n return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)", "_____no_output_____" ], [ "model = torch.nn.Sequential(\n torch.nn.Linear(5, 200),\n torch.nn.ELU(),\n torch.nn.Linear(200, 2000),\n torch.nn.ELU(),\n torch.nn.Linear(2000, 200),\n torch.nn.ELU(),\n torch.nn.Linear(200, 1),\n).cuda()", "_____no_output_____" ], [ "likelihood = gpytorch.likelihoods.GaussianLikelihood().cuda()\n\ngpmodel = ExactGPModel(torch.randn(10, 5).cuda(), torch.randn(10).cuda(), likelihood, model).cuda()\nparspace_gpmodel = ExactGPModel(torch.randn(10, 5).cuda(), torch.randn(10).cuda(), \n likelihood, model, use_linearstrategy=True).cuda()", "_____no_output_____" ], [ "def run_model_list(mm, n_list):\n num_data_list = []\n for n in num_data_points:\n mm.train()\n #parspace_gpmodel.train()\n\n print('N: ', n)\n\n data = torch.randn(n, 5).cuda()\n y = torch.randn(n).cuda()\n\n mm.set_train_data(data, y, strict=False)\n #parspace_gpmodel.set_train_data(data, y, strict=False)\n\n start = time.time()\n logprob = likelihood(mm(data)).log_prob(y)\n log_end = time.time() - start\n\n #start = time.time()\n #logprob = likelihood(parspace_gpmodel(data)).log_prob(y)\n #plog_end = time.time() - start\n\n mm.eval()\n #parspace_gpmodel.eval()\n\n with gpytorch.settings.fast_pred_var(), gpytorch.settings.max_eager_kernel_size(200):\n test_data = torch.randn(50, 5).cuda()\n\n start = time.time()\n pred_vars = mm(test_data).mean\n var_end = time.time() - start\n\n # start = time.time()\n # pred_vars = parspace_gpmodel(data).variance\n # pvar_end = time.time() - start\n\n #timings = [log_end, plog_end, var_end, pvar_end]\n #timings = [log_end, plog_end]\n #print(timings)\n num_data_list.append([log_end, var_end])\n \n mm.prediction_strategy = None\n \n return num_data_list", "_____no_output_____" ], [ "num_data_points = [300, 500, 1000, 5000, 10000, 25000, 50000, 100000]\n\nfun_space_list = run_model_list(gpmodel, num_data_points)\ndel gpmodel\n\n", "N: 300\nN: 500\nN: 1000\nN: 5000\nN: 10000\n" ], [ "par_space_list = run_model_list(parspace_gpmodel, num_data_points)\ndel parspace_gpmodel", "N: 300\ntorch.Size([803601])\nN: 500\ntorch.Size([803601])\nN: 1000\ntorch.Size([803601])\nN: 5000\ntorch.Size([803601])\nN: 10000\ntorch.Size([803601])\nN: 25000\ntorch.Size([803601])\nN: 50000\ntorch.Size([803601])\nN: 100000\ntorch.Size([803601])\n" ], [ "plt.plot(num_data_points, np.stack(fun_space_list)[:,1], marker = 'x', label = 'Function Space')\nplt.plot(num_data_points, np.stack(par_space_list)[:,1], marker = 'x', label = 'Parameter Space')\nplt.xscale('log')\nplt.yscale('log')\nplt.grid()\nplt.legend()", "_____no_output_____" ], [ "numpars = 0\nfor p in model.parameters():\n numpars += p.numel()\nprint(numpars)", "803601\n" ], [ "with open('../data/ntk_mlp_varying_data_speed_gp.pkl', 'wb') as handle:\n plot_dict = {\n 'N': num_data_points,\n 'ntk': fun_space_list,\n 'fisher': par_space_list,\n 'numpars': numpars\n }\n pickle.dump(plot_dict, handle, pickle.HIGHEST_PROTOCOL)", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2f3bfbe9571ad7da2621ff2b3c4b14bcd082ef

408,838

ipynb

Jupyter Notebook

lab/ML2_lab3.ipynb

pascalesser/Machine_Learning_2

c7c4352cfa56301f2d794436fb710329f1dfcd38

[ "MIT" ]

null

lab/ML2_lab3.ipynb

pascalesser/Machine_Learning_2

c7c4352cfa56301f2d794436fb710329f1dfcd38

[ "MIT" ]

null

lab/ML2_lab3.ipynb

pascalesser/Machine_Learning_2

c7c4352cfa56301f2d794436fb710329f1dfcd38

[ "MIT" ]

null

131.586096

47,664

0.860204

[ [ [ "### Lab 3: Expectation Maximization and Variational Autoencoder\n\n### Machine Learning 2 (2017/2018)\n\n* The lab exercises should be made in groups of two or three people.\n* The deadline is Friday, 01.06.\n* Assignment should be submitted through BlackBoard! Make sure to include your and your teammates' names with the submission.\n* Attach the .IPYNB (IPython Notebook) file containing your code and answers. Naming of the file should be \"studentid1\\_studentid2\\_lab#\", for example, the attached file should be \"12345\\_12346\\_lab1.ipynb\". Only use underscores (\"\\_\") to connect ids, otherwise the files cannot be parsed.\n\nNotes on implementation:\n\n* You should write your code and answers in an IPython Notebook: http://ipython.org/notebook.html. If you have problems, please ask.\n* Use __one cell__ for code and markdown answers only!\n * Put all code in the cell with the ```# YOUR CODE HERE``` comment and overwrite the ```raise NotImplementedError()``` line.\n * For theoretical questions, put your solution using LaTeX style formatting in the YOUR ANSWER HERE cell.\n* Among the first lines of your notebook should be \"%pylab inline\". This imports all required modules, and your plots will appear inline.\n* Large parts of you notebook will be graded automatically. Therefore it is important that your notebook can be run completely without errors and within a reasonable time limit. To test your notebook before submission, select Kernel -> Restart \\& Run All.\n$\\newcommand{\\bx}{\\mathbf{x}} \\newcommand{\\bpi}{\\mathbf{\\pi}} \\newcommand{\\bmu}{\\mathbf{\\mu}} \\newcommand{\\bX}{\\mathbf{X}} \\newcommand{\\bZ}{\\mathbf{Z}} \\newcommand{\\bz}{\\mathbf{z}}$", "_____no_output_____" ], [ "### Installing PyTorch\n\nIn this lab we will use PyTorch. PyTorch is an open source deep learning framework primarily developed by Facebook's artificial-intelligence research group. In order to install PyTorch in your conda environment go to https://pytorch.org and select your operating system, conda, Python 3.6, no cuda. Copy the text from the \"Run this command:\" box. Now open a terminal and activate your 'ml2labs' conda environment. Paste the text and run. After the installation is done you should restart Jupyter.", "_____no_output_____" ], [ "### MNIST data\n\nIn this Lab we will use several methods for unsupervised learning on the MNIST dataset of written digits. The dataset contains digital images of handwritten numbers $0$ through $9$. Each image has 28x28 pixels that each take 256 values in a range from white ($= 0$) to black ($=1$). The labels belonging to the images are also included. \nFortunately, PyTorch comes with a MNIST data loader. The first time you run the box below it will download the MNIST data set. That can take a couple of minutes.\nThe main data types in PyTorch are tensors. For Part 1, we will convert those tensors to numpy arrays. In Part 2, we will use the torch module to directly work with PyTorch tensors.", "_____no_output_____" ] ], [ [ "%pylab inline\nimport torch\nfrom torchvision import datasets, transforms\n\ntrain_dataset = datasets.MNIST('../data', train=True, download=True,\n transform=transforms.Compose([\n transforms.ToTensor(),\n transforms.Normalize((0.1307,), (0.3081,))\n ]))\n\ntrain_labels = train_dataset.train_labels.numpy()\ntrain_data = train_dataset.train_data.numpy()\n# For EM we will use flattened data\ntrain_data = train_data.reshape(train_data.shape[0], -1)\n", "Populating the interactive namespace from numpy and matplotlib\n" ] ], [ [ "## Part 1: Expectation Maximization\nWe will use the Expectation Maximization (EM) algorithm for the recognition of handwritten digits in the MNIST dataset. The images are modelled as a Bernoulli mixture model (see Bishop $\\S9.3.3$):\n$$\np(\\bx|\\bmu, \\bpi) = \\sum_{k=1}^K \\pi_k \\prod_{i=1}^D \\mu_{ki}^{x_i}(1-\\mu_{ki})^{(1-x_i)}\n$$\nwhere $x_i$ is the value of pixel $i$ in an image, $\\mu_{ki}$ represents the probability that pixel $i$ in class $k$ is black, and $\\{\\pi_1, \\ldots, \\pi_K\\}$ are the mixing coefficients of classes in the data. We want to use this data set to classify new images of handwritten numbers.", "_____no_output_____" ], [ "### 1.1 Binary data (5 points)\nAs we like to apply our Bernoulli mixture model, write a function `binarize` to convert the (flattened) MNIST data to binary images, where each pixel $x_i \\in \\{0,1\\}$, by thresholding at an appropriate level.", "_____no_output_____" ] ], [ [ "def binarize(X):\n ######################## ######################## ########################\n # YOUR CODE HERE\n \n X_ = np.around(X.astype(np.double)/255)\n return X_", "_____no_output_____" ], [ "# Test test test!\nbin_train_data = binarize(train_data)\nassert bin_train_data.dtype == np.float\nassert bin_train_data.shape == train_data.shape\n", "_____no_output_____" ] ], [ [ "Sample a few images of digits $2$, $3$ and $4$; and show both the original and the binarized image together with their label.", "_____no_output_____" ] ], [ [ "# YOUR CODE HERE\n######################## ######################## ########################\n\ndef plot_MNIST_digits(data):\n \n i = data.shape[0]\n \n for j in range(i):\n plt.subplot(1,i,j+1)\n plt.imshow(data[j].reshape(28,28), interpolation = 'nearest',\n cmap ='Greys')\n plt.axis('off')\n plt.show()\n\n\ndef plot_bin_MNIST_digits(digits, bin_train_data, train_labels, train_data):\n \n for digit in digits:\n\n print('\\n\\n'+'='*50+'\\n\\n')\n print('plotting label {}:\\n'.format(digit))\n\n bin_zip = zip(bin_train_data, train_labels)\n float_zip = zip(train_data, train_labels)\n bin_ = np.array([i for i,n in bin_zip if n == digit])\n float_ = np.array([i for i,n in float_zip if n == digit])\n\n print('... float')\n plot_MNIST_digits(np.vstack((float_[0:5])))\n\n print('... binary')\n plot_MNIST_digits(np.vstack((bin_[0:5])))\n\n print('\\n\\n'+'='*50+'\\n\\n')\n\n\nplot_bin_MNIST_digits([2,3,4], bin_train_data, train_labels, train_data)\n\n######################## ######################## ########################", "\n\n==================================================\n\n\nplotting label 2:\n\n... float\n" ] ], [ [ "### 1.2 Implementation (40 points)\nYou are going to write a function ```EM(X, K, max_iter)``` that implements the EM algorithm on the Bernoulli mixture model. \n\nThe only parameters the function has are:\n* ```X``` :: (NxD) array of input training images\n* ```K``` :: size of the latent space\n* ```max_iter``` :: maximum number of iterations, i.e. one E-step and one M-step\n\nYou are free to specify your return statement.\n\nMake sure you use a sensible way of terminating the iteration process early to prevent unnecessarily running through all epochs. Vectorize computations using ```numpy``` as much as possible.\n\nYou should implement the `E_step(X, mu, pi)` and `M_step(X, gamma)` separately in the functions defined below. These you can then use in your function `EM(X, K, max_iter)`.", "_____no_output_____" ] ], [ [ "def E_step(X, mu, pi):\n \n # YOUR CODE HERE\n ######################## ######################## ########################\n \n # expand X over axis 1 which gives us from (NxD) for X to (Nx1xD) for X_ \n X_ = np.expand_dims(X,axis=1)\n \n # calculate unnormalized gamma \n g = pi*np.prod(mu**X_ * (1-mu)**(1-X_), axis=2)\n \n # calculate normalization and expend it from N to Nx1\n normal = np.expand_dims(np.sum(g,axis=1),axis = 1)\n \n # get normalized gamma and handle devision by zero\n gamma = np.divide(g, normal, out=np.zeros_like(g), where=normal!=0)\n \n ######################## ######################## ########################\n return gamma", "_____no_output_____" ], [ "# Let's test on 5 datapoints\nn_test = 5\nX_test = bin_train_data[:n_test]\nD_test, K_test = X_test.shape[1], 10\n\nnp.random.seed(2018)\nmu_test = np.random.uniform(low=.25, high=.75, size=(K_test,D_test))\npi_test = np.ones(K_test) / K_test\n\ngamma_test = E_step(X_test, mu_test, pi_test)\nassert gamma_test.shape == (n_test, K_test)\n", "_____no_output_____" ], [ "def M_step(X, gamma):\n \n # YOUR CODE HERE\n ######################## ######################## ########################\n \n N_k = np.sum(gamma, axis=0) \n pi = N_k / np.sum(N_k)\n \n # we expend similar to the E-step but now over the second dimension of gamma\n X_ = np.expand_dims(X,axis=1)\n X__ = np.repeat(X_,gamma.shape[1],axis=1)\n \n # expend from Nxk to NxKx1\n gamma_ = np.expand_dims(gamma,axis=2)\n \n mu_ = np.sum(X__*gamma_,axis=0)\n \n mu = mu_/np.expand_dims(N_k,axis=1)\n\n ######################## ######################## ########################\n return mu, pi", "_____no_output_____" ], [ "# Oh, let's test again\nmu_test, pi_test = M_step(X_test, gamma_test)\n\nassert mu_test.shape == (K_test,D_test)\nassert pi_test.shape == (K_test, )\n", "_____no_output_____" ], [ "import time\ndef EM(X, K, max_iter, mu=None, pi=None, plotting = False, threshold = 1e-1):\n \n # YOUR CODE HERE\n ######################## ######################## ########################\n \n start_total = time.time() \n \n print('='*50+'\\ninitialize EM\\n')\n \n # init mu and pi if not given (reuse initialisation from above tests.) \n if mu is None:\n mu = np.random.uniform(low=.25, high=.75, size=(K,X_test.shape[1]))\n if pi is None:\n pi = np.ones(K) / K\n \n mu_ = mu\n pi_ = pi\n\n if plotting:\n print('initialize mu:')\n plot_MNIST_digits(mu)\n print('='*50+'\\n')\n \n \n # loop over epochs\n for i in range(max_iter):\n \n start = time.time()\n \n print('iteration {}'.format(i+1))\n \n gamma = E_step(X,mu,pi)\n mu, pi = M_step(X,gamma)\n \n # plotting latent space\n if plotting: plot_MNIST_digits(mu)\n \n # break if differences in mu and pi are small -> converged\n if all([i>0,np.linalg.norm(mu_-mu)<threshold , \n np.linalg.norm(pi_-pi)<threshold]):\n print('stop because of convergence after {} iterations'.format(i+1))\n break\n \n mu_ = mu \n pi_ = pi\n \n print('\\n\\n'+'='*50+'\\n\\n{} iterations in {} min\\n\\n'.format(\n i+1,(time.time()-start_total)/60)+'='*50+'\\n\\n')\n \n return mu, pi\n \n ######################## ######################## ########################", "_____no_output_____" ] ], [ [ "### 1.3 Three digits experiment (10 points)\nIn analogue with Bishop $\\S9.3.3$, sample a training set consisting of only __binary__ images of written digits $2$, $3$, and $4$. Run your EM algorithm and show the reconstructed digits.", "_____no_output_____" ] ], [ [ "# YOUR CODE HERE\n######################## ######################## ########################\n\n# fast version: only use part of the data\nbin_zip = zip(bin_train_data[:5000], train_labels[:5000])\n\nX = np.array([i for i,n in bin_zip if any([n==2, n==3, n==4])])\n\nK = 3\nepochs = 10\nmu,pi = EM(X,K,epochs,plotting=True)\n\n######################## ######################## ########################", "==================================================\ninitialize EM\n\ninitialize mu:\n" ] ], [ [ "Can you identify which element in the latent space corresponds to which digit? What are the identified mixing coefficients for digits $2$, $3$ and $4$, and how do these compare to the true ones?", "_____no_output_____" ], [ "YOUR ANSWER HERE\n\nYes, we can identify which element in the latent space corresponds to which digit, as there is one element for each of the digits $2,3$ and $4$.\n\nThe mixing coefficients for the digits are $0.35, 0.30, 0.35$. This is slightly different to the true values, where each number should appear $\\frac{1}{3}$ of the time.", "_____no_output_____" ] ], [ [ "print(pi)", "[0.34954996 0.29628561 0.35416443]\n" ] ], [ [ "### 1.4 Experiments (20 points)\nPerform the follow-up experiments listed below using your implementation of the EM algorithm. For each of these, describe/comment on the obtained results and give an explanation. You may still use your dataset with only digits 2, 3 and 4 as otherwise computations can take very long.", "_____no_output_____" ], [ "#### 1.4.1 Size of the latent space (5 points)\nRun EM with $K$ larger or smaller than the true number of classes. Describe your results.", "_____no_output_____" ] ], [ [ "# YOUR CODE HERE\n######################## ######################## ########################\n\n# smaller\nK = 2\n_, _ = EM(X,K,epochs,plotting=True) \n\n######################## ######################## ########################", "==================================================\ninitialize EM\n\ninitialize mu:\n" ] ], [ [ "###YOUR ANSWER HERE\n\nWhen we use $K=2$, the latent space can only represent two different classes, while there are still three classes present. As a result, the latent representation starts mixing the representations for the different numbers. We can see this especially for the digits $2$ and $4$, which are merged into a joined representation. Additionally, we can see that in contrast to the setting with three classes in the latent space, the algorithm fails to converge within ten epochs.", "_____no_output_____" ] ], [ [ "# YOUR CODE HERE\n######################## ######################## ########################\n\n# larger\nK = 5\n_, _ = EM(X,K,epochs,plotting=True) \n\n######################## ######################## ########################", "==================================================\ninitialize EM\n\ninitialize mu:\n" ] ], [ [ "###YOUR ANSWER HERE\n\nWhen we use $K=5$, the latent space can represent five different classes, while there are still three classes present. As a result, the latent representation starts splitting the representations of the given numbers. We can see this especially for the digits $2$ and $3$. For the $2$, we can see that we learn two depictions: one which encompasses a distinctive loop, while the other does not. For the $3$, we get one representation that is squeezed more than the other and one of them seems to be mixed with a representation of the digit two.", "_____no_output_____" ], [ "#### 1.4.2 Identify misclassifications (10 points)\nHow can you use the data labels to assign a label to each of the clusters/latent variables? Use this to identify images that are 'misclassified' and try to understand why they are. Report your findings.", "_____no_output_____" ] ], [ [ "# YOUR CODE HERE\n######################## ######################## ########################\n\ndef get_true_mu(bin_train_data,train_labels):\n\n true_mu = np.zeros((3,bin_train_data.shape[1]))\n \n for i in range(2,5):\n #find indices of images belonging to this label\n indx = np.argwhere(train_labels==i)\n \n # average over these images\n true_mu[i-2] = np.average(bin_train_data[indx],axis=0)\n\n return true_mu\n\n\ndef classify_image(image, mu):\n \"\"\"\n takes image and mu as an input and maps the image to the closest mu\n \"\"\"\n \n # L1 distance between mu and image\n dist = np.zeros((mu.shape[0],))\n for c in range(mu.shape[0]):\n dist[c] = numpy.linalg.norm(image-mu[c])\n \n # minimal distance is class\n classification = np.argmin(dist)\n \n return classification\n\n\ndef find_misclassification(mu, bin_train_data, train_labels, number_mc = 5): \n \n #find true labels of the latent space\n true_mu = get_true_mu(bin_train_data,train_labels)\n \n mu_label = np.zeros((mu.shape[0],))\n for i in range(len(mu)):\n mu_label[i] = classify_image(mu[i], true_mu) + 2\n \n #initializing arrays to save the misclassified results\n mc_pic = np.zeros((number_mc,mu.shape[1]))\n mc_pred = np.zeros((number_mc,))\n mc_label = np.zeros((number_mc,))\n i = 0\n mc_counter = 0\n\n while mc_counter < number_mc: \n if train_labels[i] >= 2 and train_labels[i] <= 4: ## only consider images with true labels 2, 3 or 4\n c_pred = mu_label[classify_image(bin_train_data[i], mu)]\n \n if c_pred != train_labels[i]:\n mc_pic[mc_counter] = bin_train_data[i]\n mc_pred[mc_counter] = c_pred\n mc_label[mc_counter] = train_labels[i]\n mc_counter = mc_counter + 1\n i = i + 1 \n \n print('True label - predicted label:')\n for j in range(number_mc):\n plt.subplot(1,number_mc,j+1)\n plt.imshow(mc_pic[j].reshape(28,28), interpolation = 'nearest',\n cmap ='Greys')\n plt.title(\"{0:d} - {1:d}\".format(int(mc_label[j]), int(mc_pred[j])))\n plt.axis('off')\n plt.show()\n \n# using mu from the run above with the correct number of classes\n\nfind_misclassification(mu, bin_train_data, train_labels, number_mc=10)\nprint('Comparing to the mus found using EM:')\nplot_MNIST_digits(mu)\n\n######################## ######################## ########################", "True label - predicted label:\n" ] ], [ [ "YOUR ANSWER HERE\n\nWe can use the data labels in order to calculate the true values of the mus by averaging over all images that are assigned with this label. Then, we compare these true values to the mus we found using the EM-algorithm and label them with the according label if they show the smallest difference between one another.\n\nUsing the same technique, we can label the images of the dataset by comparing the to the mus we found using the EM-algorithm and assigning them with the correponding label of the most similar one. Comparing our result to the true labels, gives us a number of misclassifications as shown above.\n\nWe can see that a lot of twos get misclassified, especially if they do not encompass the loop as it is present in the latent representation. We can conclude that in general samples that are too different from the latent representation will be misclassified.", "_____no_output_____" ], [ "#### 1.4.3 Initialize with true values (5 points)\nInitialize the three classes with the true values of the parameters and see what happens. Report your results.", "_____no_output_____" ] ], [ [ "# YOUR CODE HERE\n######################## ######################## ########################\n\nK = 3\ntrue_mu = get_true_mu(bin_train_data,train_labels)\n_, _ = EM(X,K,epochs,mu = true_mu, plotting=True) \n\n######################## ######################## ########################", "==================================================\ninitialize EM\n\ninitialize mu:\n" ] ], [ [ "YOUR ANSWER HERE\n\nWhen we initialize with the true values for mu, we can see that the algorithm changes this representation only marginally. For example, the loop of the two slightly increases. The algorithm manages to converge within 3 epochs.", "_____no_output_____" ], [ "## Part 2: Variational Auto-Encoder\n\nA Variational Auto-Encoder (VAE) is a probabilistic model $p(\\bx, \\bz)$ over observed variables $\\bx$ and latent variables and/or parameters $\\bz$. Here we distinguish the decoder part, $p(\\bx | \\bz) p(\\bz)$ and an encoder part $p(\\bz | \\bx)$ that are both specified with a neural network. A lower bound on the log marginal likelihood $\\log p(\\bx)$ can be obtained by approximately inferring the latent variables z from the observed data x using an encoder distribution $q(\\bz| \\bx)$ that is also specified as a neural network. This lower bound is then optimized to fit the model to the data. \n\nThe model was introduced by Diederik Kingma (during his PhD at the UVA) and Max Welling in 2013, https://arxiv.org/abs/1312.6114. \n\nSince it is such an important model there are plenty of well written tutorials that should help you with the assignment. E.g: https://jaan.io/what-is-variational-autoencoder-vae-tutorial/.\n\nIn the following, we will make heavily use of the torch module, https://pytorch.org/docs/stable/index.html. Most of the time replacing `np.` with `torch.` will do the trick, e.g. `np.sum` becomes `torch.sum` and `np.log` becomes `torch.log`. In addition, we will use `torch.FloatTensor()` as an equivalent to `np.array()`. In order to train our VAE efficiently we will make use of batching. The number of data points in a batch will become the first dimension of our data tensor, e.g. A batch of 128 MNIST images has the dimensions [128, 1, 28, 28]. To check check the dimensions of a tensor you can call `.size()`.", "_____no_output_____" ], [ "### 2.1 Loss function\nThe objective function (variational lower bound), that we will use to train the VAE, consists of two terms: a log Bernoulli loss (reconstruction loss) and a Kullback–Leibler divergence. We implement the two terms separately and combine them in the end.\nAs seen in Part 1: Expectation Maximization, we can use a multivariate Bernoulli distribution to model the likelihood $p(\\bx | \\bz)$ of black and white images. Formally, the variational lower bound is maximized but in PyTorch we are always minimizing therefore we need to calculate the negative log Bernoulli loss and Kullback–Leibler divergence.", "_____no_output_____" ], [ "### 2.1.1 Negative Log Bernoulli loss (5 points)\nThe negative log Bernoulli loss is defined as,\n\n\\begin{align}\nloss = - (\\sum_i^D \\bx_i \\log \\hat{\\bx_i} + (1 − \\bx_i) \\log(1 − \\hat{\\bx_i})).\n\\end{align}\n\nWrite a function `log_bernoulli_loss` that takes a D dimensional vector `x`, its reconstruction `x_hat` and returns the negative log Bernoulli loss. Make sure that your function works for batches of arbitrary size.", "_____no_output_____" ] ], [ [ "def log_bernoulli_loss(x_hat, x):\n \n # YOUR CODE HERE\n ######################## ######################## ########################\n \n n = torch.mul(x, torch.log(x_hat)) + torch.mul(1 - x, torch.log(1 - x_hat))\n loss = -n.sum()\n \n ######################## ######################## ########################\n return loss\n", "_____no_output_____" ], [ "### Test test test\nx_test = torch.FloatTensor([[0.1, 0.2, 0.3, 0.4], [0.5, 0.6, 0.7, 0.8], [0.9, 0.9, 0.9, 0.9]])\nx_hat_test = torch.FloatTensor([[0.11, 0.22, 0.33, 0.44], [0.55, 0.66, 0.77, 0.88], [0.99, 0.99, 0.99, 0.99]])\n\nassert log_bernoulli_loss(x_hat_test, x_test) > 0.0\nassert log_bernoulli_loss(x_hat_test, x_test) < 10.0\n", "_____no_output_____" ] ], [ [ "### 2.1.2 Negative Kullback–Leibler divergence (10 Points)\nThe variational lower bound (the objective to be maximized) contains a KL term $D_{KL}(q(\\bz)||p(\\bz))$ that can often be calculated analytically. In the VAE we assume $q = N(\\bz, \\mu, \\sigma^2I)$ and $p = N(\\bz, 0, I)$. Solve analytically!", "_____no_output_____" ], [ "YOUR ANSWER HERE\n\n\n\\begin{align*} \n\\newcommand{\\xscalar}{x}\n\\newcommand{\\xvec}{{\\bf z}}\n\\newcommand{\\Lmat}{{\\sigma^2 \\bf I}}\n\\newcommand{\\Sigmamat}{\\bf I}\n\\newcommand{\\SigmamatInv}{\\Sigmamat^{-1}}\n\\newcommand{\\mvec}{\\boldsymbol{\\mu}}\n \\mathcal{KL}(q||p) &= - \\int q(\\xvec) \\log \\left(\\frac{p(\\xvec)}{q(\\xvec)}\\right) d\\xvec \\\\\n &= \\int q(\\xvec) \\log (p(\\xvec) - q(\\xvec)) d\\xvec \\\\ \n &= \\int q(\\xvec) [ - \\frac{D}{2} \\log(2\\pi) - \\frac{1}{2} \\log(|\\Sigmamat|) - \\frac{1}{2} (\\xvec)^T \\SigmamatInv(\\xvec) \\\\\n & + \\frac{D}{2} \\log(2\\pi) + \\frac{1}{2} \\log(|\\Lmat|) + \\frac{1}{2} (\\xvec-\\mvec)^T \\Lmat^{-1}(\\xvec-\\mvec) ] d\\xvec \\\\\n &= \\frac{1}{2} \\log \\left(\\frac{|\\Lmat|}{|\\Sigmamat|}\\right) \\int q(\\xvec) d\\xvec \\int q(\\xvec) [ - \\frac{1}{2} (\\xvec)^T \\SigmamatInv(\\xvec) \\\\\n & + \\frac{1}{2} (\\xvec-\\mvec)^T \\Lmat^{-1}(\\xvec-\\mvec) ] d\\xvec\n \\end{align*}\n We use $\\int q(\\xvec) d\\xvec = 1$ and the law of the unconscious statistician to get \n \\begin{align*}\n &= \\frac{1}{2} \\log \\left(\\frac{|\\Lmat|}{|\\Sigmamat|}\\right) - \\frac{1}{2} \\mathbb{E}[ (\\xvec)^T \\SigmamatInv(\\xvec)] + \n \\frac{1}{2} \\mathbb{E}[(\\xvec-\\mvec)^T \\Lmat^{-1}(\\xvec-\\mvec)] \n \\end{align*}\n Since $p$ is considered to be the original distribution, it follows that $\\xvec \\sim \\mathcal{N}(\\xvec|0, \\Sigmamat)$. Therefore, we can use equation 380 from the matrix cookbook to get: \n \\begin{align*}\n &= \\frac{1}{2} \\log \\left(\\frac{|\\Lmat|}{|\\Sigmamat|}\\right) - \\frac{1}{2}[\\SigmamatInv + Tr(\\SigmamatInv\\Sigmamat)] \\\\\n & + \\frac{1}{2}[(-\\mvec)^T \\Lmat^{-1}(-\\mvec) + Tr(\\Lmat^{-1}\\Sigmamat)] \\\\\n &= \\frac{1}{2} \\left[\\log \\left(\\frac{|\\Lmat|}{|\\Sigmamat|}\\right) - Tr(\\Sigmamat)+ (-\\mvec)^T \\Lmat^{-1}(-\\mvec) + Tr(\\Lmat^{-1}\\Sigmamat)\\right] \\\\\n &= \\frac{1}{2} \\left[\\log \\left(\\frac{|\\Lmat|}{|\\Sigmamat|}\\right) - D + (-\\mvec)^T \\Lmat^{-1}(-\\mvec) + Tr(\\Lmat^{-1}\\Sigmamat)\\right]\\\\\n \\end{align*}", "_____no_output_____" ], [ "Write a function `KL_loss` that takes two J dimensional vectors `mu` and `logvar` and returns the negative Kullback–Leibler divergence. Where `logvar` is $\\log(\\sigma^2)$. Make sure that your function works for batches of arbitrary size.", "_____no_output_____" ] ], [ [ "def KL_loss(mu, logvar):\n \n # YOUR CODE HERE\n ######################## ######################## ########################\n \n loss = -0.5 * torch.sum(1 + logvar - torch.pow(mu, 2) - torch.exp(logvar))\n \n ######################## ######################## ########################\n return loss\n", "_____no_output_____" ], [ "### Test test test\nmu_test = torch.FloatTensor([[0.1, 0.2], [0.3, 0.4], [0.5, 0.6]])\nlogvar_test = torch.FloatTensor([[0.01, 0.02], [0.03, 0.04], [0.05, 0.06]])\n\nassert KL_loss(mu_test, logvar_test) > 0.0\nassert KL_loss(mu_test, logvar_test) < 10.0\n", "_____no_output_____" ] ], [ [ "### 2.1.3 Putting the losses together (5 points)\nWrite a function `loss_function` that takes a D dimensional vector `x`, its reconstruction `x_hat`, two J dimensional vectors `mu` and `logvar` and returns the final loss. Make sure that your function works for batches of arbitrary size.", "_____no_output_____" ] ], [ [ "def loss_function(x_hat, x, mu, logvar):\n \n # YOUR CODE HERE\n ######################## ######################## ########################\n \n entropy_loss = log_bernoulli_loss(x_hat, x)\n kl_loss = KL_loss(mu,logvar)\n loss = entropy_loss+kl_loss \n \n ######################## ######################## ########################\n \n return loss\n", "_____no_output_____" ], [ "x_test = torch.FloatTensor([[0.1, 0.2, 0.3], [0.4, 0.5, 0.6], [0.7, 0.8, 0.9]])\nx_hat_test = torch.FloatTensor([[0.11, 0.22, 0.33], [0.44, 0.55, 0.66], [0.77, 0.88, 0.99]])\nmu_test = torch.FloatTensor([[0.1, 0.2], [0.3, 0.4], [0.5, 0.6]])\nlogvar_test = torch.FloatTensor([[0.01, 0.02], [0.03, 0.04], [0.05, 0.06]])\n\nassert loss_function(x_hat_test, x_test, mu_test, logvar_test) > 0.0\nassert loss_function(x_hat_test, x_test, mu_test, logvar_test) < 10.0\n", "_____no_output_____" ] ], [ [ "### 2.2 The model\nBelow you see a data structure for the VAE. The modell itself consists of two main parts the encoder (images $\\bx$ to latent variables $\\bz$) and the decoder (latent variables $\\bz$ to images $\\bx$). The encoder is using 3 fully-connected layers, whereas the decoder is using fully-connected layers. Right now the data structure is quite empty, step by step will update its functionality. For test purposes we will initialize a VAE for you. After the data structure is completed you will do the hyperparameter search.\n", "_____no_output_____" ] ], [ [ "from torch import nn\nfrom torch.nn import functional as F \n\nclass VAE(nn.Module):\n def __init__(self, fc1_dims, fc21_dims, fc22_dims, fc3_dims, fc4_dims):\n super(VAE, self).__init__()\n\n self.fc1 = nn.Linear(*fc1_dims)\n self.fc21 = nn.Linear(*fc21_dims)\n self.fc22 = nn.Linear(*fc22_dims)\n self.fc3 = nn.Linear(*fc3_dims)\n self.fc4 = nn.Linear(*fc4_dims)\n\n def encode(self, x):\n # To be implemented\n raise Exception('Method not implemented')\n\n def reparameterize(self, mu, logvar):\n # To be implemented\n raise Exception('Method not implemented')\n\n def decode(self, z):\n # To be implemented\n raise Exception('Method not implemented')\n\n def forward(self, x):\n # To be implemented\n raise Exception('Method not implemented')\n\nVAE_test = VAE(fc1_dims=(784, 4), fc21_dims=(4, 2), fc22_dims=(4, 2), fc3_dims=(2, 4), fc4_dims=(4, 784))\n", "_____no_output_____" ] ], [ [ "### 2.3 Encoding (10 points)\nWrite a function `encode` that gets a vector `x` with 784 elements (flattened MNIST image) and returns `mu` and `logvar`. Your function should use three fully-connected layers (`self.fc1()`, `self.fc21()`, `self.fc22()`). First, you should use `self.fc1()` to embed `x`. Second, you should use `self.fc21()` and `self.fc22()` on the embedding of `x` to compute `mu` and `logvar` respectively. PyTorch comes with a variety of activation functions, the most common calls are `F.relu()`, `F.sigmoid()`, `F.tanh()`. Make sure that your function works for batches of arbitrary size. ", "_____no_output_____" ] ], [ [ "def encode(self, x):\n \n # YOUR CODE HERE\n ######################## ######################## ########################\n \n z = F.relu(self.fc1(x))\n mu = self.fc21(z)\n logvar = self.fc22(z)\n \n ######################## ######################## ########################\n \n return mu, logvar\n", "_____no_output_____" ], [ "### Test, test, test\nVAE.encode = encode\n\nx_test = torch.ones((5,784))\nmu_test, logvar_test = VAE_test.encode(x_test)\n\nassert np.allclose(mu_test.size(), [5, 2])\nassert np.allclose(logvar_test.size(), [5, 2])\n", "_____no_output_____" ] ], [ [ "### 2.4 Reparameterization (10 points)\nOne of the major question that the VAE is answering, is 'how to take derivatives with respect to the parameters of a stochastic variable?', i.e. if we are given $\\bz$ that is drawn from a distribution $q(\\bz|\\bx)$, and we want to take derivatives. This step is necessary to be able to use gradient-based optimization algorithms like SGD.\nFor some distributions, it is possible to reparameterize samples in a clever way, such that the stochasticity is independent of the parameters. We want our samples to deterministically depend on the parameters of the distribution. For example, in a normally-distributed variable with mean $\\mu$ and standard deviation $\\sigma$, we can sample from it like this:\n\n\\begin{align}\n\\bz = \\mu + \\sigma \\odot \\epsilon,\n\\end{align}\n\nwhere $\\odot$ is the element-wise multiplication and $\\epsilon$ is sampled from $N(0, I)$.\n\n\nWrite a function `reparameterize` that takes two J dimensional vectors `mu` and `logvar`. It should return $\\bz = \\mu + \\sigma \\odot \\epsilon$.\n", "_____no_output_____" ] ], [ [ "def reparameterize(self, mu, logvar):\n\n # YOUR CODE HERE\n ######################## ######################## ########################\n\n sigma = torch.sqrt(torch.exp(logvar))\n z = mu + sigma * torch.randn(mu.size())\n\n ######################## ######################## ########################\n return z\n", "_____no_output_____" ], [ "### Test, test, test\nVAE.reparameterize = reparameterize\nVAE_test.train()\n\nmu_test = torch.FloatTensor([[0.1, 0.2], [0.3, 0.4], [0.5, 0.6]])\nlogvar_test = torch.FloatTensor([[0.01, 0.02], [0.03, 0.04], [0.05, 0.06]])\n\nz_test = VAE_test.reparameterize(mu_test, logvar_test)\n\nassert np.allclose(z_test.size(), [3, 2])\nassert z_test[0][0] < 5.0\nassert z_test[0][0] > -5.0\n", "_____no_output_____" ] ], [ [ "### 2.5 Decoding (10 points)\nWrite a function `decode` that gets a vector `z` with J elements and returns a vector `x_hat` with 784 elements (flattened MNIST image). Your function should use two fully-connected layers (`self.fc3()`, `self.fc4()`). PyTorch comes with a variety of activation functions, the most common calls are `F.relu()`, `F.sigmoid()`, `F.tanh()`. Make sure that your function works for batches of arbitrary size.", "_____no_output_____" ] ], [ [ "def decode(self, z):\n \n # YOUR CODE HERE\n ######################## ######################## ########################\n \n out3 = F.relu(self.fc3(z))\n x_hat = F.sigmoid(self.fc4(out3))\n \n ######################## ######################## ########################\n return x_hat\n", "_____no_output_____" ], [ "# test test test\nVAE.decode = decode\n\nz_test = torch.ones((5,2))\nx_hat_test = VAE_test.decode(z_test)\n\nassert np.allclose(x_hat_test.size(), [5, 784])\nassert (x_hat_test <= 1).all()\nassert (x_hat_test >= 0).all()\n", "_____no_output_____" ] ], [ [ "### 2.6 Forward pass (10)\nTo complete the data structure you have to define a forward pass through the VAE. A single forward pass consists of the encoding of an MNIST image $\\bx$ into latent space $\\bz$, the reparameterization of $\\bz$ and the decoding of $\\bz$ into an image $\\bx$.\n\nWrite a function `forward` that gets a a vector `x` with 784 elements (flattened MNIST image) and returns a vector `x_hat` with 784 elements (flattened MNIST image), `mu` and `logvar`.", "_____no_output_____" ] ], [ [ "def forward(self, x):\n x = x.view(-1, 784)\n \n # YOUR CODE HERE\n ######################## ######################## ########################\n mu, logvar = self.encode(x)\n z = self.reparameterize(mu, logvar)\n x_hat = self.decode(z)\n \n ######################## ######################## ########################\n return x_hat, mu, logvar\n", "_____no_output_____" ], [ "# test test test \nVAE.forward = forward\n\nx_test = torch.ones((5,784))\nx_hat_test, mu_test, logvar_test = VAE_test.forward(x_test)\n\nassert np.allclose(x_hat_test.size(), [5, 784])\nassert np.allclose(mu_test.size(), [5, 2])\nassert np.allclose(logvar_test.size(), [5, 2])\n", "_____no_output_____" ] ], [ [ "### 2.7 Training (15)\nWe will now train the VAE using an optimizer called Adam, https://arxiv.org/abs/1412.6980. The code to train a model in PyTorch is given below.", "_____no_output_____" ] ], [ [ "from torch.autograd import Variable\n\ndef train(epoch, train_loader, model, optimizer):\n model.train()\n train_loss = 0\n for batch_idx, (data, _) in enumerate(train_loader):\n data = Variable(data)\n optimizer.zero_grad()\n recon_batch, mu, logvar = model(data)\n loss = loss_function(recon_batch, data.view(-1, 784), mu, logvar)\n loss.backward()\n train_loss += loss.data\n optimizer.step()\n if batch_idx % 100 == 0:\n print('Train Epoch: {} [{}/{} ({:.0f}%)]\\tLoss: {:.6f}'.format(\n epoch, batch_idx * len(data), len(train_loader.dataset),\n 100. * batch_idx / len(train_loader),\n loss.data / len(data)))\n\n print('====> Epoch: {} Average loss: {:.4f}'.format(\n epoch, train_loss / len(train_loader.dataset)))\n", "_____no_output_____" ] ], [ [ "Let's train. You have to choose the hyperparameters. Make sure your loss is going down in a reasonable amount of epochs (around 10).", "_____no_output_____" ] ], [ [ "# Hyperparameters\n# fc1_dims = (?,?)\n# fc21_dims =\n# fc22_dims =\n# fc3_dims =\n# fc4_dims =\n# lr =\n# batch_size =\n# epochs =\n\n# YOUR CODE HERE\n######################## ######################## ########################\n# using the parameters as given in: https://github.com/pytorch/examples/tree/master/vae \nfc1_dims = (784,400)\nfc21_dims = (400,20)\nfc22_dims = (400,20)\nfc3_dims = (20,400)\nfc4_dims = (400,784)\nlr = 1e-3\nbatch_size = 128\nepochs = 10\n######################## ######################## ########################", "_____no_output_____" ], [ "# This cell contains a hidden test, please don't delete it, thx", "_____no_output_____" ] ], [ [ "Run the box below to train the model using the hyperparameters you entered above.", "_____no_output_____" ] ], [ [ "from torchvision import datasets, transforms\nfrom torch import nn, optim\n\n# Load data\ntrain_data = datasets.MNIST('../data', train=True, download=True,\n transform=transforms.ToTensor())\n\ntrain_loader = torch.utils.data.DataLoader(train_data,\n batch_size=batch_size, shuffle=True, **{})\n\n# Init model\nVAE_MNIST = VAE(fc1_dims=fc1_dims, fc21_dims=fc21_dims, fc22_dims=fc22_dims, fc3_dims=fc3_dims, fc4_dims=fc4_dims)\n\n# Init optimizer\noptimizer = optim.Adam(VAE_MNIST.parameters(), lr=lr)\n\n# Train\nfor epoch in range(1, epochs + 1):\n train(epoch, train_loader, VAE_MNIST, optimizer)\n", "Train Epoch: 1 [0/60000 (0%)]\tLoss: 549.927795\nTrain Epoch: 1 [12800/60000 (21%)]\tLoss: 187.774139\nTrain Epoch: 1 [25600/60000 (43%)]\tLoss: 151.297928\nTrain Epoch: 1 [38400/60000 (64%)]\tLoss: 135.530563\nTrain Epoch: 1 [51200/60000 (85%)]\tLoss: 133.712051\n====> Epoch: 1 Average loss: 162.9749\nTrain Epoch: 2 [0/60000 (0%)]\tLoss: 129.225845\nTrain Epoch: 2 [12800/60000 (21%)]\tLoss: 124.249214\nTrain Epoch: 2 [25600/60000 (43%)]\tLoss: 119.403214\nTrain Epoch: 2 [38400/60000 (64%)]\tLoss: 117.094475\nTrain Epoch: 2 [51200/60000 (85%)]\tLoss: 110.436165\n====> Epoch: 2 Average loss: 120.6739\nTrain Epoch: 3 [0/60000 (0%)]\tLoss: 114.500031\nTrain Epoch: 3 [12800/60000 (21%)]\tLoss: 111.776672\nTrain Epoch: 3 [25600/60000 (43%)]\tLoss: 114.054794\nTrain Epoch: 3 [38400/60000 (64%)]\tLoss: 111.648720\nTrain Epoch: 3 [51200/60000 (85%)]\tLoss: 111.599319\n====> Epoch: 3 Average loss: 114.1491\nTrain Epoch: 4 [0/60000 (0%)]\tLoss: 110.490540\nTrain Epoch: 4 [12800/60000 (21%)]\tLoss: 111.640862\nTrain Epoch: 4 [25600/60000 (43%)]\tLoss: 110.019012\nTrain Epoch: 4 [38400/60000 (64%)]\tLoss: 111.838921\nTrain Epoch: 4 [51200/60000 (85%)]\tLoss: 110.753128\n====> Epoch: 4 Average loss: 111.4047\nTrain Epoch: 5 [0/60000 (0%)]\tLoss: 111.950302\nTrain Epoch: 5 [12800/60000 (21%)]\tLoss: 109.241913\nTrain Epoch: 5 [25600/60000 (43%)]\tLoss: 107.332108\nTrain Epoch: 5 [38400/60000 (64%)]\tLoss: 110.472519\nTrain Epoch: 5 [51200/60000 (85%)]\tLoss: 109.508560\n====> Epoch: 5 Average loss: 109.7302\nTrain Epoch: 6 [0/60000 (0%)]\tLoss: 110.585701\nTrain Epoch: 6 [12800/60000 (21%)]\tLoss: 108.586479\nTrain Epoch: 6 [25600/60000 (43%)]\tLoss: 107.371269\nTrain Epoch: 6 [38400/60000 (64%)]\tLoss: 105.153595\nTrain Epoch: 6 [51200/60000 (85%)]\tLoss: 105.446297\n====> Epoch: 6 Average loss: 108.5776\nTrain Epoch: 7 [0/60000 (0%)]\tLoss: 109.831375\nTrain Epoch: 7 [12800/60000 (21%)]\tLoss: 110.046555\nTrain Epoch: 7 [25600/60000 (43%)]\tLoss: 104.801361\nTrain Epoch: 7 [38400/60000 (64%)]\tLoss: 103.717628\nTrain Epoch: 7 [51200/60000 (85%)]\tLoss: 111.997604\n====> Epoch: 7 Average loss: 107.8022\nTrain Epoch: 8 [0/60000 (0%)]\tLoss: 107.858582\nTrain Epoch: 8 [12800/60000 (21%)]\tLoss: 108.593163\nTrain Epoch: 8 [25600/60000 (43%)]\tLoss: 108.067123\nTrain Epoch: 8 [38400/60000 (64%)]\tLoss: 110.446304\nTrain Epoch: 8 [51200/60000 (85%)]\tLoss: 105.854263\n====> Epoch: 8 Average loss: 107.1581\nTrain Epoch: 9 [0/60000 (0%)]\tLoss: 104.720139\nTrain Epoch: 9 [12800/60000 (21%)]\tLoss: 106.817406\nTrain Epoch: 9 [25600/60000 (43%)]\tLoss: 104.800179\nTrain Epoch: 9 [38400/60000 (64%)]\tLoss: 105.337631\nTrain Epoch: 9 [51200/60000 (85%)]\tLoss: 109.797195\n====> Epoch: 9 Average loss: 106.6367\nTrain Epoch: 10 [0/60000 (0%)]\tLoss: 103.187050\nTrain Epoch: 10 [12800/60000 (21%)]\tLoss: 106.347107\nTrain Epoch: 10 [25600/60000 (43%)]\tLoss: 105.634209\nTrain Epoch: 10 [38400/60000 (64%)]\tLoss: 108.781830\nTrain Epoch: 10 [51200/60000 (85%)]\tLoss: 108.425758\n====> Epoch: 10 Average loss: 106.2243\n" ] ], [ [ "Run the box below to check if the model you trained above is able to correctly reconstruct images.", "_____no_output_____" ] ], [ [ "### Let's check if the reconstructions make sense\n# Set model to test mode\nVAE_MNIST.eval()\n \n# Reconstructed\ntrain_data_plot = datasets.MNIST('../data', train=True, download=True,\n transform=transforms.ToTensor())\n\ntrain_loader_plot = torch.utils.data.DataLoader(train_data_plot,\n batch_size=1, shuffle=False, **{})\n\nfor batch_idx, (data, _) in enumerate(train_loader_plot):\n x_hat, mu, logvar = VAE_MNIST(data)\n plt.imshow(x_hat.view(1,28,28).squeeze().data.numpy(), cmap='gray')\n plt.title('%i' % train_data.train_labels[batch_idx])\n plt.show()\n if batch_idx == 3:\n break\n", "_____no_output_____" ] ], [ [ "### 2.8 Visualize latent space (20 points)\nNow, implement the auto-encoder now with a 2-dimensional latent space, and train again over the MNIST data. Make a visualization of the learned manifold by using a linearly spaced coordinate grid as input for the latent space, as seen in https://arxiv.org/abs/1312.6114 Figure 4.", "_____no_output_____" ] ], [ [ "# YOUR CODE HERE\n######################## ######################## ########################\nfc1_dims = (784,400)\nfc21_dims = (400,2)\nfc22_dims = (400,2)\nfc3_dims = (2,400)\nfc4_dims = (400,784)\nlr = 1e-3\nbatch_size = 128\nepochs = 10\n\n# Init model\nVAE_MNIST = VAE(fc1_dims=fc1_dims, fc21_dims=fc21_dims, fc22_dims=fc22_dims, fc3_dims=fc3_dims, fc4_dims=fc4_dims)\n\n# Init optimizer\noptimizer = optim.Adam(VAE_MNIST.parameters(), lr=lr)\n\n# Train\nfor epoch in range(1, epochs + 1):\n train(epoch, train_loader, VAE_MNIST, optimizer)\n\n######################## ######################## ########################", "Train Epoch: 1 [0/60000 (0%)]\tLoss: 547.188660\nTrain Epoch: 1 [12800/60000 (21%)]\tLoss: 190.724518\nTrain Epoch: 1 [25600/60000 (43%)]\tLoss: 183.475037\nTrain Epoch: 1 [38400/60000 (64%)]\tLoss: 178.626740\nTrain Epoch: 1 [51200/60000 (85%)]\tLoss: 181.308685\n====> Epoch: 1 Average loss: 190.5039\nTrain Epoch: 2 [0/60000 (0%)]\tLoss: 173.734924\nTrain Epoch: 2 [12800/60000 (21%)]\tLoss: 171.191605\nTrain Epoch: 2 [25600/60000 (43%)]\tLoss: 172.238831\nTrain Epoch: 2 [38400/60000 (64%)]\tLoss: 155.479813\nTrain Epoch: 2 [51200/60000 (85%)]\tLoss: 168.183075\n====> Epoch: 2 Average loss: 166.9514\nTrain Epoch: 3 [0/60000 (0%)]\tLoss: 170.649994\nTrain Epoch: 3 [12800/60000 (21%)]\tLoss: 162.990494\nTrain Epoch: 3 [25600/60000 (43%)]\tLoss: 158.472961\nTrain Epoch: 3 [38400/60000 (64%)]\tLoss: 166.178955\nTrain Epoch: 3 [51200/60000 (85%)]\tLoss: 159.786560\n====> Epoch: 3 Average loss: 163.5314\nTrain Epoch: 4 [0/60000 (0%)]\tLoss: 162.653625\nTrain Epoch: 4 [12800/60000 (21%)]\tLoss: 167.145065\nTrain Epoch: 4 [25600/60000 (43%)]\tLoss: 160.325531\nTrain Epoch: 4 [38400/60000 (64%)]\tLoss: 162.656601\nTrain Epoch: 4 [51200/60000 (85%)]\tLoss: 171.967133\n====> Epoch: 4 Average loss: 161.6073\nTrain Epoch: 5 [0/60000 (0%)]\tLoss: 158.492798\nTrain Epoch: 5 [12800/60000 (21%)]\tLoss: 161.623306\nTrain Epoch: 5 [25600/60000 (43%)]\tLoss: 154.071381\nTrain Epoch: 5 [38400/60000 (64%)]\tLoss: 158.868637\nTrain Epoch: 5 [51200/60000 (85%)]\tLoss: 147.898712\n====> Epoch: 5 Average loss: 160.2289\nTrain Epoch: 6 [0/60000 (0%)]\tLoss: 159.335892\nTrain Epoch: 6 [12800/60000 (21%)]\tLoss: 161.691116\nTrain Epoch: 6 [25600/60000 (43%)]\tLoss: 156.913315\nTrain Epoch: 6 [38400/60000 (64%)]\tLoss: 157.479507\nTrain Epoch: 6 [51200/60000 (85%)]\tLoss: 162.400757\n====> Epoch: 6 Average loss: 159.0768\nTrain Epoch: 7 [0/60000 (0%)]\tLoss: 163.747528\nTrain Epoch: 7 [12800/60000 (21%)]\tLoss: 154.155258\nTrain Epoch: 7 [25600/60000 (43%)]\tLoss: 157.765182\nTrain Epoch: 7 [38400/60000 (64%)]\tLoss: 152.845505\nTrain Epoch: 7 [51200/60000 (85%)]\tLoss: 157.339355\n====> Epoch: 7 Average loss: 157.9870\nTrain Epoch: 8 [0/60000 (0%)]\tLoss: 154.260925\nTrain Epoch: 8 [12800/60000 (21%)]\tLoss: 158.054810\nTrain Epoch: 8 [25600/60000 (43%)]\tLoss: 151.418488\nTrain Epoch: 8 [38400/60000 (64%)]\tLoss: 152.102722\nTrain Epoch: 8 [51200/60000 (85%)]\tLoss: 157.490784\n====> Epoch: 8 Average loss: 157.0406\nTrain Epoch: 9 [0/60000 (0%)]\tLoss: 163.825485\nTrain Epoch: 9 [12800/60000 (21%)]\tLoss: 155.307663\nTrain Epoch: 9 [25600/60000 (43%)]\tLoss: 157.243729\nTrain Epoch: 9 [38400/60000 (64%)]\tLoss: 148.323654\nTrain Epoch: 9 [51200/60000 (85%)]\tLoss: 157.200607\n====> Epoch: 9 Average loss: 156.2460\nTrain Epoch: 10 [0/60000 (0%)]\tLoss: 150.685394\nTrain Epoch: 10 [12800/60000 (21%)]\tLoss: 162.164215\nTrain Epoch: 10 [25600/60000 (43%)]\tLoss: 157.070526\nTrain Epoch: 10 [38400/60000 (64%)]\tLoss: 153.022583\nTrain Epoch: 10 [51200/60000 (85%)]\tLoss: 148.663284\n====> Epoch: 10 Average loss: 155.4347\n" ], [ "######################## ######################## ########################\n\nVAE_MNIST.eval()\n\nsize = 5\nf, axarr = plt.subplots(size*2,size*2)\n\nfor i in range(-size,size):\n for j in range(-size,size):\n pos = torch.zeros((1,2))\n pos[0,0] = i\n pos[0,1] = j\n x_hat = VAE_MNIST.decode(torch.autograd.Variable(pos))\n axarr[i+size,j+size].imshow(x_hat.view(1,28,28).squeeze().data.numpy(), interpolation = 'nearest',\n cmap ='Greys')\n axarr[i+size,j+size].axis('off')\n \nplt.show()\n \n######################## ######################## ########################", "_____no_output_____" ] ], [ [ "### 2.8 Amortized inference (10 points)\nWhat is amortized inference? Where in the code of Part 2 is it used? What is the benefit of using it?\n", "_____no_output_____" ], [ "YOUR ANSWER HERE\n\nIn amortized inference, we share the variational parameters $\\lambda$ across datapoints. In the Variational Autoencoder in Part 2, this is the case, since we use the same parameters, i.e. the same weights and biases in the encoding network, for all datapoints, i.e. samples from the dataset.\n\nIf we see a new datapoint, we can use the learned network in order to approximate its posterior $q(z)$, which can be an advantage over the alternative mean-field approach, where we would have to run variational inference for each new datapoint again.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ] ]

cb2f4e000bf33499d87f83d1a8bcc02b5c688bb3

32,482

ipynb

Jupyter Notebook

notebooks/W2D1_Wine_Amr_Sara_Sascha_assignment_2Reduction.ipynb

amrshaawkyy/w2d2

67583a89c85cc0914bada3c29ff7a2cd843961aa

[ "MIT" ]

null

notebooks/W2D1_Wine_Amr_Sara_Sascha_assignment_2Reduction.ipynb

amrshaawkyy/w2d2

67583a89c85cc0914bada3c29ff7a2cd843961aa

[ "MIT" ]

null

notebooks/W2D1_Wine_Amr_Sara_Sascha_assignment_2Reduction.ipynb

amrshaawkyy/w2d2

67583a89c85cc0914bada3c29ff7a2cd843961aa

[ "MIT" ]

null

32,482

0.749461

[ [ [ "## Set up", "_____no_output_____" ], [ "### package install", "_____no_output_____" ] ], [ [ "!sudo apt-get install build-essential swig\n!curl https://raw.githubusercontent.com/automl/auto-sklearn/master/requirements.txt | xargs -n 1 -L 1 pip install\n!pip install auto-sklearn\n!pip install pipelineprofiler # visualize the pipelines created by auto-sklearn\n!pip install shap\n!pip install --upgrade plotly\n!pip3 install -U scikit-learn", "_____no_output_____" ] ], [ [ "### Packages imports", "_____no_output_____" ] ], [ [ "import numpy as np\nimport pandas as pd\n\nfrom sklearn.model_selection import train_test_split\nfrom sklearn import metrics\nfrom sklearn import set_config\nfrom sklearn.pipeline import Pipeline\nfrom sklearn.metrics import mean_squared_error\nimport autosklearn.regression\n\n\nimport plotly.express as px\nimport plotly.graph_objects as go\n\nfrom joblib import dump\n\nimport shap\n\nimport datetime\n\nimport logging\n\nimport matplotlib.pyplot as plt", "/usr/local/lib/python3.7/dist-packages/pyparsing.py:3190: FutureWarning: Possible set intersection at position 3\n self.re = re.compile(self.reString)\n" ] ], [ [ "### Google Drive connection", "_____no_output_____" ] ], [ [ "from google.colab import drive\ndrive.mount('/content/drive', force_remount=True)", "Mounted at /content/drive\n" ] ], [ [ "### options and settings", "_____no_output_____" ] ], [ [ "data_path = \"/content/drive/MyDrive/Introduction2DataScience/tutorials/w2d2/data/raw/\"", "_____no_output_____" ], [ "model_path = \"/content/drive/MyDrive/Introduction2DataScience/tutorials/w2d2/models/\"", "_____no_output_____" ], [ "timesstr = str(datetime.datetime.now()).replace(' ', '_')", "_____no_output_____" ], [ "logging.basicConfig(filename=f\"{model_path}explog_{timesstr}.log\", level=logging.INFO)", "_____no_output_____" ] ], [ [ "Please Download the data from [this source](https://drive.google.com/file/d/1MUZrfW214Pv9p5cNjNNEEosiruIlLUXz/view?usp=sharing), and upload it on your Introduction2DataScience/data google drive folder.", "_____no_output_____" ], [ "## Loading Data and Train-Test Split", "_____no_output_____" ] ], [ [ "df = pd.read_csv(f'{data_path}winequality-red.csv')", "_____no_output_____" ], [ "test_size = 0.2\nrandom_state = 0", "_____no_output_____" ], [ "train, test = train_test_split(df, test_size=test_size, random_state=random_state)", "_____no_output_____" ], [ "logging.info(f'train test split with test_size={test_size} and random state={random_state}')", "INFO:root:train test split with test_size=0.2 and random state=0\n" ], [ "train.to_csv(f'{data_path}winequality-red.csv', index=False)", "_____no_output_____" ], [ "train= train.copy()", "_____no_output_____" ], [ "test.to_csv(f'{data_path}winequality-red.csv', index=False)", "_____no_output_____" ], [ "test = test.copy()", "_____no_output_____" ] ], [ [ "## Modelling", "_____no_output_____" ] ], [ [ "X_train, y_train = train.iloc[:,:-1], train.iloc[:,-1] ", "_____no_output_____" ], [ "total_time = 600\nper_run_time_limit = 30", "_____no_output_____" ], [ "automl = autosklearn.regression.AutoSklearnRegressor(\n time_left_for_this_task=total_time,\n per_run_time_limit=per_run_time_limit,\n)\nautoml.fit(X_train, y_train)", "[WARNING] [2021-04-19 17:23:56,986:Client-EnsembleBuilder] No models better than random - using Dummy Score!Number of models besides current dummy model: 1. Number of dummy models: 1\n[WARNING] [2021-04-19 17:24:34,421:Client-EnsembleBuilder] No models better than random - using Dummy Score!Number of models besides current dummy model: 1. Number of dummy models: 1\n" ], [ "logging.info(f'Ran autosklearn regressor for a total time of {total_time} seconds, with a maximum of {per_run_time_limit} seconds per model run')", "_____no_output_____" ], [ "dump(automl, f'{model_path}model{timesstr}.pkl')", "_____no_output_____" ], [ "logging.info(f'Saved regressor model at {model_path}model{timesstr}.pkl ')", "_____no_output_____" ], [ "logging.info(f'autosklearn model statistics:')\nlogging.info(automl.sprint_statistics())", "_____no_output_____" ], [ "#profiler_data= PipelineProfiler.import_autosklearn(automl)\n#PipelineProfiler.plot_pipeline_matrix(profiler_data)", "_____no_output_____" ] ], [ [ "## Model Evluation and Explainability", "_____no_output_____" ], [ "Let's separate our test dataframe into a feature variable (X_test), and a target variable (y_test):", "_____no_output_____" ] ], [ [ "X_test, y_test = test.iloc[:,:-1], test.iloc[:,-1]", "_____no_output_____" ] ], [ [ "#### Model Evaluation", "_____no_output_____" ], [ "Now, we can attempt to predict the median house value from our test set. To do that, we just use the .predict method on the object \"automl\" that we created and trained in the last sections:", "_____no_output_____" ] ], [ [ "y_pred = automl.predict(X_test)", "_____no_output_____" ] ], [ [ "Let's now evaluate it using the mean_squared_error function from scikit learn:", "_____no_output_____" ] ], [ [ "logging.info(f\"Mean Squared Error is {mean_squared_error(y_test, y_pred)}, \\n R2 score is {automl.score(X_test, y_test)}\")", "_____no_output_____" ] ], [ [ "we can also plot the y_test vs y_pred scatter:", "_____no_output_____" ] ], [ [ "df = pd.DataFrame(np.concatenate((X_test, y_test.to_numpy().reshape(-1,1), y_pred.reshape(-1,1)), axis=1))", "_____no_output_____" ], [ "df.columns = ['fixed acidity', 'volatile acidity', 'citric acid', 'residual sugar',\n 'chlorides', 'free sulfur dioxide',\n 'total sulfur dioxide', 'density', 'pH', 'sulphates', 'alcohol', 'Actual Target', 'Predicted Target']", "_____no_output_____" ], [ "fig = px.scatter(df, x='Predicted Target', y='Actual Target')\nfig.write_html(f\"{model_path}residualfig_{timesstr}.html\")", "_____no_output_____" ], [ "logging.info(f\"Figure of residuals saved as {model_path}residualfig_{timesstr}.html\")", "_____no_output_____" ] ], [ [ "#### Model Explainability", "_____no_output_____" ] ], [ [ "explainer = shap.KernelExplainer(model = automl.predict, data = X_test.iloc[:50, :], link = \"identity\")", "_____no_output_____" ], [ "# Set the index of the specific example to explain\nX_idx = 0\nshap_value_single = explainer.shap_values(X = X_test.iloc[X_idx:X_idx+1,:], nsamples = 100)\nX_test.iloc[X_idx:X_idx+1,:]\n# print the JS visualization code to the notebook\n#shap.initjs()\nshap.force_plot(base_value = explainer.expected_value,\n shap_values = shap_value_single,\n features = X_test.iloc[X_idx:X_idx+1,:], \n show=False,\n matplotlib=True\n )\nplt.savefig(f\"{model_path}shap_example_{timesstr}.png\")\nlogging.info(f\"Shapley example saved as {model_path}shap_example_{timesstr}.png\")", "_____no_output_____" ], [ "shap_values = explainer.shap_values(X = X_test.iloc[0:50,:], nsamples = 100)", "_____no_output_____" ], [ "# print the JS visualization code to the notebook\n#shap.initjs()\nfig = shap.summary_plot(shap_values = shap_values,\n features = X_test.iloc[0:50,:],\n show=False)\nplt.savefig(f\"{model_path}shap_summary_{timesstr}.png\")\nlogging.info(f\"Shapley summary saved as {model_path}shap_summary_{timesstr}.png\")", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ] ]

cb2f5ba67d933126e548b3ac593eebcca8b4cb64

160,425

ipynb

Jupyter Notebook

02B_RESULT_LongDocPreProcessing.ipynb

Herais/Synopsis

d3d9c4bd3777a8eca0204f1a5c2bc015a7133038

[ "MIT" ]

null

02B_RESULT_LongDocPreProcessing.ipynb

Herais/Synopsis

d3d9c4bd3777a8eca0204f1a5c2bc015a7133038

[ "MIT" ]

null

02B_RESULT_LongDocPreProcessing.ipynb

Herais/Synopsis

d3d9c4bd3777a8eca0204f1a5c2bc015a7133038

[ "MIT" ]

null

160,425

0.597307

[ [ [ "#[1] Mount Drive", "_____no_output_____" ] ], [ [ "from google.colab import drive\ndrive.mount('/content/drive')", "Drive already mounted at /content/drive; to attempt to forcibly remount, call drive.mount(\"/content/drive\", force_remount=True).\n" ] ], [ [ "# [2] Install Requirements and Load Libs", "_____no_output_____" ], [ "## Install RequirementsRequirements", "_____no_output_____" ] ], [ [ "!pip install datasets &> /dev/null\n!pip install rouge_score &> /dev/null\n!pip install -q transformers==4.8.2 &> /dev/null\n!pip install sentencepiece\n!pip install nltk", "Collecting sentencepiece\n Downloading sentencepiece-0.1.96-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (1.2 MB)\n\u001b[?25l\r\u001b[K |▎ | 10 kB 23.0 MB/s eta 0:00:01\r\u001b[K |▌ | 20 kB 26.1 MB/s eta 0:00:01\r\u001b[K |▉ | 30 kB 14.0 MB/s eta 0:00:01\r\u001b[K |█ | 40 kB 10.4 MB/s eta 0:00:01\r\u001b[K |█▍ | 51 kB 5.3 MB/s eta 0:00:01\r\u001b[K |█▋ | 61 kB 5.3 MB/s eta 0:00:01\r\u001b[K |██ | 71 kB 5.6 MB/s eta 0:00:01\r\u001b[K |██▏ | 81 kB 6.3 MB/s eta 0:00:01\r\u001b[K |██▍ | 92 kB 4.6 MB/s eta 0:00:01\r\u001b[K |██▊ | 102 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███ | 112 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███▎ | 122 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███▌ | 133 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███▉ | 143 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████ | 153 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████▎ | 163 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████▋ | 174 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████▉ | 184 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████▏ | 194 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████▍ | 204 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████▊ | 215 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████ | 225 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████▏ | 235 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████▌ | 245 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████▊ | 256 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████ | 266 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████▎ | 276 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████▋ | 286 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████▉ | 296 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████ | 307 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████▍ | 317 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████▋ | 327 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████ | 337 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████▏ | 348 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████▌ | 358 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████▊ | 368 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████ | 378 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████▎ | 389 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████▌ | 399 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████▉ | 409 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████ | 419 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████▍ | 430 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████▋ | 440 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████▉ | 450 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████▏ | 460 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████▍ | 471 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████▊ | 481 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████ | 491 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████▎ | 501 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████▌ | 512 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████▊ | 522 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████ | 532 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████▎ | 542 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████▋ | 552 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████▉ | 563 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████▏ | 573 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████▍ | 583 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████▋ | 593 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████ | 604 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████▏ | 614 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████▌ | 624 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████▊ | 634 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████ | 645 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████▎ | 655 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████▌ | 665 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████▉ | 675 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████ | 686 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████▍ | 696 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████▋ | 706 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████ | 716 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████▏ | 727 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████▍ | 737 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████▊ | 747 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████ | 757 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████▎ | 768 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████▌ | 778 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████▉ | 788 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████████ | 798 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████████▎ | 808 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████████▋ | 819 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████████▉ | 829 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████▏ | 839 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████▍ | 849 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████▊ | 860 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████ | 870 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████▏ | 880 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████▌ | 890 kB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████▊ | 901 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████████ | 911 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████████▎ | 921 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████████▋ | 931 kB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████████▉ | 942 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████████████ | 952 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████████████▍ | 962 kB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████████████▋ | 972 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████████ | 983 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████████▏ | 993 kB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████████▌ | 1.0 MB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████████▊ | 1.0 MB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████████ | 1.0 MB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████████▎ | 1.0 MB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████████▌ | 1.0 MB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████████▉ | 1.1 MB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████████████ | 1.1 MB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████████████▍ | 1.1 MB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████████████▋ | 1.1 MB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████████████▉ | 1.1 MB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████████████████▏ | 1.1 MB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████████████████▍ | 1.1 MB 5.0 MB/s eta 0:00:01\r\u001b[K |█████████████████████████████▊ | 1.1 MB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████████████ | 1.1 MB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████████████▎ | 1.1 MB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████████████▌ | 1.2 MB 5.0 MB/s eta 0:00:01\r\u001b[K |██████████████████████████████▊ | 1.2 MB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████████████ | 1.2 MB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████████████▎| 1.2 MB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████████████▋| 1.2 MB 5.0 MB/s eta 0:00:01\r\u001b[K |███████████████████████████████▉| 1.2 MB 5.0 MB/s eta 0:00:01\r\u001b[K |████████████████████████████████| 1.2 MB 5.0 MB/s \n\u001b[?25hInstalling collected packages: sentencepiece\nSuccessfully installed sentencepiece-0.1.96\nRequirement already satisfied: nltk in /usr/local/lib/python3.7/dist-packages (3.2.5)\nRequirement already satisfied: six in /usr/local/lib/python3.7/dist-packages (from nltk) (1.15.0)\n" ], [ "# Import Python Lib\nimport os\nimport shutil\nimport pandas as pd\nimport numpy as np\nfrom ast import literal_eval\nimport re\nimport torch\nimport nltk\n\n\nfrom rouge_score import rouge_scorer\nfrom IPython.display import display, HTML", "_____no_output_____" ], [ "# Import local lib\n%load_ext autoreload\n%autoreload 2\npath_utils = '/content/drive/MyDrive/Github/Synopsis/utils'\nos.chdir(path_utils)\n#importlib.reload(utils_lsstr)\n#importlib.reload(utils_model)\n\nfrom utils_model import Summarization_Model, Tokenizer, \\\n str_summarize, segment_to_split_size, str_seg_and_summarize, str_led_summarize\nfrom utils_lsstr import str_word_count, ls_word_count\nfrom utils_lsstr import split_str_to_batch_ls, \\\n str_remove_duplicated_consective_token\n\nfrom Screenplay import SC_Elements\n# instantiate SC_Element\nsc = SC_Elements()", "[nltk_data] Downloading package punkt to /root/nltk_data...\n[nltk_data] Unzipping tokenizers/punkt.zip.\n" ] ], [ [ "## Set Common Paths", "_____no_output_____" ] ], [ [ "path_datasets ='/content/drive/MyDrive/Github/Synopsis/Datasets'\npath_results = '/content/drive/MyDrive/Github/Synopsis/results'", "_____no_output_____" ] ], [ [ "# [3] Compare Segmentation Methods\n", "_____no_output_____" ], [ "## Load Various Tokenizer\ngoogle/pegasus-large, 500/1000\ngoogle/pegasus-cnn_dailymail, 500 (no large version)\n\nfacebook/bart-large, 500/1000\nfacebook/bart-large-cnn, 500/1000\n\ngoogle/bigbird-pegasus-large-arxiv, 512/1000/4000\n\nallenai/led-large-16384, 512/1000/4000/16000\nallenai/led-large-16384-arxiv, 512/1000/4000/16000", "_____no_output_____" ], [ "", "_____no_output_____" ] ], [ [ "# initalize tokenizer by model\nmodel_name = 'allenai/led-base-16384'\ntokenizer = Tokenizer(model_name)\n\n# Instantiate word tokenizer and detokenizer\nfrom nltk.tokenize import RegexpTokenizer\nfrom nltk.tokenize import line_tokenize, sent_tokenize, word_tokenize\nfrom nltk.tokenize import TreebankWordTokenizer\nfrom nltk.tokenize.treebank import TreebankWordDetokenizer\nnltk.download('punkt')", "_____no_output_____" ] ], [ [ "## Preprocessing Test Data Overview", "_____no_output_____" ] ], [ [ "# Load SSGD\npath_datasets = '/content/drive/MyDrive/Github/Synopsis/Datasets'\npath_dfssgd = '/content/drive/MyDrive/Github/Synopsis/Datasets/SSGD-2021-07-23-719SC-TVTbl.json'\ndf_wscript = pd.read_json(path_dfssgd)\ndf_wscript['dfsc'] = df_wscript['dfsc'].apply(lambda x: pd.DataFrame(x))\n\n# Load Turning Points from TRIPOD (for testing splits methods using turning poitns\npath_TRIPOD = '/content/drive/MyDrive/Github/Synopsis/Datasets/TRIPOD-master'\npath_tps= path_TRIPOD + '/Synopses_and_annotations/TRIPOD_screenplays_test.csv'\ndf_tps = pd.read_csv(path_tps, header=0)\n\n# for each film title with turniing points, find the corresponding SSGD record\n# Save to df_cases, use df_cases for Long Document Processing Experiments\ndf_cases = df_wscript[df_wscript['title'].isin(df_tps['movie_name'])]\ndf_tmp = df_tps.melt(id_vars=['movie_name'])\ndf_tmp['value'] = df_tmp['value'].apply(lambda x: literal_eval(x)).apply(lambda x: [x])\ndf_tmp = df_tmp.groupby('movie_name')['value'].sum().reset_index()\ndf_tmp.columns = ['title', 'ls_tps']\ndf_cases = df_cases.merge(df_tmp, on='title', how='left')\ndf_cases = df_cases.drop_duplicates('title')\n\n# assign tps to scenes in dfsc\nfor i, row in df_cases.iterrows():\n df_cases.loc[i,'dfsc'] ['tps'] = 0\n for j, ls in enumerate(df_cases.loc[i, 'ls_tps']):\n df_cases.loc[i,'dfsc'].loc[df_cases.loc[i,'dfsc']['Scene'].isin(ls),'tps'] = j+1\n\n# fillna for Scene numbers and insure type as i\nfor i, case in df_cases.iterrows():\n df_cases.loc[i, 'dfsc']['Scene'] =\\\n df_cases.loc[i, 'dfsc']['Scene'].fillna('-1').astype('int')", "_____no_output_____" ], [ "df_cases['gold'] = df_cases['ls_sums_sorted'].apply(lambda x: x[0])\ndf_cases['nScenes'] = df_cases['dfsc'].apply(lambda x: x['Scene'].nunique())\ndf_cases['gold_wc'] = df_cases['gold'].apply(lambda x: len(word_tokenize(x)))\ndf_cases['nScenes_tps'] = df_cases['ls_tps'].apply(lambda x: sum([len(ls) for ls in x]))\ndf_cases['dict_AF']= df_cases['dfsc'].apply(sc.extract_str_by_method, method='AF', return_type='df').apply(lambda x: x.dropna().to_dict(), axis=1)", "_____no_output_____" ], [ "def calc_tc(x):\n for k, v in x.items():\n x[k] = len(tokenizer(v)['input_ids'])\n return list(x.values())\n\ndf_cases['Scene_tc'] = df_cases['dict_AF'].apply(calc_tc)", "_____no_output_____" ], [ "Scene_tc = pd.DataFrame(df_cases['Scene_tc'].sum()).describe().astype('int')\nScene_tc.columns =['分词数量']", "_____no_output_____" ], [ "df_cases", "_____no_output_____" ] ], [ [ "### 长文本预测试集概览 ", "_____no_output_____" ] ], [ [ "overview = df_cases[['title', 'word_count', 'nScenes', '%Dialog', 'gold_wc', 'nScenes_tps']].copy()\noverview.columns = ['片名', '剧本单词量', '场次数量', '对白占比', '参考总结单词量', '重点场次数量']\noverview['压缩倍数'] = overview['剧本单词量'] / overview['参考总结单词量']\noverview.loc['均数'] = overview.mean()\noverview = overview.fillna('均数')\noverview.round()", "_____no_output_____" ], [ "df_cases.columns", "_____no_output_____" ], [ "# Specify selection methods or define custom\n# methods are in utils/Screenplay.py\n\n# SELECTION METHOD\n#####################\nselection_method = 'PSentAO_F1'\n#####################\n\npath_utils = '/content/drive/MyDrive/Github/Synopsis/utils'\nos.chdir(path_utils)\n#%load_ext autoreload\n%autoreload 2\nfrom Screenplay import SC_Elements\nsc = SC_Elements()\n\n# Initialize df\ndf = df_cases[['title', 'ls_sums_sorted', 'dfsc']].copy()\n\n# Get selection by selection_method\ndf['selection'] = df['dfsc'].apply(sc.extract_str_by_method, \n method=selection_method, return_type='df').apply(\n lambda x: x.dropna().to_dict(),\n axis=1\n )\ndf['selection']", "_____no_output_____" ], [ "# Input Huggingface model name or local model path\n\n#####################################\nmodel_name = 'facebook/bart-large'\n#####################################\n\n# assign cuda to device if it exists\nif torch.cuda.device_count() > 0:\n device = 'cuda:' + str(torch.cuda.current_device())\nelse:\n device = 'cpu'\n\n# Instantiate tokenizer and model\ntokenizer = Tokenizer(model_name=None)\n#model = Summarization_Model(model_name=model_name, device=device)", "_____no_output_____" ], [ "tmp", "_____no_output_____" ] ], [ [ "## by token count vs. by scene", "_____no_output_____" ] ], [ [ "path_compare_segmentation_methods = '/content/drive/MyDrive/Github/Synopsis/results/by_SegMethod'\nfor root, dirs, files in os.walk(path_compare_segmentation_methods):\n if root == path_compare_segmentation_methods:\n fns = files\n break\n\nrouge_scores = []\nfor fn in fns:\n record = [fn[3:-5]]\n dftmp = pd.read_json(path_compare_segmentation_methods + '/' + fn)\n record.extend(dftmp[['R1', 'R2', 'RL', 's0_wc', 's0_tc', \n 'sum_wc_max', 'sum_tc_max', 's1_wc', 's1_tc']].mean().tolist())\n rouge_scores.append(record)\n\ndfscores = pd.DataFrame(rouge_scores)\ndfscores.columns = ['method', 'R1', 'R2', 'RL', 's0_wc', 's0_tc', \n 'sum_wc_max', 'sum_tc_max', 's1_wc', 's1_tc']\ndfscores['s0_wc'] = dfscores['s0_wc'].astype('int')\ndfscores['s0_tc'] = dfscores['s0_tc'].astype('int')\ndfscores['s1_wc'] = dfscores['s1_wc'].astype('int')\ndfscores['s1_tc'] = dfscores['s1_tc'].astype('int')\ndfscores['sum_tc_max'] = dfscores['sum_tc_max'].astype('int')\n\nmethods = dfscores['method'].str.split('_', expand=True)\nmethods.columns = ['筛选方法', '分段方法', '模型', '分段tc距离']\ndfscores = dfscores.merge(methods, left_index=True, right_index=True).drop('method', axis=1)", "_____no_output_____" ], [ "# create view\nview = dfscores[[\n '分段方法', '模型', '分段tc距离', 'R1', 'R2', 'RL', \n 's0_wc', 'sum_wc_max', 's1_wc',\n 's0_tc', 'sum_tc_max', 's1_tc']].sort_values(['R2'], ascending=[False])\n\nview.columns = ['分段方法', '模型', '分段tc', 'R1', 'R2', 'RL',\n '输入wc', '参考梗概wc', '生成梗概wc',\n '输入tc', '参考梗概tc', '生成梗概tc']\nview['参考梗概wc'] = view['参考梗概wc'].astype('int')\nview.round(2)", "_____no_output_____" ] ], [ [ "# [4] Compare Selection Method", "_____no_output_____" ] ], [ [ "path_selections = '/content/drive/MyDrive/Github/Synopsis/results/by_selections'\n# Get result file names\nfor root, dirs, files in os.walk(path_selections):\n if root == path_selections:\n fns = files\n break\n\nfrom rouge_score import rouge_scorer\nscorer = rouge_scorer.RougeScorer(['rouge1', 'rouge2', 'rougeL'], \n use_stemmer=True)\n\nrouge_scores = []\nfor fn in fns:\n record = [fn[3:-5]]\n dftmp = pd.read_json(path_selections + '/' + fn)\n dftmp['s0_wc'] = dftmp['s0'].apply(lambda x: len(word_tokenize(x)))\n record.extend(dftmp[['R1', 'R2', 'RL', 's0_wc']].mean().tolist())\n rouge_scores.append(record)\n\ndfscores = pd.DataFrame(rouge_scores)\ndfscores.columns = ['method', 'R1', 'R2',\t'RL', 's0_wc']\n\nmethods = dfscores['method'].str.split('_', expand=True)\nmethods.columns = ['selection_method', 'model', 'split-size']\n\ndfscores = dfscores.merge(methods, left_index=True, right_index=True).drop('method', axis=1)", "_____no_output_____" ], [ "# Create View\nview = dfscores[['selection_method', 's0_wc', 'R1', 'R2', 'RL']].copy()\nview.columns = ['筛选方式', '输入wc','R1', 'R2', 'RL']\nview['输入wc'] = view['输入wc'].astype('int')\nview.sort_values('R2', ascending=False).round(2)", "_____no_output_____" ], [ "view.sort_values('R2', ascending=False).round(2)", "_____no_output_____" ], [ "view.sort_values('输入wc').round(2)", "_____no_output_____" ] ], [ [ "# [5] Compare Finetuning Method", "_____no_output_____" ], [ "## by window size", "_____no_output_____" ] ], [ [ "path_wsize = '/content/drive/MyDrive/Github/Synopsis/results/by_FTmodel/by_window_size'\n# Get result file names\nfor root, dirs, files in os.walk(path_wsize):\n if root == path_wsize:\n fns = files\n break\n\nfrom rouge_score import rouge_scorer\nscorer = rouge_scorer.RougeScorer(['rouge1', 'rouge2', 'rougeL'], \n use_stemmer=True)\n\nrouge_scores = []\nfor fn in fns:\n record = [fn[3:-5]]\n dftmp = pd.read_json(path_wsize + '/' + fn)\n record.extend(dftmp[['R1', 'R2', 'RL']].mean().tolist())\n rouge_scores.append(record)\n\ndfscores = pd.DataFrame(rouge_scores)\ndfscores.columns = ['method', 'R1', 'R2', 'RL']\n\nmethods = dfscores['method'].str.split('_', expand=True)\nmethods.columns = ['selection_method', 'model', 'pred GA', 'split-size']\ndfscores = dfscores.merge(methods, left_index=True, right_index=True).drop('method', axis=1)", "_____no_output_____" ], [ "# Create View\nview = dfscores.sort_values(\n ['selection_method', 'R2'], ascending=[True, False])\nview = view[['model', 'R1', 'R2', 'RL']]\nview.columns = ['模型', 'R1', 'R2', 'RL']\nview['窗口'] = view['模型'].str.extract('([0-9]*)W')\nview = view[['窗口', 'R1', 'R2', 'RL', '模型']]\nview.round(2)", "_____no_output_____" ] ], [ [ "## by global attention application", "_____no_output_____" ] ], [ [ "path_global_attention = '/content/drive/MyDrive/Github/Synopsis/results/by_FTmodel/by_global_attention'\n# Get result file names\nfor root, dirs, files in os.walk(path_global_attention):\n if root == path_global_attention:\n fns = files\n break\n\nfrom rouge_score import rouge_scorer\nscorer = rouge_scorer.RougeScorer(['rouge1', 'rouge2', 'rougeL'], \n use_stemmer=True)\nrouge_scores = []\nfor fn in fns:\n record = [fn[3:-5]]\n dftmp = pd.read_json(path_global_attention + '/' + fn)\n record.extend(dftmp[['R1', 'R2', 'RL']].mean().tolist())\n rouge_scores.append(record)\n\ndfscores = pd.DataFrame(rouge_scores)\ndfscores.columns = ['method', 'R1', 'R2', 'RL']\nmethods =dfscores['method'].str.split('-', expand=True)\ndfscores['训练GA'] = methods[5].apply(lambda x: x[2:])\ndfscores['预测GA'] = methods[7].str.extract('_(.*)_')", "_____no_output_____" ], [ "view = dfscores[['训练GA', '预测GA', 'R1', 'R2', 'RL', 'method']].sort_values('R2', ascending=False)\nview['模型'] = view['method'].apply(lambda x: x[10:])\nview.drop('method', axis=1).round(2)", "_____no_output_____" ], [ "pd.read_json(path_global_attention + '/' + fn)", "_____no_output_____" ] ], [ [ "## by expanding gold tc range", "_____no_output_____" ] ], [ [ "fp_goldtcrange= '/content/drive/MyDrive/Github/Synopsis/results/by_FTmodel/by_expand_goldtcrange'\n# Get result file names\nfor root, dirs, files in os.walk(fp_goldtcrange):\n if root == fp_goldtcrange:\n fns = files\n break\n\nfrom rouge_score import rouge_scorer\nscorer = rouge_scorer.RougeScorer(['rouge1', 'rouge2', 'rougeL'], \n use_stemmer=True)\nrouge_scores = []\nfor fn in fns:\n record = [fn[3:-5]]\n dftmp = pd.read_json(fp_goldtcrange + '/' + fn)\n record.extend(dftmp[['R1', 'R2', 'RL', 's1_wc']].mean().tolist())\n rouge_scores.append(record)\n\ndfscores = pd.DataFrame(rouge_scores)\ndfscores.columns = ['method', 'R1', 'R2', 'RL', 's1_wc']\ndfscores['s1_wc'] = dfscores['s1_wc'].astype('int')\n\nmethods = dfscores['method'].str.split('_', expand=True)\nmethods.columns = ['预测集筛选方法', 'model', '预测GA', 'split-size']\ndfscores = dfscores.merge(methods, left_index=True, right_index=True).drop('method', axis=1)\n\nselection_methods = ['Grp_n06', 'Grp_n06', 'Grp_n06']\ngold_tc_range = [[256,1024], [0,1024], [512, 1024]]\ntraining_time = ['1小时06分钟', '5小时07分钟', '3分钟15秒']\n\nmethods = dfscores['model'].str.split('-', expand=True)\ndfscores['训练步数'] = methods[7].apply(lambda x: re.sub('steps', '', x))\ndfscores['训练样本量'] = methods[6].apply(lambda x: re.split('T', x)[0])\ndfscores['训练输入筛选法'] = selection_methods\ndfscores['参考总结tc范围'] = gold_tc_range\ndfscores['训练耗时'] = training_time\ndfscores['基础模型'] = dfscores['model'].apply(\n lambda x: re.split('-6L', x)[0])", "_____no_output_____" ], [ "view = dfscores.sort_values('R2', ascending=False)\nview = view[['训练输入筛选法','参考总结tc范围', \n '训练样本量', '训练步数',\n 'R1', 'R2', 'RL', '训练耗时', 's1_wc']]\n\nview.columns = ['训练输入筛选方式','参考总结tc范围', \n '训练样本', '训练步数',\n 'R1', 'R2', 'RL', '训练耗时', '生成梗概wc均值']\nview.round(2)", "_____no_output_____" ] ], [ [ "## by augmentaiton with selection methods\n", "_____no_output_____" ] ], [ [ "fp_aug_sm = '/content/drive/MyDrive/Github/Synopsis/results/by_FTmodel/by_augmentation_w_selections'\n# Get result file names\nfor root, dirs, files in os.walk(fp_aug_sm):\n if root == fp_aug_sm:\n fns = files\n break\n\nfrom rouge_score import rouge_scorer\nscorer = rouge_scorer.RougeScorer(['rouge1', 'rouge2', 'rougeL'], \n use_stemmer=True)\nrouge_scores = []\nfor fn in fns:\n record = [fn[3:-5]]\n dftmp = pd.read_json(fp_aug_sm + '/' + fn)\n record.extend(dftmp[['R1', 'R2', 'RL', 's0_wc', 's1_wc']].mean().tolist())\n rouge_scores.append(record)\n\ndfscores = pd.DataFrame(rouge_scores)\ndfscores.columns = ['method', 'R1', 'R2', 'RL','s0_wc', 's1_wc']\ndfscores['s0_wc'] = dfscores['s0_wc'].astype('int')\ndfscores['s1_wc'] = dfscores['s1_wc'].astype('int')\n\nmethods = dfscores['method'].str.split('_', expand=True)\nmethods.columns = ['预测集筛选方法', 'model', '预测GA', 'split-size']\n\nselection_methods = ['Grp_n12', 'Grp_n06', 'Grp_n19', 'Grp_n24']\ngold_tc_range = [[512,1024], [512,1024], [512, 1024], [512, 1024]]\ntraining_time = ['11分钟24秒', '3分钟15秒', '15分钟47秒', '48分钟02秒']\n\ndfscores = dfscores.merge(methods, left_index=True, right_index=True).drop('method', axis=1)\n\nmethods = dfscores['model'].str.split('-', expand=True)\ndfscores['训练步数'] = methods[7].apply(lambda x: re.sub('steps', '', x))\ndfscores['训练样本量'] = methods[6].apply(lambda x: re.split('T', x)[0])\ndfscores['训练输入筛选法'] = selection_methods\ndfscores['参考总结tc范围'] = gold_tc_range\ndfscores['训练耗时'] = training_time\n", "_____no_output_____" ], [ "# create view\nview = dfscores[['训练输入筛选法','参考总结tc范围', \n '训练样本量', '训练步数',\n 'R1', 'R2', 'RL', '训练耗时', 's1_wc']].sort_values('R2', ascending=False)\nview.columns = ['训练输入筛选方式','参考总结tc范围', \n '训练样本量', '训练步数',\n 'R1', 'R2', 'RL', '训练耗时', '输出wc均值']\nview.round(2)", "_____no_output_____" ] ], [ [ "## by prediction with selection methods", "_____no_output_____" ] ], [ [ "fp_pred_sm = '/content/drive/MyDrive/Github/Synopsis/results/by_FTmodel/by_pred_selection_methods'\n# Get result file names\nfor root, dirs, files in os.walk(fp_pred_sm):\n if root == fp_pred_sm:\n fns = files\n break\n\nfrom rouge_score import rouge_scorer\nscorer = rouge_scorer.RougeScorer(['rouge1', 'rouge2', 'rougeL'], \n use_stemmer=True)\nrouge_scores = []\nfor fn in fns:\n record = [fn[3:-5]]\n dftmp = pd.read_json(fp_pred_sm + '/' + fn)\n record.extend(dftmp[['R1', 'R2', 'RL', 's0_wc', 's1_wc']].mean().tolist())\n rouge_scores.append(record)\n\ndfscores = pd.DataFrame(rouge_scores)\ndfscores.columns = ['method', 'R1', 'R2', 'RL','s0_wc', 's1_wc']\ndfscores['s0_wc'] = dfscores['s0_wc'].astype('int')\ndfscores['s1_wc'] = dfscores['s1_wc'].astype('int')\n\nmethods = dfscores['method'].str.split('_', expand=True)\nmethods.columns = ['预测输入筛选方法', 'model', '预测GA', 'split-size']\n\ndfscores = dfscores.merge(methods, left_index=True, right_index=True).drop('method', axis=1)", "_____no_output_____" ], [ "view = dfscores.sort_values('R2', ascending=False).round(2)\nview = view[['预测输入筛选方法', '预测GA', 'R1', 'R2', 'RL', 's0_wc', 's1_wc']]\nleft = view[view['预测GA'] == 'None'].sort_values('预测输入筛选方法')\nleft = left[['s0_wc', 's1_wc', 'R1', 'R2', 'RL', '预测GA', '预测输入筛选方法']]\nleft.loc['均值'] = left.mean()\nleft.fillna('')", "_____no_output_____" ], [ "right = view[view.预测GA == 'boScene'].sort_values('预测输入筛选方法')\nright.loc['均值'] = right.mean()\nright.fillna('')", "_____no_output_____" ], [ "view.loc[view['预测GA'] == 'boScene'].sort_values('预测输入筛选方法')", "_____no_output_____" ], [ "view.sort_values(['预测输入筛选方法', 'R2'], ascending=[True, False])", "_____no_output_____" ], [ "", "_____no_output_____" ], [ "view.sort_values(\n ['预测输入筛选方法', 'R2'], \n ascending=[True, False]\n )[['预测输入筛选方法', 'R1', 'R2', 'RL', '预测GA', 's0_wc', 's1_wc']]", "_____no_output_____" ] ], [ [ "## Pred", "_____no_output_____" ] ], [ [ "fptest = '/content/drive/MyDrive/Github/Synopsis/results/df_results_pt_then_ft.json'\n#dftest.to_json(fptest)\ndftest = pd.read_json(fptest)\ndftest['dfsc'] = dftest['dfsc'].apply(lambda x: pd.DataFrame(x))\ndftest['s0_EVERY4at0'] = dftest['dfsc'].apply(sc.extract_str_by_method, method='EVERY4at0')\ndftest", "_____no_output_____" ] ], [ [ "# [8] View Generated Summaries", "_____no_output_____" ] ], [ [ "path_global_training = '/content/drive/MyDrive/Github/Synopsis/results/by_FTmodel'\n# Get result file names\nfor root, dirs, files in os.walk(path_global_training):\n if root == path_global_training:\n fns = files\n break\n\ndfs = pd.read_json(path_global_training + '/' + fns[0])[['title', 'ls_sums_sorted']]\ndfs['gold'] = dfs['ls_sums_sorted'].apply(lambda x: x[0])\n\nfor fn in fns:\n # append method\n df = pd.read_json(path_global_training + '/' + fn)\n # append title\n dftmp = df[['title']].copy()\n # append predicted summary\n dftmp['pred_sum_{}'.format(fn[3:-5])] = df['s1']\n # append rouge2_f1\n dftmp['rouge2_f1_{}'.format(fn[3:-5])] = df['rouge2_f1']\n # merge summary to dfc\n dfs = dfs.merge(dftmp, on='title', how='left')", "_____no_output_____" ], [ "dfs.T", "_____no_output_____" ], [ "HTML(dfs.T[[10]].to_html())", "_____no_output_____" ], [ "dfs.columns", "_____no_output_____" ] ], [ [ "", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ] ]

cb2f5c8bdc1b27e72a608d6ae09110ab1447ccda

440,791

ipynb

Jupyter Notebook

notebooks/era5_validation/precip_metrics.ipynb

brews/downscaleCMIP6

7ce377f50c5a1b9d554668efeb30e969dd6ede18

[ "MIT" ]

6

2017-08-14T21:41:33.000Z

2020-07-24T16:53:43.000Z

notebooks/era5_validation/precip_metrics.ipynb

brews/downscaleCMIP6

7ce377f50c5a1b9d554668efeb30e969dd6ede18

[ "MIT" ]

29

2017-09-04T13:14:11.000Z

2020-08-12T19:53:42.000Z

notebooks/era5_validation/precip_metrics.ipynb

brews/downscaleCMIP6

7ce377f50c5a1b9d554668efeb30e969dd6ede18

[ "MIT" ]

null

668.878604

267,988

0.95114

[ [ [ "Precipitation Metrics (consecutive dry days, rolling 5-day precip accumulation, return period)", "_____no_output_____" ] ], [ [ "! pip install xclim", "_____no_output_____" ], [ "%matplotlib inline\nimport xarray as xr\nimport numpy as np \nimport matplotlib.pyplot as plt\nimport os\nimport pandas as pd\nfrom datetime import datetime, timedelta, date\n\nimport dask\nimport dask.array as dda\nimport dask.distributed as dd\n\n# rhodium-specific kubernetes cluster configuration\nimport rhg_compute_tools.kubernetes as rhgk", "_____no_output_____" ], [ "client, cluster = rhgk.get_big_cluster()\ncluster.scale(30)", "_____no_output_____" ], [ "client", "_____no_output_____" ], [ "cluster.close()", "_____no_output_____" ], [ "def pull_ERA5_variable(filevar, variable):\n filenames = []\n \n for num_yrs in range(len(yrs)):\n filename = '/gcs/impactlab-data/climate/source_data/ERA-5/{}/daily/netcdf/v1.3/{}_daily_{}-{}.nc'.format(filevar, filevar, yrs[num_yrs], yrs[num_yrs])\n filenames.append(filename)\n \n era5_var = xr.open_mfdataset(filenames, \n concat_dim='time', combine='by_coords')\n \n var_all = era5_var[variable]\n \n return var_all", "_____no_output_____" ], [ "yrs = np.arange(1995,2015) ", "_____no_output_____" ], [ "da = pull_ERA5_variable('pr', 'tp')", "_____no_output_____" ], [ "import xclim as xc\nfrom xclim.core.calendar import convert_calendar\n\n# remove leap days and convert calendar to no-leap\nda = convert_calendar(da, 'noleap')", "_____no_output_____" ], [ "da_mm = da*1000\nda_mm.attrs[\"units\"] = \"mm/day\"", "_____no_output_____" ], [ "da_mm = da_mm.persist()", "_____no_output_____" ] ], [ [ "Calculate the max number of consecutive dry days per year. Use the threshold value for the wet day frequency correction", "_____no_output_____" ] ], [ [ "dry_days = xc.indicators.atmos.maximum_consecutive_dry_days(da_mm, thresh=0.0005, freq='YS')", "_____no_output_____" ], [ "dry_days = dry_days.compute()", "_____no_output_____" ], [ "#dry_days.sel(latitude=50.0, longitude=0.0).plot()", "_____no_output_____" ], [ "avg_dry_days = dry_days.mean(dim='time').compute()", "_____no_output_____" ], [ "avg_dry_days.plot(robust=True)", "_____no_output_____" ], [ "from matplotlib import cm\nfrom cartopy import config\nimport cartopy.crs as ccrs\nimport cartopy.feature as cfeature", "_____no_output_____" ], [ "def plot_average_dry_days(da, years, fname): \n fig = plt.figure(figsize=(10, 5))\n ax = plt.axes(projection=ccrs.Robinson())\n cmap = cm.pink_r \n\n da.plot(\n ax=ax,\n cmap=cmap,\n transform=ccrs.PlateCarree(),\n cbar_kwargs={'shrink': 0.8, 'pad': 0.02, \"label\": \"# of days\"},\n vmin=0,\n vmax=180,\n )\n\n ax.coastlines()\n ax.add_feature(cfeature.BORDERS, linestyle=\":\")\n ax.set_title(\"Mean number of consecutive dry days annually ({})\".format(years))\n \n plt.savefig(fname, dpi=600, bbox_inches='tight')", "_____no_output_____" ], [ "plot_average_dry_days(avg_dry_days, '1995-2014', 'avg_dry_days_era5')", "_____no_output_____" ] ], [ [ "Calculate the highest precipitation amount cumulated over a 5-day moving window", "_____no_output_____" ] ], [ [ "max_5day_dailyprecip = xc.indicators.icclim.RX5day(da_mm, freq='YS')\n\n# there is a different function for a n-day moving window", "_____no_output_____" ], [ "max_5day_dailyprecip = max_5day_dailyprecip.compute()", "_____no_output_____" ], [ "avg_5day_dailyprecip = max_5day_dailyprecip.mean(dim='time').compute()", "_____no_output_____" ], [ "avg_5day_dailyprecip.plot()", "_____no_output_____" ], [ "def plot_average_5day_max_precip(da, years, fname): \n fig = plt.figure(figsize=(10, 5))\n ax = plt.axes(projection=ccrs.Robinson())\n cmap = cm.GnBu\n\n da.plot(\n ax=ax,\n cmap=cmap,\n transform=ccrs.PlateCarree(),\n cbar_kwargs={'shrink': 0.8, 'pad': 0.02, \"label\": \"5-day accumulated precip (mm)\"},\n vmin=0,\n vmax=250,\n )\n\n ax.coastlines()\n ax.add_feature(cfeature.BORDERS, linestyle=\":\")\n ax.set_title(\"Maximum annual 5-day rolling precipitation accumulation ({})\".format(years))\n \n plt.savefig(fname, dpi=600, bbox_inches='tight')", "_____no_output_____" ], [ "plot_average_5day_max_precip(avg_5day_dailyprecip, '1995-2014', 'avg_max_5day_precip_era5')", "_____no_output_____" ] ], [ [ "Comparing difference of mean with nans and mean without taking into account nans", "_____no_output_____" ] ], [ [ "avg_5day_dailyprecip = max_5day_dailyprecip.mean(dim='time', skipna=True).compute()", "_____no_output_____" ], [ "avg_5day_dailyprecip", "_____no_output_____" ], [ "plot_average_5day_max_precip(avg_5day_dailyprecip, '1995-2014')", "_____no_output_____" ], [ "max_5day_dailyprecip.sel(latitude=-89.0, longitude=0.0).plot()", "_____no_output_____" ] ], [ [ "Basics for calculating the return period of daily precipitation. More testing needed as it blows up currently.", "_____no_output_____" ] ], [ [ "def calculate_return(da, return_interval):\n '''\n calculate return period of daily precip data per grid point\n '''\n # Sort data smallest to largest\n sorted_data = da.sortby(da, ascending=True).compute()\n \n # Count total obervations\n n = sorted_data.shape[0]\n \n # Compute rank position\n rank = np.arange(1, 1 + n)\n \n # Calculate probability\n probability = (n - rank + 1) / (n + 1)\n \n # Calculate return - data are daily to then divide by 365?\n return_year = (1 / probability)\n \n # Round return period\n return_yr_rnd = np.around(return_year, decimals=1)\n \n # identify daily precip for specified return interval\n indices = np.where(return_yr_rnd == return_interval)\n \n # Compute over daily accumulation for the X return period\n mean_return_period_value = sorted_data[indices].mean().compute()\n\n return(mean_return_period_value)", "_____no_output_____" ], [ "da_grid_cell = da.sel(latitude=lat, longitude=lon)\nda_grid_cell", "_____no_output_____" ], [ "# applyufunc --> this applies a function to a single grid cell", "_____no_output_____" ], [ "return_values = []\n\nfor ilat in range(0, len(da.latitude)):\n for ilon in range(0, len(da.longitude):\n # create array to store lon values per lat\n values_per_lat = []\n # select da per grid cell\n da_grid_cell = da.sel(latitude=latitude[ilat], longitude=longitude[ilon])\n # compute return period value & append\n mean_return_value = calculate_return(da_grid_cell, 5.0)\n values_per_lat.append(mean_return_value)\n \n # for each latitude save all longitude values\n return_values.append(values_per_lat)", "_____no_output_____" ], [ "return_values", "_____no_output_____" ], [ "for lat in da.latitude:\n for lon in da.longitude:\n da_grid_cell = da.sel(latitude=lat, longitude=lon)\n \n mean_return_value = calculate_return(da_grid_cell, 5.0) ", "_____no_output_____" ] ], [ [ "Breakdown of per step testing of return period", "_____no_output_____" ] ], [ [ "da_test = da.sel(latitude=75.0, longitude=18.0).persist()\nda_test", "_____no_output_____" ], [ "mean = calculate_return(da_test, 5.0)\nmean", "_____no_output_____" ], [ "sorted_data = da_test.sortby(da_test, ascending=True).compute()\nsorted_data", "_____no_output_____" ], [ "n = sorted_data.shape[0]\nn", "_____no_output_____" ], [ "rank = np.arange(1, 1 + n) # sorted_data.insert(0, 'rank', range(1, 1 + n))\nrank", "_____no_output_____" ], [ "probability = (n - rank + 1) / (n + 1)\nprobability", "_____no_output_____" ], [ "return_year = (1 / probability)\nreturn_year", "_____no_output_____" ], [ "return_yr_rnd = np.around(return_year, decimals=1)\nreturn_yr_rnd[5679]", "_____no_output_____" ], [ "indices = np.where(return_yr_rnd == 5.0)\nindices", "_____no_output_____" ], [ "sorted_data[indices].mean().compute()", "_____no_output_____" ], [ "sorted_test = np.sort(da_test, axis=0)\n", "_____no_output_____" ], [ "sorted_test = xr.DataArray(sorted_test)\nsorted_test", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb2f5ed0d727bc5e94f8e6578825eb5b54b6fb49

13,747

ipynb

Jupyter Notebook

notebooks/cugraph_benchmarks/pagerank_benchmark.ipynb

jwyles/cugraph

1758d085e03d1d62ccd7064fda8cb0257011f50b

[ "Apache-2.0" ]

null

notebooks/cugraph_benchmarks/pagerank_benchmark.ipynb

jwyles/cugraph

1758d085e03d1d62ccd7064fda8cb0257011f50b

[ "Apache-2.0" ]

null

notebooks/cugraph_benchmarks/pagerank_benchmark.ipynb

jwyles/cugraph

1758d085e03d1d62ccd7064fda8cb0257011f50b

[ "Apache-2.0" ]

null

26.902153

316

0.503674

[ [ [ "# PageRank Performance Benchmarking\n\nThis notebook benchmarks performance of running PageRank within cuGraph against NetworkX. NetworkX contains several implementations of PageRank. This benchmark will compare cuGraph versus the defaukt Nx implementation as well as the SciPy version\n\nNotebook Credits\n\n Original Authors: Bradley Rees\n Last Edit: 06/10/2019\n \nRAPIDS Versions: 0.15\n\nTest Hardware\n\n GV100 32G, CUDA 10,0\n Intel(R) Core(TM) CPU i7-7800X @ 3.50GHz\n 32GB system memory\n \n", "_____no_output_____" ], [ "### Test Data\n\n| File Name | Num of Vertices | Num of Edges |\n|:---------------------- | --------------: | -----------: |\n| preferentialAttachment | 100,000 | 999,970 |\n| caidaRouterLevel | 192,244 | 1,218,132 |\n| coAuthorsDBLP | 299,067 | 1,955,352 |\n| dblp-2010 | 326,186 | 1,615,400 |\n| citationCiteseer | 268,495 | 2,313,294 |\n| coPapersDBLP | 540,486 | 30,491,458 |\n| coPapersCiteseer | 434,102 | 32,073,440 |\n| as-Skitter | 1,696,415 | 22,190,596 |\n\n\n", "_____no_output_____" ], [ "### Timing \nWhat is not timed: Reading the data\n\nWhat is timmed: (1) creating a Graph, (2) running PageRank\n\nThe data file is read in once for all flavors of PageRank. Each timed block will craete a Graph and then execute the algorithm. The results of the algorithm are not compared. If you are interested in seeing the comparison of results, then please see PageRank in the __notebooks__ repo. ", "_____no_output_____" ], [ "## NOTICE\n_You must have run the __dataPrep__ script prior to running this notebook so that the data is downloaded_\n\nSee the README file in this folder for a discription of how to get the data", "_____no_output_____" ], [ "## If you have more than one GPU, set the GPU to use\nThis is not needed on a Single GPU system or if the default GPU is to be used", "_____no_output_____" ] ], [ [ "!nvidia-smi", "_____no_output_____" ], [ "# since this is a shared machine - let's pick a GPU that no one else is using\nimport os\nos.environ[\"CUDA_VISIBLE_DEVICES\"]=\"0\"", "_____no_output_____" ] ], [ [ "## Now load the required libraries", "_____no_output_____" ] ], [ [ "# Import needed libraries\nimport gc\nimport time\nimport rmm\nimport cugraph\nimport cudf", "_____no_output_____" ], [ "# NetworkX libraries\nimport networkx as nx\nfrom scipy.io import mmread", "_____no_output_____" ], [ "try: \n import matplotlib\nexcept ModuleNotFoundError:\n os.system('pip install matplotlib')", "_____no_output_____" ], [ "import matplotlib.pyplot as plt; plt.rcdefaults()\nimport numpy as np", "_____no_output_____" ], [ "# Print out GPU Name\ncudf._cuda.gpu.deviceGetName(0)", "_____no_output_____" ] ], [ [ "### Define the test data", "_____no_output_____" ] ], [ [ "# Test File\ndata = {\n 'preferentialAttachment' : './data/preferentialAttachment.mtx',\n 'caidaRouterLevel' : './data/caidaRouterLevel.mtx',\n 'coAuthorsDBLP' : './data/coAuthorsDBLP.mtx',\n 'dblp' : './data/dblp-2010.mtx',\n 'citationCiteseer' : './data/citationCiteseer.mtx',\n 'coPapersDBLP' : './data/coPapersDBLP.mtx',\n 'coPapersCiteseer' : './data/coPapersCiteseer.mtx',\n 'as-Skitter' : './data/as-Skitter.mtx'\n}", "_____no_output_____" ] ], [ [ "### Define the testing functions", "_____no_output_____" ] ], [ [ "# Data reader - the file format is MTX, so we will use the reader from SciPy\ndef read_mtx_file(mm_file):\n print('Reading ' + str(mm_file) + '...')\n M = mmread(mm_file).asfptype()\n \n return M", "_____no_output_____" ], [ "# CuGraph PageRank\n\ndef cugraph_call(M, max_iter, tol, alpha):\n\n gdf = cudf.DataFrame()\n gdf['src'] = M.row\n gdf['dst'] = M.col\n \n print('\\tcuGraph Solving... ')\n \n t1 = time.time()\n \n # cugraph Pagerank Call\n G = cugraph.DiGraph()\n G.from_cudf_edgelist(gdf, source='src', destination='dst', renumber=False)\n \n df = cugraph.pagerank(G, alpha=alpha, max_iter=max_iter, tol=tol)\n t2 = time.time() - t1\n \n return t2\n ", "_____no_output_____" ], [ "# Basic NetworkX PageRank\n\ndef networkx_call(M, max_iter, tol, alpha):\n nnz_per_row = {r: 0 for r in range(M.get_shape()[0])}\n for nnz in range(M.getnnz()):\n nnz_per_row[M.row[nnz]] = 1 + nnz_per_row[M.row[nnz]]\n for nnz in range(M.getnnz()):\n M.data[nnz] = 1.0/float(nnz_per_row[M.row[nnz]])\n\n M = M.tocsr()\n if M is None:\n raise TypeError('Could not read the input graph')\n if M.shape[0] != M.shape[1]:\n raise TypeError('Shape is not square')\n\n # should be autosorted, but check just to make sure\n if not M.has_sorted_indices:\n print('sort_indices ... ')\n M.sort_indices()\n\n z = {k: 1.0/M.shape[0] for k in range(M.shape[0])}\n \n print('\\tNetworkX Solving... ')\n \n # start timer\n t1 = time.time()\n \n Gnx = nx.DiGraph(M)\n\n pr = nx.pagerank(Gnx, alpha, z, max_iter, tol)\n \n t2 = time.time() - t1\n\n return t2", "_____no_output_____" ], [ "# SciPy PageRank\n\ndef networkx_scipy_call(M, max_iter, tol, alpha):\n nnz_per_row = {r: 0 for r in range(M.get_shape()[0])}\n for nnz in range(M.getnnz()):\n nnz_per_row[M.row[nnz]] = 1 + nnz_per_row[M.row[nnz]]\n for nnz in range(M.getnnz()):\n M.data[nnz] = 1.0/float(nnz_per_row[M.row[nnz]])\n\n M = M.tocsr()\n if M is None:\n raise TypeError('Could not read the input graph')\n if M.shape[0] != M.shape[1]:\n raise TypeError('Shape is not square')\n\n # should be autosorted, but check just to make sure\n if not M.has_sorted_indices:\n print('sort_indices ... ')\n M.sort_indices()\n\n z = {k: 1.0/M.shape[0] for k in range(M.shape[0])}\n\n # SciPy Pagerank Call\n print('\\tSciPy Solving... ')\n t1 = time.time()\n \n Gnx = nx.DiGraph(M) \n \n pr = nx.pagerank_scipy(Gnx, alpha, z, max_iter, tol)\n t2 = time.time() - t1\n\n return t2", "_____no_output_____" ] ], [ [ "### Run the benchmarks", "_____no_output_____" ] ], [ [ "# arrays to capture performance gains\ntime_cu = []\ntime_nx = []\ntime_sp = []\nperf_nx = []\nperf_sp = []\nnames = []\n\n# init libraries by doing a simple task \nv = './data/preferentialAttachment.mtx'\nM = read_mtx_file(v)\ntrapids = cugraph_call(M, 100, 0.00001, 0.85)\ndel M\n\n\nfor k,v in data.items():\n gc.collect()\n\n # Saved the file Name\n names.append(k)\n \n # read the data\n M = read_mtx_file(v)\n \n # call cuGraph - this will be the baseline\n trapids = cugraph_call(M, 100, 0.00001, 0.85)\n time_cu.append(trapids)\n \n # Now call NetworkX\n tn = networkx_call(M, 100, 0.00001, 0.85)\n speedUp = (tn / trapids)\n perf_nx.append(speedUp)\n time_nx.append(tn)\n \n # Now call SciPy\n tsp = networkx_scipy_call(M, 100, 0.00001, 0.85)\n speedUp = (tsp / trapids)\n perf_sp.append(speedUp) \n time_sp.append(tsp)\n \n print(\"cuGraph (\" + str(trapids) + \") Nx (\" + str(tn) + \") SciPy (\" + str(tsp) + \")\" )\n del M", "_____no_output_____" ] ], [ [ "### plot the output", "_____no_output_____" ] ], [ [ "%matplotlib inline\n\nplt.figure(figsize=(10,8))\n\nbar_width = 0.35\nindex = np.arange(len(names))\n\n_ = plt.bar(index, perf_nx, bar_width, color='g', label='vs Nx')\n_ = plt.bar(index + bar_width, perf_sp, bar_width, color='b', label='vs SciPy')\n\nplt.xlabel('Datasets')\nplt.ylabel('Speedup')\nplt.title('PageRank Performance Speedup')\nplt.xticks(index + (bar_width / 2), names)\nplt.xticks(rotation=90) \n\n# Text on the top of each barplot\nfor i in range(len(perf_nx)):\n plt.text(x = (i - 0.55) + bar_width, y = perf_nx[i] + 25, s = round(perf_nx[i], 1), size = 12)\n\nfor i in range(len(perf_sp)):\n plt.text(x = (i - 0.1) + bar_width, y = perf_sp[i] + 25, s = round(perf_sp[i], 1), size = 12)\n\n\nplt.legend()\nplt.show()", "_____no_output_____" ] ], [ [ "# Dump the raw stats", "_____no_output_____" ] ], [ [ "perf_nx", "_____no_output_____" ], [ "perf_sp", "_____no_output_____" ], [ "time_cu", "_____no_output_____" ], [ "time_nx", "_____no_output_____" ], [ "time_sp", "_____no_output_____" ] ], [ [ "___\nCopyright (c) 2020, NVIDIA CORPORATION.\n\nLicensed under the Apache License, Version 2.0 (the \"License\"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0\n\nUnless required by applicable law or agreed to in writing, software distributed under the License is distributed on an \"AS IS\" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.\n___", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ] ]

cb2f604f27992511d8efade7d779d80bf41104f6

51,335

ipynb

Jupyter Notebook

lab 4.ipynb

Kalisl8/340

25d666ac19adada34ddc64b4bbc26d7698d91dc6

[ "MIT" ]

null

lab 4.ipynb

Kalisl8/340

25d666ac19adada34ddc64b4bbc26d7698d91dc6

[ "MIT" ]

null

lab 4.ipynb

Kalisl8/340

25d666ac19adada34ddc64b4bbc26d7698d91dc6

[ "MIT" ]

null

50.826733

13,768

0.659686

[ [ [ "# lab 4", "_____no_output_____" ], [ "## import libs and connect db", "_____no_output_____" ] ], [ [ "!pip install psycopg2", "Requirement already satisfied: psycopg2 in /home/ec2-user/anaconda3/envs/python3/lib/python3.6/site-packages (2.7.5)\n\u001b[33mWARNING: You are using pip version 20.0.2; however, version 20.2.3 is available.\nYou should consider upgrading via the '/home/ec2-user/anaconda3/envs/python3/bin/python -m pip install --upgrade pip' command.\u001b[0m\n" ], [ "import pandas\nimport configparser\nimport psycopg2", "_____no_output_____" ], [ "config = configparser.ConfigParser()\nconfig.read('config.ini')\n\nhost = config['my aws']['host']\ndb = config['my aws']['db']\nuser = config['my aws']['user']\npassword = config['my aws']['password']\n\n\n", "_____no_output_____" ], [ "conn = psycopg2.connect(\n\n host=host,\n user=user,\n password=password,\n database=db\n )\n\nprint(user)", "gp13\n" ], [ "cur=conn.cursor()", "_____no_output_____" ] ], [ [ "# Q1", "_____no_output_____" ] ], [ [ "sql_q1 = \"\"\"\n select * from gp13.student\n \"\"\"", "_____no_output_____" ], [ "df=pandas.read_sql_query(sql_q1,conn) \ndf[:]", "_____no_output_____" ] ], [ [ "## Q2", "_____no_output_____" ] ], [ [ "sql_q2= \"\"\"\n select gp13.professor.p_name,\n gp13.course.course_name\n from gp13.professor\n inner join gp13.course\n on gp13.professor.p_email = gp13.course.p_email\n \n \"\"\"", "_____no_output_____" ], [ "df=pandas.read_sql_query(sql_q2, conn) \ndf[:]", "_____no_output_____" ] ], [ [ "# Q3", "_____no_output_____" ] ], [ [ "sql_q3= \"\"\"\n select course_number, \n count(course_number) as enrolled\n from gp13.enroll_list\n group by course_number\n order by enrolled desc\n \"\"\"\n ", "_____no_output_____" ], [ "df=pandas.read_sql_query(sql_q3, conn) \ndf.plot.bar(y='enrolled',x='course_number')", "_____no_output_____" ] ], [ [ "# Q4", "_____no_output_____" ] ], [ [ "sql_q4= \"\"\"\n select gp13.professor.p_name,\n count(gp13.course.course_name) as teaching_number\n from gp13.professor\n inner join gp13.course\n on gp13.professor.p_email = gp13.course.p_email\n group by professor.p_name\n order by teaching_number desc\n \"\"\"", "_____no_output_____" ], [ "df=pandas.read_sql_query(sql_q4, conn) \ndf.plot.bar(y='teaching_number',x='p_name')", "_____no_output_____" ] ], [ [ "# Q5", "_____no_output_____" ] ], [ [ "sql_q5_professor= \"\"\"\n insert into gp13.professor(p_email,p_name, office)\n values('{}','{}','{}')\n \"\"\" .format('[email protected]','new','new_office')", "_____no_output_____" ], [ "conn.commit()", "_____no_output_____" ], [ "df=pandas.read_sql_query('select * from gp13.professor',conn)\ndf[:]", "_____no_output_____" ], [ "sql_q5_course= \"\"\"\n insert into gp13.course(course_number,course_name,room,p_email)\n values('{}','{}','{}','{}')\n \"\"\" .format('ia_new','new_c_name','new_room','[email protected]')", "_____no_output_____" ], [ "cur.execute(sql_q5_course)", "_____no_output_____" ], [ "df=pandas.read_sql_query('select * from gp13.course',conn)\ndf[:]", "_____no_output_____" ] ], [ [ "# Q6", "_____no_output_____" ] ], [ [ "sql_q6_course = \"\"\"\n update gp13.course\n set p_email = '{}'\n where p_email ='{}'\n \"\"\".format('[email protected]','[email protected]')", "_____no_output_____" ], [ "cur.execute(sql_q6_course)", "_____no_output_____" ], [ "conn.commit()", "_____no_output_____" ], [ "df=pandas.read_sql_query('select * from gp13.course',conn)\ndf[:]", "_____no_output_____" ], [ "sql_q6_professor= \"\"\"\n delete from gp13.professor\n where p_email ='{}'\n \"\"\".format('[email protected]')", "_____no_output_____" ], [ "cur.execute(sql_q6_professor)", "_____no_output_____" ], [ "df=pandas.read_sql_query('select * from gp13.course',conn)\ndf[:]", "_____no_output_____" ] ], [ [ "# close connection", "_____no_output_____" ] ], [ [ "cur.close()\nconn.close()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ] ]

cb2f64b626d6b6988720194c9f6e0c4062eba07a

40,840

ipynb

Jupyter Notebook

resources/example.ipynb

naru-hiyoko/IElixir

48be2845fcf48e4fc86c0a0ab3fc9784e4b8fa76

[ "Apache-2.0" ]

363

2015-07-12T07:36:38.000Z

2022-03-23T22:48:41.000Z

resources/example.ipynb

naru-hiyoko/IElixir

48be2845fcf48e4fc86c0a0ab3fc9784e4b8fa76

[ "Apache-2.0" ]

51

2015-07-30T08:40:46.000Z

2021-12-03T09:18:58.000Z

resources/example.ipynb

naru-hiyoko/IElixir

48be2845fcf48e4fc86c0a0ab3fc9784e4b8fa76

[ "Apache-2.0" ]

50

2015-07-30T05:31:58.000Z

2021-12-03T09:15:58.000Z

21.3934

4,357

0.478501

[ [ [ "# IElixir - Elixir kernel for Jupyter Project\n\n<img src=\"logo.png\" title=\"Hosted by imgur.com\" style=\"margin: 0 0;\"/>\n\n---\n\n## Google Summer of Code 2015\n> Developed by [Piotr Przetacznik](https://twitter.com/pprzetacznik)\n\n> Mentored by [José Valim](https://twitter.com/josevalim)\n\n---\n## References\n\n* [Elixir language](http://elixir-lang.org/)\n* [Jupyter Project](https://jupyter.org/)\n* [IElixir sources](https://github.com/pprzetacznik/IElixir)", "_____no_output_____" ], [ "## Getting Started\n\n### Basic Types\n\n<pre>\n1 # integer\n0x1F # integer\n1.0 # float\ntrue # boolean\n:atom # atom / symbol\n\"elixir\" # string\n[1, 2, 3] # list\n{1, 2, 3} # tuple\n</pre>\n\n### Basic arithmetic", "_____no_output_____" ] ], [ [ "1 + 2", "_____no_output_____" ], [ "5 * 5", "_____no_output_____" ], [ "10 / 2", "_____no_output_____" ], [ "div(10, 2)", "_____no_output_____" ], [ "div 10, 2", "_____no_output_____" ], [ "rem 10, 3", "_____no_output_____" ], [ "0b1010", "_____no_output_____" ], [ "0o777", "_____no_output_____" ], [ "0x1F", "_____no_output_____" ], [ "1.0", "_____no_output_____" ], [ "1.0e-10", "_____no_output_____" ], [ "round 3.58", "_____no_output_____" ], [ "trunc 3.58", "_____no_output_____" ] ], [ [ "### Booleans", "_____no_output_____" ] ], [ [ "true", "_____no_output_____" ], [ "true == false", "_____no_output_____" ], [ "is_boolean(true)", "_____no_output_____" ], [ "is_boolean(1)", "_____no_output_____" ], [ "is_integer(5)", "_____no_output_____" ], [ "is_float(5)", "_____no_output_____" ], [ "is_number(\"5.0\")", "_____no_output_____" ] ], [ [ "### Atoms", "_____no_output_____" ] ], [ [ ":hello", "_____no_output_____" ], [ ":hello == :world", "_____no_output_____" ], [ "true == :true", "_____no_output_____" ], [ "is_atom(false)", "_____no_output_____" ], [ "is_boolean(:false)", "_____no_output_____" ] ], [ [ "### Strings", "_____no_output_____" ] ], [ [ "\"hellö\"", "_____no_output_____" ], [ "\"hellö #{:world}\"", "_____no_output_____" ], [ "IO.puts \"hello\\nworld\"", "hello\nworld\n" ], [ "is_binary(\"hellö\")", "_____no_output_____" ], [ "byte_size(\"hellö\")", "_____no_output_____" ], [ "String.length(\"hellö\")", "_____no_output_____" ], [ "String.upcase(\"hellö\")", "_____no_output_____" ] ], [ [ "### Anonymous functions", "_____no_output_____" ] ], [ [ "add = fn a, b -> a + b end", "_____no_output_____" ], [ "is_function(add)", "_____no_output_____" ], [ "is_function(add, 2)", "_____no_output_____" ], [ "is_function(add, 1)", "_____no_output_____" ], [ "add.(1, 2)", "_____no_output_____" ], [ "add_two = fn a -> add.(a, 2) end", "_____no_output_____" ], [ "add_two.(2)", "_____no_output_____" ], [ "x = 42\n(fn -> x = 0 end).()\nx", "\u001b[33mwarning: \u001b[0mvariable \"x\" is unused\n\nNote variables defined inside case, cond, fn, if and similar do not leak. If you want to conditionally override an existing variable \"x\", you will have to explicitly return the variable. For example:\n\n if some_condition? do\n atom = :one\n else\n atom = :two\n end\n\nshould be written as\n\n atom =\n if some_condition? do\n :one\n else\n :two\n end\n\nUnused variable found at:\n nofile:2\n\n" ] ], [ [ "### (Linked) Lists", "_____no_output_____" ] ], [ [ "a = [1, 2, true, 3]", "_____no_output_____" ], [ "length [1, 2, 3]", "_____no_output_____" ], [ "[1, 2, 3] ++ [4, 5, 6]", "_____no_output_____" ], [ "[1, true, 2, false, 3, true] -- [true, false]", "_____no_output_____" ], [ "hd(a)", "_____no_output_____" ], [ "tl(a)", "_____no_output_____" ], [ "hd []", "_____no_output_____" ], [ "[11, 12, 13]", "_____no_output_____" ], [ "[104, 101, 108, 108, 111]", "_____no_output_____" ], [ "'hello' == \"hello\"", "_____no_output_____" ] ], [ [ "### Tuples", "_____no_output_____" ] ], [ [ "{:ok, \"hello\"}", "_____no_output_____" ], [ "tuple_size {:ok, \"hello\"}", "_____no_output_____" ], [ "tuple = {:ok, \"hello\"}", "_____no_output_____" ], [ "elem(tuple, 1)", "_____no_output_____" ], [ "tuple_size(tuple)", "_____no_output_____" ], [ "put_elem(tuple, 1, \"world\")", "_____no_output_____" ], [ "tuple", "_____no_output_____" ] ], [ [ "### Lists or tuples?", "_____no_output_____" ] ], [ [ "list = [1|[2|[3|[]]]]", "_____no_output_____" ], [ "[0] ++ list", "_____no_output_____" ], [ "list ++ [4]", "_____no_output_____" ], [ "File.read(\"LICENSE\")", "_____no_output_____" ], [ "File.read(\"path/to/unknown/file\")", "_____no_output_____" ] ], [ [ "### Other examples", "_____no_output_____" ] ], [ [ "0x1F", "_____no_output_____" ], [ "a = 25\nb = 150\nIO.puts(a+b)", "175\n" ], [ "defmodule Math do\n def sum(a, b) do\n a + b\n end\nend", "\u001b[33mwarning: \u001b[0mredefining module Math (current version defined in memory)\n nofile:1\n\n" ], [ "Math.sum(1, 2)", "_____no_output_____" ], [ "import ExUnit.CaptureIO\ncapture_io(fn -> IO.write \"john\" end) == \"john\"", "_____no_output_____" ], [ "?a", "_____no_output_____" ], [ "<<98>> == <<?b>>", "_____no_output_____" ], [ "<<?g, ?o, ?\\n>> == \"go\n\"", "_____no_output_____" ], [ "{hlen, blen} = {4, 4}\n<<header :: binary-size(hlen), body :: binary-size(blen)>> = \"headbody\"\n{header, body}", "_____no_output_____" ], [ "h()", "\u001b[0m\n\u001b[7m\u001b[33m IEx.Helpers \u001b[0m\n\u001b[0m\nWelcome to Interactive Elixir. You are currently seeing the documentation for\nthe module \u001b[36mIEx.Helpers\u001b[0m which provides many helpers to make Elixir's shell more\njoyful to work with.\n\u001b[0m\nThis message was triggered by invoking the helper \u001b[36mh()\u001b[0m, usually referred to as\n\u001b[36mh/0\u001b[0m (since it expects 0 arguments).\n\u001b[0m\nYou can use the \u001b[36mh/1\u001b[0m function to invoke the documentation for any Elixir module\nor function:\n\u001b[0m\n\u001b[36m iex> h(Enum)\n iex> h(Enum.map)\n iex> h(Enum.reverse/1)\u001b[0m\n\u001b[0m\nYou can also use the \u001b[36mi/1\u001b[0m function to introspect any value you have in the\nshell:\n\u001b[0m\n\u001b[36m iex> i(\"hello\")\u001b[0m\n\u001b[0m\nThere are many other helpers available, here are some examples:\n\u001b[0m\n • \u001b[36mb/1\u001b[0m - prints callbacks info and docs for a given module\n • \u001b[36mc/1\u001b[0m - compiles a file\n • \u001b[36mc/2\u001b[0m - compiles a file and writes bytecode to the given path\n • \u001b[36mcd/1\u001b[0m - changes the current directory\n • \u001b[36mclear/0\u001b[0m - clears the screen\n • \u001b[36mexports/1\u001b[0m - shows all exports (functions + macros) in a module\n • \u001b[36mflush/0\u001b[0m - flushes all messages sent to the shell\n • \u001b[36mh/0\u001b[0m - prints this help message\n • \u001b[36mh/1\u001b[0m - prints help for the given module, function or macro\n • \u001b[36mi/0\u001b[0m - prints information about the last value\n • \u001b[36mi/1\u001b[0m - prints information about the given term\n • \u001b[36mls/0\u001b[0m - lists the contents of the current directory\n • \u001b[36mls/1\u001b[0m - lists the contents of the specified directory\n • \u001b[36mopen/1\u001b[0m - opens the source for the given module or function in\n your editor\n • \u001b[36mpid/1\u001b[0m - creates a PID from a string\n • \u001b[36mpid/3\u001b[0m - creates a PID with the 3 integer arguments passed\n • \u001b[36mref/1\u001b[0m - creates a Reference from a string\n • \u001b[36mref/4\u001b[0m - creates a Reference with the 4 integer arguments\n passed\n • \u001b[36mpwd/0\u001b[0m - prints the current working directory\n • \u001b[36mr/1\u001b[0m - recompiles the given module's source file\n • \u001b[36mrecompile/0\u001b[0m - recompiles the current project\n • \u001b[36mruntime_info/0\u001b[0m - prints runtime info (versions, memory usage, stats)\n • \u001b[36mv/0\u001b[0m - retrieves the last value from the history\n • \u001b[36mv/1\u001b[0m - retrieves the nth value from the history\n\u001b[0m\nHelp for all of those functions can be consulted directly from the command line\nusing the \u001b[36mh/1\u001b[0m helper itself. Try:\n\u001b[0m\n\u001b[36m iex> h(v/0)\u001b[0m\n\u001b[0m\nTo list all IEx helpers available, which is effectively all exports (functions\nand macros) in the \u001b[36mIEx.Helpers\u001b[0m module:\n\u001b[0m\n\u001b[36m iex> exports(IEx.Helpers)\u001b[0m\n\u001b[0m\nThis module also includes helpers for debugging purposes, see \u001b[36mIEx.break!/4\u001b[0m for\nmore information.\n\u001b[0m\nTo learn more about IEx as a whole, type \u001b[36mh(IEx)\u001b[0m.\n\u001b[0m\n" ], [ "defmodule KV.Registry do\n use GenServer\n\n ## Client API\n\n @doc \"\"\"\n Starts the registry.\n \"\"\"\n def start_link(opts \\\\ []) do\n GenServer.start_link(__MODULE__, :ok, opts)\n end\n\n @doc \"\"\"\n Looks up the bucket pid for `name` stored in `server`.\n\n Returns `{:ok, pid}` if the bucket exists, `:error` otherwise.\n \"\"\"\n def lookup(server, name) do\n GenServer.call(server, {:lookup, name})\n end\n\n @doc \"\"\"\n Ensures there is a bucket associated to the given `name` in `server`.\n \"\"\"\n def create(server, name) do\n GenServer.cast(server, {:create, name})\n end\n\n ## Server Callbacks\n\n def init(:ok) do\n {:ok, HashDict.new}\n end\n\n def handle_call({:lookup, name}, _from, names) do\n {:reply, HashDict.fetch(names, name), names}\n end\n\n def handle_cast({:create, name}, names) do\n if HashDict.has_key?(names, name) do\n {:noreply, names}\n else\n {:ok, bucket} = KV.Bucket.start_link()\n {:noreply, HashDict.put(names, name, bucket)}\n end\n end\nend", "\u001b[33mwarning: \u001b[0mredefining module KV.Registry (current version defined in memory)\n nofile:1\n\n\u001b[33mwarning: \u001b[0mHashDict.new/0 is deprecated. Use maps and the Map module instead\n nofile:32\n\n\u001b[33mwarning: \u001b[0mHashDict.fetch/2 is deprecated. Use maps and the Map module instead\n nofile:36\n\n\u001b[33mwarning: \u001b[0mHashDict.has_key?/2 is deprecated. Use maps and the Map module instead\n nofile:40\n\n\u001b[33mwarning: \u001b[0mHashDict.put/3 is deprecated. Use maps and the Map module instead\n nofile:44\n\n" ], [ "ExUnit.start()", "_____no_output_____" ], [ "defmodule KV.RegistryTest do\n use ExUnit.Case, async: true\n\n setup do\n {:ok, registry} = KV.Registry.start_link\n {:ok, registry: registry}\n end\n\n test \"spawns buckets\", %{registry: registry} do\n assert KV.Registry.lookup(registry, \"shopping\") == :error\n\n KV.Registry.create(registry, \"shopping\")\n assert {:ok, bucket} = KV.Registry.lookup(registry, \"shopping\")\n\n KV.Bucket.put(bucket, \"milk\", 1)\n assert KV.Bucket.get(bucket, \"milk\") == 1\n end\nend", "\u001b[33mwarning: \u001b[0mredefining module KV.RegistryTest (current version defined in memory)\n nofile:1\n\n" ] ], [ [ "## IElixir magic commands\n\nGet output of previous cell.", "_____no_output_____" ] ], [ [ "ans", "_____no_output_____" ] ], [ [ "You can also access output of any cell using it's number.", "_____no_output_____" ] ], [ [ "out[142]", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2f91043ef893db9b81ba403b0082b351f5d4ba

48,165

ipynb

Jupyter Notebook

1 Supervised Learning/Classification/Sequence_Tagging_NER.ipynb

HJJ256/Machine-Learning-2018-present-

f01d2f13025b02792612ee42e2e58f13f461b999

[ "MIT" ]

1

2020-09-26T20:02:57.000Z

1 Supervised Learning/Classification/Sequence_Tagging_NER.ipynb

HJJ256/Machine-Learning-2018-present-

f01d2f13025b02792612ee42e2e58f13f461b999

[ "MIT" ]

null

1 Supervised Learning/Classification/Sequence_Tagging_NER.ipynb

HJJ256/Machine-Learning-2018-present-

f01d2f13025b02792612ee42e2e58f13f461b999

[ "MIT" ]

null

41.557377

9,450

0.552455

[ [ [ "import pandas as pd\nimport numpy as np\nimport matplotlib.pyplot as plt", "_____no_output_____" ], [ "A = np.random.randn(4,3)\nB = np.sum(A, axis = 1, keepdims = True)\nB.shape", "_____no_output_____" ] ], [ [ "# Data Loading", "_____no_output_____" ] ], [ [ "data = pd.read_csv(\"ner_dataset.csv\", encoding=\"latin1\")\ndata = data.drop(['POS'], axis =1)\ndata.head()", "_____no_output_____" ], [ "plt.style.use(\"ggplot\")\ndata = pd.read_csv(\"ner_dataset.csv\", encoding=\"latin1\")\ndata = data.drop(['POS'], axis =1)\ndata = data.fillna(method=\"ffill\")\nwords = set(list(data['Word'].values)) #Vocabulary\nwords.add('PADword')\nn_words = len(words)\ntags = list(set(data[\"Tag\"].values))\nn_tags = len(tags)\nprint(n_words,n_tags)", "35179 17\n" ] ], [ [ "# Data Preprocessing", "_____no_output_____" ] ], [ [ "class SentenceGetter(object):\n def __init__(self, data):\n self.n_sent = 1\n self.data = data\n self.empty = False\n agg_func = lambda s: [(w, t) for w, t in zip(s[\"Word\"].\n values.tolist(),s[\"Tag\"].values.tolist())]\n self.grouped = self.data.groupby(\"Sentence #\").apply(agg_func)\n self.sentences = [s for s in self.grouped]\n\n def get_next(self):\n try:\n s = self.grouped[\"Sentence: {}\".format(self.n_sent)]\n self.n_sent += 1\n return s\n except:\n return None", "_____no_output_____" ], [ "getter = SentenceGetter(data)\n", "[('Thousands', 'O'), ('of', 'O'), ('demonstrators', 'O'), ('have', 'O'), ('marched', 'O'), ('through', 'O'), ('London', 'B-geo'), ('to', 'O'), ('protest', 'O'), ('the', 'O'), ('war', 'O'), ('in', 'O'), ('Iraq', 'B-geo'), ('and', 'O'), ('demand', 'O'), ('the', 'O'), ('withdrawal', 'O'), ('of', 'O'), ('British', 'B-gpe'), ('troops', 'O'), ('from', 'O'), ('that', 'O'), ('country', 'O'), ('.', 'O')]\n" ], [ "sent = getter.get_next()\nprint(sent)", "_____no_output_____" ], [ "sentences = getter.sentences\nprint(len(sentences))", "47959\n" ], [ "largest_sen = max(len(sen) for sen in sentences)\nprint('biggest sentence has {} words'.format(largest_sen))", "biggest sentence has 104 words\n" ], [ "%matplotlib inline\nplt.hist([len(sen) for sen in sentences],bins=50)\nplt.xlabel('Sentence Length')\nplt.ylabel('Frequency')\nplt.show()", "_____no_output_____" ], [ "max_len = 50\nX = [[w[0]for w in s] for s in sentences]\nnew_X = []\nfor seq in X:\n new_seq = []\n for i in range(max_len):\n try:\n new_seq.append(seq[i])\n except:\n new_seq.append(\"PADword\")\n new_X.append(new_seq)\nprint(new_X[0])\nsentences[0]", "_____no_output_____" ], [ "list(enumerate(tags))", "_____no_output_____" ], [ "", "_____no_output_____" ], [ "tags2index", "_____no_output_____" ], [ "from keras.preprocessing.sequence import pad_sequences\ntags2index = {t:i for i,t in enumerate(tags)}\ny = [[tags2index[w[1]] for w in s] for s in sentences]\ny = pad_sequences(maxlen=max_len, sequences=y, padding=\"post\", value=tags2index[\"O\"])\ny", "Using TensorFlow backend.\n" ] ], [ [ "# Model Building and Training", "_____no_output_____" ] ], [ [ "from sklearn.model_selection import train_test_split\nimport tensorflow as tf\nimport tensorflow_hub as hub\nfrom keras import backend as K\nX_tr, X_te, y_tr, y_te = train_test_split(new_X, y, test_size=0.1, random_state=2018)\nsess = tf.Session()\nK.set_session(sess)\nelmo_model = hub.Module(\"https://tfhub.dev/google/elmo/2\", trainable=True)\nsess.run(tf.global_variables_initializer())\nsess.run(tf.tables_initializer())", "_____no_output_____" ], [ "batch_size = 32\ndef ElmoEmbedding(x):\n return elmo_model(inputs={\"tokens\": tf.squeeze(tf.cast(x,\n tf.string)),\"sequence_len\": tf.constant(batch_size*[max_len])\n },signature=\"tokens\",as_dict=True)[\"elmo\"]", "_____no_output_____" ], [ "", "_____no_output_____" ], [ "from keras.models import Model, Input\nfrom keras.layers.merge import add\nfrom keras.layers import LSTM, Embedding, Dense, TimeDistributed, Dropout, Bidirectional, Lambda\ninput_text = Input(shape=(max_len,), dtype=tf.string)\nembedding = Lambda(ElmoEmbedding, output_shape=(max_len, 1024))(input_text)\nx = Bidirectional(LSTM(units=512, return_sequences=True,\n recurrent_dropout=0.2, dropout=0.2))(embedding)\nx_rnn = Bidirectional(LSTM(units=512, return_sequences=True,\n recurrent_dropout=0.2, dropout=0.2))(x)\nx = add([x, x_rnn]) # residual connection to the first biLSTM\nout = TimeDistributed(Dense(n_tags, activation=\"softmax\"))(x)\nmodel = Model(input_text, out)\nmodel.compile(optimizer=\"adam\", loss=\"sparse_categorical_crossentropy\", metrics=[\"accuracy\"])\nmodel.summary()", "WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/keras/backend/tensorflow_backend.py:66: The name tf.get_default_graph is deprecated. Please use tf.compat.v1.get_default_graph instead.\n\n" ], [ "X_tr, X_val = X_tr[:1213*batch_size], X_tr[-135*batch_size:]\ny_tr, y_val = y_tr[:1213*batch_size], y_tr[-135*batch_size:]\ny_tr = y_tr.reshape(y_tr.shape[0], y_tr.shape[1], 1)\ny_val = y_val.reshape(y_val.shape[0], y_val.shape[1], 1)\nhistory = model.fit(np.array(X_tr), y_tr, validation_data=(np.array(X_val), y_val),batch_size=batch_size, epochs=3, verbose=1)", "WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow_core/python/ops/math_grad.py:1424: where (from tensorflow.python.ops.array_ops) is deprecated and will be removed in a future version.\nInstructions for updating:\nUse tf.where in 2.0, which has the same broadcast rule as np.where\n" ], [ "model.save_weights('bilstm_model.hdf5')", "_____no_output_____" ], [ "!pip install seqeval", "_____no_output_____" ] ], [ [ "# Model Evaluation", "_____no_output_____" ] ], [ [ "from seqeval.metrics import precision_score, recall_score, f1_score, classification_report\nX_te = X_te[:149*batch_size]\ntest_pred = model.predict(np.array(X_te), verbose=1)", "_____no_output_____" ], [ "idx2tag = {i: w for w, i in tags2index.items()}\ndef pred2label(pred):\n out = []\n for pred_i in pred:\n out_i = []\n for p in pred_i:\n p_i = np.argmax(p)\n out_i.append(idx2tag[p_i].replace(\"PADword\", \"O\"))\n out.append(out_i)\n return out\ndef test2label(pred):\n out = []\n for pred_i in pred:\n out_i = []\n for p in pred_i:\n out_i.append(idx2tag[p].replace(\"PADword\", \"O\"))\n out.append(out_i)\n return out\n \npred_labels = pred2label(test_pred)\ntest_labels = test2label(y_te[:149*32])\nprint(classification_report(test_labels, pred_labels))", "_____no_output_____" ], [ "i = 390\np = model.predict(np.array(X_te[i:i+batch_size]))[0]\np = np.argmax(p, axis=-1)\nprint(\"{:15} {:5}: ({})\".format(\"Word\", \"Pred\", \"True\"))\nprint(\"=\"*30)\nfor w, true, pred in zip(X_te[i], y_te[i], p):\n if w != \"__PAD__\":\n print(\"{:15}:{:5} ({})\".format(w, tags[pred], tags[true]))", "_____no_output_____" ], [ "history.history", "_____no_output_____" ], [ "?(figsize=(12,12))\n?(history.history[\"acc\"],c = 'b')\n?(history.history[\"val_acc\"], c = 'g')\nplt.show()", "_____no_output_____" ], [ "test_sentence = [[\"Hawking\", \"is\", \"a\", \"Fellow\", \"of\", \"the\", \"Royal\", \"Society\", \",\", \"a\", \"lifetime\", \"member\",\n \"of\", \"the\", \"Pontifical\", \"Academy\", \"of\", \"Sciences\", \",\", \"and\", \"a\", \"recipient\", \"of\",\n \"the\", \"Presidential\", \"Medal\", \"of\", \"Freedom\", \",\", \"the\", \"highest\", \"civilian\", \"award\",\n \"in\", \"the\", \"United\", \"States\", \".\"]]", "_____no_output_____" ], [ "max_len = 50\nX_test = [[w for w in s] for s in test_sentence]\nnew_X_test = []\nfor seq in X_test:\n new_seq = []\n for i in range(max_len):\n try:\n new_seq.append(seq[i])\n except:\n new_seq.append(\"PADword\")\n new_X_test.append(new_seq)\nnew_X_test", "_____no_output_____" ], [ "np.array(new_X_test,dtype='<U26')", "_____no_output_____" ], [ "np.array(X_te)[1]", "_____no_output_____" ] ], [ [ "# Inference", "_____no_output_____" ] ], [ [ "#model.load_weights('bilstm_model.hdf5')\n#model.compile(optimizer=\"adam\", loss=\"sparse_categorical_crossentropy\", metrics=[\"accuracy\"])\np = ?(np.array(new_X_test*32,dtype='<U26'))[0]\np = ?(p, axis=-1)\nprint(\"{:15} {:5}\".format(\"Word\", \"Pred\"))\nprint(\"=\"*30)\nfor w, pred in zip(new_X_test[0], p):\n if w != \"__PAD__\":\n print(\"{:15}:{:5}\".format(w, tags[pred]))", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ] ]

cb2f92fc8791cd443e83b12e56000d2dfbf88fc7

3,582

ipynb

Jupyter Notebook

regression/ridge_regression/residence.ipynb

fumiphys/data-science

4d9a73bd7ce025d409936eb9713513247f71b5a5

[ "MIT" ]

null

regression/ridge_regression/residence.ipynb

fumiphys/data-science

4d9a73bd7ce025d409936eb9713513247f71b5a5

[ "MIT" ]

null

regression/ridge_regression/residence.ipynb

fumiphys/data-science

4d9a73bd7ce025d409936eb9713513247f71b5a5

[ "MIT" ]

null

22.670886

103

0.544389

[ [ [ "# Ridge regression\nadd L2 regularization term to cost function", "_____no_output_____" ] ], [ [ "import numpy as np\nimport pandas as pd\nfrom matplotlib import pyplot as plt\nfrom sklearn import linear_model, datasets, cross_validation", "_____no_output_____" ], [ "# datasets\nboston = datasets.load_boston()\ndata = boston.data\ntarget = boston.target\nx_train, x_test, y_train, y_test = cross_validation.train_test_split(data, target, test_size=0.2)", "_____no_output_____" ], [ "# define model\nmodel = linear_model.Ridge(alpha=1.0)\nmodel.fit(x_train, y_train)", "_____no_output_____" ], [ "# predict for test set\ny_pred = model.predict(x_test)\nprint(np.mean((y_pred - y_test)**2))\nprint(model.coef_)", "19.822190013923926\n[-1.02467275e-01 5.73494319e-02 -5.71244270e-03 1.92386560e+00\n -1.03094322e+01 3.33806179e+00 -8.22167035e-04 -1.42200049e+00\n 3.03853320e-01 -1.26939146e-02 -8.32930802e-01 9.96107585e-03\n -5.99081520e-01]\n" ], [ "# linear regression\nmodel_l = linear_model.LinearRegression()\nmodel_l.fit(x_train, y_train)", "_____no_output_____" ], [ "y_pred_l = model_l.predict(x_test)\nprint(np.mean((y_pred_l - y_test)**2))\nprint(model_l.coef_)", "19.666581156998216\n[-1.06446116e-01 5.61459693e-02 3.47899554e-02 2.16209691e+00\n -1.84908000e+01 3.27759494e+00 7.04083277e-03 -1.53412749e+00\n 3.22856037e-01 -1.21758363e-02 -9.42201760e-01 9.53050841e-03\n -5.86782791e-01]\n" ] ] ]

[ "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ] ]

cb2f9c76b8af7c5856c5624d554f97e61bc04215

26,532

ipynb

Jupyter Notebook

docs/tutorials/10_checkpointer_policysaver_tutorial.ipynb

lucifer2288/agents

63a8ea8ea9095cb9ab9f7c9fcf3aa2f9ac5fa280

[ "Apache-2.0" ]

null

docs/tutorials/10_checkpointer_policysaver_tutorial.ipynb

lucifer2288/agents

63a8ea8ea9095cb9ab9f7c9fcf3aa2f9ac5fa280

[ "Apache-2.0" ]

null

docs/tutorials/10_checkpointer_policysaver_tutorial.ipynb

lucifer2288/agents

63a8ea8ea9095cb9ab9f7c9fcf3aa2f9ac5fa280

[ "Apache-2.0" ]

null

29.912063

267

0.51779

[ [ [ "##### Copyright 2019 The TF-Agents Authors.\n", "_____no_output_____" ] ], [ [ "#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n# you may not use this file except in compliance with the License.\n# You may obtain a copy of the License at\n#\n# https://www.apache.org/licenses/LICENSE-2.0\n#\n# Unless required by applicable law or agreed to in writing, software\n# distributed under the License is distributed on an \"AS IS\" BASIS,\n# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n# See the License for the specific language governing permissions and\n# limitations under the License.", "_____no_output_____" ] ], [ [ "### Checkpointer and PolicySaver\n\n<table class=\"tfo-notebook-buttons\" align=\"left\">\n <td>\n <a target=\"_blank\" href=\"https://www.tensorflow.org/agents/tutorials/10_checkpointer_policysaver_tutorial\">\n <img src=\"https://www.tensorflow.org/images/tf_logo_32px.png\" />\n View on TensorFlow.org</a>\n </td>\n <td>\n <a target=\"_blank\" href=\"https://colab.research.google.com/github/tensorflow/agents/blob/master/docs/tutorials/10_checkpointer_policysaver_tutorial.ipynb\">\n <img src=\"https://www.tensorflow.org/images/colab_logo_32px.png\" />\n Run in Google Colab</a>\n </td>\n <td>\n <a target=\"_blank\" href=\"https://github.com/tensorflow/agents/blob/master/docs/tutorials/10_checkpointer_policysaver_tutorial.ipynb\">\n <img src=\"https://www.tensorflow.org/images/GitHub-Mark-32px.png\" />\n View source on GitHub</a>\n </td>\n <td>\n <a href=\"https://storage.googleapis.com/tensorflow_docs/agents/docs/tutorials/10_checkpointer_policysaver_tutorial.ipynb\"><img src=\"https://www.tensorflow.org/images/download_logo_32px.png\" />Download notebook</a>\n </td>\n</table>", "_____no_output_____" ], [ "## Introduction\n\n`tf_agents.utils.common.Checkpointer` is a utility to save/load the training state, policy state, and replay_buffer state to/from a local storage.\n\n`tf_agents.policies.policy_saver.PolicySaver` is a tool to save/load only the policy, and is lighter than `Checkpointer`. You can use `PolicySaver` to deploy the model as well without any knowledge of the code that created the policy.\n\nIn this tutorial, we will use DQN to train a model, then use `Checkpointer` and `PolicySaver` to show how we can store and load the states and model in an interactive way. Note that we will use TF2.0's new saved_model tooling and format for `PolicySaver`.\n", "_____no_output_____" ], [ "## Setup", "_____no_output_____" ], [ " If you haven't installed the following dependencies, run:", "_____no_output_____" ] ], [ [ "#@test {\"skip\": true}\n!sudo apt-get install -y xvfb ffmpeg\n!pip install 'gym==0.10.11'\n!pip install 'imageio==2.4.0'\n!pip install 'pyglet==1.3.2'\n!pip install 'xvfbwrapper==0.2.9'\n!pip install tf-agents", "_____no_output_____" ], [ "from __future__ import absolute_import\nfrom __future__ import division\nfrom __future__ import print_function\n\nimport base64\nimport imageio\nimport io\nimport matplotlib\nimport matplotlib.pyplot as plt\nimport os\nimport shutil\nimport tempfile\nimport tensorflow as tf\nimport zipfile\nimport IPython\n\ntry:\n from google.colab import files\nexcept ImportError:\n files = None\nfrom tf_agents.agents.dqn import dqn_agent\nfrom tf_agents.drivers import dynamic_step_driver\nfrom tf_agents.environments import suite_gym\nfrom tf_agents.environments import tf_py_environment\nfrom tf_agents.eval import metric_utils\nfrom tf_agents.metrics import tf_metrics\nfrom tf_agents.networks import q_network\nfrom tf_agents.policies import policy_saver\nfrom tf_agents.policies import py_tf_eager_policy\nfrom tf_agents.policies import random_tf_policy\nfrom tf_agents.replay_buffers import tf_uniform_replay_buffer\nfrom tf_agents.trajectories import trajectory\nfrom tf_agents.utils import common\n\ntf.compat.v1.enable_v2_behavior()\n\ntempdir = os.getenv(\"TEST_TMPDIR\", tempfile.gettempdir())", "_____no_output_____" ], [ "#@test {\"skip\": true}\n# Set up a virtual display for rendering OpenAI gym environments.\nimport xvfbwrapper\nxvfbwrapper.Xvfb(1400, 900, 24).start()", "_____no_output_____" ] ], [ [ "## DQN agent\nWe are going to set up DQN agent, just like in the previous colab. The details are hidden by default as they are not core part of this colab, but you can click on 'SHOW CODE' to see the details.", "_____no_output_____" ], [ "### Hyperparameters", "_____no_output_____" ] ], [ [ "env_name = \"CartPole-v1\"\n\ncollect_steps_per_iteration = 100\nreplay_buffer_capacity = 100000\n\nfc_layer_params = (100,)\n\nbatch_size = 64\nlearning_rate = 1e-3\nlog_interval = 5\n\nnum_eval_episodes = 10\neval_interval = 1000", "_____no_output_____" ] ], [ [ "### Environment", "_____no_output_____" ] ], [ [ "train_py_env = suite_gym.load(env_name)\neval_py_env = suite_gym.load(env_name)\n\ntrain_env = tf_py_environment.TFPyEnvironment(train_py_env)\neval_env = tf_py_environment.TFPyEnvironment(eval_py_env)", "_____no_output_____" ] ], [ [ "### Agent", "_____no_output_____" ] ], [ [ "#@title\nq_net = q_network.QNetwork(\n train_env.observation_spec(),\n train_env.action_spec(),\n fc_layer_params=fc_layer_params)\n\noptimizer = tf.compat.v1.train.AdamOptimizer(learning_rate=learning_rate)\n\nglobal_step = tf.compat.v1.train.get_or_create_global_step()\n\nagent = dqn_agent.DqnAgent(\n train_env.time_step_spec(),\n train_env.action_spec(),\n q_network=q_net,\n optimizer=optimizer,\n td_errors_loss_fn=common.element_wise_squared_loss,\n train_step_counter=global_step)\nagent.initialize()", "_____no_output_____" ] ], [ [ "### Data Collection", "_____no_output_____" ] ], [ [ "#@title\nreplay_buffer = tf_uniform_replay_buffer.TFUniformReplayBuffer(\n data_spec=agent.collect_data_spec,\n batch_size=train_env.batch_size,\n max_length=replay_buffer_capacity)\n\ncollect_driver = dynamic_step_driver.DynamicStepDriver(\n train_env,\n agent.collect_policy,\n observers=[replay_buffer.add_batch],\n num_steps=collect_steps_per_iteration)\n\n# Initial data collection\ncollect_driver.run()\n\n# Dataset generates trajectories with shape [BxTx...] where\n# T = n_step_update + 1.\ndataset = replay_buffer.as_dataset(\n num_parallel_calls=3, sample_batch_size=batch_size,\n num_steps=2).prefetch(3)\n\niterator = iter(dataset)", "_____no_output_____" ] ], [ [ "### Train the agent", "_____no_output_____" ] ], [ [ "#@title\n# (Optional) Optimize by wrapping some of the code in a graph using TF function.\nagent.train = common.function(agent.train)\n\ndef train_one_iteration():\n\n # Collect a few steps using collect_policy and save to the replay buffer.\n collect_driver.run()\n\n # Sample a batch of data from the buffer and update the agent's network.\n experience, unused_info = next(iterator)\n train_loss = agent.train(experience)\n\n iteration = agent.train_step_counter.numpy()\n print ('iteration: {0} loss: {1}'.format(iteration, train_loss.loss))", "_____no_output_____" ] ], [ [ "### Video Generation", "_____no_output_____" ] ], [ [ "#@title\ndef embed_gif(gif_buffer):\n \"\"\"Embeds a gif file in the notebook.\"\"\"\n tag = '<img src=\"data:image/gif;base64,{0}\"/>'.format(base64.b64encode(gif_buffer).decode())\n return IPython.display.HTML(tag)\n\ndef run_episodes_and_create_video(policy, eval_tf_env, eval_py_env):\n num_episodes = 3\n frames = []\n for _ in range(num_episodes):\n time_step = eval_tf_env.reset()\n frames.append(eval_py_env.render())\n while not time_step.is_last():\n action_step = policy.action(time_step)\n time_step = eval_tf_env.step(action_step.action)\n frames.append(eval_py_env.render())\n gif_file = io.BytesIO()\n imageio.mimsave(gif_file, frames, format='gif', fps=60)\n IPython.display.display(embed_gif(gif_file.getvalue()))", "_____no_output_____" ] ], [ [ "### Generate a video\nCheck the performance of the policy by generating a video.", "_____no_output_____" ] ], [ [ "print ('global_step:')\nprint (global_step)\nrun_episodes_and_create_video(agent.policy, eval_env, eval_py_env)", "_____no_output_____" ] ], [ [ "## Setup Checkpointer and PolicySaver\n\nNow we are ready to use Checkpointer and PolicySaver.", "_____no_output_____" ], [ "### Checkpointer\n", "_____no_output_____" ] ], [ [ "checkpoint_dir = os.path.join(tempdir, 'checkpoint')\ntrain_checkpointer = common.Checkpointer(\n ckpt_dir=checkpoint_dir,\n max_to_keep=1,\n agent=agent,\n policy=agent.policy,\n replay_buffer=replay_buffer,\n global_step=global_step\n)", "_____no_output_____" ] ], [ [ "### Policy Saver", "_____no_output_____" ] ], [ [ "policy_dir = os.path.join(tempdir, 'policy')\ntf_policy_saver = policy_saver.PolicySaver(agent.policy)", "_____no_output_____" ] ], [ [ "### Train one iteration", "_____no_output_____" ] ], [ [ "#@test {\"skip\": true}\nprint('Training one iteration....')\ntrain_one_iteration()", "_____no_output_____" ] ], [ [ "### Save to checkpoint", "_____no_output_____" ] ], [ [ "train_checkpointer.save(global_step)", "_____no_output_____" ] ], [ [ "### Restore checkpoint\n\nFor this to work, the whole set of objects should be recreated the same way as when the checkpoint was created.", "_____no_output_____" ] ], [ [ "train_checkpointer.initialize_or_restore()\nglobal_step = tf.compat.v1.train.get_global_step()", "_____no_output_____" ] ], [ [ "Also save policy and export to a location", "_____no_output_____" ] ], [ [ "tf_policy_saver.save(policy_dir)", "_____no_output_____" ] ], [ [ "The policy can be loaded without having any knowledge of what agent or network was used to create it. This makes deployment of the policy much easier.\n\nLoad the saved policy and check how it performs", "_____no_output_____" ] ], [ [ "saved_policy = tf.compat.v2.saved_model.load(policy_dir)\nrun_episodes_and_create_video(saved_policy, eval_env, eval_py_env)", "_____no_output_____" ] ], [ [ "## Export and import\nThe rest of the colab will help you export / import checkpointer and policy directories such that you can continue training at a later point and deploy the model without having to train again.\n\nNow you can go back to 'Train one iteration' and train a few more times such that you can understand the difference later on. Once you start to see slightly better results, continue below.", "_____no_output_____" ] ], [ [ "#@title Create zip file and upload zip file (double-click to see the code)\ndef create_zip_file(dirname, base_filename):\n return shutil.make_archive(base_filename, 'zip', dirname)\n\ndef upload_and_unzip_file_to(dirname):\n if files is None:\n return\n uploaded = files.upload()\n for fn in uploaded.keys():\n print('User uploaded file \"{name}\" with length {length} bytes'.format(\n name=fn, length=len(uploaded[fn])))\n shutil.rmtree(dirname)\n zip_files = zipfile.ZipFile(io.BytesIO(uploaded[fn]), 'r')\n zip_files.extractall(dirname)\n zip_files.close()", "_____no_output_____" ] ], [ [ "Create a zipped file from the checkpoint directory.", "_____no_output_____" ] ], [ [ "train_checkpointer.save(global_step)\ncheckpoint_zip_filename = create_zip_file(checkpoint_dir, os.path.join(tempdir, 'exported_cp'))", "_____no_output_____" ] ], [ [ "Download the zip file.", "_____no_output_____" ] ], [ [ "#@test {\"skip\": true}\nif files is not None:\n files.download(checkpoint_zip_filename) # try again if this fails: https://github.com/googlecolab/colabtools/issues/469", "_____no_output_____" ] ], [ [ "After training for some time (10-15 times), download the checkpoint zip file,\nand go to \"Runtime > Restart and run all\" to reset the training,\nand come back to this cell. Now you can upload the downloaded zip file,\nand continue the training.", "_____no_output_____" ] ], [ [ "#@test {\"skip\": true}\nupload_and_unzip_file_to(checkpoint_dir)\ntrain_checkpointer.initialize_or_restore()\nglobal_step = tf.compat.v1.train.get_global_step()", "_____no_output_____" ] ], [ [ "Once you have uploaded checkpoint directory, go back to 'Train one iteration' to continue training or go back to 'Generate a video' to check the performance of the loaded poliicy.", "_____no_output_____" ], [ "Alternatively, you can save the policy (model) and restore it.\nUnlike checkpointer, you cannot continue with the training, but you can still deploy the model. Note that the downloaded file is much smaller than that of the checkpointer.", "_____no_output_____" ] ], [ [ "tf_policy_saver.save(policy_dir)\npolicy_zip_filename = create_zip_file(policy_dir, os.path.join(tempdir, 'exported_policy'))", "_____no_output_____" ], [ "#@test {\"skip\": true}\nif files is not None:\n files.download(policy_zip_filename) # try again if this fails: https://github.com/googlecolab/colabtools/issues/469", "_____no_output_____" ] ], [ [ "Upload the downloaded policy directory (exported_policy.zip) and check how the saved policy performs.", "_____no_output_____" ] ], [ [ "#@test {\"skip\": true}\nupload_and_unzip_file_to(policy_dir)\nsaved_policy = tf.compat.v2.saved_model.load(policy_dir)\nrun_episodes_and_create_video(saved_policy, eval_env, eval_py_env)\n", "_____no_output_____" ] ], [ [ "## SavedModelPyTFEagerPolicy\n\nIf you don't want to use TF policy, then you can also use the saved_model directly with the Python env through the use of `py_tf_eager_policy.SavedModelPyTFEagerPolicy`.\n\nNote that this only works when eager mode is enabled.", "_____no_output_____" ] ], [ [ "eager_py_policy = py_tf_eager_policy.SavedModelPyTFEagerPolicy(\n policy_dir, eval_py_env.time_step_spec(), eval_py_env.action_spec())\n\n# Note that we're passing eval_py_env not eval_env.\nrun_episodes_and_create_video(eager_py_policy, eval_py_env, eval_py_env)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2fa5b0083960921180c2274262539db9ab173f

328,477

ipynb

Jupyter Notebook

examples/quantum_annealing/Dwave_TravelingSalesmanProblem/Dwave_TravelingSalesmanProblem.ipynb

dumplingsforbreakfast/amazon-braket-examples

2efbc0a425d1b2a0ca3627ea94df9cc81ea638f2

[ "Apache-2.0" ]

null

examples/quantum_annealing/Dwave_TravelingSalesmanProblem/Dwave_TravelingSalesmanProblem.ipynb

dumplingsforbreakfast/amazon-braket-examples

2efbc0a425d1b2a0ca3627ea94df9cc81ea638f2

[ "Apache-2.0" ]

null

examples/quantum_annealing/Dwave_TravelingSalesmanProblem/Dwave_TravelingSalesmanProblem.ipynb

dumplingsforbreakfast/amazon-braket-examples

2efbc0a425d1b2a0ca3627ea94df9cc81ea638f2

[ "Apache-2.0" ]

null

197.639591

143,388

0.894467

[ [ [ "# TUTORIAL FOR TRAVELING SALESMAN PROBLEM", "_____no_output_____" ], [ "__Introduction__: The famous travelling salesman problem (also called the travelling salesperson problem or in short TSP) is a well-known NP-hard problem in combinatorial optimization, asking for the shortest possible route that visits each city exactly once, given a list of cities and the distances between each pair of cities [1]. \nApplications of the TSP can be found in planning, logistics, and the manufacture of microchips. \nIn these applications, the general concept of a city represents, for example, customers, or points on a chip. \n\n__Methods__: Using brute-force search one could try all permutations (ordered combinations) and see which one is cheapest. \nThe running time for this approach, however, lies within a polynomial factor of $O(n!)$, the factorial of the number of cities $n$. \nThus, this solution becomes impractical already for only $\\sim 20$ cities. \nStill, many heuristics are known, and some instances with tens of thousands of cities can be solved completely [1]. \nIn this hello-world tutorial we will solve small instances of the TSP with one particular approach, that is simulated annealing and quantum annealing, as made available with D-Wave on Amazon Braket. \nSpecifically, we will leverage two different quantum devices made available through Amazon Braket, namely D-Wave's 2000Q QPU (with 2000 qubits and 6000 couplers) and D-Wave's Advantage QPU (with more than 5000 qubits and more than 35,000 couplers). \n\n__TSP as graph problem__: \nThe solution to the TSP can be viewed as a specific ordering of the vertices in a weighted graph.\nTaking an undirected weighted graph, cities correspond to the graph's nodes, with paths corresponding to the graph's edges, and a path's distance is the edge's weight. \nTypically, the graph is complete where each pair of nodes is connected by an edge. \nIf no connection exists between two cities, one can add an arbitrarily long edge to complete the graph without affecting the optimal tour [1].\nThe goal is then to find a Hamiltonian cycle with the least weight. \nWe will provide figures for visualization below. \n\n__Binary encoding__: To solve the TSP with (quantum) annealing we need to formulate the TSP as a QUBO problem of the general form \n\n$$\n\\mathrm{min} \\hspace{0.1cm} y=x^{\\intercal}Qx + x^{\\intercal}B + c,\n$$ \n\nwhere $x=(x_{1}, x_{2}, \\dots)$ is a vector of binary decision variables $x_{i}=0,1$. \nTo this end, here we introduce double-indexed binary variables $x_{i,j}$ with $x_{i,j}=1$ if city $i$is located at position $j$ in the cycle and $x_{i,j}=0$ otherwise. \nConsider for example three cities: New York indexed with $i=0$, Los Angeles ($i=1$), and Chicago ($i=2$). \nThen, $x_{0,0}=x_{1,2}=x_{2,1}=1$ means that we visit these cities in the order New York - Chicago - Los Angeles. \nWith this encoding $x_{i,j}$ with $i=0,\\dots, N-1$ and $j=0,\\dots, N-1$ in total we deal with $N^2$ binary variables for a problem with $N$ cities (nodes in the graph), causing a quadratic overhead. \n\nOur goal is then to find the Hamiltonian cycle with the shortest length, as described by the following objective function\n\n$$\nH_{\\mathrm{dist}} = \\sum_{i,j} D_{i,j} \\sum_{k} x_{i,k}x_{j,k+1},\n$$\n\nwith $D_{i,j}$ being the distance between city $i$ and city $j$. Note that the product $x_{i,k}x_{j,k+1}=1$, only if city $i$ is at position $k$ in the cycle and city $j$ is visited right after city $i$; in that case we add the distance $D_{i,j}$ to our objective function which we would like to minimize. \nOverall, we sum all costs of the distances between successive cities. \n\nFinally, we need to account for the following constraints: \n(i) First, each city should occur exactly once in the cycle. This can be written as: \n$$\n\\sum_{j=0}^{N-1} x_{i,j}=1 \\hspace{0.5cm} \\forall i=0,...,N-1.\n$$\n(ii) Second, each position in the cycle should be assigned to exactly one city. Mathematically this means:\n$$\n\\sum_{i=0}^{N-1} x_{i,j}=1 \\hspace{0.5cm} \\forall j=0,...,N-1.\n$$\n\nFor illustration a valid solution for $N=4$ for the route $[1,3,2,4]$ could look as follows (note that every row and column sums up to one, as desired):\n\n<div>\n<img src=\"attachment:image.png\" width=\"300\"/>\n</div>\n\nTo enforce solutions that satisfy these constraints we add the following penalty terms to our Hamiltonian\n\n$$\nH_{\\mathrm{constraint}} = P \\sum_{i=0}^{N-1} \\left(1-\\sum_{j=0}^{N-1} x_{i,j}\\right)^{2} + P \\sum_{j=0}^{N-1} \\left(1-\\sum_{i=0}^{N-1} x_{i,j}\\right)^{2}\n$$\n\nWith these terms we enforce solutions where every city is visited exactly once as part of the tour. \nOtherwise, a high penalty value $P$ would be added to the solution, making it unfavorable. \nFor simplicity we use the same penalty parameter $P$ for the two types of constraints covered in $H_{\\mathrm{constraint}}$. \n\nThe total Hamiltonian for the TSP problem then reads\n\n$$\nH = H_{\\mathrm{dist}} + H_{\\mathrm{constraint}}.\n$$\n\nWe will perform hyperparameter optimization on the penalty parameter $P$ in order to find a good solution that complies with the constraints outlined above. \nIf $P$ is not chosen properly it is possible that the algorithm provides solutions that are not acceptable, for example routes that do not cover all cities or routes that visit some cities multiple times. \nIn our code below we apply simple heuristic postprocessing steps to account for these issues. ", "_____no_output_____" ], [ "## IMPORTS AND SETUP", "_____no_output_____" ] ], [ [ "!pip install pandas -q", "_____no_output_____" ], [ "import boto3\nfrom braket.aws import AwsDevice\nfrom braket.ocean_plugin import BraketSampler, BraketDWaveSampler", "_____no_output_____" ], [ "import numpy as np\nimport networkx as nx\nimport dimod\nimport dwave_networkx as dnx\nfrom dimod.binary_quadratic_model import BinaryQuadraticModel\nfrom dwave.system.composites import EmbeddingComposite\nimport matplotlib.pyplot as plt\n# magic word for producing visualizations in notebook\n%matplotlib inline\nfrom collections import defaultdict\nimport itertools\nimport pandas as pd", "_____no_output_____" ], [ "# local imports\nfrom utils_tsp import get_distance, traveling_salesperson\n\n%load_ext autoreload\n%autoreload 2", "_____no_output_____" ], [ "# Please enter the S3 bucket you created during onboarding in the code below\nmy_bucket = f\"amazon-braket-Your-Bucket-Name\" # the name of the bucket\nmy_prefix = \"Your-Folder-Name\" # the name of the folder in the bucket\ns3_folder = (my_bucket, my_prefix)", "_____no_output_____" ], [ "# fix random seed for reproducibility\nseed = 1\nnp.random.seed(seed)", "_____no_output_____" ] ], [ [ "## IMPORT DATASET", "_____no_output_____" ], [ "Sample datasets for TSP are available [here](https://people.sc.fsu.edu/~jburkardt/datasets/tsp/tsp.html).\nHere, we start with a very small dataset comprising five cities only. \nThe minimal tour is known to have length 19.", "_____no_output_____" ] ], [ [ "# load dataset\ndata = pd.read_csv('tsp_data/five_d.txt', sep='\\s+', header=None)", "_____no_output_____" ], [ "# show data set for inter-city distances\ndata", "_____no_output_____" ], [ "# distance between two example cities\nidx_city1 = 0\nidx_city2 = 1\ndistance = data[idx_city1][idx_city2]\nprint('Distance between city {} and city {} is {}.'.format(idx_city1, idx_city2, distance))", "Distance between city 0 and city 1 is 3.0.\n" ], [ "# get number of cities\nnumber_cities = data.shape[0]\nprint('Total number of cities:', number_cities)", "Total number of cities: 5\n" ] ], [ [ "## SET UP GRAPH", "_____no_output_____" ], [ "We can generate ```networkx``` graphs from ```pandas``` data frames, as explained [here](https://networkx.github.io/documentation/stable/reference/convert.html#pandas) and in particular [here](https://networkx.github.io/documentation/stable/reference/generated/networkx.convert_matrix.from_pandas_adjacency.html?highlight=from%20pandas#networkx.convert_matrix.from_pandas_adjacency).", "_____no_output_____" ] ], [ [ "# G = nx.from_pandas_dataframe(data) \nG = nx.from_pandas_adjacency(data)\n# pos = nx.random_layout(G) \npos = nx.spring_layout(G, seed=seed)\n\n# get characteristics of graph\nnodes = G.nodes()\nedges = G.edges()\nweights = nx.get_edge_attributes(G,'weight');", "_____no_output_____" ], [ "# print weights of graph\nprint('Weights of graph:', weights)", "Weights of graph: {(0, 1): 3.0, (0, 2): 4.0, (0, 3): 2.0, (0, 4): 7.0, (1, 2): 4.0, (1, 3): 6.0, (1, 4): 3.0, (2, 3): 5.0, (2, 4): 8.0, (3, 4): 6.0}\n" ], [ "# show graph with weigths\nplt.axis('off'); \nnx.draw_networkx(G, pos, with_labels=True);\nnx.draw_networkx_edge_labels(G, pos, edge_labels=weights);", "_____no_output_____" ] ], [ [ "The weights of this fully-connected graph correspond to the distances between the cities. ", "_____no_output_____" ], [ "## QUBO FOR TSP", "_____no_output_____" ], [ "We can get the QUBO matrix using the ```traveling_salesperson_qubo``` method as described [here](https://docs.ocean.dwavesys.com/projects/dwave-networkx/en/latest/reference/algorithms/generated/dwave_networkx.algorithms.tsp.traveling_salesperson_qubo.html#dwave_networkx.algorithms.tsp.traveling_salesperson_qubo).\nThis method will return the QUBO with ground states corresponding to a minimum TSP route.\nHere, if $|G|$ is the number of nodes (cities) in the original graph, the resulting QUBO will have $|G|^2$ variables/nodes\nand $|G|^2(|G|^2-1)/2$ edges. \nThere is a quadratic overhead because of the binary encoding $x_{i,j}=1$ if city $i$ is at position $j$ on the route and zero otherwise. \nThe Lagrange penalty parameter enforces the constraints that every city should be visited exactly once in our route (i.e., we do not leave out any city and we do not visit cities multiple times). \nAs this parameter can be tuned we will run hyperparameter optimization (HPO) to find a good value for this hyperparameter. ", "_____no_output_____" ] ], [ [ "# get QUBO for TSP\ntsp_qubo = dnx.algorithms.tsp.traveling_salesperson_qubo(G)", "_____no_output_____" ], [ "# find default Langrange parameter for enforcing constraints\n\n# set parameters\nlagrange = None\nweight='weight'\n\n# get corresponding QUBO step by step\nN = G.number_of_nodes()\n\nif lagrange is None:\n # If no lagrange parameter provided, set to 'average' tour length.\n # Usually a good estimate for a lagrange parameter is between 75-150%\n # of the objective function value, so we come up with an estimate for \n # tour length and use that.\n if G.number_of_edges()>0:\n lagrange = G.size(weight=weight)*G.number_of_nodes()/G.number_of_edges()\n else:\n lagrange = 2\n\nprint('Default Lagrange parameter:', lagrange) ", "Default Lagrange parameter: 24.0\n" ], [ "# create list around default value for HPO \nlagrange_list= list(np.arange(int(0.8*lagrange), int(1.1*lagrange)))\nprint('Lagrange parameter for HPO:', lagrange_list)", "Lagrange parameter for HPO: [19, 20, 21, 22, 23, 24, 25]\n" ] ], [ [ "## SOLUTION WITH SIMULATED ANNEALING", "_____no_output_____" ], [ "First let us solve the TSP problem with classical simulated annealing.\nTo this end we can simply call the built-in ```traveling_salesperson(...)``` routine from the ```dwave_networkx``` package using the ```SimulatedAnnealingSampler``` sampler as provided in the standard Ocean tool suite. ", "_____no_output_____" ] ], [ [ "# use (classical) simulated annealing\nsampler = dimod.SimulatedAnnealingSampler()\n# route = dnx.traveling_salesperson(G, dimod.ExactSolver(), start=0)\nroute = dnx.traveling_salesperson(G, sampler, start=0)\nprint('Route found with simulated annealing:', route)", "Route found with simulated annealing: [0, 3, 4, 1, 2]\n" ], [ "# get the total distance\ntotal_dist = 0\nfor idx, node in enumerate(route[:-1]):\n dist = data[route[idx+1]][route[idx]]\n total_dist += dist\n\nprint('Total distance (without return):', total_dist)", "Total distance (without return): 15.0\n" ], [ "# add distance between start and end point to complete cycle\nreturn_distance = data[route[0]][route[-1]]\nprint('Distance between start and end:', return_distance)", "Distance between start and end: 4.0\n" ], [ "# get distance for full cyle \ndistance = total_dist + return_distance\nprint('Total distance (including return):', distance)", "Total distance (including return): 19.0\n" ] ], [ [ "## SOLUTION WITH QUANTUM ANNEALING ON D-WAVE WITH HPO FOR LAGRANGE PARAMETER", "_____no_output_____" ], [ "Now let us run the TSP problem on D-Wave's 2000Q QPU, together with hyperparameter optimization for the Langrange parameter.\nTo this end, we augment the ```traveling_salesperson(...)``` routine with post-processing heuristics that correct for invalid solutions if some cities are not present in the sample produced by D-Wave or if some cities are duplicates in the route. \nThe original source code for ```traveling_salesperson(...)``` can be found in the Appendix. ", "_____no_output_____" ] ], [ [ "# run TSP with imported TSP routine\nsampler = BraketDWaveSampler(s3_folder,'arn:aws:braket:::device/qpu/d-wave/DW_2000Q_6')\nsampler = EmbeddingComposite(sampler)\n\n# set parameters\nnum_shots = 1000\nstart_city = 0\nbest_distance = sum(weights.values())\nbest_route = [None]*len(G)\n\n# run HPO to find route\nfor lagrange in lagrange_list:\n print('Running quantum annealing for TSP with Lagrange parameter=', lagrange)\n route = traveling_salesperson(G, sampler, lagrange=lagrange, \n start=start_city, num_reads=num_shots, answer_mode=\"histogram\")\n # print route \n print('Route found with D-Wave:', route)\n \n # print distance\n total_dist, distance_with_return = get_distance(route, data)\n \n # update best values\n if distance_with_return < best_distance:\n best_distance = distance_with_return\n best_route = route\n\nprint('---FINAL SOLUTION---')\nprint('Best solution found with D-Wave:', best_route)\nprint('Total distance (including return):', best_distance)", "Running quantum annealing for TSP with Langrgange parameter= 19\nRoute found with D-Wave: [0, 2, 1, 4, 3]\nTotal distance (without return): 17.0\nTotal distance (including return): 19.0\nRunning quantum annealing for TSP with Langrgange parameter= 20\nRoute found with D-Wave: [0, 3, 4, 1, 2]\nTotal distance (without return): 15.0\nTotal distance (including return): 19.0\nRunning quantum annealing for TSP with Langrgange parameter= 21\nRoute found with D-Wave: [0, 3, 4, 1, 2]\nTotal distance (without return): 15.0\nTotal distance (including return): 19.0\nRunning quantum annealing for TSP with Langrgange parameter= 22\nRoute found with D-Wave: [0, 3, 4, 1, 2]\nTotal distance (without return): 15.0\nTotal distance (including return): 19.0\nRunning quantum annealing for TSP with Langrgange parameter= 23\nRoute found with D-Wave: [0, 2, 1, 4, 3]\nTotal distance (without return): 17.0\nTotal distance (including return): 19.0\nRunning quantum annealing for TSP with Langrgange parameter= 24\nRoute found with D-Wave: [0, 2, 1, 4, 3]\nTotal distance (without return): 17.0\nTotal distance (including return): 19.0\nRunning quantum annealing for TSP with Langrgange parameter= 25\nRoute found with D-Wave: [0, 3, 4, 1, 2]\nTotal distance (without return): 15.0\nTotal distance (including return): 19.0\n---FINAL SOLUTION---\nBest solution found with D-Wave: [0, 2, 1, 4, 3]\nTotal distance (including return): 19.0\n" ] ], [ [ "Now let us visualize the solution found by the D-Wave QPU. \nFirst we plot again the original graph with nodes representing cities and weighted edges representing distances between the cities. \nIt is a complete graph showing the distance for every pair of cities. \nThen, we plot below the graph showing the proposed route, with steps labelling the specific sequence connecting the individual stops on the route. ", "_____no_output_____" ] ], [ [ "# show original graph with weigths\nplt.axis('off'); \nnx.draw_networkx(G, pos, with_labels=True, font_color='w');\nnx.draw_networkx_edge_labels(G, pos, edge_labels=weights);", "_____no_output_____" ], [ "# get mapping from original nodes to position in cycle\nnode_labels = {list(nodes)[ii]: best_route[ii] for ii in range(number_cities)}", "_____no_output_____" ], [ "# Construct route as list of (node_i, node_i+1)\nsol_graph_base = [(best_route[idx], best_route[idx+1]) for idx in range(len(best_route)-1)]\n# Establish weights between nodes along route, allowing for mirrored keys (i.e. weights[(0, 1)] = weights[(1, 0)])\nbest_weights = {k: weights[k] if k in weights.keys() else weights[(k[1],k[0])] for k in sol_graph_base}\n# Rebuild graph containing only route connections\nG_best = nx.Graph(sol_graph_base)\n\nroute_labels = {x: f'step_{i}={best_weights[x]}' for i, x in enumerate(sol_graph_base)}", "_____no_output_____" ], [ "# show solution\nplt.axis('off'); \nnx.draw_networkx(G_best, pos, font_color='w');\nnx.draw_networkx_edge_labels(G_best, pos, edge_labels=route_labels, label_pos=0.25);", "_____no_output_____" ] ], [ [ "In conclusion, in this part of our tutorial we have solved a very small instance of the famous NP-hard TSP problem using both (classical) simulated annealing and quantum annealing using D-Wave's Ocean tool suite that is natively supported on Amazon Braket. \nWhile there are classical methods that can solve this problem very efficiently, at least to a very good approximation, this is an educational tutorial focused on the formulation of a specific QUBO problem and the approximate solution thereof using (quantum) annealing methods. \nBelow we extend our analysis to larger problem sizes that cannot be embedded on the 2000Q D-Wave chip with Chimera connectivity, but can be run on the larger Advantage chip with $\\sim 5000$ physical variables and Pegasus connectivity. ", "_____no_output_____" ], [ "## LARGER TSP PROBLEM ON D-WAVE ADVANTAGE CHIP", "_____no_output_____" ], [ "Next we run a larger problem instance of TSP on D-Wave's Advantage chip with over 5000 physical qubits and Pegasus connectivity graph. \nWe take a dataset comprising ten cities; we have taken the original data set with 15 cities from [here](https://people.sc.fsu.edu/~jburkardt/datasets/tsp/tsp.html) and cut it down to a smaller dataset containing only the first ten cities. \nFirst let us load and inspect the data set for the inter-city distances. ", "_____no_output_____" ] ], [ [ "# load dataset\ndata10 = pd.read_csv('tsp_data/data10cities.csv')\n# rename columns from object to int \ndic_map = {}\nfor key in data10.columns:\n d = {key: int(key)}\n dic_map.update(d)\ndata10 = data10.rename(columns=dic_map)\n# show data set for inter-city distances\ndata10", "_____no_output_____" ] ], [ [ "Next, using the ```networkx``` library again we display this problem as a complete graph with a single node per city and weighted edges specifying the intercity distances. ", "_____no_output_____" ] ], [ [ "# G = nx.from_pandas_dataframe(data) \nG = nx.from_pandas_adjacency(data10)\n# pos = nx.random_layout(G) \npos = nx.spring_layout(G, seed=seed)\n\n# get characteristics of graph\nnodes = G.nodes()\nedges = G.edges()\nweights = nx.get_edge_attributes(G,'weight');\n\n# show graph with weigths\nplt.figure(figsize=(10,10))\nplt.axis('off'); \nnx.draw_networkx(G, pos, with_labels=True);\nnx.draw_networkx_edge_labels(G, pos, edge_labels=weights, label_pos=0.25);", "_____no_output_____" ] ], [ [ "Now that the problem is set up as a graph problem, we first use classical simulated annealing to easily build a classical benchmark, using the ```SimulatedAnnealingSampler``` that comes out of the box with the ```dimod``` library. ", "_____no_output_____" ] ], [ [ "# use (classical) simulated annealing\nsampler = dimod.SimulatedAnnealingSampler()\n# route = dnx.traveling_salesperson(G, dimod.ExactSolver(), start=0)\nroute = dnx.traveling_salesperson(G, sampler, start=0)\nprint('Route found with simulated annealing:', route)", "Route found with simulated annealing: [0, 7, 9, 3, 5, 1, 6, 8, 2, 4]\n" ], [ "# print distance\ntotal_dist, distance_with_return = get_distance(route, data10)", "Total distance (without return): 310\nTotal distance (including return): 378\n" ] ], [ [ "Below again we will run HPO to try several numerical values for the hyperparameter $P$ enforcing the constraints within the cost function.\nTo this end we first set up a list of parameters to loop over later in our simulation routine. ", "_____no_output_____" ] ], [ [ "# find default Langrange parameter for enforcing constraints\n\n# set parameters\nlagrange = None\nweight='weight'\n\n# get corresponding QUBO step by step\nN = G.number_of_nodes()\n\nif lagrange is None:\n # If no lagrange parameter provided, set to 'average' tour length.\n # Usually a good estimate for a lagrange parameter is between 75-150%\n # of the objective function value, so we come up with an estimate for \n # tour length and use that.\n if G.number_of_edges()>0:\n lagrange = G.size(weight=weight)*G.number_of_nodes()/G.number_of_edges()\n else:\n lagrange = 2\n\nprint('Default Lagrange parameter:', lagrange) ", "Default Lagrange parameter: 438.0\n" ], [ "# create list around default value for HPO \n# lagrange_list= list(np.arange(int(0.99*lagrange), int(1.01*lagrange)))\nlagrange_list= [int(lagrange)-10, int(lagrange), int(lagrange)+10]\nprint('Lagrange parameter for HPO:', lagrange_list)", "Lagrange parameter for HPO: [428, 438, 448]\n" ] ], [ [ "Next, we try to run this problem on D-Wave's 2000Q backend with Chimera connectivity. \nHere, we will run into an ```ValueError: no embedding found```, because a problem with 10 cities results in a fully-connected problem with 100 logical variables. \nThis problem size cannot be embedded onto the sparse Chimera graph with $\\sim 2000$ physical qubits. \nTherefore we will try to run the same problem on the larger Advantage chip below. ", "_____no_output_____" ] ], [ [ "# run TSP on 2000Q chip\nsampler = BraketDWaveSampler(s3_folder,'arn:aws:braket:::device/qpu/d-wave/DW_2000Q_6')\nsampler = EmbeddingComposite(sampler)\n\n# set parameters\nnum_shots = 1000\nstart_city = 0\n\ntry: \n print('Running quantum annealing for TSP with Lagrange parameter=', lagrange)\n route = traveling_salesperson(G, sampler, lagrange=lagrange_list[0], \n start=start_city, num_reads=num_shots, answer_mode=\"histogram\")\n # print route \n print('Route found with D-Wave:', route)\nexcept ValueError:\n print(\"ValueError: no embedding found. This problem is too large to be embedded on the 2000Q chip.\")", "Running quantum annealing for TSP with Langrgange parameter= 438.0\nValueError: no embedding found. This problem is too large to be embedded on the 2000Q chip.\n" ] ], [ [ "Next we simply switch to the D-Wave's Advantage chip with over 5000 physical qubits and Pegasus connectivity graph. \nThis switch amounts to changing one line of code. ", "_____no_output_____" ] ], [ [ "# run TSP on Advantage chip\nsampler = BraketDWaveSampler(s3_folder,'arn:aws:braket:::device/qpu/d-wave/Advantage_system4')\nsampler = EmbeddingComposite(sampler)\n\n# set parameters\nnum_shots = 1000\nstart_city = 0\nbest_distance = sum(weights.values())\nbest_route = [None]*len(G)\n\n# run HPO to find route\nfor lagrange in lagrange_list:\n print('Running quantum annealing for TSP with Lagrange parameter=', lagrange)\n route = traveling_salesperson(G, sampler, lagrange=lagrange, \n start=start_city, num_reads=num_shots, answer_mode=\"histogram\")\n # print route \n print('Route found with D-Wave:', route)\n \n # print distance\n total_dist, distance_with_return = get_distance(route, data10)\n \n # update best values\n if distance_with_return < best_distance:\n best_distance = distance_with_return\n best_route = route\n\nprint('---FINAL SOLUTION---')\nprint('Best solution found with D-Wave:', best_route)\nprint('Total distance (including return):', best_distance)", "Running quantum annealing for TSP with Langrgange parameter= 428\nRoute found with D-Wave: [0, 1, 7, 2, 6, 4, 5, 8, 9, 3]\nTotal distance (without return): 341\nTotal distance (including return): 387\nRunning quantum annealing for TSP with Langrgange parameter= 438\nRoute found with D-Wave: [0, 2, 1, 9, 5, 7, 3, 4, 8, 6]\nTotal distance (without return): 379\nTotal distance (including return): 451\nRunning quantum annealing for TSP with Langrgange parameter= 448\nRoute found with D-Wave: [0, 7, 2, 6, 4, 8, 1, 3, 9, 5]\nTotal distance (without return): 294\nTotal distance (including return): 346\n---FINAL SOLUTION---\nBest solution found with D-Wave: [0, 7, 2, 6, 4, 8, 1, 3, 9, 5]\nTotal distance (including return): 346\n" ] ], [ [ "In conclusion in this tutorial we have mapped the canonical TSP to a QUBO problem using the Ocean tool suite that is natively supported on Amazon Braket. \nWe have used classical simulated annealing and quantum annealing to find solutions to this problem. \nSpecifically, we have seen that we can solve larger problem instances with the Advantage chip (that has more than 5000 qubits and more than 35,000 couplers) than what we could solve for using the previous-generation 2000Q QPU with roughly 2000 qubits and 6000 couplers. ", "_____no_output_____" ], [ "---\n## APPENDIX", "_____no_output_____" ], [ "### APPENDIX FOR HEURISTIC POSTPROCESSING", "_____no_output_____" ], [ "If there are cities unassigned to route, we just fill the route with these without optimization. \nFirst, we can take care of filling ```None``` values. ", "_____no_output_____" ] ], [ [ "# set example route\nroute = [None, 4, 0, 3, 1]\nprint('Original route:', route)\n# get lists with all cities\nlist_cities = list(nodes)\n# get not assigned cities\ncities_unassigned = [city for city in list_cities if city not in route] \n# fill None values\nfor idx, city in enumerate(route):\n if city == None:\n route[idx] = cities_unassigned[0]\n cities_unassigned.remove(route[idx])\nprint('Route after filling heuristic:', route)", "Original route: [None, 4, 0, 3, 1]\nRoute after filling heuristic: [2, 4, 0, 3, 1]\n" ], [ "# randomly permute\ncities_unassigned = [0, 4, 7]\nnp.random.permutation(cities_unassigned)", "_____no_output_____" ] ], [ [ "Second, we can still have proposed routes with cities appearing multiple times in exchange for some cities not visited at all. ", "_____no_output_____" ] ], [ [ "# set example route\nroute = [0, 2, 3, 4, 4]\nprint('Original route:', route)\nunique_entries = set(route)\nnumber_unique_entries = len(unique_entries)\nif number_unique_entries != len(route):\n print('Solution not valid.')\n# get unassigned cities\ncities_unassigned = [city for city in list_cities if city not in route]\nprint('Unassigned cities:', cities_unassigned)\n\n# replace duplicates\nroute_new = []\nfor city in route:\n if city not in route_new:\n route_new.append(city)\n else:\n route_new.append(cities_unassigned[0])\n cities_unassigned.remove(route_new[-1])\nprint('Route after heuristics:', route_new)", "Original route: [0, 2, 3, 4, 4]\nSolution not valid.\nUnassigned cities: [1, 5, 6, 7, 8, 9]\nRoute after heuristics: [0, 2, 3, 4, 1]\n" ], [ "# set example route\nroute = [0, 0, 1, 1, 1]\nprint('Original route:', route)\nunique_entries = set(route)\nnumber_unique_entries = len(unique_entries)\nif number_unique_entries != len(route):\n print('Solution not valid.')\n# get unassigned cities\ncities_unassigned = [city for city in list_cities if city not in route]\nprint('Unassigned cities:', cities_unassigned)\n\n# replace duplicates\nroute_new = []\nfor city in route:\n if city not in route_new:\n route_new.append(city)\n else:\n route_new.append(cities_unassigned[0])\n cities_unassigned.remove(route_new[-1])\nprint('Route after heuristics:', route_new)", "Original route: [0, 0, 1, 1, 1]\nSolution not valid.\nUnassigned cities: [2, 3, 4, 5, 6, 7, 8, 9]\nRoute after heuristics: [0, 2, 1, 3, 4]\n" ] ], [ [ "### APPENDIX: ORIGINAL SOURCE CODE WITH LINKS", "_____no_output_____" ], [ "Here we display the ocean source code used above for solving the TSP problem. \nWe show the code for both ```traveling_salesperson(...)``` taken from [here](https://docs.ocean.dwavesys.com/projects/dwave-networkx/en/latest/_modules/dwave_networkx/algorithms/tsp.html#traveling_salesperson) and ```traveling_salesperson_qubo(...)``` taken from [here](https://docs.ocean.dwavesys.com/projects/dwave-networkx/en/latest/_modules/dwave_networkx/algorithms/tsp.html#traveling_salesperson_qubo).", "_____no_output_____" ], [ "```python\n@binary_quadratic_model_sampler(1)\ndef traveling_salesperson(G, sampler=None, lagrange=None, weight='weight',\n start=None, **sampler_args):\n \"\"\"Returns an approximate minimum traveling salesperson route.\n\n Defines a QUBO with ground states corresponding to the\n minimum routes and uses the sampler to sample\n from it.\n\n A route is a cycle in the graph that reaches each node exactly once.\n A minimum route is a route with the smallest total edge weight.\n\n Parameters\n ----------\n G : NetworkX graph\n The graph on which to find a minimum traveling salesperson route.\n This should be a complete graph with non-zero weights on every edge.\n\n sampler :\n A binary quadratic model sampler. A sampler is a process that\n samples from low energy states in models defined by an Ising\n equation or a Quadratic Unconstrained Binary Optimization\n Problem (QUBO). A sampler is expected to have a 'sample_qubo'\n and 'sample_ising' method. A sampler is expected to return an\n iterable of samples, in order of increasing energy. If no\n sampler is provided, one must be provided using the\n `set_default_sampler` function.\n\n lagrange : number, optional (default None)\n Lagrange parameter to weight constraints (visit every city once)\n versus objective (shortest distance route).\n\n weight : optional (default 'weight')\n The name of the edge attribute containing the weight.\n\n start : node, optional\n If provided, the route will begin at `start`.\n\n sampler_args :\n Additional keyword parameters are passed to the sampler.\n\n Returns\n -------\n route : list\n List of nodes in order to be visited on a route\n\n Examples\n --------\n\n >>> import dimod\n ...\n >>> G = nx.Graph()\n >>> G.add_weighted_edges_from({(0, 1, .1), (0, 2, .5), (0, 3, .1), (1, 2, .1),\n ... (1, 3, .5), (2, 3, .1)})\n >>> dnx.traveling_salesperson(G, dimod.ExactSolver(), start=0) # doctest: +SKIP\n [0, 1, 2, 3]\n\n Notes\n -----\n Samplers by their nature may not return the optimal solution. This\n function does not attempt to confirm the quality of the returned\n sample.\n\n \"\"\"\n # Get a QUBO representation of the problem\n Q = traveling_salesperson_qubo(G, lagrange, weight)\n\n # use the sampler to find low energy states\n response = sampler.sample_qubo(Q, **sampler_args)\n\n sample = response.first.sample\n\n route = [None]*len(G)\n for (city, time), val in sample.items():\n if val:\n route[time] = city\n\n if start is not None and route[0] != start:\n # rotate to put the start in front\n idx = route.index(start)\n route = route[idx:] + route[:idx]\n\n return route\n```", "_____no_output_____" ], [ "```python\ndef traveling_salesperson_qubo(G, lagrange=None, weight='weight'):\n \"\"\"Return the QUBO with ground states corresponding to a minimum TSP route.\n\n If :math:`|G|` is the number of nodes in the graph, the resulting qubo will have:\n\n * :math:`|G|^2` variables/nodes\n * :math:`2 |G|^2 (|G| - 1)` interactions/edges\n\n Parameters\n ----------\n G : NetworkX graph\n A complete graph in which each edge has a attribute giving its weight.\n\n lagrange : number, optional (default None)\n Lagrange parameter to weight constraints (no edges within set)\n versus objective (largest set possible).\n\n weight : optional (default 'weight')\n The name of the edge attribute containing the weight.\n\n Returns\n -------\n QUBO : dict\n The QUBO with ground states corresponding to a minimum travelling\n salesperson route. The QUBO variables are labelled `(c, t)` where `c`\n is a node in `G` and `t` is the time index. For instance, if `('a', 0)`\n is 1 in the ground state, that means the node 'a' is visted first.\n\n \"\"\"\n N = G.number_of_nodes()\n\n if lagrange is None:\n # If no lagrange parameter provided, set to 'average' tour length.\n # Usually a good estimate for a lagrange parameter is between 75-150%\n # of the objective function value, so we come up with an estimate for \n # tour length and use that.\n if G.number_of_edges()>0:\n lagrange = G.size(weight=weight)*G.number_of_nodes()/G.number_of_edges()\n else:\n lagrange = 2\n\n # some input checking\n if N in (1, 2) or len(G.edges) != N*(N-1)//2:\n msg = \"graph must be a complete graph with at least 3 nodes or empty\"\n raise ValueError(msg)\n\n # Creating the QUBO\n Q = defaultdict(float)\n\n # Constraint that each row has exactly one 1\n for node in G:\n for pos_1 in range(N):\n Q[((node, pos_1), (node, pos_1))] -= lagrange\n for pos_2 in range(pos_1+1, N):\n Q[((node, pos_1), (node, pos_2))] += 2.0*lagrange\n\n # Constraint that each col has exactly one 1\n for pos in range(N):\n for node_1 in G:\n Q[((node_1, pos), (node_1, pos))] -= lagrange\n for node_2 in set(G)-{node_1}:\n # QUBO coefficient is 2*lagrange, but we are placing this value \n # above *and* below the diagonal, so we put half in each position.\n Q[((node_1, pos), (node_2, pos))] += lagrange\n\n # Objective that minimizes distance\n for u, v in itertools.combinations(G.nodes, 2):\n for pos in range(N):\n nextpos = (pos + 1) % N\n\n # going from u -> v\n Q[((u, pos), (v, nextpos))] += G[u][v][weight]\n\n # going from v -> u\n Q[((v, pos), (u, nextpos))] += G[u][v][weight]\n\n return Q\n\n```", "_____no_output_____" ], [ "---\n## REFERENCES\n\n[1] Wikipedia: [Travelling salesman problem](https://en.wikipedia.org/wiki/Travelling_salesman_problem).", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown" ] ]

cb2fa93097a579b60e5518b8e25c2a1406d224c8

365,984

ipynb

Jupyter Notebook

example.ipynb

marcopost-it/TaughtNet

3d5d15e6d16c5592aa36ee59867e322f0353fee9

[ "Apache-2.0" ]

null

example.ipynb

marcopost-it/TaughtNet

3d5d15e6d16c5592aa36ee59867e322f0353fee9

[ "Apache-2.0" ]

null

example.ipynb

marcopost-it/TaughtNet

3d5d15e6d16c5592aa36ee59867e322f0353fee9

[ "Apache-2.0" ]

null

365,984

0.607204

[ [ [ "# This code has ben run on Google Colab.\n# To execute it, you have to move to the right folder.\n\n% cd drive/MyDrive/TaughtNet", "[Errno 2] No such file or directory: 'drive/MyDrive/TaughtNet'\n/content/drive/MyDrive/TaughtNet\n" ], [ "!pip install transformers\n!pip install seqeval", "Requirement already satisfied: transformers in /usr/local/lib/python3.7/dist-packages (4.4.2)\nRequirement already satisfied: filelock in /usr/local/lib/python3.7/dist-packages (from transformers) (3.0.12)\nRequirement already satisfied: requests in /usr/local/lib/python3.7/dist-packages (from transformers) (2.23.0)\nRequirement already satisfied: packaging in /usr/local/lib/python3.7/dist-packages (from transformers) (20.9)\nRequirement already satisfied: regex!=2019.12.17 in /usr/local/lib/python3.7/dist-packages (from transformers) (2019.12.20)\nRequirement already satisfied: numpy>=1.17 in /usr/local/lib/python3.7/dist-packages (from transformers) (1.19.5)\nRequirement already satisfied: sacremoses in /usr/local/lib/python3.7/dist-packages (from transformers) (0.0.43)\nRequirement already satisfied: tokenizers<0.11,>=0.10.1 in /usr/local/lib/python3.7/dist-packages (from transformers) (0.10.1)\nRequirement already satisfied: tqdm>=4.27 in /usr/local/lib/python3.7/dist-packages (from transformers) (4.41.1)\nRequirement already satisfied: importlib-metadata; python_version < \"3.8\" in /usr/local/lib/python3.7/dist-packages (from transformers) (3.7.2)\nRequirement already satisfied: certifi>=2017.4.17 in /usr/local/lib/python3.7/dist-packages (from requests->transformers) (2020.12.5)\nRequirement already satisfied: idna<3,>=2.5 in /usr/local/lib/python3.7/dist-packages (from requests->transformers) (2.10)\nRequirement already satisfied: chardet<4,>=3.0.2 in /usr/local/lib/python3.7/dist-packages (from requests->transformers) (3.0.4)\nRequirement already satisfied: urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1 in /usr/local/lib/python3.7/dist-packages (from requests->transformers) (1.24.3)\nRequirement already satisfied: pyparsing>=2.0.2 in /usr/local/lib/python3.7/dist-packages (from packaging->transformers) (2.4.7)\nRequirement already satisfied: joblib in /usr/local/lib/python3.7/dist-packages (from sacremoses->transformers) (1.0.1)\nRequirement already satisfied: click in /usr/local/lib/python3.7/dist-packages (from sacremoses->transformers) (7.1.2)\nRequirement already satisfied: six in /usr/local/lib/python3.7/dist-packages (from sacremoses->transformers) (1.15.0)\nRequirement already satisfied: typing-extensions>=3.6.4; python_version < \"3.8\" in /usr/local/lib/python3.7/dist-packages (from importlib-metadata; python_version < \"3.8\"->transformers) (3.7.4.3)\nRequirement already satisfied: zipp>=0.5 in /usr/local/lib/python3.7/dist-packages (from importlib-metadata; python_version < \"3.8\"->transformers) (3.4.1)\nRequirement already satisfied: seqeval in /usr/local/lib/python3.7/dist-packages (1.2.2)\nRequirement already satisfied: scikit-learn>=0.21.3 in /usr/local/lib/python3.7/dist-packages (from seqeval) (0.22.2.post1)\nRequirement already satisfied: numpy>=1.14.0 in /usr/local/lib/python3.7/dist-packages (from seqeval) (1.19.5)\nRequirement already satisfied: joblib>=0.11 in /usr/local/lib/python3.7/dist-packages (from scikit-learn>=0.21.3->seqeval) (1.0.1)\nRequirement already satisfied: scipy>=0.17.0 in /usr/local/lib/python3.7/dist-packages (from scikit-learn>=0.21.3->seqeval) (1.4.1)\n" ] ], [ [ "## Teachers training\n\nIn this example, we will train one teacher for each of the following datasets: *BC2GM*, *BC5CDR-chem*, *NCBI-disease*.", "_____no_output_____" ] ], [ [ "!python train_teacher.py \\\n--data_dir 'data/BC2GM' \\\n--model_name_or_path 'dmis-lab/biobert-base-cased-v1.1' \\\n--output_dir 'models/Teachers/BC2GM' \\\n--logging_dir 'models/Teachers/BC2GM' \\\n--save_steps 10000 ", "2021-03-29 16:16:06.961537: I tensorflow/stream_executor/platform/default/dso_loader.cc:49] Successfully opened dynamic library libcudart.so.11.0\nNamespace(data_dir='data/BC2GM', do_eval=True, do_predict=True, do_train=True, evaluation_strategy='epoch', logging_dir='models/Teachers/BC2GM', logging_steps=100, max_seq_length=128, model_name_or_path='dmis-lab/biobert-base-cased-v1.1', num_train_epochs=3, output_dir='models/Teachers/BC2GM', per_device_train_batch_size=32, save_steps=10000, seed=1)\n03/29/2021 16:16:08 - WARNING - __main__ - Process rank: -1, device: cuda:0, n_gpu: 1, distributed training: False, 16-bits training: False\n03/29/2021 16:16:08 - INFO - __main__ - Training/evaluation parameters TrainingArguments(output_dir=models/Teachers/BC2GM, overwrite_output_dir=False, do_train=True, do_eval=True, do_predict=True, evaluation_strategy=IntervalStrategy.EPOCH, prediction_loss_only=False, per_device_train_batch_size=32, per_device_eval_batch_size=8, gradient_accumulation_steps=1, eval_accumulation_steps=None, learning_rate=5e-05, weight_decay=0.0, adam_beta1=0.9, adam_beta2=0.999, adam_epsilon=1e-08, max_grad_norm=1.0, num_train_epochs=3, max_steps=-1, lr_scheduler_type=SchedulerType.LINEAR, warmup_ratio=0.0, warmup_steps=0, logging_dir=models/Teachers/BC2GM, logging_strategy=IntervalStrategy.STEPS, logging_first_step=False, logging_steps=100, save_strategy=IntervalStrategy.STEPS, save_steps=10000, save_total_limit=None, no_cuda=False, seed=1, fp16=False, fp16_opt_level=O1, fp16_backend=auto, fp16_full_eval=False, local_rank=-1, tpu_num_cores=None, tpu_metrics_debug=False, debug=False, dataloader_drop_last=False, eval_steps=100, dataloader_num_workers=0, past_index=-1, run_name=models/Teachers/BC2GM, disable_tqdm=False, remove_unused_columns=True, label_names=None, load_best_model_at_end=False, metric_for_best_model=None, greater_is_better=None, ignore_data_skip=False, sharded_ddp=[], deepspeed=None, label_smoothing_factor=0.0, adafactor=False, group_by_length=False, report_to=['tensorboard'], ddp_find_unused_parameters=None, dataloader_pin_memory=True, skip_memory_metrics=False, _n_gpu=1)\n03/29/2021 16:16:10 - INFO - filelock - Lock 140593573243600 acquired on data/BC2GM/cached_train_dev_BertTokenizer_128.lock\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - Creating features from dataset file at data/BC2GM\ntrain_dev\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - Writing example 0 of 15093\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - *** Example ***\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - guid: train_dev-1\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - tokens: [CLS] im ##mu ##no ##his ##to ##chemical stain ##ing was positive for s - 100 in all 9 cases stained , positive for h ##mb - 45 in 9 ( 90 % ) of 10 , and negative for c ##yt ##oker ##ati ##n in all 9 cases in which my ##x ##oid me ##lan ##oma remained in the block after previous sections . [SEP]\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - input_ids: 101 13280 13601 2728 27516 2430 16710 24754 1158 1108 3112 1111 188 118 1620 1107 1155 130 2740 9729 117 3112 1111 177 12913 118 2532 1107 130 113 3078 110 114 1104 1275 117 1105 4366 1111 172 25669 26218 11745 1179 1107 1155 130 2740 1107 1134 1139 1775 7874 1143 4371 7903 1915 1107 1103 3510 1170 2166 4886 119 102 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - input_mask: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - segment_ids: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - label_ids: -100 2 -100 -100 -100 -100 -100 2 -100 2 2 2 0 1 1 2 2 2 2 2 2 2 2 0 -100 1 1 2 2 2 2 2 2 2 2 2 2 2 2 0 -100 -100 -100 -100 2 2 2 2 2 2 2 -100 -100 2 -100 -100 2 2 2 2 2 2 2 2 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - *** Example ***\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - guid: train_dev-2\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - tokens: [CLS] ch ##lora ##mp ##hen ##ico ##l ace ##ty ##lt ##ran ##s ##fer ##ase ass ##ays examining the ability of i ##e ##86 to re ##press activity from the h ##c ##m ##v major i ##e promoter or activate the h ##c ##m ##v early promoter for the 2 . 2 - k ##b class of r ##nas demonstrated the functional integrity of the i ##e ##86 protein . [SEP]\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - input_ids: 101 22572 24171 8223 10436 10658 1233 20839 2340 6066 4047 1116 6732 6530 3919 22979 13766 1103 2912 1104 178 1162 22392 1106 1231 11135 3246 1121 1103 177 1665 1306 1964 1558 178 1162 17110 1137 23162 1103 177 1665 1306 1964 1346 17110 1111 1103 123 119 123 118 180 1830 1705 1104 187 13146 7160 1103 8458 12363 1104 1103 178 1162 22392 4592 119 102 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - input_mask: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - segment_ids: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - label_ids: -100 0 -100 -100 -100 -100 -100 1 -100 -100 -100 -100 -100 -100 2 -100 2 2 2 2 0 -100 -100 2 2 -100 2 2 2 2 -100 -100 -100 2 0 -100 1 2 2 2 0 -100 -100 -100 1 1 2 2 2 2 2 2 2 -100 2 2 2 -100 2 2 2 2 2 2 0 -100 -100 1 2 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - *** Example ***\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - guid: train_dev-3\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - tokens: [CLS] a new d ##na repair gene from s ##chi ##zo ##sa ##cc ##har ##omy ##ces p ##omb ##e with ho ##mology to re ##ca was identified and characterized . [SEP]\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - input_ids: 101 170 1207 173 1605 6949 5565 1121 188 4313 6112 3202 19515 7111 18574 7723 185 20972 1162 1114 16358 19969 1106 1231 2599 1108 3626 1105 6858 119 102 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - input_mask: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - segment_ids: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - label_ids: -100 2 2 0 -100 1 1 2 2 -100 -100 -100 -100 -100 -100 -100 2 -100 -100 2 2 -100 2 0 -100 2 2 2 2 2 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - *** Example ***\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - guid: train_dev-4\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - tokens: [CLS] our study also demonstrated significant increases in the number of larger my ##elin ##ated fibers crossing the repair site in comparison with the neon ##ata ##l and adult groups ( p < 0 . 04 ) . [SEP]\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - input_ids: 101 1412 2025 1145 7160 2418 6986 1107 1103 1295 1104 2610 1139 24247 2913 18064 4905 1103 6949 1751 1107 7577 1114 1103 24762 6575 1233 1105 4457 2114 113 185 133 121 119 5129 114 119 102 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - input_mask: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - segment_ids: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - label_ids: -100 2 2 2 2 2 2 2 2 2 2 2 2 -100 -100 2 2 2 2 2 2 2 2 2 2 -100 -100 2 2 2 2 2 2 2 2 2 2 2 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - *** Example ***\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - guid: train_dev-5\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - tokens: [CLS] c ##lon ##ing and se ##quencing of the upstream region of p ##ep ##x revealed the presence of two or ##fs of 360 and 1 , 33 ##8 b ##p that were shown to be able to en ##code proteins with high ho ##mology to g ##ln ##r and g ##ln ##a proteins , respectively . [SEP]\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - input_ids: 101 172 4934 1158 1105 14516 27276 1104 1103 15011 1805 1104 185 8043 1775 3090 1103 2915 1104 1160 1137 22816 1104 9174 1105 122 117 3081 1604 171 1643 1115 1127 2602 1106 1129 1682 1106 4035 13775 7865 1114 1344 16358 19969 1106 176 21615 1197 1105 176 21615 1161 7865 117 3569 119 102 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - input_mask: 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - segment_ids: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\n03/29/2021 16:16:10 - INFO - src.data_handling.DataHandlers - label_ids: -100 2 -100 -100 2 2 -100 2 2 2 2 2 0 -100 -100 2 2 2 2 2 2 -100 2 2 2 2 2 2 -100 2 -100 2 2 2 2 2 2 2 2 -100 2 2 2 2 -100 2 0 -100 -100 2 0 -100 -100 1 2 2 2 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100 -100\n03/29/2021 16:16:28 - INFO - src.data_handling.DataHandlers - Writing example 10000 of 15093\n03/29/2021 16:16:37 - INFO - src.data_handling.DataHandlers - Saving features into cached file data/BC2GM/cached_train_dev_BertTokenizer_128\n03/29/2021 16:16:40 - INFO - filelock - Lock 140593573243600 released on data/BC2GM/cached_train_dev_BertTokenizer_128.lock\n03/29/2021 16:16:40 - INFO - filelock - Lock 140593573699728 acquired on data/BC2GM/cached_test_BertTokenizer_128.lock\n03/29/2021 16:16:40 - INFO - src.data_handling.DataHandlers - Loading features from cached file data/BC2GM/cached_test_BertTokenizer_128\n03/29/2021 16:16:40 - INFO - filelock - Lock 140593573699728 released on data/BC2GM/cached_test_BertTokenizer_128.lock\nSome weights of the model checkpoint at dmis-lab/biobert-base-cased-v1.1 were not used when initializing BertForTokenClassification: ['cls.predictions.bias', 'cls.predictions.transform.dense.weight', 'cls.predictions.transform.dense.bias', 'cls.predictions.transform.LayerNorm.weight', 'cls.predictions.transform.LayerNorm.bias', 'cls.predictions.decoder.weight', 'cls.predictions.decoder.bias', 'cls.seq_relationship.weight', 'cls.seq_relationship.bias']\n- This IS expected if you are initializing BertForTokenClassification from the checkpoint of a model trained on another task or with another architecture (e.g. initializing a BertForSequenceClassification model from a BertForPreTraining model).\n- This IS NOT expected if you are initializing BertForTokenClassification from the checkpoint of a model that you expect to be exactly identical (initializing a BertForSequenceClassification model from a BertForSequenceClassification model).\nSome weights of BertForTokenClassification were not initialized from the model checkpoint at dmis-lab/biobert-base-cased-v1.1 and are newly initialized: ['classifier.weight', 'classifier.bias']\nYou should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.\n/usr/local/lib/python3.7/dist-packages/transformers/trainer.py:836: FutureWarning: `model_path` is deprecated and will be removed in a future version. Use `resume_from_checkpoint` instead.\n FutureWarning,\n{'loss': 0.156, 'learning_rate': 4.646892655367232e-05, 'epoch': 0.21}\n{'loss': 0.0856, 'learning_rate': 4.2937853107344634e-05, 'epoch': 0.42}\n{'loss': 0.0702, 'learning_rate': 3.940677966101695e-05, 'epoch': 0.64}\n{'loss': 0.0658, 'learning_rate': 3.587570621468927e-05, 'epoch': 0.85}\n 33% 472/1416 [05:17<09:46, 1.61it/s]\n 0% 0/630 [00:00<?, ?it/s]\u001b[A\n 0% 3/630 [00:00<00:28, 22.00it/s]\u001b[A\n 1% 5/630 [00:00<00:32, 19.27it/s]\u001b[A\n 1% 7/630 [00:00<00:35, 17.44it/s]\u001b[A\n 1% 9/630 [00:00<00:36, 16.81it/s]\u001b[A\n 2% 11/630 [00:00<00:39, 15.82it/s]\u001b[A\n 2% 13/630 [00:00<00:40, 15.39it/s]\u001b[A\n 2% 15/630 [00:00<00:40, 15.07it/s]\u001b[A\n 3% 17/630 [00:01<00:40, 15.13it/s]\u001b[A\n 3% 19/630 [00:01<00:40, 15.08it/s]\u001b[A\n 3% 21/630 [00:01<00:40, 14.91it/s]\u001b[A\n 4% 23/630 [00:01<00:40, 15.01it/s]\u001b[A\n 4% 25/630 [00:01<00:40, 14.81it/s]\u001b[A\n 4% 27/630 [00:01<00:41, 14.61it/s]\u001b[A\n 5% 29/630 [00:01<00:41, 14.61it/s]\u001b[A\n 5% 31/630 [00:02<00:40, 14.84it/s]\u001b[A\n 5% 33/630 [00:02<00:40, 14.90it/s]\u001b[A\n 6% 35/630 [00:02<00:39, 14.90it/s]\u001b[A\n 6% 37/630 [00:02<00:39, 14.86it/s]\u001b[A\n 6% 39/630 [00:02<00:39, 14.79it/s]\u001b[A\n 7% 41/630 [00:02<00:39, 14.73it/s]\u001b[A\n 7% 43/630 [00:02<00:39, 14.69it/s]\u001b[A\n 7% 45/630 [00:02<00:39, 14.74it/s]\u001b[A\n 7% 47/630 [00:03<00:39, 14.82it/s]\u001b[A\n 8% 49/630 [00:03<00:38, 14.91it/s]\u001b[A\n 8% 51/630 [00:03<00:39, 14.83it/s]\u001b[A\n 8% 53/630 [00:03<00:38, 14.87it/s]\u001b[A\n 9% 55/630 [00:03<00:39, 14.71it/s]\u001b[A\n 9% 57/630 [00:03<00:39, 14.64it/s]\u001b[A\n 9% 59/630 [00:03<00:39, 14.64it/s]\u001b[A\n 10% 61/630 [00:04<00:38, 14.76it/s]\u001b[A\n 10% 63/630 [00:04<00:38, 14.83it/s]\u001b[A\n 10% 65/630 [00:04<00:37, 14.91it/s]\u001b[A\n 11% 67/630 [00:04<00:37, 14.93it/s]\u001b[A\n 11% 69/630 [00:04<00:37, 14.80it/s]\u001b[A\n 11% 71/630 [00:04<00:38, 14.68it/s]\u001b[A\n 12% 73/630 [00:04<00:38, 14.58it/s]\u001b[A\n 12% 75/630 [00:05<00:37, 14.72it/s]\u001b[A\n 12% 77/630 [00:05<00:37, 14.78it/s]\u001b[A\n 13% 79/630 [00:05<00:37, 14.76it/s]\u001b[A\n 13% 81/630 [00:05<00:36, 14.84it/s]\u001b[A\n 13% 83/630 [00:05<00:37, 14.78it/s]\u001b[A\n 13% 85/630 [00:05<00:37, 14.71it/s]\u001b[A\n 14% 87/630 [00:05<00:36, 14.69it/s]\u001b[A\n 14% 89/630 [00:05<00:36, 14.67it/s]\u001b[A\n 14% 91/630 [00:06<00:36, 14.77it/s]\u001b[A\n 15% 93/630 [00:06<00:36, 14.88it/s]\u001b[A\n 15% 95/630 [00:06<00:36, 14.82it/s]\u001b[A\n 15% 97/630 [00:06<00:35, 14.84it/s]\u001b[A\n 16% 99/630 [00:06<00:35, 14.83it/s]\u001b[A\n 16% 101/630 [00:06<00:35, 14.71it/s]\u001b[A\n 16% 103/630 [00:06<00:35, 14.66it/s]\u001b[A\n 17% 105/630 [00:07<00:35, 14.69it/s]\u001b[A\n 17% 107/630 [00:07<00:35, 14.84it/s]\u001b[A\n 17% 109/630 [00:07<00:35, 14.89it/s]\u001b[A\n 18% 111/630 [00:07<00:34, 14.88it/s]\u001b[A\n 18% 113/630 [00:07<00:34, 14.82it/s]\u001b[A\n 18% 115/630 [00:07<00:34, 14.86it/s]\u001b[A\n 19% 117/630 [00:07<00:34, 14.85it/s]\u001b[A\n 19% 119/630 [00:07<00:34, 14.72it/s]\u001b[A\n 19% 121/630 [00:08<00:34, 14.73it/s]\u001b[A\n 20% 123/630 [00:08<00:34, 14.82it/s]\u001b[A\n 20% 125/630 [00:08<00:34, 14.80it/s]\u001b[A\n 20% 127/630 [00:08<00:33, 14.85it/s]\u001b[A\n 20% 129/630 [00:08<00:33, 14.83it/s]\u001b[A\n 21% 131/630 [00:08<00:33, 14.83it/s]\u001b[A\n 21% 133/630 [00:08<00:33, 14.78it/s]\u001b[A\n 21% 135/630 [00:09<00:33, 14.82it/s]\u001b[A\n 22% 137/630 [00:09<00:33, 14.88it/s]\u001b[A\n 22% 139/630 [00:09<00:33, 14.81it/s]\u001b[A\n 22% 141/630 [00:09<00:32, 14.83it/s]\u001b[A\n 23% 143/630 [00:09<00:32, 14.86it/s]\u001b[A\n 23% 145/630 [00:09<00:32, 14.78it/s]\u001b[A\n 23% 147/630 [00:09<00:32, 14.84it/s]\u001b[A\n 24% 149/630 [00:10<00:32, 14.74it/s]\u001b[A\n 24% 151/630 [00:10<00:32, 14.84it/s]\u001b[A\n 24% 153/630 [00:10<00:32, 14.90it/s]\u001b[A\n 25% 155/630 [00:10<00:32, 14.80it/s]\u001b[A\n 25% 157/630 [00:10<00:31, 14.79it/s]\u001b[A\n 25% 159/630 [00:10<00:31, 14.79it/s]\u001b[A\n 26% 161/630 [00:10<00:31, 14.78it/s]\u001b[A\n 26% 163/630 [00:10<00:31, 14.74it/s]\u001b[A\n 26% 165/630 [00:11<00:31, 14.79it/s]\u001b[A\n 27% 167/630 [00:11<00:31, 14.82it/s]\u001b[A\n 27% 169/630 [00:11<00:31, 14.78it/s]\u001b[A\n 27% 171/630 [00:11<00:30, 14.85it/s]\u001b[A\n 27% 173/630 [00:11<00:30, 14.78it/s]\u001b[A\n 28% 175/630 [00:11<00:30, 14.77it/s]\u001b[A\n 28% 177/630 [00:11<00:30, 14.80it/s]\u001b[A\n 28% 179/630 [00:12<00:30, 14.72it/s]\u001b[A\n 29% 181/630 [00:12<00:30, 14.76it/s]\u001b[A\n 29% 183/630 [00:12<00:30, 14.83it/s]\u001b[A\n 29% 185/630 [00:12<00:30, 14.82it/s]\u001b[A\n 30% 187/630 [00:12<00:29, 14.85it/s]\u001b[A\n 30% 189/630 [00:12<00:29, 14.85it/s]\u001b[A\n 30% 191/630 [00:12<00:29, 14.79it/s]\u001b[A\n 31% 193/630 [00:12<00:29, 14.74it/s]\u001b[A\n 31% 195/630 [00:13<00:29, 14.84it/s]\u001b[A\n 31% 197/630 [00:13<00:29, 14.75it/s]\u001b[A\n 32% 199/630 [00:13<00:29, 14.80it/s]\u001b[A\n 32% 201/630 [00:13<00:28, 14.81it/s]\u001b[A\n 32% 203/630 [00:13<00:28, 14.74it/s]\u001b[A\n 33% 205/630 [00:13<00:28, 14.72it/s]\u001b[A\n 33% 207/630 [00:13<00:28, 14.77it/s]\u001b[A\n 33% 209/630 [00:14<00:28, 14.73it/s]\u001b[A\n 33% 211/630 [00:14<00:28, 14.80it/s]\u001b[A\n 34% 213/630 [00:14<00:28, 14.84it/s]\u001b[A\n 34% 215/630 [00:14<00:27, 14.84it/s]\u001b[A\n 34% 217/630 [00:14<00:27, 14.82it/s]\u001b[A\n 35% 219/630 [00:14<00:27, 14.91it/s]\u001b[A\n 35% 221/630 [00:14<00:27, 14.94it/s]\u001b[A\n 35% 223/630 [00:15<00:27, 14.92it/s]\u001b[A\n 36% 225/630 [00:15<00:27, 14.89it/s]\u001b[A\n 36% 227/630 [00:15<00:27, 14.84it/s]\u001b[A\n 36% 229/630 [00:15<00:26, 14.86it/s]\u001b[A\n 37% 231/630 [00:15<00:26, 14.81it/s]\u001b[A\n 37% 233/630 [00:15<00:26, 14.82it/s]\u001b[A\n 37% 235/630 [00:15<00:26, 14.88it/s]\u001b[A\n 38% 237/630 [00:15<00:26, 14.84it/s]\u001b[A\n 38% 239/630 [00:16<00:26, 14.85it/s]\u001b[A\n 38% 241/630 [00:16<00:26, 14.85it/s]\u001b[A\n 39% 243/630 [00:16<00:26, 14.76it/s]\u001b[A\n 39% 245/630 [00:16<00:26, 14.72it/s]\u001b[A\n 39% 247/630 [00:16<00:25, 14.78it/s]\u001b[A\n 40% 249/630 [00:16<00:25, 14.82it/s]\u001b[A\n 40% 251/630 [00:16<00:25, 14.84it/s]\u001b[A\n 40% 253/630 [00:17<00:25, 14.88it/s]\u001b[A\n 40% 255/630 [00:17<00:25, 14.81it/s]\u001b[A\n 41% 257/630 [00:17<00:25, 14.77it/s]\u001b[A\n 41% 259/630 [00:17<00:25, 14.74it/s]\u001b[A\n 41% 261/630 [00:17<00:25, 14.73it/s]\u001b[A\n 42% 263/630 [00:17<00:24, 14.79it/s]\u001b[A\n 42% 265/630 [00:17<00:24, 14.81it/s]\u001b[A\n 42% 267/630 [00:17<00:24, 14.75it/s]\u001b[A\n 43% 269/630 [00:18<00:24, 14.78it/s]\u001b[A\n 43% 271/630 [00:18<00:24, 14.80it/s]\u001b[A\n 43% 273/630 [00:18<00:24, 14.78it/s]\u001b[A\n 44% 275/630 [00:18<00:24, 14.75it/s]\u001b[A\n 44% 277/630 [00:18<00:23, 14.73it/s]\u001b[A\n 44% 279/630 [00:18<00:23, 14.71it/s]\u001b[A\n 45% 281/630 [00:18<00:23, 14.67it/s]\u001b[A\n 45% 283/630 [00:19<00:23, 14.72it/s]\u001b[A\n 45% 285/630 [00:19<00:23, 14.80it/s]\u001b[A\n 46% 287/630 [00:19<00:23, 14.75it/s]\u001b[A\n 46% 289/630 [00:19<00:23, 14.75it/s]\u001b[A\n 46% 291/630 [00:19<00:22, 14.75it/s]\u001b[A\n 47% 293/630 [00:19<00:22, 14.68it/s]\u001b[A\n 47% 295/630 [00:19<00:22, 14.62it/s]\u001b[A\n 47% 297/630 [00:20<00:22, 14.64it/s]\u001b[A\n 47% 299/630 [00:20<00:22, 14.73it/s]\u001b[A\n 48% 301/630 [00:20<00:22, 14.73it/s]\u001b[A\n 48% 303/630 [00:20<00:22, 14.68it/s]\u001b[A\n 48% 305/630 [00:20<00:21, 14.78it/s]\u001b[A\n 49% 307/630 [00:20<00:21, 14.76it/s]\u001b[A\n 49% 309/630 [00:20<00:21, 14.76it/s]\u001b[A\n 49% 311/630 [00:20<00:21, 14.81it/s]\u001b[A\n 50% 313/630 [00:21<00:21, 14.78it/s]\u001b[A\n 50% 315/630 [00:21<00:21, 14.77it/s]\u001b[A\n 50% 317/630 [00:21<00:21, 14.80it/s]\u001b[A\n 51% 319/630 [00:21<00:21, 14.75it/s]\u001b[A\n 51% 321/630 [00:21<00:20, 14.74it/s]\u001b[A\n 51% 323/630 [00:21<00:20, 14.81it/s]\u001b[A\n 52% 325/630 [00:21<00:20, 14.78it/s]\u001b[A\n 52% 327/630 [00:22<00:20, 14.71it/s]\u001b[A\n 52% 329/630 [00:22<00:20, 14.72it/s]\u001b[A\n 53% 331/630 [00:22<00:20, 14.78it/s]\u001b[A\n 53% 333/630 [00:22<00:20, 14.72it/s]\u001b[A\n 53% 335/630 [00:22<00:19, 14.76it/s]\u001b[A\n 53% 337/630 [00:22<00:19, 14.80it/s]\u001b[A\n 54% 339/630 [00:22<00:19, 14.77it/s]\u001b[A\n 54% 341/630 [00:23<00:19, 14.73it/s]\u001b[A\n 54% 343/630 [00:23<00:19, 14.73it/s]\u001b[A\n 55% 345/630 [00:23<00:19, 14.74it/s]\u001b[A\n 55% 347/630 [00:23<00:19, 14.70it/s]\u001b[A\n 55% 349/630 [00:23<00:19, 14.78it/s]\u001b[A\n 56% 351/630 [00:23<00:18, 14.78it/s]\u001b[A\n 56% 353/630 [00:23<00:18, 14.75it/s]\u001b[A\n 56% 355/630 [00:23<00:18, 14.75it/s]\u001b[A\n 57% 357/630 [00:24<00:18, 14.76it/s]\u001b[A\n 57% 359/630 [00:24<00:18, 14.73it/s]\u001b[A\n 57% 361/630 [00:24<00:18, 14.73it/s]\u001b[A\n 58% 363/630 [00:24<00:18, 14.80it/s]\u001b[A\n 58% 365/630 [00:24<00:17, 14.74it/s]\u001b[A\n 58% 367/630 [00:24<00:17, 14.78it/s]\u001b[A\n 59% 369/630 [00:24<00:17, 14.78it/s]\u001b[A\n 59% 371/630 [00:25<00:17, 14.80it/s]\u001b[A\n 59% 373/630 [00:25<00:17, 14.75it/s]\u001b[A\n 60% 375/630 [00:25<00:17, 14.77it/s]\u001b[A\n 60% 377/630 [00:25<00:17, 14.79it/s]\u001b[A\n 60% 379/630 [00:25<00:17, 14.70it/s]\u001b[A\n 60% 381/630 [00:25<00:16, 14.80it/s]\u001b[A\n 61% 383/630 [00:25<00:16, 14.78it/s]\u001b[A\n 61% 385/630 [00:25<00:16, 14.83it/s]\u001b[A\n 61% 387/630 [00:26<00:16, 14.81it/s]\u001b[A\n 62% 389/630 [00:26<00:16, 14.79it/s]\u001b[A\n 62% 391/630 [00:26<00:16, 14.78it/s]\u001b[A\n 62% 393/630 [00:26<00:16, 14.77it/s]\u001b[A\n 63% 395/630 [00:26<00:15, 14.75it/s]\u001b[A\n 63% 397/630 [00:26<00:15, 14.77it/s]\u001b[A\n 63% 399/630 [00:26<00:15, 14.84it/s]\u001b[A\n 64% 401/630 [00:27<00:15, 14.86it/s]\u001b[A\n 64% 403/630 [00:27<00:15, 14.73it/s]\u001b[A\n 64% 405/630 [00:27<00:15, 14.75it/s]\u001b[A\n 65% 407/630 [00:27<00:15, 14.73it/s]\u001b[A\n 65% 409/630 [00:27<00:14, 14.81it/s]\u001b[A\n 65% 411/630 [00:27<00:14, 14.78it/s]\u001b[A\n 66% 413/630 [00:27<00:14, 14.70it/s]\u001b[A\n 66% 415/630 [00:28<00:14, 14.70it/s]\u001b[A\n 66% 417/630 [00:28<00:14, 14.80it/s]\u001b[A\n 67% 419/630 [00:28<00:14, 14.76it/s]\u001b[A\n 67% 421/630 [00:28<00:14, 14.66it/s]\u001b[A\n 67% 423/630 [00:28<00:14, 14.73it/s]\u001b[A\n 67% 425/630 [00:28<00:13, 14.72it/s]\u001b[A\n 68% 427/630 [00:28<00:13, 14.66it/s]\u001b[A\n 68% 429/630 [00:28<00:13, 14.63it/s]\u001b[A\n 68% 431/630 [00:29<00:13, 14.73it/s]\u001b[A\n 69% 433/630 [00:29<00:13, 14.73it/s]\u001b[A\n 69% 435/630 [00:29<00:13, 14.72it/s]\u001b[A\n 69% 437/630 [00:29<00:13, 14.68it/s]\u001b[A\n 70% 439/630 [00:29<00:12, 14.70it/s]\u001b[A\n 70% 441/630 [00:29<00:12, 14.69it/s]\u001b[A\n 70% 443/630 [00:29<00:12, 14.74it/s]\u001b[A\n 71% 445/630 [00:30<00:12, 14.78it/s]\u001b[A\n 71% 447/630 [00:30<00:12, 14.65it/s]\u001b[A\n 71% 449/630 [00:30<00:12, 14.68it/s]\u001b[A\n 72% 451/630 [00:30<00:12, 14.72it/s]\u001b[A\n 72% 453/630 [00:30<00:11, 14.76it/s]\u001b[A\n 72% 455/630 [00:30<00:11, 14.70it/s]\u001b[A\n 73% 457/630 [00:30<00:11, 14.69it/s]\u001b[A\n 73% 459/630 [00:31<00:11, 14.73it/s]\u001b[A\n 73% 461/630 [00:31<00:11, 14.71it/s]\u001b[A\n 73% 463/630 [00:31<00:11, 14.75it/s]\u001b[A\n 74% 465/630 [00:31<00:11, 14.75it/s]\u001b[A\n 74% 467/630 [00:31<00:11, 14.64it/s]\u001b[A\n 74% 469/630 [00:31<00:11, 14.57it/s]\u001b[A\n 75% 471/630 [00:31<00:10, 14.65it/s]\u001b[A\n 75% 473/630 [00:31<00:10, 14.69it/s]\u001b[A\n 75% 475/630 [00:32<00:10, 14.63it/s]\u001b[A\n 76% 477/630 [00:32<00:10, 14.57it/s]\u001b[A\n 76% 479/630 [00:32<00:10, 14.64it/s]\u001b[A\n 76% 481/630 [00:32<00:10, 14.71it/s]\u001b[A\n 77% 483/630 [00:32<00:10, 14.64it/s]\u001b[A\n 77% 485/630 [00:32<00:09, 14.68it/s]\u001b[A\n 77% 487/630 [00:32<00:09, 14.75it/s]\u001b[A\n 78% 489/630 [00:33<00:09, 14.68it/s]\u001b[A\n 78% 491/630 [00:33<00:09, 14.67it/s]\u001b[A\n 78% 493/630 [00:33<00:09, 14.75it/s]\u001b[A\n 79% 495/630 [00:33<00:09, 14.79it/s]\u001b[A\n 79% 497/630 [00:33<00:09, 14.67it/s]\u001b[A\n 79% 499/630 [00:33<00:08, 14.75it/s]\u001b[A\n 80% 501/630 [00:33<00:08, 14.77it/s]\u001b[A\n 80% 503/630 [00:34<00:08, 14.68it/s]\u001b[A\n 80% 505/630 [00:34<00:08, 14.65it/s]\u001b[A\n 80% 507/630 [00:34<00:08, 14.70it/s]\u001b[A\n 81% 509/630 [00:34<00:08, 14.78it/s]\u001b[A\n 81% 511/630 [00:34<00:08, 14.69it/s]\u001b[A\n 81% 513/630 [00:34<00:07, 14.67it/s]\u001b[A\n 82% 515/630 [00:34<00:07, 14.74it/s]\u001b[A\n 82% 517/630 [00:34<00:07, 14.65it/s]\u001b[A\n 82% 519/630 [00:35<00:07, 14.71it/s]\u001b[A\n 83% 521/630 [00:35<00:07, 14.77it/s]\u001b[A\n 83% 523/630 [00:35<00:07, 14.81it/s]\u001b[A\n 83% 525/630 [00:35<00:07, 14.82it/s]\u001b[A\n 84% 527/630 [00:35<00:06, 14.82it/s]\u001b[A\n 84% 529/630 [00:35<00:06, 14.78it/s]\u001b[A\n 84% 531/630 [00:35<00:06, 14.72it/s]\u001b[A\n 85% 533/630 [00:36<00:06, 14.64it/s]\u001b[A\n 85% 535/630 [00:36<00:06, 14.75it/s]\u001b[A\n 85% 537/630 [00:36<00:06, 14.69it/s]\u001b[A\n 86% 539/630 [00:36<00:06, 14.69it/s]\u001b[A\n 86% 541/630 [00:36<00:06, 14.61it/s]\u001b[A\n 86% 543/630 [00:36<00:05, 14.61it/s]\u001b[A\n 87% 545/630 [00:36<00:05, 14.65it/s]\u001b[A\n 87% 547/630 [00:36<00:05, 14.67it/s]\u001b[A\n 87% 549/630 [00:37<00:05, 14.74it/s]\u001b[A\n 87% 551/630 [00:37<00:05, 14.72it/s]\u001b[A\n 88% 553/630 [00:37<00:05, 14.79it/s]\u001b[A\n 88% 555/630 [00:37<00:05, 14.82it/s]\u001b[A\n 88% 557/630 [00:37<00:04, 14.70it/s]\u001b[A\n 89% 559/630 [00:37<00:04, 14.67it/s]\u001b[A\n 89% 561/630 [00:37<00:04, 14.61it/s]\u001b[A\n 89% 563/630 [00:38<00:04, 14.70it/s]\u001b[A\n 90% 565/630 [00:38<00:04, 14.73it/s]\u001b[A\n 90% 567/630 [00:38<00:04, 14.72it/s]\u001b[A\n 90% 569/630 [00:38<00:04, 14.74it/s]\u001b[A\n 91% 571/630 [00:38<00:04, 14.65it/s]\u001b[A\n 91% 573/630 [00:38<00:03, 14.56it/s]\u001b[A\n 91% 575/630 [00:38<00:03, 14.54it/s]\u001b[A\n 92% 577/630 [00:39<00:03, 14.63it/s]\u001b[A\n 92% 579/630 [00:39<00:03, 14.64it/s]\u001b[A\n 92% 581/630 [00:39<00:03, 14.62it/s]\u001b[A\n 93% 583/630 [00:39<00:03, 14.65it/s]\u001b[A\n 93% 585/630 [00:39<00:03, 14.70it/s]\u001b[A\n 93% 587/630 [00:39<00:02, 14.65it/s]\u001b[A\n 93% 589/630 [00:39<00:02, 14.58it/s]\u001b[A\n 94% 591/630 [00:39<00:02, 14.63it/s]\u001b[A\n 94% 593/630 [00:40<00:02, 14.66it/s]\u001b[A\n 94% 595/630 [00:40<00:02, 14.69it/s]\u001b[A\n 95% 597/630 [00:40<00:02, 14.75it/s]\u001b[A\n 95% 599/630 [00:40<00:02, 14.79it/s]\u001b[A\n 95% 601/630 [00:40<00:01, 14.77it/s]\u001b[A\n 96% 603/630 [00:40<00:01, 14.70it/s]\u001b[A\n 96% 605/630 [00:40<00:01, 14.74it/s]\u001b[A\n 96% 607/630 [00:41<00:01, 14.70it/s]\u001b[A\n 97% 609/630 [00:41<00:01, 14.67it/s]\u001b[A\n 97% 611/630 [00:41<00:01, 14.67it/s]\u001b[A\n 97% 613/630 [00:41<00:01, 14.71it/s]\u001b[A\n 98% 615/630 [00:41<00:01, 14.67it/s]\u001b[A\n 98% 617/630 [00:41<00:00, 14.65it/s]\u001b[A\n 98% 619/630 [00:41<00:00, 14.67it/s]\u001b[A\n 99% 621/630 [00:42<00:00, 14.68it/s]\u001b[A\n 99% 623/630 [00:42<00:00, 14.66it/s]\u001b[A\n 99% 625/630 [00:42<00:00, 14.72it/s]\u001b[A\n100% 627/630 [00:42<00:00, 14.76it/s]\u001b[A\n \n\u001b[A{'eval_loss': 0.05860723555088043, 'eval_accuracy_score': 0.9765879265091864, 'eval_precision': 0.7703681798018631, 'eval_recall': 0.8268528804951595, 'eval_f1': 0.7976117575015308, 'eval_runtime': 62.0653, 'eval_samples_per_second': 81.173, 'epoch': 1.0}\n 33% 472/1416 [06:19<09:46, 1.61it/s]\n100% 630/630 [01:02<00:00, 14.78it/s]\u001b[A\n{'loss': 0.0557, 'learning_rate': 3.234463276836158e-05, 'epoch': 1.06}\n{'loss': 0.0398, 'learning_rate': 2.88135593220339e-05, 'epoch': 1.27}\n{'loss': 0.0381, 'learning_rate': 2.5282485875706215e-05, 'epoch': 1.48}\n{'loss': 0.0361, 'learning_rate': 2.175141242937853e-05, 'epoch': 1.69}\n{'loss': 0.0379, 'learning_rate': 1.8220338983050846e-05, 'epoch': 1.91}\n 67% 944/1416 [11:44<04:55, 1.60it/s]\n 0% 0/630 [00:00<?, ?it/s]\u001b[A\n 0% 3/630 [00:00<00:29, 21.19it/s]\u001b[A\n 1% 5/630 [00:00<00:33, 18.65it/s]\u001b[A\n 1% 7/630 [00:00<00:36, 17.06it/s]\u001b[A\n 1% 9/630 [00:00<00:37, 16.48it/s]\u001b[A\n 2% 11/630 [00:00<00:39, 15.74it/s]\u001b[A\n 2% 13/630 [00:00<00:40, 15.39it/s]\u001b[A\n 2% 15/630 [00:00<00:40, 15.26it/s]\u001b[A\n 3% 17/630 [00:01<00:40, 15.09it/s]\u001b[A\n 3% 19/630 [00:01<00:40, 14.92it/s]\u001b[A\n 3% 21/630 [00:01<00:41, 14.80it/s]\u001b[A\n 4% 23/630 [00:01<00:40, 14.88it/s]\u001b[A\n 4% 25/630 [00:01<00:41, 14.74it/s]\u001b[A\n 4% 27/630 [00:01<00:41, 14.67it/s]\u001b[A\n 5% 29/630 [00:01<00:40, 14.72it/s]\u001b[A\n 5% 31/630 [00:02<00:40, 14.77it/s]\u001b[A\n 5% 33/630 [00:02<00:40, 14.65it/s]\u001b[A\n 6% 35/630 [00:02<00:40, 14.60it/s]\u001b[A\n 6% 37/630 [00:02<00:40, 14.74it/s]\u001b[A\n 6% 39/630 [00:02<00:40, 14.70it/s]\u001b[A\n 7% 41/630 [00:02<00:40, 14.63it/s]\u001b[A\n 7% 43/630 [00:02<00:40, 14.65it/s]\u001b[A\n 7% 45/630 [00:03<00:39, 14.74it/s]\u001b[A\n 7% 47/630 [00:03<00:39, 14.71it/s]\u001b[A\n 8% 49/630 [00:03<00:39, 14.63it/s]\u001b[A\n 8% 51/630 [00:03<00:39, 14.54it/s]\u001b[A\n 8% 53/630 [00:03<00:39, 14.62it/s]\u001b[A\n 9% 55/630 [00:03<00:39, 14.61it/s]\u001b[A\n 9% 57/630 [00:03<00:39, 14.62it/s]\u001b[A\n 9% 59/630 [00:03<00:39, 14.61it/s]\u001b[A\n 10% 61/630 [00:04<00:38, 14.62it/s]\u001b[A\n 10% 63/630 [00:04<00:38, 14.61it/s]\u001b[A\n 10% 65/630 [00:04<00:38, 14.63it/s]\u001b[A\n 11% 67/630 [00:04<00:38, 14.67it/s]\u001b[A\n 11% 69/630 [00:04<00:38, 14.65it/s]\u001b[A\n 11% 71/630 [00:04<00:38, 14.68it/s]\u001b[A\n 12% 73/630 [00:04<00:37, 14.74it/s]\u001b[A\n 12% 75/630 [00:05<00:37, 14.65it/s]\u001b[A\n 12% 77/630 [00:05<00:37, 14.56it/s]\u001b[A\n 13% 79/630 [00:05<00:37, 14.61it/s]\u001b[A\n 13% 81/630 [00:05<00:37, 14.50it/s]\u001b[A\n 13% 83/630 [00:05<00:37, 14.55it/s]\u001b[A\n 13% 85/630 [00:05<00:37, 14.61it/s]\u001b[A\n 14% 87/630 [00:05<00:36, 14.70it/s]\u001b[A\n 14% 89/630 [00:06<00:36, 14.70it/s]\u001b[A\n 14% 91/630 [00:06<00:36, 14.63it/s]\u001b[A\n 15% 93/630 [00:06<00:36, 14.57it/s]\u001b[A\n 15% 95/630 [00:06<00:36, 14.75it/s]\u001b[A\n 15% 97/630 [00:06<00:36, 14.66it/s]\u001b[A\n 16% 99/630 [00:06<00:36, 14.57it/s]\u001b[A\n 16% 101/630 [00:06<00:36, 14.66it/s]\u001b[A\n 16% 103/630 [00:06<00:35, 14.67it/s]\u001b[A\n 17% 105/630 [00:07<00:35, 14.69it/s]\u001b[A\n 17% 107/630 [00:07<00:35, 14.64it/s]\u001b[A\n 17% 109/630 [00:07<00:35, 14.65it/s]\u001b[A\n 18% 111/630 [00:07<00:35, 14.59it/s]\u001b[A\n 18% 113/630 [00:07<00:35, 14.54it/s]\u001b[A\n 18% 115/630 [00:07<00:35, 14.58it/s]\u001b[A\n 19% 117/630 [00:07<00:35, 14.61it/s]\u001b[A\n 19% 119/630 [00:08<00:34, 14.66it/s]\u001b[A\n 19% 121/630 [00:08<00:34, 14.63it/s]\u001b[A\n 20% 123/630 [00:08<00:34, 14.66it/s]\u001b[A\n 20% 125/630 [00:08<00:34, 14.70it/s]\u001b[A\n 20% 127/630 [00:08<00:34, 14.60it/s]\u001b[A\n 20% 129/630 [00:08<00:34, 14.54it/s]\u001b[A\n 21% 131/630 [00:08<00:34, 14.61it/s]\u001b[A\n 21% 133/630 [00:09<00:33, 14.66it/s]\u001b[A\n 21% 135/630 [00:09<00:33, 14.63it/s]\u001b[A\n 22% 137/630 [00:09<00:33, 14.66it/s]\u001b[A\n 22% 139/630 [00:09<00:33, 14.73it/s]\u001b[A\n 22% 141/630 [00:09<00:33, 14.64it/s]\u001b[A\n 23% 143/630 [00:09<00:33, 14.64it/s]\u001b[A\n 23% 145/630 [00:09<00:33, 14.65it/s]\u001b[A\n 23% 147/630 [00:09<00:32, 14.65it/s]\u001b[A\n 24% 149/630 [00:10<00:33, 14.55it/s]\u001b[A\n 24% 151/630 [00:10<00:33, 14.51it/s]\u001b[A\n 24% 153/630 [00:10<00:32, 14.61it/s]\u001b[A\n 25% 155/630 [00:10<00:32, 14.66it/s]\u001b[A\n 25% 157/630 [00:10<00:32, 14.59it/s]\u001b[A\n 25% 159/630 [00:10<00:32, 14.60it/s]\u001b[A\n 26% 161/630 [00:10<00:31, 14.71it/s]\u001b[A\n 26% 163/630 [00:11<00:31, 14.68it/s]\u001b[A\n 26% 165/630 [00:11<00:31, 14.58it/s]\u001b[A\n 27% 167/630 [00:11<00:31, 14.68it/s]\u001b[A\n 27% 169/630 [00:11<00:31, 14.68it/s]\u001b[A\n 27% 171/630 [00:11<00:31, 14.65it/s]\u001b[A\n 27% 173/630 [00:11<00:31, 14.64it/s]\u001b[A\n 28% 175/630 [00:11<00:31, 14.57it/s]\u001b[A\n 28% 177/630 [00:12<00:30, 14.63it/s]\u001b[A\n 28% 179/630 [00:12<00:31, 14.53it/s]\u001b[A\n 29% 181/630 [00:12<00:30, 14.49it/s]\u001b[A\n 29% 183/630 [00:12<00:30, 14.57it/s]\u001b[A\n 29% 185/630 [00:12<00:30, 14.64it/s]\u001b[A\n 30% 187/630 [00:12<00:30, 14.62it/s]\u001b[A\n 30% 189/630 [00:12<00:30, 14.63it/s]\u001b[A\n 30% 191/630 [00:12<00:30, 14.56it/s]\u001b[A\n 31% 193/630 [00:13<00:30, 14.54it/s]\u001b[A\n 31% 195/630 [00:13<00:29, 14.56it/s]\u001b[A\n 31% 197/630 [00:13<00:29, 14.53it/s]\u001b[A\n 32% 199/630 [00:13<00:29, 14.59it/s]\u001b[A\n 32% 201/630 [00:13<00:29, 14.66it/s]\u001b[A\n 32% 203/630 [00:13<00:29, 14.65it/s]\u001b[A\n 33% 205/630 [00:13<00:28, 14.69it/s]\u001b[A\n 33% 207/630 [00:14<00:28, 14.71it/s]\u001b[A\n 33% 209/630 [00:14<00:28, 14.64it/s]\u001b[A\n 33% 211/630 [00:14<00:28, 14.59it/s]\u001b[A\n 34% 213/630 [00:14<00:28, 14.65it/s]\u001b[A\n 34% 215/630 [00:14<00:28, 14.75it/s]\u001b[A\n 34% 217/630 [00:14<00:28, 14.71it/s]\u001b[A\n 35% 219/630 [00:14<00:27, 14.77it/s]\u001b[A\n 35% 221/630 [00:15<00:27, 14.72it/s]\u001b[A\n 35% 223/630 [00:15<00:27, 14.61it/s]\u001b[A\n 36% 225/630 [00:15<00:27, 14.55it/s]\u001b[A\n 36% 227/630 [00:15<00:27, 14.56it/s]\u001b[A\n 36% 229/630 [00:15<00:27, 14.66it/s]\u001b[A\n 37% 231/630 [00:15<00:27, 14.62it/s]\u001b[A\n 37% 233/630 [00:15<00:26, 14.73it/s]\u001b[A\n 37% 235/630 [00:15<00:26, 14.73it/s]\u001b[A\n 38% 237/630 [00:16<00:26, 14.67it/s]\u001b[A\n 38% 239/630 [00:16<00:26, 14.61it/s]\u001b[A\n 38% 241/630 [00:16<00:26, 14.56it/s]\u001b[A\n 39% 243/630 [00:16<00:26, 14.65it/s]\u001b[A\n 39% 245/630 [00:16<00:26, 14.63it/s]\u001b[A\n 39% 247/630 [00:16<00:26, 14.67it/s]\u001b[A\n 40% 249/630 [00:16<00:25, 14.67it/s]\u001b[A\n 40% 251/630 [00:17<00:25, 14.68it/s]\u001b[A\n 40% 253/630 [00:17<00:25, 14.58it/s]\u001b[A\n 40% 255/630 [00:17<00:25, 14.55it/s]\u001b[A\n 41% 257/630 [00:17<00:25, 14.59it/s]\u001b[A\n 41% 259/630 [00:17<00:25, 14.63it/s]\u001b[A\n 41% 261/630 [00:17<00:25, 14.64it/s]\u001b[A\n 42% 263/630 [00:17<00:24, 14.69it/s]\u001b[A\n 42% 265/630 [00:18<00:24, 14.72it/s]\u001b[A\n 42% 267/630 [00:18<00:24, 14.67it/s]\u001b[A\n 43% 269/630 [00:18<00:24, 14.60it/s]\u001b[A\n 43% 271/630 [00:18<00:24, 14.65it/s]\u001b[A\n 43% 273/630 [00:18<00:24, 14.69it/s]\u001b[A\n 44% 275/630 [00:18<00:24, 14.64it/s]\u001b[A\n 44% 277/630 [00:18<00:24, 14.63it/s]\u001b[A\n 44% 279/630 [00:19<00:24, 14.59it/s]\u001b[A\n 45% 281/630 [00:19<00:23, 14.64it/s]\u001b[A\n 45% 283/630 [00:19<00:23, 14.58it/s]\u001b[A\n 45% 285/630 [00:19<00:23, 14.53it/s]\u001b[A\n 46% 287/630 [00:19<00:23, 14.64it/s]\u001b[A\n 46% 289/630 [00:19<00:23, 14.62it/s]\u001b[A\n 46% 291/630 [00:19<00:23, 14.61it/s]\u001b[A\n 47% 293/630 [00:19<00:23, 14.58it/s]\u001b[A\n 47% 295/630 [00:20<00:22, 14.62it/s]\u001b[A\n 47% 297/630 [00:20<00:22, 14.64it/s]\u001b[A\n 47% 299/630 [00:20<00:22, 14.59it/s]\u001b[A\n 48% 301/630 [00:20<00:22, 14.54it/s]\u001b[A\n 48% 303/630 [00:20<00:22, 14.52it/s]\u001b[A\n 48% 305/630 [00:20<00:22, 14.57it/s]\u001b[A\n 49% 307/630 [00:20<00:22, 14.65it/s]\u001b[A\n 49% 309/630 [00:21<00:21, 14.64it/s]\u001b[A\n 49% 311/630 [00:21<00:21, 14.61it/s]\u001b[A\n 50% 313/630 [00:21<00:21, 14.67it/s]\u001b[A\n 50% 315/630 [00:21<00:21, 14.62it/s]\u001b[A\n 50% 317/630 [00:21<00:21, 14.57it/s]\u001b[A\n 51% 319/630 [00:21<00:21, 14.62it/s]\u001b[A\n 51% 321/630 [00:21<00:21, 14.64it/s]\u001b[A\n 51% 323/630 [00:22<00:20, 14.65it/s]\u001b[A\n 52% 325/630 [00:22<00:20, 14.61it/s]\u001b[A\n 52% 327/630 [00:22<00:20, 14.61it/s]\u001b[A\n 52% 329/630 [00:22<00:20, 14.67it/s]\u001b[A\n 53% 331/630 [00:22<00:20, 14.62it/s]\u001b[A\n 53% 333/630 [00:22<00:20, 14.61it/s]\u001b[A\n 53% 335/630 [00:22<00:20, 14.63it/s]\u001b[A\n 53% 337/630 [00:22<00:20, 14.64it/s]\u001b[A\n 54% 339/630 [00:23<00:19, 14.59it/s]\u001b[A\n 54% 341/630 [00:23<00:19, 14.55it/s]\u001b[A\n 54% 343/630 [00:23<00:19, 14.65it/s]\u001b[A\n 55% 345/630 [00:23<00:19, 14.66it/s]\u001b[A\n 55% 347/630 [00:23<00:19, 14.65it/s]\u001b[A\n 55% 349/630 [00:23<00:19, 14.63it/s]\u001b[A\n 56% 351/630 [00:23<00:19, 14.56it/s]\u001b[A\n 56% 353/630 [00:24<00:19, 14.45it/s]\u001b[A\n 56% 355/630 [00:24<00:18, 14.51it/s]\u001b[A\n 57% 357/630 [00:24<00:18, 14.58it/s]\u001b[A\n 57% 359/630 [00:24<00:18, 14.59it/s]\u001b[A\n 57% 361/630 [00:24<00:18, 14.64it/s]\u001b[A\n 58% 363/630 [00:24<00:18, 14.67it/s]\u001b[A\n 58% 365/630 [00:24<00:18, 14.67it/s]\u001b[A\n 58% 367/630 [00:25<00:17, 14.77it/s]\u001b[A\n 59% 369/630 [00:25<00:17, 14.71it/s]\u001b[A\n 59% 371/630 [00:25<00:17, 14.64it/s]\u001b[A\n 59% 373/630 [00:25<00:17, 14.62it/s]\u001b[A\n 60% 375/630 [00:25<00:17, 14.69it/s]\u001b[A\n 60% 377/630 [00:25<00:17, 14.67it/s]\u001b[A\n 60% 379/630 [00:25<00:17, 14.68it/s]\u001b[A\n 60% 381/630 [00:25<00:17, 14.60it/s]\u001b[A\n 61% 383/630 [00:26<00:16, 14.68it/s]\u001b[A\n 61% 385/630 [00:26<00:16, 14.63it/s]\u001b[A\n 61% 387/630 [00:26<00:16, 14.68it/s]\u001b[A\n 62% 389/630 [00:26<00:16, 14.76it/s]\u001b[A\n 62% 391/630 [00:26<00:16, 14.67it/s]\u001b[A\n 62% 393/630 [00:26<00:16, 14.69it/s]\u001b[A\n 63% 395/630 [00:26<00:16, 14.66it/s]\u001b[A\n 63% 397/630 [00:27<00:15, 14.68it/s]\u001b[A\n 63% 399/630 [00:27<00:15, 14.69it/s]\u001b[A\n 64% 401/630 [00:27<00:15, 14.70it/s]\u001b[A\n 64% 403/630 [00:27<00:15, 14.59it/s]\u001b[A\n 64% 405/630 [00:27<00:15, 14.62it/s]\u001b[A\n 65% 407/630 [00:27<00:15, 14.57it/s]\u001b[A\n 65% 409/630 [00:27<00:15, 14.46it/s]\u001b[A\n 65% 411/630 [00:28<00:15, 14.52it/s]\u001b[A\n 66% 413/630 [00:28<00:14, 14.63it/s]\u001b[A\n 66% 415/630 [00:28<00:14, 14.70it/s]\u001b[A\n 66% 417/630 [00:28<00:14, 14.66it/s]\u001b[A\n 67% 419/630 [00:28<00:14, 14.64it/s]\u001b[A\n 67% 421/630 [00:28<00:14, 14.67it/s]\u001b[A\n 67% 423/630 [00:28<00:14, 14.64it/s]\u001b[A\n 67% 425/630 [00:28<00:14, 14.63it/s]\u001b[A\n 68% 427/630 [00:29<00:13, 14.61it/s]\u001b[A\n 68% 429/630 [00:29<00:13, 14.61it/s]\u001b[A\n 68% 431/630 [00:29<00:13, 14.55it/s]\u001b[A\n 69% 433/630 [00:29<00:13, 14.52it/s]\u001b[A\n 69% 435/630 [00:29<00:13, 14.59it/s]\u001b[A\n 69% 437/630 [00:29<00:13, 14.65it/s]\u001b[A\n 70% 439/630 [00:29<00:13, 14.63it/s]\u001b[A\n 70% 441/630 [00:30<00:12, 14.59it/s]\u001b[A\n 70% 443/630 [00:30<00:12, 14.57it/s]\u001b[A\n 71% 445/630 [00:30<00:12, 14.60it/s]\u001b[A\n 71% 447/630 [00:30<00:12, 14.62it/s]\u001b[A\n 71% 449/630 [00:30<00:12, 14.55it/s]\u001b[A\n 72% 451/630 [00:30<00:12, 14.55it/s]\u001b[A\n 72% 453/630 [00:30<00:12, 14.62it/s]\u001b[A\n 72% 455/630 [00:31<00:11, 14.62it/s]\u001b[A\n 73% 457/630 [00:31<00:11, 14.60it/s]\u001b[A\n 73% 459/630 [00:31<00:11, 14.65it/s]\u001b[A\n 73% 461/630 [00:31<00:11, 14.64it/s]\u001b[A\n 73% 463/630 [00:31<00:11, 14.61it/s]\u001b[A\n 74% 465/630 [00:31<00:11, 14.54it/s]\u001b[A\n 74% 467/630 [00:31<00:11, 14.55it/s]\u001b[A\n 74% 469/630 [00:31<00:10, 14.67it/s]\u001b[A\n 75% 471/630 [00:32<00:10, 14.68it/s]\u001b[A\n 75% 473/630 [00:32<00:10, 14.62it/s]\u001b[A\n 75% 475/630 [00:32<00:10, 14.57it/s]\u001b[A\n 76% 477/630 [00:32<00:10, 14.62it/s]\u001b[A\n 76% 479/630 [00:32<00:10, 14.64it/s]\u001b[A\n 76% 481/630 [00:32<00:10, 14.57it/s]\u001b[A\n 77% 483/630 [00:32<00:10, 14.60it/s]\u001b[A\n 77% 485/630 [00:33<00:09, 14.61it/s]\u001b[A\n 77% 487/630 [00:33<00:09, 14.58it/s]\u001b[A\n 78% 489/630 [00:33<00:09, 14.54it/s]\u001b[A\n 78% 491/630 [00:33<00:09, 14.50it/s]\u001b[A\n 78% 493/630 [00:33<00:09, 14.56it/s]\u001b[A\n 79% 495/630 [00:33<00:09, 14.57it/s]\u001b[A\n 79% 497/630 [00:33<00:09, 14.56it/s]\u001b[A\n 79% 499/630 [00:34<00:09, 14.54it/s]\u001b[A\n 80% 501/630 [00:34<00:08, 14.54it/s]\u001b[A\n 80% 503/630 [00:34<00:08, 14.58it/s]\u001b[A\n 80% 505/630 [00:34<00:08, 14.62it/s]\u001b[A\n 80% 507/630 [00:34<00:08, 14.62it/s]\u001b[A\n 81% 509/630 [00:34<00:08, 14.61it/s]\u001b[A\n 81% 511/630 [00:34<00:08, 14.62it/s]\u001b[A\n 81% 513/630 [00:35<00:08, 14.60it/s]\u001b[A\n 82% 515/630 [00:35<00:07, 14.60it/s]\u001b[A\n 82% 517/630 [00:35<00:07, 14.64it/s]\u001b[A\n 82% 519/630 [00:35<00:07, 14.65it/s]\u001b[A\n 83% 521/630 [00:35<00:07, 14.59it/s]\u001b[A\n 83% 523/630 [00:35<00:07, 14.61it/s]\u001b[A\n 83% 525/630 [00:35<00:07, 14.68it/s]\u001b[A\n 84% 527/630 [00:35<00:07, 14.71it/s]\u001b[A\n 84% 529/630 [00:36<00:06, 14.65it/s]\u001b[A\n 84% 531/630 [00:36<00:06, 14.68it/s]\u001b[A\n 85% 533/630 [00:36<00:06, 14.59it/s]\u001b[A\n 85% 535/630 [00:36<00:06, 14.60it/s]\u001b[A\n 85% 537/630 [00:36<00:06, 14.56it/s]\u001b[A\n 86% 539/630 [00:36<00:06, 14.52it/s]\u001b[A\n 86% 541/630 [00:36<00:06, 14.59it/s]\u001b[A\n 86% 543/630 [00:37<00:05, 14.65it/s]\u001b[A\n 87% 545/630 [00:37<00:05, 14.61it/s]\u001b[A\n 87% 547/630 [00:37<00:05, 14.62it/s]\u001b[A\n 87% 549/630 [00:37<00:05, 14.66it/s]\u001b[A\n 87% 551/630 [00:37<00:05, 14.66it/s]\u001b[A\n 88% 553/630 [00:37<00:05, 14.55it/s]\u001b[A\n 88% 555/630 [00:37<00:05, 14.57it/s]\u001b[A\n 88% 557/630 [00:38<00:05, 14.57it/s]\u001b[A\n 89% 559/630 [00:38<00:04, 14.65it/s]\u001b[A\n 89% 561/630 [00:38<00:04, 14.66it/s]\u001b[A\n 89% 563/630 [00:38<00:04, 14.69it/s]\u001b[A\n 90% 565/630 [00:38<00:04, 14.71it/s]\u001b[A\n 90% 567/630 [00:38<00:04, 14.71it/s]\u001b[A\n 90% 569/630 [00:38<00:04, 14.68it/s]\u001b[A\n 91% 571/630 [00:38<00:03, 14.81it/s]\u001b[A\n 91% 573/630 [00:39<00:03, 14.79it/s]\u001b[A\n 91% 575/630 [00:39<00:03, 14.83it/s]\u001b[A\n 92% 577/630 [00:39<00:03, 14.82it/s]\u001b[A\n 92% 579/630 [00:39<00:03, 14.73it/s]\u001b[A\n 92% 581/630 [00:39<00:03, 14.67it/s]\u001b[A\n 93% 583/630 [00:39<00:03, 14.63it/s]\u001b[A\n 93% 585/630 [00:39<00:03, 14.74it/s]\u001b[A\n 93% 587/630 [00:40<00:02, 14.72it/s]\u001b[A\n 93% 589/630 [00:40<00:02, 14.70it/s]\u001b[A\n 94% 591/630 [00:40<00:02, 14.71it/s]\u001b[A\n 94% 593/630 [00:40<00:02, 14.66it/s]\u001b[A\n 94% 595/630 [00:40<00:02, 14.57it/s]\u001b[A\n 95% 597/630 [00:40<00:02, 14.58it/s]\u001b[A\n 95% 599/630 [00:40<00:02, 14.59it/s]\u001b[A\n 95% 601/630 [00:41<00:01, 14.68it/s]\u001b[A\n 96% 603/630 [00:41<00:01, 14.67it/s]\u001b[A\n 96% 605/630 [00:41<00:01, 14.66it/s]\u001b[A\n 96% 607/630 [00:41<00:01, 14.61it/s]\u001b[A\n 97% 609/630 [00:41<00:01, 14.62it/s]\u001b[A\n 97% 611/630 [00:41<00:01, 14.51it/s]\u001b[A\n 97% 613/630 [00:41<00:01, 14.50it/s]\u001b[A\n 98% 615/630 [00:41<00:01, 14.50it/s]\u001b[A\n 98% 617/630 [00:42<00:00, 14.57it/s]\u001b[A\n 98% 619/630 [00:42<00:00, 14.61it/s]\u001b[A\n 99% 621/630 [00:42<00:00, 14.60it/s]\u001b[A\n 99% 623/630 [00:42<00:00, 14.57it/s]\u001b[A\n 99% 625/630 [00:42<00:00, 14.46it/s]\u001b[A\n100% 627/630 [00:42<00:00, 14.56it/s]\u001b[A\n100% 629/630 [00:42<00:00, 14.62it/s]\u001b[A\n \n\u001b[A{'eval_loss': 0.05753315985202789, 'eval_accuracy_score': 0.9774768153980753, 'eval_precision': 0.7869513287548522, 'eval_recall': 0.8365338835105539, 'eval_f1': 0.8109854604200323, 'eval_runtime': 62.4658, 'eval_samples_per_second': 80.652, 'epoch': 2.0}\n 67% 944/1416 [12:47<04:55, 1.60it/s]\n100% 630/630 [01:02<00:00, 14.62it/s]\u001b[A\n{'loss': 0.0289, 'learning_rate': 1.4689265536723165e-05, 'epoch': 2.12}\n{'loss': 0.02, 'learning_rate': 1.115819209039548e-05, 'epoch': 2.33}\n{'loss': 0.0221, 'learning_rate': 7.627118644067798e-06, 'epoch': 2.54}\n{'loss': 0.0216, 'learning_rate': 4.096045197740113e-06, 'epoch': 2.75}\n{'loss': 0.0196, 'learning_rate': 5.649717514124295e-07, 'epoch': 2.97}\n100% 1416/1416 [18:11<00:00, 1.60it/s]\n 0% 0/630 [00:00<?, ?it/s]\u001b[A\n 0% 3/630 [00:00<00:29, 21.32it/s]\u001b[A\n 1% 5/630 [00:00<00:32, 18.97it/s]\u001b[A\n 1% 7/630 [00:00<00:36, 17.26it/s]\u001b[A\n 1% 9/630 [00:00<00:37, 16.53it/s]\u001b[A\n 2% 11/630 [00:00<00:39, 15.73it/s]\u001b[A\n 2% 13/630 [00:00<00:40, 15.31it/s]\u001b[A\n 2% 15/630 [00:00<00:40, 15.13it/s]\u001b[A\n 3% 17/630 [00:01<00:40, 15.05it/s]\u001b[A\n 3% 19/630 [00:01<00:40, 14.96it/s]\u001b[A\n 3% 21/630 [00:01<00:41, 14.85it/s]\u001b[A\n 4% 23/630 [00:01<00:40, 14.84it/s]\u001b[A\n 4% 25/630 [00:01<00:41, 14.70it/s]\u001b[A\n 4% 27/630 [00:01<00:41, 14.62it/s]\u001b[A\n 5% 29/630 [00:01<00:41, 14.64it/s]\u001b[A\n 5% 31/630 [00:02<00:40, 14.72it/s]\u001b[A\n 5% 33/630 [00:02<00:40, 14.71it/s]\u001b[A\n 6% 35/630 [00:02<00:40, 14.65it/s]\u001b[A\n 6% 37/630 [00:02<00:40, 14.74it/s]\u001b[A\n 6% 39/630 [00:02<00:40, 14.69it/s]\u001b[A\n 7% 41/630 [00:02<00:40, 14.65it/s]\u001b[A\n 7% 43/630 [00:02<00:40, 14.65it/s]\u001b[A\n 7% 45/630 [00:03<00:39, 14.73it/s]\u001b[A\n 7% 47/630 [00:03<00:39, 14.78it/s]\u001b[A\n 8% 49/630 [00:03<00:39, 14.82it/s]\u001b[A\n 8% 51/630 [00:03<00:39, 14.70it/s]\u001b[A\n 8% 53/630 [00:03<00:39, 14.62it/s]\u001b[A\n 9% 55/630 [00:03<00:39, 14.60it/s]\u001b[A\n 9% 57/630 [00:03<00:39, 14.65it/s]\u001b[A\n 9% 59/630 [00:03<00:38, 14.68it/s]\u001b[A\n 10% 61/630 [00:04<00:38, 14.67it/s]\u001b[A\n 10% 63/630 [00:04<00:38, 14.73it/s]\u001b[A\n 10% 65/630 [00:04<00:38, 14.74it/s]\u001b[A\n 11% 67/630 [00:04<00:38, 14.61it/s]\u001b[A\n 11% 69/630 [00:04<00:38, 14.61it/s]\u001b[A\n 11% 71/630 [00:04<00:38, 14.65it/s]\u001b[A\n 12% 73/630 [00:04<00:37, 14.67it/s]\u001b[A\n 12% 75/630 [00:05<00:38, 14.60it/s]\u001b[A\n 12% 77/630 [00:05<00:37, 14.66it/s]\u001b[A\n 13% 79/630 [00:05<00:37, 14.60it/s]\u001b[A\n 13% 81/630 [00:05<00:37, 14.63it/s]\u001b[A\n 13% 83/630 [00:05<00:37, 14.59it/s]\u001b[A\n 13% 85/630 [00:05<00:37, 14.60it/s]\u001b[A\n 14% 87/630 [00:05<00:37, 14.63it/s]\u001b[A\n 14% 89/630 [00:06<00:36, 14.67it/s]\u001b[A\n 14% 91/630 [00:06<00:36, 14.70it/s]\u001b[A\n 15% 93/630 [00:06<00:36, 14.74it/s]\u001b[A\n 15% 95/630 [00:06<00:36, 14.76it/s]\u001b[A\n 15% 97/630 [00:06<00:36, 14.63it/s]\u001b[A\n 16% 99/630 [00:06<00:36, 14.59it/s]\u001b[A\n 16% 101/630 [00:06<00:35, 14.71it/s]\u001b[A\n 16% 103/630 [00:06<00:35, 14.66it/s]\u001b[A\n 17% 105/630 [00:07<00:35, 14.62it/s]\u001b[A\n 17% 107/630 [00:07<00:35, 14.71it/s]\u001b[A\n 17% 109/630 [00:07<00:35, 14.74it/s]\u001b[A\n 18% 111/630 [00:07<00:35, 14.75it/s]\u001b[A\n 18% 113/630 [00:07<00:35, 14.68it/s]\u001b[A\n 18% 115/630 [00:07<00:34, 14.74it/s]\u001b[A\n 19% 117/630 [00:07<00:34, 14.70it/s]\u001b[A\n 19% 119/630 [00:08<00:34, 14.61it/s]\u001b[A\n 19% 121/630 [00:08<00:34, 14.61it/s]\u001b[A\n 20% 123/630 [00:08<00:34, 14.54it/s]\u001b[A\n 20% 125/630 [00:08<00:34, 14.64it/s]\u001b[A\n 20% 127/630 [00:08<00:34, 14.51it/s]\u001b[A\n 20% 129/630 [00:08<00:34, 14.52it/s]\u001b[A\n 21% 131/630 [00:08<00:34, 14.60it/s]\u001b[A\n 21% 133/630 [00:09<00:33, 14.63it/s]\u001b[A\n 21% 135/630 [00:09<00:33, 14.66it/s]\u001b[A\n 22% 137/630 [00:09<00:33, 14.72it/s]\u001b[A\n 22% 139/630 [00:09<00:33, 14.76it/s]\u001b[A\n 22% 141/630 [00:09<00:33, 14.67it/s]\u001b[A\n 23% 143/630 [00:09<00:33, 14.63it/s]\u001b[A\n 23% 145/630 [00:09<00:33, 14.66it/s]\u001b[A\n 23% 147/630 [00:09<00:32, 14.70it/s]\u001b[A\n 24% 149/630 [00:10<00:32, 14.70it/s]\u001b[A\n 24% 151/630 [00:10<00:32, 14.73it/s]\u001b[A\n 24% 153/630 [00:10<00:32, 14.76it/s]\u001b[A\n 25% 155/630 [00:10<00:32, 14.65it/s]\u001b[A\n 25% 157/630 [00:10<00:32, 14.59it/s]\u001b[A\n 25% 159/630 [00:10<00:32, 14.59it/s]\u001b[A\n 26% 161/630 [00:10<00:31, 14.69it/s]\u001b[A\n 26% 163/630 [00:11<00:31, 14.67it/s]\u001b[A\n 26% 165/630 [00:11<00:31, 14.71it/s]\u001b[A\n 27% 167/630 [00:11<00:31, 14.60it/s]\u001b[A\n 27% 169/630 [00:11<00:31, 14.64it/s]\u001b[A\n 27% 171/630 [00:11<00:31, 14.56it/s]\u001b[A\n 27% 173/630 [00:11<00:31, 14.48it/s]\u001b[A\n 28% 175/630 [00:11<00:31, 14.50it/s]\u001b[A\n 28% 177/630 [00:12<00:31, 14.55it/s]\u001b[A\n 28% 179/630 [00:12<00:30, 14.55it/s]\u001b[A\n 29% 181/630 [00:12<00:30, 14.53it/s]\u001b[A\n 29% 183/630 [00:12<00:30, 14.51it/s]\u001b[A\n 29% 185/630 [00:12<00:30, 14.60it/s]\u001b[A\n 30% 187/630 [00:12<00:30, 14.64it/s]\u001b[A\n 30% 189/630 [00:12<00:30, 14.66it/s]\u001b[A\n 30% 191/630 [00:12<00:29, 14.69it/s]\u001b[A\n 31% 193/630 [00:13<00:29, 14.68it/s]\u001b[A\n 31% 195/630 [00:13<00:29, 14.73it/s]\u001b[A\n 31% 197/630 [00:13<00:29, 14.64it/s]\u001b[A\n 32% 199/630 [00:13<00:29, 14.74it/s]\u001b[A\n 32% 201/630 [00:13<00:29, 14.71it/s]\u001b[A\n 32% 203/630 [00:13<00:29, 14.60it/s]\u001b[A\n 33% 205/630 [00:13<00:29, 14.60it/s]\u001b[A\n 33% 207/630 [00:14<00:28, 14.64it/s]\u001b[A\n 33% 209/630 [00:14<00:28, 14.75it/s]\u001b[A\n 33% 211/630 [00:14<00:28, 14.72it/s]\u001b[A\n 34% 213/630 [00:14<00:28, 14.69it/s]\u001b[A\n 34% 215/630 [00:14<00:28, 14.66it/s]\u001b[A\n 34% 217/630 [00:14<00:28, 14.68it/s]\u001b[A\n 35% 219/630 [00:14<00:28, 14.66it/s]\u001b[A\n 35% 221/630 [00:15<00:27, 14.61it/s]\u001b[A\n 35% 223/630 [00:15<00:27, 14.70it/s]\u001b[A\n 36% 225/630 [00:15<00:27, 14.71it/s]\u001b[A\n 36% 227/630 [00:15<00:27, 14.72it/s]\u001b[A\n 36% 229/630 [00:15<00:27, 14.71it/s]\u001b[A\n 37% 231/630 [00:15<00:27, 14.63it/s]\u001b[A\n 37% 233/630 [00:15<00:27, 14.59it/s]\u001b[A\n 37% 235/630 [00:15<00:27, 14.62it/s]\u001b[A\n 38% 237/630 [00:16<00:26, 14.65it/s]\u001b[A\n 38% 239/630 [00:16<00:26, 14.65it/s]\u001b[A\n 38% 241/630 [00:16<00:26, 14.57it/s]\u001b[A\n 39% 243/630 [00:16<00:26, 14.57it/s]\u001b[A\n 39% 245/630 [00:16<00:26, 14.51it/s]\u001b[A\n 39% 247/630 [00:16<00:26, 14.57it/s]\u001b[A\n 40% 249/630 [00:16<00:26, 14.60it/s]\u001b[A\n 40% 251/630 [00:17<00:25, 14.67it/s]\u001b[A\n 40% 253/630 [00:17<00:25, 14.72it/s]\u001b[A\n 40% 255/630 [00:17<00:25, 14.69it/s]\u001b[A\n 41% 257/630 [00:17<00:25, 14.64it/s]\u001b[A\n 41% 259/630 [00:17<00:25, 14.63it/s]\u001b[A\n 41% 261/630 [00:17<00:25, 14.66it/s]\u001b[A\n 42% 263/630 [00:17<00:25, 14.67it/s]\u001b[A\n 42% 265/630 [00:18<00:24, 14.65it/s]\u001b[A\n 42% 267/630 [00:18<00:24, 14.75it/s]\u001b[A\n 43% 269/630 [00:18<00:24, 14.73it/s]\u001b[A\n 43% 271/630 [00:18<00:24, 14.65it/s]\u001b[A\n 43% 273/630 [00:18<00:24, 14.65it/s]\u001b[A\n 44% 275/630 [00:18<00:24, 14.52it/s]\u001b[A\n 44% 277/630 [00:18<00:24, 14.55it/s]\u001b[A\n 44% 279/630 [00:18<00:24, 14.60it/s]\u001b[A\n 45% 281/630 [00:19<00:24, 14.53it/s]\u001b[A\n 45% 283/630 [00:19<00:23, 14.62it/s]\u001b[A\n 45% 285/630 [00:19<00:23, 14.70it/s]\u001b[A\n 46% 287/630 [00:19<00:23, 14.66it/s]\u001b[A\n 46% 289/630 [00:19<00:23, 14.64it/s]\u001b[A\n 46% 291/630 [00:19<00:23, 14.60it/s]\u001b[A\n 47% 293/630 [00:19<00:23, 14.65it/s]\u001b[A\n 47% 295/630 [00:20<00:22, 14.63it/s]\u001b[A\n 47% 297/630 [00:20<00:22, 14.69it/s]\u001b[A\n 47% 299/630 [00:20<00:22, 14.71it/s]\u001b[A\n 48% 301/630 [00:20<00:22, 14.62it/s]\u001b[A\n 48% 303/630 [00:20<00:22, 14.56it/s]\u001b[A\n 48% 305/630 [00:20<00:22, 14.57it/s]\u001b[A\n 49% 307/630 [00:20<00:22, 14.62it/s]\u001b[A\n 49% 309/630 [00:21<00:21, 14.66it/s]\u001b[A\n 49% 311/630 [00:21<00:21, 14.54it/s]\u001b[A\n 50% 313/630 [00:21<00:21, 14.63it/s]\u001b[A\n 50% 315/630 [00:21<00:21, 14.64it/s]\u001b[A\n 50% 317/630 [00:21<00:21, 14.58it/s]\u001b[A\n 51% 319/630 [00:21<00:21, 14.61it/s]\u001b[A\n 51% 321/630 [00:21<00:21, 14.58it/s]\u001b[A\n 51% 323/630 [00:21<00:20, 14.72it/s]\u001b[A\n 52% 325/630 [00:22<00:20, 14.56it/s]\u001b[A\n 52% 327/630 [00:22<00:20, 14.54it/s]\u001b[A\n 52% 329/630 [00:22<00:20, 14.66it/s]\u001b[A\n 53% 331/630 [00:22<00:20, 14.67it/s]\u001b[A\n 53% 333/630 [00:22<00:20, 14.67it/s]\u001b[A\n 53% 335/630 [00:22<00:20, 14.66it/s]\u001b[A\n 53% 337/630 [00:22<00:19, 14.66it/s]\u001b[A\n 54% 339/630 [00:23<00:19, 14.67it/s]\u001b[A\n 54% 341/630 [00:23<00:19, 14.64it/s]\u001b[A\n 54% 343/630 [00:23<00:19, 14.70it/s]\u001b[A\n 55% 345/630 [00:23<00:19, 14.73it/s]\u001b[A\n 55% 347/630 [00:23<00:19, 14.62it/s]\u001b[A\n 55% 349/630 [00:23<00:19, 14.54it/s]\u001b[A\n 56% 351/630 [00:23<00:19, 14.60it/s]\u001b[A\n 56% 353/630 [00:24<00:18, 14.60it/s]\u001b[A\n 56% 355/630 [00:24<00:18, 14.59it/s]\u001b[A\n 57% 357/630 [00:24<00:18, 14.54it/s]\u001b[A\n 57% 359/630 [00:24<00:18, 14.60it/s]\u001b[A\n 57% 361/630 [00:24<00:18, 14.59it/s]\u001b[A\n 58% 363/630 [00:24<00:18, 14.63it/s]\u001b[A\n 58% 365/630 [00:24<00:18, 14.60it/s]\u001b[A\n 58% 367/630 [00:24<00:17, 14.72it/s]\u001b[A\n 59% 369/630 [00:25<00:17, 14.67it/s]\u001b[A\n 59% 371/630 [00:25<00:17, 14.62it/s]\u001b[A\n 59% 373/630 [00:25<00:17, 14.65it/s]\u001b[A\n 60% 375/630 [00:25<00:17, 14.65it/s]\u001b[A\n 60% 377/630 [00:25<00:17, 14.60it/s]\u001b[A\n 60% 379/630 [00:25<00:17, 14.55it/s]\u001b[A\n 60% 381/630 [00:25<00:17, 14.54it/s]\u001b[A\n 61% 383/630 [00:26<00:16, 14.55it/s]\u001b[A\n 61% 385/630 [00:26<00:16, 14.62it/s]\u001b[A\n 61% 387/630 [00:26<00:16, 14.66it/s]\u001b[A\n 62% 389/630 [00:26<00:16, 14.69it/s]\u001b[A\n 62% 391/630 [00:26<00:16, 14.58it/s]\u001b[A\n 62% 393/630 [00:26<00:16, 14.58it/s]\u001b[A\n 63% 395/630 [00:26<00:16, 14.61it/s]\u001b[A\n 63% 397/630 [00:27<00:15, 14.69it/s]\u001b[A\n 63% 399/630 [00:27<00:15, 14.67it/s]\u001b[A\n 64% 401/630 [00:27<00:15, 14.70it/s]\u001b[A\n 64% 403/630 [00:27<00:15, 14.70it/s]\u001b[A\n 64% 405/630 [00:27<00:15, 14.73it/s]\u001b[A\n 65% 407/630 [00:27<00:15, 14.66it/s]\u001b[A\n 65% 409/630 [00:27<00:15, 14.63it/s]\u001b[A\n 65% 411/630 [00:28<00:14, 14.70it/s]\u001b[A\n 66% 413/630 [00:28<00:14, 14.63it/s]\u001b[A\n 66% 415/630 [00:28<00:14, 14.59it/s]\u001b[A\n 66% 417/630 [00:28<00:14, 14.59it/s]\u001b[A\n 67% 419/630 [00:28<00:14, 14.62it/s]\u001b[A\n 67% 421/630 [00:28<00:14, 14.63it/s]\u001b[A\n 67% 423/630 [00:28<00:14, 14.58it/s]\u001b[A\n 67% 425/630 [00:28<00:14, 14.55it/s]\u001b[A\n 68% 427/630 [00:29<00:13, 14.54it/s]\u001b[A\n 68% 429/630 [00:29<00:13, 14.65it/s]\u001b[A\n 68% 431/630 [00:29<00:13, 14.63it/s]\u001b[A\n 69% 433/630 [00:29<00:13, 14.64it/s]\u001b[A\n 69% 435/630 [00:29<00:13, 14.71it/s]\u001b[A\n 69% 437/630 [00:29<00:13, 14.70it/s]\u001b[A\n 70% 439/630 [00:29<00:13, 14.68it/s]\u001b[A\n 70% 441/630 [00:30<00:12, 14.76it/s]\u001b[A\n 70% 443/630 [00:30<00:12, 14.66it/s]\u001b[A\n 71% 445/630 [00:30<00:12, 14.65it/s]\u001b[A\n 71% 447/630 [00:30<00:12, 14.63it/s]\u001b[A\n 71% 449/630 [00:30<00:12, 14.68it/s]\u001b[A\n 72% 451/630 [00:30<00:12, 14.64it/s]\u001b[A\n 72% 453/630 [00:30<00:12, 14.61it/s]\u001b[A\n 72% 455/630 [00:31<00:11, 14.67it/s]\u001b[A\n 73% 457/630 [00:31<00:11, 14.67it/s]\u001b[A\n 73% 459/630 [00:31<00:11, 14.65it/s]\u001b[A\n 73% 461/630 [00:31<00:11, 14.67it/s]\u001b[A\n 73% 463/630 [00:31<00:11, 14.66it/s]\u001b[A\n 74% 465/630 [00:31<00:11, 14.64it/s]\u001b[A\n 74% 467/630 [00:31<00:11, 14.61it/s]\u001b[A\n 74% 469/630 [00:31<00:11, 14.60it/s]\u001b[A\n 75% 471/630 [00:32<00:10, 14.64it/s]\u001b[A\n 75% 473/630 [00:32<00:10, 14.66it/s]\u001b[A\n 75% 475/630 [00:32<00:10, 14.66it/s]\u001b[A\n 76% 477/630 [00:32<00:10, 14.66it/s]\u001b[A\n 76% 479/630 [00:32<00:10, 14.65it/s]\u001b[A\n 76% 481/630 [00:32<00:10, 14.63it/s]\u001b[A\n 77% 483/630 [00:32<00:10, 14.62it/s]\u001b[A\n 77% 485/630 [00:33<00:09, 14.65it/s]\u001b[A\n 77% 487/630 [00:33<00:09, 14.62it/s]\u001b[A\n 78% 489/630 [00:33<00:09, 14.67it/s]\u001b[A\n 78% 491/630 [00:33<00:09, 14.72it/s]\u001b[A\n 78% 493/630 [00:33<00:09, 14.67it/s]\u001b[A\n 79% 495/630 [00:33<00:09, 14.62it/s]\u001b[A\n 79% 497/630 [00:33<00:09, 14.55it/s]\u001b[A\n 79% 499/630 [00:34<00:08, 14.63it/s]\u001b[A\n 80% 501/630 [00:34<00:08, 14.60it/s]\u001b[A\n 80% 503/630 [00:34<00:08, 14.62it/s]\u001b[A\n 80% 505/630 [00:34<00:08, 14.62it/s]\u001b[A\n 80% 507/630 [00:34<00:08, 14.61it/s]\u001b[A\n 81% 509/630 [00:34<00:08, 14.66it/s]\u001b[A\n 81% 511/630 [00:34<00:08, 14.59it/s]\u001b[A\n 81% 513/630 [00:34<00:07, 14.68it/s]\u001b[A\n 82% 515/630 [00:35<00:07, 14.66it/s]\u001b[A\n 82% 517/630 [00:35<00:07, 14.59it/s]\u001b[A\n 82% 519/630 [00:35<00:07, 14.65it/s]\u001b[A\n 83% 521/630 [00:35<00:07, 14.64it/s]\u001b[A\n 83% 523/630 [00:35<00:07, 14.66it/s]\u001b[A\n 83% 525/630 [00:35<00:07, 14.64it/s]\u001b[A\n 84% 527/630 [00:35<00:07, 14.64it/s]\u001b[A\n 84% 529/630 [00:36<00:06, 14.66it/s]\u001b[A\n 84% 531/630 [00:36<00:06, 14.65it/s]\u001b[A\n 85% 533/630 [00:36<00:06, 14.69it/s]\u001b[A\n 85% 535/630 [00:36<00:06, 14.68it/s]\u001b[A\n 85% 537/630 [00:36<00:06, 14.59it/s]\u001b[A\n 86% 539/630 [00:36<00:06, 14.59it/s]\u001b[A\n 86% 541/630 [00:36<00:06, 14.64it/s]\u001b[A\n 86% 543/630 [00:37<00:05, 14.67it/s]\u001b[A\n 87% 545/630 [00:37<00:05, 14.55it/s]\u001b[A\n 87% 547/630 [00:37<00:05, 14.51it/s]\u001b[A\n 87% 549/630 [00:37<00:05, 14.53it/s]\u001b[A\n 87% 551/630 [00:37<00:05, 14.57it/s]\u001b[A\n 88% 553/630 [00:37<00:05, 14.55it/s]\u001b[A\n 88% 555/630 [00:37<00:05, 14.57it/s]\u001b[A\n 88% 557/630 [00:37<00:05, 14.48it/s]\u001b[A\n 89% 559/630 [00:38<00:04, 14.57it/s]\u001b[A\n 89% 561/630 [00:38<00:04, 14.60it/s]\u001b[A\n 89% 563/630 [00:38<00:04, 14.63it/s]\u001b[A\n 90% 565/630 [00:38<00:04, 14.63it/s]\u001b[A\n 90% 567/630 [00:38<00:04, 14.57it/s]\u001b[A\n 90% 569/630 [00:38<00:04, 14.51it/s]\u001b[A\n 91% 571/630 [00:38<00:04, 14.60it/s]\u001b[A\n 91% 573/630 [00:39<00:03, 14.56it/s]\u001b[A\n 91% 575/630 [00:39<00:03, 14.63it/s]\u001b[A\n 92% 577/630 [00:39<00:03, 14.70it/s]\u001b[A\n 92% 579/630 [00:39<00:03, 14.72it/s]\u001b[A\n 92% 581/630 [00:39<00:03, 14.69it/s]\u001b[A\n 93% 583/630 [00:39<00:03, 14.65it/s]\u001b[A\n 93% 585/630 [00:39<00:03, 14.70it/s]\u001b[A\n 93% 587/630 [00:40<00:02, 14.61it/s]\u001b[A\n 93% 589/630 [00:40<00:02, 14.69it/s]\u001b[A\n 94% 591/630 [00:40<00:02, 14.69it/s]\u001b[A\n 94% 593/630 [00:40<00:02, 14.67it/s]\u001b[A\n 94% 595/630 [00:40<00:02, 14.69it/s]\u001b[A\n 95% 597/630 [00:40<00:02, 14.65it/s]\u001b[A\n 95% 599/630 [00:40<00:02, 14.70it/s]\u001b[A\n 95% 601/630 [00:40<00:01, 14.59it/s]\u001b[A\n 96% 603/630 [00:41<00:01, 14.63it/s]\u001b[A\n 96% 605/630 [00:41<00:01, 14.58it/s]\u001b[A\n 96% 607/630 [00:41<00:01, 14.61it/s]\u001b[A\n 97% 609/630 [00:41<00:01, 14.58it/s]\u001b[A\n 97% 611/630 [00:41<00:01, 14.52it/s]\u001b[A\n 97% 613/630 [00:41<00:01, 14.63it/s]\u001b[A\n 98% 615/630 [00:41<00:01, 14.53it/s]\u001b[A\n 98% 617/630 [00:42<00:00, 14.62it/s]\u001b[A\n 98% 619/630 [00:42<00:00, 14.55it/s]\u001b[A\n 99% 621/630 [00:42<00:00, 14.62it/s]\u001b[A\n 99% 623/630 [00:42<00:00, 14.62it/s]\u001b[A\n 99% 625/630 [00:42<00:00, 14.62it/s]\u001b[A\n100% 627/630 [00:42<00:00, 14.68it/s]\u001b[A\n100% 629/630 [00:42<00:00, 14.65it/s]\u001b[A\n \n\u001b[A{'eval_loss': 0.06635135412216187, 'eval_accuracy_score': 0.9786596675415573, 'eval_precision': 0.8015325670498085, 'eval_recall': 0.8300269798444692, 'eval_f1': 0.815530952752222, 'eval_runtime': 62.2005, 'eval_samples_per_second': 80.996, 'epoch': 3.0}\n100% 1416/1416 [19:13<00:00, 1.60it/s]\n100% 630/630 [01:02<00:00, 14.65it/s]\u001b[A\n{'train_runtime': 1154.0141, 'train_samples_per_second': 1.227, 'epoch': 3.0}\n100% 1416/1416 [19:13<00:00, 1.23it/s]\n" ], [ "!python train_teacher.py \\\n--data_dir 'data/BC5CDR-chem' \\\n--model_name_or_path 'dmis-lab/biobert-base-cased-v1.1' \\\n--output_dir 'models/Teachers/BC5CDR-chem' \\\n--logging_dir 'models/Teachers/BC5CDR-chem' \\\n--save_steps 10000", "2021-03-29 16:36:06.082885: I tensorflow/stream_executor/platform/default/dso_loader.cc:49] Successfully opened dynamic library libcudart.so.11.0\nNamespace(data_dir='data/BC5CDR-chem', do_eval=True, do_predict=True, do_train=True, evaluation_strategy='epoch', logging_dir='models/Teachers/BC5CDR-chem', logging_steps=100, max_seq_length=128, model_name_or_path='dmis-lab/biobert-base-cased-v1.1', num_train_epochs=3, output_dir='models/Teachers/BC5CDR-chem', per_device_train_batch_size=32, save_steps=10000, seed=1)\n03/29/2021 16:36:07 - WARNING - __main__ - Process rank: -1, device: cuda:0, n_gpu: 1, distributed training: False, 16-bits training: False\n03/29/2021 16:36:07 - INFO - __main__ - Training/evaluation parameters TrainingArguments(output_dir=models/Teachers/BC5CDR-chem, overwrite_output_dir=False, do_train=True, do_eval=True, do_predict=True, evaluation_strategy=IntervalStrategy.EPOCH, prediction_loss_only=False, per_device_train_batch_size=32, per_device_eval_batch_size=8, gradient_accumulation_steps=1, eval_accumulation_steps=None, learning_rate=5e-05, weight_decay=0.0, adam_beta1=0.9, adam_beta2=0.999, adam_epsilon=1e-08, max_grad_norm=1.0, num_train_epochs=3, max_steps=-1, lr_scheduler_type=SchedulerType.LINEAR, warmup_ratio=0.0, warmup_steps=0, logging_dir=models/Teachers/BC5CDR-chem, logging_strategy=IntervalStrategy.STEPS, logging_first_step=False, logging_steps=100, save_strategy=IntervalStrategy.STEPS, save_steps=10000, save_total_limit=None, no_cuda=False, seed=1, fp16=False, fp16_opt_level=O1, fp16_backend=auto, fp16_full_eval=False, local_rank=-1, tpu_num_cores=None, tpu_metrics_debug=False, debug=False, dataloader_drop_last=False, eval_steps=100, dataloader_num_workers=0, past_index=-1, run_name=models/Teachers/BC5CDR-chem, disable_tqdm=False, remove_unused_columns=True, label_names=None, load_best_model_at_end=False, metric_for_best_model=None, greater_is_better=None, ignore_data_skip=False, sharded_ddp=[], deepspeed=None, label_smoothing_factor=0.0, adafactor=False, group_by_length=False, report_to=['tensorboard'], ddp_find_unused_parameters=None, dataloader_pin_memory=True, skip_memory_metrics=False, _n_gpu=1)\n03/29/2021 16:36:09 - INFO - filelock - Lock 139803467959376 acquired on data/BC5CDR-chem/cached_train_dev_BertTokenizer_128.lock\n03/29/2021 16:36:09 - INFO - src.data_handling.DataHandlers - Loading features from cached file data/BC5CDR-chem/cached_train_dev_BertTokenizer_128\n03/29/2021 16:36:10 - INFO - filelock - Lock 139803467959376 released on data/BC5CDR-chem/cached_train_dev_BertTokenizer_128.lock\n03/29/2021 16:36:10 - INFO - filelock - Lock 139803468389456 acquired on data/BC5CDR-chem/cached_test_BertTokenizer_128.lock\n03/29/2021 16:36:10 - INFO - src.data_handling.DataHandlers - Loading features from cached file data/BC5CDR-chem/cached_test_BertTokenizer_128\n03/29/2021 16:36:10 - INFO - filelock - Lock 139803468389456 released on data/BC5CDR-chem/cached_test_BertTokenizer_128.lock\nSome weights of the model checkpoint at dmis-lab/biobert-base-cased-v1.1 were not used when initializing BertForTokenClassification: ['cls.predictions.bias', 'cls.predictions.transform.dense.weight', 'cls.predictions.transform.dense.bias', 'cls.predictions.transform.LayerNorm.weight', 'cls.predictions.transform.LayerNorm.bias', 'cls.predictions.decoder.weight', 'cls.predictions.decoder.bias', 'cls.seq_relationship.weight', 'cls.seq_relationship.bias']\n- This IS expected if you are initializing BertForTokenClassification from the checkpoint of a model trained on another task or with another architecture (e.g. initializing a BertForSequenceClassification model from a BertForPreTraining model).\n- This IS NOT expected if you are initializing BertForTokenClassification from the checkpoint of a model that you expect to be exactly identical (initializing a BertForSequenceClassification model from a BertForSequenceClassification model).\nSome weights of BertForTokenClassification were not initialized from the model checkpoint at dmis-lab/biobert-base-cased-v1.1 and are newly initialized: ['classifier.weight', 'classifier.bias']\nYou should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.\n/usr/local/lib/python3.7/dist-packages/transformers/trainer.py:836: FutureWarning: `model_path` is deprecated and will be removed in a future version. Use `resume_from_checkpoint` instead.\n FutureWarning,\n{'loss': 0.0813, 'learning_rate': 4.4172494172494175e-05, 'epoch': 0.35}\n{'loss': 0.024, 'learning_rate': 3.834498834498835e-05, 'epoch': 0.7}\n 33% 286/858 [03:16<05:56, 1.60it/s]\n 0% 0/600 [00:00<?, ?it/s]\u001b[A\n 0% 3/600 [00:00<00:27, 21.45it/s]\u001b[A\n 1% 5/600 [00:00<00:31, 18.84it/s]\u001b[A\n 1% 7/600 [00:00<00:34, 17.22it/s]\u001b[A\n 2% 9/600 [00:00<00:35, 16.55it/s]\u001b[A\n 2% 11/600 [00:00<00:37, 15.77it/s]\u001b[A\n 2% 13/600 [00:00<00:38, 15.36it/s]\u001b[A\n 2% 15/600 [00:00<00:38, 15.21it/s]\u001b[A\n 3% 17/600 [00:01<00:38, 15.23it/s]\u001b[A\n 3% 19/600 [00:01<00:38, 15.09it/s]\u001b[A\n 4% 21/600 [00:01<00:38, 14.91it/s]\u001b[A\n 4% 23/600 [00:01<00:38, 14.96it/s]\u001b[A\n 4% 25/600 [00:01<00:38, 14.77it/s]\u001b[A\n 4% 27/600 [00:01<00:39, 14.68it/s]\u001b[A\n 5% 29/600 [00:01<00:38, 14.69it/s]\u001b[A\n 5% 31/600 [00:02<00:38, 14.84it/s]\u001b[A\n 6% 33/600 [00:02<00:38, 14.81it/s]\u001b[A\n 6% 35/600 [00:02<00:38, 14.64it/s]\u001b[A\n 6% 37/600 [00:02<00:38, 14.71it/s]\u001b[A\n 6% 39/600 [00:02<00:38, 14.63it/s]\u001b[A\n 7% 41/600 [00:02<00:38, 14.57it/s]\u001b[A\n 7% 43/600 [00:02<00:37, 14.68it/s]\u001b[A\n 8% 45/600 [00:02<00:37, 14.81it/s]\u001b[A\n 8% 47/600 [00:03<00:37, 14.77it/s]\u001b[A\n 8% 49/600 [00:03<00:37, 14.86it/s]\u001b[A\n 8% 51/600 [00:03<00:37, 14.78it/s]\u001b[A\n 9% 53/600 [00:03<00:37, 14.78it/s]\u001b[A\n 9% 55/600 [00:03<00:37, 14.66it/s]\u001b[A\n 10% 57/600 [00:03<00:37, 14.66it/s]\u001b[A\n 10% 59/600 [00:03<00:36, 14.72it/s]\u001b[A\n 10% 61/600 [00:04<00:36, 14.73it/s]\u001b[A\n 10% 63/600 [00:04<00:36, 14.78it/s]\u001b[A\n 11% 65/600 [00:04<00:36, 14.79it/s]\u001b[A\n 11% 67/600 [00:04<00:36, 14.72it/s]\u001b[A\n 12% 69/600 [00:04<00:36, 14.66it/s]\u001b[A\n 12% 71/600 [00:04<00:36, 14.66it/s]\u001b[A\n 12% 73/600 [00:04<00:35, 14.69it/s]\u001b[A\n 12% 75/600 [00:05<00:35, 14.74it/s]\u001b[A\n 13% 77/600 [00:05<00:35, 14.82it/s]\u001b[A\n 13% 79/600 [00:05<00:35, 14.73it/s]\u001b[A\n 14% 81/600 [00:05<00:35, 14.75it/s]\u001b[A\n 14% 83/600 [00:05<00:35, 14.76it/s]\u001b[A\n 14% 85/600 [00:05<00:35, 14.71it/s]\u001b[A\n 14% 87/600 [00:05<00:35, 14.60it/s]\u001b[A\n 15% 89/600 [00:05<00:35, 14.59it/s]\u001b[A\n 15% 91/600 [00:06<00:34, 14.67it/s]\u001b[A\n 16% 93/600 [00:06<00:34, 14.65it/s]\u001b[A\n 16% 95/600 [00:06<00:34, 14.63it/s]\u001b[A\n 16% 97/600 [00:06<00:34, 14.64it/s]\u001b[A\n 16% 99/600 [00:06<00:34, 14.67it/s]\u001b[A\n 17% 101/600 [00:06<00:34, 14.62it/s]\u001b[A\n 17% 103/600 [00:06<00:33, 14.67it/s]\u001b[A\n 18% 105/600 [00:07<00:33, 14.64it/s]\u001b[A\n 18% 107/600 [00:07<00:33, 14.55it/s]\u001b[A\n 18% 109/600 [00:07<00:33, 14.64it/s]\u001b[A\n 18% 111/600 [00:07<00:33, 14.57it/s]\u001b[A\n 19% 113/600 [00:07<00:33, 14.62it/s]\u001b[A\n 19% 115/600 [00:07<00:33, 14.58it/s]\u001b[A\n 20% 117/600 [00:07<00:33, 14.63it/s]\u001b[A\n 20% 119/600 [00:08<00:32, 14.63it/s]\u001b[A\n 20% 121/600 [00:08<00:32, 14.61it/s]\u001b[A\n 20% 123/600 [00:08<00:32, 14.59it/s]\u001b[A\n 21% 125/600 [00:08<00:32, 14.65it/s]\u001b[A\n 21% 127/600 [00:08<00:32, 14.62it/s]\u001b[A\n 22% 129/600 [00:08<00:32, 14.69it/s]\u001b[A\n 22% 131/600 [00:08<00:31, 14.72it/s]\u001b[A\n 22% 133/600 [00:08<00:31, 14.75it/s]\u001b[A\n 22% 135/600 [00:09<00:31, 14.72it/s]\u001b[A\n 23% 137/600 [00:09<00:31, 14.65it/s]\u001b[A\n 23% 139/600 [00:09<00:31, 14.61it/s]\u001b[A\n 24% 141/600 [00:09<00:31, 14.56it/s]\u001b[A\n 24% 143/600 [00:09<00:31, 14.59it/s]\u001b[A\n 24% 145/600 [00:09<00:31, 14.66it/s]\u001b[A\n 24% 147/600 [00:09<00:30, 14.68it/s]\u001b[A\n 25% 149/600 [00:10<00:30, 14.64it/s]\u001b[A\n 25% 151/600 [00:10<00:30, 14.72it/s]\u001b[A\n 26% 153/600 [00:10<00:30, 14.70it/s]\u001b[A\n 26% 155/600 [00:10<00:30, 14.65it/s]\u001b[A\n 26% 157/600 [00:10<00:30, 14.59it/s]\u001b[A\n 26% 159/600 [00:10<00:30, 14.70it/s]\u001b[A\n 27% 161/600 [00:10<00:29, 14.73it/s]\u001b[A\n 27% 163/600 [00:11<00:29, 14.72it/s]\u001b[A\n 28% 165/600 [00:11<00:29, 14.71it/s]\u001b[A\n 28% 167/600 [00:11<00:29, 14.64it/s]\u001b[A\n 28% 169/600 [00:11<00:29, 14.57it/s]\u001b[A\n 28% 171/600 [00:11<00:29, 14.62it/s]\u001b[A\n 29% 173/600 [00:11<00:29, 14.65it/s]\u001b[A\n 29% 175/600 [00:11<00:28, 14.77it/s]\u001b[A\n 30% 177/600 [00:11<00:28, 14.67it/s]\u001b[A\n 30% 179/600 [00:12<00:28, 14.59it/s]\u001b[A\n 30% 181/600 [00:12<00:28, 14.66it/s]\u001b[A\n 30% 183/600 [00:12<00:28, 14.68it/s]\u001b[A\n 31% 185/600 [00:12<00:28, 14.68it/s]\u001b[A\n 31% 187/600 [00:12<00:27, 14.76it/s]\u001b[A\n 32% 189/600 [00:12<00:27, 14.80it/s]\u001b[A\n 32% 191/600 [00:12<00:27, 14.68it/s]\u001b[A\n 32% 193/600 [00:13<00:27, 14.63it/s]\u001b[A\n 32% 195/600 [00:13<00:27, 14.68it/s]\u001b[A\n 33% 197/600 [00:13<00:27, 14.70it/s]\u001b[A\n 33% 199/600 [00:13<00:27, 14.65it/s]\u001b[A\n 34% 201/600 [00:13<00:27, 14.66it/s]\u001b[A\n 34% 203/600 [00:13<00:27, 14.63it/s]\u001b[A\n 34% 205/600 [00:13<00:26, 14.69it/s]\u001b[A\n 34% 207/600 [00:14<00:26, 14.69it/s]\u001b[A\n 35% 209/600 [00:14<00:26, 14.69it/s]\u001b[A\n 35% 211/600 [00:14<00:26, 14.63it/s]\u001b[A\n 36% 213/600 [00:14<00:26, 14.61it/s]\u001b[A\n 36% 215/600 [00:14<00:26, 14.59it/s]\u001b[A\n 36% 217/600 [00:14<00:26, 14.69it/s]\u001b[A\n 36% 219/600 [00:14<00:25, 14.69it/s]\u001b[A\n 37% 221/600 [00:14<00:25, 14.67it/s]\u001b[A\n 37% 223/600 [00:15<00:25, 14.73it/s]\u001b[A\n 38% 225/600 [00:15<00:25, 14.78it/s]\u001b[A\n 38% 227/600 [00:15<00:25, 14.69it/s]\u001b[A\n 38% 229/600 [00:15<00:25, 14.62it/s]\u001b[A\n 38% 231/600 [00:15<00:25, 14.73it/s]\u001b[A\n 39% 233/600 [00:15<00:24, 14.72it/s]\u001b[A\n 39% 235/600 [00:15<00:24, 14.62it/s]\u001b[A\n 40% 237/600 [00:16<00:24, 14.64it/s]\u001b[A\n 40% 239/600 [00:16<00:24, 14.57it/s]\u001b[A\n 40% 241/600 [00:16<00:24, 14.61it/s]\u001b[A\n 40% 243/600 [00:16<00:24, 14.51it/s]\u001b[A\n 41% 245/600 [00:16<00:24, 14.59it/s]\u001b[A\n 41% 247/600 [00:16<00:24, 14.66it/s]\u001b[A\n 42% 249/600 [00:16<00:23, 14.68it/s]\u001b[A\n 42% 251/600 [00:17<00:23, 14.64it/s]\u001b[A\n 42% 253/600 [00:17<00:23, 14.67it/s]\u001b[A\n 42% 255/600 [00:17<00:23, 14.65it/s]\u001b[A\n 43% 257/600 [00:17<00:23, 14.61it/s]\u001b[A\n 43% 259/600 [00:17<00:23, 14.58it/s]\u001b[A\n 44% 261/600 [00:17<00:23, 14.60it/s]\u001b[A\n 44% 263/600 [00:17<00:22, 14.65it/s]\u001b[A\n 44% 265/600 [00:18<00:22, 14.59it/s]\u001b[A\n 44% 267/600 [00:18<00:22, 14.62it/s]\u001b[A\n 45% 269/600 [00:18<00:22, 14.49it/s]\u001b[A\n 45% 271/600 [00:18<00:22, 14.53it/s]\u001b[A\n 46% 273/600 [00:18<00:22, 14.52it/s]\u001b[A\n 46% 275/600 [00:18<00:22, 14.57it/s]\u001b[A\n 46% 277/600 [00:18<00:22, 14.60it/s]\u001b[A\n 46% 279/600 [00:18<00:22, 14.53it/s]\u001b[A\n 47% 281/600 [00:19<00:21, 14.63it/s]\u001b[A\n 47% 283/600 [00:19<00:21, 14.57it/s]\u001b[A\n 48% 285/600 [00:19<00:21, 14.60it/s]\u001b[A\n 48% 287/600 [00:19<00:21, 14.54it/s]\u001b[A\n 48% 289/600 [00:19<00:21, 14.61it/s]\u001b[A\n 48% 291/600 [00:19<00:21, 14.60it/s]\u001b[A\n 49% 293/600 [00:19<00:21, 14.54it/s]\u001b[A\n 49% 295/600 [00:20<00:20, 14.66it/s]\u001b[A\n 50% 297/600 [00:20<00:20, 14.61it/s]\u001b[A\n 50% 299/600 [00:20<00:20, 14.58it/s]\u001b[A\n 50% 301/600 [00:20<00:20, 14.59it/s]\u001b[A\n 50% 303/600 [00:20<00:20, 14.70it/s]\u001b[A\n 51% 305/600 [00:20<00:20, 14.71it/s]\u001b[A\n 51% 307/600 [00:20<00:19, 14.71it/s]\u001b[A\n 52% 309/600 [00:21<00:19, 14.73it/s]\u001b[A\n 52% 311/600 [00:21<00:19, 14.65it/s]\u001b[A\n 52% 313/600 [00:21<00:19, 14.63it/s]\u001b[A\n 52% 315/600 [00:21<00:19, 14.62it/s]\u001b[A\n 53% 317/600 [00:21<00:19, 14.64it/s]\u001b[A\n 53% 319/600 [00:21<00:19, 14.61it/s]\u001b[A\n 54% 321/600 [00:21<00:19, 14.58it/s]\u001b[A\n 54% 323/600 [00:21<00:18, 14.61it/s]\u001b[A\n 54% 325/600 [00:22<00:18, 14.63it/s]\u001b[A\n 55% 327/600 [00:22<00:18, 14.69it/s]\u001b[A\n 55% 329/600 [00:22<00:18, 14.64it/s]\u001b[A\n 55% 331/600 [00:22<00:18, 14.70it/s]\u001b[A\n 56% 333/600 [00:22<00:18, 14.67it/s]\u001b[A\n 56% 335/600 [00:22<00:18, 14.62it/s]\u001b[A\n 56% 337/600 [00:22<00:17, 14.62it/s]\u001b[A\n 56% 339/600 [00:23<00:17, 14.61it/s]\u001b[A\n 57% 341/600 [00:23<00:17, 14.67it/s]\u001b[A\n 57% 343/600 [00:23<00:17, 14.61it/s]\u001b[A\n 57% 345/600 [00:23<00:17, 14.59it/s]\u001b[A\n 58% 347/600 [00:23<00:17, 14.60it/s]\u001b[A\n 58% 349/600 [00:23<00:17, 14.56it/s]\u001b[A\n 58% 351/600 [00:23<00:17, 14.57it/s]\u001b[A\n 59% 353/600 [00:24<00:16, 14.59it/s]\u001b[A\n 59% 355/600 [00:24<00:16, 14.63it/s]\u001b[A\n 60% 357/600 [00:24<00:16, 14.57it/s]\u001b[A\n 60% 359/600 [00:24<00:16, 14.60it/s]\u001b[A\n 60% 361/600 [00:24<00:16, 14.60it/s]\u001b[A\n 60% 363/600 [00:24<00:16, 14.67it/s]\u001b[A\n 61% 365/600 [00:24<00:16, 14.62it/s]\u001b[A\n 61% 367/600 [00:24<00:15, 14.67it/s]\u001b[A\n 62% 369/600 [00:25<00:15, 14.58it/s]\u001b[A\n 62% 371/600 [00:25<00:15, 14.58it/s]\u001b[A\n 62% 373/600 [00:25<00:15, 14.56it/s]\u001b[A\n 62% 375/600 [00:25<00:15, 14.54it/s]\u001b[A\n 63% 377/600 [00:25<00:15, 14.59it/s]\u001b[A\n 63% 379/600 [00:25<00:15, 14.61it/s]\u001b[A\n 64% 381/600 [00:25<00:14, 14.62it/s]\u001b[A\n 64% 383/600 [00:26<00:14, 14.64it/s]\u001b[A\n 64% 385/600 [00:26<00:14, 14.61it/s]\u001b[A\n 64% 387/600 [00:26<00:14, 14.64it/s]\u001b[A\n 65% 389/600 [00:26<00:14, 14.56it/s]\u001b[A\n 65% 391/600 [00:26<00:14, 14.57it/s]\u001b[A\n 66% 393/600 [00:26<00:14, 14.66it/s]\u001b[A\n 66% 395/600 [00:26<00:13, 14.67it/s]\u001b[A\n 66% 397/600 [00:27<00:13, 14.64it/s]\u001b[A\n 66% 399/600 [00:27<00:13, 14.71it/s]\u001b[A\n 67% 401/600 [00:27<00:13, 14.76it/s]\u001b[A\n 67% 403/600 [00:27<00:13, 14.68it/s]\u001b[A\n 68% 405/600 [00:27<00:13, 14.68it/s]\u001b[A\n 68% 407/600 [00:27<00:13, 14.70it/s]\u001b[A\n 68% 409/600 [00:27<00:12, 14.71it/s]\u001b[A\n 68% 411/600 [00:27<00:12, 14.64it/s]\u001b[A\n 69% 413/600 [00:28<00:12, 14.63it/s]\u001b[A\n 69% 415/600 [00:28<00:12, 14.70it/s]\u001b[A\n 70% 417/600 [00:28<00:12, 14.58it/s]\u001b[A\n 70% 419/600 [00:28<00:12, 14.54it/s]\u001b[A\n 70% 421/600 [00:28<00:12, 14.56it/s]\u001b[A\n 70% 423/600 [00:28<00:12, 14.60it/s]\u001b[A\n 71% 425/600 [00:28<00:12, 14.56it/s]\u001b[A\n 71% 427/600 [00:29<00:11, 14.62it/s]\u001b[A\n 72% 429/600 [00:29<00:11, 14.62it/s]\u001b[A\n 72% 431/600 [00:29<00:11, 14.64it/s]\u001b[A\n 72% 433/600 [00:29<00:11, 14.62it/s]\u001b[A\n 72% 435/600 [00:29<00:11, 14.61it/s]\u001b[A\n 73% 437/600 [00:29<00:11, 14.54it/s]\u001b[A\n 73% 439/600 [00:29<00:11, 14.63it/s]\u001b[A\n 74% 441/600 [00:30<00:10, 14.68it/s]\u001b[A\n 74% 443/600 [00:30<00:10, 14.69it/s]\u001b[A\n 74% 445/600 [00:30<00:10, 14.73it/s]\u001b[A\n 74% 447/600 [00:30<00:10, 14.65it/s]\u001b[A\n 75% 449/600 [00:30<00:10, 14.68it/s]\u001b[A\n 75% 451/600 [00:30<00:10, 14.63it/s]\u001b[A\n 76% 453/600 [00:30<00:10, 14.62it/s]\u001b[A\n 76% 455/600 [00:30<00:09, 14.66it/s]\u001b[A\n 76% 457/600 [00:31<00:09, 14.73it/s]\u001b[A\n 76% 459/600 [00:31<00:09, 14.78it/s]\u001b[A\n 77% 461/600 [00:31<00:09, 14.73it/s]\u001b[A\n 77% 463/600 [00:31<00:09, 14.67it/s]\u001b[A\n 78% 465/600 [00:31<00:09, 14.71it/s]\u001b[A\n 78% 467/600 [00:31<00:09, 14.66it/s]\u001b[A\n 78% 469/600 [00:31<00:08, 14.63it/s]\u001b[A\n 78% 471/600 [00:32<00:08, 14.60it/s]\u001b[A\n 79% 473/600 [00:32<00:08, 14.73it/s]\u001b[A\n 79% 475/600 [00:32<00:08, 14.70it/s]\u001b[A\n 80% 477/600 [00:32<00:08, 14.71it/s]\u001b[A\n 80% 479/600 [00:32<00:08, 14.56it/s]\u001b[A\n 80% 481/600 [00:32<00:08, 14.60it/s]\u001b[A\n 80% 483/600 [00:32<00:08, 14.62it/s]\u001b[A\n 81% 485/600 [00:33<00:07, 14.62it/s]\u001b[A\n 81% 487/600 [00:33<00:07, 14.64it/s]\u001b[A\n 82% 489/600 [00:33<00:07, 14.72it/s]\u001b[A\n 82% 491/600 [00:33<00:07, 14.64it/s]\u001b[A\n 82% 493/600 [00:33<00:07, 14.64it/s]\u001b[A\n 82% 495/600 [00:33<00:07, 14.53it/s]\u001b[A\n 83% 497/600 [00:33<00:07, 14.62it/s]\u001b[A\n 83% 499/600 [00:33<00:06, 14.58it/s]\u001b[A\n 84% 501/600 [00:34<00:06, 14.52it/s]\u001b[A\n 84% 503/600 [00:34<00:06, 14.61it/s]\u001b[A\n 84% 505/600 [00:34<00:06, 14.66it/s]\u001b[A\n 84% 507/600 [00:34<00:06, 14.64it/s]\u001b[A\n 85% 509/600 [00:34<00:06, 14.61it/s]\u001b[A\n 85% 511/600 [00:34<00:06, 14.65it/s]\u001b[A\n 86% 513/600 [00:34<00:05, 14.75it/s]\u001b[A\n 86% 515/600 [00:35<00:05, 14.65it/s]\u001b[A\n 86% 517/600 [00:35<00:05, 14.64it/s]\u001b[A\n 86% 519/600 [00:35<00:05, 14.56it/s]\u001b[A\n 87% 521/600 [00:35<00:05, 14.71it/s]\u001b[A\n 87% 523/600 [00:35<00:05, 14.61it/s]\u001b[A\n 88% 525/600 [00:35<00:05, 14.58it/s]\u001b[A\n 88% 527/600 [00:35<00:05, 14.57it/s]\u001b[A\n 88% 529/600 [00:36<00:04, 14.63it/s]\u001b[A\n 88% 531/600 [00:36<00:04, 14.64it/s]\u001b[A\n 89% 533/600 [00:36<00:04, 14.61it/s]\u001b[A\n 89% 535/600 [00:36<00:04, 14.72it/s]\u001b[A\n 90% 537/600 [00:36<00:04, 14.69it/s]\u001b[A\n 90% 539/600 [00:36<00:04, 14.63it/s]\u001b[A\n 90% 541/600 [00:36<00:04, 14.69it/s]\u001b[A\n 90% 543/600 [00:36<00:03, 14.73it/s]\u001b[A\n 91% 545/600 [00:37<00:03, 14.72it/s]\u001b[A\n 91% 547/600 [00:37<00:03, 14.66it/s]\u001b[A\n 92% 549/600 [00:37<00:03, 14.72it/s]\u001b[A\n 92% 551/600 [00:37<00:03, 14.65it/s]\u001b[A\n 92% 553/600 [00:37<00:03, 14.56it/s]\u001b[A\n 92% 555/600 [00:37<00:03, 14.66it/s]\u001b[A\n 93% 557/600 [00:37<00:02, 14.69it/s]\u001b[A\n 93% 559/600 [00:38<00:02, 14.66it/s]\u001b[A\n 94% 561/600 [00:38<00:02, 14.60it/s]\u001b[A\n 94% 563/600 [00:38<00:02, 14.65it/s]\u001b[A\n 94% 565/600 [00:38<00:02, 14.67it/s]\u001b[A\n 94% 567/600 [00:38<00:02, 14.61it/s]\u001b[A\n 95% 569/600 [00:38<00:02, 14.63it/s]\u001b[A\n 95% 571/600 [00:38<00:01, 14.62it/s]\u001b[A\n 96% 573/600 [00:39<00:01, 14.70it/s]\u001b[A\n 96% 575/600 [00:39<00:01, 14.69it/s]\u001b[A\n 96% 577/600 [00:39<00:01, 14.74it/s]\u001b[A\n 96% 579/600 [00:39<00:01, 14.78it/s]\u001b[A\n 97% 581/600 [00:39<00:01, 14.65it/s]\u001b[A\n 97% 583/600 [00:39<00:01, 14.59it/s]\u001b[A\n 98% 585/600 [00:39<00:01, 14.63it/s]\u001b[A\n 98% 587/600 [00:40<00:00, 14.67it/s]\u001b[A\n 98% 589/600 [00:40<00:00, 14.61it/s]\u001b[A\n 98% 591/600 [00:40<00:00, 14.56it/s]\u001b[A\n 99% 593/600 [00:40<00:00, 14.64it/s]\u001b[A\n 99% 595/600 [00:40<00:00, 14.70it/s]\u001b[A\n100% 597/600 [00:40<00:00, 14.70it/s]\u001b[A\n100% 599/600 [00:40<00:00, 14.68it/s]\u001b[A\n \n\u001b[A{'eval_loss': 0.02725045755505562, 'eval_accuracy_score': 0.9915078740789495, 'eval_precision': 0.9328655414375119, 'eval_recall': 0.9143122676579926, 'eval_f1': 0.9234957289026565, 'eval_runtime': 59.3763, 'eval_samples_per_second': 80.79, 'epoch': 1.0}\n 33% 286/858 [04:15<05:56, 1.60it/s]\n100% 600/600 [00:59<00:00, 14.68it/s]\u001b[A\n{'loss': 0.0178, 'learning_rate': 3.251748251748252e-05, 'epoch': 1.05}\n{'loss': 0.0088, 'learning_rate': 2.6689976689976692e-05, 'epoch': 1.4}\n{'loss': 0.0095, 'learning_rate': 2.0862470862470865e-05, 'epoch': 1.75}\n 67% 572/858 [07:31<02:58, 1.60it/s]\n 0% 0/600 [00:00<?, ?it/s]\u001b[A\n 0% 3/600 [00:00<00:28, 21.21it/s]\u001b[A\n 1% 5/600 [00:00<00:31, 18.61it/s]\u001b[A\n 1% 7/600 [00:00<00:34, 17.01it/s]\u001b[A\n 2% 9/600 [00:00<00:36, 16.29it/s]\u001b[A\n 2% 11/600 [00:00<00:37, 15.54it/s]\u001b[A\n 2% 13/600 [00:00<00:38, 15.12it/s]\u001b[A\n 2% 15/600 [00:00<00:38, 15.10it/s]\u001b[A\n 3% 17/600 [00:01<00:38, 15.07it/s]\u001b[A\n 3% 19/600 [00:01<00:38, 15.04it/s]\u001b[A\n 4% 21/600 [00:01<00:39, 14.83it/s]\u001b[A\n 4% 23/600 [00:01<00:39, 14.79it/s]\u001b[A\n 4% 25/600 [00:01<00:39, 14.66it/s]\u001b[A\n 4% 27/600 [00:01<00:39, 14.54it/s]\u001b[A\n 5% 29/600 [00:01<00:39, 14.51it/s]\u001b[A\n 5% 31/600 [00:02<00:38, 14.69it/s]\u001b[A\n 6% 33/600 [00:02<00:38, 14.71it/s]\u001b[A\n 6% 35/600 [00:02<00:38, 14.66it/s]\u001b[A\n 6% 37/600 [00:02<00:38, 14.70it/s]\u001b[A\n 6% 39/600 [00:02<00:38, 14.62it/s]\u001b[A\n 7% 41/600 [00:02<00:38, 14.59it/s]\u001b[A\n 7% 43/600 [00:02<00:38, 14.54it/s]\u001b[A\n 8% 45/600 [00:03<00:37, 14.69it/s]\u001b[A\n 8% 47/600 [00:03<00:37, 14.75it/s]\u001b[A\n 8% 49/600 [00:03<00:37, 14.66it/s]\u001b[A\n 8% 51/600 [00:03<00:37, 14.71it/s]\u001b[A\n 9% 53/600 [00:03<00:37, 14.67it/s]\u001b[A\n 9% 55/600 [00:03<00:37, 14.62it/s]\u001b[A\n 10% 57/600 [00:03<00:37, 14.56it/s]\u001b[A\n 10% 59/600 [00:03<00:36, 14.68it/s]\u001b[A\n 10% 61/600 [00:04<00:36, 14.73it/s]\u001b[A\n 10% 63/600 [00:04<00:36, 14.68it/s]\u001b[A\n 11% 65/600 [00:04<00:36, 14.70it/s]\u001b[A\n 11% 67/600 [00:04<00:36, 14.65it/s]\u001b[A\n 12% 69/600 [00:04<00:36, 14.51it/s]\u001b[A\n 12% 71/600 [00:04<00:36, 14.51it/s]\u001b[A\n 12% 73/600 [00:04<00:36, 14.59it/s]\u001b[A\n 12% 75/600 [00:05<00:35, 14.66it/s]\u001b[A\n 13% 77/600 [00:05<00:35, 14.71it/s]\u001b[A\n 13% 79/600 [00:05<00:35, 14.71it/s]\u001b[A\n 14% 81/600 [00:05<00:35, 14.68it/s]\u001b[A\n 14% 83/600 [00:05<00:35, 14.62it/s]\u001b[A\n 14% 85/600 [00:05<00:35, 14.59it/s]\u001b[A\n 14% 87/600 [00:05<00:35, 14.58it/s]\u001b[A\n 15% 89/600 [00:06<00:34, 14.72it/s]\u001b[A\n 15% 91/600 [00:06<00:34, 14.68it/s]\u001b[A\n 16% 93/600 [00:06<00:34, 14.74it/s]\u001b[A\n 16% 95/600 [00:06<00:34, 14.73it/s]\u001b[A\n 16% 97/600 [00:06<00:34, 14.61it/s]\u001b[A\n 16% 99/600 [00:06<00:34, 14.57it/s]\u001b[A\n 17% 101/600 [00:06<00:34, 14.61it/s]\u001b[A\n 17% 103/600 [00:06<00:34, 14.54it/s]\u001b[A\n 18% 105/600 [00:07<00:33, 14.66it/s]\u001b[A\n 18% 107/600 [00:07<00:33, 14.62it/s]\u001b[A\n 18% 109/600 [00:07<00:33, 14.62it/s]\u001b[A\n 18% 111/600 [00:07<00:33, 14.67it/s]\u001b[A\n 19% 113/600 [00:07<00:33, 14.66it/s]\u001b[A\n 19% 115/600 [00:07<00:33, 14.57it/s]\u001b[A\n 20% 117/600 [00:07<00:33, 14.58it/s]\u001b[A\n 20% 119/600 [00:08<00:32, 14.68it/s]\u001b[A\n 20% 121/600 [00:08<00:32, 14.65it/s]\u001b[A\n 20% 123/600 [00:08<00:32, 14.60it/s]\u001b[A\n 21% 125/600 [00:08<00:32, 14.66it/s]\u001b[A\n 21% 127/600 [00:08<00:32, 14.67it/s]\u001b[A\n 22% 129/600 [00:08<00:32, 14.64it/s]\u001b[A\n 22% 131/600 [00:08<00:32, 14.60it/s]\u001b[A\n 22% 133/600 [00:09<00:31, 14.65it/s]\u001b[A\n 22% 135/600 [00:09<00:31, 14.63it/s]\u001b[A\n 23% 137/600 [00:09<00:31, 14.65it/s]\u001b[A\n 23% 139/600 [00:09<00:31, 14.68it/s]\u001b[A\n 24% 141/600 [00:09<00:31, 14.56it/s]\u001b[A\n 24% 143/600 [00:09<00:31, 14.60it/s]\u001b[A\n 24% 145/600 [00:09<00:31, 14.55it/s]\u001b[A\n 24% 147/600 [00:09<00:31, 14.55it/s]\u001b[A\n 25% 149/600 [00:10<00:30, 14.55it/s]\u001b[A\n 25% 151/600 [00:10<00:31, 14.46it/s]\u001b[A\n 26% 153/600 [00:10<00:30, 14.62it/s]\u001b[A\n 26% 155/600 [00:10<00:30, 14.60it/s]\u001b[A\n 26% 157/600 [00:10<00:30, 14.60it/s]\u001b[A\n 26% 159/600 [00:10<00:29, 14.72it/s]\u001b[A\n 27% 161/600 [00:10<00:29, 14.67it/s]\u001b[A\n 27% 163/600 [00:11<00:29, 14.72it/s]\u001b[A\n 28% 165/600 [00:11<00:29, 14.62it/s]\u001b[A\n 28% 167/600 [00:11<00:29, 14.63it/s]\u001b[A\n 28% 169/600 [00:11<00:29, 14.59it/s]\u001b[A\n 28% 171/600 [00:11<00:29, 14.57it/s]\u001b[A\n 29% 173/600 [00:11<00:29, 14.68it/s]\u001b[A\n 29% 175/600 [00:11<00:29, 14.64it/s]\u001b[A\n 30% 177/600 [00:12<00:28, 14.65it/s]\u001b[A\n 30% 179/600 [00:12<00:28, 14.64it/s]\u001b[A\n 30% 181/600 [00:12<00:28, 14.66it/s]\u001b[A\n 30% 183/600 [00:12<00:28, 14.68it/s]\u001b[A\n 31% 185/600 [00:12<00:28, 14.62it/s]\u001b[A\n 31% 187/600 [00:12<00:28, 14.68it/s]\u001b[A\n 32% 189/600 [00:12<00:27, 14.76it/s]\u001b[A\n 32% 191/600 [00:12<00:27, 14.72it/s]\u001b[A\n 32% 193/600 [00:13<00:27, 14.75it/s]\u001b[A\n 32% 195/600 [00:13<00:27, 14.80it/s]\u001b[A\n 33% 197/600 [00:13<00:27, 14.70it/s]\u001b[A\n 33% 199/600 [00:13<00:27, 14.64it/s]\u001b[A\n 34% 201/600 [00:13<00:27, 14.67it/s]\u001b[A\n 34% 203/600 [00:13<00:26, 14.73it/s]\u001b[A\n 34% 205/600 [00:13<00:26, 14.64it/s]\u001b[A\n 34% 207/600 [00:14<00:26, 14.67it/s]\u001b[A\n 35% 209/600 [00:14<00:26, 14.60it/s]\u001b[A\n 35% 211/600 [00:14<00:26, 14.66it/s]\u001b[A\n 36% 213/600 [00:14<00:26, 14.59it/s]\u001b[A\n 36% 215/600 [00:14<00:26, 14.55it/s]\u001b[A\n 36% 217/600 [00:14<00:26, 14.66it/s]\u001b[A\n 36% 219/600 [00:14<00:25, 14.67it/s]\u001b[A\n 37% 221/600 [00:15<00:25, 14.67it/s]\u001b[A\n 37% 223/600 [00:15<00:25, 14.72it/s]\u001b[A\n 38% 225/600 [00:15<00:25, 14.76it/s]\u001b[A\n 38% 227/600 [00:15<00:25, 14.67it/s]\u001b[A\n 38% 229/600 [00:15<00:25, 14.58it/s]\u001b[A\n 38% 231/600 [00:15<00:25, 14.60it/s]\u001b[A\n 39% 233/600 [00:15<00:24, 14.73it/s]\u001b[A\n 39% 235/600 [00:15<00:24, 14.70it/s]\u001b[A\n 40% 237/600 [00:16<00:24, 14.71it/s]\u001b[A\n 40% 239/600 [00:16<00:24, 14.64it/s]\u001b[A\n 40% 241/600 [00:16<00:24, 14.64it/s]\u001b[A\n 40% 243/600 [00:16<00:24, 14.60it/s]\u001b[A\n 41% 245/600 [00:16<00:24, 14.59it/s]\u001b[A\n 41% 247/600 [00:16<00:24, 14.62it/s]\u001b[A\n 42% 249/600 [00:16<00:23, 14.68it/s]\u001b[A\n 42% 251/600 [00:17<00:23, 14.70it/s]\u001b[A\n 42% 253/600 [00:17<00:23, 14.71it/s]\u001b[A\n 42% 255/600 [00:17<00:23, 14.75it/s]\u001b[A\n 43% 257/600 [00:17<00:23, 14.70it/s]\u001b[A\n 43% 259/600 [00:17<00:23, 14.65it/s]\u001b[A\n 44% 261/600 [00:17<00:23, 14.71it/s]\u001b[A\n 44% 263/600 [00:17<00:22, 14.78it/s]\u001b[A\n 44% 265/600 [00:18<00:22, 14.68it/s]\u001b[A\n 44% 267/600 [00:18<00:22, 14.64it/s]\u001b[A\n 45% 269/600 [00:18<00:22, 14.64it/s]\u001b[A\n 45% 271/600 [00:18<00:22, 14.64it/s]\u001b[A\n 46% 273/600 [00:18<00:22, 14.56it/s]\u001b[A\n 46% 275/600 [00:18<00:22, 14.60it/s]\u001b[A\n 46% 277/600 [00:18<00:22, 14.62it/s]\u001b[A\n 46% 279/600 [00:18<00:21, 14.68it/s]\u001b[A\n 47% 281/600 [00:19<00:21, 14.72it/s]\u001b[A\n 47% 283/600 [00:19<00:21, 14.78it/s]\u001b[A\n 48% 285/600 [00:19<00:21, 14.68it/s]\u001b[A\n 48% 287/600 [00:19<00:21, 14.65it/s]\u001b[A\n 48% 289/600 [00:19<00:21, 14.63it/s]\u001b[A\n 48% 291/600 [00:19<00:21, 14.62it/s]\u001b[A\n 49% 293/600 [00:19<00:20, 14.69it/s]\u001b[A\n 49% 295/600 [00:20<00:20, 14.71it/s]\u001b[A\n 50% 297/600 [00:20<00:20, 14.79it/s]\u001b[A\n 50% 299/600 [00:20<00:20, 14.66it/s]\u001b[A\n 50% 301/600 [00:20<00:20, 14.53it/s]\u001b[A\n 50% 303/600 [00:20<00:20, 14.51it/s]\u001b[A\n 51% 305/600 [00:20<00:20, 14.62it/s]\u001b[A\n 51% 307/600 [00:20<00:20, 14.54it/s]\u001b[A\n 52% 309/600 [00:21<00:19, 14.69it/s]\u001b[A\n 52% 311/600 [00:21<00:19, 14.74it/s]\u001b[A\n 52% 313/600 [00:21<00:19, 14.75it/s]\u001b[A\n 52% 315/600 [00:21<00:19, 14.63it/s]\u001b[A\n 53% 317/600 [00:21<00:19, 14.60it/s]\u001b[A\n 53% 319/600 [00:21<00:19, 14.63it/s]\u001b[A\n 54% 321/600 [00:21<00:19, 14.66it/s]\u001b[A\n 54% 323/600 [00:21<00:18, 14.66it/s]\u001b[A\n 54% 325/600 [00:22<00:18, 14.71it/s]\u001b[A\n 55% 327/600 [00:22<00:18, 14.75it/s]\u001b[A\n 55% 329/600 [00:22<00:18, 14.62it/s]\u001b[A\n 55% 331/600 [00:22<00:18, 14.57it/s]\u001b[A\n 56% 333/600 [00:22<00:18, 14.60it/s]\u001b[A\n 56% 335/600 [00:22<00:18, 14.65it/s]\u001b[A\n 56% 337/600 [00:22<00:17, 14.73it/s]\u001b[A\n 56% 339/600 [00:23<00:17, 14.75it/s]\u001b[A\n 57% 341/600 [00:23<00:17, 14.86it/s]\u001b[A\n 57% 343/600 [00:23<00:17, 14.70it/s]\u001b[A\n 57% 345/600 [00:23<00:17, 14.66it/s]\u001b[A\n 58% 347/600 [00:23<00:17, 14.69it/s]\u001b[A\n 58% 349/600 [00:23<00:17, 14.75it/s]\u001b[A\n 58% 351/600 [00:23<00:16, 14.80it/s]\u001b[A\n 59% 353/600 [00:24<00:16, 14.76it/s]\u001b[A\n 59% 355/600 [00:24<00:16, 14.82it/s]\u001b[A\n 60% 357/600 [00:24<00:16, 14.75it/s]\u001b[A\n 60% 359/600 [00:24<00:16, 14.74it/s]\u001b[A\n 60% 361/600 [00:24<00:16, 14.59it/s]\u001b[A\n 60% 363/600 [00:24<00:16, 14.70it/s]\u001b[A\n 61% 365/600 [00:24<00:15, 14.71it/s]\u001b[A\n 61% 367/600 [00:24<00:15, 14.75it/s]\u001b[A\n 62% 369/600 [00:25<00:15, 14.83it/s]\u001b[A\n 62% 371/600 [00:25<00:15, 14.69it/s]\u001b[A\n 62% 373/600 [00:25<00:15, 14.70it/s]\u001b[A\n 62% 375/600 [00:25<00:15, 14.56it/s]\u001b[A\n 63% 377/600 [00:25<00:15, 14.64it/s]\u001b[A\n 63% 379/600 [00:25<00:15, 14.67it/s]\u001b[A\n 64% 381/600 [00:25<00:14, 14.68it/s]\u001b[A\n 64% 383/600 [00:26<00:14, 14.62it/s]\u001b[A\n 64% 385/600 [00:26<00:14, 14.67it/s]\u001b[A\n 64% 387/600 [00:26<00:14, 14.64it/s]\u001b[A\n 65% 389/600 [00:26<00:14, 14.62it/s]\u001b[A\n 65% 391/600 [00:26<00:14, 14.69it/s]\u001b[A\n 66% 393/600 [00:26<00:14, 14.68it/s]\u001b[A\n 66% 395/600 [00:26<00:13, 14.74it/s]\u001b[A\n 66% 397/600 [00:27<00:13, 14.78it/s]\u001b[A\n 66% 399/600 [00:27<00:13, 14.78it/s]\u001b[A\n 67% 401/600 [00:27<00:13, 14.73it/s]\u001b[A\n 67% 403/600 [00:27<00:13, 14.74it/s]\u001b[A\n 68% 405/600 [00:27<00:13, 14.68it/s]\u001b[A\n 68% 407/600 [00:27<00:13, 14.65it/s]\u001b[A\n 68% 409/600 [00:27<00:12, 14.70it/s]\u001b[A\n 68% 411/600 [00:27<00:12, 14.66it/s]\u001b[A\n 69% 413/600 [00:28<00:12, 14.70it/s]\u001b[A\n 69% 415/600 [00:28<00:12, 14.77it/s]\u001b[A\n 70% 417/600 [00:28<00:12, 14.75it/s]\u001b[A\n 70% 419/600 [00:28<00:12, 14.62it/s]\u001b[A\n 70% 421/600 [00:28<00:12, 14.52it/s]\u001b[A\n 70% 423/600 [00:28<00:12, 14.61it/s]\u001b[A\n 71% 425/600 [00:28<00:11, 14.59it/s]\u001b[A\n 71% 427/600 [00:29<00:11, 14.66it/s]\u001b[A\n 72% 429/600 [00:29<00:11, 14.73it/s]\u001b[A\n 72% 431/600 [00:29<00:11, 14.74it/s]\u001b[A\n 72% 433/600 [00:29<00:11, 14.75it/s]\u001b[A\n 72% 435/600 [00:29<00:11, 14.63it/s]\u001b[A\n 73% 437/600 [00:29<00:11, 14.71it/s]\u001b[A\n 73% 439/600 [00:29<00:10, 14.73it/s]\u001b[A\n 74% 441/600 [00:30<00:10, 14.73it/s]\u001b[A\n 74% 443/600 [00:30<00:10, 14.68it/s]\u001b[A\n 74% 445/600 [00:30<00:10, 14.81it/s]\u001b[A\n 74% 447/600 [00:30<00:10, 14.74it/s]\u001b[A\n 75% 449/600 [00:30<00:10, 14.74it/s]\u001b[A\n 75% 451/600 [00:30<00:10, 14.83it/s]\u001b[A\n 76% 453/600 [00:30<00:09, 14.79it/s]\u001b[A\n 76% 455/600 [00:30<00:09, 14.82it/s]\u001b[A\n 76% 457/600 [00:31<00:09, 14.84it/s]\u001b[A\n 76% 459/600 [00:31<00:09, 14.72it/s]\u001b[A\n 77% 461/600 [00:31<00:09, 14.79it/s]\u001b[A\n 77% 463/600 [00:31<00:09, 14.77it/s]\u001b[A\n 78% 465/600 [00:31<00:09, 14.77it/s]\u001b[A\n 78% 467/600 [00:31<00:09, 14.70it/s]\u001b[A\n 78% 469/600 [00:31<00:08, 14.67it/s]\u001b[A\n 78% 471/600 [00:32<00:08, 14.69it/s]\u001b[A\n 79% 473/600 [00:32<00:08, 14.65it/s]\u001b[A\n 79% 475/600 [00:32<00:08, 14.74it/s]\u001b[A\n 80% 477/600 [00:32<00:08, 14.71it/s]\u001b[A\n 80% 479/600 [00:32<00:08, 14.73it/s]\u001b[A\n 80% 481/600 [00:32<00:08, 14.70it/s]\u001b[A\n 80% 483/600 [00:32<00:07, 14.77it/s]\u001b[A\n 81% 485/600 [00:33<00:07, 14.74it/s]\u001b[A\n 81% 487/600 [00:33<00:07, 14.79it/s]\u001b[A\n 82% 489/600 [00:33<00:07, 14.79it/s]\u001b[A\n 82% 491/600 [00:33<00:07, 14.70it/s]\u001b[A\n 82% 493/600 [00:33<00:07, 14.68it/s]\u001b[A\n 82% 495/600 [00:33<00:07, 14.76it/s]\u001b[A\n 83% 497/600 [00:33<00:06, 14.72it/s]\u001b[A\n 83% 499/600 [00:33<00:06, 14.62it/s]\u001b[A\n 84% 501/600 [00:34<00:06, 14.68it/s]\u001b[A\n 84% 503/600 [00:34<00:06, 14.74it/s]\u001b[A\n 84% 505/600 [00:34<00:06, 14.73it/s]\u001b[A\n 84% 507/600 [00:34<00:06, 14.70it/s]\u001b[A\n 85% 509/600 [00:34<00:06, 14.72it/s]\u001b[A\n 85% 511/600 [00:34<00:06, 14.68it/s]\u001b[A\n 86% 513/600 [00:34<00:05, 14.70it/s]\u001b[A\n 86% 515/600 [00:35<00:05, 14.70it/s]\u001b[A\n 86% 517/600 [00:35<00:05, 14.78it/s]\u001b[A\n 86% 519/600 [00:35<00:05, 14.69it/s]\u001b[A\n 87% 521/600 [00:35<00:05, 14.70it/s]\u001b[A\n 87% 523/600 [00:35<00:05, 14.78it/s]\u001b[A\n 88% 525/600 [00:35<00:05, 14.70it/s]\u001b[A\n 88% 527/600 [00:35<00:04, 14.78it/s]\u001b[A\n 88% 529/600 [00:35<00:04, 14.83it/s]\u001b[A\n 88% 531/600 [00:36<00:04, 14.73it/s]\u001b[A\n 89% 533/600 [00:36<00:04, 14.74it/s]\u001b[A\n 89% 535/600 [00:36<00:04, 14.71it/s]\u001b[A\n 90% 537/600 [00:36<00:04, 14.73it/s]\u001b[A\n 90% 539/600 [00:36<00:04, 14.66it/s]\u001b[A\n 90% 541/600 [00:36<00:04, 14.68it/s]\u001b[A\n 90% 543/600 [00:36<00:03, 14.78it/s]\u001b[A\n 91% 545/600 [00:37<00:03, 14.75it/s]\u001b[A\n 91% 547/600 [00:37<00:03, 14.75it/s]\u001b[A\n 92% 549/600 [00:37<00:03, 14.77it/s]\u001b[A\n 92% 551/600 [00:37<00:03, 14.70it/s]\u001b[A\n 92% 553/600 [00:37<00:03, 14.73it/s]\u001b[A\n 92% 555/600 [00:37<00:03, 14.74it/s]\u001b[A\n 93% 557/600 [00:37<00:02, 14.71it/s]\u001b[A\n 93% 559/600 [00:38<00:02, 14.76it/s]\u001b[A\n 94% 561/600 [00:38<00:02, 14.75it/s]\u001b[A\n 94% 563/600 [00:38<00:02, 14.75it/s]\u001b[A\n 94% 565/600 [00:38<00:02, 14.70it/s]\u001b[A\n 94% 567/600 [00:38<00:02, 14.74it/s]\u001b[A\n 95% 569/600 [00:38<00:02, 14.69it/s]\u001b[A\n 95% 571/600 [00:38<00:01, 14.59it/s]\u001b[A\n 96% 573/600 [00:38<00:01, 14.68it/s]\u001b[A\n 96% 575/600 [00:39<00:01, 14.71it/s]\u001b[A\n 96% 577/600 [00:39<00:01, 14.62it/s]\u001b[A\n 96% 579/600 [00:39<00:01, 14.64it/s]\u001b[A\n 97% 581/600 [00:39<00:01, 14.64it/s]\u001b[A\n 97% 583/600 [00:39<00:01, 14.67it/s]\u001b[A\n 98% 585/600 [00:39<00:01, 14.66it/s]\u001b[A\n 98% 587/600 [00:39<00:00, 14.74it/s]\u001b[A\n 98% 589/600 [00:40<00:00, 14.80it/s]\u001b[A\n 98% 591/600 [00:40<00:00, 14.73it/s]\u001b[A\n 99% 593/600 [00:40<00:00, 14.68it/s]\u001b[A\n 99% 595/600 [00:40<00:00, 14.75it/s]\u001b[A\n100% 597/600 [00:40<00:00, 14.76it/s]\u001b[A\n100% 599/600 [00:40<00:00, 14.72it/s]\u001b[A\n \n\u001b[A{'eval_loss': 0.030171476304531097, 'eval_accuracy_score': 0.9918851235291285, 'eval_precision': 0.9204462326261887, 'eval_recall': 0.9355018587360595, 'eval_f1': 0.9279129793510326, 'eval_runtime': 58.9654, 'eval_samples_per_second': 81.353, 'epoch': 2.0}\n 67% 572/858 [08:30<02:58, 1.60it/s]\n100% 600/600 [00:58<00:00, 14.72it/s]\u001b[A\n{'loss': 0.0073, 'learning_rate': 1.5034965034965034e-05, 'epoch': 2.1}\n{'loss': 0.0044, 'learning_rate': 9.207459207459208e-06, 'epoch': 2.45}\n{'loss': 0.0032, 'learning_rate': 3.3799533799533803e-06, 'epoch': 2.8}\n100% 858/858 [11:46<00:00, 1.60it/s]\n 0% 0/600 [00:00<?, ?it/s]\u001b[A\n 0% 3/600 [00:00<00:27, 21.61it/s]\u001b[A\n 1% 5/600 [00:00<00:31, 18.89it/s]\u001b[A\n 1% 7/600 [00:00<00:34, 17.13it/s]\u001b[A\n 2% 9/600 [00:00<00:35, 16.61it/s]\u001b[A\n 2% 11/600 [00:00<00:37, 15.77it/s]\u001b[A\n 2% 13/600 [00:00<00:38, 15.43it/s]\u001b[A\n 2% 15/600 [00:00<00:38, 15.31it/s]\u001b[A\n 3% 17/600 [00:01<00:38, 15.26it/s]\u001b[A\n 3% 19/600 [00:01<00:38, 15.06it/s]\u001b[A\n 4% 21/600 [00:01<00:39, 14.81it/s]\u001b[A\n 4% 23/600 [00:01<00:38, 14.86it/s]\u001b[A\n 4% 25/600 [00:01<00:39, 14.72it/s]\u001b[A\n 4% 27/600 [00:01<00:39, 14.55it/s]\u001b[A\n 5% 29/600 [00:01<00:39, 14.61it/s]\u001b[A\n 5% 31/600 [00:02<00:38, 14.79it/s]\u001b[A\n 6% 33/600 [00:02<00:38, 14.76it/s]\u001b[A\n 6% 35/600 [00:02<00:38, 14.70it/s]\u001b[A\n 6% 37/600 [00:02<00:38, 14.69it/s]\u001b[A\n 6% 39/600 [00:02<00:38, 14.62it/s]\u001b[A\n 7% 41/600 [00:02<00:38, 14.57it/s]\u001b[A\n 7% 43/600 [00:02<00:38, 14.53it/s]\u001b[A\n 8% 45/600 [00:03<00:37, 14.65it/s]\u001b[A\n 8% 47/600 [00:03<00:37, 14.68it/s]\u001b[A\n 8% 49/600 [00:03<00:37, 14.63it/s]\u001b[A\n 8% 51/600 [00:03<00:37, 14.66it/s]\u001b[A\n 9% 53/600 [00:03<00:37, 14.59it/s]\u001b[A\n 9% 55/600 [00:03<00:37, 14.64it/s]\u001b[A\n 10% 57/600 [00:03<00:37, 14.54it/s]\u001b[A\n 10% 59/600 [00:03<00:36, 14.68it/s]\u001b[A\n 10% 61/600 [00:04<00:36, 14.77it/s]\u001b[A\n 10% 63/600 [00:04<00:36, 14.64it/s]\u001b[A\n 11% 65/600 [00:04<00:36, 14.68it/s]\u001b[A\n 11% 67/600 [00:04<00:36, 14.65it/s]\u001b[A\n 12% 69/600 [00:04<00:36, 14.65it/s]\u001b[A\n 12% 71/600 [00:04<00:36, 14.60it/s]\u001b[A\n 12% 73/600 [00:04<00:36, 14.62it/s]\u001b[A\n 12% 75/600 [00:05<00:35, 14.69it/s]\u001b[A\n 13% 77/600 [00:05<00:35, 14.76it/s]\u001b[A\n 13% 79/600 [00:05<00:35, 14.67it/s]\u001b[A\n 14% 81/600 [00:05<00:35, 14.67it/s]\u001b[A\n 14% 83/600 [00:05<00:35, 14.72it/s]\u001b[A\n 14% 85/600 [00:05<00:35, 14.61it/s]\u001b[A\n 14% 87/600 [00:05<00:35, 14.63it/s]\u001b[A\n 15% 89/600 [00:06<00:34, 14.69it/s]\u001b[A\n 15% 91/600 [00:06<00:34, 14.76it/s]\u001b[A\n 16% 93/600 [00:06<00:34, 14.75it/s]\u001b[A\n 16% 95/600 [00:06<00:34, 14.71it/s]\u001b[A\n 16% 97/600 [00:06<00:34, 14.68it/s]\u001b[A\n 16% 99/600 [00:06<00:34, 14.64it/s]\u001b[A\n 17% 101/600 [00:06<00:34, 14.67it/s]\u001b[A\n 17% 103/600 [00:06<00:33, 14.76it/s]\u001b[A\n 18% 105/600 [00:07<00:33, 14.69it/s]\u001b[A\n 18% 107/600 [00:07<00:33, 14.62it/s]\u001b[A\n 18% 109/600 [00:07<00:33, 14.62it/s]\u001b[A\n 18% 111/600 [00:07<00:33, 14.70it/s]\u001b[A\n 19% 113/600 [00:07<00:33, 14.60it/s]\u001b[A\n 19% 115/600 [00:07<00:33, 14.61it/s]\u001b[A\n 20% 117/600 [00:07<00:32, 14.69it/s]\u001b[A\n 20% 119/600 [00:08<00:32, 14.71it/s]\u001b[A\n 20% 121/600 [00:08<00:32, 14.67it/s]\u001b[A\n 20% 123/600 [00:08<00:32, 14.66it/s]\u001b[A\n 21% 125/600 [00:08<00:32, 14.57it/s]\u001b[A\n 21% 127/600 [00:08<00:32, 14.68it/s]\u001b[A\n 22% 129/600 [00:08<00:32, 14.64it/s]\u001b[A\n 22% 131/600 [00:08<00:31, 14.72it/s]\u001b[A\n 22% 133/600 [00:09<00:31, 14.75it/s]\u001b[A\n 22% 135/600 [00:09<00:31, 14.68it/s]\u001b[A\n 23% 137/600 [00:09<00:31, 14.70it/s]\u001b[A\n 23% 139/600 [00:09<00:31, 14.65it/s]\u001b[A\n 24% 141/600 [00:09<00:31, 14.70it/s]\u001b[A\n 24% 143/600 [00:09<00:31, 14.54it/s]\u001b[A\n 24% 145/600 [00:09<00:31, 14.52it/s]\u001b[A\n 24% 147/600 [00:09<00:31, 14.55it/s]\u001b[A\n 25% 149/600 [00:10<00:31, 14.50it/s]\u001b[A\n 25% 151/600 [00:10<00:30, 14.59it/s]\u001b[A\n 26% 153/600 [00:10<00:30, 14.55it/s]\u001b[A\n 26% 155/600 [00:10<00:30, 14.62it/s]\u001b[A\n 26% 157/600 [00:10<00:30, 14.66it/s]\u001b[A\n 26% 159/600 [00:10<00:30, 14.63it/s]\u001b[A\n 27% 161/600 [00:10<00:30, 14.56it/s]\u001b[A\n 27% 163/600 [00:11<00:29, 14.64it/s]\u001b[A\n 28% 165/600 [00:11<00:29, 14.64it/s]\u001b[A\n 28% 167/600 [00:11<00:29, 14.62it/s]\u001b[A\n 28% 169/600 [00:11<00:29, 14.57it/s]\u001b[A\n 28% 171/600 [00:11<00:29, 14.60it/s]\u001b[A\n 29% 173/600 [00:11<00:29, 14.63it/s]\u001b[A\n 29% 175/600 [00:11<00:28, 14.66it/s]\u001b[A\n 30% 177/600 [00:12<00:28, 14.65it/s]\u001b[A\n 30% 179/600 [00:12<00:28, 14.67it/s]\u001b[A\n 30% 181/600 [00:12<00:28, 14.67it/s]\u001b[A\n 30% 183/600 [00:12<00:28, 14.59it/s]\u001b[A\n 31% 185/600 [00:12<00:28, 14.62it/s]\u001b[A\n 31% 187/600 [00:12<00:28, 14.69it/s]\u001b[A\n 32% 189/600 [00:12<00:27, 14.74it/s]\u001b[A\n 32% 191/600 [00:12<00:27, 14.64it/s]\u001b[A\n 32% 193/600 [00:13<00:27, 14.70it/s]\u001b[A\n 32% 195/600 [00:13<00:27, 14.64it/s]\u001b[A\n 33% 197/600 [00:13<00:27, 14.70it/s]\u001b[A\n 33% 199/600 [00:13<00:27, 14.62it/s]\u001b[A\n 34% 201/600 [00:13<00:27, 14.59it/s]\u001b[A\n 34% 203/600 [00:13<00:27, 14.67it/s]\u001b[A\n 34% 205/600 [00:13<00:27, 14.61it/s]\u001b[A\n 34% 207/600 [00:14<00:26, 14.61it/s]\u001b[A\n 35% 209/600 [00:14<00:26, 14.58it/s]\u001b[A\n 35% 211/600 [00:14<00:26, 14.67it/s]\u001b[A\n 36% 213/600 [00:14<00:26, 14.60it/s]\u001b[A\n 36% 215/600 [00:14<00:26, 14.56it/s]\u001b[A\n 36% 217/600 [00:14<00:26, 14.61it/s]\u001b[A\n 36% 219/600 [00:14<00:25, 14.67it/s]\u001b[A\n 37% 221/600 [00:15<00:25, 14.70it/s]\u001b[A\n 37% 223/600 [00:15<00:25, 14.67it/s]\u001b[A\n 38% 225/600 [00:15<00:25, 14.62it/s]\u001b[A\n 38% 227/600 [00:15<00:25, 14.65it/s]\u001b[A\n 38% 229/600 [00:15<00:25, 14.52it/s]\u001b[A\n 38% 231/600 [00:15<00:25, 14.57it/s]\u001b[A\n 39% 233/600 [00:15<00:25, 14.60it/s]\u001b[A\n 39% 235/600 [00:15<00:24, 14.64it/s]\u001b[A\n 40% 237/600 [00:16<00:24, 14.54it/s]\u001b[A\n 40% 239/600 [00:16<00:24, 14.55it/s]\u001b[A\n 40% 241/600 [00:16<00:24, 14.57it/s]\u001b[A\n 40% 243/600 [00:16<00:24, 14.57it/s]\u001b[A\n 41% 245/600 [00:16<00:24, 14.64it/s]\u001b[A\n 41% 247/600 [00:16<00:24, 14.64it/s]\u001b[A\n 42% 249/600 [00:16<00:23, 14.70it/s]\u001b[A\n 42% 251/600 [00:17<00:23, 14.66it/s]\u001b[A\n 42% 253/600 [00:17<00:23, 14.57it/s]\u001b[A\n 42% 255/600 [00:17<00:23, 14.52it/s]\u001b[A\n 43% 257/600 [00:17<00:23, 14.57it/s]\u001b[A\n 43% 259/600 [00:17<00:23, 14.53it/s]\u001b[A\n 44% 261/600 [00:17<00:23, 14.59it/s]\u001b[A\n 44% 263/600 [00:17<00:23, 14.56it/s]\u001b[A\n 44% 265/600 [00:18<00:22, 14.62it/s]\u001b[A\n 44% 267/600 [00:18<00:22, 14.57it/s]\u001b[A\n 45% 269/600 [00:18<00:22, 14.55it/s]\u001b[A\n 45% 271/600 [00:18<00:22, 14.51it/s]\u001b[A\n 46% 273/600 [00:18<00:22, 14.54it/s]\u001b[A\n 46% 275/600 [00:18<00:22, 14.58it/s]\u001b[A\n 46% 277/600 [00:18<00:22, 14.66it/s]\u001b[A\n 46% 279/600 [00:18<00:21, 14.67it/s]\u001b[A\n 47% 281/600 [00:19<00:21, 14.66it/s]\u001b[A\n 47% 283/600 [00:19<00:21, 14.61it/s]\u001b[A\n 48% 285/600 [00:19<00:21, 14.64it/s]\u001b[A\n 48% 287/600 [00:19<00:21, 14.62it/s]\u001b[A\n 48% 289/600 [00:19<00:21, 14.57it/s]\u001b[A\n 48% 291/600 [00:19<00:21, 14.62it/s]\u001b[A\n 49% 293/600 [00:19<00:20, 14.69it/s]\u001b[A\n 49% 295/600 [00:20<00:20, 14.59it/s]\u001b[A\n 50% 297/600 [00:20<00:20, 14.53it/s]\u001b[A\n 50% 299/600 [00:20<00:20, 14.57it/s]\u001b[A\n 50% 301/600 [00:20<00:20, 14.61it/s]\u001b[A\n 50% 303/600 [00:20<00:20, 14.56it/s]\u001b[A\n 51% 305/600 [00:20<00:20, 14.52it/s]\u001b[A\n 51% 307/600 [00:20<00:20, 14.64it/s]\u001b[A\n 52% 309/600 [00:21<00:19, 14.65it/s]\u001b[A\n 52% 311/600 [00:21<00:19, 14.61it/s]\u001b[A\n 52% 313/600 [00:21<00:19, 14.62it/s]\u001b[A\n 52% 315/600 [00:21<00:19, 14.64it/s]\u001b[A\n 53% 317/600 [00:21<00:19, 14.71it/s]\u001b[A\n 53% 319/600 [00:21<00:19, 14.56it/s]\u001b[A\n 54% 321/600 [00:21<00:19, 14.57it/s]\u001b[A\n 54% 323/600 [00:22<00:18, 14.59it/s]\u001b[A\n 54% 325/600 [00:22<00:18, 14.63it/s]\u001b[A\n 55% 327/600 [00:22<00:18, 14.55it/s]\u001b[A\n 55% 329/600 [00:22<00:18, 14.53it/s]\u001b[A\n 55% 331/600 [00:22<00:18, 14.54it/s]\u001b[A\n 56% 333/600 [00:22<00:18, 14.62it/s]\u001b[A\n 56% 335/600 [00:22<00:18, 14.64it/s]\u001b[A\n 56% 337/600 [00:22<00:18, 14.55it/s]\u001b[A\n 56% 339/600 [00:23<00:17, 14.56it/s]\u001b[A\n 57% 341/600 [00:23<00:17, 14.61it/s]\u001b[A\n 57% 343/600 [00:23<00:17, 14.61it/s]\u001b[A\n 57% 345/600 [00:23<00:17, 14.60it/s]\u001b[A\n 58% 347/600 [00:23<00:17, 14.66it/s]\u001b[A\n 58% 349/600 [00:23<00:17, 14.71it/s]\u001b[A\n 58% 351/600 [00:23<00:17, 14.63it/s]\u001b[A\n 59% 353/600 [00:24<00:16, 14.63it/s]\u001b[A\n 59% 355/600 [00:24<00:16, 14.63it/s]\u001b[A\n 60% 357/600 [00:24<00:16, 14.66it/s]\u001b[A\n 60% 359/600 [00:24<00:16, 14.61it/s]\u001b[A\n 60% 361/600 [00:24<00:16, 14.63it/s]\u001b[A\n 60% 363/600 [00:24<00:16, 14.61it/s]\u001b[A\n 61% 365/600 [00:24<00:16, 14.53it/s]\u001b[A\n 61% 367/600 [00:25<00:15, 14.58it/s]\u001b[A\n 62% 369/600 [00:25<00:15, 14.61it/s]\u001b[A\n 62% 371/600 [00:25<00:15, 14.63it/s]\u001b[A\n 62% 373/600 [00:25<00:15, 14.60it/s]\u001b[A\n 62% 375/600 [00:25<00:15, 14.59it/s]\u001b[A\n 63% 377/600 [00:25<00:15, 14.66it/s]\u001b[A\n 63% 379/600 [00:25<00:15, 14.71it/s]\u001b[A\n 64% 381/600 [00:25<00:14, 14.76it/s]\u001b[A\n 64% 383/600 [00:26<00:14, 14.71it/s]\u001b[A\n 64% 385/600 [00:26<00:14, 14.64it/s]\u001b[A\n 64% 387/600 [00:26<00:14, 14.63it/s]\u001b[A\n 65% 389/600 [00:26<00:14, 14.68it/s]\u001b[A\n 65% 391/600 [00:26<00:14, 14.69it/s]\u001b[A\n 66% 393/600 [00:26<00:14, 14.71it/s]\u001b[A\n 66% 395/600 [00:26<00:13, 14.74it/s]\u001b[A\n 66% 397/600 [00:27<00:13, 14.73it/s]\u001b[A\n 66% 399/600 [00:27<00:13, 14.70it/s]\u001b[A\n 67% 401/600 [00:27<00:13, 14.59it/s]\u001b[A\n 67% 403/600 [00:27<00:13, 14.66it/s]\u001b[A\n 68% 405/600 [00:27<00:13, 14.65it/s]\u001b[A\n 68% 407/600 [00:27<00:13, 14.61it/s]\u001b[A\n 68% 409/600 [00:27<00:12, 14.70it/s]\u001b[A\n 68% 411/600 [00:28<00:12, 14.68it/s]\u001b[A\n 69% 413/600 [00:28<00:12, 14.67it/s]\u001b[A\n 69% 415/600 [00:28<00:12, 14.66it/s]\u001b[A\n 70% 417/600 [00:28<00:12, 14.69it/s]\u001b[A\n 70% 419/600 [00:28<00:12, 14.66it/s]\u001b[A\n 70% 421/600 [00:28<00:12, 14.66it/s]\u001b[A\n 70% 423/600 [00:28<00:12, 14.65it/s]\u001b[A\n 71% 425/600 [00:28<00:11, 14.64it/s]\u001b[A\n 71% 427/600 [00:29<00:11, 14.60it/s]\u001b[A\n 72% 429/600 [00:29<00:11, 14.53it/s]\u001b[A\n 72% 431/600 [00:29<00:11, 14.62it/s]\u001b[A\n 72% 433/600 [00:29<00:11, 14.51it/s]\u001b[A\n 72% 435/600 [00:29<00:11, 14.58it/s]\u001b[A\n 73% 437/600 [00:29<00:11, 14.58it/s]\u001b[A\n 73% 439/600 [00:29<00:11, 14.60it/s]\u001b[A\n 74% 441/600 [00:30<00:10, 14.65it/s]\u001b[A\n 74% 443/600 [00:30<00:10, 14.55it/s]\u001b[A\n 74% 445/600 [00:30<00:10, 14.60it/s]\u001b[A\n 74% 447/600 [00:30<00:10, 14.57it/s]\u001b[A\n 75% 449/600 [00:30<00:10, 14.59it/s]\u001b[A\n 75% 451/600 [00:30<00:10, 14.63it/s]\u001b[A\n 76% 453/600 [00:30<00:10, 14.58it/s]\u001b[A\n 76% 455/600 [00:31<00:09, 14.66it/s]\u001b[A\n 76% 457/600 [00:31<00:09, 14.67it/s]\u001b[A\n 76% 459/600 [00:31<00:09, 14.64it/s]\u001b[A\n 77% 461/600 [00:31<00:09, 14.55it/s]\u001b[A\n 77% 463/600 [00:31<00:09, 14.51it/s]\u001b[A\n 78% 465/600 [00:31<00:09, 14.54it/s]\u001b[A\n 78% 467/600 [00:31<00:09, 14.64it/s]\u001b[A\n 78% 469/600 [00:31<00:08, 14.59it/s]\u001b[A\n 78% 471/600 [00:32<00:08, 14.65it/s]\u001b[A\n 79% 473/600 [00:32<00:08, 14.72it/s]\u001b[A\n 79% 475/600 [00:32<00:08, 14.66it/s]\u001b[A\n 80% 477/600 [00:32<00:08, 14.55it/s]\u001b[A\n 80% 479/600 [00:32<00:08, 14.60it/s]\u001b[A\n 80% 481/600 [00:32<00:08, 14.62it/s]\u001b[A\n 80% 483/600 [00:32<00:07, 14.65it/s]\u001b[A\n 81% 485/600 [00:33<00:07, 14.58it/s]\u001b[A\n 81% 487/600 [00:33<00:07, 14.60it/s]\u001b[A\n 82% 489/600 [00:33<00:07, 14.63it/s]\u001b[A\n 82% 491/600 [00:33<00:07, 14.59it/s]\u001b[A\n 82% 493/600 [00:33<00:07, 14.65it/s]\u001b[A\n 82% 495/600 [00:33<00:07, 14.62it/s]\u001b[A\n 83% 497/600 [00:33<00:07, 14.63it/s]\u001b[A\n 83% 499/600 [00:34<00:06, 14.65it/s]\u001b[A\n 84% 501/600 [00:34<00:06, 14.62it/s]\u001b[A\n 84% 503/600 [00:34<00:06, 14.66it/s]\u001b[A\n 84% 505/600 [00:34<00:06, 14.62it/s]\u001b[A\n 84% 507/600 [00:34<00:06, 14.66it/s]\u001b[A\n 85% 509/600 [00:34<00:06, 14.58it/s]\u001b[A\n 85% 511/600 [00:34<00:06, 14.61it/s]\u001b[A\n 86% 513/600 [00:35<00:05, 14.60it/s]\u001b[A\n 86% 515/600 [00:35<00:05, 14.64it/s]\u001b[A\n 86% 517/600 [00:35<00:05, 14.67it/s]\u001b[A\n 86% 519/600 [00:35<00:05, 14.72it/s]\u001b[A\n 87% 521/600 [00:35<00:05, 14.76it/s]\u001b[A\n 87% 523/600 [00:35<00:05, 14.67it/s]\u001b[A\n 88% 525/600 [00:35<00:05, 14.66it/s]\u001b[A\n 88% 527/600 [00:35<00:04, 14.67it/s]\u001b[A\n 88% 529/600 [00:36<00:04, 14.74it/s]\u001b[A\n 88% 531/600 [00:36<00:04, 14.66it/s]\u001b[A\n 89% 533/600 [00:36<00:04, 14.64it/s]\u001b[A\n 89% 535/600 [00:36<00:04, 14.60it/s]\u001b[A\n 90% 537/600 [00:36<00:04, 14.56it/s]\u001b[A\n 90% 539/600 [00:36<00:04, 14.56it/s]\u001b[A\n 90% 541/600 [00:36<00:04, 14.57it/s]\u001b[A\n 90% 543/600 [00:37<00:03, 14.60it/s]\u001b[A\n 91% 545/600 [00:37<00:03, 14.53it/s]\u001b[A\n 91% 547/600 [00:37<00:03, 14.64it/s]\u001b[A\n 92% 549/600 [00:37<00:03, 14.60it/s]\u001b[A\n 92% 551/600 [00:37<00:03, 14.64it/s]\u001b[A\n 92% 553/600 [00:37<00:03, 14.72it/s]\u001b[A\n 92% 555/600 [00:37<00:03, 14.69it/s]\u001b[A\n 93% 557/600 [00:38<00:02, 14.77it/s]\u001b[A\n 93% 559/600 [00:38<00:02, 14.71it/s]\u001b[A\n 94% 561/600 [00:38<00:02, 14.58it/s]\u001b[A\n 94% 563/600 [00:38<00:02, 14.51it/s]\u001b[A\n 94% 565/600 [00:38<00:02, 14.45it/s]\u001b[A\n 94% 567/600 [00:38<00:02, 14.54it/s]\u001b[A\n 95% 569/600 [00:38<00:02, 14.62it/s]\u001b[A\n 95% 571/600 [00:38<00:01, 14.64it/s]\u001b[A\n 96% 573/600 [00:39<00:01, 14.62it/s]\u001b[A\n 96% 575/600 [00:39<00:01, 14.68it/s]\u001b[A\n 96% 577/600 [00:39<00:01, 14.70it/s]\u001b[A\n 96% 579/600 [00:39<00:01, 14.61it/s]\u001b[A\n 97% 581/600 [00:39<00:01, 14.68it/s]\u001b[A\n 97% 583/600 [00:39<00:01, 14.73it/s]\u001b[A\n 98% 585/600 [00:39<00:01, 14.65it/s]\u001b[A\n 98% 587/600 [00:40<00:00, 14.60it/s]\u001b[A\n 98% 589/600 [00:40<00:00, 14.58it/s]\u001b[A\n 98% 591/600 [00:40<00:00, 14.51it/s]\u001b[A\n 99% 593/600 [00:40<00:00, 14.58it/s]\u001b[A\n 99% 595/600 [00:40<00:00, 14.64it/s]\u001b[A\n100% 597/600 [00:40<00:00, 14.67it/s]\u001b[A\n100% 599/600 [00:40<00:00, 14.69it/s]\u001b[A\n \n\u001b[A{'eval_loss': 0.03536759689450264, 'eval_accuracy_score': 0.991740645016294, 'eval_precision': 0.9202487653191879, 'eval_recall': 0.9351301115241636, 'eval_f1': 0.9276297593804739, 'eval_runtime': 59.0665, 'eval_samples_per_second': 81.214, 'epoch': 3.0}\n100% 858/858 [12:45<00:00, 1.60it/s]\n100% 600/600 [00:59<00:00, 14.69it/s]\u001b[A\n{'train_runtime': 765.69, 'train_samples_per_second': 1.121, 'epoch': 3.0}\n100% 858/858 [12:45<00:00, 1.12it/s]\n" ], [ "!python train_teacher.py \\\n--data_dir 'data/NCBI-disease' \\\n--model_name_or_path 'dmis-lab/biobert-base-cased-v1.1' \\\n--output_dir 'models/Teachers/NCBI-disease' \\\n--logging_dir 'models/Teachers/NCBI-disease' \\\n--save_steps 10000", "2021-03-29 16:49:08.663349: I tensorflow/stream_executor/platform/default/dso_loader.cc:49] Successfully opened dynamic library libcudart.so.11.0\nNamespace(data_dir='data/NCBI-disease', do_eval=True, do_predict=True, do_train=True, evaluation_strategy='epoch', logging_dir='models/Teachers/NCBI-disease', logging_steps=100, max_seq_length=128, model_name_or_path='dmis-lab/biobert-base-cased-v1.1', num_train_epochs=3, output_dir='models/Teachers/NCBI-disease', per_device_train_batch_size=32, save_steps=10000, seed=1)\n03/29/2021 16:49:10 - WARNING - __main__ - Process rank: -1, device: cuda:0, n_gpu: 1, distributed training: False, 16-bits training: False\n03/29/2021 16:49:10 - INFO - __main__ - Training/evaluation parameters TrainingArguments(output_dir=models/Teachers/NCBI-disease, overwrite_output_dir=False, do_train=True, do_eval=True, do_predict=True, evaluation_strategy=IntervalStrategy.EPOCH, prediction_loss_only=False, per_device_train_batch_size=32, per_device_eval_batch_size=8, gradient_accumulation_steps=1, eval_accumulation_steps=None, learning_rate=5e-05, weight_decay=0.0, adam_beta1=0.9, adam_beta2=0.999, adam_epsilon=1e-08, max_grad_norm=1.0, num_train_epochs=3, max_steps=-1, lr_scheduler_type=SchedulerType.LINEAR, warmup_ratio=0.0, warmup_steps=0, logging_dir=models/Teachers/NCBI-disease, logging_strategy=IntervalStrategy.STEPS, logging_first_step=False, logging_steps=100, save_strategy=IntervalStrategy.STEPS, save_steps=10000, save_total_limit=None, no_cuda=False, seed=1, fp16=False, fp16_opt_level=O1, fp16_backend=auto, fp16_full_eval=False, local_rank=-1, tpu_num_cores=None, tpu_metrics_debug=False, debug=False, dataloader_drop_last=False, eval_steps=100, dataloader_num_workers=0, past_index=-1, run_name=models/Teachers/NCBI-disease, disable_tqdm=False, remove_unused_columns=True, label_names=None, load_best_model_at_end=False, metric_for_best_model=None, greater_is_better=None, ignore_data_skip=False, sharded_ddp=[], deepspeed=None, label_smoothing_factor=0.0, adafactor=False, group_by_length=False, report_to=['tensorboard'], ddp_find_unused_parameters=None, dataloader_pin_memory=True, skip_memory_metrics=False, _n_gpu=1)\n03/29/2021 16:49:12 - INFO - filelock - Lock 139759777279312 acquired on data/NCBI-disease/cached_train_dev_BertTokenizer_128.lock\n03/29/2021 16:49:12 - INFO - src.data_handling.DataHandlers - Loading features from cached file data/NCBI-disease/cached_train_dev_BertTokenizer_128\n03/29/2021 16:49:12 - INFO - filelock - Lock 139759777279312 released on data/NCBI-disease/cached_train_dev_BertTokenizer_128.lock\n03/29/2021 16:49:12 - INFO - filelock - Lock 139759777718224 acquired on data/NCBI-disease/cached_test_BertTokenizer_128.lock\n03/29/2021 16:49:12 - INFO - src.data_handling.DataHandlers - Loading features from cached file data/NCBI-disease/cached_test_BertTokenizer_128\n03/29/2021 16:49:12 - INFO - filelock - Lock 139759777718224 released on data/NCBI-disease/cached_test_BertTokenizer_128.lock\nSome weights of the model checkpoint at dmis-lab/biobert-base-cased-v1.1 were not used when initializing BertForTokenClassification: ['cls.predictions.bias', 'cls.predictions.transform.dense.weight', 'cls.predictions.transform.dense.bias', 'cls.predictions.transform.LayerNorm.weight', 'cls.predictions.transform.LayerNorm.bias', 'cls.predictions.decoder.weight', 'cls.predictions.decoder.bias', 'cls.seq_relationship.weight', 'cls.seq_relationship.bias']\n- This IS expected if you are initializing BertForTokenClassification from the checkpoint of a model trained on another task or with another architecture (e.g. initializing a BertForSequenceClassification model from a BertForPreTraining model).\n- This IS NOT expected if you are initializing BertForTokenClassification from the checkpoint of a model that you expect to be exactly identical (initializing a BertForSequenceClassification model from a BertForSequenceClassification model).\nSome weights of BertForTokenClassification were not initialized from the model checkpoint at dmis-lab/biobert-base-cased-v1.1 and are newly initialized: ['classifier.weight', 'classifier.bias']\nYou should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.\n/usr/local/lib/python3.7/dist-packages/transformers/trainer.py:836: FutureWarning: `model_path` is deprecated and will be removed in a future version. Use `resume_from_checkpoint` instead.\n FutureWarning,\n{'loss': 0.1303, 'learning_rate': 4.16247906197655e-05, 'epoch': 0.5}\n 33% 199/597 [02:16<03:44, 1.77it/s]\n 0% 0/118 [00:00<?, ?it/s]\u001b[A\n 3% 3/118 [00:00<00:05, 22.01it/s]\u001b[A\n 4% 5/118 [00:00<00:05, 18.96it/s]\u001b[A\n 6% 7/118 [00:00<00:06, 17.49it/s]\u001b[A\n 8% 9/118 [00:00<00:06, 16.48it/s]\u001b[A\n 9% 11/118 [00:00<00:06, 15.80it/s]\u001b[A\n 11% 13/118 [00:00<00:06, 15.28it/s]\u001b[A\n 13% 15/118 [00:00<00:06, 15.06it/s]\u001b[A\n 14% 17/118 [00:01<00:06, 15.09it/s]\u001b[A\n 16% 19/118 [00:01<00:06, 14.98it/s]\u001b[A\n 18% 21/118 [00:01<00:06, 14.94it/s]\u001b[A\n 19% 23/118 [00:01<00:06, 14.82it/s]\u001b[A\n 21% 25/118 [00:01<00:06, 14.79it/s]\u001b[A\n 23% 27/118 [00:01<00:06, 14.61it/s]\u001b[A\n 25% 29/118 [00:01<00:06, 14.60it/s]\u001b[A\n 26% 31/118 [00:02<00:05, 14.76it/s]\u001b[A\n 28% 33/118 [00:02<00:05, 14.81it/s]\u001b[A\n 30% 35/118 [00:02<00:05, 14.77it/s]\u001b[A\n 31% 37/118 [00:02<00:05, 14.82it/s]\u001b[A\n 33% 39/118 [00:02<00:05, 14.71it/s]\u001b[A\n 35% 41/118 [00:02<00:05, 14.65it/s]\u001b[A\n 36% 43/118 [00:02<00:05, 14.61it/s]\u001b[A\n 38% 45/118 [00:03<00:04, 14.72it/s]\u001b[A\n 40% 47/118 [00:03<00:04, 14.72it/s]\u001b[A\n 42% 49/118 [00:03<00:04, 14.71it/s]\u001b[A\n 43% 51/118 [00:03<00:04, 14.74it/s]\u001b[A\n 45% 53/118 [00:03<00:04, 14.66it/s]\u001b[A\n 47% 55/118 [00:03<00:04, 14.62it/s]\u001b[A\n 48% 57/118 [00:03<00:04, 14.54it/s]\u001b[A\n 50% 59/118 [00:03<00:04, 14.60it/s]\u001b[A\n 52% 61/118 [00:04<00:03, 14.69it/s]\u001b[A\n 53% 63/118 [00:04<00:03, 14.74it/s]\u001b[A\n 55% 65/118 [00:04<00:03, 14.74it/s]\u001b[A\n 57% 67/118 [00:04<00:03, 14.74it/s]\u001b[A\n 58% 69/118 [00:04<00:03, 14.66it/s]\u001b[A\n 60% 71/118 [00:04<00:03, 14.59it/s]\u001b[A\n 62% 73/118 [00:04<00:03, 14.68it/s]\u001b[A\n 64% 75/118 [00:05<00:02, 14.73it/s]\u001b[A\n 65% 77/118 [00:05<00:02, 14.73it/s]\u001b[A\n 67% 79/118 [00:05<00:02, 14.71it/s]\u001b[A\n 69% 81/118 [00:05<00:02, 14.77it/s]\u001b[A\n 70% 83/118 [00:05<00:02, 14.67it/s]\u001b[A\n 72% 85/118 [00:05<00:02, 14.63it/s]\u001b[A\n 74% 87/118 [00:05<00:02, 14.74it/s]\u001b[A\n 75% 89/118 [00:06<00:01, 14.66it/s]\u001b[A\n 77% 91/118 [00:06<00:01, 14.66it/s]\u001b[A\n 79% 93/118 [00:06<00:01, 14.66it/s]\u001b[A\n 81% 95/118 [00:06<00:01, 14.74it/s]\u001b[A\n 82% 97/118 [00:06<00:01, 14.60it/s]\u001b[A\n 84% 99/118 [00:06<00:01, 14.58it/s]\u001b[A\n 86% 101/118 [00:06<00:01, 14.64it/s]\u001b[A\n 87% 103/118 [00:06<00:01, 14.73it/s]\u001b[A\n 89% 105/118 [00:07<00:00, 14.68it/s]\u001b[A\n 91% 107/118 [00:07<00:00, 14.73it/s]\u001b[A\n 92% 109/118 [00:07<00:00, 14.80it/s]\u001b[A\n 94% 111/118 [00:07<00:00, 14.73it/s]\u001b[A\n 96% 113/118 [00:07<00:00, 14.61it/s]\u001b[A\n 97% 115/118 [00:07<00:00, 14.63it/s]\u001b[A\n \n\u001b[A{'eval_loss': 0.048421476036310196, 'eval_accuracy_score': 0.9833748621379845, 'eval_precision': 0.8003802281368821, 'eval_recall': 0.8770833333333333, 'eval_f1': 0.8369781312127236, 'eval_runtime': 11.5173, 'eval_samples_per_second': 81.616, 'epoch': 1.0}\n 33% 199/597 [02:27<03:44, 1.77it/s]\n100% 118/118 [00:11<00:00, 14.76it/s]\u001b[A\n{'loss': 0.0449, 'learning_rate': 3.324958123953099e-05, 'epoch': 1.01}\n{'loss': 0.0221, 'learning_rate': 2.4874371859296484e-05, 'epoch': 1.51}\n 67% 398/597 [04:43<01:52, 1.77it/s]\n 0% 0/118 [00:00<?, ?it/s]\u001b[A\n 3% 3/118 [00:00<00:05, 21.99it/s]\u001b[A\n 4% 5/118 [00:00<00:05, 18.85it/s]\u001b[A\n 6% 7/118 [00:00<00:06, 17.36it/s]\u001b[A\n 8% 9/118 [00:00<00:06, 16.34it/s]\u001b[A\n 9% 11/118 [00:00<00:06, 15.76it/s]\u001b[A\n 11% 13/118 [00:00<00:06, 15.29it/s]\u001b[A\n 13% 15/118 [00:00<00:06, 15.13it/s]\u001b[A\n 14% 17/118 [00:01<00:06, 15.17it/s]\u001b[A\n 16% 19/118 [00:01<00:06, 15.05it/s]\u001b[A\n 18% 21/118 [00:01<00:06, 14.87it/s]\u001b[A\n 19% 23/118 [00:01<00:06, 14.76it/s]\u001b[A\n 21% 25/118 [00:01<00:06, 14.74it/s]\u001b[A\n 23% 27/118 [00:01<00:06, 14.65it/s]\u001b[A\n 25% 29/118 [00:01<00:06, 14.58it/s]\u001b[A\n 26% 31/118 [00:02<00:05, 14.73it/s]\u001b[A\n 28% 33/118 [00:02<00:05, 14.76it/s]\u001b[A\n 30% 35/118 [00:02<00:05, 14.77it/s]\u001b[A\n 31% 37/118 [00:02<00:05, 14.66it/s]\u001b[A\n 33% 39/118 [00:02<00:05, 14.64it/s]\u001b[A\n 35% 41/118 [00:02<00:05, 14.51it/s]\u001b[A\n 36% 43/118 [00:02<00:05, 14.46it/s]\u001b[A\n 38% 45/118 [00:03<00:04, 14.64it/s]\u001b[A\n 40% 47/118 [00:03<00:04, 14.70it/s]\u001b[A\n 42% 49/118 [00:03<00:04, 14.69it/s]\u001b[A\n 43% 51/118 [00:03<00:04, 14.70it/s]\u001b[A\n 45% 53/118 [00:03<00:04, 14.61it/s]\u001b[A\n 47% 55/118 [00:03<00:04, 14.50it/s]\u001b[A\n 48% 57/118 [00:03<00:04, 14.52it/s]\u001b[A\n 50% 59/118 [00:03<00:04, 14.64it/s]\u001b[A\n 52% 61/118 [00:04<00:03, 14.66it/s]\u001b[A\n 53% 63/118 [00:04<00:03, 14.72it/s]\u001b[A\n 55% 65/118 [00:04<00:03, 14.70it/s]\u001b[A\n 57% 67/118 [00:04<00:03, 14.67it/s]\u001b[A\n 58% 69/118 [00:04<00:03, 14.59it/s]\u001b[A\n 60% 71/118 [00:04<00:03, 14.58it/s]\u001b[A\n 62% 73/118 [00:04<00:03, 14.68it/s]\u001b[A\n 64% 75/118 [00:05<00:02, 14.76it/s]\u001b[A\n 65% 77/118 [00:05<00:02, 14.87it/s]\u001b[A\n 67% 79/118 [00:05<00:02, 14.88it/s]\u001b[A\n 69% 81/118 [00:05<00:02, 14.75it/s]\u001b[A\n 70% 83/118 [00:05<00:02, 14.73it/s]\u001b[A\n 72% 85/118 [00:05<00:02, 14.67it/s]\u001b[A\n 74% 87/118 [00:05<00:02, 14.75it/s]\u001b[A\n 75% 89/118 [00:06<00:01, 14.71it/s]\u001b[A\n 77% 91/118 [00:06<00:01, 14.85it/s]\u001b[A\n 79% 93/118 [00:06<00:01, 14.80it/s]\u001b[A\n 81% 95/118 [00:06<00:01, 14.69it/s]\u001b[A\n 82% 97/118 [00:06<00:01, 14.67it/s]\u001b[A\n 84% 99/118 [00:06<00:01, 14.63it/s]\u001b[A\n 86% 101/118 [00:06<00:01, 14.62it/s]\u001b[A\n 87% 103/118 [00:06<00:01, 14.59it/s]\u001b[A\n 89% 105/118 [00:07<00:00, 14.68it/s]\u001b[A\n 91% 107/118 [00:07<00:00, 14.75it/s]\u001b[A\n 92% 109/118 [00:07<00:00, 14.70it/s]\u001b[A\n 94% 111/118 [00:07<00:00, 14.71it/s]\u001b[A\n 96% 113/118 [00:07<00:00, 14.68it/s]\u001b[A\n 97% 115/118 [00:07<00:00, 14.64it/s]\u001b[A\n \n\u001b[A{'eval_loss': 0.04439317435026169, 'eval_accuracy_score': 0.9848862383072587, 'eval_precision': 0.8467741935483871, 'eval_recall': 0.875, 'eval_f1': 0.8606557377049181, 'eval_runtime': 11.5254, 'eval_samples_per_second': 81.559, 'epoch': 2.0}\n 67% 398/597 [04:55<01:52, 1.77it/s]\n100% 118/118 [00:11<00:00, 14.57it/s]\u001b[A\n{'loss': 0.0187, 'learning_rate': 1.6499162479061976e-05, 'epoch': 2.01}\n{'loss': 0.0093, 'learning_rate': 8.123953098827471e-06, 'epoch': 2.51}\n100% 597/597 [07:11<00:00, 1.79it/s]\n 0% 0/118 [00:00<?, ?it/s]\u001b[A\n 3% 3/118 [00:00<00:05, 21.90it/s]\u001b[A\n 4% 5/118 [00:00<00:05, 18.91it/s]\u001b[A\n 6% 7/118 [00:00<00:06, 17.40it/s]\u001b[A\n 8% 9/118 [00:00<00:06, 16.43it/s]\u001b[A\n 9% 11/118 [00:00<00:06, 15.76it/s]\u001b[A\n 11% 13/118 [00:00<00:06, 15.36it/s]\u001b[A\n 13% 15/118 [00:00<00:06, 15.16it/s]\u001b[A\n 14% 17/118 [00:01<00:06, 15.24it/s]\u001b[A\n 16% 19/118 [00:01<00:06, 15.07it/s]\u001b[A\n 18% 21/118 [00:01<00:06, 15.04it/s]\u001b[A\n 19% 23/118 [00:01<00:06, 14.89it/s]\u001b[A\n 21% 25/118 [00:01<00:06, 14.82it/s]\u001b[A\n 23% 27/118 [00:01<00:06, 14.68it/s]\u001b[A\n 25% 29/118 [00:01<00:06, 14.72it/s]\u001b[A\n 26% 31/118 [00:02<00:05, 14.87it/s]\u001b[A\n 28% 33/118 [00:02<00:05, 14.74it/s]\u001b[A\n 30% 35/118 [00:02<00:05, 14.79it/s]\u001b[A\n 31% 37/118 [00:02<00:05, 14.77it/s]\u001b[A\n 33% 39/118 [00:02<00:05, 14.73it/s]\u001b[A\n 35% 41/118 [00:02<00:05, 14.65it/s]\u001b[A\n 36% 43/118 [00:02<00:05, 14.61it/s]\u001b[A\n 38% 45/118 [00:02<00:04, 14.74it/s]\u001b[A\n 40% 47/118 [00:03<00:04, 14.77it/s]\u001b[A\n 42% 49/118 [00:03<00:04, 14.85it/s]\u001b[A\n 43% 51/118 [00:03<00:04, 14.78it/s]\u001b[A\n 45% 53/118 [00:03<00:04, 14.75it/s]\u001b[A\n 47% 55/118 [00:03<00:04, 14.71it/s]\u001b[A\n 48% 57/118 [00:03<00:04, 14.72it/s]\u001b[A\n 50% 59/118 [00:03<00:04, 14.68it/s]\u001b[A\n 52% 61/118 [00:04<00:03, 14.79it/s]\u001b[A\n 53% 63/118 [00:04<00:03, 14.89it/s]\u001b[A\n 55% 65/118 [00:04<00:03, 14.74it/s]\u001b[A\n 57% 67/118 [00:04<00:03, 14.72it/s]\u001b[A\n 58% 69/118 [00:04<00:03, 14.74it/s]\u001b[A\n 60% 71/118 [00:04<00:03, 14.69it/s]\u001b[A\n 62% 73/118 [00:04<00:03, 14.62it/s]\u001b[A\n 64% 75/118 [00:05<00:02, 14.72it/s]\u001b[A\n 65% 77/118 [00:05<00:02, 14.87it/s]\u001b[A\n 67% 79/118 [00:05<00:02, 14.75it/s]\u001b[A\n 69% 81/118 [00:05<00:02, 14.84it/s]\u001b[A\n 70% 83/118 [00:05<00:02, 14.81it/s]\u001b[A\n 72% 85/118 [00:05<00:02, 14.73it/s]\u001b[A\n 74% 87/118 [00:05<00:02, 14.75it/s]\u001b[A\n 75% 89/118 [00:05<00:01, 14.81it/s]\u001b[A\n 77% 91/118 [00:06<00:01, 14.77it/s]\u001b[A\n 79% 93/118 [00:06<00:01, 14.75it/s]\u001b[A\n 81% 95/118 [00:06<00:01, 14.82it/s]\u001b[A\n 82% 97/118 [00:06<00:01, 14.72it/s]\u001b[A\n 84% 99/118 [00:06<00:01, 14.67it/s]\u001b[A\n 86% 101/118 [00:06<00:01, 14.63it/s]\u001b[A\n 87% 103/118 [00:06<00:01, 14.78it/s]\u001b[A\n 89% 105/118 [00:07<00:00, 14.81it/s]\u001b[A\n 91% 107/118 [00:07<00:00, 14.84it/s]\u001b[A\n 92% 109/118 [00:07<00:00, 14.79it/s]\u001b[A\n 94% 111/118 [00:07<00:00, 14.81it/s]\u001b[A\n 96% 113/118 [00:07<00:00, 14.81it/s]\u001b[A\n 97% 115/118 [00:07<00:00, 14.75it/s]\u001b[A\n \n\u001b[A{'eval_loss': 0.05127991735935211, 'eval_accuracy_score': 0.9853764143621584, 'eval_precision': 0.8384236453201971, 'eval_recall': 0.8864583333333333, 'eval_f1': 0.8617721518987341, 'eval_runtime': 11.5073, 'eval_samples_per_second': 81.687, 'epoch': 3.0}\n100% 597/597 [07:22<00:00, 1.79it/s]\n100% 118/118 [00:11<00:00, 14.76it/s]\u001b[A\n{'train_runtime': 442.8327, 'train_samples_per_second': 1.348, 'epoch': 3.0}\n100% 597/597 [07:22<00:00, 1.35it/s]\n" ] ], [ [ "## Global datasets\n\nWe need the aggregated datasets for *teachers* in order to obtain their predictions over the whole set of data. Furthermore, we need the aggregated dataset with teachers' labels to train our Student.", "_____no_output_____" ] ], [ [ "!python generate_global_datasets.py", "Namespace(data_path='data')\nGenerating file: data/GLOBAL/BC2GM/train.tsv\nGenerating file: data/GLOBAL/BC5CDR-chem/train.tsv\nGenerating file: data/GLOBAL/NCBI-disease/train.tsv\nGenerating file: data/GLOBAL/BC2GM/dev.tsv\nGenerating file: data/GLOBAL/BC5CDR-chem/dev.tsv\nGenerating file: data/GLOBAL/NCBI-disease/dev.tsv\nGenerating file: data/GLOBAL/BC2GM/train_dev.tsv\nGenerating file: data/GLOBAL/BC5CDR-chem/train_dev.tsv\nGenerating file: data/GLOBAL/NCBI-disease/train_dev.tsv\nGenerating file: data/GLOBAL/BC2GM/test.tsv\nGenerating file: data/GLOBAL/BC5CDR-chem/test.tsv\nGenerating file: data/GLOBAL/NCBI-disease/test.tsv\nGenerating file: data/GLOBAL/Student/train.tsv\nGenerating file: data/GLOBAL/Student/dev.tsv\nGenerating file: data/GLOBAL/Student/train_dev.tsv\nGenerating file: data/GLOBAL/Student/test.tsv\n" ] ], [ [ "## Offline generation of teachers' distribution\n\nWe obtain the output distribution of each teacher. The $i$-th teacher outputs the probabilities $p_B^i, p_I^i, p_O^i$, $i = \\{1,...,k\\}$, $k$ being the number of teachers.\n\nWe have to aggregate them in a distribution with $2k+1$ labels ($B$ and $O$ for each teacher and the global $O$):\n\n- $P_{Bi} = p_B^i \\prod_{j\\ne i}{\\big(p_I^j + p_O^j\\big)}$, \n- $P_{Ii} = p_I^i \\prod_{j\\ne i}{\\big(p_I^j + p_O^j\\big)}$, \n- $P_{O} = \\prod_i{p_O^i}$", "_____no_output_____" ] ], [ [ "!python generate_teachers_distributions.py \\\n--data_dir 'data' \\\n--teachers_dir 'models/Teachers' \\\n--model_name_or_path 'dmis-lab/biobert-base-cased-v1.1'", "\u001b[1;30;43mStreaming output truncated to the last 5000 lines.\u001b[0m\n\n 35% 1326/3823 [02:29<04:42, 8.85it/s]\u001b[A\u001b[A\n\n 35% 1327/3823 [02:29<04:42, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1328/3823 [02:29<04:42, 8.82it/s]\u001b[A\u001b[A\n\n 35% 1329/3823 [02:30<04:42, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1330/3823 [02:30<04:41, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1331/3823 [02:30<04:41, 8.85it/s]\u001b[A\u001b[A\n\n 35% 1332/3823 [02:30<04:41, 8.85it/s]\u001b[A\u001b[A\n\n 35% 1333/3823 [02:30<04:41, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1334/3823 [02:30<04:42, 8.81it/s]\u001b[A\u001b[A\n\n 35% 1335/3823 [02:30<04:42, 8.81it/s]\u001b[A\u001b[A\n\n 35% 1336/3823 [02:30<04:42, 8.82it/s]\u001b[A\u001b[A\n\n 35% 1337/3823 [02:30<04:41, 8.82it/s]\u001b[A\u001b[A\n\n 35% 1338/3823 [02:31<04:41, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1339/3823 [02:31<04:41, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1340/3823 [02:31<04:41, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1341/3823 [02:31<04:41, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1342/3823 [02:31<04:40, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1343/3823 [02:31<04:40, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1344/3823 [02:31<04:40, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1345/3823 [02:31<04:40, 8.82it/s]\u001b[A\u001b[A\n\n 35% 1346/3823 [02:31<04:40, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1347/3823 [02:32<04:40, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1348/3823 [02:32<04:39, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1349/3823 [02:32<04:39, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1350/3823 [02:32<04:39, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1351/3823 [02:32<04:39, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1352/3823 [02:32<04:39, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1353/3823 [02:32<04:39, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1354/3823 [02:32<04:39, 8.83it/s]\u001b[A\u001b[A\n\n 35% 1355/3823 [02:32<04:39, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1356/3823 [02:33<04:38, 8.84it/s]\u001b[A\u001b[A\n\n 35% 1357/3823 [02:33<04:38, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1358/3823 [02:33<04:38, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1359/3823 [02:33<04:38, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1360/3823 [02:33<04:38, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1361/3823 [02:33<04:38, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1362/3823 [02:33<04:38, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1363/3823 [02:33<04:37, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1364/3823 [02:33<04:37, 8.86it/s]\u001b[A\u001b[A\n\n 36% 1365/3823 [02:34<04:37, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1366/3823 [02:34<04:37, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1367/3823 [02:34<04:37, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1368/3823 [02:34<04:38, 8.83it/s]\u001b[A\u001b[A\n\n 36% 1369/3823 [02:34<04:38, 8.80it/s]\u001b[A\u001b[A\n\n 36% 1370/3823 [02:34<04:38, 8.82it/s]\u001b[A\u001b[A\n\n 36% 1371/3823 [02:34<04:37, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1372/3823 [02:34<04:37, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1373/3823 [02:34<04:36, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1374/3823 [02:35<04:36, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1375/3823 [02:35<04:36, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1376/3823 [02:35<04:36, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1377/3823 [02:35<04:36, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1378/3823 [02:35<04:36, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1379/3823 [02:35<04:36, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1380/3823 [02:35<04:36, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1381/3823 [02:35<04:36, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1382/3823 [02:36<04:36, 8.83it/s]\u001b[A\u001b[A\n\n 36% 1383/3823 [02:36<04:36, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1384/3823 [02:36<04:35, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1385/3823 [02:36<04:35, 8.83it/s]\u001b[A\u001b[A\n\n 36% 1386/3823 [02:36<04:35, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1387/3823 [02:36<04:35, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1388/3823 [02:36<04:34, 8.86it/s]\u001b[A\u001b[A\n\n 36% 1389/3823 [02:36<04:34, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1390/3823 [02:36<04:35, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1391/3823 [02:37<04:34, 8.85it/s]\u001b[A\u001b[A\n\n 36% 1392/3823 [02:37<04:34, 8.84it/s]\u001b[A\u001b[A\n\n 36% 1393/3823 [02:37<04:35, 8.82it/s]\u001b[A\u001b[A\n\n 36% 1394/3823 [02:37<04:35, 8.82it/s]\u001b[A\u001b[A\n\n 36% 1395/3823 [02:37<04:35, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1396/3823 [02:37<04:34, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1397/3823 [02:37<04:34, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1398/3823 [02:37<04:34, 8.82it/s]\u001b[A\u001b[A\n\n 37% 1399/3823 [02:37<04:34, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1400/3823 [02:38<04:34, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1401/3823 [02:38<04:33, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1402/3823 [02:38<04:33, 8.85it/s]\u001b[A\u001b[A\n\n 37% 1403/3823 [02:38<04:33, 8.85it/s]\u001b[A\u001b[A\n\n 37% 1404/3823 [02:38<04:33, 8.85it/s]\u001b[A\u001b[A\n\n 37% 1405/3823 [02:38<04:33, 8.85it/s]\u001b[A\u001b[A\n\n 37% 1406/3823 [02:38<04:33, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1407/3823 [02:38<04:33, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1408/3823 [02:38<04:33, 8.82it/s]\u001b[A\u001b[A\n\n 37% 1409/3823 [02:39<04:33, 8.81it/s]\u001b[A\u001b[A\n\n 37% 1410/3823 [02:39<04:33, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1411/3823 [02:39<04:33, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1412/3823 [02:39<04:32, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1413/3823 [02:39<04:32, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1414/3823 [02:39<04:32, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1415/3823 [02:39<04:32, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1416/3823 [02:39<04:32, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1417/3823 [02:39<04:31, 8.85it/s]\u001b[A\u001b[A\n\n 37% 1418/3823 [02:40<04:32, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1419/3823 [02:40<04:32, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1420/3823 [02:40<04:32, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1421/3823 [02:40<04:31, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1422/3823 [02:40<04:31, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1423/3823 [02:40<04:31, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1424/3823 [02:40<04:31, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1425/3823 [02:40<04:31, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1426/3823 [02:40<04:31, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1427/3823 [02:41<04:30, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1428/3823 [02:41<04:30, 8.85it/s]\u001b[A\u001b[A\n\n 37% 1429/3823 [02:41<04:30, 8.84it/s]\u001b[A\u001b[A\n\n 37% 1430/3823 [02:41<04:31, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1431/3823 [02:41<04:31, 8.83it/s]\u001b[A\u001b[A\n\n 37% 1432/3823 [02:41<04:31, 8.82it/s]\u001b[A\u001b[A\n\n 37% 1433/3823 [02:41<04:30, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1434/3823 [02:41<04:30, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1435/3823 [02:42<04:30, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1436/3823 [02:42<04:30, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1437/3823 [02:42<04:30, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1438/3823 [02:42<04:30, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1439/3823 [02:42<04:30, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1440/3823 [02:42<04:30, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1441/3823 [02:42<04:30, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1442/3823 [02:42<04:29, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1443/3823 [02:42<04:30, 8.81it/s]\u001b[A\u001b[A\n\n 38% 1444/3823 [02:43<04:30, 8.80it/s]\u001b[A\u001b[A\n\n 38% 1445/3823 [02:43<04:29, 8.81it/s]\u001b[A\u001b[A\n\n 38% 1446/3823 [02:43<04:29, 8.81it/s]\u001b[A\u001b[A\n\n 38% 1447/3823 [02:43<04:29, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1448/3823 [02:43<04:28, 8.83it/s]\u001b[A\u001b[A\n\n 38% 1449/3823 [02:43<04:28, 8.84it/s]\u001b[A\u001b[A\n\n 38% 1450/3823 [02:43<04:28, 8.84it/s]\u001b[A\u001b[A\n\n 38% 1451/3823 [02:43<04:28, 8.85it/s]\u001b[A\u001b[A\n\n 38% 1452/3823 [02:43<04:28, 8.83it/s]\u001b[A\u001b[A\n\n 38% 1453/3823 [02:44<04:28, 8.82it/s]\u001b[A\u001b[A\n\n 38% 1454/3823 [02:44<04:28, 8.83it/s]\u001b[A\u001b[A\n\n 38% 1455/3823 [02:44<04:27, 8.84it/s]\u001b[A\u001b[A\n\n 38% 1456/3823 [02:44<04:27, 8.84it/s]\u001b[A\u001b[A\n\n 38% 1457/3823 [02:44<04:27, 8.85it/s]\u001b[A\u001b[A\n\n 38% 1458/3823 [02:44<04:27, 8.85it/s]\u001b[A\u001b[A\n\n 38% 1459/3823 [02:44<04:27, 8.84it/s]\u001b[A\u001b[A\n\n 38% 1460/3823 [02:44<04:27, 8.84it/s]\u001b[A\u001b[A\n\n 38% 1461/3823 [02:44<04:27, 8.84it/s]\u001b[A\u001b[A\n\n 38% 1462/3823 [02:45<04:27, 8.83it/s]\u001b[A\u001b[A\n\n 38% 1463/3823 [02:45<04:26, 8.85it/s]\u001b[A\u001b[A\n\n 38% 1464/3823 [02:45<04:26, 8.85it/s]\u001b[A\u001b[A\n\n 38% 1465/3823 [02:45<04:26, 8.85it/s]\u001b[A\u001b[A\n\n 38% 1466/3823 [02:45<04:26, 8.85it/s]\u001b[A\u001b[A\n\n 38% 1467/3823 [02:45<04:26, 8.85it/s]\u001b[A\u001b[A\n\n 38% 1468/3823 [02:45<04:25, 8.85it/s]\u001b[A\u001b[A\n\n 38% 1469/3823 [02:45<04:26, 8.85it/s]\u001b[A\u001b[A\n\n 38% 1470/3823 [02:45<04:26, 8.84it/s]\u001b[A\u001b[A\n\n 38% 1471/3823 [02:46<04:25, 8.85it/s]\u001b[A\u001b[A\n\n 39% 1472/3823 [02:46<04:25, 8.85it/s]\u001b[A\u001b[A\n\n 39% 1473/3823 [02:46<04:25, 8.85it/s]\u001b[A\u001b[A\n\n 39% 1474/3823 [02:46<04:25, 8.85it/s]\u001b[A\u001b[A\n\n 39% 1475/3823 [02:46<04:25, 8.85it/s]\u001b[A\u001b[A\n\n 39% 1476/3823 [02:46<04:25, 8.85it/s]\u001b[A\u001b[A\n\n 39% 1477/3823 [02:46<04:25, 8.85it/s]\u001b[A\u001b[A\n\n 39% 1478/3823 [02:46<04:25, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1479/3823 [02:46<04:25, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1480/3823 [02:47<04:24, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1481/3823 [02:47<04:24, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1482/3823 [02:47<04:24, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1483/3823 [02:47<04:24, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1484/3823 [02:47<04:24, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1485/3823 [02:47<04:24, 8.83it/s]\u001b[A\u001b[A\n\n 39% 1486/3823 [02:47<04:25, 8.81it/s]\u001b[A\u001b[A\n\n 39% 1487/3823 [02:47<04:24, 8.82it/s]\u001b[A\u001b[A\n\n 39% 1488/3823 [02:48<04:24, 8.81it/s]\u001b[A\u001b[A\n\n 39% 1489/3823 [02:48<04:24, 8.81it/s]\u001b[A\u001b[A\n\n 39% 1490/3823 [02:48<04:24, 8.82it/s]\u001b[A\u001b[A\n\n 39% 1491/3823 [02:48<04:23, 8.83it/s]\u001b[A\u001b[A\n\n 39% 1492/3823 [02:48<04:23, 8.83it/s]\u001b[A\u001b[A\n\n 39% 1493/3823 [02:48<04:23, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1494/3823 [02:48<04:23, 8.83it/s]\u001b[A\u001b[A\n\n 39% 1495/3823 [02:48<04:23, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1496/3823 [02:48<04:23, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1497/3823 [02:49<04:23, 8.83it/s]\u001b[A\u001b[A\n\n 39% 1498/3823 [02:49<04:23, 8.82it/s]\u001b[A\u001b[A\n\n 39% 1499/3823 [02:49<04:23, 8.82it/s]\u001b[A\u001b[A\n\n 39% 1500/3823 [02:49<04:23, 8.82it/s]\u001b[A\u001b[A\n\n 39% 1501/3823 [02:49<04:22, 8.83it/s]\u001b[A\u001b[A\n\n 39% 1502/3823 [02:49<04:22, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1503/3823 [02:49<04:22, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1504/3823 [02:49<04:22, 8.85it/s]\u001b[A\u001b[A\n\n 39% 1505/3823 [02:49<04:21, 8.85it/s]\u001b[A\u001b[A\n\n 39% 1506/3823 [02:50<04:22, 8.84it/s]\u001b[A\u001b[A\n\n 39% 1507/3823 [02:50<04:22, 8.82it/s]\u001b[A\u001b[A\n\n 39% 1508/3823 [02:50<04:22, 8.82it/s]\u001b[A\u001b[A\n\n 39% 1509/3823 [02:50<04:22, 8.83it/s]\u001b[A\u001b[A\n\n 39% 1510/3823 [02:50<04:21, 8.83it/s]\u001b[A\u001b[A\n\n 40% 1511/3823 [02:50<04:21, 8.83it/s]\u001b[A\u001b[A\n\n 40% 1512/3823 [02:50<04:21, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1513/3823 [02:50<04:21, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1514/3823 [02:50<04:21, 8.83it/s]\u001b[A\u001b[A\n\n 40% 1515/3823 [02:51<04:21, 8.83it/s]\u001b[A\u001b[A\n\n 40% 1516/3823 [02:51<04:21, 8.81it/s]\u001b[A\u001b[A\n\n 40% 1517/3823 [02:51<04:21, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1518/3823 [02:51<04:21, 8.83it/s]\u001b[A\u001b[A\n\n 40% 1519/3823 [02:51<04:21, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1520/3823 [02:51<04:20, 8.83it/s]\u001b[A\u001b[A\n\n 40% 1521/3823 [02:51<04:20, 8.84it/s]\u001b[A\u001b[A\n\n 40% 1522/3823 [02:51<04:20, 8.84it/s]\u001b[A\u001b[A\n\n 40% 1523/3823 [02:51<04:20, 8.84it/s]\u001b[A\u001b[A\n\n 40% 1524/3823 [02:52<04:20, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1525/3823 [02:52<04:20, 8.81it/s]\u001b[A\u001b[A\n\n 40% 1526/3823 [02:52<04:20, 8.81it/s]\u001b[A\u001b[A\n\n 40% 1527/3823 [02:52<04:21, 8.79it/s]\u001b[A\u001b[A\n\n 40% 1528/3823 [02:52<04:20, 8.79it/s]\u001b[A\u001b[A\n\n 40% 1529/3823 [02:52<04:20, 8.80it/s]\u001b[A\u001b[A\n\n 40% 1530/3823 [02:52<04:20, 8.81it/s]\u001b[A\u001b[A\n\n 40% 1531/3823 [02:52<04:20, 8.81it/s]\u001b[A\u001b[A\n\n 40% 1532/3823 [02:53<04:20, 8.80it/s]\u001b[A\u001b[A\n\n 40% 1533/3823 [02:53<04:19, 8.81it/s]\u001b[A\u001b[A\n\n 40% 1534/3823 [02:53<04:19, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1535/3823 [02:53<04:19, 8.83it/s]\u001b[A\u001b[A\n\n 40% 1536/3823 [02:53<04:18, 8.84it/s]\u001b[A\u001b[A\n\n 40% 1537/3823 [02:53<04:19, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1538/3823 [02:53<04:18, 8.83it/s]\u001b[A\u001b[A\n\n 40% 1539/3823 [02:53<04:18, 8.83it/s]\u001b[A\u001b[A\n\n 40% 1540/3823 [02:53<04:18, 8.83it/s]\u001b[A\u001b[A\n\n 40% 1541/3823 [02:54<04:18, 8.84it/s]\u001b[A\u001b[A\n\n 40% 1542/3823 [02:54<04:18, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1543/3823 [02:54<04:18, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1544/3823 [02:54<04:17, 8.84it/s]\u001b[A\u001b[A\n\n 40% 1545/3823 [02:54<04:17, 8.84it/s]\u001b[A\u001b[A\n\n 40% 1546/3823 [02:54<04:18, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1547/3823 [02:54<04:17, 8.82it/s]\u001b[A\u001b[A\n\n 40% 1548/3823 [02:54<04:17, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1549/3823 [02:54<04:17, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1550/3823 [02:55<04:17, 8.82it/s]\u001b[A\u001b[A\n\n 41% 1551/3823 [02:55<04:17, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1552/3823 [02:55<04:17, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1553/3823 [02:55<04:17, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1554/3823 [02:55<04:16, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1555/3823 [02:55<04:16, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1556/3823 [02:55<04:16, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1557/3823 [02:55<04:16, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1558/3823 [02:55<04:16, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1559/3823 [02:56<04:16, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1560/3823 [02:56<04:16, 8.82it/s]\u001b[A\u001b[A\n\n 41% 1561/3823 [02:56<04:16, 8.82it/s]\u001b[A\u001b[A\n\n 41% 1562/3823 [02:56<04:16, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1563/3823 [02:56<04:15, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1564/3823 [02:56<04:15, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1565/3823 [02:56<04:15, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1566/3823 [02:56<04:15, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1567/3823 [02:56<04:15, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1568/3823 [02:57<04:15, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1569/3823 [02:57<04:14, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1570/3823 [02:57<04:14, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1571/3823 [02:57<04:14, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1572/3823 [02:57<04:15, 8.82it/s]\u001b[A\u001b[A\n\n 41% 1573/3823 [02:57<04:15, 8.80it/s]\u001b[A\u001b[A\n\n 41% 1574/3823 [02:57<04:15, 8.80it/s]\u001b[A\u001b[A\n\n 41% 1575/3823 [02:57<04:15, 8.78it/s]\u001b[A\u001b[A\n\n 41% 1576/3823 [02:57<04:15, 8.80it/s]\u001b[A\u001b[A\n\n 41% 1577/3823 [02:58<04:14, 8.81it/s]\u001b[A\u001b[A\n\n 41% 1578/3823 [02:58<04:14, 8.82it/s]\u001b[A\u001b[A\n\n 41% 1579/3823 [02:58<04:14, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1580/3823 [02:58<04:14, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1581/3823 [02:58<04:14, 8.81it/s]\u001b[A\u001b[A\n\n 41% 1582/3823 [02:58<04:14, 8.82it/s]\u001b[A\u001b[A\n\n 41% 1583/3823 [02:58<04:13, 8.83it/s]\u001b[A\u001b[A\n\n 41% 1584/3823 [02:58<04:13, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1585/3823 [02:59<04:13, 8.84it/s]\u001b[A\u001b[A\n\n 41% 1586/3823 [02:59<04:13, 8.82it/s]\u001b[A\u001b[A\n\n 42% 1587/3823 [02:59<04:13, 8.83it/s]\u001b[A\u001b[A\n\n 42% 1588/3823 [02:59<04:13, 8.82it/s]\u001b[A\u001b[A\n\n 42% 1589/3823 [02:59<04:13, 8.82it/s]\u001b[A\u001b[A\n\n 42% 1590/3823 [02:59<04:12, 8.83it/s]\u001b[A\u001b[A\n\n 42% 1591/3823 [02:59<04:12, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1592/3823 [02:59<04:12, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1593/3823 [02:59<04:11, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1594/3823 [03:00<04:11, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1595/3823 [03:00<04:12, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1596/3823 [03:00<04:11, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1597/3823 [03:00<04:11, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1598/3823 [03:00<04:11, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1599/3823 [03:00<04:11, 8.83it/s]\u001b[A\u001b[A\n\n 42% 1600/3823 [03:00<04:11, 8.82it/s]\u001b[A\u001b[A\n\n 42% 1601/3823 [03:00<04:11, 8.82it/s]\u001b[A\u001b[A\n\n 42% 1602/3823 [03:00<04:11, 8.82it/s]\u001b[A\u001b[A\n\n 42% 1603/3823 [03:01<04:11, 8.83it/s]\u001b[A\u001b[A\n\n 42% 1604/3823 [03:01<04:11, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1605/3823 [03:01<04:11, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1606/3823 [03:01<04:10, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1607/3823 [03:01<04:10, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1608/3823 [03:01<04:10, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1609/3823 [03:01<04:10, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1610/3823 [03:01<04:10, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1611/3823 [03:01<04:09, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1612/3823 [03:02<04:09, 8.86it/s]\u001b[A\u001b[A\n\n 42% 1613/3823 [03:02<04:09, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1614/3823 [03:02<04:09, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1615/3823 [03:02<04:09, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1616/3823 [03:02<04:09, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1617/3823 [03:02<04:09, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1618/3823 [03:02<04:09, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1619/3823 [03:02<04:09, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1620/3823 [03:02<04:09, 8.85it/s]\u001b[A\u001b[A\n\n 42% 1621/3823 [03:03<04:09, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1622/3823 [03:03<04:08, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1623/3823 [03:03<04:08, 8.84it/s]\u001b[A\u001b[A\n\n 42% 1624/3823 [03:03<04:08, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1625/3823 [03:03<04:08, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1626/3823 [03:03<04:08, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1627/3823 [03:03<04:08, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1628/3823 [03:03<04:08, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1629/3823 [03:03<04:08, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1630/3823 [03:04<04:08, 8.82it/s]\u001b[A\u001b[A\n\n 43% 1631/3823 [03:04<04:08, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1632/3823 [03:04<04:08, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1633/3823 [03:04<04:07, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1634/3823 [03:04<04:07, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1635/3823 [03:04<04:07, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1636/3823 [03:04<04:07, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1637/3823 [03:04<04:07, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1638/3823 [03:05<04:07, 8.82it/s]\u001b[A\u001b[A\n\n 43% 1639/3823 [03:05<04:07, 8.82it/s]\u001b[A\u001b[A\n\n 43% 1640/3823 [03:05<04:07, 8.81it/s]\u001b[A\u001b[A\n\n 43% 1641/3823 [03:05<04:07, 8.82it/s]\u001b[A\u001b[A\n\n 43% 1642/3823 [03:05<04:07, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1643/3823 [03:05<04:07, 8.82it/s]\u001b[A\u001b[A\n\n 43% 1644/3823 [03:05<04:07, 8.80it/s]\u001b[A\u001b[A\n\n 43% 1645/3823 [03:05<04:07, 8.80it/s]\u001b[A\u001b[A\n\n 43% 1646/3823 [03:05<04:07, 8.81it/s]\u001b[A\u001b[A\n\n 43% 1647/3823 [03:06<04:06, 8.82it/s]\u001b[A\u001b[A\n\n 43% 1648/3823 [03:06<04:06, 8.82it/s]\u001b[A\u001b[A\n\n 43% 1649/3823 [03:06<04:06, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1650/3823 [03:06<04:05, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1651/3823 [03:06<04:05, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1652/3823 [03:06<04:05, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1653/3823 [03:06<04:05, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1654/3823 [03:06<04:05, 8.83it/s]\u001b[A\u001b[A\n\n 43% 1655/3823 [03:06<04:05, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1656/3823 [03:07<04:05, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1657/3823 [03:07<04:04, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1658/3823 [03:07<04:04, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1659/3823 [03:07<04:04, 8.85it/s]\u001b[A\u001b[A\n\n 43% 1660/3823 [03:07<04:04, 8.85it/s]\u001b[A\u001b[A\n\n 43% 1661/3823 [03:07<04:04, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1662/3823 [03:07<04:04, 8.84it/s]\u001b[A\u001b[A\n\n 43% 1663/3823 [03:07<04:04, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1664/3823 [03:07<04:04, 8.85it/s]\u001b[A\u001b[A\n\n 44% 1665/3823 [03:08<04:03, 8.85it/s]\u001b[A\u001b[A\n\n 44% 1666/3823 [03:08<04:03, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1667/3823 [03:08<04:03, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1668/3823 [03:08<04:03, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1669/3823 [03:08<04:03, 8.83it/s]\u001b[A\u001b[A\n\n 44% 1670/3823 [03:08<04:03, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1671/3823 [03:08<04:03, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1672/3823 [03:08<04:03, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1673/3823 [03:08<04:03, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1674/3823 [03:09<04:03, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1675/3823 [03:09<04:02, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1676/3823 [03:09<04:02, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1677/3823 [03:09<04:02, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1678/3823 [03:09<04:02, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1679/3823 [03:09<04:02, 8.83it/s]\u001b[A\u001b[A\n\n 44% 1680/3823 [03:09<04:02, 8.82it/s]\u001b[A\u001b[A\n\n 44% 1681/3823 [03:09<04:02, 8.82it/s]\u001b[A\u001b[A\n\n 44% 1682/3823 [03:09<04:02, 8.83it/s]\u001b[A\u001b[A\n\n 44% 1683/3823 [03:10<04:02, 8.83it/s]\u001b[A\u001b[A\n\n 44% 1684/3823 [03:10<04:02, 8.83it/s]\u001b[A\u001b[A\n\n 44% 1685/3823 [03:10<04:01, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1686/3823 [03:10<04:01, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1687/3823 [03:10<04:01, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1688/3823 [03:10<04:01, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1689/3823 [03:10<04:01, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1690/3823 [03:10<04:01, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1691/3823 [03:11<04:01, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1692/3823 [03:11<04:01, 8.83it/s]\u001b[A\u001b[A\n\n 44% 1693/3823 [03:11<04:01, 8.83it/s]\u001b[A\u001b[A\n\n 44% 1694/3823 [03:11<04:01, 8.83it/s]\u001b[A\u001b[A\n\n 44% 1695/3823 [03:11<04:00, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1696/3823 [03:11<04:00, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1697/3823 [03:11<04:00, 8.84it/s]\u001b[A\u001b[A\n\n 44% 1698/3823 [03:11<04:00, 8.85it/s]\u001b[A\u001b[A\n\n 44% 1699/3823 [03:11<03:59, 8.85it/s]\u001b[A\u001b[A\n\n 44% 1700/3823 [03:12<03:59, 8.86it/s]\u001b[A\u001b[A\n\n 44% 1701/3823 [03:12<03:59, 8.85it/s]\u001b[A\u001b[A\n\n 45% 1702/3823 [03:12<03:59, 8.85it/s]\u001b[A\u001b[A\n\n 45% 1703/3823 [03:12<03:59, 8.86it/s]\u001b[A\u001b[A\n\n 45% 1704/3823 [03:12<03:59, 8.86it/s]\u001b[A\u001b[A\n\n 45% 1705/3823 [03:12<03:59, 8.85it/s]\u001b[A\u001b[A\n\n 45% 1706/3823 [03:12<03:59, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1707/3823 [03:12<03:59, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1708/3823 [03:12<03:59, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1709/3823 [03:13<03:59, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1710/3823 [03:13<03:59, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1711/3823 [03:13<03:58, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1712/3823 [03:13<03:58, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1713/3823 [03:13<03:58, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1714/3823 [03:13<03:58, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1715/3823 [03:13<03:58, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1716/3823 [03:13<03:58, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1717/3823 [03:13<03:58, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1718/3823 [03:14<03:58, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1719/3823 [03:14<03:58, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1720/3823 [03:14<03:58, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1721/3823 [03:14<03:57, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1722/3823 [03:14<03:57, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1723/3823 [03:14<03:57, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1724/3823 [03:14<03:57, 8.82it/s]\u001b[A\u001b[A\n\n 45% 1725/3823 [03:14<03:57, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1726/3823 [03:14<03:57, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1727/3823 [03:15<03:57, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1728/3823 [03:15<03:56, 8.85it/s]\u001b[A\u001b[A\n\n 45% 1729/3823 [03:15<03:56, 8.85it/s]\u001b[A\u001b[A\n\n 45% 1730/3823 [03:15<03:56, 8.85it/s]\u001b[A\u001b[A\n\n 45% 1731/3823 [03:15<03:56, 8.85it/s]\u001b[A\u001b[A\n\n 45% 1732/3823 [03:15<03:56, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1733/3823 [03:15<03:56, 8.83it/s]\u001b[A\u001b[A\n\n 45% 1734/3823 [03:15<03:56, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1735/3823 [03:15<03:56, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1736/3823 [03:16<03:56, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1737/3823 [03:16<03:55, 8.84it/s]\u001b[A\u001b[A\n\n 45% 1738/3823 [03:16<03:55, 8.85it/s]\u001b[A\u001b[A\n\n 45% 1739/3823 [03:16<03:55, 8.85it/s]\u001b[A\u001b[A\n\n 46% 1740/3823 [03:16<03:55, 8.83it/s]\u001b[A\u001b[A\n\n 46% 1741/3823 [03:16<03:55, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1742/3823 [03:16<03:55, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1743/3823 [03:16<03:55, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1744/3823 [03:16<03:54, 8.85it/s]\u001b[A\u001b[A\n\n 46% 1745/3823 [03:17<03:55, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1746/3823 [03:17<03:55, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1747/3823 [03:17<03:55, 8.83it/s]\u001b[A\u001b[A\n\n 46% 1748/3823 [03:17<03:54, 8.83it/s]\u001b[A\u001b[A\n\n 46% 1749/3823 [03:17<03:54, 8.83it/s]\u001b[A\u001b[A\n\n 46% 1750/3823 [03:17<03:54, 8.83it/s]\u001b[A\u001b[A\n\n 46% 1751/3823 [03:17<03:54, 8.82it/s]\u001b[A\u001b[A\n\n 46% 1752/3823 [03:17<03:54, 8.82it/s]\u001b[A\u001b[A\n\n 46% 1753/3823 [03:18<03:54, 8.82it/s]\u001b[A\u001b[A\n\n 46% 1754/3823 [03:18<03:54, 8.82it/s]\u001b[A\u001b[A\n\n 46% 1755/3823 [03:18<03:54, 8.82it/s]\u001b[A\u001b[A\n\n 46% 1756/3823 [03:18<03:54, 8.83it/s]\u001b[A\u001b[A\n\n 46% 1757/3823 [03:18<03:53, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1758/3823 [03:18<03:53, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1759/3823 [03:18<03:53, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1760/3823 [03:18<03:53, 8.82it/s]\u001b[A\u001b[A\n\n 46% 1761/3823 [03:18<03:53, 8.82it/s]\u001b[A\u001b[A\n\n 46% 1762/3823 [03:19<03:53, 8.81it/s]\u001b[A\u001b[A\n\n 46% 1763/3823 [03:19<03:53, 8.82it/s]\u001b[A\u001b[A\n\n 46% 1764/3823 [03:19<03:53, 8.82it/s]\u001b[A\u001b[A\n\n 46% 1765/3823 [03:19<03:52, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1766/3823 [03:19<03:52, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1767/3823 [03:19<03:52, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1768/3823 [03:19<03:52, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1769/3823 [03:19<03:52, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1770/3823 [03:19<03:52, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1771/3823 [03:20<03:52, 8.84it/s]\u001b[A\u001b[A\n\n 46% 1772/3823 [03:20<03:52, 8.82it/s]\u001b[A\u001b[A\n\n 46% 1773/3823 [03:20<03:52, 8.81it/s]\u001b[A\u001b[A\n\n 46% 1774/3823 [03:20<03:52, 8.81it/s]\u001b[A\u001b[A\n\n 46% 1775/3823 [03:20<03:52, 8.81it/s]\u001b[A\u001b[A\n\n 46% 1776/3823 [03:20<03:52, 8.81it/s]\u001b[A\u001b[A\n\n 46% 1777/3823 [03:20<03:52, 8.82it/s]\u001b[A\u001b[A\n\n 47% 1778/3823 [03:20<03:51, 8.83it/s]\u001b[A\u001b[A\n\n 47% 1779/3823 [03:20<03:51, 8.83it/s]\u001b[A\u001b[A\n\n 47% 1780/3823 [03:21<03:51, 8.82it/s]\u001b[A\u001b[A\n\n 47% 1781/3823 [03:21<03:51, 8.82it/s]\u001b[A\u001b[A\n\n 47% 1782/3823 [03:21<03:51, 8.81it/s]\u001b[A\u001b[A\n\n 47% 1783/3823 [03:21<03:51, 8.81it/s]\u001b[A\u001b[A\n\n 47% 1784/3823 [03:21<03:51, 8.81it/s]\u001b[A\u001b[A\n\n 47% 1785/3823 [03:21<03:51, 8.82it/s]\u001b[A\u001b[A\n\n 47% 1786/3823 [03:21<03:51, 8.82it/s]\u001b[A\u001b[A\n\n 47% 1787/3823 [03:21<03:51, 8.81it/s]\u001b[A\u001b[A\n\n 47% 1788/3823 [03:21<03:50, 8.82it/s]\u001b[A\u001b[A\n\n 47% 1789/3823 [03:22<03:50, 8.82it/s]\u001b[A\u001b[A\n\n 47% 1790/3823 [03:22<03:50, 8.82it/s]\u001b[A\u001b[A\n\n 47% 1791/3823 [03:22<03:50, 8.81it/s]\u001b[A\u001b[A\n\n 47% 1792/3823 [03:22<03:50, 8.81it/s]\u001b[A\u001b[A\n\n 47% 1793/3823 [03:22<03:50, 8.81it/s]\u001b[A\u001b[A\n\n 47% 1794/3823 [03:22<03:50, 8.81it/s]\u001b[A\u001b[A\n\n 47% 1795/3823 [03:22<03:49, 8.83it/s]\u001b[A\u001b[A\n\n 47% 1796/3823 [03:22<03:49, 8.82it/s]\u001b[A\u001b[A\n\n 47% 1797/3823 [03:23<03:49, 8.84it/s]\u001b[A\u001b[A\n\n 47% 1798/3823 [03:23<03:48, 8.85it/s]\u001b[A\u001b[A\n\n 47% 1799/3823 [03:23<03:49, 8.84it/s]\u001b[A\u001b[A\n\n 47% 1800/3823 [03:23<03:48, 8.83it/s]\u001b[A\u001b[A\n\n 47% 1801/3823 [03:23<03:48, 8.84it/s]\u001b[A\u001b[A\n\n 47% 1802/3823 [03:23<03:48, 8.85it/s]\u001b[A\u001b[A\n\n 47% 1803/3823 [03:23<03:48, 8.84it/s]\u001b[A\u001b[A\n\n 47% 1804/3823 [03:23<03:48, 8.83it/s]\u001b[A\u001b[A\n\n 47% 1805/3823 [03:23<03:48, 8.83it/s]\u001b[A\u001b[A\n\n 47% 1806/3823 [03:24<03:48, 8.84it/s]\u001b[A\u001b[A\n\n 47% 1807/3823 [03:24<03:48, 8.84it/s]\u001b[A\u001b[A\n\n 47% 1808/3823 [03:24<03:48, 8.83it/s]\u001b[A\u001b[A\n\n 47% 1809/3823 [03:24<03:48, 8.81it/s]\u001b[A\u001b[A\n\n 47% 1810/3823 [03:24<03:49, 8.79it/s]\u001b[A\u001b[A\n\n 47% 1811/3823 [03:24<03:48, 8.79it/s]\u001b[A\u001b[A\n\n 47% 1812/3823 [03:24<03:49, 8.75it/s]\u001b[A\u001b[A\n\n 47% 1813/3823 [03:24<03:49, 8.76it/s]\u001b[A\u001b[A\n\n 47% 1814/3823 [03:24<03:48, 8.78it/s]\u001b[A\u001b[A\n\n 47% 1815/3823 [03:25<03:48, 8.80it/s]\u001b[A\u001b[A\n\n 48% 1816/3823 [03:25<03:47, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1817/3823 [03:25<03:47, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1818/3823 [03:25<03:47, 8.80it/s]\u001b[A\u001b[A\n\n 48% 1819/3823 [03:25<03:47, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1820/3823 [03:25<03:47, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1821/3823 [03:25<03:47, 8.80it/s]\u001b[A\u001b[A\n\n 48% 1822/3823 [03:25<03:47, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1823/3823 [03:25<03:47, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1824/3823 [03:26<03:46, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1825/3823 [03:26<03:46, 8.80it/s]\u001b[A\u001b[A\n\n 48% 1826/3823 [03:26<03:47, 8.79it/s]\u001b[A\u001b[A\n\n 48% 1827/3823 [03:26<03:46, 8.80it/s]\u001b[A\u001b[A\n\n 48% 1828/3823 [03:26<03:46, 8.82it/s]\u001b[A\u001b[A\n\n 48% 1829/3823 [03:26<03:46, 8.82it/s]\u001b[A\u001b[A\n\n 48% 1830/3823 [03:26<03:46, 8.82it/s]\u001b[A\u001b[A\n\n 48% 1831/3823 [03:26<03:45, 8.83it/s]\u001b[A\u001b[A\n\n 48% 1832/3823 [03:26<03:45, 8.84it/s]\u001b[A\u001b[A\n\n 48% 1833/3823 [03:27<03:45, 8.84it/s]\u001b[A\u001b[A\n\n 48% 1834/3823 [03:27<03:45, 8.84it/s]\u001b[A\u001b[A\n\n 48% 1835/3823 [03:27<03:44, 8.84it/s]\u001b[A\u001b[A\n\n 48% 1836/3823 [03:27<03:44, 8.84it/s]\u001b[A\u001b[A\n\n 48% 1837/3823 [03:27<03:44, 8.84it/s]\u001b[A\u001b[A\n\n 48% 1838/3823 [03:27<03:44, 8.84it/s]\u001b[A\u001b[A\n\n 48% 1839/3823 [03:27<03:45, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1840/3823 [03:27<03:45, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1841/3823 [03:27<03:44, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1842/3823 [03:28<03:44, 8.82it/s]\u001b[A\u001b[A\n\n 48% 1843/3823 [03:28<03:44, 8.83it/s]\u001b[A\u001b[A\n\n 48% 1844/3823 [03:28<03:44, 8.83it/s]\u001b[A\u001b[A\n\n 48% 1845/3823 [03:28<03:43, 8.84it/s]\u001b[A\u001b[A\n\n 48% 1846/3823 [03:28<03:43, 8.83it/s]\u001b[A\u001b[A\n\n 48% 1847/3823 [03:28<03:44, 8.82it/s]\u001b[A\u001b[A\n\n 48% 1848/3823 [03:28<03:44, 8.81it/s]\u001b[A\u001b[A\n\n 48% 1849/3823 [03:28<03:43, 8.82it/s]\u001b[A\u001b[A\n\n 48% 1850/3823 [03:29<03:43, 8.82it/s]\u001b[A\u001b[A\n\n 48% 1851/3823 [03:29<03:43, 8.82it/s]\u001b[A\u001b[A\n\n 48% 1852/3823 [03:29<03:43, 8.82it/s]\u001b[A\u001b[A\n\n 48% 1853/3823 [03:29<03:43, 8.82it/s]\u001b[A\u001b[A\n\n 48% 1854/3823 [03:29<03:43, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1855/3823 [03:29<03:43, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1856/3823 [03:29<03:42, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1857/3823 [03:29<03:43, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1858/3823 [03:29<03:42, 8.81it/s]\u001b[A\u001b[A\n\n 49% 1859/3823 [03:30<03:42, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1860/3823 [03:30<03:42, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1861/3823 [03:30<03:42, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1862/3823 [03:30<03:42, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1863/3823 [03:30<03:41, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1864/3823 [03:30<03:41, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1865/3823 [03:30<03:41, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1866/3823 [03:30<03:41, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1867/3823 [03:30<03:41, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1868/3823 [03:31<03:41, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1869/3823 [03:31<03:41, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1870/3823 [03:31<03:41, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1871/3823 [03:31<03:41, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1872/3823 [03:31<03:40, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1873/3823 [03:31<03:40, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1874/3823 [03:31<03:41, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1875/3823 [03:31<03:40, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1876/3823 [03:31<03:40, 8.84it/s]\u001b[A\u001b[A\n\n 49% 1877/3823 [03:32<03:40, 8.84it/s]\u001b[A\u001b[A\n\n 49% 1878/3823 [03:32<03:40, 8.84it/s]\u001b[A\u001b[A\n\n 49% 1879/3823 [03:32<03:40, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1880/3823 [03:32<03:40, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1881/3823 [03:32<03:40, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1882/3823 [03:32<03:39, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1883/3823 [03:32<03:40, 8.81it/s]\u001b[A\u001b[A\n\n 49% 1884/3823 [03:32<03:39, 8.81it/s]\u001b[A\u001b[A\n\n 49% 1885/3823 [03:32<03:39, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1886/3823 [03:33<03:39, 8.83it/s]\u001b[A\u001b[A\n\n 49% 1887/3823 [03:33<03:39, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1888/3823 [03:33<03:39, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1889/3823 [03:33<03:39, 8.82it/s]\u001b[A\u001b[A\n\n 49% 1890/3823 [03:33<03:38, 8.84it/s]\u001b[A\u001b[A\n\n 49% 1891/3823 [03:33<03:38, 8.84it/s]\u001b[A\u001b[A\n\n 49% 1892/3823 [03:33<03:38, 8.85it/s]\u001b[A\u001b[A\n\n 50% 1893/3823 [03:33<03:38, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1894/3823 [03:33<03:38, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1895/3823 [03:34<03:38, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1896/3823 [03:34<03:38, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1897/3823 [03:34<03:37, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1898/3823 [03:34<03:38, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1899/3823 [03:34<03:37, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1900/3823 [03:34<03:37, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1901/3823 [03:34<03:37, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1902/3823 [03:34<03:37, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1903/3823 [03:35<03:37, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1904/3823 [03:35<03:37, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1905/3823 [03:35<03:37, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1906/3823 [03:35<03:36, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1907/3823 [03:35<03:36, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1908/3823 [03:35<03:36, 8.85it/s]\u001b[A\u001b[A\n\n 50% 1909/3823 [03:35<03:36, 8.85it/s]\u001b[A\u001b[A\n\n 50% 1910/3823 [03:35<03:36, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1911/3823 [03:35<03:36, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1912/3823 [03:36<03:36, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1913/3823 [03:36<03:36, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1914/3823 [03:36<03:36, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1915/3823 [03:36<03:35, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1916/3823 [03:36<03:35, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1917/3823 [03:36<03:35, 8.84it/s]\u001b[A\u001b[A\n\n 50% 1918/3823 [03:36<03:35, 8.85it/s]\u001b[A\u001b[A\n\n 50% 1919/3823 [03:36<03:35, 8.85it/s]\u001b[A\u001b[A\n\n 50% 1920/3823 [03:36<03:35, 8.85it/s]\u001b[A\u001b[A\n\n 50% 1921/3823 [03:37<03:34, 8.85it/s]\u001b[A\u001b[A\n\n 50% 1922/3823 [03:37<03:34, 8.86it/s]\u001b[A\u001b[A\n\n 50% 1923/3823 [03:37<03:34, 8.86it/s]\u001b[A\u001b[A\n\n 50% 1924/3823 [03:37<03:34, 8.86it/s]\u001b[A\u001b[A\n\n 50% 1925/3823 [03:37<03:34, 8.86it/s]\u001b[A\u001b[A\n\n 50% 1926/3823 [03:37<03:34, 8.85it/s]\u001b[A\u001b[A\n\n 50% 1927/3823 [03:37<03:34, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1928/3823 [03:37<03:34, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1929/3823 [03:37<03:34, 8.83it/s]\u001b[A\u001b[A\n\n 50% 1930/3823 [03:38<03:34, 8.82it/s]\u001b[A\u001b[A\n\n 51% 1931/3823 [03:38<03:34, 8.83it/s]\u001b[A\u001b[A\n\n 51% 1932/3823 [03:38<03:33, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1933/3823 [03:38<03:33, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1934/3823 [03:38<03:33, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1935/3823 [03:38<03:33, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1936/3823 [03:38<03:33, 8.83it/s]\u001b[A\u001b[A\n\n 51% 1937/3823 [03:38<03:33, 8.83it/s]\u001b[A\u001b[A\n\n 51% 1938/3823 [03:38<03:33, 8.82it/s]\u001b[A\u001b[A\n\n 51% 1939/3823 [03:39<03:33, 8.82it/s]\u001b[A\u001b[A\n\n 51% 1940/3823 [03:39<03:33, 8.82it/s]\u001b[A\u001b[A\n\n 51% 1941/3823 [03:39<03:33, 8.83it/s]\u001b[A\u001b[A\n\n 51% 1942/3823 [03:39<03:32, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1943/3823 [03:39<03:32, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1944/3823 [03:39<03:33, 8.82it/s]\u001b[A\u001b[A\n\n 51% 1945/3823 [03:39<03:32, 8.82it/s]\u001b[A\u001b[A\n\n 51% 1946/3823 [03:39<03:32, 8.83it/s]\u001b[A\u001b[A\n\n 51% 1947/3823 [03:39<03:32, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1948/3823 [03:40<03:31, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1949/3823 [03:40<03:31, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1950/3823 [03:40<03:31, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1951/3823 [03:40<03:31, 8.83it/s]\u001b[A\u001b[A\n\n 51% 1952/3823 [03:40<03:31, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1953/3823 [03:40<03:31, 8.83it/s]\u001b[A\u001b[A\n\n 51% 1954/3823 [03:40<03:31, 8.83it/s]\u001b[A\u001b[A\n\n 51% 1955/3823 [03:40<03:31, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1956/3823 [03:41<03:31, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1957/3823 [03:41<03:30, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1958/3823 [03:41<03:30, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1959/3823 [03:41<03:30, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1960/3823 [03:41<03:30, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1961/3823 [03:41<03:30, 8.84it/s]\u001b[A\u001b[A\n\n 51% 1962/3823 [03:41<03:30, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1963/3823 [03:41<03:30, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1964/3823 [03:41<03:29, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1965/3823 [03:42<03:29, 8.86it/s]\u001b[A\u001b[A\n\n 51% 1966/3823 [03:42<03:29, 8.85it/s]\u001b[A\u001b[A\n\n 51% 1967/3823 [03:42<03:30, 8.83it/s]\u001b[A\u001b[A\n\n 51% 1968/3823 [03:42<03:30, 8.83it/s]\u001b[A\u001b[A\n\n 52% 1969/3823 [03:42<03:30, 8.82it/s]\u001b[A\u001b[A\n\n 52% 1970/3823 [03:42<03:29, 8.82it/s]\u001b[A\u001b[A\n\n 52% 1971/3823 [03:42<03:29, 8.83it/s]\u001b[A\u001b[A\n\n 52% 1972/3823 [03:42<03:29, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1973/3823 [03:42<03:29, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1974/3823 [03:43<03:29, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1975/3823 [03:43<03:28, 8.85it/s]\u001b[A\u001b[A\n\n 52% 1976/3823 [03:43<03:28, 8.85it/s]\u001b[A\u001b[A\n\n 52% 1977/3823 [03:43<03:28, 8.86it/s]\u001b[A\u001b[A\n\n 52% 1978/3823 [03:43<03:28, 8.85it/s]\u001b[A\u001b[A\n\n 52% 1979/3823 [03:43<03:28, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1980/3823 [03:43<03:28, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1981/3823 [03:43<03:28, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1982/3823 [03:43<03:28, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1983/3823 [03:44<03:28, 8.83it/s]\u001b[A\u001b[A\n\n 52% 1984/3823 [03:44<03:28, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1985/3823 [03:44<03:28, 8.83it/s]\u001b[A\u001b[A\n\n 52% 1986/3823 [03:44<03:27, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1987/3823 [03:44<03:27, 8.85it/s]\u001b[A\u001b[A\n\n 52% 1988/3823 [03:44<03:27, 8.85it/s]\u001b[A\u001b[A\n\n 52% 1989/3823 [03:44<03:27, 8.85it/s]\u001b[A\u001b[A\n\n 52% 1990/3823 [03:44<03:27, 8.85it/s]\u001b[A\u001b[A\n\n 52% 1991/3823 [03:44<03:27, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1992/3823 [03:45<03:27, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1993/3823 [03:45<03:27, 8.83it/s]\u001b[A\u001b[A\n\n 52% 1994/3823 [03:45<03:27, 8.83it/s]\u001b[A\u001b[A\n\n 52% 1995/3823 [03:45<03:26, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1996/3823 [03:45<03:26, 8.84it/s]\u001b[A\u001b[A\n\n 52% 1997/3823 [03:45<03:26, 8.85it/s]\u001b[A\u001b[A\n\n 52% 1998/3823 [03:45<03:26, 8.85it/s]\u001b[A\u001b[A\n\n 52% 1999/3823 [03:45<03:26, 8.84it/s]\u001b[A\u001b[A\n\n 52% 2000/3823 [03:45<03:26, 8.85it/s]\u001b[A\u001b[A\n\n 52% 2001/3823 [03:46<03:25, 8.85it/s]\u001b[A\u001b[A\n\n 52% 2002/3823 [03:46<03:26, 8.84it/s]\u001b[A\u001b[A\n\n 52% 2003/3823 [03:46<03:25, 8.84it/s]\u001b[A\u001b[A\n\n 52% 2004/3823 [03:46<03:25, 8.84it/s]\u001b[A\u001b[A\n\n 52% 2005/3823 [03:46<03:25, 8.84it/s]\u001b[A\u001b[A\n\n 52% 2006/3823 [03:46<03:25, 8.83it/s]\u001b[A\u001b[A\n\n 52% 2007/3823 [03:46<03:26, 8.81it/s]\u001b[A\u001b[A\n\n 53% 2008/3823 [03:46<03:25, 8.82it/s]\u001b[A\u001b[A\n\n 53% 2009/3823 [03:47<03:25, 8.83it/s]\u001b[A\u001b[A\n\n 53% 2010/3823 [03:47<03:25, 8.83it/s]\u001b[A\u001b[A\n\n 53% 2011/3823 [03:47<03:25, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2012/3823 [03:47<03:24, 8.85it/s]\u001b[A\u001b[A\n\n 53% 2013/3823 [03:47<03:24, 8.86it/s]\u001b[A\u001b[A\n\n 53% 2014/3823 [03:47<03:24, 8.85it/s]\u001b[A\u001b[A\n\n 53% 2015/3823 [03:47<03:24, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2016/3823 [03:47<03:24, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2017/3823 [03:47<03:24, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2018/3823 [03:48<03:24, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2019/3823 [03:48<03:24, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2020/3823 [03:48<03:24, 8.83it/s]\u001b[A\u001b[A\n\n 53% 2021/3823 [03:48<03:24, 8.83it/s]\u001b[A\u001b[A\n\n 53% 2022/3823 [03:48<03:24, 8.82it/s]\u001b[A\u001b[A\n\n 53% 2023/3823 [03:48<03:24, 8.82it/s]\u001b[A\u001b[A\n\n 53% 2024/3823 [03:48<03:23, 8.83it/s]\u001b[A\u001b[A\n\n 53% 2025/3823 [03:48<03:23, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2026/3823 [03:48<03:23, 8.83it/s]\u001b[A\u001b[A\n\n 53% 2027/3823 [03:49<03:23, 8.83it/s]\u001b[A\u001b[A\n\n 53% 2028/3823 [03:49<03:23, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2029/3823 [03:49<03:22, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2030/3823 [03:49<03:22, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2031/3823 [03:49<03:23, 8.82it/s]\u001b[A\u001b[A\n\n 53% 2032/3823 [03:49<03:22, 8.83it/s]\u001b[A\u001b[A\n\n 53% 2033/3823 [03:49<03:22, 8.83it/s]\u001b[A\u001b[A\n\n 53% 2034/3823 [03:49<03:22, 8.83it/s]\u001b[A\u001b[A\n\n 53% 2035/3823 [03:49<03:22, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2036/3823 [03:50<03:22, 8.84it/s]\u001b[A\u001b[A\n\n 53% 2037/3823 [03:50<03:21, 8.85it/s]\u001b[A\u001b[A\n\n 53% 2038/3823 [03:50<03:21, 8.85it/s]\u001b[A\u001b[A\n\n 53% 2039/3823 [03:50<03:21, 8.85it/s]\u001b[A\u001b[A\n\n 53% 2040/3823 [03:50<03:21, 8.85it/s]\u001b[A\u001b[A\n\n 53% 2041/3823 [03:50<03:21, 8.85it/s]\u001b[A\u001b[A\n\n 53% 2042/3823 [03:50<03:21, 8.85it/s]\u001b[A\u001b[A\n\n 53% 2043/3823 [03:50<03:20, 8.86it/s]\u001b[A\u001b[A\n\n 53% 2044/3823 [03:50<03:20, 8.86it/s]\u001b[A\u001b[A\n\n 53% 2045/3823 [03:51<03:20, 8.85it/s]\u001b[A\u001b[A\n\n 54% 2046/3823 [03:51<03:20, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2047/3823 [03:51<03:21, 8.83it/s]\u001b[A\u001b[A\n\n 54% 2048/3823 [03:51<03:20, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2049/3823 [03:51<03:20, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2050/3823 [03:51<03:20, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2051/3823 [03:51<03:20, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2052/3823 [03:51<03:20, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2053/3823 [03:51<03:20, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2054/3823 [03:52<03:20, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2055/3823 [03:52<03:20, 8.83it/s]\u001b[A\u001b[A\n\n 54% 2056/3823 [03:52<03:19, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2057/3823 [03:52<03:19, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2058/3823 [03:52<03:19, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2059/3823 [03:52<03:19, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2060/3823 [03:52<03:19, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2061/3823 [03:52<03:19, 8.85it/s]\u001b[A\u001b[A\n\n 54% 2062/3823 [03:53<03:19, 8.85it/s]\u001b[A\u001b[A\n\n 54% 2063/3823 [03:53<03:19, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2064/3823 [03:53<03:18, 8.85it/s]\u001b[A\u001b[A\n\n 54% 2065/3823 [03:53<03:18, 8.85it/s]\u001b[A\u001b[A\n\n 54% 2066/3823 [03:53<03:18, 8.85it/s]\u001b[A\u001b[A\n\n 54% 2067/3823 [03:53<03:18, 8.85it/s]\u001b[A\u001b[A\n\n 54% 2068/3823 [03:53<03:18, 8.85it/s]\u001b[A\u001b[A\n\n 54% 2069/3823 [03:53<03:18, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2070/3823 [03:53<03:18, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2071/3823 [03:54<03:18, 8.83it/s]\u001b[A\u001b[A\n\n 54% 2072/3823 [03:54<03:18, 8.83it/s]\u001b[A\u001b[A\n\n 54% 2073/3823 [03:54<03:18, 8.82it/s]\u001b[A\u001b[A\n\n 54% 2074/3823 [03:54<03:17, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2075/3823 [03:54<03:17, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2076/3823 [03:54<03:17, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2077/3823 [03:54<03:17, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2078/3823 [03:54<03:17, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2079/3823 [03:54<03:17, 8.83it/s]\u001b[A\u001b[A\n\n 54% 2080/3823 [03:55<03:17, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2081/3823 [03:55<03:17, 8.84it/s]\u001b[A\u001b[A\n\n 54% 2082/3823 [03:55<03:16, 8.85it/s]\u001b[A\u001b[A\n\n 54% 2083/3823 [03:55<03:16, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2084/3823 [03:55<03:16, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2085/3823 [03:55<03:16, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2086/3823 [03:55<03:16, 8.82it/s]\u001b[A\u001b[A\n\n 55% 2087/3823 [03:55<03:16, 8.82it/s]\u001b[A\u001b[A\n\n 55% 2088/3823 [03:55<03:16, 8.82it/s]\u001b[A\u001b[A\n\n 55% 2089/3823 [03:56<03:16, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2090/3823 [03:56<03:16, 8.83it/s]\u001b[A\u001b[A\n\n 55% 2091/3823 [03:56<03:15, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2092/3823 [03:56<03:15, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2093/3823 [03:56<03:15, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2094/3823 [03:56<03:15, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2095/3823 [03:56<03:15, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2096/3823 [03:56<03:15, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2097/3823 [03:56<03:15, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2098/3823 [03:57<03:14, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2099/3823 [03:57<03:14, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2100/3823 [03:57<03:14, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2101/3823 [03:57<03:14, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2102/3823 [03:57<03:14, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2103/3823 [03:57<03:14, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2104/3823 [03:57<03:14, 8.83it/s]\u001b[A\u001b[A\n\n 55% 2105/3823 [03:57<03:14, 8.83it/s]\u001b[A\u001b[A\n\n 55% 2106/3823 [03:57<03:14, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2107/3823 [03:58<03:14, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2108/3823 [03:58<03:13, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2109/3823 [03:58<03:13, 8.85it/s]\u001b[A\u001b[A\n\n 55% 2110/3823 [03:58<03:13, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2111/3823 [03:58<03:13, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2112/3823 [03:58<03:13, 8.83it/s]\u001b[A\u001b[A\n\n 55% 2113/3823 [03:58<03:13, 8.83it/s]\u001b[A\u001b[A\n\n 55% 2114/3823 [03:58<03:13, 8.83it/s]\u001b[A\u001b[A\n\n 55% 2115/3823 [03:59<03:13, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2116/3823 [03:59<03:13, 8.83it/s]\u001b[A\u001b[A\n\n 55% 2117/3823 [03:59<03:13, 8.84it/s]\u001b[A\u001b[A\n\n 55% 2118/3823 [03:59<03:13, 8.83it/s]\u001b[A\u001b[A\n\n 55% 2119/3823 [03:59<03:13, 8.82it/s]\u001b[A\u001b[A\n\n 55% 2120/3823 [03:59<03:13, 8.82it/s]\u001b[A\u001b[A\n\n 55% 2121/3823 [03:59<03:12, 8.83it/s]\u001b[A\u001b[A\n\n 56% 2122/3823 [03:59<03:12, 8.82it/s]\u001b[A\u001b[A\n\n 56% 2123/3823 [03:59<03:12, 8.82it/s]\u001b[A\u001b[A\n\n 56% 2124/3823 [04:00<03:12, 8.82it/s]\u001b[A\u001b[A\n\n 56% 2125/3823 [04:00<03:12, 8.80it/s]\u001b[A\u001b[A\n\n 56% 2126/3823 [04:00<03:12, 8.81it/s]\u001b[A\u001b[A\n\n 56% 2127/3823 [04:00<03:12, 8.81it/s]\u001b[A\u001b[A\n\n 56% 2128/3823 [04:00<03:12, 8.82it/s]\u001b[A\u001b[A\n\n 56% 2129/3823 [04:00<03:11, 8.83it/s]\u001b[A\u001b[A\n\n 56% 2130/3823 [04:00<03:11, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2131/3823 [04:00<03:11, 8.85it/s]\u001b[A\u001b[A\n\n 56% 2132/3823 [04:00<03:11, 8.85it/s]\u001b[A\u001b[A\n\n 56% 2133/3823 [04:01<03:10, 8.85it/s]\u001b[A\u001b[A\n\n 56% 2134/3823 [04:01<03:10, 8.85it/s]\u001b[A\u001b[A\n\n 56% 2135/3823 [04:01<03:10, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2136/3823 [04:01<03:10, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2137/3823 [04:01<03:10, 8.83it/s]\u001b[A\u001b[A\n\n 56% 2138/3823 [04:01<03:10, 8.82it/s]\u001b[A\u001b[A\n\n 56% 2139/3823 [04:01<03:10, 8.82it/s]\u001b[A\u001b[A\n\n 56% 2140/3823 [04:01<03:10, 8.83it/s]\u001b[A\u001b[A\n\n 56% 2141/3823 [04:01<03:10, 8.83it/s]\u001b[A\u001b[A\n\n 56% 2142/3823 [04:02<03:10, 8.83it/s]\u001b[A\u001b[A\n\n 56% 2143/3823 [04:02<03:10, 8.83it/s]\u001b[A\u001b[A\n\n 56% 2144/3823 [04:02<03:10, 8.83it/s]\u001b[A\u001b[A\n\n 56% 2145/3823 [04:02<03:09, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2146/3823 [04:02<03:09, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2147/3823 [04:02<03:09, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2148/3823 [04:02<03:09, 8.85it/s]\u001b[A\u001b[A\n\n 56% 2149/3823 [04:02<03:09, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2150/3823 [04:02<03:09, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2151/3823 [04:03<03:09, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2152/3823 [04:03<03:09, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2153/3823 [04:03<03:08, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2154/3823 [04:03<03:08, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2155/3823 [04:03<03:08, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2156/3823 [04:03<03:08, 8.84it/s]\u001b[A\u001b[A\n\n 56% 2157/3823 [04:03<03:08, 8.85it/s]\u001b[A\u001b[A\n\n 56% 2158/3823 [04:03<03:08, 8.85it/s]\u001b[A\u001b[A\n\n 56% 2159/3823 [04:03<03:08, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2160/3823 [04:04<03:08, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2161/3823 [04:04<03:07, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2162/3823 [04:04<03:07, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2163/3823 [04:04<03:07, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2164/3823 [04:04<03:07, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2165/3823 [04:04<03:07, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2166/3823 [04:04<03:07, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2167/3823 [04:04<03:07, 8.82it/s]\u001b[A\u001b[A\n\n 57% 2168/3823 [04:04<03:07, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2169/3823 [04:05<03:07, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2170/3823 [04:05<03:07, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2171/3823 [04:05<03:07, 8.82it/s]\u001b[A\u001b[A\n\n 57% 2172/3823 [04:05<03:07, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2173/3823 [04:05<03:06, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2174/3823 [04:05<03:06, 8.82it/s]\u001b[A\u001b[A\n\n 57% 2175/3823 [04:05<03:06, 8.81it/s]\u001b[A\u001b[A\n\n 57% 2176/3823 [04:05<03:06, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2177/3823 [04:06<03:06, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2178/3823 [04:06<03:06, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2179/3823 [04:06<03:05, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2180/3823 [04:06<03:05, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2181/3823 [04:06<03:05, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2182/3823 [04:06<03:05, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2183/3823 [04:06<03:05, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2184/3823 [04:06<03:05, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2185/3823 [04:06<03:05, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2186/3823 [04:07<03:05, 8.85it/s]\u001b[A\u001b[A\n\n 57% 2187/3823 [04:07<03:05, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2188/3823 [04:07<03:05, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2189/3823 [04:07<03:04, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2190/3823 [04:07<03:04, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2191/3823 [04:07<03:04, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2192/3823 [04:07<03:04, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2193/3823 [04:07<03:04, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2194/3823 [04:07<03:04, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2195/3823 [04:08<03:04, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2196/3823 [04:08<03:04, 8.84it/s]\u001b[A\u001b[A\n\n 57% 2197/3823 [04:08<03:04, 8.83it/s]\u001b[A\u001b[A\n\n 57% 2198/3823 [04:08<03:04, 8.83it/s]\u001b[A\u001b[A\n\n 58% 2199/3823 [04:08<03:03, 8.84it/s]\u001b[A\u001b[A\n\n 58% 2200/3823 [04:08<03:03, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2201/3823 [04:08<03:04, 8.81it/s]\u001b[A\u001b[A\n\n 58% 2202/3823 [04:08<03:03, 8.81it/s]\u001b[A\u001b[A\n\n 58% 2203/3823 [04:08<03:03, 8.81it/s]\u001b[A\u001b[A\n\n 58% 2204/3823 [04:09<03:03, 8.81it/s]\u001b[A\u001b[A\n\n 58% 2205/3823 [04:09<03:03, 8.81it/s]\u001b[A\u001b[A\n\n 58% 2206/3823 [04:09<03:03, 8.80it/s]\u001b[A\u001b[A\n\n 58% 2207/3823 [04:09<03:03, 8.80it/s]\u001b[A\u001b[A\n\n 58% 2208/3823 [04:09<03:03, 8.80it/s]\u001b[A\u001b[A\n\n 58% 2209/3823 [04:09<03:03, 8.81it/s]\u001b[A\u001b[A\n\n 58% 2210/3823 [04:09<03:02, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2211/3823 [04:09<03:02, 8.83it/s]\u001b[A\u001b[A\n\n 58% 2212/3823 [04:09<03:02, 8.83it/s]\u001b[A\u001b[A\n\n 58% 2213/3823 [04:10<03:02, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2214/3823 [04:10<03:02, 8.80it/s]\u001b[A\u001b[A\n\n 58% 2215/3823 [04:10<03:02, 8.81it/s]\u001b[A\u001b[A\n\n 58% 2216/3823 [04:10<03:02, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2217/3823 [04:10<03:01, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2218/3823 [04:10<03:01, 8.83it/s]\u001b[A\u001b[A\n\n 58% 2219/3823 [04:10<03:01, 8.83it/s]\u001b[A\u001b[A\n\n 58% 2220/3823 [04:10<03:01, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2221/3823 [04:11<03:01, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2222/3823 [04:11<03:01, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2223/3823 [04:11<03:01, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2224/3823 [04:11<03:01, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2225/3823 [04:11<03:01, 8.81it/s]\u001b[A\u001b[A\n\n 58% 2226/3823 [04:11<03:01, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2227/3823 [04:11<03:00, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2228/3823 [04:11<03:00, 8.83it/s]\u001b[A\u001b[A\n\n 58% 2229/3823 [04:11<03:00, 8.83it/s]\u001b[A\u001b[A\n\n 58% 2230/3823 [04:12<03:00, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2231/3823 [04:12<03:00, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2232/3823 [04:12<03:00, 8.83it/s]\u001b[A\u001b[A\n\n 58% 2233/3823 [04:12<03:00, 8.83it/s]\u001b[A\u001b[A\n\n 58% 2234/3823 [04:12<03:00, 8.82it/s]\u001b[A\u001b[A\n\n 58% 2235/3823 [04:12<02:59, 8.83it/s]\u001b[A\u001b[A\n\n 58% 2236/3823 [04:12<02:59, 8.83it/s]\u001b[A\u001b[A\n\n 59% 2237/3823 [04:12<02:59, 8.83it/s]\u001b[A\u001b[A\n\n 59% 2238/3823 [04:12<02:59, 8.83it/s]\u001b[A\u001b[A\n\n 59% 2239/3823 [04:13<02:59, 8.84it/s]\u001b[A\u001b[A\n\n 59% 2240/3823 [04:13<02:59, 8.83it/s]\u001b[A\u001b[A\n\n 59% 2241/3823 [04:13<02:59, 8.82it/s]\u001b[A\u001b[A\n\n 59% 2242/3823 [04:13<02:59, 8.80it/s]\u001b[A\u001b[A\n\n 59% 2243/3823 [04:13<03:00, 8.76it/s]\u001b[A\u001b[A\n\n 59% 2244/3823 [04:13<02:59, 8.77it/s]\u001b[A\u001b[A\n\n 59% 2245/3823 [04:13<02:59, 8.79it/s]\u001b[A\u001b[A\n\n 59% 2246/3823 [04:13<02:59, 8.80it/s]\u001b[A\u001b[A\n\n 59% 2247/3823 [04:13<02:58, 8.81it/s]\u001b[A\u001b[A\n\n 59% 2248/3823 [04:14<02:58, 8.82it/s]\u001b[A\u001b[A\n\n 59% 2249/3823 [04:14<02:58, 8.83it/s]\u001b[A\u001b[A\n\n 59% 2250/3823 [04:14<02:58, 8.83it/s]\u001b[A\u001b[A\n\n 59% 2251/3823 [04:14<02:58, 8.82it/s]\u001b[A\u001b[A\n\n 59% 2252/3823 [04:14<02:58, 8.81it/s]\u001b[A\u001b[A\n\n 59% 2253/3823 [04:14<02:58, 8.81it/s]\u001b[A\u001b[A\n\n 59% 2254/3823 [04:14<02:58, 8.81it/s]\u001b[A\u001b[A\n\n 59% 2255/3823 [04:14<02:57, 8.82it/s]\u001b[A\u001b[A\n\n 59% 2256/3823 [04:14<02:57, 8.83it/s]\u001b[A\u001b[A\n\n 59% 2257/3823 [04:15<02:57, 8.84it/s]\u001b[A\u001b[A\n\n 59% 2258/3823 [04:15<02:56, 8.84it/s]\u001b[A\u001b[A\n\n 59% 2259/3823 [04:15<02:56, 8.85it/s]\u001b[A\u001b[A\n\n 59% 2260/3823 [04:15<02:56, 8.84it/s]\u001b[A\u001b[A\n\n 59% 2261/3823 [04:15<02:57, 8.82it/s]\u001b[A\u001b[A\n\n 59% 2262/3823 [04:15<02:57, 8.82it/s]\u001b[A\u001b[A\n\n 59% 2263/3823 [04:15<02:56, 8.82it/s]\u001b[A\u001b[A\n\n 59% 2264/3823 [04:15<02:56, 8.83it/s]\u001b[A\u001b[A\n\n 59% 2265/3823 [04:15<02:56, 8.83it/s]\u001b[A\u001b[A\n\n 59% 2266/3823 [04:16<02:56, 8.83it/s]\u001b[A\u001b[A\n\n 59% 2267/3823 [04:16<02:56, 8.82it/s]\u001b[A\u001b[A\n\n 59% 2268/3823 [04:16<02:56, 8.81it/s]\u001b[A\u001b[A\n\n 59% 2269/3823 [04:16<02:56, 8.79it/s]\u001b[A\u001b[A\n\n 59% 2270/3823 [04:16<02:56, 8.80it/s]\u001b[A\u001b[A\n\n 59% 2271/3823 [04:16<02:55, 8.85it/s]\u001b[A\u001b[A\n\n 59% 2272/3823 [04:16<02:55, 8.85it/s]\u001b[A\u001b[A\n\n 59% 2273/3823 [04:16<02:55, 8.85it/s]\u001b[A\u001b[A\n\n 59% 2274/3823 [04:17<02:54, 8.86it/s]\u001b[A\u001b[A\n\n 60% 2275/3823 [04:17<02:54, 8.85it/s]\u001b[A\u001b[A\n\n 60% 2276/3823 [04:17<02:54, 8.86it/s]\u001b[A\u001b[A\n\n 60% 2277/3823 [04:17<02:54, 8.86it/s]\u001b[A\u001b[A\n\n 60% 2278/3823 [04:17<02:54, 8.85it/s]\u001b[A\u001b[A\n\n 60% 2279/3823 [04:17<02:54, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2280/3823 [04:17<02:54, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2281/3823 [04:17<02:54, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2282/3823 [04:17<02:54, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2283/3823 [04:18<02:54, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2284/3823 [04:18<02:54, 8.82it/s]\u001b[A\u001b[A\n\n 60% 2285/3823 [04:18<02:54, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2286/3823 [04:18<02:54, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2287/3823 [04:18<02:54, 8.81it/s]\u001b[A\u001b[A\n\n 60% 2288/3823 [04:18<02:54, 8.81it/s]\u001b[A\u001b[A\n\n 60% 2289/3823 [04:18<02:53, 8.82it/s]\u001b[A\u001b[A\n\n 60% 2290/3823 [04:18<02:53, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2291/3823 [04:18<02:53, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2292/3823 [04:19<02:53, 8.81it/s]\u001b[A\u001b[A\n\n 60% 2293/3823 [04:19<02:53, 8.81it/s]\u001b[A\u001b[A\n\n 60% 2294/3823 [04:19<02:53, 8.82it/s]\u001b[A\u001b[A\n\n 60% 2295/3823 [04:19<02:53, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2296/3823 [04:19<02:52, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2297/3823 [04:19<02:52, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2298/3823 [04:19<02:52, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2299/3823 [04:19<02:52, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2300/3823 [04:19<02:52, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2301/3823 [04:20<02:52, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2302/3823 [04:20<02:52, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2303/3823 [04:20<02:51, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2304/3823 [04:20<02:51, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2305/3823 [04:20<02:51, 8.84it/s]\u001b[A\u001b[A\n\n 60% 2306/3823 [04:20<02:51, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2307/3823 [04:20<02:51, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2308/3823 [04:20<02:51, 8.82it/s]\u001b[A\u001b[A\n\n 60% 2309/3823 [04:20<02:51, 8.82it/s]\u001b[A\u001b[A\n\n 60% 2310/3823 [04:21<02:51, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2311/3823 [04:21<02:51, 8.83it/s]\u001b[A\u001b[A\n\n 60% 2312/3823 [04:21<02:51, 8.84it/s]\u001b[A\u001b[A\n\n 61% 2313/3823 [04:21<02:50, 8.84it/s]\u001b[A\u001b[A\n\n 61% 2314/3823 [04:21<02:50, 8.84it/s]\u001b[A\u001b[A\n\n 61% 2315/3823 [04:21<02:50, 8.82it/s]\u001b[A\u001b[A\n\n 61% 2316/3823 [04:21<02:51, 8.80it/s]\u001b[A\u001b[A\n\n 61% 2317/3823 [04:21<02:51, 8.80it/s]\u001b[A\u001b[A\n\n 61% 2318/3823 [04:21<02:51, 8.80it/s]\u001b[A\u001b[A\n\n 61% 2319/3823 [04:22<02:50, 8.80it/s]\u001b[A\u001b[A\n\n 61% 2320/3823 [04:22<02:50, 8.81it/s]\u001b[A\u001b[A\n\n 61% 2321/3823 [04:22<02:50, 8.82it/s]\u001b[A\u001b[A\n\n 61% 2322/3823 [04:22<02:50, 8.82it/s]\u001b[A\u001b[A\n\n 61% 2323/3823 [04:22<02:49, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2324/3823 [04:22<02:49, 8.82it/s]\u001b[A\u001b[A\n\n 61% 2325/3823 [04:22<02:49, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2326/3823 [04:22<02:49, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2327/3823 [04:23<02:49, 8.84it/s]\u001b[A\u001b[A\n\n 61% 2328/3823 [04:23<02:49, 8.84it/s]\u001b[A\u001b[A\n\n 61% 2329/3823 [04:23<02:48, 8.84it/s]\u001b[A\u001b[A\n\n 61% 2330/3823 [04:23<02:48, 8.84it/s]\u001b[A\u001b[A\n\n 61% 2331/3823 [04:23<02:48, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2332/3823 [04:23<02:49, 8.81it/s]\u001b[A\u001b[A\n\n 61% 2333/3823 [04:23<02:49, 8.81it/s]\u001b[A\u001b[A\n\n 61% 2334/3823 [04:23<02:48, 8.81it/s]\u001b[A\u001b[A\n\n 61% 2335/3823 [04:23<02:48, 8.82it/s]\u001b[A\u001b[A\n\n 61% 2336/3823 [04:24<02:48, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2337/3823 [04:24<02:48, 8.84it/s]\u001b[A\u001b[A\n\n 61% 2338/3823 [04:24<02:48, 8.84it/s]\u001b[A\u001b[A\n\n 61% 2339/3823 [04:24<02:48, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2340/3823 [04:24<02:48, 8.82it/s]\u001b[A\u001b[A\n\n 61% 2341/3823 [04:24<02:47, 8.84it/s]\u001b[A\u001b[A\n\n 61% 2342/3823 [04:24<02:47, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2343/3823 [04:24<02:47, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2344/3823 [04:24<02:47, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2345/3823 [04:25<02:47, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2346/3823 [04:25<02:47, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2347/3823 [04:25<02:47, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2348/3823 [04:25<02:47, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2349/3823 [04:25<02:46, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2350/3823 [04:25<02:46, 8.83it/s]\u001b[A\u001b[A\n\n 61% 2351/3823 [04:25<02:47, 8.81it/s]\u001b[A\u001b[A\n\n 62% 2352/3823 [04:25<02:47, 8.80it/s]\u001b[A\u001b[A\n\n 62% 2353/3823 [04:25<02:46, 8.81it/s]\u001b[A\u001b[A\n\n 62% 2354/3823 [04:26<02:46, 8.81it/s]\u001b[A\u001b[A\n\n 62% 2355/3823 [04:26<02:46, 8.81it/s]\u001b[A\u001b[A\n\n 62% 2356/3823 [04:26<02:46, 8.82it/s]\u001b[A\u001b[A\n\n 62% 2357/3823 [04:26<02:46, 8.83it/s]\u001b[A\u001b[A\n\n 62% 2358/3823 [04:26<02:45, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2359/3823 [04:26<02:45, 8.83it/s]\u001b[A\u001b[A\n\n 62% 2360/3823 [04:26<02:45, 8.82it/s]\u001b[A\u001b[A\n\n 62% 2361/3823 [04:26<02:45, 8.83it/s]\u001b[A\u001b[A\n\n 62% 2362/3823 [04:26<02:45, 8.83it/s]\u001b[A\u001b[A\n\n 62% 2363/3823 [04:27<02:45, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2364/3823 [04:27<02:45, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2365/3823 [04:27<02:45, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2366/3823 [04:27<02:44, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2367/3823 [04:27<02:44, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2368/3823 [04:27<02:44, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2369/3823 [04:27<02:44, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2370/3823 [04:27<02:44, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2371/3823 [04:27<02:44, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2372/3823 [04:28<02:44, 8.83it/s]\u001b[A\u001b[A\n\n 62% 2373/3823 [04:28<02:44, 8.81it/s]\u001b[A\u001b[A\n\n 62% 2374/3823 [04:28<02:44, 8.82it/s]\u001b[A\u001b[A\n\n 62% 2375/3823 [04:28<02:44, 8.83it/s]\u001b[A\u001b[A\n\n 62% 2376/3823 [04:28<02:43, 8.83it/s]\u001b[A\u001b[A\n\n 62% 2377/3823 [04:28<02:43, 8.83it/s]\u001b[A\u001b[A\n\n 62% 2378/3823 [04:28<02:43, 8.83it/s]\u001b[A\u001b[A\n\n 62% 2379/3823 [04:28<02:43, 8.84it/s]\u001b[A\u001b[A\n\n 62% 2380/3823 [04:29<02:43, 8.82it/s]\u001b[A\u001b[A\n\n 62% 2381/3823 [04:29<02:43, 8.81it/s]\u001b[A\u001b[A\n\n 62% 2382/3823 [04:29<02:43, 8.82it/s]\u001b[A\u001b[A\n\n 62% 2383/3823 [04:29<02:43, 8.82it/s]\u001b[A\u001b[A\n\n 62% 2384/3823 [04:29<02:43, 8.82it/s]\u001b[A\u001b[A\n\n 62% 2385/3823 [04:29<02:43, 8.82it/s]\u001b[A\u001b[A\n\n 62% 2386/3823 [04:29<02:43, 8.81it/s]\u001b[A\u001b[A\n\n 62% 2387/3823 [04:29<02:42, 8.81it/s]\u001b[A\u001b[A\n\n 62% 2388/3823 [04:29<02:42, 8.81it/s]\u001b[A\u001b[A\n\n 62% 2389/3823 [04:30<02:42, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2390/3823 [04:30<02:42, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2391/3823 [04:30<02:42, 8.81it/s]\u001b[A\u001b[A\n\n 63% 2392/3823 [04:30<02:42, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2393/3823 [04:30<02:42, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2394/3823 [04:30<02:42, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2395/3823 [04:30<02:42, 8.81it/s]\u001b[A\u001b[A\n\n 63% 2396/3823 [04:30<02:41, 8.81it/s]\u001b[A\u001b[A\n\n 63% 2397/3823 [04:30<02:41, 8.81it/s]\u001b[A\u001b[A\n\n 63% 2398/3823 [04:31<02:41, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2399/3823 [04:31<02:41, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2400/3823 [04:31<02:41, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2401/3823 [04:31<02:41, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2402/3823 [04:31<02:41, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2403/3823 [04:31<02:41, 8.81it/s]\u001b[A\u001b[A\n\n 63% 2404/3823 [04:31<02:41, 8.80it/s]\u001b[A\u001b[A\n\n 63% 2405/3823 [04:31<02:41, 8.80it/s]\u001b[A\u001b[A\n\n 63% 2406/3823 [04:31<02:40, 8.81it/s]\u001b[A\u001b[A\n\n 63% 2407/3823 [04:32<02:40, 8.83it/s]\u001b[A\u001b[A\n\n 63% 2408/3823 [04:32<02:40, 8.83it/s]\u001b[A\u001b[A\n\n 63% 2409/3823 [04:32<02:40, 8.83it/s]\u001b[A\u001b[A\n\n 63% 2410/3823 [04:32<02:40, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2411/3823 [04:32<02:40, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2412/3823 [04:32<02:40, 8.81it/s]\u001b[A\u001b[A\n\n 63% 2413/3823 [04:32<02:40, 8.80it/s]\u001b[A\u001b[A\n\n 63% 2414/3823 [04:32<02:39, 8.81it/s]\u001b[A\u001b[A\n\n 63% 2415/3823 [04:32<02:39, 8.82it/s]\u001b[A\u001b[A\n\n 63% 2416/3823 [04:33<02:39, 8.83it/s]\u001b[A\u001b[A\n\n 63% 2417/3823 [04:33<02:39, 8.84it/s]\u001b[A\u001b[A\n\n 63% 2418/3823 [04:33<02:38, 8.84it/s]\u001b[A\u001b[A\n\n 63% 2419/3823 [04:33<02:38, 8.84it/s]\u001b[A\u001b[A\n\n 63% 2420/3823 [04:33<02:38, 8.84it/s]\u001b[A\u001b[A\n\n 63% 2421/3823 [04:33<02:38, 8.84it/s]\u001b[A\u001b[A\n\n 63% 2422/3823 [04:33<02:38, 8.84it/s]\u001b[A\u001b[A\n\n 63% 2423/3823 [04:33<02:38, 8.84it/s]\u001b[A\u001b[A\n\n 63% 2424/3823 [04:34<02:38, 8.84it/s]\u001b[A\u001b[A\n\n 63% 2425/3823 [04:34<02:38, 8.83it/s]\u001b[A\u001b[A\n\n 63% 2426/3823 [04:34<02:38, 8.83it/s]\u001b[A\u001b[A\n\n 63% 2427/3823 [04:34<02:38, 8.83it/s]\u001b[A\u001b[A\n\n 64% 2428/3823 [04:34<02:38, 8.83it/s]\u001b[A\u001b[A\n\n 64% 2429/3823 [04:34<02:37, 8.83it/s]\u001b[A\u001b[A\n\n 64% 2430/3823 [04:34<02:37, 8.83it/s]\u001b[A\u001b[A\n\n 64% 2431/3823 [04:34<02:37, 8.83it/s]\u001b[A\u001b[A\n\n 64% 2432/3823 [04:34<02:37, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2433/3823 [04:35<02:37, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2434/3823 [04:35<02:37, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2435/3823 [04:35<02:37, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2436/3823 [04:35<02:36, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2437/3823 [04:35<02:36, 8.83it/s]\u001b[A\u001b[A\n\n 64% 2438/3823 [04:35<02:37, 8.81it/s]\u001b[A\u001b[A\n\n 64% 2439/3823 [04:35<02:37, 8.81it/s]\u001b[A\u001b[A\n\n 64% 2440/3823 [04:35<02:36, 8.82it/s]\u001b[A\u001b[A\n\n 64% 2441/3823 [04:35<02:36, 8.81it/s]\u001b[A\u001b[A\n\n 64% 2442/3823 [04:36<02:36, 8.82it/s]\u001b[A\u001b[A\n\n 64% 2443/3823 [04:36<02:36, 8.82it/s]\u001b[A\u001b[A\n\n 64% 2444/3823 [04:36<02:36, 8.82it/s]\u001b[A\u001b[A\n\n 64% 2445/3823 [04:36<02:36, 8.81it/s]\u001b[A\u001b[A\n\n 64% 2446/3823 [04:36<02:36, 8.82it/s]\u001b[A\u001b[A\n\n 64% 2447/3823 [04:36<02:35, 8.82it/s]\u001b[A\u001b[A\n\n 64% 2448/3823 [04:36<02:35, 8.83it/s]\u001b[A\u001b[A\n\n 64% 2449/3823 [04:36<02:35, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2450/3823 [04:36<02:35, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2451/3823 [04:37<02:35, 8.85it/s]\u001b[A\u001b[A\n\n 64% 2452/3823 [04:37<02:35, 8.83it/s]\u001b[A\u001b[A\n\n 64% 2453/3823 [04:37<02:35, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2454/3823 [04:37<02:34, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2455/3823 [04:37<02:34, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2456/3823 [04:37<02:34, 8.85it/s]\u001b[A\u001b[A\n\n 64% 2457/3823 [04:37<02:34, 8.85it/s]\u001b[A\u001b[A\n\n 64% 2458/3823 [04:37<02:34, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2459/3823 [04:37<02:34, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2460/3823 [04:38<02:34, 8.83it/s]\u001b[A\u001b[A\n\n 64% 2461/3823 [04:38<02:34, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2462/3823 [04:38<02:33, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2463/3823 [04:38<02:33, 8.84it/s]\u001b[A\u001b[A\n\n 64% 2464/3823 [04:38<02:33, 8.85it/s]\u001b[A\u001b[A\n\n 64% 2465/3823 [04:38<02:33, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2466/3823 [04:38<02:33, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2467/3823 [04:38<02:33, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2468/3823 [04:38<02:33, 8.82it/s]\u001b[A\u001b[A\n\n 65% 2469/3823 [04:39<02:33, 8.82it/s]\u001b[A\u001b[A\n\n 65% 2470/3823 [04:39<02:33, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2471/3823 [04:39<02:32, 8.84it/s]\u001b[A\u001b[A\n\n 65% 2472/3823 [04:39<02:32, 8.84it/s]\u001b[A\u001b[A\n\n 65% 2473/3823 [04:39<02:32, 8.84it/s]\u001b[A\u001b[A\n\n 65% 2474/3823 [04:39<02:32, 8.84it/s]\u001b[A\u001b[A\n\n 65% 2475/3823 [04:39<02:32, 8.85it/s]\u001b[A\u001b[A\n\n 65% 2476/3823 [04:39<02:32, 8.85it/s]\u001b[A\u001b[A\n\n 65% 2477/3823 [04:40<02:32, 8.84it/s]\u001b[A\u001b[A\n\n 65% 2478/3823 [04:40<02:32, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2479/3823 [04:40<02:32, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2480/3823 [04:40<02:32, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2481/3823 [04:40<02:31, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2482/3823 [04:40<02:31, 8.84it/s]\u001b[A\u001b[A\n\n 65% 2483/3823 [04:40<02:31, 8.84it/s]\u001b[A\u001b[A\n\n 65% 2484/3823 [04:40<02:31, 8.84it/s]\u001b[A\u001b[A\n\n 65% 2485/3823 [04:40<02:31, 8.84it/s]\u001b[A\u001b[A\n\n 65% 2486/3823 [04:41<02:31, 8.85it/s]\u001b[A\u001b[A\n\n 65% 2487/3823 [04:41<02:30, 8.85it/s]\u001b[A\u001b[A\n\n 65% 2488/3823 [04:41<02:30, 8.85it/s]\u001b[A\u001b[A\n\n 65% 2489/3823 [04:41<02:30, 8.85it/s]\u001b[A\u001b[A\n\n 65% 2490/3823 [04:41<02:30, 8.85it/s]\u001b[A\u001b[A\n\n 65% 2491/3823 [04:41<02:30, 8.85it/s]\u001b[A\u001b[A\n\n 65% 2492/3823 [04:41<02:30, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2493/3823 [04:41<02:30, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2494/3823 [04:41<02:30, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2495/3823 [04:42<02:30, 8.82it/s]\u001b[A\u001b[A\n\n 65% 2496/3823 [04:42<02:30, 8.82it/s]\u001b[A\u001b[A\n\n 65% 2497/3823 [04:42<02:30, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2498/3823 [04:42<02:30, 8.82it/s]\u001b[A\u001b[A\n\n 65% 2499/3823 [04:42<02:29, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2500/3823 [04:42<02:29, 8.82it/s]\u001b[A\u001b[A\n\n 65% 2501/3823 [04:42<02:29, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2502/3823 [04:42<02:29, 8.83it/s]\u001b[A\u001b[A\n\n 65% 2503/3823 [04:42<02:29, 8.84it/s]\u001b[A\u001b[A\n\n 65% 2504/3823 [04:43<02:29, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2505/3823 [04:43<02:29, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2506/3823 [04:43<02:28, 8.85it/s]\u001b[A\u001b[A\n\n 66% 2507/3823 [04:43<02:28, 8.85it/s]\u001b[A\u001b[A\n\n 66% 2508/3823 [04:43<02:28, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2509/3823 [04:43<02:28, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2510/3823 [04:43<02:28, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2511/3823 [04:43<02:28, 8.85it/s]\u001b[A\u001b[A\n\n 66% 2512/3823 [04:43<02:28, 8.85it/s]\u001b[A\u001b[A\n\n 66% 2513/3823 [04:44<02:28, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2514/3823 [04:44<02:28, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2515/3823 [04:44<02:27, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2516/3823 [04:44<02:27, 8.83it/s]\u001b[A\u001b[A\n\n 66% 2517/3823 [04:44<02:27, 8.83it/s]\u001b[A\u001b[A\n\n 66% 2518/3823 [04:44<02:27, 8.83it/s]\u001b[A\u001b[A\n\n 66% 2519/3823 [04:44<02:27, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2520/3823 [04:44<02:27, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2521/3823 [04:44<02:27, 8.85it/s]\u001b[A\u001b[A\n\n 66% 2522/3823 [04:45<02:27, 8.85it/s]\u001b[A\u001b[A\n\n 66% 2523/3823 [04:45<02:26, 8.85it/s]\u001b[A\u001b[A\n\n 66% 2524/3823 [04:45<02:26, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2525/3823 [04:45<02:26, 8.85it/s]\u001b[A\u001b[A\n\n 66% 2526/3823 [04:45<02:26, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2527/3823 [04:45<02:26, 8.83it/s]\u001b[A\u001b[A\n\n 66% 2528/3823 [04:45<02:26, 8.81it/s]\u001b[A\u001b[A\n\n 66% 2529/3823 [04:45<02:26, 8.82it/s]\u001b[A\u001b[A\n\n 66% 2530/3823 [04:46<02:26, 8.82it/s]\u001b[A\u001b[A\n\n 66% 2531/3823 [04:46<02:26, 8.83it/s]\u001b[A\u001b[A\n\n 66% 2532/3823 [04:46<02:26, 8.83it/s]\u001b[A\u001b[A\n\n 66% 2533/3823 [04:46<02:26, 8.83it/s]\u001b[A\u001b[A\n\n 66% 2534/3823 [04:46<02:25, 8.83it/s]\u001b[A\u001b[A\n\n 66% 2535/3823 [04:46<02:25, 8.83it/s]\u001b[A\u001b[A\n\n 66% 2536/3823 [04:46<02:25, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2537/3823 [04:46<02:25, 8.85it/s]\u001b[A\u001b[A\n\n 66% 2538/3823 [04:46<02:25, 8.85it/s]\u001b[A\u001b[A\n\n 66% 2539/3823 [04:47<02:25, 8.84it/s]\u001b[A\u001b[A\n\n 66% 2540/3823 [04:47<02:25, 8.82it/s]\u001b[A\u001b[A\n\n 66% 2541/3823 [04:47<02:25, 8.83it/s]\u001b[A\u001b[A\n\n 66% 2542/3823 [04:47<02:24, 8.84it/s]\u001b[A\u001b[A\n\n 67% 2543/3823 [04:47<02:24, 8.84it/s]\u001b[A\u001b[A\n\n 67% 2544/3823 [04:47<02:24, 8.84it/s]\u001b[A\u001b[A\n\n 67% 2545/3823 [04:47<02:24, 8.84it/s]\u001b[A\u001b[A\n\n 67% 2546/3823 [04:47<02:24, 8.83it/s]\u001b[A\u001b[A\n\n 67% 2547/3823 [04:47<02:24, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2548/3823 [04:48<02:24, 8.81it/s]\u001b[A\u001b[A\n\n 67% 2549/3823 [04:48<02:24, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2550/3823 [04:48<02:24, 8.83it/s]\u001b[A\u001b[A\n\n 67% 2551/3823 [04:48<02:23, 8.84it/s]\u001b[A\u001b[A\n\n 67% 2552/3823 [04:48<02:23, 8.84it/s]\u001b[A\u001b[A\n\n 67% 2553/3823 [04:48<02:23, 8.83it/s]\u001b[A\u001b[A\n\n 67% 2554/3823 [04:48<02:23, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2555/3823 [04:48<02:23, 8.83it/s]\u001b[A\u001b[A\n\n 67% 2556/3823 [04:48<02:23, 8.80it/s]\u001b[A\u001b[A\n\n 67% 2557/3823 [04:49<02:23, 8.79it/s]\u001b[A\u001b[A\n\n 67% 2558/3823 [04:49<02:23, 8.81it/s]\u001b[A\u001b[A\n\n 67% 2559/3823 [04:49<02:23, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2560/3823 [04:49<02:23, 8.83it/s]\u001b[A\u001b[A\n\n 67% 2561/3823 [04:49<02:23, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2562/3823 [04:49<02:23, 8.80it/s]\u001b[A\u001b[A\n\n 67% 2563/3823 [04:49<02:22, 8.81it/s]\u001b[A\u001b[A\n\n 67% 2564/3823 [04:49<02:22, 8.81it/s]\u001b[A\u001b[A\n\n 67% 2565/3823 [04:49<02:22, 8.81it/s]\u001b[A\u001b[A\n\n 67% 2566/3823 [04:50<02:22, 8.80it/s]\u001b[A\u001b[A\n\n 67% 2567/3823 [04:50<02:22, 8.81it/s]\u001b[A\u001b[A\n\n 67% 2568/3823 [04:50<02:22, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2569/3823 [04:50<02:22, 8.83it/s]\u001b[A\u001b[A\n\n 67% 2570/3823 [04:50<02:21, 8.83it/s]\u001b[A\u001b[A\n\n 67% 2571/3823 [04:50<02:21, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2572/3823 [04:50<02:21, 8.83it/s]\u001b[A\u001b[A\n\n 67% 2573/3823 [04:50<02:21, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2574/3823 [04:50<02:21, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2575/3823 [04:51<02:21, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2576/3823 [04:51<02:21, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2577/3823 [04:51<02:21, 8.83it/s]\u001b[A\u001b[A\n\n 67% 2578/3823 [04:51<02:21, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2579/3823 [04:51<02:21, 8.82it/s]\u001b[A\u001b[A\n\n 67% 2580/3823 [04:51<02:20, 8.82it/s]\u001b[A\u001b[A\n\n 68% 2581/3823 [04:51<02:20, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2582/3823 [04:51<02:20, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2583/3823 [04:52<02:20, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2584/3823 [04:52<02:20, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2585/3823 [04:52<02:20, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2586/3823 [04:52<02:20, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2587/3823 [04:52<02:20, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2588/3823 [04:52<02:19, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2589/3823 [04:52<02:19, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2590/3823 [04:52<02:19, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2591/3823 [04:52<02:19, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2592/3823 [04:53<02:19, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2593/3823 [04:53<02:19, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2594/3823 [04:53<02:19, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2595/3823 [04:53<02:19, 8.82it/s]\u001b[A\u001b[A\n\n 68% 2596/3823 [04:53<02:19, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2597/3823 [04:53<02:18, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2598/3823 [04:53<02:18, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2599/3823 [04:53<02:18, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2600/3823 [04:53<02:18, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2601/3823 [04:54<02:18, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2602/3823 [04:54<02:18, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2603/3823 [04:54<02:18, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2604/3823 [04:54<02:17, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2605/3823 [04:54<02:17, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2606/3823 [04:54<02:18, 8.82it/s]\u001b[A\u001b[A\n\n 68% 2607/3823 [04:54<02:17, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2608/3823 [04:54<02:17, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2609/3823 [04:54<02:17, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2610/3823 [04:55<02:17, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2611/3823 [04:55<02:17, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2612/3823 [04:55<02:17, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2613/3823 [04:55<02:17, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2614/3823 [04:55<02:16, 8.83it/s]\u001b[A\u001b[A\n\n 68% 2615/3823 [04:55<02:16, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2616/3823 [04:55<02:16, 8.84it/s]\u001b[A\u001b[A\n\n 68% 2617/3823 [04:55<02:16, 8.85it/s]\u001b[A\u001b[A\n\n 68% 2618/3823 [04:55<02:16, 8.84it/s]\u001b[A\u001b[A\n\n 69% 2619/3823 [04:56<02:16, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2620/3823 [04:56<02:16, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2621/3823 [04:56<02:16, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2622/3823 [04:56<02:15, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2623/3823 [04:56<02:15, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2624/3823 [04:56<02:15, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2625/3823 [04:56<02:15, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2626/3823 [04:56<02:15, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2627/3823 [04:56<02:15, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2628/3823 [04:57<02:15, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2629/3823 [04:57<02:15, 8.81it/s]\u001b[A\u001b[A\n\n 69% 2630/3823 [04:57<02:15, 8.81it/s]\u001b[A\u001b[A\n\n 69% 2631/3823 [04:57<02:15, 8.81it/s]\u001b[A\u001b[A\n\n 69% 2632/3823 [04:57<02:15, 8.81it/s]\u001b[A\u001b[A\n\n 69% 2633/3823 [04:57<02:15, 8.81it/s]\u001b[A\u001b[A\n\n 69% 2634/3823 [04:57<02:14, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2635/3823 [04:57<02:14, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2636/3823 [04:58<02:14, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2637/3823 [04:58<02:14, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2638/3823 [04:58<02:14, 8.84it/s]\u001b[A\u001b[A\n\n 69% 2639/3823 [04:58<02:13, 8.84it/s]\u001b[A\u001b[A\n\n 69% 2640/3823 [04:58<02:13, 8.84it/s]\u001b[A\u001b[A\n\n 69% 2641/3823 [04:58<02:13, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2642/3823 [04:58<02:13, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2643/3823 [04:58<02:13, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2644/3823 [04:58<02:13, 8.81it/s]\u001b[A\u001b[A\n\n 69% 2645/3823 [04:59<02:13, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2646/3823 [04:59<02:13, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2647/3823 [04:59<02:13, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2648/3823 [04:59<02:13, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2649/3823 [04:59<02:13, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2650/3823 [04:59<02:12, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2651/3823 [04:59<02:12, 8.82it/s]\u001b[A\u001b[A\n\n 69% 2652/3823 [04:59<02:12, 8.84it/s]\u001b[A\u001b[A\n\n 69% 2653/3823 [04:59<02:12, 8.84it/s]\u001b[A\u001b[A\n\n 69% 2654/3823 [05:00<02:12, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2655/3823 [05:00<02:12, 8.83it/s]\u001b[A\u001b[A\n\n 69% 2656/3823 [05:00<02:12, 8.83it/s]\u001b[A\u001b[A\n\n 70% 2657/3823 [05:00<02:12, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2658/3823 [05:00<02:12, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2659/3823 [05:00<02:11, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2660/3823 [05:00<02:11, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2661/3823 [05:00<02:11, 8.81it/s]\u001b[A\u001b[A\n\n 70% 2662/3823 [05:00<02:11, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2663/3823 [05:01<02:11, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2664/3823 [05:01<02:11, 8.83it/s]\u001b[A\u001b[A\n\n 70% 2665/3823 [05:01<02:11, 8.83it/s]\u001b[A\u001b[A\n\n 70% 2666/3823 [05:01<02:11, 8.83it/s]\u001b[A\u001b[A\n\n 70% 2667/3823 [05:01<02:10, 8.83it/s]\u001b[A\u001b[A\n\n 70% 2668/3823 [05:01<02:10, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2669/3823 [05:01<02:10, 8.81it/s]\u001b[A\u001b[A\n\n 70% 2670/3823 [05:01<02:10, 8.81it/s]\u001b[A\u001b[A\n\n 70% 2671/3823 [05:01<02:10, 8.80it/s]\u001b[A\u001b[A\n\n 70% 2672/3823 [05:02<02:10, 8.80it/s]\u001b[A\u001b[A\n\n 70% 2673/3823 [05:02<02:10, 8.79it/s]\u001b[A\u001b[A\n\n 70% 2674/3823 [05:02<02:10, 8.80it/s]\u001b[A\u001b[A\n\n 70% 2675/3823 [05:02<02:10, 8.81it/s]\u001b[A\u001b[A\n\n 70% 2676/3823 [05:02<02:10, 8.81it/s]\u001b[A\u001b[A\n\n 70% 2677/3823 [05:02<02:09, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2678/3823 [05:02<02:09, 8.83it/s]\u001b[A\u001b[A\n\n 70% 2679/3823 [05:02<02:09, 8.83it/s]\u001b[A\u001b[A\n\n 70% 2680/3823 [05:03<02:09, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2681/3823 [05:03<02:09, 8.80it/s]\u001b[A\u001b[A\n\n 70% 2682/3823 [05:03<02:09, 8.80it/s]\u001b[A\u001b[A\n\n 70% 2683/3823 [05:03<02:09, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2684/3823 [05:03<02:09, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2685/3823 [05:03<02:09, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2686/3823 [05:03<02:09, 8.81it/s]\u001b[A\u001b[A\n\n 70% 2687/3823 [05:03<02:08, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2688/3823 [05:03<02:08, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2689/3823 [05:04<02:08, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2690/3823 [05:04<02:08, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2691/3823 [05:04<02:08, 8.82it/s]\u001b[A\u001b[A\n\n 70% 2692/3823 [05:04<02:08, 8.83it/s]\u001b[A\u001b[A\n\n 70% 2693/3823 [05:04<02:08, 8.83it/s]\u001b[A\u001b[A\n\n 70% 2694/3823 [05:04<02:07, 8.83it/s]\u001b[A\u001b[A\n\n 70% 2695/3823 [05:04<02:07, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2696/3823 [05:04<02:07, 8.82it/s]\u001b[A\u001b[A\n\n 71% 2697/3823 [05:04<02:07, 8.82it/s]\u001b[A\u001b[A\n\n 71% 2698/3823 [05:05<02:07, 8.82it/s]\u001b[A\u001b[A\n\n 71% 2699/3823 [05:05<02:07, 8.82it/s]\u001b[A\u001b[A\n\n 71% 2700/3823 [05:05<02:07, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2701/3823 [05:05<02:07, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2702/3823 [05:05<02:06, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2703/3823 [05:05<02:06, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2704/3823 [05:05<02:06, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2705/3823 [05:05<02:06, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2706/3823 [05:05<02:06, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2707/3823 [05:06<02:06, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2708/3823 [05:06<02:06, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2709/3823 [05:06<02:06, 8.84it/s]\u001b[A\u001b[A\n\n 71% 2710/3823 [05:06<02:05, 8.84it/s]\u001b[A\u001b[A\n\n 71% 2711/3823 [05:06<02:05, 8.84it/s]\u001b[A\u001b[A\n\n 71% 2712/3823 [05:06<02:05, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2713/3823 [05:06<02:05, 8.82it/s]\u001b[A\u001b[A\n\n 71% 2714/3823 [05:06<02:05, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2715/3823 [05:06<02:05, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2716/3823 [05:07<02:05, 8.82it/s]\u001b[A\u001b[A\n\n 71% 2717/3823 [05:07<02:05, 8.82it/s]\u001b[A\u001b[A\n\n 71% 2718/3823 [05:07<02:05, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2719/3823 [05:07<02:04, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2720/3823 [05:07<02:04, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2721/3823 [05:07<02:04, 8.82it/s]\u001b[A\u001b[A\n\n 71% 2722/3823 [05:07<02:04, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2723/3823 [05:07<02:04, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2724/3823 [05:07<02:04, 8.84it/s]\u001b[A\u001b[A\n\n 71% 2725/3823 [05:08<02:04, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2726/3823 [05:08<02:04, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2727/3823 [05:08<02:04, 8.84it/s]\u001b[A\u001b[A\n\n 71% 2728/3823 [05:08<02:03, 8.84it/s]\u001b[A\u001b[A\n\n 71% 2729/3823 [05:08<02:03, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2730/3823 [05:08<02:03, 8.84it/s]\u001b[A\u001b[A\n\n 71% 2731/3823 [05:08<02:03, 8.83it/s]\u001b[A\u001b[A\n\n 71% 2732/3823 [05:08<02:03, 8.82it/s]\u001b[A\u001b[A\n\n 71% 2733/3823 [05:09<02:03, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2734/3823 [05:09<02:03, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2735/3823 [05:09<02:03, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2736/3823 [05:09<02:03, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2737/3823 [05:09<02:03, 8.80it/s]\u001b[A\u001b[A\n\n 72% 2738/3823 [05:09<02:03, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2739/3823 [05:09<02:03, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2740/3823 [05:09<02:02, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2741/3823 [05:09<02:02, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2742/3823 [05:10<02:02, 8.83it/s]\u001b[A\u001b[A\n\n 72% 2743/3823 [05:10<02:02, 8.83it/s]\u001b[A\u001b[A\n\n 72% 2744/3823 [05:10<02:02, 8.83it/s]\u001b[A\u001b[A\n\n 72% 2745/3823 [05:10<02:02, 8.83it/s]\u001b[A\u001b[A\n\n 72% 2746/3823 [05:10<02:02, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2747/3823 [05:10<02:02, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2748/3823 [05:10<02:01, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2749/3823 [05:10<02:01, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2750/3823 [05:10<02:01, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2751/3823 [05:11<02:01, 8.79it/s]\u001b[A\u001b[A\n\n 72% 2752/3823 [05:11<02:01, 8.80it/s]\u001b[A\u001b[A\n\n 72% 2753/3823 [05:11<02:01, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2754/3823 [05:11<02:01, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2755/3823 [05:11<02:01, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2756/3823 [05:11<02:01, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2757/3823 [05:11<02:01, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2758/3823 [05:11<02:00, 8.80it/s]\u001b[A\u001b[A\n\n 72% 2759/3823 [05:11<02:00, 8.80it/s]\u001b[A\u001b[A\n\n 72% 2760/3823 [05:12<02:00, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2761/3823 [05:12<02:00, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2762/3823 [05:12<02:00, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2763/3823 [05:12<02:00, 8.83it/s]\u001b[A\u001b[A\n\n 72% 2764/3823 [05:12<02:00, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2765/3823 [05:12<01:59, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2766/3823 [05:12<02:00, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2767/3823 [05:12<02:00, 8.80it/s]\u001b[A\u001b[A\n\n 72% 2768/3823 [05:12<01:59, 8.81it/s]\u001b[A\u001b[A\n\n 72% 2769/3823 [05:13<01:59, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2770/3823 [05:13<01:59, 8.82it/s]\u001b[A\u001b[A\n\n 72% 2771/3823 [05:13<01:59, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2772/3823 [05:13<01:59, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2773/3823 [05:13<01:58, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2774/3823 [05:13<01:58, 8.82it/s]\u001b[A\u001b[A\n\n 73% 2775/3823 [05:13<01:58, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2776/3823 [05:13<01:58, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2777/3823 [05:13<01:58, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2778/3823 [05:14<01:58, 8.84it/s]\u001b[A\u001b[A\n\n 73% 2779/3823 [05:14<01:58, 8.84it/s]\u001b[A\u001b[A\n\n 73% 2780/3823 [05:14<01:57, 8.84it/s]\u001b[A\u001b[A\n\n 73% 2781/3823 [05:14<01:57, 8.84it/s]\u001b[A\u001b[A\n\n 73% 2782/3823 [05:14<01:57, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2783/3823 [05:14<01:57, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2784/3823 [05:14<01:57, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2785/3823 [05:14<01:57, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2786/3823 [05:15<01:57, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2787/3823 [05:15<01:57, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2788/3823 [05:15<01:57, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2789/3823 [05:15<01:57, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2790/3823 [05:15<01:57, 8.82it/s]\u001b[A\u001b[A\n\n 73% 2791/3823 [05:15<01:56, 8.82it/s]\u001b[A\u001b[A\n\n 73% 2792/3823 [05:15<01:56, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2793/3823 [05:15<01:56, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2794/3823 [05:15<01:56, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2795/3823 [05:16<01:56, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2796/3823 [05:16<01:56, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2797/3823 [05:16<01:56, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2798/3823 [05:16<01:56, 8.82it/s]\u001b[A\u001b[A\n\n 73% 2799/3823 [05:16<01:56, 8.82it/s]\u001b[A\u001b[A\n\n 73% 2800/3823 [05:16<01:56, 8.81it/s]\u001b[A\u001b[A\n\n 73% 2801/3823 [05:16<01:55, 8.82it/s]\u001b[A\u001b[A\n\n 73% 2802/3823 [05:16<01:55, 8.82it/s]\u001b[A\u001b[A\n\n 73% 2803/3823 [05:16<01:55, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2804/3823 [05:17<01:55, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2805/3823 [05:17<01:55, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2806/3823 [05:17<01:55, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2807/3823 [05:17<01:55, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2808/3823 [05:17<01:54, 8.83it/s]\u001b[A\u001b[A\n\n 73% 2809/3823 [05:17<01:54, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2810/3823 [05:17<01:54, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2811/3823 [05:17<01:54, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2812/3823 [05:17<01:54, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2813/3823 [05:18<01:54, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2814/3823 [05:18<01:54, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2815/3823 [05:18<01:54, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2816/3823 [05:18<01:54, 8.81it/s]\u001b[A\u001b[A\n\n 74% 2817/3823 [05:18<01:54, 8.80it/s]\u001b[A\u001b[A\n\n 74% 2818/3823 [05:18<01:54, 8.80it/s]\u001b[A\u001b[A\n\n 74% 2819/3823 [05:18<01:54, 8.80it/s]\u001b[A\u001b[A\n\n 74% 2820/3823 [05:18<01:53, 8.81it/s]\u001b[A\u001b[A\n\n 74% 2821/3823 [05:18<01:53, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2822/3823 [05:19<01:53, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2823/3823 [05:19<01:53, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2824/3823 [05:19<01:53, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2825/3823 [05:19<01:52, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2826/3823 [05:19<01:52, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2827/3823 [05:19<01:52, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2828/3823 [05:19<01:52, 8.81it/s]\u001b[A\u001b[A\n\n 74% 2829/3823 [05:19<01:53, 8.79it/s]\u001b[A\u001b[A\n\n 74% 2830/3823 [05:20<01:52, 8.80it/s]\u001b[A\u001b[A\n\n 74% 2831/3823 [05:20<01:52, 8.80it/s]\u001b[A\u001b[A\n\n 74% 2832/3823 [05:20<01:52, 8.81it/s]\u001b[A\u001b[A\n\n 74% 2833/3823 [05:20<01:52, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2834/3823 [05:20<01:52, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2835/3823 [05:20<01:52, 8.81it/s]\u001b[A\u001b[A\n\n 74% 2836/3823 [05:20<01:51, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2837/3823 [05:20<01:51, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2838/3823 [05:20<01:51, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2839/3823 [05:21<01:51, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2840/3823 [05:21<01:51, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2841/3823 [05:21<01:51, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2842/3823 [05:21<01:51, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2843/3823 [05:21<01:51, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2844/3823 [05:21<01:51, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2845/3823 [05:21<01:50, 8.82it/s]\u001b[A\u001b[A\n\n 74% 2846/3823 [05:21<01:50, 8.83it/s]\u001b[A\u001b[A\n\n 74% 2847/3823 [05:21<01:50, 8.84it/s]\u001b[A\u001b[A\n\n 74% 2848/3823 [05:22<01:50, 8.83it/s]\u001b[A\u001b[A\n\n 75% 2849/3823 [05:22<01:50, 8.84it/s]\u001b[A\u001b[A\n\n 75% 2850/3823 [05:22<01:50, 8.83it/s]\u001b[A\u001b[A\n\n 75% 2851/3823 [05:22<01:50, 8.83it/s]\u001b[A\u001b[A\n\n 75% 2852/3823 [05:22<01:50, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2853/3823 [05:22<01:50, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2854/3823 [05:22<01:49, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2855/3823 [05:22<01:49, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2856/3823 [05:22<01:49, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2857/3823 [05:23<01:49, 8.83it/s]\u001b[A\u001b[A\n\n 75% 2858/3823 [05:23<01:49, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2859/3823 [05:23<01:49, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2860/3823 [05:23<01:49, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2861/3823 [05:23<01:49, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2862/3823 [05:23<01:49, 8.80it/s]\u001b[A\u001b[A\n\n 75% 2863/3823 [05:23<01:48, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2864/3823 [05:23<01:48, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2865/3823 [05:23<01:48, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2866/3823 [05:24<01:48, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2867/3823 [05:24<01:48, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2868/3823 [05:24<01:48, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2869/3823 [05:24<01:48, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2870/3823 [05:24<01:48, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2871/3823 [05:24<01:47, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2872/3823 [05:24<01:47, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2873/3823 [05:24<01:47, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2874/3823 [05:24<01:47, 8.83it/s]\u001b[A\u001b[A\n\n 75% 2875/3823 [05:25<01:47, 8.83it/s]\u001b[A\u001b[A\n\n 75% 2876/3823 [05:25<01:47, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2877/3823 [05:25<01:47, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2878/3823 [05:25<01:47, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2879/3823 [05:25<01:47, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2880/3823 [05:25<01:47, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2881/3823 [05:25<01:46, 8.81it/s]\u001b[A\u001b[A\n\n 75% 2882/3823 [05:25<01:46, 8.82it/s]\u001b[A\u001b[A\n\n 75% 2883/3823 [05:26<01:46, 8.83it/s]\u001b[A\u001b[A\n\n 75% 2884/3823 [05:26<01:46, 8.83it/s]\u001b[A\u001b[A\n\n 75% 2885/3823 [05:26<01:46, 8.83it/s]\u001b[A\u001b[A\n\n 75% 2886/3823 [05:26<01:46, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2887/3823 [05:26<01:45, 8.84it/s]\u001b[A\u001b[A\n\n 76% 2888/3823 [05:26<01:45, 8.84it/s]\u001b[A\u001b[A\n\n 76% 2889/3823 [05:26<01:45, 8.84it/s]\u001b[A\u001b[A\n\n 76% 2890/3823 [05:26<01:45, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2891/3823 [05:26<01:45, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2892/3823 [05:27<01:45, 8.81it/s]\u001b[A\u001b[A\n\n 76% 2893/3823 [05:27<01:45, 8.81it/s]\u001b[A\u001b[A\n\n 76% 2894/3823 [05:27<01:45, 8.81it/s]\u001b[A\u001b[A\n\n 76% 2895/3823 [05:27<01:45, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2896/3823 [05:27<01:45, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2897/3823 [05:27<01:44, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2898/3823 [05:27<01:44, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2899/3823 [05:27<01:44, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2900/3823 [05:27<01:44, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2901/3823 [05:28<01:44, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2902/3823 [05:28<01:44, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2903/3823 [05:28<01:44, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2904/3823 [05:28<01:44, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2905/3823 [05:28<01:43, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2906/3823 [05:28<01:44, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2907/3823 [05:28<01:43, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2908/3823 [05:28<01:43, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2909/3823 [05:28<01:43, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2910/3823 [05:29<01:43, 8.81it/s]\u001b[A\u001b[A\n\n 76% 2911/3823 [05:29<01:43, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2912/3823 [05:29<01:43, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2913/3823 [05:29<01:43, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2914/3823 [05:29<01:42, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2915/3823 [05:29<01:42, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2916/3823 [05:29<01:42, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2917/3823 [05:29<01:42, 8.83it/s]\u001b[A\u001b[A\n\n 76% 2918/3823 [05:29<01:42, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2919/3823 [05:30<01:42, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2920/3823 [05:30<01:42, 8.81it/s]\u001b[A\u001b[A\n\n 76% 2921/3823 [05:30<01:42, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2922/3823 [05:30<01:42, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2923/3823 [05:30<01:42, 8.82it/s]\u001b[A\u001b[A\n\n 76% 2924/3823 [05:30<01:41, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2925/3823 [05:30<01:41, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2926/3823 [05:30<01:41, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2927/3823 [05:30<01:41, 8.84it/s]\u001b[A\u001b[A\n\n 77% 2928/3823 [05:31<01:41, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2929/3823 [05:31<01:41, 8.84it/s]\u001b[A\u001b[A\n\n 77% 2930/3823 [05:31<01:41, 8.84it/s]\u001b[A\u001b[A\n\n 77% 2931/3823 [05:31<01:40, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2932/3823 [05:31<01:40, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2933/3823 [05:31<01:40, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2934/3823 [05:31<01:40, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2935/3823 [05:31<01:40, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2936/3823 [05:32<01:40, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2937/3823 [05:32<01:40, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2938/3823 [05:32<01:40, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2939/3823 [05:32<01:40, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2940/3823 [05:32<01:40, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2941/3823 [05:32<01:39, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2942/3823 [05:32<01:39, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2943/3823 [05:32<01:39, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2944/3823 [05:32<01:39, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2945/3823 [05:33<01:39, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2946/3823 [05:33<01:39, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2947/3823 [05:33<01:39, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2948/3823 [05:33<01:39, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2949/3823 [05:33<01:39, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2950/3823 [05:33<01:38, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2951/3823 [05:33<01:38, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2952/3823 [05:33<01:38, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2953/3823 [05:33<01:38, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2954/3823 [05:34<01:38, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2955/3823 [05:34<01:38, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2956/3823 [05:34<01:38, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2957/3823 [05:34<01:38, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2958/3823 [05:34<01:37, 8.84it/s]\u001b[A\u001b[A\n\n 77% 2959/3823 [05:34<01:37, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2960/3823 [05:34<01:37, 8.83it/s]\u001b[A\u001b[A\n\n 77% 2961/3823 [05:34<01:37, 8.82it/s]\u001b[A\u001b[A\n\n 77% 2962/3823 [05:34<01:37, 8.81it/s]\u001b[A\u001b[A\n\n 78% 2963/3823 [05:35<01:37, 8.81it/s]\u001b[A\u001b[A\n\n 78% 2964/3823 [05:35<01:37, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2965/3823 [05:35<01:37, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2966/3823 [05:35<01:37, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2967/3823 [05:35<01:36, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2968/3823 [05:35<01:36, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2969/3823 [05:35<01:36, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2970/3823 [05:35<01:36, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2971/3823 [05:35<01:36, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2972/3823 [05:36<01:36, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2973/3823 [05:36<01:36, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2974/3823 [05:36<01:36, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2975/3823 [05:36<01:36, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2976/3823 [05:36<01:35, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2977/3823 [05:36<01:35, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2978/3823 [05:36<01:35, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2979/3823 [05:36<01:35, 8.81it/s]\u001b[A\u001b[A\n\n 78% 2980/3823 [05:37<01:35, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2981/3823 [05:37<01:35, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2982/3823 [05:37<01:35, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2983/3823 [05:37<01:35, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2984/3823 [05:37<01:35, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2985/3823 [05:37<01:34, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2986/3823 [05:37<01:34, 8.81it/s]\u001b[A\u001b[A\n\n 78% 2987/3823 [05:37<01:34, 8.81it/s]\u001b[A\u001b[A\n\n 78% 2988/3823 [05:37<01:34, 8.81it/s]\u001b[A\u001b[A\n\n 78% 2989/3823 [05:38<01:34, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2990/3823 [05:38<01:34, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2991/3823 [05:38<01:34, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2992/3823 [05:38<01:34, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2993/3823 [05:38<01:34, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2994/3823 [05:38<01:33, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2995/3823 [05:38<01:33, 8.82it/s]\u001b[A\u001b[A\n\n 78% 2996/3823 [05:38<01:33, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2997/3823 [05:38<01:33, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2998/3823 [05:39<01:33, 8.83it/s]\u001b[A\u001b[A\n\n 78% 2999/3823 [05:39<01:33, 8.82it/s]\u001b[A\u001b[A\n\n 78% 3000/3823 [05:39<01:33, 8.81it/s]\u001b[A\u001b[A\n\n 78% 3001/3823 [05:39<01:33, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3002/3823 [05:39<01:33, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3003/3823 [05:39<01:32, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3004/3823 [05:39<01:32, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3005/3823 [05:39<01:32, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3006/3823 [05:39<01:32, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3007/3823 [05:40<01:32, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3008/3823 [05:40<01:32, 8.84it/s]\u001b[A\u001b[A\n\n 79% 3009/3823 [05:40<01:32, 8.84it/s]\u001b[A\u001b[A\n\n 79% 3010/3823 [05:40<01:32, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3011/3823 [05:40<01:31, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3012/3823 [05:40<01:31, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3013/3823 [05:40<01:31, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3014/3823 [05:40<01:31, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3015/3823 [05:40<01:31, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3016/3823 [05:41<01:31, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3017/3823 [05:41<01:31, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3018/3823 [05:41<01:31, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3019/3823 [05:41<01:31, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3020/3823 [05:41<01:31, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3021/3823 [05:41<01:30, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3022/3823 [05:41<01:30, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3023/3823 [05:41<01:30, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3024/3823 [05:41<01:30, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3025/3823 [05:42<01:30, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3026/3823 [05:42<01:30, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3027/3823 [05:42<01:30, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3028/3823 [05:42<01:30, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3029/3823 [05:42<01:29, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3030/3823 [05:42<01:29, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3031/3823 [05:42<01:29, 8.84it/s]\u001b[A\u001b[A\n\n 79% 3032/3823 [05:42<01:29, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3033/3823 [05:43<01:29, 8.82it/s]\u001b[A\u001b[A\n\n 79% 3034/3823 [05:43<01:29, 8.80it/s]\u001b[A\u001b[A\n\n 79% 3035/3823 [05:43<01:29, 8.81it/s]\u001b[A\u001b[A\n\n 79% 3036/3823 [05:43<01:29, 8.81it/s]\u001b[A\u001b[A\n\n 79% 3037/3823 [05:43<01:29, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3038/3823 [05:43<01:28, 8.83it/s]\u001b[A\u001b[A\n\n 79% 3039/3823 [05:43<01:28, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3040/3823 [05:43<01:28, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3041/3823 [05:43<01:28, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3042/3823 [05:44<01:28, 8.82it/s]\u001b[A\u001b[A\n\n 80% 3043/3823 [05:44<01:28, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3044/3823 [05:44<01:28, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3045/3823 [05:44<01:28, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3046/3823 [05:44<01:28, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3047/3823 [05:44<01:27, 8.82it/s]\u001b[A\u001b[A\n\n 80% 3048/3823 [05:44<01:27, 8.81it/s]\u001b[A\u001b[A\n\n 80% 3049/3823 [05:44<01:27, 8.81it/s]\u001b[A\u001b[A\n\n 80% 3050/3823 [05:44<01:27, 8.81it/s]\u001b[A\u001b[A\n\n 80% 3051/3823 [05:45<01:27, 8.82it/s]\u001b[A\u001b[A\n\n 80% 3052/3823 [05:45<01:27, 8.82it/s]\u001b[A\u001b[A\n\n 80% 3053/3823 [05:45<01:27, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3054/3823 [05:45<01:27, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3055/3823 [05:45<01:26, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3056/3823 [05:45<01:26, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3057/3823 [05:45<01:26, 8.82it/s]\u001b[A\u001b[A\n\n 80% 3058/3823 [05:45<01:26, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3059/3823 [05:45<01:26, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3060/3823 [05:46<01:26, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3061/3823 [05:46<01:26, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3062/3823 [05:46<01:26, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3063/3823 [05:46<01:26, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3064/3823 [05:46<01:26, 8.82it/s]\u001b[A\u001b[A\n\n 80% 3065/3823 [05:46<01:25, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3066/3823 [05:46<01:25, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3067/3823 [05:46<01:25, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3068/3823 [05:46<01:25, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3069/3823 [05:47<01:25, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3070/3823 [05:47<01:25, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3071/3823 [05:47<01:25, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3072/3823 [05:47<01:25, 8.83it/s]\u001b[A\u001b[A\n\n 80% 3073/3823 [05:47<01:25, 8.81it/s]\u001b[A\u001b[A\n\n 80% 3074/3823 [05:47<01:25, 8.80it/s]\u001b[A\u001b[A\n\n 80% 3075/3823 [05:47<01:24, 8.81it/s]\u001b[A\u001b[A\n\n 80% 3076/3823 [05:47<01:24, 8.81it/s]\u001b[A\u001b[A\n\n 80% 3077/3823 [05:47<01:24, 8.80it/s]\u001b[A\u001b[A\n\n 81% 3078/3823 [05:48<01:24, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3079/3823 [05:48<01:24, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3080/3823 [05:48<01:24, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3081/3823 [05:48<01:24, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3082/3823 [05:48<01:23, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3083/3823 [05:48<01:23, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3084/3823 [05:48<01:23, 8.83it/s]\u001b[A\u001b[A\n\n 81% 3085/3823 [05:48<01:23, 8.84it/s]\u001b[A\u001b[A\n\n 81% 3086/3823 [05:49<01:23, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3087/3823 [05:49<01:23, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3088/3823 [05:49<01:23, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3089/3823 [05:49<01:23, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3090/3823 [05:49<01:23, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3091/3823 [05:49<01:22, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3092/3823 [05:49<01:22, 8.83it/s]\u001b[A\u001b[A\n\n 81% 3093/3823 [05:49<01:22, 8.83it/s]\u001b[A\u001b[A\n\n 81% 3094/3823 [05:49<01:22, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3095/3823 [05:50<01:22, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3096/3823 [05:50<01:22, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3097/3823 [05:50<01:22, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3098/3823 [05:50<01:22, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3099/3823 [05:50<01:22, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3100/3823 [05:50<01:22, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3101/3823 [05:50<01:21, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3102/3823 [05:50<01:21, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3103/3823 [05:50<01:21, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3104/3823 [05:51<01:21, 8.80it/s]\u001b[A\u001b[A\n\n 81% 3105/3823 [05:51<01:21, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3106/3823 [05:51<01:21, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3107/3823 [05:51<01:21, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3108/3823 [05:51<01:21, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3109/3823 [05:51<01:20, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3110/3823 [05:51<01:20, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3111/3823 [05:51<01:20, 8.82it/s]\u001b[A\u001b[A\n\n 81% 3112/3823 [05:51<01:20, 8.81it/s]\u001b[A\u001b[A\n\n 81% 3113/3823 [05:52<01:20, 8.80it/s]\u001b[A\u001b[A\n\n 81% 3114/3823 [05:52<01:20, 8.80it/s]\u001b[A\u001b[A\n\n 81% 3115/3823 [05:52<01:20, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3116/3823 [05:52<01:20, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3117/3823 [05:52<01:20, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3118/3823 [05:52<01:19, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3119/3823 [05:52<01:19, 8.83it/s]\u001b[A\u001b[A\n\n 82% 3120/3823 [05:52<01:19, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3121/3823 [05:52<01:19, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3122/3823 [05:53<01:19, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3123/3823 [05:53<01:19, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3124/3823 [05:53<01:19, 8.83it/s]\u001b[A\u001b[A\n\n 82% 3125/3823 [05:53<01:19, 8.83it/s]\u001b[A\u001b[A\n\n 82% 3126/3823 [05:53<01:19, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3127/3823 [05:53<01:19, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3128/3823 [05:53<01:18, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3129/3823 [05:53<01:18, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3130/3823 [05:54<01:18, 8.79it/s]\u001b[A\u001b[A\n\n 82% 3131/3823 [05:54<01:18, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3132/3823 [05:54<01:17, 8.86it/s]\u001b[A\u001b[A\n\n 82% 3133/3823 [05:54<01:17, 8.85it/s]\u001b[A\u001b[A\n\n 82% 3134/3823 [05:54<01:17, 8.85it/s]\u001b[A\u001b[A\n\n 82% 3135/3823 [05:54<01:17, 8.84it/s]\u001b[A\u001b[A\n\n 82% 3136/3823 [05:54<01:17, 8.83it/s]\u001b[A\u001b[A\n\n 82% 3137/3823 [05:54<01:17, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3138/3823 [05:54<01:17, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3139/3823 [05:55<01:17, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3140/3823 [05:55<01:17, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3141/3823 [05:55<01:17, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3142/3823 [05:55<01:17, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3143/3823 [05:55<01:17, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3144/3823 [05:55<01:17, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3145/3823 [05:55<01:16, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3146/3823 [05:55<01:16, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3147/3823 [05:55<01:16, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3148/3823 [05:56<01:16, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3149/3823 [05:56<01:16, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3150/3823 [05:56<01:16, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3151/3823 [05:56<01:16, 8.82it/s]\u001b[A\u001b[A\n\n 82% 3152/3823 [05:56<01:16, 8.81it/s]\u001b[A\u001b[A\n\n 82% 3153/3823 [05:56<01:15, 8.82it/s]\u001b[A\u001b[A\n\n 83% 3154/3823 [05:56<01:15, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3155/3823 [05:56<01:15, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3156/3823 [05:56<01:15, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3157/3823 [05:57<01:15, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3158/3823 [05:57<01:15, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3159/3823 [05:57<01:15, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3160/3823 [05:57<01:15, 8.78it/s]\u001b[A\u001b[A\n\n 83% 3161/3823 [05:57<01:15, 8.77it/s]\u001b[A\u001b[A\n\n 83% 3162/3823 [05:57<01:15, 8.79it/s]\u001b[A\u001b[A\n\n 83% 3163/3823 [05:57<01:15, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3164/3823 [05:57<01:14, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3165/3823 [05:57<01:14, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3166/3823 [05:58<01:14, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3167/3823 [05:58<01:14, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3168/3823 [05:58<01:14, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3169/3823 [05:58<01:14, 8.82it/s]\u001b[A\u001b[A\n\n 83% 3170/3823 [05:58<01:14, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3171/3823 [05:58<01:13, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3172/3823 [05:58<01:13, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3173/3823 [05:58<01:13, 8.82it/s]\u001b[A\u001b[A\n\n 83% 3174/3823 [05:59<01:13, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3175/3823 [05:59<01:13, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3176/3823 [05:59<01:13, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3177/3823 [05:59<01:13, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3178/3823 [05:59<01:13, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3179/3823 [05:59<01:13, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3180/3823 [05:59<01:12, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3181/3823 [05:59<01:12, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3182/3823 [05:59<01:12, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3183/3823 [06:00<01:12, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3184/3823 [06:00<01:12, 8.79it/s]\u001b[A\u001b[A\n\n 83% 3185/3823 [06:00<01:12, 8.79it/s]\u001b[A\u001b[A\n\n 83% 3186/3823 [06:00<01:12, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3187/3823 [06:00<01:12, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3188/3823 [06:00<01:12, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3189/3823 [06:00<01:12, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3190/3823 [06:00<01:11, 8.81it/s]\u001b[A\u001b[A\n\n 83% 3191/3823 [06:00<01:11, 8.80it/s]\u001b[A\u001b[A\n\n 83% 3192/3823 [06:01<01:11, 8.79it/s]\u001b[A\u001b[A\n\n 84% 3193/3823 [06:01<01:11, 8.78it/s]\u001b[A\u001b[A\n\n 84% 3194/3823 [06:01<01:11, 8.79it/s]\u001b[A\u001b[A\n\n 84% 3195/3823 [06:01<01:11, 8.80it/s]\u001b[A\u001b[A\n\n 84% 3196/3823 [06:01<01:11, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3197/3823 [06:01<01:11, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3198/3823 [06:01<01:10, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3199/3823 [06:01<01:10, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3200/3823 [06:01<01:10, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3201/3823 [06:02<01:10, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3202/3823 [06:02<01:10, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3203/3823 [06:02<01:10, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3204/3823 [06:02<01:10, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3205/3823 [06:02<01:10, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3206/3823 [06:02<01:10, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3207/3823 [06:02<01:09, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3208/3823 [06:02<01:09, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3209/3823 [06:02<01:09, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3210/3823 [06:03<01:09, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3211/3823 [06:03<01:09, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3212/3823 [06:03<01:09, 8.83it/s]\u001b[A\u001b[A\n\n 84% 3213/3823 [06:03<01:09, 8.83it/s]\u001b[A\u001b[A\n\n 84% 3214/3823 [06:03<01:09, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3215/3823 [06:03<01:08, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3216/3823 [06:03<01:08, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3217/3823 [06:03<01:08, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3218/3823 [06:03<01:08, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3219/3823 [06:04<01:08, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3220/3823 [06:04<01:08, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3221/3823 [06:04<01:08, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3222/3823 [06:04<01:08, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3223/3823 [06:04<01:08, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3224/3823 [06:04<01:07, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3225/3823 [06:04<01:07, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3226/3823 [06:04<01:07, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3227/3823 [06:05<01:07, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3228/3823 [06:05<01:07, 8.82it/s]\u001b[A\u001b[A\n\n 84% 3229/3823 [06:05<01:07, 8.81it/s]\u001b[A\u001b[A\n\n 84% 3230/3823 [06:05<01:07, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3231/3823 [06:05<01:07, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3232/3823 [06:05<01:07, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3233/3823 [06:05<01:06, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3234/3823 [06:05<01:06, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3235/3823 [06:05<01:06, 8.82it/s]\u001b[A\u001b[A\n\n 85% 3236/3823 [06:06<01:06, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3237/3823 [06:06<01:06, 8.80it/s]\u001b[A\u001b[A\n\n 85% 3238/3823 [06:06<01:06, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3239/3823 [06:06<01:06, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3240/3823 [06:06<01:06, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3241/3823 [06:06<01:06, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3242/3823 [06:06<01:05, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3243/3823 [06:06<01:05, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3244/3823 [06:06<01:05, 8.80it/s]\u001b[A\u001b[A\n\n 85% 3245/3823 [06:07<01:05, 8.79it/s]\u001b[A\u001b[A\n\n 85% 3246/3823 [06:07<01:05, 8.80it/s]\u001b[A\u001b[A\n\n 85% 3247/3823 [06:07<01:05, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3248/3823 [06:07<01:05, 8.82it/s]\u001b[A\u001b[A\n\n 85% 3249/3823 [06:07<01:05, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3250/3823 [06:07<01:05, 8.80it/s]\u001b[A\u001b[A\n\n 85% 3251/3823 [06:07<01:04, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3252/3823 [06:07<01:04, 8.80it/s]\u001b[A\u001b[A\n\n 85% 3253/3823 [06:07<01:04, 8.80it/s]\u001b[A\u001b[A\n\n 85% 3254/3823 [06:08<01:04, 8.80it/s]\u001b[A\u001b[A\n\n 85% 3255/3823 [06:08<01:04, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3256/3823 [06:08<01:04, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3257/3823 [06:08<01:04, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3258/3823 [06:08<01:04, 8.79it/s]\u001b[A\u001b[A\n\n 85% 3259/3823 [06:08<01:04, 8.79it/s]\u001b[A\u001b[A\n\n 85% 3260/3823 [06:08<01:04, 8.79it/s]\u001b[A\u001b[A\n\n 85% 3261/3823 [06:08<01:03, 8.80it/s]\u001b[A\u001b[A\n\n 85% 3262/3823 [06:08<01:03, 8.79it/s]\u001b[A\u001b[A\n\n 85% 3263/3823 [06:09<01:03, 8.80it/s]\u001b[A\u001b[A\n\n 85% 3264/3823 [06:09<01:03, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3265/3823 [06:09<01:03, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3266/3823 [06:09<01:03, 8.81it/s]\u001b[A\u001b[A\n\n 85% 3267/3823 [06:09<01:03, 8.82it/s]\u001b[A\u001b[A\n\n 85% 3268/3823 [06:09<01:02, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3269/3823 [06:09<01:02, 8.82it/s]\u001b[A\u001b[A\n\n 86% 3270/3823 [06:09<01:02, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3271/3823 [06:10<01:02, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3272/3823 [06:10<01:02, 8.80it/s]\u001b[A\u001b[A\n\n 86% 3273/3823 [06:10<01:02, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3274/3823 [06:10<01:02, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3275/3823 [06:10<01:02, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3276/3823 [06:10<01:02, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3277/3823 [06:10<01:01, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3278/3823 [06:10<01:01, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3279/3823 [06:10<01:01, 8.82it/s]\u001b[A\u001b[A\n\n 86% 3280/3823 [06:11<01:01, 8.82it/s]\u001b[A\u001b[A\n\n 86% 3281/3823 [06:11<01:01, 8.83it/s]\u001b[A\u001b[A\n\n 86% 3282/3823 [06:11<01:01, 8.83it/s]\u001b[A\u001b[A\n\n 86% 3283/3823 [06:11<01:01, 8.82it/s]\u001b[A\u001b[A\n\n 86% 3284/3823 [06:11<01:01, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3285/3823 [06:11<01:01, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3286/3823 [06:11<01:00, 8.80it/s]\u001b[A\u001b[A\n\n 86% 3287/3823 [06:11<01:00, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3288/3823 [06:11<01:00, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3289/3823 [06:12<01:00, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3290/3823 [06:12<01:00, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3291/3823 [06:12<01:00, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3292/3823 [06:12<01:00, 8.80it/s]\u001b[A\u001b[A\n\n 86% 3293/3823 [06:12<01:00, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3294/3823 [06:12<00:59, 8.82it/s]\u001b[A\u001b[A\n\n 86% 3295/3823 [06:12<00:59, 8.83it/s]\u001b[A\u001b[A\n\n 86% 3296/3823 [06:12<00:59, 8.83it/s]\u001b[A\u001b[A\n\n 86% 3297/3823 [06:12<00:59, 8.83it/s]\u001b[A\u001b[A\n\n 86% 3298/3823 [06:13<00:59, 8.80it/s]\u001b[A\u001b[A\n\n 86% 3299/3823 [06:13<00:59, 8.80it/s]\u001b[A\u001b[A\n\n 86% 3300/3823 [06:13<00:59, 8.80it/s]\u001b[A\u001b[A\n\n 86% 3301/3823 [06:13<00:59, 8.80it/s]\u001b[A\u001b[A\n\n 86% 3302/3823 [06:13<00:59, 8.80it/s]\u001b[A\u001b[A\n\n 86% 3303/3823 [06:13<00:59, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3304/3823 [06:13<00:58, 8.81it/s]\u001b[A\u001b[A\n\n 86% 3305/3823 [06:13<00:58, 8.82it/s]\u001b[A\u001b[A\n\n 86% 3306/3823 [06:13<00:58, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3307/3823 [06:14<00:58, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3308/3823 [06:14<00:58, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3309/3823 [06:14<00:58, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3310/3823 [06:14<00:58, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3311/3823 [06:14<00:58, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3312/3823 [06:14<00:58, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3313/3823 [06:14<00:57, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3314/3823 [06:14<00:57, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3315/3823 [06:15<00:57, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3316/3823 [06:15<00:57, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3317/3823 [06:15<00:57, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3318/3823 [06:15<00:57, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3319/3823 [06:15<00:57, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3320/3823 [06:15<00:57, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3321/3823 [06:15<00:56, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3322/3823 [06:15<00:56, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3323/3823 [06:15<00:56, 8.82it/s]\u001b[A\u001b[A\n\n 87% 3324/3823 [06:16<00:56, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3325/3823 [06:16<00:56, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3326/3823 [06:16<00:56, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3327/3823 [06:16<00:56, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3328/3823 [06:16<00:56, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3329/3823 [06:16<00:56, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3330/3823 [06:16<00:56, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3331/3823 [06:16<00:55, 8.79it/s]\u001b[A\u001b[A\n\n 87% 3332/3823 [06:16<00:55, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3333/3823 [06:17<00:55, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3334/3823 [06:17<00:55, 8.82it/s]\u001b[A\u001b[A\n\n 87% 3335/3823 [06:17<00:55, 8.81it/s]\u001b[A\u001b[A\n\n 87% 3336/3823 [06:17<00:55, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3337/3823 [06:17<00:55, 8.79it/s]\u001b[A\u001b[A\n\n 87% 3338/3823 [06:17<00:55, 8.78it/s]\u001b[A\u001b[A\n\n 87% 3339/3823 [06:17<00:55, 8.77it/s]\u001b[A\u001b[A\n\n 87% 3340/3823 [06:17<00:55, 8.78it/s]\u001b[A\u001b[A\n\n 87% 3341/3823 [06:17<00:54, 8.79it/s]\u001b[A\u001b[A\n\n 87% 3342/3823 [06:18<00:54, 8.79it/s]\u001b[A\u001b[A\n\n 87% 3343/3823 [06:18<00:54, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3344/3823 [06:18<00:54, 8.80it/s]\u001b[A\u001b[A\n\n 87% 3345/3823 [06:18<00:54, 8.79it/s]\u001b[A\u001b[A\n\n 88% 3346/3823 [06:18<00:54, 8.79it/s]\u001b[A\u001b[A\n\n 88% 3347/3823 [06:18<00:54, 8.78it/s]\u001b[A\u001b[A\n\n 88% 3348/3823 [06:18<00:54, 8.79it/s]\u001b[A\u001b[A\n\n 88% 3349/3823 [06:18<00:53, 8.80it/s]\u001b[A\u001b[A\n\n 88% 3350/3823 [06:18<00:53, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3351/3823 [06:19<00:53, 8.80it/s]\u001b[A\u001b[A\n\n 88% 3352/3823 [06:19<00:53, 8.80it/s]\u001b[A\u001b[A\n\n 88% 3353/3823 [06:19<00:53, 8.80it/s]\u001b[A\u001b[A\n\n 88% 3354/3823 [06:19<00:53, 8.80it/s]\u001b[A\u001b[A\n\n 88% 3355/3823 [06:19<00:53, 8.80it/s]\u001b[A\u001b[A\n\n 88% 3356/3823 [06:19<00:53, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3357/3823 [06:19<00:52, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3358/3823 [06:19<00:52, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3359/3823 [06:20<00:52, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3360/3823 [06:20<00:52, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3361/3823 [06:20<00:52, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3362/3823 [06:20<00:52, 8.80it/s]\u001b[A\u001b[A\n\n 88% 3363/3823 [06:20<00:52, 8.79it/s]\u001b[A\u001b[A\n\n 88% 3364/3823 [06:20<00:52, 8.79it/s]\u001b[A\u001b[A\n\n 88% 3365/3823 [06:20<00:52, 8.79it/s]\u001b[A\u001b[A\n\n 88% 3366/3823 [06:20<00:51, 8.79it/s]\u001b[A\u001b[A\n\n 88% 3367/3823 [06:20<00:51, 8.80it/s]\u001b[A\u001b[A\n\n 88% 3368/3823 [06:21<00:51, 8.80it/s]\u001b[A\u001b[A\n\n 88% 3369/3823 [06:21<00:51, 8.80it/s]\u001b[A\u001b[A\n\n 88% 3370/3823 [06:21<00:51, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3371/3823 [06:21<00:51, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3372/3823 [06:21<00:51, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3373/3823 [06:21<00:51, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3374/3823 [06:21<00:50, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3375/3823 [06:21<00:50, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3376/3823 [06:21<00:50, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3377/3823 [06:22<00:50, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3378/3823 [06:22<00:50, 8.81it/s]\u001b[A\u001b[A\n\n 88% 3379/3823 [06:22<00:50, 8.82it/s]\u001b[A\u001b[A\n\n 88% 3380/3823 [06:22<00:50, 8.82it/s]\u001b[A\u001b[A\n\n 88% 3381/3823 [06:22<00:50, 8.82it/s]\u001b[A\u001b[A\n\n 88% 3382/3823 [06:22<00:50, 8.82it/s]\u001b[A\u001b[A\n\n 88% 3383/3823 [06:22<00:49, 8.82it/s]\u001b[A\u001b[A\n\n 89% 3384/3823 [06:22<00:49, 8.82it/s]\u001b[A\u001b[A\n\n 89% 3385/3823 [06:22<00:49, 8.82it/s]\u001b[A\u001b[A\n\n 89% 3386/3823 [06:23<00:49, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3387/3823 [06:23<00:49, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3388/3823 [06:23<00:49, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3389/3823 [06:23<00:49, 8.82it/s]\u001b[A\u001b[A\n\n 89% 3390/3823 [06:23<00:49, 8.82it/s]\u001b[A\u001b[A\n\n 89% 3391/3823 [06:23<00:49, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3392/3823 [06:23<00:48, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3393/3823 [06:23<00:48, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3394/3823 [06:23<00:48, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3395/3823 [06:24<00:48, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3396/3823 [06:24<00:48, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3397/3823 [06:24<00:48, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3398/3823 [06:24<00:48, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3399/3823 [06:24<00:48, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3400/3823 [06:24<00:48, 8.79it/s]\u001b[A\u001b[A\n\n 89% 3401/3823 [06:24<00:47, 8.79it/s]\u001b[A\u001b[A\n\n 89% 3402/3823 [06:24<00:47, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3403/3823 [06:25<00:47, 8.79it/s]\u001b[A\u001b[A\n\n 89% 3404/3823 [06:25<00:47, 8.79it/s]\u001b[A\u001b[A\n\n 89% 3405/3823 [06:25<00:47, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3406/3823 [06:25<00:47, 8.79it/s]\u001b[A\u001b[A\n\n 89% 3407/3823 [06:25<00:47, 8.79it/s]\u001b[A\u001b[A\n\n 89% 3408/3823 [06:25<00:47, 8.79it/s]\u001b[A\u001b[A\n\n 89% 3409/3823 [06:25<00:47, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3410/3823 [06:25<00:46, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3411/3823 [06:25<00:46, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3412/3823 [06:26<00:46, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3413/3823 [06:26<00:46, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3414/3823 [06:26<00:46, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3415/3823 [06:26<00:46, 8.79it/s]\u001b[A\u001b[A\n\n 89% 3416/3823 [06:26<00:46, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3417/3823 [06:26<00:46, 8.80it/s]\u001b[A\u001b[A\n\n 89% 3418/3823 [06:26<00:45, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3419/3823 [06:26<00:45, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3420/3823 [06:26<00:45, 8.81it/s]\u001b[A\u001b[A\n\n 89% 3421/3823 [06:27<00:45, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3422/3823 [06:27<00:45, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3423/3823 [06:27<00:45, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3424/3823 [06:27<00:45, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3425/3823 [06:27<00:45, 8.80it/s]\u001b[A\u001b[A\n\n 90% 3426/3823 [06:27<00:45, 8.80it/s]\u001b[A\u001b[A\n\n 90% 3427/3823 [06:27<00:44, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3428/3823 [06:27<00:44, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3429/3823 [06:27<00:44, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3430/3823 [06:28<00:44, 8.80it/s]\u001b[A\u001b[A\n\n 90% 3431/3823 [06:28<00:44, 8.80it/s]\u001b[A\u001b[A\n\n 90% 3432/3823 [06:28<00:44, 8.80it/s]\u001b[A\u001b[A\n\n 90% 3433/3823 [06:28<00:44, 8.80it/s]\u001b[A\u001b[A\n\n 90% 3434/3823 [06:28<00:44, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3435/3823 [06:28<00:44, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3436/3823 [06:28<00:43, 8.82it/s]\u001b[A\u001b[A\n\n 90% 3437/3823 [06:28<00:43, 8.82it/s]\u001b[A\u001b[A\n\n 90% 3438/3823 [06:28<00:43, 8.82it/s]\u001b[A\u001b[A\n\n 90% 3439/3823 [06:29<00:43, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3440/3823 [06:29<00:43, 8.80it/s]\u001b[A\u001b[A\n\n 90% 3441/3823 [06:29<00:43, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3442/3823 [06:29<00:43, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3443/3823 [06:29<00:43, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3444/3823 [06:29<00:42, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3445/3823 [06:29<00:42, 8.82it/s]\u001b[A\u001b[A\n\n 90% 3446/3823 [06:29<00:42, 8.82it/s]\u001b[A\u001b[A\n\n 90% 3447/3823 [06:29<00:42, 8.82it/s]\u001b[A\u001b[A\n\n 90% 3448/3823 [06:30<00:42, 8.82it/s]\u001b[A\u001b[A\n\n 90% 3449/3823 [06:30<00:42, 8.82it/s]\u001b[A\u001b[A\n\n 90% 3450/3823 [06:30<00:42, 8.82it/s]\u001b[A\u001b[A\n\n 90% 3451/3823 [06:30<00:42, 8.82it/s]\u001b[A\u001b[A\n\n 90% 3452/3823 [06:30<00:42, 8.80it/s]\u001b[A\u001b[A\n\n 90% 3453/3823 [06:30<00:42, 8.78it/s]\u001b[A\u001b[A\n\n 90% 3454/3823 [06:30<00:42, 8.78it/s]\u001b[A\u001b[A\n\n 90% 3455/3823 [06:30<00:41, 8.79it/s]\u001b[A\u001b[A\n\n 90% 3456/3823 [06:31<00:41, 8.79it/s]\u001b[A\u001b[A\n\n 90% 3457/3823 [06:31<00:41, 8.80it/s]\u001b[A\u001b[A\n\n 90% 3458/3823 [06:31<00:41, 8.81it/s]\u001b[A\u001b[A\n\n 90% 3459/3823 [06:31<00:41, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3460/3823 [06:31<00:41, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3461/3823 [06:31<00:41, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3462/3823 [06:31<00:40, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3463/3823 [06:31<00:40, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3464/3823 [06:31<00:40, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3465/3823 [06:32<00:40, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3466/3823 [06:32<00:40, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3467/3823 [06:32<00:40, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3468/3823 [06:32<00:40, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3469/3823 [06:32<00:40, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3470/3823 [06:32<00:40, 8.80it/s]\u001b[A\u001b[A\n\n 91% 3471/3823 [06:32<00:40, 8.79it/s]\u001b[A\u001b[A\n\n 91% 3472/3823 [06:32<00:39, 8.80it/s]\u001b[A\u001b[A\n\n 91% 3473/3823 [06:32<00:39, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3474/3823 [06:33<00:39, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3475/3823 [06:33<00:39, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3476/3823 [06:33<00:39, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3477/3823 [06:33<00:39, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3478/3823 [06:33<00:39, 8.80it/s]\u001b[A\u001b[A\n\n 91% 3479/3823 [06:33<00:39, 8.80it/s]\u001b[A\u001b[A\n\n 91% 3480/3823 [06:33<00:38, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3481/3823 [06:33<00:38, 8.80it/s]\u001b[A\u001b[A\n\n 91% 3482/3823 [06:33<00:38, 8.80it/s]\u001b[A\u001b[A\n\n 91% 3483/3823 [06:34<00:38, 8.80it/s]\u001b[A\u001b[A\n\n 91% 3484/3823 [06:34<00:38, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3485/3823 [06:34<00:38, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3486/3823 [06:34<00:38, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3487/3823 [06:34<00:38, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3488/3823 [06:34<00:37, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3489/3823 [06:34<00:37, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3490/3823 [06:34<00:37, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3491/3823 [06:34<00:37, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3492/3823 [06:35<00:37, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3493/3823 [06:35<00:37, 8.80it/s]\u001b[A\u001b[A\n\n 91% 3494/3823 [06:35<00:37, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3495/3823 [06:35<00:37, 8.81it/s]\u001b[A\u001b[A\n\n 91% 3496/3823 [06:35<00:37, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3497/3823 [06:35<00:36, 8.82it/s]\u001b[A\u001b[A\n\n 91% 3498/3823 [06:35<00:36, 8.82it/s]\u001b[A\u001b[A\n\n 92% 3499/3823 [06:35<00:36, 8.82it/s]\u001b[A\u001b[A\n\n 92% 3500/3823 [06:36<00:36, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3501/3823 [06:36<00:36, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3502/3823 [06:36<00:36, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3503/3823 [06:36<00:36, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3504/3823 [06:36<00:36, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3505/3823 [06:36<00:36, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3506/3823 [06:36<00:35, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3507/3823 [06:36<00:35, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3508/3823 [06:36<00:35, 8.80it/s]\u001b[A\u001b[A\n\n 92% 3509/3823 [06:37<00:35, 8.80it/s]\u001b[A\u001b[A\n\n 92% 3510/3823 [06:37<00:35, 8.80it/s]\u001b[A\u001b[A\n\n 92% 3511/3823 [06:37<00:35, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3512/3823 [06:37<00:35, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3513/3823 [06:37<00:35, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3514/3823 [06:37<00:35, 8.82it/s]\u001b[A\u001b[A\n\n 92% 3515/3823 [06:37<00:34, 8.82it/s]\u001b[A\u001b[A\n\n 92% 3516/3823 [06:37<00:34, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3517/3823 [06:37<00:34, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3518/3823 [06:38<00:34, 8.80it/s]\u001b[A\u001b[A\n\n 92% 3519/3823 [06:38<00:34, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3520/3823 [06:38<00:34, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3521/3823 [06:38<00:34, 8.82it/s]\u001b[A\u001b[A\n\n 92% 3522/3823 [06:38<00:34, 8.82it/s]\u001b[A\u001b[A\n\n 92% 3523/3823 [06:38<00:34, 8.82it/s]\u001b[A\u001b[A\n\n 92% 3524/3823 [06:38<00:33, 8.82it/s]\u001b[A\u001b[A\n\n 92% 3525/3823 [06:38<00:33, 8.82it/s]\u001b[A\u001b[A\n\n 92% 3526/3823 [06:38<00:33, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3527/3823 [06:39<00:33, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3528/3823 [06:39<00:33, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3529/3823 [06:39<00:33, 8.82it/s]\u001b[A\u001b[A\n\n 92% 3530/3823 [06:39<00:33, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3531/3823 [06:39<00:33, 8.80it/s]\u001b[A\u001b[A\n\n 92% 3532/3823 [06:39<00:33, 8.80it/s]\u001b[A\u001b[A\n\n 92% 3533/3823 [06:39<00:32, 8.80it/s]\u001b[A\u001b[A\n\n 92% 3534/3823 [06:39<00:32, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3535/3823 [06:39<00:32, 8.81it/s]\u001b[A\u001b[A\n\n 92% 3536/3823 [06:40<00:32, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3537/3823 [06:40<00:32, 8.80it/s]\u001b[A\u001b[A\n\n 93% 3538/3823 [06:40<00:32, 8.80it/s]\u001b[A\u001b[A\n\n 93% 3539/3823 [06:40<00:32, 8.80it/s]\u001b[A\u001b[A\n\n 93% 3540/3823 [06:40<00:32, 8.80it/s]\u001b[A\u001b[A\n\n 93% 3541/3823 [06:40<00:32, 8.80it/s]\u001b[A\u001b[A\n\n 93% 3542/3823 [06:40<00:31, 8.80it/s]\u001b[A\u001b[A\n\n 93% 3543/3823 [06:40<00:31, 8.80it/s]\u001b[A\u001b[A\n\n 93% 3544/3823 [06:41<00:31, 8.79it/s]\u001b[A\u001b[A\n\n 93% 3545/3823 [06:41<00:31, 8.78it/s]\u001b[A\u001b[A\n\n 93% 3546/3823 [06:41<00:31, 8.79it/s]\u001b[A\u001b[A\n\n 93% 3547/3823 [06:41<00:31, 8.80it/s]\u001b[A\u001b[A\n\n 93% 3548/3823 [06:41<00:31, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3549/3823 [06:41<00:31, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3550/3823 [06:41<00:30, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3551/3823 [06:41<00:30, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3552/3823 [06:41<00:30, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3553/3823 [06:42<00:30, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3554/3823 [06:42<00:30, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3555/3823 [06:42<00:30, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3556/3823 [06:42<00:30, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3557/3823 [06:42<00:30, 8.80it/s]\u001b[A\u001b[A\n\n 93% 3558/3823 [06:42<00:30, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3559/3823 [06:42<00:29, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3560/3823 [06:42<00:29, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3561/3823 [06:42<00:29, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3562/3823 [06:43<00:29, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3563/3823 [06:43<00:29, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3564/3823 [06:43<00:29, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3565/3823 [06:43<00:29, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3566/3823 [06:43<00:29, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3567/3823 [06:43<00:29, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3568/3823 [06:43<00:28, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3569/3823 [06:43<00:28, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3570/3823 [06:43<00:28, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3571/3823 [06:44<00:28, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3572/3823 [06:44<00:28, 8.82it/s]\u001b[A\u001b[A\n\n 93% 3573/3823 [06:44<00:28, 8.81it/s]\u001b[A\u001b[A\n\n 93% 3574/3823 [06:44<00:28, 8.82it/s]\u001b[A\u001b[A\n\n 94% 3575/3823 [06:44<00:28, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3576/3823 [06:44<00:28, 8.82it/s]\u001b[A\u001b[A\n\n 94% 3577/3823 [06:44<00:27, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3578/3823 [06:44<00:27, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3579/3823 [06:44<00:27, 8.80it/s]\u001b[A\u001b[A\n\n 94% 3580/3823 [06:45<00:27, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3581/3823 [06:45<00:27, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3582/3823 [06:45<00:27, 8.82it/s]\u001b[A\u001b[A\n\n 94% 3583/3823 [06:45<00:27, 8.82it/s]\u001b[A\u001b[A\n\n 94% 3584/3823 [06:45<00:27, 8.82it/s]\u001b[A\u001b[A\n\n 94% 3585/3823 [06:45<00:27, 8.80it/s]\u001b[A\u001b[A\n\n 94% 3586/3823 [06:45<00:26, 8.79it/s]\u001b[A\u001b[A\n\n 94% 3587/3823 [06:45<00:26, 8.80it/s]\u001b[A\u001b[A\n\n 94% 3588/3823 [06:46<00:26, 8.80it/s]\u001b[A\u001b[A\n\n 94% 3589/3823 [06:46<00:26, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3590/3823 [06:46<00:26, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3591/3823 [06:46<00:26, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3592/3823 [06:46<00:26, 8.82it/s]\u001b[A\u001b[A\n\n 94% 3593/3823 [06:46<00:26, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3594/3823 [06:46<00:26, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3595/3823 [06:46<00:25, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3596/3823 [06:46<00:25, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3597/3823 [06:47<00:25, 8.80it/s]\u001b[A\u001b[A\n\n 94% 3598/3823 [06:47<00:25, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3599/3823 [06:47<00:25, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3600/3823 [06:47<00:25, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3601/3823 [06:47<00:25, 8.80it/s]\u001b[A\u001b[A\n\n 94% 3602/3823 [06:47<00:25, 8.80it/s]\u001b[A\u001b[A\n\n 94% 3603/3823 [06:47<00:25, 8.80it/s]\u001b[A\u001b[A\n\n 94% 3604/3823 [06:47<00:24, 8.80it/s]\u001b[A\u001b[A\n\n 94% 3605/3823 [06:47<00:24, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3606/3823 [06:48<00:24, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3607/3823 [06:48<00:24, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3608/3823 [06:48<00:24, 8.82it/s]\u001b[A\u001b[A\n\n 94% 3609/3823 [06:48<00:24, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3610/3823 [06:48<00:24, 8.80it/s]\u001b[A\u001b[A\n\n 94% 3611/3823 [06:48<00:24, 8.81it/s]\u001b[A\u001b[A\n\n 94% 3612/3823 [06:48<00:23, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3613/3823 [06:48<00:23, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3614/3823 [06:48<00:23, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3615/3823 [06:49<00:23, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3616/3823 [06:49<00:23, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3617/3823 [06:49<00:23, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3618/3823 [06:49<00:23, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3619/3823 [06:49<00:23, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3620/3823 [06:49<00:23, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3621/3823 [06:49<00:22, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3622/3823 [06:49<00:22, 8.82it/s]\u001b[A\u001b[A\n\n 95% 3623/3823 [06:49<00:22, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3624/3823 [06:50<00:22, 8.79it/s]\u001b[A\u001b[A\n\n 95% 3625/3823 [06:50<00:22, 8.79it/s]\u001b[A\u001b[A\n\n 95% 3626/3823 [06:50<00:22, 8.79it/s]\u001b[A\u001b[A\n\n 95% 3627/3823 [06:50<00:22, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3628/3823 [06:50<00:22, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3629/3823 [06:50<00:22, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3630/3823 [06:50<00:21, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3631/3823 [06:50<00:21, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3632/3823 [06:51<00:21, 8.79it/s]\u001b[A\u001b[A\n\n 95% 3633/3823 [06:51<00:21, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3634/3823 [06:51<00:21, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3635/3823 [06:51<00:21, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3636/3823 [06:51<00:21, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3637/3823 [06:51<00:21, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3638/3823 [06:51<00:21, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3639/3823 [06:51<00:20, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3640/3823 [06:51<00:20, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3641/3823 [06:52<00:20, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3642/3823 [06:52<00:20, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3643/3823 [06:52<00:20, 8.80it/s]\u001b[A\u001b[A\n\n 95% 3644/3823 [06:52<00:20, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3645/3823 [06:52<00:20, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3646/3823 [06:52<00:20, 8.82it/s]\u001b[A\u001b[A\n\n 95% 3647/3823 [06:52<00:19, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3648/3823 [06:52<00:19, 8.82it/s]\u001b[A\u001b[A\n\n 95% 3649/3823 [06:52<00:19, 8.81it/s]\u001b[A\u001b[A\n\n 95% 3650/3823 [06:53<00:19, 8.79it/s]\u001b[A\u001b[A\n\n 96% 3651/3823 [06:53<00:19, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3652/3823 [06:53<00:19, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3653/3823 [06:53<00:19, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3654/3823 [06:53<00:19, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3655/3823 [06:53<00:19, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3656/3823 [06:53<00:18, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3657/3823 [06:53<00:18, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3658/3823 [06:53<00:18, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3659/3823 [06:54<00:18, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3660/3823 [06:54<00:18, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3661/3823 [06:54<00:18, 8.82it/s]\u001b[A\u001b[A\n\n 96% 3662/3823 [06:54<00:18, 8.82it/s]\u001b[A\u001b[A\n\n 96% 3663/3823 [06:54<00:18, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3664/3823 [06:54<00:18, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3665/3823 [06:54<00:17, 8.79it/s]\u001b[A\u001b[A\n\n 96% 3666/3823 [06:54<00:17, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3667/3823 [06:54<00:17, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3668/3823 [06:55<00:17, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3669/3823 [06:55<00:17, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3670/3823 [06:55<00:17, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3671/3823 [06:55<00:17, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3672/3823 [06:55<00:17, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3673/3823 [06:55<00:17, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3674/3823 [06:55<00:16, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3675/3823 [06:55<00:16, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3676/3823 [06:55<00:16, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3677/3823 [06:56<00:16, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3678/3823 [06:56<00:16, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3679/3823 [06:56<00:16, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3680/3823 [06:56<00:16, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3681/3823 [06:56<00:16, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3682/3823 [06:56<00:16, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3683/3823 [06:56<00:15, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3684/3823 [06:56<00:15, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3685/3823 [06:57<00:15, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3686/3823 [06:57<00:15, 8.81it/s]\u001b[A\u001b[A\n\n 96% 3687/3823 [06:57<00:15, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3688/3823 [06:57<00:15, 8.80it/s]\u001b[A\u001b[A\n\n 96% 3689/3823 [06:57<00:15, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3690/3823 [06:57<00:15, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3691/3823 [06:57<00:15, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3692/3823 [06:57<00:14, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3693/3823 [06:57<00:14, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3694/3823 [06:58<00:14, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3695/3823 [06:58<00:14, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3696/3823 [06:58<00:14, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3697/3823 [06:58<00:14, 8.78it/s]\u001b[A\u001b[A\n\n 97% 3698/3823 [06:58<00:14, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3699/3823 [06:58<00:14, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3700/3823 [06:58<00:13, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3701/3823 [06:58<00:13, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3702/3823 [06:58<00:13, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3703/3823 [06:59<00:13, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3704/3823 [06:59<00:13, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3705/3823 [06:59<00:13, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3706/3823 [06:59<00:13, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3707/3823 [06:59<00:13, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3708/3823 [06:59<00:13, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3709/3823 [06:59<00:12, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3710/3823 [06:59<00:12, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3711/3823 [06:59<00:12, 8.81it/s]\u001b[A\u001b[A\n\n 97% 3712/3823 [07:00<00:12, 8.81it/s]\u001b[A\u001b[A\n\n 97% 3713/3823 [07:00<00:12, 8.81it/s]\u001b[A\u001b[A\n\n 97% 3714/3823 [07:00<00:12, 8.81it/s]\u001b[A\u001b[A\n\n 97% 3715/3823 [07:00<00:12, 8.81it/s]\u001b[A\u001b[A\n\n 97% 3716/3823 [07:00<00:12, 8.81it/s]\u001b[A\u001b[A\n\n 97% 3717/3823 [07:00<00:12, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3718/3823 [07:00<00:11, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3719/3823 [07:00<00:11, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3720/3823 [07:01<00:11, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3721/3823 [07:01<00:11, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3722/3823 [07:01<00:11, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3723/3823 [07:01<00:11, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3724/3823 [07:01<00:11, 8.80it/s]\u001b[A\u001b[A\n\n 97% 3725/3823 [07:01<00:11, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3726/3823 [07:01<00:11, 8.79it/s]\u001b[A\u001b[A\n\n 97% 3727/3823 [07:01<00:10, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3728/3823 [07:01<00:10, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3729/3823 [07:02<00:10, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3730/3823 [07:02<00:10, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3731/3823 [07:02<00:10, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3732/3823 [07:02<00:10, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3733/3823 [07:02<00:10, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3734/3823 [07:02<00:10, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3735/3823 [07:02<00:10, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3736/3823 [07:02<00:09, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3737/3823 [07:02<00:09, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3738/3823 [07:03<00:09, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3739/3823 [07:03<00:09, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3740/3823 [07:03<00:09, 8.81it/s]\u001b[A\u001b[A\n\n 98% 3741/3823 [07:03<00:09, 8.81it/s]\u001b[A\u001b[A\n\n 98% 3742/3823 [07:03<00:09, 8.81it/s]\u001b[A\u001b[A\n\n 98% 3743/3823 [07:03<00:09, 8.82it/s]\u001b[A\u001b[A\n\n 98% 3744/3823 [07:03<00:08, 8.81it/s]\u001b[A\u001b[A\n\n 98% 3745/3823 [07:03<00:08, 8.81it/s]\u001b[A\u001b[A\n\n 98% 3746/3823 [07:03<00:08, 8.81it/s]\u001b[A\u001b[A\n\n 98% 3747/3823 [07:04<00:08, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3748/3823 [07:04<00:08, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3749/3823 [07:04<00:08, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3750/3823 [07:04<00:08, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3751/3823 [07:04<00:08, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3752/3823 [07:04<00:08, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3753/3823 [07:04<00:07, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3754/3823 [07:04<00:07, 8.80it/s]\u001b[A\u001b[A\n\n 98% 3755/3823 [07:04<00:07, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3756/3823 [07:05<00:07, 8.78it/s]\u001b[A\u001b[A\n\n 98% 3757/3823 [07:05<00:07, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3758/3823 [07:05<00:07, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3759/3823 [07:05<00:07, 8.78it/s]\u001b[A\u001b[A\n\n 98% 3760/3823 [07:05<00:07, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3761/3823 [07:05<00:07, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3762/3823 [07:05<00:06, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3763/3823 [07:05<00:06, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3764/3823 [07:06<00:06, 8.79it/s]\u001b[A\u001b[A\n\n 98% 3765/3823 [07:06<00:06, 8.79it/s]\u001b[A\u001b[A\n\n 99% 3766/3823 [07:06<00:06, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3767/3823 [07:06<00:06, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3768/3823 [07:06<00:06, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3769/3823 [07:06<00:06, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3770/3823 [07:06<00:06, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3771/3823 [07:06<00:05, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3772/3823 [07:06<00:05, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3773/3823 [07:07<00:05, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3774/3823 [07:07<00:05, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3775/3823 [07:07<00:05, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3776/3823 [07:07<00:05, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3777/3823 [07:07<00:05, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3778/3823 [07:07<00:05, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3779/3823 [07:07<00:04, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3780/3823 [07:07<00:04, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3781/3823 [07:07<00:04, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3782/3823 [07:08<00:04, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3783/3823 [07:08<00:04, 8.81it/s]\u001b[A\u001b[A\n\n 99% 3784/3823 [07:08<00:04, 8.82it/s]\u001b[A\u001b[A\n\n 99% 3785/3823 [07:08<00:04, 8.82it/s]\u001b[A\u001b[A\n\n 99% 3786/3823 [07:08<00:04, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3787/3823 [07:08<00:04, 8.79it/s]\u001b[A\u001b[A\n\n 99% 3788/3823 [07:08<00:03, 8.79it/s]\u001b[A\u001b[A\n\n 99% 3789/3823 [07:08<00:03, 8.78it/s]\u001b[A\u001b[A\n\n 99% 3790/3823 [07:08<00:03, 8.79it/s]\u001b[A\u001b[A\n\n 99% 3791/3823 [07:09<00:03, 8.79it/s]\u001b[A\u001b[A\n\n 99% 3792/3823 [07:09<00:03, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3793/3823 [07:09<00:03, 8.79it/s]\u001b[A\u001b[A\n\n 99% 3794/3823 [07:09<00:03, 8.79it/s]\u001b[A\u001b[A\n\n 99% 3795/3823 [07:09<00:03, 8.79it/s]\u001b[A\u001b[A\n\n 99% 3796/3823 [07:09<00:03, 8.79it/s]\u001b[A\u001b[A\n\n 99% 3797/3823 [07:09<00:02, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3798/3823 [07:09<00:02, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3799/3823 [07:09<00:02, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3800/3823 [07:10<00:02, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3801/3823 [07:10<00:02, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3802/3823 [07:10<00:02, 8.80it/s]\u001b[A\u001b[A\n\n 99% 3803/3823 [07:10<00:02, 8.79it/s]\u001b[A\u001b[A\n\n100% 3804/3823 [07:10<00:02, 8.79it/s]\u001b[A\u001b[A\n\n100% 3805/3823 [07:10<00:02, 8.78it/s]\u001b[A\u001b[A\n\n100% 3806/3823 [07:10<00:01, 8.78it/s]\u001b[A\u001b[A\n\n100% 3807/3823 [07:10<00:01, 8.78it/s]\u001b[A\u001b[A\n\n100% 3808/3823 [07:11<00:01, 8.79it/s]\u001b[A\u001b[A\n\n100% 3809/3823 [07:11<00:01, 8.79it/s]\u001b[A\u001b[A\n\n100% 3810/3823 [07:11<00:01, 8.78it/s]\u001b[A\u001b[A\n\n100% 3811/3823 [07:11<00:01, 8.79it/s]\u001b[A\u001b[A\n\n100% 3812/3823 [07:11<00:01, 8.79it/s]\u001b[A\u001b[A\n\n100% 3813/3823 [07:11<00:01, 8.80it/s]\u001b[A\u001b[A\n\n100% 3814/3823 [07:11<00:01, 8.80it/s]\u001b[A\u001b[A\n\n100% 3815/3823 [07:11<00:00, 8.80it/s]\u001b[A\u001b[A\n\n100% 3816/3823 [07:11<00:00, 8.80it/s]\u001b[A\u001b[A\n\n100% 3817/3823 [07:12<00:00, 8.79it/s]\u001b[A\u001b[A\n\n100% 3818/3823 [07:12<00:00, 8.79it/s]\u001b[A\u001b[A\n\n100% 3819/3823 [07:12<00:00, 8.80it/s]\u001b[A\u001b[A\n\n100% 3820/3823 [07:12<00:00, 8.80it/s]\u001b[A\u001b[A\n\n100% 3821/3823 [07:12<00:00, 8.79it/s]\u001b[A\u001b[A\n\n100% 3822/3823 [07:12<00:00, 8.79it/s]\u001b[A\u001b[AAggregating distributions...\n\n\n100% 3823/3823 [15:59<00:00, 3.98it/s]\n\n100% 3823/3823 [24:43<00:00, 2.58it/s]\n100% 3823/3823 [07:17<00:00, 8.74it/s]\n" ] ], [ [ "## Student Training", "_____no_output_____" ] ], [ [ "!python train_student.py \\\n--data_dir 'data/GLOBAL/Student' \\\n--model_name_or_path 'dmis-lab/biobert-base-cased-v1.1' \\\n--output_dir 'models/Student' \\\n--logging_dir 'models/Student' \\\n--save_steps 956 ", "2021-03-30 15:43:22.368091: I tensorflow/stream_executor/platform/default/dso_loader.cc:49] Successfully opened dynamic library libcudart.so.11.0\nNamespace(data_dir='data/GLOBAL/Student', logging_dir='models/Student', logging_steps=100, max_seq_length=128, model_name_or_path='dmis-lab/biobert-base-cased-v1.1', num_train_epochs=3, output_dir='models/Student', per_device_train_batch_size=32, save_steps=956, seed=1)\n03/30/2021 15:43:24 - WARNING - __main__ - Process rank: -1, device: cuda:0, n_gpu: 1, distributed training: False, 16-bits training: False\n03/30/2021 15:43:24 - INFO - __main__ - Training/evaluation parameters TrainingArguments(output_dir=models/Student, overwrite_output_dir=False, do_train=False, do_eval=None, do_predict=False, evaluation_strategy=IntervalStrategy.NO, prediction_loss_only=False, per_device_train_batch_size=32, per_device_eval_batch_size=8, gradient_accumulation_steps=1, eval_accumulation_steps=None, learning_rate=5e-05, weight_decay=0.0, adam_beta1=0.9, adam_beta2=0.999, adam_epsilon=1e-08, max_grad_norm=1.0, num_train_epochs=3, max_steps=-1, lr_scheduler_type=SchedulerType.LINEAR, warmup_ratio=0.0, warmup_steps=0, logging_dir=models/Student, logging_strategy=IntervalStrategy.STEPS, logging_first_step=False, logging_steps=100, save_strategy=IntervalStrategy.STEPS, save_steps=956, save_total_limit=None, no_cuda=False, seed=1, fp16=False, fp16_opt_level=O1, fp16_backend=auto, fp16_full_eval=False, local_rank=-1, tpu_num_cores=None, tpu_metrics_debug=False, debug=False, dataloader_drop_last=False, eval_steps=100, dataloader_num_workers=0, past_index=-1, run_name=models/Student, disable_tqdm=False, remove_unused_columns=True, label_names=None, load_best_model_at_end=False, metric_for_best_model=None, greater_is_better=None, ignore_data_skip=False, sharded_ddp=[], deepspeed=None, label_smoothing_factor=0.0, adafactor=False, group_by_length=False, report_to=['tensorboard'], ddp_find_unused_parameters=None, dataloader_pin_memory=True, skip_memory_metrics=False, _n_gpu=1)\n03/30/2021 15:43:28 - INFO - filelock - Lock 139997681852240 acquired on data/GLOBAL/Student/cached_train_dev_BertTokenizer_128.lock\n03/30/2021 15:43:28 - INFO - src.data_handling.DataHandlers - Loading features from cached file data/GLOBAL/Student/cached_train_dev_BertTokenizer_128\n03/30/2021 15:43:35 - INFO - filelock - Lock 139997681852240 released on data/GLOBAL/Student/cached_train_dev_BertTokenizer_128.lock\nSome weights of the model checkpoint at dmis-lab/biobert-base-cased-v1.1 were not used when initializing BertForTokenClassification: ['cls.predictions.bias', 'cls.predictions.transform.dense.weight', 'cls.predictions.transform.dense.bias', 'cls.predictions.transform.LayerNorm.weight', 'cls.predictions.transform.LayerNorm.bias', 'cls.predictions.decoder.weight', 'cls.predictions.decoder.bias', 'cls.seq_relationship.weight', 'cls.seq_relationship.bias']\n- This IS expected if you are initializing BertForTokenClassification from the checkpoint of a model trained on another task or with another architecture (e.g. initializing a BertForSequenceClassification model from a BertForPreTraining model).\n- This IS NOT expected if you are initializing BertForTokenClassification from the checkpoint of a model that you expect to be exactly identical (initializing a BertForSequenceClassification model from a BertForSequenceClassification model).\nSome weights of BertForTokenClassification were not initialized from the model checkpoint at dmis-lab/biobert-base-cased-v1.1 and are newly initialized: ['classifier.weight', 'classifier.bias']\nYou should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.\n03/30/2021 15:43:47 - INFO - filelock - Lock 139997473662864 acquired on data/BC2GM/cached_test_BertTokenizer_128.lock\n03/30/2021 15:43:47 - INFO - src.data_handling.DataHandlers - Loading features from cached file data/BC2GM/cached_test_BertTokenizer_128\n03/30/2021 15:43:47 - INFO - filelock - Lock 139997473662864 released on data/BC2GM/cached_test_BertTokenizer_128.lock\n03/30/2021 15:43:47 - INFO - filelock - Lock 139997473662480 acquired on data/BC5CDR-chem/cached_test_BertTokenizer_128.lock\n03/30/2021 15:43:47 - INFO - src.data_handling.DataHandlers - Loading features from cached file data/BC5CDR-chem/cached_test_BertTokenizer_128\n03/30/2021 15:43:48 - INFO - filelock - Lock 139997473662480 released on data/BC5CDR-chem/cached_test_BertTokenizer_128.lock\n03/30/2021 15:43:48 - INFO - filelock - Lock 139997681910672 acquired on data/NCBI-disease/cached_test_BertTokenizer_128.lock\n03/30/2021 15:43:48 - INFO - src.data_handling.DataHandlers - Loading features from cached file data/NCBI-disease/cached_test_BertTokenizer_128\n03/30/2021 15:43:48 - INFO - filelock - Lock 139997681910672 released on data/NCBI-disease/cached_test_BertTokenizer_128.lock\n/usr/local/lib/python3.7/dist-packages/transformers/trainer.py:836: FutureWarning: `model_path` is deprecated and will be removed in a future version. Use `resume_from_checkpoint` instead.\n FutureWarning,\n 0% 0/2868 [00:00<?, ?it/s]/usr/local/lib/python3.7/dist-packages/torch/nn/functional.py:2608: UserWarning: reduction: 'mean' divides the total loss by both the batch size and the support size.'batchmean' divides only by the batch size, and aligns with the KL div math definition.'mean' will be changed to behave the same as 'batchmean' in the next major release.\n \"reduction: 'mean' divides the total loss by both the batch size and the support size.\"\n{'loss': 0.0156, 'learning_rate': 4.825662482566248e-05, 'epoch': 0.1}\n{'loss': 0.0115, 'learning_rate': 4.651324965132497e-05, 'epoch': 0.21}\n{'loss': 0.0109, 'learning_rate': 4.476987447698745e-05, 'epoch': 0.31}\n{'loss': 0.0108, 'learning_rate': 4.302649930264993e-05, 'epoch': 0.42}\n{'loss': 0.0105, 'learning_rate': 4.128312412831242e-05, 'epoch': 0.52}\n{'loss': 0.0105, 'learning_rate': 3.95397489539749e-05, 'epoch': 0.63}\n{'loss': 0.0103, 'learning_rate': 3.779637377963738e-05, 'epoch': 0.73}\n{'loss': 0.01, 'learning_rate': 3.6052998605299864e-05, 'epoch': 0.84}\n{'loss': 0.01, 'learning_rate': 3.4309623430962344e-05, 'epoch': 0.94}\n 33% 956/2868 [19:46<35:51, 1.13s/it]\n 0% 0/118 [00:00<?, ?it/s]\u001b[A\n 2% 2/118 [00:00<00:07, 16.23it/s]\u001b[A\n 3% 3/118 [00:00<00:09, 12.74it/s]\u001b[A\n 3% 4/118 [00:00<00:10, 11.15it/s]\u001b[A\n 4% 5/118 [00:00<00:11, 10.25it/s]\u001b[A\n 5% 6/118 [00:00<00:11, 9.66it/s]\u001b[A\n 6% 7/118 [00:00<00:11, 9.28it/s]\u001b[A\n 7% 8/118 [00:00<00:12, 9.08it/s]\u001b[A\n 8% 9/118 [00:00<00:12, 8.90it/s]\u001b[A\n 8% 10/118 [00:01<00:12, 8.82it/s]\u001b[A\n 9% 11/118 [00:01<00:12, 8.75it/s]\u001b[A\n 10% 12/118 [00:01<00:12, 8.73it/s]\u001b[A\n 11% 13/118 [00:01<00:12, 8.70it/s]\u001b[A\n 12% 14/118 [00:01<00:11, 8.67it/s]\u001b[A\n 13% 15/118 [00:01<00:11, 8.67it/s]\u001b[A\n 14% 16/118 [00:01<00:11, 8.70it/s]\u001b[A\n 14% 17/118 [00:01<00:11, 8.73it/s]\u001b[A\n 15% 18/118 [00:01<00:11, 8.75it/s]\u001b[A\n 16% 19/118 [00:02<00:11, 8.75it/s]\u001b[A\n 17% 20/118 [00:02<00:11, 8.77it/s]\u001b[A\n 18% 21/118 [00:02<00:11, 8.77it/s]\u001b[A\n 19% 22/118 [00:02<00:10, 8.78it/s]\u001b[A\n 19% 23/118 [00:02<00:10, 8.79it/s]\u001b[A\n 20% 24/118 [00:02<00:10, 8.78it/s]\u001b[A\n 21% 25/118 [00:02<00:10, 8.79it/s]\u001b[A\n 22% 26/118 [00:02<00:10, 8.77it/s]\u001b[A\n 23% 27/118 [00:03<00:10, 8.78it/s]\u001b[A\n 24% 28/118 [00:03<00:10, 8.79it/s]\u001b[A\n 25% 29/118 [00:03<00:10, 8.80it/s]\u001b[A\n 25% 30/118 [00:03<00:10, 8.80it/s]\u001b[A\n 26% 31/118 [00:03<00:09, 8.79it/s]\u001b[A\n 27% 32/118 [00:03<00:09, 8.77it/s]\u001b[A\n 28% 33/118 [00:03<00:09, 8.77it/s]\u001b[A\n 29% 34/118 [00:03<00:09, 8.77it/s]\u001b[A\n 30% 35/118 [00:03<00:09, 8.78it/s]\u001b[A\n 31% 36/118 [00:04<00:09, 8.78it/s]\u001b[A\n 31% 37/118 [00:04<00:09, 8.78it/s]\u001b[A\n 32% 38/118 [00:04<00:09, 8.79it/s]\u001b[A\n 33% 39/118 [00:04<00:08, 8.80it/s]\u001b[A\n 34% 40/118 [00:04<00:08, 8.80it/s]\u001b[A\n 35% 41/118 [00:04<00:08, 8.79it/s]\u001b[A\n 36% 42/118 [00:04<00:08, 8.79it/s]\u001b[A\n 36% 43/118 [00:04<00:08, 8.79it/s]\u001b[A\n 37% 44/118 [00:04<00:08, 8.81it/s]\u001b[A\n 38% 45/118 [00:05<00:08, 8.81it/s]\u001b[A\n 39% 46/118 [00:05<00:08, 8.81it/s]\u001b[A\n 40% 47/118 [00:05<00:08, 8.83it/s]\u001b[A\n 41% 48/118 [00:05<00:07, 8.84it/s]\u001b[A\n 42% 49/118 [00:05<00:07, 8.84it/s]\u001b[A\n 42% 50/118 [00:05<00:07, 8.84it/s]\u001b[A\n 43% 51/118 [00:05<00:07, 8.84it/s]\u001b[A\n 44% 52/118 [00:05<00:07, 8.83it/s]\u001b[A\n 45% 53/118 [00:05<00:07, 8.83it/s]\u001b[A\n 46% 54/118 [00:06<00:07, 8.80it/s]\u001b[A\n 47% 55/118 [00:06<00:07, 8.79it/s]\u001b[A\n 47% 56/118 [00:06<00:07, 8.79it/s]\u001b[A\n 48% 57/118 [00:06<00:06, 8.80it/s]\u001b[A\n 49% 58/118 [00:06<00:06, 8.80it/s]\u001b[A\n 50% 59/118 [00:06<00:06, 8.79it/s]\u001b[A\n 51% 60/118 [00:06<00:06, 8.76it/s]\u001b[A\n 52% 61/118 [00:06<00:06, 8.74it/s]\u001b[A\n 53% 62/118 [00:06<00:06, 8.75it/s]\u001b[A\n 53% 63/118 [00:07<00:06, 8.75it/s]\u001b[A\n 54% 64/118 [00:07<00:06, 8.77it/s]\u001b[A\n 55% 65/118 [00:07<00:06, 8.79it/s]\u001b[A\n 56% 66/118 [00:07<00:05, 8.80it/s]\u001b[A\n 57% 67/118 [00:07<00:05, 8.79it/s]\u001b[A\n 58% 68/118 [00:07<00:05, 8.77it/s]\u001b[A\n 58% 69/118 [00:07<00:05, 8.75it/s]\u001b[A\n 59% 70/118 [00:07<00:05, 8.77it/s]\u001b[A\n 60% 71/118 [00:08<00:05, 8.76it/s]\u001b[A\n 61% 72/118 [00:08<00:05, 8.78it/s]\u001b[A\n 62% 73/118 [00:08<00:05, 8.77it/s]\u001b[A\n 63% 74/118 [00:08<00:05, 8.77it/s]\u001b[A\n 64% 75/118 [00:08<00:04, 8.78it/s]\u001b[A\n 64% 76/118 [00:08<00:04, 8.76it/s]\u001b[A\n 65% 77/118 [00:08<00:04, 8.77it/s]\u001b[A\n 66% 78/118 [00:08<00:04, 8.78it/s]\u001b[A\n 67% 79/118 [00:08<00:04, 8.79it/s]\u001b[A\n 68% 80/118 [00:09<00:04, 8.80it/s]\u001b[A\n 69% 81/118 [00:09<00:04, 8.79it/s]\u001b[A\n 69% 82/118 [00:09<00:04, 8.77it/s]\u001b[A\n 70% 83/118 [00:09<00:03, 8.77it/s]\u001b[A\n 71% 84/118 [00:09<00:03, 8.74it/s]\u001b[A\n 72% 85/118 [00:09<00:03, 8.73it/s]\u001b[A\n 73% 86/118 [00:09<00:03, 8.74it/s]\u001b[A\n 74% 87/118 [00:09<00:03, 8.74it/s]\u001b[A\n 75% 88/118 [00:09<00:03, 8.77it/s]\u001b[A\n 75% 89/118 [00:10<00:03, 8.78it/s]\u001b[A\n 76% 90/118 [00:10<00:03, 8.77it/s]\u001b[A\n 77% 91/118 [00:10<00:03, 8.78it/s]\u001b[A\n 78% 92/118 [00:10<00:02, 8.77it/s]\u001b[A\n 79% 93/118 [00:10<00:02, 8.77it/s]\u001b[A\n 80% 94/118 [00:10<00:02, 8.77it/s]\u001b[A\n 81% 95/118 [00:10<00:02, 8.76it/s]\u001b[A\n 81% 96/118 [00:10<00:02, 8.74it/s]\u001b[A\n 82% 97/118 [00:10<00:02, 8.76it/s]\u001b[A\n 83% 98/118 [00:11<00:02, 8.79it/s]\u001b[A\n 84% 99/118 [00:11<00:02, 8.80it/s]\u001b[A\n 85% 100/118 [00:11<00:02, 8.80it/s]\u001b[A\n 86% 101/118 [00:11<00:01, 8.79it/s]\u001b[A\n 86% 102/118 [00:11<00:01, 8.78it/s]\u001b[A\n 87% 103/118 [00:11<00:01, 8.77it/s]\u001b[A\n 88% 104/118 [00:11<00:01, 8.77it/s]\u001b[A\n 89% 105/118 [00:11<00:01, 8.77it/s]\u001b[A\n 90% 106/118 [00:11<00:01, 8.76it/s]\u001b[A\n 91% 107/118 [00:12<00:01, 8.77it/s]\u001b[A\n 92% 108/118 [00:12<00:01, 8.79it/s]\u001b[A\n 92% 109/118 [00:12<00:01, 8.80it/s]\u001b[A\n 93% 110/118 [00:12<00:00, 8.79it/s]\u001b[A\n 94% 111/118 [00:12<00:00, 8.79it/s]\u001b[A\n 95% 112/118 [00:12<00:00, 8.79it/s]\u001b[A\n 96% 113/118 [00:12<00:00, 8.78it/s]\u001b[A\n 97% 114/118 [00:12<00:00, 8.78it/s]\u001b[A\n 97% 115/118 [00:13<00:00, 8.76it/s]\u001b[A\n 98% 116/118 [00:13<00:00, 8.77it/s]\u001b[A\n 99% 117/118 [00:13<00:00, 8.78it/s]\u001b[A\n119it [00:14, 3.47it/s] \u001b[A\n120it [00:14, 4.27it/s]\u001b[A\n121it [00:14, 5.12it/s]\u001b[A\n122it [00:14, 5.87it/s]\u001b[A\n123it [00:15, 6.48it/s]\u001b[A\n124it [00:15, 6.98it/s]\u001b[A\n125it [00:15, 7.39it/s]\u001b[A\n126it [00:15, 7.74it/s]\u001b[A\n127it [00:15, 8.03it/s]\u001b[A\n128it [00:15, 8.25it/s]\u001b[A\n129it [00:15, 8.40it/s]\u001b[A\n130it [00:15, 8.49it/s]\u001b[A\n131it [00:16, 8.58it/s]\u001b[A\n132it [00:16, 8.64it/s]\u001b[A\n133it [00:16, 8.68it/s]\u001b[A\n134it [00:16, 8.72it/s]\u001b[A\n135it [00:16, 8.74it/s]\u001b[A\n136it [00:16, 8.75it/s]\u001b[A\n137it [00:16, 8.77it/s]\u001b[A\n138it [00:16, 8.77it/s]\u001b[A\n139it [00:16, 8.79it/s]\u001b[A\n140it [00:17, 8.76it/s]\u001b[A\n141it [00:17, 8.73it/s]\u001b[A\n142it [00:17, 8.76it/s]\u001b[A\n143it [00:17, 8.77it/s]\u001b[A\n144it [00:17, 8.73it/s]\u001b[A\n145it [00:17, 8.71it/s]\u001b[A\n146it [00:17, 8.72it/s]\u001b[A\n147it [00:17, 8.70it/s]\u001b[A\n148it [00:17, 8.71it/s]\u001b[A\n149it [00:18, 8.73it/s]\u001b[A\n150it [00:18, 8.76it/s]\u001b[A\n151it [00:18, 8.77it/s]\u001b[A\n152it [00:18, 8.75it/s]\u001b[A\n153it [00:18, 8.76it/s]\u001b[A\n154it [00:18, 8.77it/s]\u001b[A\n155it [00:18, 8.79it/s]\u001b[A\n156it [00:18, 8.78it/s]\u001b[A\n157it [00:18, 8.75it/s]\u001b[A\n158it [00:19, 8.75it/s]\u001b[A\n159it [00:19, 8.77it/s]\u001b[A\n160it [00:19, 8.79it/s]\u001b[A\n161it [00:19, 8.80it/s]\u001b[A\n162it [00:19, 8.81it/s]\u001b[A\n163it [00:19, 8.79it/s]\u001b[A\n164it [00:19, 8.79it/s]\u001b[A\n165it [00:19, 8.78it/s]\u001b[A\n166it [00:19, 8.79it/s]\u001b[A\n167it [00:20, 8.80it/s]\u001b[A\n168it [00:20, 8.81it/s]\u001b[A\n169it [00:20, 8.81it/s]\u001b[A\n170it [00:20, 8.82it/s]\u001b[A\n171it [00:20, 8.81it/s]\u001b[A\n172it [00:20, 8.79it/s]\u001b[A\n173it [00:20, 8.81it/s]\u001b[A\n174it [00:20, 8.80it/s]\u001b[A\n175it [00:21, 8.77it/s]\u001b[A\n176it [00:21, 8.79it/s]\u001b[A\n177it [00:21, 8.80it/s]\u001b[A\n178it [00:21, 8.79it/s]\u001b[A\n179it [00:21, 8.80it/s]\u001b[A\n180it [00:21, 8.78it/s]\u001b[A\n181it [00:21, 8.78it/s]\u001b[A\n182it [00:21, 8.79it/s]\u001b[A\n183it [00:21, 8.76it/s]\u001b[A\n184it [00:22, 8.76it/s]\u001b[A\n185it [00:22, 8.76it/s]\u001b[A\n186it [00:22, 8.78it/s]\u001b[A\n187it [00:22, 8.73it/s]\u001b[A\n188it [00:22, 8.72it/s]\u001b[A\n189it [00:22, 8.70it/s]\u001b[A\n190it [00:22, 8.73it/s]\u001b[A\n191it [00:22, 8.73it/s]\u001b[A\n192it [00:22, 8.75it/s]\u001b[A\n193it [00:23, 8.75it/s]\u001b[A\n194it [00:23, 8.71it/s]\u001b[A\n195it [00:23, 8.69it/s]\u001b[A\n196it [00:23, 8.66it/s]\u001b[A\n197it [00:23, 8.70it/s]\u001b[A\n198it [00:23, 8.72it/s]\u001b[A\n199it [00:23, 8.73it/s]\u001b[A\n200it [00:23, 8.73it/s]\u001b[A\n201it [00:23, 8.73it/s]\u001b[A\n202it [00:24, 8.76it/s]\u001b[A\n203it [00:24, 8.78it/s]\u001b[A\n204it [00:24, 8.79it/s]\u001b[A\n205it [00:24, 8.80it/s]\u001b[A\n206it [00:24, 8.79it/s]\u001b[A\n207it [00:24, 8.78it/s]\u001b[A\n208it [00:24, 8.78it/s]\u001b[A\n209it [00:24, 8.76it/s]\u001b[A\n210it [00:25, 8.75it/s]\u001b[A\n211it [00:25, 8.75it/s]\u001b[A\n212it [00:25, 8.77it/s]\u001b[A\n213it [00:25, 8.79it/s]\u001b[A\n214it [00:25, 8.80it/s]\u001b[A\n215it [00:25, 8.81it/s]\u001b[A\n216it [00:25, 8.82it/s]\u001b[A\n217it [00:25, 8.81it/s]\u001b[A\n218it [00:25, 8.81it/s]\u001b[A\n219it [00:26, 8.81it/s]\u001b[A\n220it [00:26, 8.80it/s]\u001b[A\n221it [00:26, 8.80it/s]\u001b[A\n222it [00:26, 8.79it/s]\u001b[A\n223it [00:26, 8.80it/s]\u001b[A\n224it [00:26, 8.81it/s]\u001b[A\n225it [00:26, 8.81it/s]\u001b[A\n226it [00:26, 8.82it/s]\u001b[A\n227it [00:26, 8.82it/s]\u001b[A\n228it [00:27, 8.82it/s]\u001b[A\n229it [00:27, 8.82it/s]\u001b[A\n230it [00:27, 8.83it/s]\u001b[A\n231it [00:27, 8.84it/s]\u001b[A\n232it [00:27, 8.84it/s]\u001b[A\n233it [00:27, 8.84it/s]\u001b[A\n234it [00:27, 8.84it/s]\u001b[A\n235it [00:27, 8.83it/s]\u001b[A\n236it [00:27, 8.83it/s]\u001b[A\n237it [00:28, 8.83it/s]\u001b[A\n238it [00:28, 8.83it/s]\u001b[A\n239it [00:28, 8.83it/s]\u001b[A\n240it [00:28, 8.84it/s]\u001b[A\n241it [00:28, 8.83it/s]\u001b[A\n242it [00:28, 8.83it/s]\u001b[A\n243it [00:28, 8.83it/s]\u001b[A\n244it [00:28, 8.82it/s]\u001b[A\n245it [00:28, 8.80it/s]\u001b[A\n246it [00:29, 8.81it/s]\u001b[A\n247it [00:29, 8.81it/s]\u001b[A\n248it [00:29, 8.81it/s]\u001b[A\n249it [00:29, 8.81it/s]\u001b[A\n250it [00:29, 8.81it/s]\u001b[A\n251it [00:29, 8.80it/s]\u001b[A\n252it [00:29, 8.79it/s]\u001b[A\n253it [00:29, 8.78it/s]\u001b[A\n254it [00:30, 8.78it/s]\u001b[A\n255it [00:30, 8.78it/s]\u001b[A\n256it [00:30, 8.78it/s]\u001b[A\n257it [00:30, 8.80it/s]\u001b[A\n258it [00:30, 8.81it/s]\u001b[A\n259it [00:30, 8.82it/s]\u001b[A\n260it [00:30, 8.81it/s]\u001b[A\n261it [00:30, 8.79it/s]\u001b[A\n262it [00:30, 8.79it/s]\u001b[A\n263it [00:31, 8.79it/s]\u001b[A\n264it [00:31, 8.80it/s]\u001b[A\n265it [00:31, 8.81it/s]\u001b[A\n266it [00:31, 8.82it/s]\u001b[A\n267it [00:31, 8.81it/s]\u001b[A\n268it [00:31, 8.81it/s]\u001b[A\n269it [00:31, 8.80it/s]\u001b[A\n270it [00:31, 8.80it/s]\u001b[A\n271it [00:31, 8.80it/s]\u001b[A\n272it [00:32, 8.81it/s]\u001b[A\n273it [00:32, 8.81it/s]\u001b[A\n274it [00:32, 8.82it/s]\u001b[A\n275it [00:32, 8.81it/s]\u001b[A\n276it [00:32, 8.82it/s]\u001b[A\n277it [00:32, 8.82it/s]\u001b[A\n278it [00:32, 8.77it/s]\u001b[A\n279it [00:32, 8.72it/s]\u001b[A\n280it [00:32, 8.70it/s]\u001b[A\n281it [00:33, 8.73it/s]\u001b[A\n282it [00:33, 8.75it/s]\u001b[A\n283it [00:33, 8.77it/s]\u001b[A\n284it [00:33, 8.79it/s]\u001b[A\n285it [00:33, 8.80it/s]\u001b[A\n286it [00:33, 8.81it/s]\u001b[A\n287it [00:33, 8.81it/s]\u001b[A\n288it [00:33, 8.81it/s]\u001b[A\n289it [00:33, 8.81it/s]\u001b[A\n290it [00:34, 8.81it/s]\u001b[A\n291it [00:34, 8.81it/s]\u001b[A\n292it [00:34, 8.80it/s]\u001b[A\n293it [00:34, 8.81it/s]\u001b[A\n294it [00:34, 8.82it/s]\u001b[A\n295it [00:34, 8.81it/s]\u001b[A\n296it [00:34, 8.81it/s]\u001b[A\n297it [00:34, 8.82it/s]\u001b[A\n298it [00:35, 8.82it/s]\u001b[A\n299it [00:35, 8.82it/s]\u001b[A\n300it [00:35, 8.82it/s]\u001b[A\n301it [00:35, 8.80it/s]\u001b[A\n302it [00:35, 8.80it/s]\u001b[A\n303it [00:35, 8.79it/s]\u001b[A\n304it [00:35, 8.79it/s]\u001b[A\n305it [00:35, 8.79it/s]\u001b[A\n306it [00:35, 8.79it/s]\u001b[A\n307it [00:36, 8.80it/s]\u001b[A\n308it [00:36, 8.82it/s]\u001b[A\n309it [00:36, 8.81it/s]\u001b[A\n310it [00:36, 8.82it/s]\u001b[A\n311it [00:36, 8.82it/s]\u001b[A\n312it [00:36, 8.82it/s]\u001b[A\n313it [00:36, 8.81it/s]\u001b[A\n314it [00:36, 8.80it/s]\u001b[A\n315it [00:36, 8.79it/s]\u001b[A\n316it [00:37, 8.79it/s]\u001b[A\n317it [00:37, 8.78it/s]\u001b[A\n318it [00:37, 8.79it/s]\u001b[A\n319it [00:37, 8.80it/s]\u001b[A\n320it [00:37, 8.80it/s]\u001b[A\n321it [00:37, 8.79it/s]\u001b[A\n322it [00:37, 8.76it/s]\u001b[A\n323it [00:37, 8.76it/s]\u001b[A\n324it [00:37, 8.78it/s]\u001b[A\n325it [00:38, 8.78it/s]\u001b[A\n326it [00:38, 8.78it/s]\u001b[A\n327it [00:38, 8.78it/s]\u001b[A\n328it [00:38, 8.78it/s]\u001b[A\n329it [00:38, 8.79it/s]\u001b[A\n330it [00:38, 8.79it/s]\u001b[A\n331it [00:38, 8.79it/s]\u001b[A\n332it [00:38, 8.80it/s]\u001b[A\n333it [00:38, 8.79it/s]\u001b[A\n334it [00:39, 8.80it/s]\u001b[A\n335it [00:39, 8.80it/s]\u001b[A\n336it [00:39, 8.79it/s]\u001b[A\n337it [00:39, 8.79it/s]\u001b[A\n338it [00:39, 8.80it/s]\u001b[A\n339it [00:39, 8.81it/s]\u001b[A\n340it [00:39, 8.81it/s]\u001b[A\n341it [00:39, 8.81it/s]\u001b[A\n342it [00:40, 8.80it/s]\u001b[A\n343it [00:40, 8.80it/s]\u001b[A\n344it [00:40, 8.79it/s]\u001b[A\n345it [00:40, 8.79it/s]\u001b[A\n346it [00:40, 8.79it/s]\u001b[A\n347it [00:40, 8.79it/s]\u001b[A\n348it [00:40, 8.79it/s]\u001b[A\n349it [00:40, 8.80it/s]\u001b[A\n350it [00:40, 8.80it/s]\u001b[A\n351it [00:41, 8.80it/s]\u001b[A\n352it [00:41, 8.80it/s]\u001b[A\n353it [00:41, 8.81it/s]\u001b[A\n354it [00:41, 8.81it/s]\u001b[A\n355it [00:41, 8.81it/s]\u001b[A\n356it [00:41, 8.80it/s]\u001b[A\n357it [00:41, 8.80it/s]\u001b[A\n358it [00:41, 8.79it/s]\u001b[A\n359it [00:41, 8.79it/s]\u001b[A\n360it [00:42, 8.79it/s]\u001b[A\n361it [00:42, 8.80it/s]\u001b[A\n362it [00:42, 8.80it/s]\u001b[A\n363it [00:42, 8.80it/s]\u001b[A\n364it [00:42, 8.79it/s]\u001b[A\n365it [00:42, 8.78it/s]\u001b[A\n366it [00:42, 8.78it/s]\u001b[A\n367it [00:42, 8.79it/s]\u001b[A\n368it [00:42, 8.79it/s]\u001b[A\n369it [00:43, 8.80it/s]\u001b[A\n370it [00:43, 8.80it/s]\u001b[A\n371it [00:43, 8.81it/s]\u001b[A\n372it [00:43, 8.81it/s]\u001b[A\n373it [00:43, 8.80it/s]\u001b[A\n374it [00:43, 8.80it/s]\u001b[A\n375it [00:43, 8.80it/s]\u001b[A\n376it [00:43, 8.81it/s]\u001b[A\n377it [00:43, 8.80it/s]\u001b[A\n378it [00:44, 8.79it/s]\u001b[A\n379it [00:44, 8.77it/s]\u001b[A\n380it [00:44, 8.78it/s]\u001b[A\n381it [00:44, 8.77it/s]\u001b[A\n382it [00:44, 8.78it/s]\u001b[A\n383it [00:44, 8.79it/s]\u001b[A\n384it [00:44, 8.79it/s]\u001b[A\n385it [00:44, 8.79it/s]\u001b[A\n386it [00:45, 8.79it/s]\u001b[A\n387it [00:45, 8.80it/s]\u001b[A\n388it [00:45, 8.80it/s]\u001b[A\n389it [00:45, 8.80it/s]\u001b[A\n390it [00:45, 8.81it/s]\u001b[A\n391it [00:45, 8.81it/s]\u001b[A\n392it [00:45, 8.80it/s]\u001b[A\n393it [00:45, 8.79it/s]\u001b[A\n394it [00:45, 8.79it/s]\u001b[A\n395it [00:46, 8.78it/s]\u001b[A\n396it [00:46, 8.80it/s]\u001b[A\n397it [00:46, 8.80it/s]\u001b[A\n398it [00:46, 8.80it/s]\u001b[A\n399it [00:46, 8.80it/s]\u001b[A\n400it [00:46, 8.80it/s]\u001b[A\n401it [00:46, 8.79it/s]\u001b[A\n402it [00:46, 8.78it/s]\u001b[A\n403it [00:46, 8.79it/s]\u001b[A\n404it [00:47, 8.79it/s]\u001b[A\n405it [00:47, 8.80it/s]\u001b[A\n406it [00:47, 8.80it/s]\u001b[A\n407it [00:47, 8.80it/s]\u001b[A\n408it [00:47, 8.80it/s]\u001b[A\n409it [00:47, 8.79it/s]\u001b[A\n410it [00:47, 8.78it/s]\u001b[A\n411it [00:47, 8.79it/s]\u001b[A\n412it [00:47, 8.79it/s]\u001b[A\n413it [00:48, 8.80it/s]\u001b[A\n414it [00:48, 8.81it/s]\u001b[A\n415it [00:48, 8.81it/s]\u001b[A\n416it [00:48, 8.81it/s]\u001b[A\n417it [00:48, 8.81it/s]\u001b[A\n418it [00:48, 8.80it/s]\u001b[A\n419it [00:48, 8.80it/s]\u001b[A\n420it [00:48, 8.81it/s]\u001b[A\n421it [00:48, 8.80it/s]\u001b[A\n422it [00:49, 8.79it/s]\u001b[A\n423it [00:49, 8.79it/s]\u001b[A\n424it [00:49, 8.78it/s]\u001b[A\n425it [00:49, 8.77it/s]\u001b[A\n426it [00:49, 8.77it/s]\u001b[A\n427it [00:49, 8.77it/s]\u001b[A\n428it [00:49, 8.78it/s]\u001b[A\n429it [00:49, 8.78it/s]\u001b[A\n430it [00:50, 8.78it/s]\u001b[A\n431it [00:50, 8.79it/s]\u001b[A\n432it [00:50, 8.79it/s]\u001b[A\n433it [00:50, 8.79it/s]\u001b[A\n434it [00:50, 8.77it/s]\u001b[A\n435it [00:50, 8.75it/s]\u001b[A\n436it [00:50, 8.76it/s]\u001b[A\n437it [00:50, 8.77it/s]\u001b[A\n438it [00:50, 8.77it/s]\u001b[A\n439it [00:51, 8.78it/s]\u001b[A\n440it [00:51, 8.79it/s]\u001b[A\n441it [00:51, 8.80it/s]\u001b[A\n442it [00:51, 8.80it/s]\u001b[A\n443it [00:51, 8.79it/s]\u001b[A\n444it [00:51, 8.77it/s]\u001b[A\n445it [00:51, 8.78it/s]\u001b[A\n446it [00:51, 8.79it/s]\u001b[A\n447it [00:51, 8.79it/s]\u001b[A\n448it [00:52, 8.78it/s]\u001b[A\n449it [00:52, 8.78it/s]\u001b[A\n450it [00:52, 8.78it/s]\u001b[A\n451it [00:52, 8.79it/s]\u001b[A\n452it [00:52, 8.79it/s]\u001b[A\n453it [00:52, 8.79it/s]\u001b[A\n454it [00:52, 8.79it/s]\u001b[A\n455it [00:52, 8.79it/s]\u001b[A\n456it [00:52, 8.77it/s]\u001b[A\n457it [00:53, 8.78it/s]\u001b[A\n458it [00:53, 8.78it/s]\u001b[A\n459it [00:53, 8.79it/s]\u001b[A\n460it [00:53, 8.80it/s]\u001b[A\n461it [00:53, 8.79it/s]\u001b[A\n462it [00:53, 8.79it/s]\u001b[A\n463it [00:53, 8.78it/s]\u001b[A\n464it [00:53, 8.79it/s]\u001b[A\n465it [00:54, 8.79it/s]\u001b[A\n466it [00:54, 8.79it/s]\u001b[A\n467it [00:54, 8.80it/s]\u001b[A\n468it [00:54, 8.79it/s]\u001b[A\n469it [00:54, 8.80it/s]\u001b[A\n470it [00:54, 8.81it/s]\u001b[A\n471it [00:54, 8.80it/s]\u001b[A\n472it [00:54, 8.81it/s]\u001b[A\n473it [00:54, 8.81it/s]\u001b[A\n474it [00:55, 8.80it/s]\u001b[A\n475it [00:55, 8.80it/s]\u001b[A\n476it [00:55, 8.80it/s]\u001b[A\n477it [00:55, 8.80it/s]\u001b[A\n478it [00:55, 8.78it/s]\u001b[A\n479it [00:55, 8.78it/s]\u001b[A\n480it [00:55, 8.78it/s]\u001b[A\n481it [00:55, 8.78it/s]\u001b[A\n482it [00:55, 8.78it/s]\u001b[A\n483it [00:56, 8.78it/s]\u001b[A\n484it [00:56, 8.79it/s]\u001b[A\n485it [00:56, 8.79it/s]\u001b[A\n486it [00:56, 8.79it/s]\u001b[A\n487it [00:56, 8.79it/s]\u001b[A\n488it [00:56, 8.80it/s]\u001b[A\n489it [00:56, 8.80it/s]\u001b[A\n490it [00:56, 8.80it/s]\u001b[A\n491it [00:56, 8.80it/s]\u001b[A\n492it [00:57, 8.80it/s]\u001b[A\n493it [00:57, 8.79it/s]\u001b[A\n494it [00:57, 8.80it/s]\u001b[A\n495it [00:57, 8.80it/s]\u001b[A\n496it [00:57, 8.80it/s]\u001b[A\n497it [00:57, 8.80it/s]\u001b[A\n498it [00:57, 8.80it/s]\u001b[A\n499it [00:57, 8.79it/s]\u001b[A\n500it [00:57, 8.80it/s]\u001b[A\n501it [00:58, 8.79it/s]\u001b[A\n502it [00:58, 8.78it/s]\u001b[A\n503it [00:58, 8.79it/s]\u001b[A\n504it [00:58, 8.81it/s]\u001b[A\n505it [00:58, 8.81it/s]\u001b[A\n506it [00:58, 8.82it/s]\u001b[A\n507it [00:58, 8.81it/s]\u001b[A\n508it [00:58, 8.82it/s]\u001b[A\n509it [00:59, 8.83it/s]\u001b[A\n510it [00:59, 8.80it/s]\u001b[A\n511it [00:59, 8.82it/s]\u001b[A\n512it [00:59, 8.82it/s]\u001b[A\n513it [00:59, 8.82it/s]\u001b[A\n514it [00:59, 8.83it/s]\u001b[A\n515it [00:59, 8.83it/s]\u001b[A\n516it [00:59, 8.82it/s]\u001b[A\n517it [00:59, 8.82it/s]\u001b[A\n518it [01:00, 8.82it/s]\u001b[A\n519it [01:00, 8.82it/s]\u001b[A\n520it [01:00, 8.82it/s]\u001b[A\n521it [01:00, 8.82it/s]\u001b[A\n522it [01:00, 8.82it/s]\u001b[A\n523it [01:00, 8.82it/s]\u001b[A\n524it [01:00, 8.82it/s]\u001b[A\n525it [01:00, 8.82it/s]\u001b[A\n526it [01:00, 8.81it/s]\u001b[A\n527it [01:01, 8.81it/s]\u001b[A\n528it [01:01, 8.81it/s]\u001b[A\n529it [01:01, 8.82it/s]\u001b[A\n530it [01:01, 8.83it/s]\u001b[A\n531it [01:01, 8.83it/s]\u001b[A\n532it [01:01, 8.84it/s]\u001b[A\n533it [01:01, 8.84it/s]\u001b[A\n534it [01:01, 8.84it/s]\u001b[A\n535it [01:01, 8.84it/s]\u001b[A\n536it [01:02, 8.83it/s]\u001b[A\n537it [01:02, 8.83it/s]\u001b[A\n538it [01:02, 8.83it/s]\u001b[A\n539it [01:02, 8.82it/s]\u001b[A\n540it [01:02, 8.82it/s]\u001b[A\n541it [01:02, 8.82it/s]\u001b[A\n542it [01:02, 8.81it/s]\u001b[A\n543it [01:02, 8.79it/s]\u001b[A\n544it [01:02, 8.79it/s]\u001b[A\n545it [01:03, 8.79it/s]\u001b[A\n546it [01:03, 8.80it/s]\u001b[A\n547it [01:03, 8.81it/s]\u001b[A\n548it [01:03, 8.81it/s]\u001b[A\n549it [01:03, 8.82it/s]\u001b[A\n550it [01:03, 8.82it/s]\u001b[A\n551it [01:03, 8.82it/s]\u001b[A\n552it [01:03, 8.83it/s]\u001b[A\n553it [01:03, 8.82it/s]\u001b[A\n554it [01:04, 8.83it/s]\u001b[A\n555it [01:04, 8.82it/s]\u001b[A\n556it [01:04, 8.83it/s]\u001b[A\n557it [01:04, 8.82it/s]\u001b[A\n558it [01:04, 8.82it/s]\u001b[A\n559it [01:04, 8.82it/s]\u001b[A\n560it [01:04, 8.82it/s]\u001b[A\n561it [01:04, 8.82it/s]\u001b[A\n562it [01:05, 8.82it/s]\u001b[A\n563it [01:05, 8.82it/s]\u001b[A\n564it [01:05, 8.82it/s]\u001b[A\n565it [01:05, 8.82it/s]\u001b[A\n566it [01:05, 8.82it/s]\u001b[A\n567it [01:05, 8.82it/s]\u001b[A\n568it [01:05, 8.81it/s]\u001b[A\n569it [01:05, 8.80it/s]\u001b[A\n570it [01:05, 8.79it/s]\u001b[A\n571it [01:06, 8.79it/s]\u001b[A\n572it [01:06, 8.79it/s]\u001b[A\n573it [01:06, 8.79it/s]\u001b[A\n574it [01:06, 8.80it/s]\u001b[A\n575it [01:06, 8.81it/s]\u001b[A\n576it [01:06, 8.82it/s]\u001b[A\n577it [01:06, 8.81it/s]\u001b[A\n578it [01:06, 8.81it/s]\u001b[A\n579it [01:06, 8.80it/s]\u001b[A\n580it [01:07, 8.79it/s]\u001b[A\n581it [01:07, 8.80it/s]\u001b[A\n582it [01:07, 8.81it/s]\u001b[A\n583it [01:07, 8.81it/s]\u001b[A\n584it [01:07, 8.82it/s]\u001b[A\n585it [01:07, 8.82it/s]\u001b[A\n586it [01:07, 8.81it/s]\u001b[A\n587it [01:07, 8.79it/s]\u001b[A\n588it [01:07, 8.78it/s]\u001b[A\n589it [01:08, 8.78it/s]\u001b[A\n590it [01:08, 8.78it/s]\u001b[A\n591it [01:08, 8.78it/s]\u001b[A\n592it [01:08, 8.78it/s]\u001b[A\n593it [01:08, 8.79it/s]\u001b[A\n594it [01:08, 8.78it/s]\u001b[A\n595it [01:08, 8.79it/s]\u001b[A\n596it [01:08, 8.80it/s]\u001b[A\n597it [01:08, 8.80it/s]\u001b[A\n598it [01:09, 8.80it/s]\u001b[A\n599it [01:09, 8.79it/s]\u001b[A\n600it [01:09, 8.80it/s]\u001b[A\n601it [01:09, 8.79it/s]\u001b[A\n602it [01:09, 8.80it/s]\u001b[A\n603it [01:09, 8.79it/s]\u001b[A\n604it [01:09, 8.80it/s]\u001b[A\n605it [01:09, 8.81it/s]\u001b[A\n606it [01:10, 8.82it/s]\u001b[A\n607it [01:10, 8.82it/s]\u001b[A\n608it [01:10, 8.81it/s]\u001b[A\n609it [01:10, 8.81it/s]\u001b[A\n610it [01:10, 8.81it/s]\u001b[A\n611it [01:10, 8.79it/s]\u001b[A\n612it [01:10, 8.80it/s]\u001b[A\n613it [01:10, 8.80it/s]\u001b[A\n614it [01:10, 8.81it/s]\u001b[A\n615it [01:11, 8.82it/s]\u001b[A\n616it [01:11, 8.82it/s]\u001b[A\n617it [01:11, 8.83it/s]\u001b[A\n618it [01:11, 8.82it/s]\u001b[A\n619it [01:11, 8.82it/s]\u001b[A\n620it [01:11, 8.82it/s]\u001b[A\n621it [01:11, 8.82it/s]\u001b[A\n622it [01:11, 8.82it/s]\u001b[A\n623it [01:11, 8.81it/s]\u001b[A\n624it [01:12, 8.81it/s]\u001b[A\n625it [01:12, 8.82it/s]\u001b[A\n626it [01:12, 8.82it/s]\u001b[A\n627it [01:12, 8.82it/s]\u001b[A\n628it [01:12, 8.82it/s]\u001b[A\n629it [01:12, 8.82it/s]\u001b[A\n630it [01:12, 8.83it/s]\u001b[A\n631it [01:12, 8.82it/s]\u001b[A\n632it [01:12, 8.80it/s]\u001b[A\n633it [01:13, 8.80it/s]\u001b[A\n634it [01:13, 8.80it/s]\u001b[A\n635it [01:13, 8.80it/s]\u001b[A\n636it [01:13, 8.81it/s]\u001b[A\n637it [01:13, 8.81it/s]\u001b[A\n638it [01:13, 8.82it/s]\u001b[A\n639it [01:13, 8.82it/s]\u001b[A\n640it [01:13, 8.81it/s]\u001b[A\n641it [01:13, 8.79it/s]\u001b[A\n642it [01:14, 8.79it/s]\u001b[A\n643it [01:14, 8.80it/s]\u001b[A\n644it [01:14, 8.81it/s]\u001b[A\n645it [01:14, 8.82it/s]\u001b[A\n646it [01:14, 8.82it/s]\u001b[A\n647it [01:14, 8.82it/s]\u001b[A\n648it [01:14, 8.82it/s]\u001b[A\n649it [01:14, 8.81it/s]\u001b[A\n650it [01:15, 8.79it/s]\u001b[A\n651it [01:15, 8.80it/s]\u001b[A\n652it [01:15, 8.81it/s]\u001b[A\n653it [01:15, 8.81it/s]\u001b[A\n654it [01:15, 8.82it/s]\u001b[A\n655it [01:15, 8.82it/s]\u001b[A\n656it [01:15, 8.82it/s]\u001b[A\n657it [01:15, 8.82it/s]\u001b[A\n658it [01:15, 8.81it/s]\u001b[A\n659it [01:16, 8.80it/s]\u001b[A\n660it [01:16, 8.80it/s]\u001b[A\n661it [01:16, 8.81it/s]\u001b[A\n662it [01:16, 8.82it/s]\u001b[A\n663it [01:16, 8.82it/s]\u001b[A\n664it [01:16, 8.82it/s]\u001b[A\n665it [01:16, 8.82it/s]\u001b[A\n666it [01:16, 8.82it/s]\u001b[A\n667it [01:16, 8.81it/s]\u001b[A\n668it [01:17, 8.78it/s]\u001b[A\n669it [01:17, 8.78it/s]\u001b[A\n670it [01:17, 8.78it/s]\u001b[A\n671it [01:17, 8.78it/s]\u001b[A\n672it [01:17, 8.78it/s]\u001b[A\n673it [01:17, 8.77it/s]\u001b[A\n674it [01:17, 8.78it/s]\u001b[A\n675it [01:17, 8.79it/s]\u001b[A\n676it [01:17, 8.80it/s]\u001b[A\n677it [01:18, 8.80it/s]\u001b[A\n678it [01:18, 8.81it/s]\u001b[A\n679it [01:18, 8.82it/s]\u001b[A\n680it [01:18, 8.81it/s]\u001b[A\n681it [01:18, 8.82it/s]\u001b[A\n682it [01:18, 8.81it/s]\u001b[A\n683it [01:18, 8.80it/s]\u001b[A\n684it [01:18, 8.80it/s]\u001b[A\n685it [01:18, 8.80it/s]\u001b[A\n686it [01:19, 8.80it/s]\u001b[A\n687it [01:19, 8.81it/s]\u001b[A\n688it [01:19, 8.81it/s]\u001b[A\n689it [01:19, 8.81it/s]\u001b[A\n690it [01:19, 8.81it/s]\u001b[A\n691it [01:19, 8.80it/s]\u001b[A\n692it [01:19, 8.81it/s]\u001b[A\n693it [01:19, 8.82it/s]\u001b[A\n694it [01:20, 8.82it/s]\u001b[A\n695it [01:20, 8.82it/s]\u001b[A\n696it [01:20, 8.82it/s]\u001b[A\n697it [01:20, 8.82it/s]\u001b[A\n698it [01:20, 8.82it/s]\u001b[A\n699it [01:20, 8.82it/s]\u001b[A\n700it [01:20, 8.82it/s]\u001b[A\n701it [01:20, 8.83it/s]\u001b[A\n702it [01:20, 8.82it/s]\u001b[A\n703it [01:21, 8.81it/s]\u001b[A\n704it [01:21, 8.81it/s]\u001b[A\n705it [01:21, 8.81it/s]\u001b[A\n706it [01:21, 8.82it/s]\u001b[A\n707it [01:21, 8.83it/s]\u001b[A\n708it [01:21, 8.83it/s]\u001b[A\n709it [01:21, 8.82it/s]\u001b[A\n710it [01:21, 8.82it/s]\u001b[A\n711it [01:21, 8.82it/s]\u001b[A\n712it [01:22, 8.82it/s]\u001b[A\n713it [01:22, 8.82it/s]\u001b[A\n714it [01:22, 8.83it/s]\u001b[A\n715it [01:22, 8.83it/s]\u001b[A\n716it [01:22, 8.83it/s]\u001b[A\n717it [01:22, 8.83it/s]\u001b[A\n719it [01:25, 2.21it/s]\u001b[A\n720it [01:25, 2.86it/s]\u001b[A\n721it [01:25, 3.61it/s]\u001b[A\n722it [01:25, 4.39it/s]\u001b[A\n723it [01:25, 5.17it/s]\u001b[A\n724it [01:25, 5.87it/s]\u001b[A\n725it [01:25, 6.50it/s]\u001b[A\n726it [01:25, 7.02it/s]\u001b[A\n727it [01:26, 7.44it/s]\u001b[A\n728it [01:26, 7.80it/s]\u001b[A\n729it [01:26, 8.07it/s]\u001b[A\n730it [01:26, 8.26it/s]\u001b[A\n731it [01:26, 8.42it/s]\u001b[A\n732it [01:26, 8.53it/s]\u001b[A\n733it [01:26, 8.60it/s]\u001b[A\n734it [01:26, 8.65it/s]\u001b[A\n735it [01:26, 8.67it/s]\u001b[A\n736it [01:27, 8.70it/s]\u001b[A\n737it [01:27, 8.73it/s]\u001b[A\n738it [01:27, 8.75it/s]\u001b[A\n739it [01:27, 8.77it/s]\u001b[A\n740it [01:27, 8.77it/s]\u001b[A\n741it [01:27, 8.78it/s]\u001b[A\n742it [01:27, 8.77it/s]\u001b[A\n743it [01:27, 8.75it/s]\u001b[A\n744it [01:27, 8.75it/s]\u001b[A\n745it [01:28, 8.75it/s]\u001b[A\n746it [01:28, 8.75it/s]\u001b[A\n747it [01:28, 8.77it/s]\u001b[A\n748it [01:28, 8.78it/s]\u001b[A\n749it [01:28, 8.78it/s]\u001b[A\n750it [01:28, 8.77it/s]\u001b[A\n751it [01:28, 8.78it/s]\u001b[A\n752it [01:28, 8.78it/s]\u001b[A\n753it [01:28, 8.79it/s]\u001b[A\n754it [01:29, 8.80it/s]\u001b[A\n755it [01:29, 8.81it/s]\u001b[A\n756it [01:29, 8.81it/s]\u001b[A\n757it [01:29, 8.81it/s]\u001b[A\n758it [01:29, 8.82it/s]\u001b[A\n759it [01:29, 8.82it/s]\u001b[A\n760it [01:29, 8.83it/s]\u001b[A\n761it [01:29, 8.83it/s]\u001b[A\n762it [01:29, 8.83it/s]\u001b[A\n763it [01:30, 8.83it/s]\u001b[A\n764it [01:30, 8.83it/s]\u001b[A\n765it [01:30, 8.84it/s]\u001b[A\n766it [01:30, 8.84it/s]\u001b[A\n767it [01:30, 8.83it/s]\u001b[A\n768it [01:30, 8.83it/s]\u001b[A\n769it [01:30, 8.82it/s]\u001b[A\n770it [01:30, 8.81it/s]\u001b[A\n771it [01:31, 8.81it/s]\u001b[A\n772it [01:31, 8.81it/s]\u001b[A\n773it [01:31, 8.82it/s]\u001b[A\n774it [01:31, 8.82it/s]\u001b[A\n775it [01:31, 8.82it/s]\u001b[A\n776it [01:31, 8.82it/s]\u001b[A\n777it [01:31, 8.80it/s]\u001b[A\n778it [01:31, 8.81it/s]\u001b[A\n779it [01:31, 8.80it/s]\u001b[A\n780it [01:32, 8.78it/s]\u001b[A\n781it [01:32, 8.78it/s]\u001b[A\n782it [01:32, 8.79it/s]\u001b[A\n783it [01:32, 8.80it/s]\u001b[A\n784it [01:32, 8.80it/s]\u001b[A\n785it [01:32, 8.80it/s]\u001b[A\n786it [01:32, 8.80it/s]\u001b[A\n787it [01:32, 8.80it/s]\u001b[A\n788it [01:32, 8.79it/s]\u001b[A\n789it [01:33, 8.79it/s]\u001b[A\n790it [01:33, 8.79it/s]\u001b[A\n791it [01:33, 8.79it/s]\u001b[A\n792it [01:33, 8.79it/s]\u001b[A\n793it [01:33, 8.80it/s]\u001b[A\n794it [01:33, 8.80it/s]\u001b[A\n795it [01:33, 8.81it/s]\u001b[A\n796it [01:33, 8.82it/s]\u001b[A\n797it [01:33, 8.81it/s]\u001b[A\n798it [01:34, 8.81it/s]\u001b[A\n799it [01:34, 8.81it/s]\u001b[A\n800it [01:34, 8.80it/s]\u001b[A\n801it [01:34, 8.81it/s]\u001b[A\n802it [01:34, 8.81it/s]\u001b[A\n803it [01:34, 8.81it/s]\u001b[A\n804it [01:34, 8.81it/s]\u001b[A\n805it [01:34, 8.82it/s]\u001b[A\n806it [01:34, 8.82it/s]\u001b[A\n807it [01:35, 8.81it/s]\u001b[A\n808it [01:35, 8.80it/s]\u001b[A\n809it [01:35, 8.80it/s]\u001b[A\n810it [01:35, 8.79it/s]\u001b[A\n811it [01:35, 8.79it/s]\u001b[A\n812it [01:35, 8.81it/s]\u001b[A\n813it [01:35, 8.81it/s]\u001b[A\n814it [01:35, 8.81it/s]\u001b[A\n815it [01:36, 8.80it/s]\u001b[A\n816it [01:36, 8.80it/s]\u001b[A\n817it [01:36, 8.80it/s]\u001b[A\n818it [01:36, 8.77it/s]\u001b[A\n819it [01:36, 8.77it/s]\u001b[A\n820it [01:36, 8.77it/s]\u001b[A\n821it [01:36, 8.77it/s]\u001b[A\n822it [01:36, 8.78it/s]\u001b[A\n823it [01:36, 8.77it/s]\u001b[A\n824it [01:37, 8.77it/s]\u001b[A\n825it [01:37, 8.78it/s]\u001b[A\n826it [01:37, 8.77it/s]\u001b[A\n827it [01:37, 8.76it/s]\u001b[A\n828it [01:37, 8.77it/s]\u001b[A\n829it [01:37, 8.78it/s]\u001b[A\n830it [01:37, 8.79it/s]\u001b[A\n831it [01:37, 8.79it/s]\u001b[A\n832it [01:37, 8.80it/s]\u001b[A\n833it [01:38, 8.79it/s]\u001b[A\n834it [01:38, 8.80it/s]\u001b[A\n835it [01:38, 8.81it/s]\u001b[A\n836it [01:38, 8.81it/s]\u001b[A\n837it [01:38, 8.82it/s]\u001b[A\n838it [01:38, 8.82it/s]\u001b[A\n839it [01:38, 8.80it/s]\u001b[A\n840it [01:38, 8.81it/s]\u001b[A\n841it [01:38, 8.81it/s]\u001b[A\n842it [01:39, 8.80it/s]\u001b[A\n843it [01:39, 8.82it/s]\u001b[A\n844it [01:39, 8.81it/s]\u001b[A\n845it [01:39, 8.80it/s]\u001b[A\n846it [01:39, 8.79it/s]\u001b[A\n847it [01:39, 8.78it/s]\u001b[A\n848it [01:39, 8.78it/s]\u001b[A\n849it [01:39, 8.79it/s]\u001b[A\n850it [01:39, 8.80it/s]\u001b[A\n851it [01:40, 8.80it/s]\u001b[A\n852it [01:40, 8.80it/s]\u001b[A\n853it [01:40, 8.79it/s]\u001b[A\n854it [01:40, 8.77it/s]\u001b[A\n855it [01:40, 8.78it/s]\u001b[A\n856it [01:40, 8.79it/s]\u001b[A\n857it [01:40, 8.80it/s]\u001b[A\n858it [01:40, 8.81it/s]\u001b[A\n859it [01:41, 8.82it/s]\u001b[A\n860it [01:41, 8.82it/s]\u001b[A\n861it [01:41, 8.82it/s]\u001b[A\n862it [01:41, 8.82it/s]\u001b[A\n863it [01:41, 8.83it/s]\u001b[A\n864it [01:41, 8.84it/s]\u001b[A\n865it [01:41, 8.83it/s]\u001b[A\n866it [01:41, 8.83it/s]\u001b[A\n867it [01:41, 8.82it/s]\u001b[A\n868it [01:42, 8.82it/s]\u001b[A\n869it [01:42, 8.81it/s]\u001b[A\n870it [01:42, 8.81it/s]\u001b[A\n871it [01:42, 8.80it/s]\u001b[A\n872it [01:42, 8.79it/s]\u001b[A\n873it [01:42, 8.78it/s]\u001b[A\n874it [01:42, 8.78it/s]\u001b[A\n875it [01:42, 8.78it/s]\u001b[A\n876it [01:42, 8.78it/s]\u001b[A\n877it [01:43, 8.80it/s]\u001b[A\n878it [01:43, 8.81it/s]\u001b[A\n879it [01:43, 8.80it/s]\u001b[A\n880it [01:43, 8.81it/s]\u001b[A\n881it [01:43, 8.80it/s]\u001b[A\n882it [01:43, 8.80it/s]\u001b[A\n883it [01:43, 8.80it/s]\u001b[A\n884it [01:43, 8.79it/s]\u001b[A\n885it [01:43, 8.79it/s]\u001b[A\n886it [01:44, 8.78it/s]\u001b[A\n887it [01:44, 8.80it/s]\u001b[A\n888it [01:44, 8.80it/s]\u001b[A\n889it [01:44, 8.81it/s]\u001b[A\n890it [01:44, 8.80it/s]\u001b[A\n891it [01:44, 8.80it/s]\u001b[A\n892it [01:44, 8.80it/s]\u001b[A\n893it [01:44, 8.81it/s]\u001b[A\n894it [01:44, 8.81it/s]\u001b[A\n895it [01:45, 8.81it/s]\u001b[A\n896it [01:45, 8.82it/s]\u001b[A\n897it [01:45, 8.83it/s]\u001b[A\n898it [01:45, 8.83it/s]\u001b[A\n899it [01:45, 8.81it/s]\u001b[A\n900it [01:45, 8.81it/s]\u001b[A\n901it [01:45, 8.81it/s]\u001b[A\n902it [01:45, 8.81it/s]\u001b[A\n903it [01:46, 8.82it/s]\u001b[A\n904it [01:46, 8.82it/s]\u001b[A\n905it [01:46, 8.83it/s]\u001b[A\n906it [01:46, 8.84it/s]\u001b[A\n907it [01:46, 8.83it/s]\u001b[A\n908it [01:46, 8.82it/s]\u001b[A\n909it [01:46, 8.81it/s]\u001b[A\n910it [01:46, 8.81it/s]\u001b[A\n911it [01:46, 8.82it/s]\u001b[A\n912it [01:47, 8.82it/s]\u001b[A\n913it [01:47, 8.82it/s]\u001b[A\n914it [01:47, 8.82it/s]\u001b[A\n915it [01:47, 8.82it/s]\u001b[A\n916it [01:47, 8.81it/s]\u001b[A\n917it [01:47, 8.80it/s]\u001b[A\n918it [01:47, 8.79it/s]\u001b[A\n919it [01:47, 8.79it/s]\u001b[A\n920it [01:47, 8.78it/s]\u001b[A\n921it [01:48, 8.79it/s]\u001b[A\n922it [01:48, 8.80it/s]\u001b[A\n923it [01:48, 8.80it/s]\u001b[A\n924it [01:48, 8.81it/s]\u001b[A\n925it [01:48, 8.81it/s]\u001b[A\n926it [01:48, 8.81it/s]\u001b[A\n927it [01:48, 8.80it/s]\u001b[A\n928it [01:48, 8.79it/s]\u001b[A\n929it [01:48, 8.79it/s]\u001b[A\n930it [01:49, 8.80it/s]\u001b[A\n931it [01:49, 8.81it/s]\u001b[A\n932it [01:49, 8.80it/s]\u001b[A\n933it [01:49, 8.81it/s]\u001b[A\n934it [01:49, 8.80it/s]\u001b[A\n935it [01:49, 8.80it/s]\u001b[A\n936it [01:49, 8.79it/s]\u001b[A\n937it [01:49, 8.79it/s]\u001b[A\n938it [01:49, 8.78it/s]\u001b[A\n939it [01:50, 8.79it/s]\u001b[A\n940it [01:50, 8.80it/s]\u001b[A\n941it [01:50, 8.81it/s]\u001b[A\n942it [01:50, 8.81it/s]\u001b[A\n943it [01:50, 8.80it/s]\u001b[A\n944it [01:50, 8.79it/s]\u001b[A\n945it [01:50, 8.79it/s]\u001b[A\n946it [01:50, 8.79it/s]\u001b[A\n947it [01:51, 8.80it/s]\u001b[A\n948it [01:51, 8.81it/s]\u001b[A\n949it [01:51, 8.81it/s]\u001b[A\n950it [01:51, 8.81it/s]\u001b[A\n951it [01:51, 8.81it/s]\u001b[A\n952it [01:51, 8.80it/s]\u001b[A\n953it [01:51, 8.80it/s]\u001b[A\n954it [01:51, 8.80it/s]\u001b[A\n955it [01:51, 8.81it/s]\u001b[A\n956it [01:52, 8.81it/s]\u001b[A\n957it [01:52, 8.82it/s]\u001b[A\n958it [01:52, 8.82it/s]\u001b[A\n959it [01:52, 8.81it/s]\u001b[A\n960it [01:52, 8.80it/s]\u001b[A\n961it [01:52, 8.78it/s]\u001b[A\n962it [01:52, 8.76it/s]\u001b[A\n963it [01:52, 8.78it/s]\u001b[A\n964it [01:52, 8.80it/s]\u001b[A\n965it [01:53, 8.80it/s]\u001b[A\n966it [01:53, 8.80it/s]\u001b[A\n967it [01:53, 8.80it/s]\u001b[A\n968it [01:53, 8.79it/s]\u001b[A\n969it [01:53, 8.78it/s]\u001b[A\n970it [01:53, 8.78it/s]\u001b[A\n971it [01:53, 8.79it/s]\u001b[A\n972it [01:53, 8.80it/s]\u001b[A\n973it [01:53, 8.81it/s]\u001b[A\n974it [01:54, 8.81it/s]\u001b[A\n975it [01:54, 8.81it/s]\u001b[A\n976it [01:54, 8.80it/s]\u001b[A\n977it [01:54, 8.80it/s]\u001b[A\n978it [01:54, 8.78it/s]\u001b[A\n979it [01:54, 8.78it/s]\u001b[A\n980it [01:54, 8.78it/s]\u001b[A\n981it [01:54, 8.80it/s]\u001b[A\n982it [01:54, 8.80it/s]\u001b[A\n983it [01:55, 8.81it/s]\u001b[A\n984it [01:55, 8.81it/s]\u001b[A\n985it [01:55, 8.80it/s]\u001b[A\n986it [01:55, 8.78it/s]\u001b[A\n987it [01:55, 8.78it/s]\u001b[A\n988it [01:55, 8.78it/s]\u001b[A\n989it [01:55, 8.79it/s]\u001b[A\n990it [01:55, 8.80it/s]\u001b[A\n991it [01:56, 8.80it/s]\u001b[A\n992it [01:56, 8.79it/s]\u001b[A\n993it [01:56, 8.79it/s]\u001b[A\n994it [01:56, 8.78it/s]\u001b[A\n995it [01:56, 8.78it/s]\u001b[A\n996it [01:56, 8.77it/s]\u001b[A\n997it [01:56, 8.78it/s]\u001b[A\n998it [01:56, 8.79it/s]\u001b[A\n999it [01:56, 8.81it/s]\u001b[A\n1000it [01:57, 8.79it/s]\u001b[A\n1001it [01:57, 8.80it/s]\u001b[A\n1002it [01:57, 8.81it/s]\u001b[A\n1003it [01:57, 8.81it/s]\u001b[A\n1004it [01:57, 8.82it/s]\u001b[A\n1005it [01:57, 8.81it/s]\u001b[A\n1006it [01:57, 8.80it/s]\u001b[A\n1007it [01:57, 8.79it/s]\u001b[A\n1008it [01:57, 8.78it/s]\u001b[A\n1009it [01:58, 8.78it/s]\u001b[A\n1010it [01:58, 8.79it/s]\u001b[A\n1011it [01:58, 8.81it/s]\u001b[A\n1012it [01:58, 8.82it/s]\u001b[A\n1013it [01:58, 8.83it/s]\u001b[A\n1014it [01:58, 8.83it/s]\u001b[A\n1015it [01:58, 8.83it/s]\u001b[A\n1016it [01:58, 8.82it/s]\u001b[A\n1017it [01:58, 8.83it/s]\u001b[A\n1018it [01:59, 8.82it/s]\u001b[A\n1019it [01:59, 8.82it/s]\u001b[A\n1020it [01:59, 8.83it/s]\u001b[A\n1021it [01:59, 8.83it/s]\u001b[A\n1022it [01:59, 8.82it/s]\u001b[A\n1023it [01:59, 8.82it/s]\u001b[A\n1024it [01:59, 8.80it/s]\u001b[A\n1025it [01:59, 8.80it/s]\u001b[A\n1026it [01:59, 8.80it/s]\u001b[A\n1027it [02:00, 8.81it/s]\u001b[A\n1028it [02:00, 8.81it/s]\u001b[A\n1029it [02:00, 8.83it/s]\u001b[A\n1030it [02:00, 8.83it/s]\u001b[A\n1031it [02:00, 8.83it/s]\u001b[A\n1032it [02:00, 8.83it/s]\u001b[A\n1033it [02:00, 8.84it/s]\u001b[A\n1034it [02:00, 8.84it/s]\u001b[A\n1035it [02:00, 8.82it/s]\u001b[A\n1036it [02:01, 8.82it/s]\u001b[A\n1037it [02:01, 8.83it/s]\u001b[A\n1038it [02:01, 8.83it/s]\u001b[A\n1039it [02:01, 8.82it/s]\u001b[A\n1040it [02:01, 8.82it/s]\u001b[A\n1041it [02:01, 8.82it/s]\u001b[A\n1042it [02:01, 8.81it/s]\u001b[A\n1043it [02:01, 8.81it/s]\u001b[A\n1044it [02:02, 8.81it/s]\u001b[A\n1045it [02:02, 8.81it/s]\u001b[A\n1046it [02:02, 8.81it/s]\u001b[A\n1047it [02:02, 8.81it/s]\u001b[A\n1048it [02:02, 8.82it/s]\u001b[A\n1049it [02:02, 8.82it/s]\u001b[A\n1050it [02:02, 8.83it/s]\u001b[A\n1051it [02:02, 8.83it/s]\u001b[A\n1052it [02:02, 8.82it/s]\u001b[A\n1053it [02:03, 8.80it/s]\u001b[A\n1054it [02:03, 8.79it/s]\u001b[A\n1055it [02:03, 8.78it/s]\u001b[A\n1056it [02:03, 8.79it/s]\u001b[A\n1057it [02:03, 8.80it/s]\u001b[A\n1058it [02:03, 8.81it/s]\u001b[A\n1059it [02:03, 8.82it/s]\u001b[A\n1060it [02:03, 8.81it/s]\u001b[A\n1061it [02:03, 8.81it/s]\u001b[A\n1062it [02:04, 8.80it/s]\u001b[A\n1063it [02:04, 8.79it/s]\u001b[A\n1064it [02:04, 8.80it/s]\u001b[A\n1065it [02:04, 8.81it/s]\u001b[A\n1066it [02:04, 8.81it/s]\u001b[A\n1067it [02:04, 8.81it/s]\u001b[A\n1068it [02:04, 8.80it/s]\u001b[A\n1069it [02:04, 8.79it/s]\u001b[A\n1070it [02:04, 8.79it/s]\u001b[A\n1071it [02:05, 8.80it/s]\u001b[A\n1072it [02:05, 8.81it/s]\u001b[A\n1073it [02:05, 8.81it/s]\u001b[A\n1074it [02:05, 8.80it/s]\u001b[A\n1075it [02:05, 8.81it/s]\u001b[A\n1076it [02:05, 8.81it/s]\u001b[A\n1077it [02:05, 8.82it/s]\u001b[A\n1078it [02:05, 8.82it/s]\u001b[A\n1079it [02:05, 8.82it/s]\u001b[A\n1080it [02:06, 8.82it/s]\u001b[A\n1081it [02:06, 8.83it/s]\u001b[A\n1082it [02:06, 8.83it/s]\u001b[A\n1083it [02:06, 8.84it/s]\u001b[A\n1084it [02:06, 8.84it/s]\u001b[A\n1085it [02:06, 8.84it/s]\u001b[A\n1086it [02:06, 8.84it/s]\u001b[A\n1087it [02:06, 8.84it/s]\u001b[A\n1088it [02:07, 8.83it/s]\u001b[A\n1089it [02:07, 8.82it/s]\u001b[A\n1090it [02:07, 8.82it/s]\u001b[A\n1091it [02:07, 8.82it/s]\u001b[A\n1092it [02:07, 8.83it/s]\u001b[A\n1093it [02:07, 8.81it/s]\u001b[A\n1094it [02:07, 8.82it/s]\u001b[A\n1095it [02:07, 8.82it/s]\u001b[A\n1096it [02:07, 8.82it/s]\u001b[A\n1097it [02:08, 8.82it/s]\u001b[A\n1098it [02:08, 8.80it/s]\u001b[A\n1099it [02:08, 8.79it/s]\u001b[A\n1100it [02:08, 8.79it/s]\u001b[A\n1101it [02:08, 8.78it/s]\u001b[A\n1102it [02:08, 8.78it/s]\u001b[A\n1103it [02:08, 8.77it/s]\u001b[A\n1104it [02:08, 8.77it/s]\u001b[A\n1105it [02:08, 8.77it/s]\u001b[A\n1106it [02:09, 8.77it/s]\u001b[A\n1107it [02:09, 8.76it/s]\u001b[A\n1108it [02:09, 8.77it/s]\u001b[A\n1109it [02:09, 8.77it/s]\u001b[A\n1110it [02:09, 8.78it/s]\u001b[A\n1111it [02:09, 8.79it/s]\u001b[A\n1112it [02:09, 8.80it/s]\u001b[A\n1113it [02:09, 8.81it/s]\u001b[A\n1114it [02:09, 8.81it/s]\u001b[A\n1115it [02:10, 8.82it/s]\u001b[A\n1116it [02:10, 8.81it/s]\u001b[A\n1117it [02:10, 8.82it/s]\u001b[A\n1118it [02:10, 8.82it/s]\u001b[A\n1119it [02:10, 8.82it/s]\u001b[A\n1120it [02:10, 8.82it/s]\u001b[A\n1121it [02:10, 8.82it/s]\u001b[A\n1122it [02:10, 8.83it/s]\u001b[A\n1123it [02:10, 8.83it/s]\u001b[A\n1124it [02:11, 8.83it/s]\u001b[A\n1125it [02:11, 8.82it/s]\u001b[A\n1126it [02:11, 8.83it/s]\u001b[A\n1127it [02:11, 8.83it/s]\u001b[A\n1128it [02:11, 8.84it/s]\u001b[A\n1129it [02:11, 8.84it/s]\u001b[A\n1130it [02:11, 8.84it/s]\u001b[A\n1131it [02:11, 8.83it/s]\u001b[A\n1132it [02:12, 8.83it/s]\u001b[A\n1133it [02:12, 8.82it/s]\u001b[A\n1134it [02:12, 8.83it/s]\u001b[A\n1135it [02:12, 8.84it/s]\u001b[A\n1136it [02:12, 8.83it/s]\u001b[A\n1137it [02:12, 8.84it/s]\u001b[A\n1138it [02:12, 8.83it/s]\u001b[A\n1139it [02:12, 8.83it/s]\u001b[A\n1140it [02:12, 8.82it/s]\u001b[A\n1141it [02:13, 8.82it/s]\u001b[A\n1142it [02:13, 8.83it/s]\u001b[A\n1143it [02:13, 8.83it/s]\u001b[A\n1144it [02:13, 8.84it/s]\u001b[A\n1145it [02:13, 8.84it/s]\u001b[A\n1146it [02:13, 8.84it/s]\u001b[A\n1147it [02:13, 8.84it/s]\u001b[A\n1148it [02:13, 8.83it/s]\u001b[A\n1149it [02:13, 8.83it/s]\u001b[A\n1150it [02:14, 8.83it/s]\u001b[A\n1151it [02:14, 8.83it/s]\u001b[A\n1152it [02:14, 8.83it/s]\u001b[A\n1153it [02:14, 8.83it/s]\u001b[A\n1154it [02:14, 8.83it/s]\u001b[A\n1155it [02:14, 8.83it/s]\u001b[A\n1156it [02:14, 8.83it/s]\u001b[A\n1157it [02:14, 8.84it/s]\u001b[A\n1158it [02:14, 8.84it/s]\u001b[A\n1159it [02:15, 8.83it/s]\u001b[A\n1160it [02:15, 8.83it/s]\u001b[A\n1161it [02:15, 8.84it/s]\u001b[A\n1162it [02:15, 8.84it/s]\u001b[A\n1163it [02:15, 8.83it/s]\u001b[A\n1164it [02:15, 8.83it/s]\u001b[A\n1165it [02:15, 8.83it/s]\u001b[A\n1166it [02:15, 8.83it/s]\u001b[A\n1167it [02:15, 8.83it/s]\u001b[A\n1168it [02:16, 8.83it/s]\u001b[A\n1169it [02:16, 8.83it/s]\u001b[A\n1170it [02:16, 8.83it/s]\u001b[A\n1171it [02:16, 8.82it/s]\u001b[A\n1172it [02:16, 8.81it/s]\u001b[A\n1173it [02:16, 8.81it/s]\u001b[A\n1174it [02:16, 8.82it/s]\u001b[A\n1175it [02:16, 8.83it/s]\u001b[A\n1176it [02:16, 8.83it/s]\u001b[A\n1177it [02:17, 8.83it/s]\u001b[A\n1178it [02:17, 8.82it/s]\u001b[A\n1179it [02:17, 8.82it/s]\u001b[A\n1180it [02:17, 8.83it/s]\u001b[A\n1181it [02:17, 8.83it/s]\u001b[A\n1182it [02:17, 8.83it/s]\u001b[A\n1183it [02:17, 8.83it/s]\u001b[A\n1184it [02:17, 8.84it/s]\u001b[A\n1185it [02:18, 8.84it/s]\u001b[A\n1186it [02:18, 8.83it/s]\u001b[A\n1187it [02:18, 8.83it/s]\u001b[A\n1188it [02:18, 8.83it/s]\u001b[A\n1189it [02:18, 8.83it/s]\u001b[A\n1190it [02:18, 8.84it/s]\u001b[A\n1191it [02:18, 8.83it/s]\u001b[A\n1192it [02:18, 8.83it/s]\u001b[A\n1193it [02:18, 8.83it/s]\u001b[A\n1194it [02:19, 8.83it/s]\u001b[A\n1195it [02:19, 8.83it/s]\u001b[A\n1196it [02:19, 8.81it/s]\u001b[A\n1197it [02:19, 8.82it/s]\u001b[A\n1198it [02:19, 8.83it/s]\u001b[A\n1199it [02:19, 8.83it/s]\u001b[A\n1200it [02:19, 8.83it/s]\u001b[A\n1201it [02:19, 8.83it/s]\u001b[A\n1202it [02:19, 8.83it/s]\u001b[A\n1203it [02:20, 8.82it/s]\u001b[A\n1204it [02:20, 8.82it/s]\u001b[A\n1205it [02:20, 8.82it/s]\u001b[A\n1206it [02:20, 8.82it/s]\u001b[A\n1207it [02:20, 8.83it/s]\u001b[A\n1208it [02:20, 8.83it/s]\u001b[A\n1209it [02:20, 8.83it/s]\u001b[A\n1210it [02:20, 8.82it/s]\u001b[A\n1211it [02:20, 8.81it/s]\u001b[A\n1212it [02:21, 8.80it/s]\u001b[A\n1213it [02:21, 8.81it/s]\u001b[A\n1214it [02:21, 8.82it/s]\u001b[A\n1215it [02:21, 8.83it/s]\u001b[A\n1216it [02:21, 8.83it/s]\u001b[A\n1217it [02:21, 8.82it/s]\u001b[A\n1218it [02:21, 8.82it/s]\u001b[A\n1219it [02:21, 8.82it/s]\u001b[A\n1220it [02:21, 8.81it/s]\u001b[A\n1221it [02:22, 8.80it/s]\u001b[A\n1222it [02:22, 8.81it/s]\u001b[A\n1223it [02:22, 8.82it/s]\u001b[A\n1224it [02:22, 8.82it/s]\u001b[A\n1225it [02:22, 8.82it/s]\u001b[A\n1226it [02:22, 8.82it/s]\u001b[A\n1227it [02:22, 8.81it/s]\u001b[A\n1228it [02:22, 8.79it/s]\u001b[A\n1229it [02:22, 8.79it/s]\u001b[A\n1230it [02:23, 8.78it/s]\u001b[A\n1231it [02:23, 8.77it/s]\u001b[A\n1232it [02:23, 8.77it/s]\u001b[A\n1233it [02:23, 8.78it/s]\u001b[A\n1234it [02:23, 8.79it/s]\u001b[A\n1235it [02:23, 8.79it/s]\u001b[A\n1236it [02:23, 8.79it/s]\u001b[A\n1237it [02:23, 8.79it/s]\u001b[A\n1238it [02:24, 8.79it/s]\u001b[A\n1239it [02:24, 8.79it/s]\u001b[A\n1240it [02:24, 8.78it/s]\u001b[A\n1241it [02:24, 8.79it/s]\u001b[A\n1242it [02:24, 8.80it/s]\u001b[A\n1243it [02:24, 8.81it/s]\u001b[A\n1244it [02:24, 8.82it/s]\u001b[A\n1245it [02:24, 8.82it/s]\u001b[A\n1246it [02:24, 8.82it/s]\u001b[A\n1247it [02:25, 8.83it/s]\u001b[A\n1248it [02:25, 8.83it/s]\u001b[A\n1249it [02:25, 8.82it/s]\u001b[A\n1250it [02:25, 8.80it/s]\u001b[A\n1251it [02:25, 8.81it/s]\u001b[A\n1252it [02:25, 8.82it/s]\u001b[A\n1253it [02:25, 8.82it/s]\u001b[A\n1254it [02:25, 8.82it/s]\u001b[A\n1255it [02:25, 8.82it/s]\u001b[A\n1256it [02:26, 8.80it/s]\u001b[A\n1257it [02:26, 8.77it/s]\u001b[A\n1258it [02:26, 8.76it/s]\u001b[A\n1259it [02:26, 8.77it/s]\u001b[A\n1260it [02:26, 8.79it/s]\u001b[A\n1261it [02:26, 8.79it/s]\u001b[A\n1262it [02:26, 8.79it/s]\u001b[A\n1263it [02:26, 8.80it/s]\u001b[A\n1264it [02:26, 8.81it/s]\u001b[A\n1265it [02:27, 8.80it/s]\u001b[A\n1266it [02:27, 8.78it/s]\u001b[A\n1267it [02:27, 8.78it/s]\u001b[A\n1268it [02:27, 8.78it/s]\u001b[A\n1269it [02:27, 8.79it/s]\u001b[A\n1270it [02:27, 8.80it/s]\u001b[A\n1271it [02:27, 8.81it/s]\u001b[A\n1272it [02:27, 8.82it/s]\u001b[A\n1273it [02:27, 8.81it/s]\u001b[A\n1274it [02:28, 8.79it/s]\u001b[A\n1275it [02:28, 8.77it/s]\u001b[A\n1276it [02:28, 8.77it/s]\u001b[A\n1277it [02:28, 8.78it/s]\u001b[A\n1278it [02:28, 8.79it/s]\u001b[A\n1279it [02:28, 8.79it/s]\u001b[A\n1280it [02:28, 8.80it/s]\u001b[A\n1281it [02:28, 8.79it/s]\u001b[A\n1282it [02:29, 8.80it/s]\u001b[A\n1283it [02:29, 8.80it/s]\u001b[A\n1284it [02:29, 8.81it/s]\u001b[A\n1285it [02:29, 8.81it/s]\u001b[A\n1286it [02:29, 8.82it/s]\u001b[A\n1287it [02:29, 8.82it/s]\u001b[A\n1288it [02:29, 8.80it/s]\u001b[A\n1289it [02:29, 8.80it/s]\u001b[A\n1290it [02:29, 8.82it/s]\u001b[A\n1291it [02:30, 8.82it/s]\u001b[A\n1292it [02:30, 8.82it/s]\u001b[A\n1293it [02:30, 8.83it/s]\u001b[A\n1294it [02:30, 8.82it/s]\u001b[A\n1295it [02:30, 8.83it/s]\u001b[A\n1296it [02:30, 8.82it/s]\u001b[A\n1297it [02:30, 8.82it/s]\u001b[A\n1298it [02:30, 8.80it/s]\u001b[A\n1299it [02:30, 8.79it/s]\u001b[A\n1300it [02:31, 8.79it/s]\u001b[A\n1301it [02:31, 8.78it/s]\u001b[A\n1302it [02:31, 8.78it/s]\u001b[A\n1303it [02:31, 8.79it/s]\u001b[A\n1304it [02:31, 8.79it/s]\u001b[A\n1305it [02:31, 8.80it/s]\u001b[A\n1306it [02:31, 8.80it/s]\u001b[A\n1307it [02:31, 8.79it/s]\u001b[A\n1308it [02:31, 8.79it/s]\u001b[A\n1309it [02:32, 8.80it/s]\u001b[A\n1310it [02:32, 8.80it/s]\u001b[A\n1311it [02:32, 8.80it/s]\u001b[A\n1312it [02:32, 8.79it/s]\u001b[A\n1313it [02:32, 8.80it/s]\u001b[A\n1314it [02:32, 8.81it/s]\u001b[A\n1315it [02:32, 8.81it/s]\u001b[A\n1316it [02:32, 8.81it/s]\u001b[A\n1317it [02:32, 8.81it/s]\u001b[A\n1318it [02:33, 8.81it/s]\u001b[A\n1319it [02:33, 8.81it/s]\u001b[A\n1320it [02:33, 8.82it/s]\u001b[A\n1321it [02:33, 8.82it/s]\u001b[A\n1322it [02:33, 8.81it/s]\u001b[A\n1323it [02:33, 8.82it/s]\u001b[A\n1324it [02:33, 8.81it/s]\u001b[A\n1325it [02:33, 8.79it/s]\u001b[A\n1326it [02:34, 8.80it/s]\u001b[A\n1327it [02:34, 8.78it/s]\u001b[A\n1328it [02:34, 8.78it/s]\u001b[A\n1329it [02:34, 8.80it/s]\u001b[A\n1330it [02:34, 8.81it/s]\u001b[A\n1331it [02:34, 8.80it/s]\u001b[A\n1332it [02:34, 8.81it/s]\u001b[A\n1333it [02:34, 8.81it/s]\u001b[A\n1334it [02:34, 8.82it/s]\u001b[A\n1335it [02:35, 8.83it/s]\u001b[A\n1336it [02:35, 8.83it/s]\u001b[A\n1337it [02:35, 8.84it/s]\u001b[A\n1338it [02:35, 8.83it/s]\u001b[A\n1339it [02:35, 8.83it/s]\u001b[A\n1340it [02:35, 8.84it/s]\u001b[A\n1341it [02:35, 8.83it/s]\u001b[A\n1342it [02:35, 8.82it/s]\u001b[A\n1343it [02:35, 8.81it/s]\u001b[A\n1344it [02:36, 8.81it/s]\u001b[A\n1345it [02:36, 8.82it/s]\u001b[A\n1346it [02:36, 8.82it/s]\u001b[A\n1347it [02:36, 8.83it/s]\u001b[A0.7587131367292225, 0.884375, 0.8167388167388168, 0.8946614116804013, 0.9282527881040892, 0.9111476008027731, 0.7171814671814671, 0.8254245357879701, 0.7675053493691433\n\ndeleted\n/usr/local/lib/python3.7/dist-packages/torch/nn/functional.py:2608: UserWarning: reduction: 'mean' divides the total loss by both the batch size and the support size.'batchmean' divides only by the batch size, and aligns with the KL div math definition.'mean' will be changed to behave the same as 'batchmean' in the next major release.\n \"reduction: 'mean' divides the total loss by both the batch size and the support size.\"\n \n\u001b[A{'loss': 0.0095, 'learning_rate': 3.2566248256624825e-05, 'epoch': 1.05}\n 35% 1000/2868 [23:33<38:08, 1.22s/it]\n \n\u001b[A{'loss': 0.0093, 'learning_rate': 3.082287308228731e-05, 'epoch': 1.15}\n 38% 1100/2868 [25:35<36:01, 1.22s/it]\n \n\u001b[A{'loss': 0.0093, 'learning_rate': 2.9079497907949792e-05, 'epoch': 1.26}\n 42% 1200/2868 [27:38<34:04, 1.23s/it]\n \n\u001b[A{'loss': 0.0091, 'learning_rate': 2.7336122733612275e-05, 'epoch': 1.36}\n 45% 1300/2868 [29:40<31:55, 1.22s/it]\n \n\u001b[A{'loss': 0.0091, 'learning_rate': 2.5592747559274755e-05, 'epoch': 1.46}\n 49% 1400/2868 [31:42<29:55, 1.22s/it]\n \n\u001b[A{'loss': 0.009, 'learning_rate': 2.3849372384937242e-05, 'epoch': 1.57}\n 52% 1500/2868 [33:44<27:51, 1.22s/it]\n \n\u001b[A{'loss': 0.009, 'learning_rate': 2.2105997210599723e-05, 'epoch': 1.67}\n 56% 1600/2868 [35:47<25:45, 1.22s/it]\n \n\u001b[A{'loss': 0.0091, 'learning_rate': 2.0362622036262206e-05, 'epoch': 1.78}\n 59% 1700/2868 [37:49<23:49, 1.22s/it]\n \n\u001b[A{'loss': 0.0091, 'learning_rate': 1.8619246861924686e-05, 'epoch': 1.88}\n 63% 1800/2868 [39:51<21:45, 1.22s/it]\n \n\u001b[A{'loss': 0.0092, 'learning_rate': 1.687587168758717e-05, 'epoch': 1.99}\n 66% 1900/2868 [41:53<19:46, 1.23s/it]\n 67% 1912/2868 [42:08<17:40, 1.11s/it]\n\n 0% 0/118 [00:00<?, ?it/s]\u001b[A\u001b[A\n\n 2% 2/118 [00:00<00:07, 16.38it/s]\u001b[A\u001b[A\n\n 3% 3/118 [00:00<00:08, 13.02it/s]\u001b[A\u001b[A\n\n 3% 4/118 [00:00<00:10, 11.36it/s]\u001b[A\u001b[A\n\n 4% 5/118 [00:00<00:10, 10.42it/s]\u001b[A\u001b[A\n\n 5% 6/118 [00:00<00:11, 9.82it/s]\u001b[A\u001b[A\n\n 6% 7/118 [00:00<00:11, 9.40it/s]\u001b[A\u001b[A\n\n 7% 8/118 [00:00<00:12, 9.11it/s]\u001b[A\u001b[A\n\n 8% 9/118 [00:00<00:12, 8.91it/s]\u001b[A\u001b[A\n\n 8% 10/118 [00:01<00:12, 8.77it/s]\u001b[A\u001b[A\n\n 9% 11/118 [00:01<00:12, 8.76it/s]\u001b[A\u001b[A\n\n 10% 12/118 [00:01<00:12, 8.73it/s]\u001b[A\u001b[A\n\n 11% 13/118 [00:01<00:12, 8.69it/s]\u001b[A\u001b[A" ], [ "", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ] ]

cb2fb0f660879e721a106c80ff403551a9373959

428,483

ipynb

Jupyter Notebook

DataScience/6.Data_Visualization_using_Pandas/Exercise.ipynb

Ravi4teja/AI

89cb3dbb3c014512c46168b315c2dd3a49fd042b

[ "MIT" ]

null

DataScience/6.Data_Visualization_using_Pandas/Exercise.ipynb

Ravi4teja/AI

89cb3dbb3c014512c46168b315c2dd3a49fd042b

[ "MIT" ]

null

DataScience/6.Data_Visualization_using_Pandas/Exercise.ipynb

Ravi4teja/AI

89cb3dbb3c014512c46168b315c2dd3a49fd042b

[ "MIT" ]

null

587.768176

56,572

0.943676

[ [ [ "# Pandas Data Visualization Exercise", "_____no_output_____" ] ], [ [ "import pandas as pd\nimport matplotlib.pyplot as plt\nimport seaborn as sns\ndf3 = pd.read_csv('df3')\n%matplotlib inline", "_____no_output_____" ], [ "df3.info()", "<class 'pandas.core.frame.DataFrame'>\nRangeIndex: 500 entries, 0 to 499\nData columns (total 4 columns):\na 500 non-null float64\nb 500 non-null float64\nc 500 non-null float64\nd 500 non-null float64\ndtypes: float64(4)\nmemory usage: 15.7 KB\n" ], [ "df3.head()", "_____no_output_____" ] ], [ [ "** Recreate this scatter plot of b vs a. Note the color and size of the points. Also note the figure size. See if you can figure out how to stretch it in a similar fashion. Remeber back to your matplotlib lecture...**", "_____no_output_____" ] ], [ [ "df3.plot.scatter(x= 'a', y = 'b', color='red', s=45, figsize = (12,4))", "_____no_output_____" ] ], [ [ "** Create a histogram of the 'a' column.**", "_____no_output_____" ] ], [ [ "df3['a'].plot.hist(bins=10)", "_____no_output_____" ] ], [ [ "** These plots are okay, but they don't look very polished. Use style sheets to set the style to 'ggplot' and redo the histogram from above. Also figure out how to add more bins to it.***", "_____no_output_____" ] ], [ [ "sns.set_style('darkgrid')\ndf3['a'].plot.hist(bins=25)", "_____no_output_____" ], [ "plt.style.use('ggplot')", "_____no_output_____" ], [ "df3['a'].plot.hist(bins=25, alpha=0.5)", "_____no_output_____" ] ], [ [ "** Create a boxplot comparing the a and b columns.**", "_____no_output_____" ] ], [ [ "df3[['a', 'b']].plot.box()", "_____no_output_____" ] ], [ [ "** Create a kde plot of the 'd' column **", "_____no_output_____" ] ], [ [ "df3['d'].plot.kde()", "_____no_output_____" ], [ "df3['d'].plot.density(color='red')", "_____no_output_____" ] ], [ [ "** Figure out how to increase the linewidth and make the linestyle dashed. (Note: You would usually not dash a kde plot line)**", "_____no_output_____" ] ], [ [ "df3['d'].plot.kde(lw=5, ls=':', color='red')", "_____no_output_____" ] ], [ [ "** Create an area plot of all the columns for just the rows up to 30. (hint: use .ix).**", "_____no_output_____" ] ], [ [ "df3.iloc[0:30].plot.area(alpha=0.3)", "_____no_output_____" ] ], [ [ "## Bonus Challenge!\nNote, you may find this really hard, reference the solutions if you can't figure it out!\n** Notice how the legend in our previous figure overlapped some of actual diagram. Can you figure out how to display the legend outside of the plot as shown below?**\n\n** Try searching Google for a good stackoverflow link on this topic. If you can't find it on your own - [use this one for a hint.](http://stackoverflow.com/questions/23556153/how-to-put-legend-outside-the-plot-with-pandas)**", "_____no_output_____" ] ], [ [ "df3.iloc[0:30].plot.area(alpha=0.3)\nplt.legend(loc='center left', bbox_to_anchor=(1, 0.5))", "_____no_output_____" ] ], [ [ "# Great Job!", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ] ]

cb2fb8083b8642128c2f6213cacaa21b16cf1fcb

3,091

ipynb

Jupyter Notebook

python-deepdive/deepdive1/section02/section_02_08.ipynb

erictapia/devstacklab

2997a620c3f4d29c3a526d561ec0cfb4ba0cd6b4

[ "MIT" ]

null

python-deepdive/deepdive1/section02/section_02_08.ipynb

erictapia/devstacklab

2997a620c3f4d29c3a526d561ec0cfb4ba0cd6b4

[ "MIT" ]

null

python-deepdive/deepdive1/section02/section_02_08.ipynb

erictapia/devstacklab

2997a620c3f4d29c3a526d561ec0cfb4ba0cd6b4

[ "MIT" ]

null

16.89071

47

0.396635

[ [ [ "# Conditionals\n", "_____no_output_____" ] ], [ [ "a = 6\n\nif a < 5:\n print(\"a < 5\")\nelse:\n print(\"a >= 5\")", "a >= 5\n" ], [ "a = 5\n\nif a < 5:\n print(\"a < 5\")\nelse:\n if a < 10:\n print(\"5 <= a < 10\")\n else:\n print(\"a >= 10\")", "5 <= a < 10\n" ] ], [ [ "# else if conditionals", "_____no_output_____" ] ], [ [ "a = 5\n\nif a < 5:\n print(\"a < 5\")\nelif a < 10:\n print(\"5 <= a < 10\")\nelif a < 15:\n print(\"10 <= a < 15\")\nelif a < 20:\n print(\"15 <= a < 20\")\nelse:\n print(\"a > 20\")", "5 <= a < 10\n" ] ], [ [ "# Non Ternary operator", "_____no_output_____" ] ], [ [ "a = 25\n\nif a < 5:\n b = \"a < 5\"\nelse:\n b = \"a >= 5\"\n\nprint(b)", "a >= 5\n" ] ], [ [ "# Ternary operator", "_____no_output_____" ] ], [ [ "a = 25\n\nb = \"a < 5\" if a < 5 else \"a >= 5\"\n\nprint(b)", "a >= 5\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb2fc6983d7b91bde1d274e6e529ab428feffaf2

5,210

ipynb

Jupyter Notebook

big-docs-example2/big-docs-example02.ipynb

DavidLeoni/jubuild

0ae2c9c5e78a74bb9d7dbedd00ca2696b03f3e8e

[ "Apache-2.0" ]

null

big-docs-example2/big-docs-example02.ipynb

DavidLeoni/jubuild

0ae2c9c5e78a74bb9d7dbedd00ca2696b03f3e8e

[ "Apache-2.0" ]

85

2017-09-20T12:29:11.000Z

2022-02-22T09:42:33.000Z

big-docs-example2/big-docs-example02.ipynb

DavidLeoni/jubuild

0ae2c9c5e78a74bb9d7dbedd00ca2696b03f3e8e

[ "Apache-2.0" ]

1

2017-09-20T18:11:28.000Z

20.11583

53

0.46334

[ [ [ "# Big docs example 2", "_____no_output_____" ], [ "## reasonable paragraph \n\n### reasonable sub paragraph\n\n## reasonable paragraph \n\n### reasonable sub paragraph\n\n## paragraph with long text\n\n### sub paragraph with long text\n\n## paragraph with long text\n\n### sub paragraph with long text\n\n## paragraph with long text\n\n### sub paragraph with long text\n\n## paragraph with extra super long text\n\n### sub paragraph with extra super long text\n\n## paragraph with extra super long text\n\n### sub paragraph with extra super long text\n\n## paragraph with extra super long text\n\n### sub paragraph with extra super long text\n\n## paragraph with extra super long text\n\n### sub paragraph with extra super long text\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph", "_____no_output_____" ], [ "## reasonable paragraph \n\n### reasonable sub paragraph\n\n## reasonable paragraph \n\n### reasonable sub paragraph\n\n## paragraph with long text\n\n### sub paragraph with long text\n\n## paragraph with long text\n\n### sub paragraph with long text\n\n## paragraph with long text\n\n### sub paragraph with long text\n\n## paragraph with extra super long text\n\n### sub paragraph with extra super long text\n\n## paragraph with extra super long text\n\n### sub paragraph with extra super long text\n\n## paragraph with extra super long text\n\n### sub paragraph with extra super long text\n\n## paragraph with extra super long text\n\n### sub paragraph with extra super long text\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph\n\n## paragraph\n\n### sub paragraph", "_____no_output_____" ] ] ]

[ "markdown" ]

[ [ "markdown", "markdown", "markdown" ] ]

cb2fc9ac19972ac9fe973e63c3a23c15a38a5efd

5,713

ipynb

Jupyter Notebook

YahooFinance/YahooFinance_Display_chart_from_ticker.ipynb

Charles-de-Montigny/awesome-notebooks

79485142ba557e9c20e6f6dca4fdc12a3443813e

[ "BSD-3-Clause" ]

1

2022-01-20T22:04:48.000Z

YahooFinance/YahooFinance_Display_chart_from_ticker.ipynb

mmcfer/awesome-notebooks

8d2892e40db480a323049e04decfefac45904af4

[ "BSD-3-Clause" ]

18

2021-10-02T02:49:32.000Z

2021-12-27T21:39:14.000Z

YahooFinance/YahooFinance_Display_chart_from_ticker.ipynb

mmcfer/awesome-notebooks

8d2892e40db480a323049e04decfefac45904af4

[ "BSD-3-Clause" ]

null

25.734234

1,016

0.574479

[ [ [ "# YahooFinance - Display chart from ticker\n<a href=\"https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/YahooFinance/YahooFinance_Display_chart_from_ticker.ipynb\" target=\"_parent\"><img src=\"https://img.shields.io/badge/-Open%20in%20Naas-success?labelColor=000000&logo=data:image/svg+xml;base64,PD94bWwgdmVyc2lvbj0iMS4wIiBlbmNvZGluZz0iVVRGLTgiPz4KPHN2ZyB3aWR0aD0iMTAyNHB4IiBoZWlnaHQ9IjEwMjRweCIgdmlld0JveD0iMCAwIDEwMjQgMTAyNCIgeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIiB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGluayIgdmVyc2lvbj0iMS4xIj4KIDwhLS0gR2VuZXJhdGVkIGJ5IFBpeGVsbWF0b3IgUHJvIDIuMC41IC0tPgogPGRlZnM+CiAgPHRleHQgaWQ9InN0cmluZyIgdHJhbnNmb3JtPSJtYXRyaXgoMS4wIDAuMCAwLjAgMS4wIDIyOC4wIDU0LjUpIiBmb250LWZhbWlseT0iQ29tZm9ydGFhLVJlZ3VsYXIsIENvbWZvcnRhYSIgZm9udC1zaXplPSI4MDAiIHRleHQtZGVjb3JhdGlvbj0ibm9uZSIgZmlsbD0iI2ZmZmZmZiIgeD0iMS4xOTk5OTk5OTk5OTk5ODg2IiB5PSI3MDUuMCI+bjwvdGV4dD4KIDwvZGVmcz4KIDx1c2UgaWQ9Im4iIHhsaW5rOmhyZWY9IiNzdHJpbmciLz4KPC9zdmc+Cg==\"/></a>", "_____no_output_____" ], [ "**Tags:** #yahoofinance #trading #plotly #naas_drivers", "_____no_output_____" ], [ "With this template, you can get data from any ticker available in [Yahoo finance](https://finance.yahoo.com/quote/TSLA/).<br> ", "_____no_output_____" ], [ "## Input", "_____no_output_____" ], [ "### Import libraries", "_____no_output_____" ] ], [ [ "from naas_drivers import yahoofinance, plotly", "_____no_output_____" ] ], [ [ "### Input parameters\n👉 Here you can change the ticker, timeframe and add moving averages analysiss", "_____no_output_____" ] ], [ [ "ticker = \"TSLA\"\ndate_from = -365\ndate_to = \"today\"\ninterval = '1d'\nmoving_averages = [20, 50]", "_____no_output_____" ] ], [ [ "## Model", "_____no_output_____" ], [ "### Get dataset from Yahoo Finance", "_____no_output_____" ] ], [ [ "df_yahoo = yahoofinance.get(ticker,\n date_from=date_from,\n date_to=date_to,\n interval=interval,\n moving_averages=moving_averages)", "_____no_output_____" ] ], [ [ "## Output", "_____no_output_____" ], [ "### Display chart", "_____no_output_____" ] ], [ [ "chart = plotly.linechart(df_yahoo,\n x=\"Date\",\n y=[\"Close\", \"MA20\", \"MA50\"],\n showlegend=True,\n title=f\"{ticker} stock as of today\")", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ] ]

cb2fda7565076d25fef8ead9fc3e92ba455475ac

388,266

ipynb

Jupyter Notebook

C3.Classification_LogReg/RegresionLogistica_student.ipynb

Grarck/ML4all

41eec466353bdcd6b606404ad4c9c5c13dc7227a

[ "MIT" ]

1

2020-06-05T10:31:45.000Z

C3.Classification_LogReg/RegresionLogistica_student.ipynb

Grarck/ML4all

41eec466353bdcd6b606404ad4c9c5c13dc7227a

[ "MIT" ]

null

C3.Classification_LogReg/RegresionLogistica_student.ipynb

Grarck/ML4all

41eec466353bdcd6b606404ad4c9c5c13dc7227a

[ "MIT" ]

null

208.409018

98,640

0.886892

[ [ [ "# Logistic Regression\n\n Notebook version: 2.0 (Nov 21, 2017)\n 2.1 (Oct 19, 2018)\n\n Author: Jesús Cid Sueiro ([email protected])\n Jerónimo Arenas García ([email protected])\n\n Changes: v.1.0 - First version\n v.1.1 - Typo correction. Prepared for slide presentation\n v.2.0 - Prepared for Python 3.0 (backcompmatible with 2.7)\n Assumptions for regression model modified\n v.2.1 - Minor changes regarding notation and assumptions", "_____no_output_____" ] ], [ [ "from __future__ import print_function\n# To visualize plots in the notebook\n%matplotlib inline\n\n# Imported libraries\nimport csv\nimport random\nimport matplotlib\nimport matplotlib.pyplot as plt\nimport pylab\n\nimport numpy as np\nfrom mpl_toolkits.mplot3d import Axes3D\nfrom sklearn.preprocessing import PolynomialFeatures\nfrom sklearn import linear_model\n", "_____no_output_____" ] ], [ [ "# Logistic Regression\n\n## 1. Introduction\n\n### 1.1. Binary classification and decision theory. The MAP criterion\n\nThe goal of a classification problem is to assign a *class* or *category* to every *instance* or *observation* of a data collection. Here, we will assume that every instance ${\\bf x}$ is an $N$-dimensional vector in $\\mathbb{R}^N$, and that the class $y$ of sample ${\\bf x}$ is an element of a binary set ${\\mathcal Y} = \\{0, 1\\}$. The goal of a classifier is to predict the true value of $y$ after observing ${\\bf x}$.\n\nWe will denote as $\\hat{y}$ the classifier output or *decision*. If $y=\\hat{y}$, the decision is a *hit*, otherwise $y\\neq \\hat{y}$ and the decision is an *error*.\n", "_____no_output_____" ], [ "\nDecision theory provides a solution to the classification problem in situations where the relation between instance ${\\bf x}$ and its class $y$ is given by a known probabilistic model: assume that every tuple $({\\bf x}, y)$ is an outcome of a random vector $({\\bf X}, Y)$ with joint distribution $p_{{\\bf X},Y}({\\bf x}, y)$. A natural criteria for classification is to select predictor $\\hat{Y}=f({\\bf x})$ in such a way that the probability or error, $P\\{\\hat{Y} \\neq Y\\}$ is minimum. Noting that\n\n$$\nP\\{\\hat{Y} \\neq Y\\} = \\int P\\{\\hat{Y} \\neq Y | {\\bf x}\\} p_{\\bf X}({\\bf x}) d{\\bf x}\n$$\n\nthe optimal decision is got if, for every sample ${\\bf x}$, we make decision minimizing the conditional error probability:\n\n\\begin{align}\n\\hat{y}^* &= \\arg\\min_{\\hat{y}} P\\{\\hat{y} \\neq Y |{\\bf x}\\} \\\\\n &= \\arg\\max_{\\hat{y}} P\\{\\hat{y} = Y |{\\bf x}\\} \\\\\n\\end{align}", "_____no_output_____" ], [ "\nThus, the optimal decision rule can be expressed as\n\n$$\nP_{Y|{\\bf X}}(1|{\\bf x}) \\quad\\mathop{\\gtrless}^{\\hat{y}=1}_{\\hat{y}=0}\\quad P_{Y|{\\bf X}}(0|{\\bf x}) \n$$\n\nor, equivalently\n\n$$\nP_{Y|{\\bf X}}(1|{\\bf x}) \\quad\\mathop{\\gtrless}^{\\hat{y}=1}_{\\hat{y}=0}\\quad \\frac{1}{2} \n$$\n\nThe classifier implementing this decision rule is usually named MAP (*Maximum A Posteriori*). As we have seen, the MAP classifier minimizes the error probability for binary classification, but the result can also be generalized to multiclass classification problems.", "_____no_output_____" ], [ "### 1.2. Parametric classification.\n\nClassical decision theory is grounded on the assumption that the probabilistic model relating the observed sample ${\\bf X}$ and the true hypothesis $Y$ is known. Unfortunately, this is unrealistic in many applications, where the only available information to construct the classifier is a dataset $\\mathcal D = \\{{\\bf x}^{(k)}, y^{(k)}\\}_{k=0}^{K-1}$ of instances and their respective class labels.\n\nA more realistic formulation of the classification problem is the following: given a dataset $\\mathcal D = \\{({\\bf x}^{(k)}, y^{(k)}) \\in {\\mathbb{R}}^N \\times {\\mathcal Y}, \\, k=0,\\ldots,{K-1}\\}$ of independent and identically distributed (i.i.d.) samples from an ***unknown*** distribution $p_{{\\bf X},Y}({\\bf x}, y)$, predict the class $y$ of a new sample ${\\bf x}$ with the minimum probability of error.\n", "_____no_output_____" ], [ "\nSince the probabilistic model generating the data is unknown, the MAP decision rule cannot be applied. However, many classification algorithms use the dataset to obtain an estimate of the posterior class probabilities, and apply it to implement an approximation to the MAP decision maker.\n\nParametric classifiers based on this idea assume, additionally, that the posterior class probabilty satisfies some parametric formula:\n\n$$\nP_{Y|X}(1|{\\bf x},{\\bf w}) = f_{\\bf w}({\\bf x})\n$$\n\nwhere ${\\bf w}$ is a vector of parameters. Given the expression of the MAP decision maker, classification consists in comparing the value of $f_{\\bf w}({\\bf x})$ with the threshold $\\frac{1}{2}$, and each parameter vector would be associated to a different decision maker.\n", "_____no_output_____" ], [ "In practice, the dataset ${\\mathcal S}$ is used to select a particular parameter vector $\\hat{\\bf w}$ according to certain criterion. Accordingly, the decision rule becomes\n\n$$\nf_{\\hat{\\bf w}}({\\bf x}) \\quad\\mathop{\\gtrless}^{\\hat{y}=1}_{\\hat{y}=0}\\quad \\frac{1}{2} \n$$\n\n\nIn this lesson, we explore one of the most popular model-based parametric classification methods: **logistic regression**.\n\n<img src=\"./figs/parametric_decision.png\", width=400>", "_____no_output_____" ], [ "## 2. Logistic regression.\n\n### 2.1. The logistic function\n\nThe logistic regression model assumes that the binary class label $Y \\in \\{0,1\\}$ of observation $X\\in \\mathbb{R}^N$ satisfies the expression.\n\n$$P_{Y|{\\bf X}}(1|{\\bf x}, {\\bf w}) = g({\\bf w}^\\intercal{\\bf x})$$\n$$P_{Y|{\\bf,X}}(0|{\\bf x}, {\\bf w}) = 1-g({\\bf w}^\\intercal{\\bf x})$$\n\nwhere ${\\bf w}$ is a parameter vector and $g(·)$ is the *logistic* function, which is defined by\n\n$$g(t) = \\frac{1}{1+\\exp(-t)}$$\n", "_____no_output_____" ], [ "It is straightforward to see that the logistic function has the following properties:\n\n- **P1**: Probabilistic output: $\\quad 0 \\le g(t) \\le 1$\n- **P2**: Symmetry: $\\quad g(-t) = 1-g(t)$\n- **P3**: Monotonicity: $\\quad g'(t) = g(t)·[1-g(t)] \\ge 0$\n\nIn the following we define a logistic function in python, and use it to plot a graphical representation.", "_____no_output_____" ], [ "**Exercise 1**: Verify properties P2 and P3.\n\n**Exercise 2**: Implement a function to compute the logistic function, and use it to plot such function in the inverval $[-6,6]$.", "_____no_output_____" ] ], [ [ "# Define the logistic function\ndef logistic(t):\n #<SOL>\n #</SOL>\n\n# Plot the logistic function\nt = np.arange(-6, 6, 0.1)\nz = logistic(t)\n\nplt.plot(t, z)\nplt.xlabel('$t$', fontsize=14)\nplt.ylabel('$g(t)$', fontsize=14)\nplt.title('The logistic function')\nplt.grid()", "_____no_output_____" ] ], [ [ "### 2.2. Classifiers based on the logistic model.\n\nThe MAP classifier under a logistic model will have the form\n\n$$P_{Y|{\\bf X}}(1|{\\bf x}, {\\bf w}) = g({\\bf w}^\\intercal{\\bf x}) \\quad\\mathop{\\gtrless}^{\\hat{y}=1}_{\\hat{y}=0} \\quad \\frac{1}{2} $$\n\nTherefore\n\n$$\n2 \\quad\\mathop{\\gtrless}^{\\hat{y}=1}_{\\hat{y}=0} \\quad \n1 + \\exp(-{\\bf w}^\\intercal{\\bf x}) $$\n\nwhich is equivalent to\n\n$${\\bf w}^\\intercal{\\bf x} \n\\quad\\mathop{\\gtrless}^{\\hat{y}=1}_{\\hat{y}=0}\\quad \n0 $$\n\nTherefore, the classifiers based on the logistic model are given by linear decision boundaries passing through the origin, ${\\bf x} = {\\bf 0}$. ", "_____no_output_____" ] ], [ [ "# Weight vector:\nw = [4, 8] # Try different weights\n\n# Create a rectangular grid.\nx_min = -1\nx_max = 1\ndx = x_max - x_min\nh = float(dx) / 200\nxgrid = np.arange(x_min, x_max, h)\nxx0, xx1 = np.meshgrid(xgrid, xgrid)\n\n# Compute the logistic map for the given weights\nZ = logistic(w[0]*xx0 + w[1]*xx1)\n\n# Plot the logistic map\nfig = plt.figure()\nax = fig.gca(projection='3d')\nax.plot_surface(xx0, xx1, Z, cmap=plt.cm.copper)\nax.contour(xx0, xx1, Z, levels=[0.5], colors='b', linewidths=(3,))\nplt.xlabel('$x_0$')\nplt.ylabel('$x_1$')\nax.set_zlabel('P(1|x,w)')\n\nplt.show()", "_____no_output_____" ] ], [ [ "The next code fragment represents the output of the same classifier, representing the output of the logistic function in the $x_0$-$x_1$ plane, encoding the value of the logistic function in the representation color.", "_____no_output_____" ] ], [ [ "CS = plt.contourf(xx0, xx1, Z)\nCS2 = plt.contour(CS, levels=[0.5],\n colors='m', linewidths=(3,))\nplt.xlabel('$x_0$')\nplt.ylabel('$x_1$')\n\nplt.colorbar(CS, ticks=[0, 0.5, 1])\n\nplt.show()", "_____no_output_____" ] ], [ [ "### 3.3. Nonlinear classifiers.\n\nThe logistic model can be extended to construct non-linear classifiers by using non-linear data transformations. A general form for a nonlinear logistic regression model is\n\n$$P_{Y|{\\bf X}}(1|{\\bf x}, {\\bf w}) = g[{\\bf w}^\\intercal{\\bf z}({\\bf x})] $$\n\nwhere ${\\bf z}({\\bf x})$ is an arbitrary nonlinear transformation of the original variables. The boundary decision in that case is given by equation\n\n$$\n{\\bf w}^\\intercal{\\bf z} = 0\n$$", "_____no_output_____" ], [ "** Exercise 2**: Modify the code above to generate a 3D surface plot of the polynomial logistic regression model given by\n\n$$\nP_{Y|{\\bf X}}(1|{\\bf x}, {\\bf w}) = g(1 + 10 x_0 + 10 x_1 - 20 x_0^2 + 5 x_0 x_1 + x_1^2) \n$$", "_____no_output_____" ] ], [ [ "# Weight vector:\nw = [1, 10, 10, -20, 5, 1] # Try different weights\n\n# Create a regtangular grid.\nx_min = -1\nx_max = 1\ndx = x_max - x_min\nh = float(dx) / 200\nxgrid = np.arange(x_min, x_max, h)\nxx0, xx1 = np.meshgrid(xgrid, xgrid)\n\n# Compute the logistic map for the given weights\n# Z = <FILL IN>\n\n# Plot the logistic map\nfig = plt.figure()\nax = fig.gca(projection='3d')\nax.plot_surface(xx0, xx1, Z, cmap=plt.cm.copper)\nplt.xlabel('$x_0$')\nplt.ylabel('$x_1$')\nax.set_zlabel('P(1|x,w)')\n\nplt.show()", "_____no_output_____" ], [ "CS = plt.contourf(xx0, xx1, Z)\nCS2 = plt.contour(CS, levels=[0.5],\n colors='m', linewidths=(3,))\nplt.xlabel('$x_0$')\nplt.ylabel('$x_1$')\n\nplt.colorbar(CS, ticks=[0, 0.5, 1])\n\nplt.show()", "_____no_output_____" ] ], [ [ "## 3. Inference\n\nRemember that the idea of parametric classification is to use the training data set $\\mathcal D = \\{({\\bf x}^{(k)}, y^{(k)}) \\in {\\mathbb{R}}^N \\times \\{0,1\\}, k=0,\\ldots,{K-1}\\}$ to set the parameter vector ${\\bf w}$ according to certain criterion. Then, the estimate $\\hat{\\bf w}$ can be used to compute the label prediction for any new observation as \n\n$$\\hat{y} = \\arg\\max_y P_{Y|{\\bf X}}(y|{\\bf x},\\hat{\\bf w}).$$\n\n<img src=\"figs/parametric_decision.png\", width=400>\n\n", "_____no_output_____" ], [ "We need still to choose a criterion to optimize with the selection of the parameter vector. In the notebook, we will discuss two different approaches to the estimation of ${\\bf w}$:\n\n * Maximum Likelihood (ML): $\\hat{\\bf w}_{\\text{ML}} = \\arg\\max_{\\bf w} P_{{\\mathcal D}|{\\bf W}}({\\mathcal D}|{\\bf w})$\n * Maximum *A Posteriori* (MAP): $\\hat{\\bf w}_{\\text{MAP}} = \\arg\\max_{\\bf w} p_{{\\bf W}|{\\mathcal D}}({\\bf w}|{\\mathcal D})$\n", "_____no_output_____" ], [ "\nFor the mathematical derivation of the logistic regression algorithm, the following representation of the logistic model will be useful: noting that\n\n$$P_{Y|{\\bf X}}(0|{\\bf x}, {\\bf w}) = 1-g[{\\bf w}^\\intercal{\\bf z}({\\bf x})]\n= g[-{\\bf w}^\\intercal{\\bf z}({\\bf x})]$$\n\nwe can write\n\n$$P_{Y|{\\bf X}}(y|{\\bf x}, {\\bf w}) = g[\\overline{y}{\\bf w}^\\intercal{\\bf z}({\\bf x})]$$\n\nwhere $\\overline{y} = 2y-1$ is a *symmetrized label* ($\\overline{y}\\in\\{-1, 1\\}$). ", "_____no_output_____" ], [ "### 3.1. Model assumptions\n\nIn the following, we will make the following assumptions:\n\n- **A1**. (Logistic Regression): We assume a logistic model for the *a posteriori* probability of ${Y=1}$ given ${\\bf X}$, i.e.,\n\n$$P_{Y|{\\bf X}}(1|{\\bf x}, {\\bf w}) = g[{\\bf w}^\\intercal{\\bf z}({\\bf x})].$$\n\n- **A2**. All samples in ${\\mathcal D}$ have been generated by the same distribution, $p_{{\\bf X}, Y}({\\bf x}, y)$.\n\n- **A3**. Input variables $\\bf x$ do not depend on $\\bf w$. This implies that \n\n$$p({\\bf x}|{\\bf w}) = p({\\bf x})$$\n\n- **A4**. Targets $y^{(0)}, \\cdots, y^{(K-1)}$ are statistically independent given $\\bf w$ and the inputs ${\\bf x}^{(0)}, \\cdots, {\\bf x}^{(K-1)}$, that is:\n\n$$p(y^{(0)}, \\cdots, y^{(K-1)} | {\\bf x}^{(0)}, \\cdots, {\\bf x}^{(K-1)}, {\\bf w}) = \\prod_{k=0}^{K-1} p(s^{(k)} | {\\bf x}^{(k)}, {\\bf w})$$\n", "_____no_output_____" ], [ "### 3.2. ML estimation.\n\nThe ML estimate is defined as\n\n$$\\hat{\\bf w}_{\\text{ML}} = \\arg\\max_{\\bf w} P_{{\\mathcal D}|{\\bf W}}({\\mathcal D}|{\\bf w})$$\n\nUssing assumptions A2 and A3 above, we have that\n\n\\begin{align}\nP_{{\\mathcal D}|{\\bf W}}({\\mathcal D}|{\\bf w}) & = p(y^{(0)}, \\cdots, y^{(K-1)},{\\bf x}^{(0)}, \\cdots, {\\bf x}^{(K-1)}| {\\bf w}) \\\\\n& = P(y^{(0)}, \\cdots, y^{(K-1)}|{\\bf x}^{(0)}, \\cdots, {\\bf x}^{(K-1)}, {\\bf w}) \\; p({\\bf x}^{(0)}, \\cdots, {\\bf x}^{(K-1)}| {\\bf w}) \\\\\n& = P(y^{(0)}, \\cdots, y^{(K-1)}|{\\bf x}^{(0)}, \\cdots, {\\bf x}^{(K-1)}, {\\bf w}) \\; p({\\bf x}^{(0)}, \\cdots, {\\bf x}^{(K-1)})\\end{align}\n\nFinally, using assumption A4, we can formulate the ML estimation of $\\bf w$ as the resolution of the following optimization problem\n\n\\begin{align}\n\\hat {\\bf w}_\\text{ML} & = \\arg \\max_{\\bf w} p(y^{(0)}, \\cdots, y^{(K-1)}|{\\bf x}^{(0)}, \\cdots, {\\bf x}^{(K-1)}, {\\bf w}) \\\\\n& = \\arg \\max_{\\bf w} \\prod_{k=0}^{K-1} P(y^{(k)}|{\\bf x}^{(k)}, {\\bf w}) \\\\\n& = \\arg \\max_{\\bf w} \\sum_{k=0}^{K-1} \\log P(y^{(k)}|{\\bf x}^{(k)}, {\\bf w}) \\\\\n& = \\arg \\min_{\\bf w} \\sum_{k=0}^{K-1} - \\log P(y^{(k)}|{\\bf x}^{(k)}, {\\bf w})\n\\end{align}\n\nwhere the arguments of the maximization or minimization problems of the last three lines are usually referred to as the **likelihood**, **log-likelihood** $\\left[L(\\bf w)\\right]$, and **negative log-likelihood** $\\left[\\text{NLL}(\\bf w)\\right]$, respectively.", "_____no_output_____" ], [ "\nNow, using A1 (the logistic model)\n\n\\begin{align}\n\\text{NLL}({\\bf w}) \n &= - \\sum_{k=0}^{K-1}\\log\\left[g\\left(\\overline{y}^{(k)}{\\bf w}^\\intercal {\\bf z}^{(k)}\\right)\\right] \\\\\n &= \\sum_{k=0}^{K-1}\\log\\left[1+\\exp\\left(-\\overline{y}^{(k)}{\\bf w}^\\intercal {\\bf z}^{(k)}\\right)\\right]\n\\end{align}\n\nwhere ${\\bf z}^{(k)}={\\bf z}({\\bf x}^{(k)})$.\n", "_____no_output_____" ], [ "\nIt can be shown that $\\text{NLL}({\\bf w})$ is a convex and differentiable function of ${\\bf w}$. Therefore, its minimum is a point with zero gradient.\n\n\\begin{align}\n\\nabla_{\\bf w} \\text{NLL}(\\hat{\\bf w}_{\\text{ML}}) \n &= - \\sum_{k=0}^{K-1} \n \\frac{\\exp\\left(-\\overline{y}^{(k)}\\hat{\\bf w}_{\\text{ML}}^\\intercal {\\bf z}^{(k)}\\right) \\overline{y}^{(k)} {\\bf z}^{(k)}}\n {1+\\exp\\left(-\\overline{y}^{(k)}\\hat{\\bf w}_{\\text{ML}}^\\intercal {\\bf z}^{(k)}\n \\right)} = \\\\\n &= - \\sum_{k=0}^{K-1} \\left[y^{(k)}-g(\\hat{\\bf w}_{\\text{ML}}^T {\\bf z}^{(k)})\\right] {\\bf z}^{(k)} = 0\n\\end{align}\n\nUnfortunately, $\\hat{\\bf w}_{\\text{ML}}$ cannot be taken out from the above equation, and some iterative optimization algorithm must be used to search for the minimum.", "_____no_output_____" ], [ "### 3.2. Gradient descent.\n\nA simple iterative optimization algorithm is <a href = https://en.wikipedia.org/wiki/Gradient_descent> gradient descent</a>. \n\n\\begin{align}\n{\\bf w}_{n+1} = {\\bf w}_n - \\rho_n \\nabla_{\\bf w} L({\\bf w}_n)\n\\end{align}\n\nwhere $\\rho_n >0$ is the *learning step*.\n\nApplying the gradient descent rule to logistic regression, we get the following algorithm:\n\n\\begin{align}\n{\\bf w}_{n+1} &= {\\bf w}_n \n + \\rho_n \\sum_{k=0}^{K-1} \\left[y^{(k)}-g({\\bf w}_n^\\intercal {\\bf z}^{(k)})\\right] {\\bf z}^{(k)}\n\\end{align}\n", "_____no_output_____" ], [ "\nDefining vectors\n\n\\begin{align}\n{\\bf y} &= [y^{(0)},\\ldots,y^{(K-1)}]^\\intercal \\\\\n\\hat{\\bf p}_n &= [g({\\bf w}_n^\\intercal {\\bf z}^{(0)}), \\ldots, g({\\bf w}_n^\\intercal {\\bf z}^{(K-1)})]^\\intercal\n\\end{align}\nand matrix\n\\begin{align}\n{\\bf Z} = \\left[{\\bf z}^{(0)},\\ldots,{\\bf z}^{(K-1)}\\right]^\\intercal\n\\end{align}\n\nwe can write\n\n\\begin{align}\n{\\bf w}_{n+1} &= {\\bf w}_n \n + \\rho_n {\\bf Z}^\\intercal \\left({\\bf y}-\\hat{\\bf p}_n\\right)\n\\end{align}\n\nIn the following, we will explore the behavior of the gradient descend method using the Iris Dataset.", "_____no_output_____" ], [ "#### 3.2.1 Example: Iris Dataset.\n\nAs an illustration, consider the <a href = http://archive.ics.uci.edu/ml/datasets/Iris> Iris dataset </a>, taken from the <a href=http://archive.ics.uci.edu/ml/> UCI Machine Learning repository</a>. This data set contains 3 classes of 50 instances each, where each class refers to a type of iris plant (*setosa*, *versicolor* or *virginica*). Each instance contains 4 measurements of given flowers: sepal length, sepal width, petal length and petal width, all in centimeters. \n\nWe will try to fit the logistic regression model to discriminate between two classes using only two attributes.\n\nFirst, we load the dataset and split them in training and test subsets.", "_____no_output_____" ] ], [ [ "# Adapted from a notebook by Jason Brownlee\ndef loadDataset(filename, split):\n xTrain = []\n cTrain = []\n xTest = []\n cTest = []\n\n with open(filename, 'r') as csvfile:\n lines = csv.reader(csvfile)\n dataset = list(lines)\n for i in range(len(dataset)-1):\n for y in range(4):\n dataset[i][y] = float(dataset[i][y])\n item = dataset[i]\n if random.random() < split:\n xTrain.append(item[0:4])\n cTrain.append(item[4])\n else:\n xTest.append(item[0:4])\n cTest.append(item[4])\n return xTrain, cTrain, xTest, cTest\n\nxTrain_all, cTrain_all, xTest_all, cTest_all = loadDataset('iris.data', 0.66)\nnTrain_all = len(xTrain_all)\nnTest_all = len(xTest_all)\nprint('Train:', nTrain_all)\nprint('Test:', nTest_all)", "Train: 98\nTest: 52\n" ] ], [ [ "Now, we select two classes and two attributes.", "_____no_output_____" ] ], [ [ "# Select attributes\ni = 0 # Try 0,1,2,3\nj = 1 # Try 0,1,2,3 with j!=i\n\n# Select two classes\nc0 = 'Iris-versicolor' \nc1 = 'Iris-virginica'\n\n# Select two coordinates\nind = [i, j]\n\n# Take training test\nX_tr = np.array([[xTrain_all[n][i] for i in ind] for n in range(nTrain_all) \n if cTrain_all[n]==c0 or cTrain_all[n]==c1])\nC_tr = [cTrain_all[n] for n in range(nTrain_all) \n if cTrain_all[n]==c0 or cTrain_all[n]==c1]\nY_tr = np.array([int(c==c1) for c in C_tr])\nn_tr = len(X_tr)\n\n# Take test set\nX_tst = np.array([[xTest_all[n][i] for i in ind] for n in range(nTest_all) \n if cTest_all[n]==c0 or cTest_all[n]==c1])\nC_tst = [cTest_all[n] for n in range(nTest_all) \n if cTest_all[n]==c0 or cTest_all[n]==c1]\nY_tst = np.array([int(c==c1) for c in C_tst])\nn_tst = len(X_tst)", "_____no_output_____" ] ], [ [ "#### 3.2.2. Data normalization\n\nNormalization of data is a common pre-processing step in many machine learning algorithms. Its goal is to get a dataset where all input coordinates have a similar scale. Learning algorithms usually show less instabilities and convergence problems when data are normalized.\n\nWe will define a normalization function that returns a training data matrix with zero sample mean and unit sample variance.", "_____no_output_____" ] ], [ [ "def normalize(X, mx=None, sx=None):\n \n # Compute means and standard deviations\n if mx is None:\n mx = np.mean(X, axis=0)\n if sx is None:\n sx = np.std(X, axis=0)\n\n # Normalize\n X0 = (X-mx)/sx\n\n return X0, mx, sx", "_____no_output_____" ] ], [ [ "Now, we can normalize training and test data. Observe in the code that the same transformation should be applied to training and test data. This is the reason why normalization with the test data is done using the means and the variances computed with the training set.", "_____no_output_____" ] ], [ [ "# Normalize data\nXn_tr, mx, sx = normalize(X_tr)\nXn_tst, mx, sx = normalize(X_tst, mx, sx)", "_____no_output_____" ] ], [ [ "The following figure generates a plot of the normalized training data.", "_____no_output_____" ] ], [ [ "# Separate components of x into different arrays (just for the plots)\nx0c0 = [Xn_tr[n][0] for n in range(n_tr) if Y_tr[n]==0]\nx1c0 = [Xn_tr[n][1] for n in range(n_tr) if Y_tr[n]==0]\nx0c1 = [Xn_tr[n][0] for n in range(n_tr) if Y_tr[n]==1]\nx1c1 = [Xn_tr[n][1] for n in range(n_tr) if Y_tr[n]==1]\n\n# Scatterplot.\nlabels = {'Iris-setosa': 'Setosa', \n 'Iris-versicolor': 'Versicolor',\n 'Iris-virginica': 'Virginica'}\nplt.plot(x0c0, x1c0,'r.', label=labels[c0])\nplt.plot(x0c1, x1c1,'g+', label=labels[c1])\nplt.xlabel('$x_' + str(ind[0]) + '$')\nplt.ylabel('$x_' + str(ind[1]) + '$')\nplt.legend(loc='best')\nplt.axis('equal')\n\nplt.show()", "_____no_output_____" ] ], [ [ "In order to apply the gradient descent rule, we need to define two methods: \n - A `fit` method, that receives the training data and returns the model weights and the value of the negative log-likelihood during all iterations.\n - A `predict` method, that receives the model weight and a set of inputs, and returns the posterior class probabilities for that input, as well as their corresponding class predictions.", "_____no_output_____" ] ], [ [ "def logregFit(Z_tr, Y_tr, rho, n_it):\n\n # Data dimension\n n_dim = Z_tr.shape[1]\n\n # Initialize variables\n nll_tr = np.zeros(n_it)\n pe_tr = np.zeros(n_it)\n Y_tr2 = 2*Y_tr - 1 # Transform labels into binary symmetric.\n w = np.random.randn(n_dim,1)\n\n # Running the gradient descent algorithm\n for n in range(n_it):\n \n # Compute posterior probabilities for weight w\n p1_tr = logistic(np.dot(Z_tr, w))\n\n # Compute negative log-likelihood\n # (note that this is not required for the weight update, only for nll tracking)\n nll_tr[n] = np.sum(np.log(1 + np.exp(-np.dot(Y_tr2*Z_tr, w)))) \n\n # Update weights\n w += rho*np.dot(Z_tr.T, Y_tr - p1_tr)\n \n return w, nll_tr\n\ndef logregPredict(Z, w):\n\n # Compute posterior probability of class 1 for weights w.\n p = logistic(np.dot(Z, w)).flatten()\n \n # Class\n D = [int(round(pn)) for pn in p]\n \n return p, D", "_____no_output_____" ] ], [ [ "We can test the behavior of the gradient descent method by fitting a logistic regression model with ${\\bf z}({\\bf x}) = (1, {\\bf x}^\\intercal)^\\intercal$.", "_____no_output_____" ] ], [ [ "# Parameters of the algorithms\nrho = float(1)/50 # Learning step\nn_it = 200 # Number of iterations\n\n# Compute Z's\nZ_tr = np.c_[np.ones(n_tr), Xn_tr] \nZ_tst = np.c_[np.ones(n_tst), Xn_tst]\nn_dim = Z_tr.shape[1]\n\n# Convert target arrays to column vectors\nY_tr2 = Y_tr[np.newaxis].T\nY_tst2 = Y_tst[np.newaxis].T\n\n# Running the gradient descent algorithm\nw, nll_tr = logregFit(Z_tr, Y_tr2, rho, n_it)\n\n# Classify training and test data\np_tr, D_tr = logregPredict(Z_tr, w)\np_tst, D_tst = logregPredict(Z_tst, w)\n\n# Compute error rates\nE_tr = D_tr!=Y_tr\nE_tst = D_tst!=Y_tst\n\n# Error rates\npe_tr = float(sum(E_tr)) / n_tr\npe_tst = float(sum(E_tst)) / n_tst\n\n# NLL plot.\nplt.plot(range(n_it), nll_tr,'b.:', label='Train')\nplt.xlabel('Iteration')\nplt.ylabel('Negative Log-Likelihood')\nplt.legend()\n\nprint('The optimal weights are:')\nprint(w)\nprint('The final error rates are:')\nprint('- Training:', pe_tr)\nprint('- Test:', pe_tst)\nprint('The NLL after training is', nll_tr[len(nll_tr)-1])", "The optimal weights are:\n[[-0.06915786]\n [ 1.23157846]\n [ 0.18660814]]\nThe final error rates are:\n- Training: 0.25757575757575757\n- Test: 0.2647058823529412\nThe NLL after training is 35.901900695\n" ] ], [ [ "#### 3.2.3. Free parameters\n\nUnder certain conditions, the gradient descent method can be shown to converge asymptotically (i.e. as the number of iterations goes to infinity) to the ML estimate of the logistic model. However, in practice, the final estimate of the weights ${\\bf w}$ depend on several factors:\n\n- Number of iterations\n- Initialization\n- Learning step", "_____no_output_____" ], [ "**Exercise**: Visualize the variability of gradient descent caused by initializations. To do so, fix the number of iterations to 200 and the learning step, and execute the gradient descent 100 times, storing the training error rate of each execution. Plot the histogram of the error rate values.\n\nNote that you can do this exercise with a loop over the 100 executions, including the code in the previous code slide inside the loop, with some proper modifications. To plot a histogram of the values in array `p` with `n`bins, you can use `plt.hist(p, n)`", "_____no_output_____" ], [ "##### 3.2.3.1. Learning step\n\nThe learning step, $\\rho$, is a free parameter of the algorithm. Its choice is critical for the convergence of the algorithm. Too large values of $\\rho$ make the algorithm diverge. For too small values, the convergence gets very slow and more iterations are required for a good convergence.\n", "_____no_output_____" ], [ "**Exercise 3**: Observe the evolution of the negative log-likelihood with the number of iterations for different values of $\\rho$. It is easy to check that, for large enough $\\rho$, the gradient descent method does not converge. Can you estimate (through manual observation) an approximate value of $\\rho$ stating a boundary between convergence and divergence?", "_____no_output_____" ], [ "**Exercise 4**: In this exercise we explore the influence of the learning step more sistematically. Use the code in the previouse exercises to compute, for every value of $\\rho$, the average error rate over 100 executions. Plot the average error rate vs. $\\rho$. \n\nNote that you should explore the values of $\\rho$ in a logarithmic scale. For instance, you can take $\\rho = 1, 1/10, 1/100, 1/1000, \\ldots$", "_____no_output_____" ], [ "In practice, the selection of $\\rho$ may be a matter of trial an error. Also there is some theoretical evidence that the learning step should decrease along time up to cero, and the sequence $\\rho_n$ should satisfy two conditions:\n- C1: $\\sum_{n=0}^{\\infty} \\rho_n^2 < \\infty$ (decrease slowly)\n- C2: $\\sum_{n=0}^{\\infty} \\rho_n = \\infty$ (but not too slowly)\n\nFor instance, we can take $\\rho_n= 1/n$. Another common choice is $\\rho_n = \\alpha/(1+\\beta n)$ where $\\alpha$ and $\\beta$ are also free parameters that can be selected by trial and error with some heuristic method.", "_____no_output_____" ], [ "#### 3.2.4. Visualizing the posterior map.\n\nWe can also visualize the posterior probability map estimated by the logistic regression model for the estimated weights.", "_____no_output_____" ] ], [ [ "# Create a regtangular grid.\nx_min, x_max = Xn_tr[:, 0].min(), Xn_tr[:, 0].max() \ny_min, y_max = Xn_tr[:, 1].min(), Xn_tr[:, 1].max()\ndx = x_max - x_min\ndy = y_max - y_min\nh = dy /400\nxx, yy = np.meshgrid(np.arange(x_min - 0.1 * dx, x_max + 0.1 * dx, h),\n np.arange(y_min - 0.1 * dx, y_max + 0.1 * dy, h))\nX_grid = np.array([xx.ravel(), yy.ravel()]).T\n\n# Compute Z's\nZ_grid = np.c_[np.ones(X_grid.shape[0]), X_grid] \n\n# Compute the classifier output for all samples in the grid.\npp, dd = logregPredict(Z_grid, w)\n\n# Paint output maps\npylab.rcParams['figure.figsize'] = 6, 6 # Set figure size\n\n# Put the result into a color plot\nplt.plot(x0c0, x1c0,'r.', label=labels[c0])\nplt.plot(x0c1, x1c1,'g+', label=labels[c1])\nplt.xlabel('$x_' + str(ind[0]) + '$')\nplt.ylabel('$x_' + str(ind[1]) + '$')\nplt.legend(loc='best')\nplt.axis('equal')\npp = pp.reshape(xx.shape)\nCS = plt.contourf(xx, yy, pp, cmap=plt.cm.copper)\nplt.contour(xx, yy, pp, levels=[0.5],\n colors='b', linewidths=(3,))\n\nplt.colorbar(CS, ticks=[0, 0.5, 1])\n\n\n\nplt.show()", "_____no_output_____" ] ], [ [ "#### 3.2.5. Polynomial Logistic Regression\n\nThe error rates of the logistic regression model can be potentially reduced by using polynomial transformations.\n\nTo compute the polynomial transformation up to a given degree, we can use the `PolynomialFeatures` method in `sklearn.preprocessing`.", "_____no_output_____" ] ], [ [ "# Parameters of the algorithms\nrho = float(1)/50 # Learning step\nn_it = 500 # Number of iterations\ng = 5 # Degree of polynomial\n\n# Compute Z_tr\npoly = PolynomialFeatures(degree=g)\nZ_tr = poly.fit_transform(Xn_tr)\n# Normalize columns (this is useful to make algorithms more stable).)\nZn, mz, sz = normalize(Z_tr[:,1:])\nZ_tr = np.concatenate((np.ones((n_tr,1)), Zn), axis=1)\n\n# Compute Z_tst\nZ_tst = poly.fit_transform(Xn_tst)\nZn, mz, sz = normalize(Z_tst[:,1:], mz, sz)\nZ_tst = np.concatenate((np.ones((n_tst,1)), Zn), axis=1)\n\n# Convert target arrays to column vectors\nY_tr2 = Y_tr[np.newaxis].T\nY_tst2 = Y_tst[np.newaxis].T\n\n# Running the gradient descent algorithm\nw, nll_tr = logregFit(Z_tr, Y_tr2, rho, n_it)\n\n# Classify training and test data\np_tr, D_tr = logregPredict(Z_tr, w)\np_tst, D_tst = logregPredict(Z_tst, w)\n \n# Compute error rates\nE_tr = D_tr!=Y_tr\nE_tst = D_tst!=Y_tst\n\n# Error rates\npe_tr = float(sum(E_tr)) / n_tr\npe_tst = float(sum(E_tst)) / n_tst\n\n# NLL plot.\nplt.plot(range(n_it), nll_tr,'b.:', label='Train')\nplt.xlabel('Iteration')\nplt.ylabel('Negative Log-Likelihood')\nplt.legend()\n\nprint('The optimal weights are:')\nprint(w)\nprint('The final error rates are:')\nprint('- Training:', pe_tr)\nprint('- Test:', pe_tst)\nprint('The NLL after training is', nll_tr[len(nll_tr)-1])", "The optimal weights are:\n[[ 0.91252707]\n [ 0.37799677]\n [-0.86858232]\n [-2.22819769]\n [ 0.31935683]\n [-0.7597234 ]\n [ 1.62293685]\n [-0.59935236]\n [ 2.7594932 ]\n [ 1.0980507 ]\n [ 4.94578133]\n [-1.06423937]\n [-0.11460838]\n [ 2.65741964]\n [ 0.85181291]\n [-0.96029884]\n [-0.930799 ]\n [ 1.26419888]\n [ 3.67864276]\n [-1.17890012]\n [ 0.25785336]]\nThe final error rates are:\n- Training: 0.19696969696969696\n- Test: 0.4117647058823529\nThe NLL after training is 28.1853726886\n" ] ], [ [ "Visualizing the posterior map we can se that the polynomial transformation produces nonlinear decision boundaries.", "_____no_output_____" ] ], [ [ "# Compute Z_grid\nZ_grid = poly.fit_transform(X_grid)\nn_grid = Z_grid.shape[0]\nZn, mz, sz = normalize(Z_grid[:,1:], mz, sz)\nZ_grid = np.concatenate((np.ones((n_grid,1)), Zn), axis=1)\n\n# Compute the classifier output for all samples in the grid.\npp, dd = logregPredict(Z_grid, w)\npp = pp.reshape(xx.shape)\n\n# Paint output maps\npylab.rcParams['figure.figsize'] = 6, 6 # Set figure size\n\nplt.plot(x0c0, x1c0,'r.', label=labels[c0])\nplt.plot(x0c1, x1c1,'g+', label=labels[c1])\nplt.xlabel('$x_' + str(ind[0]) + '$')\nplt.ylabel('$x_' + str(ind[1]) + '$')\nplt.axis('equal')\nplt.legend(loc='best')\nCS = plt.contourf(xx, yy, pp, cmap=plt.cm.copper)\nplt.contour(xx, yy, pp, levels=[0.5],\n colors='b', linewidths=(3,))\n\nplt.colorbar(CS, ticks=[0, 0.5, 1])\n\nplt.show()", "_____no_output_____" ] ], [ [ "## 4. Regularization and MAP estimation.\n\nAn alternative to the ML estimation of the weights in logistic regression is Maximum A Posteriori estimation. Modelling the logistic regression weights as a random variable with prior distribution $p_{\\bf W}({\\bf w})$, the MAP estimate is defined as\n\n$$\n\\hat{\\bf w}_{\\text{MAP}} = \\arg\\max_{\\bf w} p({\\bf w}|{\\mathcal D})\n$$\n\nThe posterior density $p({\\bf w}|{\\mathcal D})$ is related to the likelihood function and the prior density of the weights, $p_{\\bf W}({\\bf w})$ through the Bayes rule\n\n$$\np({\\bf w}|{\\mathcal D}) = \n \\frac{P\\left({\\mathcal D}|{\\bf w}\\right) \\; p_{\\bf W}({\\bf w})}\n {p\\left({\\mathcal D}\\right)}\n$$\n\nIn general, the denominator in this expression cannot be computed analytically. However, it is not required for MAP estimation because it does not depend on ${\\bf w}$. Therefore, the MAP solution is given by\n\n\\begin{align}\n\\hat{\\bf w}_{\\text{MAP}} & = \\arg\\max_{\\bf w} P\\left({\\mathcal D}|{\\bf w}\\right) \\; p_{\\bf W}({\\bf w}) \\\\\n& = \\arg\\max_{\\bf w} \\left\\{ L({\\mathbf w}) + \\log p_{\\bf W}({\\bf w})\\right\\} \\\\\n& = \\arg\\min_{\\bf w} \\left\\{ \\text{NLL}({\\mathbf w}) - \\log p_{\\bf W}({\\bf w})\\right\\}\n\\end{align}", "_____no_output_____" ], [ "\nIn the light of this expression, we can conclude that the MAP solution is affected by two terms:\n\n - The likelihood, which takes large values for parameter vectors $\\bf w$ that fit well the training data\n - The prior distribution of weights $p_{\\bf W}({\\bf w})$, which expresses our *a priori* preference for some solutions. Usually, we recur to prior distributions that take large values when $\\|{\\bf w}\\|$ is small (associated to smooth classification borders).\n", "_____no_output_____" ], [ "We can check that the MAP criterion adds a penalty term to the ML objective, that penalizes parameter vectors for which the prior distribution of weights takes small values.\n\n### 4.1 MAP estimation with Gaussian prior\n\nIf we assume that ${\\bf W}$ is a zero-mean Gaussian random variable with variance matrix $v{\\bf I}$, \n\n$$\np_{\\bf W}({\\bf w}) = \\frac{1}{(2\\pi v)^{N/2}} \\exp\\left(-\\frac{1}{2v}\\|{\\bf w}\\|^2\\right)\n$$\n\nthe MAP estimate becomes\n\n\\begin{align}\n\\hat{\\bf w}_{\\text{MAP}} \n &= \\arg\\min_{\\bf w} \\left\\{L({\\bf w}) + \\frac{1}{C}\\|{\\bf w}\\|^2\n \\right\\}\n\\end{align}\n\nwhere $C = 2v$. Noting that\n\n$$\\nabla_{\\bf w}\\left\\{L({\\bf w}) + \\frac{1}{C}\\|{\\bf w}\\|^2\\right\\} \n= - {\\bf Z} \\left({\\bf y}-\\hat{\\bf p}_n\\right) + \\frac{2}{C}{\\bf w},\n$$\n\nwe obtain the following gradient descent rule for MAP estimation\n\n\\begin{align}\n{\\bf w}_{n+1} &= \\left(1-\\frac{2\\rho_n}{C}\\right){\\bf w}_n \n + \\rho_n {\\bf Z} \\left({\\bf y}-\\hat{\\bf p}_n\\right)\n\\end{align}\n", "_____no_output_____" ], [ "### 4.2 MAP estimation with Laplacian prior\n\nIf we assume that ${\\bf W}$ follows a multivariate zero-mean Laplacian distribution given by\n\n$$\np_{\\bf W}({\\bf w}) = \\frac{1}{(2 C)^{N}} \\exp\\left(-\\frac{1}{C}\\|{\\bf w}\\|_1\\right)\n$$\n\n(where $\\|{\\bf w}\\|=|w_1|+\\ldots+|w_N|$ is the $L_1$ norm of ${\\bf w}$), the MAP estimate is\n\n\\begin{align}\n\\hat{\\bf w}_{\\text{MAP}} \n &= \\arg\\min_{\\bf w} \\left\\{L({\\bf w}) + \\frac{1}{C}\\|{\\bf w}\\|_1\n \\right\\}\n\\end{align}\n\nThe additional term introduced by the prior in the optimization algorithm is usually named the *regularization term*. It is usually very effective to avoid overfitting when the dimension of the weight vectors is high. Parameter $C$ is named the *inverse regularization strength*.", "_____no_output_____" ], [ "**Exercise 5**: Derive the gradient descent rules for MAP estimation of the logistic regression weights with Laplacian prior.", "_____no_output_____" ], [ "## 5. Other optimization algorithms\n\n### 5.1. Stochastic Gradient descent.\n\nStochastic gradient descent (SGD) is based on the idea of using a single sample at each iteration of the learning algorithm. The SGD rule for ML logistic regression is\n\n\\begin{align}\n{\\bf w}_{n+1} &= {\\bf w}_n \n + \\rho_n {\\bf z}^{(n)} \\left(y^{(n)}-\\hat{p}^{(n)}_n\\right)\n\\end{align}\n\nOnce all samples in the training set have been applied, the algorith can continue by applying the training set several times.\n\nThe computational cost of each iteration of SGD is much smaller than that of gradient descent, though it usually needs more iterations to converge.", "_____no_output_____" ], [ "**Exercise 6**: Modify logregFit to implement an algorithm that applies the SGD rule.", "_____no_output_____" ], [ "### 5.2. Newton's method\n\nAssume that the function to be minimized, $C({\\bf w})$, can be approximated by its second order Taylor series expansion around ${\\bf w}_0$\n\n$$ \nC({\\bf w}) \\approx C({\\bf w}_0) \n+ \\nabla_{\\bf w}^\\intercal C({\\bf w}_0)({\\bf w}-{\\bf w}_0)\n+ \\frac{1}{2}({\\bf w}-{\\bf w}_0)^\\intercal{\\bf H}({\\bf w}_0)({\\bf w}-{\\bf w}_0)\n$$\n\nwhere ${\\bf H}({\\bf w}_k)$ is the <a href=https://en.wikipedia.org/wiki/Hessian_matrix> *Hessian* matrix</a> of $C$ at ${\\bf w}_k$. Taking the gradient of $C({\\bf w})$, and setting the result to ${\\bf 0}$, the minimum of C around ${\\bf w}_0$ can be approximated as\n\n$$ \n{\\bf w}^* = {\\bf w}_0 - {\\bf H}({\\bf w}_0)^{-1} \\nabla_{\\bf w}^\\intercal C({\\bf w}_0)\n$$\n\nSince the second order polynomial is only an approximation to $C$, ${\\bf w}^*$ is only an approximation to the optimal weight vector, but we can expect ${\\bf w}^*$ to be closer to the minimizer of $C$ than ${\\bf w}_0$. Thus, we can repeat the process, computing a second order approximation around ${\\bf w}^*$ and a new approximation to the minimizer.\n\n<a href=https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization> Newton's method</a> is based on this idea. At each optization step, the function to be minimized is approximated by a second order approximation using a Taylor series expansion around the current estimate. As a result, the learning rules becomes\n\n$$\\hat{\\bf w}_{n+1} = \\hat{\\bf w}_{n} - \\rho_n {\\bf H}({\\bf w}_k)^{-1} \\nabla_{{\\bf w}}C({\\bf w}_k)\n$$\n", "_____no_output_____" ], [ "\nFor instance, for the MAP estimate with Gaussian prior, the *Hessian* matrix becomes\n\n$$\n{\\bf H}({\\bf w}) \n = \\frac{2}{C}{\\bf I} + \\sum_{k=1}^K f({\\bf w}^T {\\bf z}^{(k)}) \\left(1-f({\\bf w}^T {\\bf z}^{(k)})\\right){\\bf z}^{(k)} ({\\bf z}^{(k)})^\\intercal\n$$\n\nDefining diagonal matrix\n\n$$\n{\\mathbf S}({\\bf w}) = \\text{diag}\\left(f({\\bf w}^T {\\bf z}^{(k)}) \\left(1-f({\\bf w}^T {\\bf z}^{(k)})\\right)\\right)\n$$\n\nthe Hessian matrix can be written in more compact form as\n\n$$\n{\\bf H}({\\bf w}) \n = \\frac{2}{C}{\\bf I} + {\\bf Z}^\\intercal {\\bf S}({\\bf w}) {\\bf Z}\n$$\n\nTherefore, the Newton's algorithm for logistic regression becomes\n\n\\begin{align}\n\\hat{\\bf w}_{n+1} = \\hat{\\bf w}_{n} + \n\\rho_n \n\\left(\\frac{2}{C}{\\bf I} + {\\bf Z}^\\intercal {\\bf S}(\\hat{\\bf w}_{n})\n{\\bf Z}\n\\right)^{-1} \n{\\bf Z}^\\intercal \\left({\\bf y}-\\hat{\\bf p}_n\\right)\n\\end{align}\n\nSome variants of the Newton method are implemented in the <a href=\"http://scikit-learn.org/stable/\"> Scikit-learn </a> package.\n\n", "_____no_output_____" ] ], [ [ "def logregFit2(Z_tr, Y_tr, rho, n_it, C=1e4):\n\n # Compute Z's\n r = 2.0/C\n n_dim = Z_tr.shape[1]\n\n # Initialize variables\n nll_tr = np.zeros(n_it)\n pe_tr = np.zeros(n_it)\n w = np.random.randn(n_dim,1)\n\n # Running the gradient descent algorithm\n for n in range(n_it):\n p_tr = logistic(np.dot(Z_tr, w))\n \n sk = np.multiply(p_tr, 1-p_tr)\n S = np.diag(np.ravel(sk.T))\n\n # Compute negative log-likelihood\n nll_tr[n] = - np.dot(Y_tr.T, np.log(p_tr)) - np.dot((1-Y_tr).T, np.log(1-p_tr))\n\n # Update weights\n invH = np.linalg.inv(r*np.identity(n_dim) + np.dot(Z_tr.T, np.dot(S, Z_tr)))\n\n w += rho*np.dot(invH, np.dot(Z_tr.T, Y_tr - p_tr))\n\n return w, nll_tr", "_____no_output_____" ], [ "# Parameters of the algorithms\nrho = float(1)/50 # Learning step\nn_it = 500 # Number of iterations\nC = 1000\ng = 4\n\n# Compute Z_tr\npoly = PolynomialFeatures(degree=g)\nZ_tr = poly.fit_transform(X_tr)\n# Normalize columns (this is useful to make algorithms more stable).)\nZn, mz, sz = normalize(Z_tr[:,1:])\nZ_tr = np.concatenate((np.ones((n_tr,1)), Zn), axis=1)\n\n# Compute Z_tst\nZ_tst = poly.fit_transform(X_tst)\nZn, mz, sz = normalize(Z_tst[:,1:], mz, sz)\nZ_tst = np.concatenate((np.ones((n_tst,1)), Zn), axis=1)\n\n# Convert target arrays to column vectors\nY_tr2 = Y_tr[np.newaxis].T\nY_tst2 = Y_tst[np.newaxis].T\n\n# Running the gradient descent algorithm\nw, nll_tr = logregFit2(Z_tr, Y_tr2, rho, n_it, C)\n\n# Classify training and test data\np_tr, D_tr = logregPredict(Z_tr, w)\np_tst, D_tst = logregPredict(Z_tst, w)\n \n# Compute error rates\nE_tr = D_tr!=Y_tr\nE_tst = D_tst!=Y_tst\n\n# Error rates\npe_tr = float(sum(E_tr)) / n_tr\npe_tst = float(sum(E_tst)) / n_tst\n\n# NLL plot.\nplt.plot(range(n_it), nll_tr,'b.:', label='Train')\nplt.xlabel('Iteration')\nplt.ylabel('Negative Log-Likelihood')\nplt.legend()\n\nprint('The final error rates are:')\nprint('- Training:', str(pe_tr))\nprint('- Test:', str(pe_tst))\nprint('The NLL after training is:', str(nll_tr[len(nll_tr)-1]))", "_____no_output_____" ] ], [ [ "## 6. Logistic regression in Scikit Learn.\n\nThe <a href=\"http://scikit-learn.org/stable/\"> scikit-learn </a> package includes an efficient implementation of <a href=\"http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression\"> logistic regression</a>. To use it, we must first create a classifier object, specifying the parameters of the logistic regression algorithm.", "_____no_output_____" ] ], [ [ "# Create a logistic regression object.\nLogReg = linear_model.LogisticRegression(C=1.0)\n\n# Compute Z_tr\npoly = PolynomialFeatures(degree=g)\nZ_tr = poly.fit_transform(Xn_tr)\n# Normalize columns (this is useful to make algorithms more stable).)\nZn, mz, sz = normalize(Z_tr[:,1:])\nZ_tr = np.concatenate((np.ones((n_tr,1)), Zn), axis=1)\n\n# Compute Z_tst\nZ_tst = poly.fit_transform(Xn_tst)\nZn, mz, sz = normalize(Z_tst[:,1:], mz, sz)\nZ_tst = np.concatenate((np.ones((n_tst,1)), Zn), axis=1)\n\n# Fit model to data.\nLogReg.fit(Z_tr, Y_tr)\n\n# Classify training and test data\nD_tr = LogReg.predict(Z_tr)\nD_tst = LogReg.predict(Z_tst)\n \n# Compute error rates\nE_tr = D_tr!=Y_tr\nE_tst = D_tst!=Y_tst\n\n# Error rates\npe_tr = float(sum(E_tr)) / n_tr\npe_tst = float(sum(E_tst)) / n_tst\n\nprint('The final error rates are:')\nprint('- Training:', str(pe_tr))\nprint('- Test:', str(pe_tst))\n\n# Compute Z_grid\nZ_grid = poly.fit_transform(X_grid)\nn_grid = Z_grid.shape[0]\nZn, mz, sz = normalize(Z_grid[:,1:], mz, sz)\nZ_grid = np.concatenate((np.ones((n_grid,1)), Zn), axis=1)\n\n# Compute the classifier output for all samples in the grid.\ndd = LogReg.predict(Z_grid)\npp = LogReg.predict_proba(Z_grid)[:,1]\npp = pp.reshape(xx.shape)\n\n# Paint output maps\npylab.rcParams['figure.figsize'] = 6, 6 # Set figure size\n\nplt.plot(x0c0, x1c0,'r.', label=labels[c0])\nplt.plot(x0c1, x1c1,'g+', label=labels[c1])\nplt.xlabel('$x_' + str(ind[0]) + '$')\nplt.ylabel('$x_' + str(ind[1]) + '$')\nplt.axis('equal')\n\nplt.contourf(xx, yy, pp, cmap=plt.cm.copper)\nplt.legend(loc='best')\n\nplt.contour(xx, yy, pp, levels=[0.5],\n colors='b', linewidths=(3,))\n\nplt.colorbar(CS, ticks=[0, 0.5, 1])\n\nplt.show()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ] ]

cb2ff30dd00c2bcfb3fe9efbedf73fc3c2384249

83,240

ipynb

Jupyter Notebook

my_code/day_0/python_basics.ipynb

mpc97/lxmls

3debbf262e35cbe3b126a2da5ac0ae2c68474cc5

[ "MIT" ]

null

my_code/day_0/python_basics.ipynb

mpc97/lxmls

3debbf262e35cbe3b126a2da5ac0ae2c68474cc5

[ "MIT" ]

null

my_code/day_0/python_basics.ipynb

mpc97/lxmls

3debbf262e35cbe3b126a2da5ac0ae2c68474cc5

[ "MIT" ]

null

80.658915

29,484

0.841579

[ [ [ "# Installation\nMake sure to have all the required software installed after proceeding. \nFor installation help, please consult the [school guide](http://lxmls.it.pt/2018/LxMLS_guide_2018.pdf).\n", "_____no_output_____" ], [ "# Python Basics", "_____no_output_____" ] ], [ [ "print('Hello World!')", "Hello World!\n" ] ], [ [ "We could also have this code in a separate file and still run it on a notebook like this: `run ./my_file.py`", "_____no_output_____" ], [ "### Basic Math Operations", "_____no_output_____" ] ], [ [ "print(3 + 5)\nprint(3 - 5)\nprint(3 * 5)\nprint(3 ** 5)", "8\n-2\n15\n243\n" ], [ "# Observation: this code gives different results for python2 and python3\n# because of the behaviour for the division operator\nprint(3 / 5.0)\nprint(3 / 5)\n\n# for compatibility, make sure to use the follow statement\nfrom __future__ import division\nprint(3 / 5.0)\nprint(3 / 5)", "_____no_output_____" ] ], [ [ "In this case I'm using Python3 but in Python2, to force floating point division instead of the default integer division, we would have to force at least one of the operands to be a floating point number, like we can see above: `print(3 / 5.0)`", "_____no_output_____" ], [ "### Data Strutures", "_____no_output_____" ] ], [ [ "countries = ['Portugal','Spain','United Kingdom']\nprint(countries)", "['Portugal', 'Spain', 'United Kingdom']\n" ] ], [ [ "## Exercise 0.1\nUse L[i:j] to return the countries in the Iberian Peninsula.", "_____no_output_____" ] ], [ [ "countries[0:2]", "_____no_output_____" ] ], [ [ "Forgetting the `0` also does the trick.", "_____no_output_____" ] ], [ [ "countries[:2]", "_____no_output_____" ] ], [ [ "### Loops and Indentation", "_____no_output_____" ] ], [ [ "i = 2\nwhile i < 10:\n print(i)\n i += 2", "2\n4\n6\n8\n" ], [ "for i in range(2,10,2):\n print(i)", "2\n4\n6\n8\n" ], [ "a=1\nwhile a <= 3:\n print(a)\n a += 1", "1\n2\n3\n" ] ], [ [ "## Exercise 0.2\nCan you then predict the output of the following code?\n\nYes, the following code results in an infinite loop that prints 1 everytime :)", "_____no_output_____" ] ], [ [ "a=1\nwhile a <= 3:\n print(a)\na += 1", "_____no_output_____" ] ], [ [ "### Control Flow", "_____no_output_____" ] ], [ [ "hour = 16\nif hour < 12:\n print('Good morning!')\nelif hour >= 12 and hour < 20:\n print('Good afternoon!')\nelse:\n print('Good evening!')", "Good afternoon!\n" ] ], [ [ "### Functions", "_____no_output_____" ] ], [ [ "def greet(hour):\n if hour < 0 or hour > 24:\n print('Invalid hour: it should be between 0 and 24.')\n elif hour < 12:\n print('Good morning!')\n elif hour >= 12 and hour < 20:\n print('Good afternoon!')\n else:\n print('Good evening!')", "_____no_output_____" ] ], [ [ "## Exercise 0.3 \nNote that the previous code allows the hour to be less than 0 or more than 24. Change the code in order to\nindicate that the hour given as input is invalid. Your output should be something like:\n\n``greet(50)\nInvalid hour: it should be between 0 and 24.\ngreet(-5)\nInvalid hour: it should be between 0 and 24.``", "_____no_output_____" ] ], [ [ "greet(50)", "Invalid hour: it should be between 0 and 24.\n" ], [ "greet(-5)", "Invalid hour: it should be between 0 and 24.\n" ] ], [ [ "### Profiling", "_____no_output_____" ] ], [ [ "%prun greet(22)", "Good evening!\n " ] ], [ [ "### Debugging in Python", "_____no_output_____" ] ], [ [ "def greet2(hour):\n if hour < 12:\n print('Good morning!')\n elif hour >= 12 and hour < 20:\n print('Good afternoon!')\n else:\n import pdb; pdb.set_trace()\n print('Good evening!')", "_____no_output_____" ], [ "greet2(22)", "> \u001b[1;32m<ipython-input-19-71eda3bc9ed1>\u001b[0m(8)\u001b[0;36mgreet2\u001b[1;34m()\u001b[0m\n\u001b[1;32m 4 \u001b[1;33m \u001b[1;32melif\u001b[0m \u001b[0mhour\u001b[0m \u001b[1;33m>=\u001b[0m \u001b[1;36m12\u001b[0m \u001b[1;32mand\u001b[0m \u001b[0mhour\u001b[0m \u001b[1;33m<\u001b[0m \u001b[1;36m20\u001b[0m\u001b[1;33m:\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 5 \u001b[1;33m \u001b[0mprint\u001b[0m\u001b[1;33m(\u001b[0m\u001b[1;34m'Good afternoon!'\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 6 \u001b[1;33m \u001b[1;32melse\u001b[0m\u001b[1;33m:\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 7 \u001b[1;33m \u001b[1;32mimport\u001b[0m \u001b[0mpdb\u001b[0m\u001b[1;33m;\u001b[0m \u001b[0mpdb\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mset_trace\u001b[0m\u001b[1;33m(\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m----> 8 \u001b[1;33m \u001b[0mprint\u001b[0m\u001b[1;33m(\u001b[0m\u001b[1;34m'Good evening!'\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m\nipdb> p hour\n22\nipdb> c\nGood evening!\n" ] ], [ [ "## Exceptions\nfor a complete list of built-in exceptions, see [http://docs.python.org/2/library/exceptions.html](http://docs.python.org/2/library/exceptions.html)", "_____no_output_____" ] ], [ [ "raise ValueError(\"Invalid input value.\")", "_____no_output_____" ], [ "while True:\n try:\n x = int(input(\"Please enter a number: \"))\n break\n except ValueError:\n print(\"Oops! That was no valid number. Try again...\")", "Please enter a number: ?\nOops! That was no valid number. Try again...\nPlease enter a number: Manuel\nOops! That was no valid number. Try again...\nPlease enter a number: 5\n" ] ], [ [ "### Extending basic Functionalities with Modules", "_____no_output_____" ] ], [ [ "import numpy as np\nnp.var?", "_____no_output_____" ], [ "np.random.normal?", "_____no_output_____" ] ], [ [ "### Organizing your Code with your own modules\nSee details in [guide](http://lxmls.it.pt/2018/LxMLS_guide_2018.pdf)", "_____no_output_____" ], [ "## Matplotlib – Plotting in Python", "_____no_output_____" ] ], [ [ "import numpy as np\nimport matplotlib.pyplot as plt\n%matplotlib inline \nX = np.linspace(-4, 4, 1000)\nplt.plot(X, X**2*np.cos(X**2))\nplt.savefig(\"simple.pdf\")", "_____no_output_____" ] ], [ [ "## Exercise 0.5 \nTry running the following on Jupyter, which will introduce you to some of the basic numeric and plotting\noperations.", "_____no_output_____" ] ], [ [ "# This will import the numpy library\n# and give it the np abbreviation\nimport numpy as np\n# This will import the plotting library\nimport matplotlib.pyplot as plt\n# Linspace will return 1000 points,\n# evenly spaced between -4 and +4\nX = np.linspace(-4, 4, 1000)\n# Y[i] = X[i]**2\nY = X**2\n# Plot using a red line ('r')\nplt.plot(X, Y, 'r')\n# arange returns integers ranging from -4 to +4\n# (the upper argument is excluded!)\nInts = np.arange(-4,5)\n# We plot these on top of the previous plot\n# using blue circles (o means a little circle)\nplt.plot(Ints, Ints**2, 'bo')\n# You may notice that the plot is tight around the line\n# Set the display limits to see better\nplt.xlim(-4.5,4.5)\nplt.ylim(-1,17)\nplt.show()", "_____no_output_____" ], [ "import matplotlib.pyplot as plt\nimport numpy as np\nX = np.linspace(0, 4 * np.pi, 1000)\nC = np.cos(X)\nS = np.sin(X)\nplt.plot(X, C)\nplt.plot(X, S)\nplt.show()", "_____no_output_____" ] ], [ [ "# Exercise 0.6 \nRun the following example and lookup the ptp function/method (use the ? functionality in Jupyter)", "_____no_output_____" ] ], [ [ "A = np.arange(100)\n# These two lines do exactly the same thing\nprint(np.mean(A))\nprint(A.mean())", "49.5\n49.5\n" ], [ "np.ptp?", "_____no_output_____" ] ], [ [ "# Exercise 0.7 ", "_____no_output_____" ], [ "Consider the following approximation to compute an integral\n\n\n\\begin{equation*}\n \\int_0^1 f(x) dx \\approx \\sum_{i=0}^{999} \\frac{f(i/1000)}{1000}\n\\end{equation*}\n\nUse numpy to implement this for $f(x) = x^2$. You should not need to use any loops. Note that integer division in Python 2.x returns the floor division (use floats – e.g. 5.0/2.0 – to obtain rationals). The exact value is 1/3. How close\nis the approximation?", "_____no_output_____" ] ], [ [ "def f(x):\n return(x**2)\n\nsum([f(x*1./1000)/1000 for x in range(0,1000)])", "_____no_output_____" ] ], [ [ "# Exercise 0.8 \nIn the rest of the school we will represent both matrices and vectors as numpy arrays. You can create arrays\nin different ways, one possible way is to create an array of zeros.", "_____no_output_____" ] ], [ [ "import numpy as np\nm = 3\nn = 2\na = np.zeros([m,n])\nprint(a)", "[[0. 0.]\n [0. 0.]\n [0. 0.]]\n" ] ], [ [ "You can check the shape and the data type of your array using the following commands:", "_____no_output_____" ] ], [ [ "print(a.shape)\nprint(a.dtype.name)", "(3, 2)\nfloat64\n" ] ], [ [ "This shows you that “a” is an 3*2 array of type float64. By default, arrays contain 64 bit6 floating point numbers. You\ncan specify the particular array type by using the keyword dtype.", "_____no_output_____" ] ], [ [ "a = np.zeros([m,n], dtype=int)\nprint(a.dtype)", "int32\n" ] ], [ [ "You can also create arrays from lists of numbers:", "_____no_output_____" ] ], [ [ "a = np.array([[2,3],[3,4]])\nprint(a)", "[[2 3]\n [3 4]]\n" ] ], [ [ "# Exercise 0.9 \nYou can multiply two matrices by looping over both indexes and multiplying the individual entries.", "_____no_output_____" ] ], [ [ "a = np.array([[2,3],[3,4]])\nb = np.array([[1,1],[1,1]])\na_dim1, a_dim2 = a.shape\nb_dim1, b_dim2 = b.shape\nc = np.zeros([a_dim1,b_dim2])\nfor i in range(a_dim1):\n for j in range(b_dim2):\n for k in range(a_dim2):\n c[i,j] += a[i,k]*b[k,j]\nprint(c)", "[[5. 5.]\n [7. 7.]]\n" ] ], [ [ "This is, however, cumbersome and inefficient. Numpy supports matrix multiplication with the dot function:", "_____no_output_____" ] ], [ [ "d = np.dot(a,b)\nprint(d)", "[[5 5]\n [7 7]]\n" ], [ "a = np.array([1,2])\nb = np.array([1,1])\nnp.dot(a,b)", "_____no_output_____" ], [ "np.outer(a,b)", "_____no_output_____" ], [ "I = np.eye(2)\nx = np.array([2.3, 3.4])\nprint(I)\nprint(np.dot(I,x))", "[[1. 0.]\n [0. 1.]]\n[2.3 3.4]\n" ], [ "A = np.array([ [1, 2], [3, 4] ])\nprint(A)\nprint(A.T)", "[[1 2]\n [3 4]]\n[[1 3]\n [2 4]]\n" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ] ]

cb3002070954753e43a7c973aa62f0a0eec3a0ce

6,038

ipynb

Jupyter Notebook

Big-Data-Clusters/CU8/Public/content/diagnose/tsg086-run-top-for-all-containers.ipynb

meenal-gupta141/tigertoolbox

5c432392f7cab091121a8879ea886b39c54f519b

[ "MIT" ]

541

2019-05-07T11:41:25.000Z

2022-03-29T17:33:19.000Z

Big-Data-Clusters/CU8/Public/content/diagnose/tsg086-run-top-for-all-containers.ipynb

sqlworldwide/tigertoolbox

2abcb62a09daf0116ab1ab9c9dd9317319b23297

[ "MIT" ]

89

2019-05-09T14:23:52.000Z

2022-01-13T20:21:04.000Z

Big-Data-Clusters/CU8/Public/content/diagnose/tsg086-run-top-for-all-containers.ipynb

sqlworldwide/tigertoolbox

2abcb62a09daf0116ab1ab9c9dd9317319b23297

[ "MIT" ]

338

2019-05-08T05:45:16.000Z

2022-03-28T15:35:03.000Z

41.356164

192

0.429944

[ [ [ "TSG086 - Run `top` in all containers\n====================================\n\nSteps\n-----\n\n### Instantiate Kubernetes client", "_____no_output_____" ] ], [ [ "# Instantiate the Python Kubernetes client into 'api' variable\n\nimport os\nfrom IPython.display import Markdown\n\ntry:\n from kubernetes import client, config\n from kubernetes.stream import stream\n\n if \"KUBERNETES_SERVICE_PORT\" in os.environ and \"KUBERNETES_SERVICE_HOST\" in os.environ:\n config.load_incluster_config()\n else:\n try:\n config.load_kube_config()\n except:\n display(Markdown(f'HINT: Use [TSG118 - Configure Kubernetes config](../repair/tsg118-configure-kube-config.ipynb) to resolve this issue.'))\n raise\n api = client.CoreV1Api()\n\n print('Kubernetes client instantiated')\nexcept ImportError:\n display(Markdown(f'HINT: Use [SOP059 - Install Kubernetes Python module](../install/sop059-install-kubernetes-module.ipynb) to resolve this issue.'))\n raise", "_____no_output_____" ] ], [ [ "### Get the namespace for the big data cluster\n\nGet the namespace of the Big Data Cluster from the Kuberenetes API.\n\n**NOTE:**\n\nIf there is more than one Big Data Cluster in the target Kubernetes\ncluster, then either:\n\n- set \\[0\\] to the correct value for the big data cluster.\n- set the environment variable AZDATA\\_NAMESPACE, before starting\n Azure Data Studio.", "_____no_output_____" ] ], [ [ "# Place Kubernetes namespace name for BDC into 'namespace' variable\n\nif \"AZDATA_NAMESPACE\" in os.environ:\n namespace = os.environ[\"AZDATA_NAMESPACE\"]\nelse:\n try:\n namespace = api.list_namespace(label_selector='MSSQL_CLUSTER').items[0].metadata.name\n except IndexError:\n from IPython.display import Markdown\n display(Markdown(f'HINT: Use [TSG081 - Get namespaces (Kubernetes)](../monitor-k8s/tsg081-get-kubernetes-namespaces.ipynb) to resolve this issue.'))\n display(Markdown(f'HINT: Use [TSG010 - Get configuration contexts](../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb) to resolve this issue.'))\n display(Markdown(f'HINT: Use [SOP011 - Set kubernetes configuration context](../common/sop011-set-kubernetes-context.ipynb) to resolve this issue.'))\n raise\n\nprint('The kubernetes namespace for your big data cluster is: ' + namespace)", "_____no_output_____" ] ], [ [ "### Run top in each container", "_____no_output_____" ] ], [ [ "cmd = \"top -b -n 1\"\n\npod_list = api.list_namespaced_pod(namespace)\npod_names = [pod.metadata.name for pod in pod_list.items]\n\nfor pod in pod_list.items:\n container_names = [container.name for container in pod.spec.containers]\n\n for container in container_names:\n print (f\"CONTAINER: {container} / POD: {pod.metadata.name}\")\n try:\n print(stream(api.connect_get_namespaced_pod_exec, pod.metadata.name, namespace, command=['/bin/sh', '-c', cmd], container=container, stderr=True, stdout=True))\n except Exception as err:\n print (f\"Failed to get run 'top' for container: {container} in pod: {pod.metadata.name}. Error: {err}\")", "_____no_output_____" ], [ "print('Notebook execution complete.')", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ] ]

cb30084b9e526cd931581381fd8678fa7437429b

50,697

ipynb

Jupyter Notebook

notebooks/kaggle_yf_wrangling.ipynb

bthodla/single_store_eval

7a7ea878a332ca4dd3d546789718f06ba1cf6ffb

[ "BSD-3-Clause" ]

null

notebooks/kaggle_yf_wrangling.ipynb

bthodla/single_store_eval

7a7ea878a332ca4dd3d546789718f06ba1cf6ffb

[ "BSD-3-Clause" ]

null

notebooks/kaggle_yf_wrangling.ipynb

bthodla/single_store_eval

7a7ea878a332ca4dd3d546789718f06ba1cf6ffb

[ "BSD-3-Clause" ]

null

32.147749

1,861

0.508038

[ [ [ "import pandas as pd", "_____no_output_____" ], [ "data_folder = '..\\\\\\\\..\\\\\\\\..\\\\\\\\..\\\\\\\\Google Drive\\\\\\\\datasets\\\\\\\\mf_data_kaggle\\\\\\\\'", "_____no_output_____" ], [ "def flip_cols2rows(src_df, col_list, item_category, key_col):\n df1 = pd.DataFrame()\n for i in col_list:\n df2 = src_df[[key_col, i]].rename(columns = {key_col: key_col, i: 'value'}).assign(item_desc=i)\n df1 = pd.concat([df1, df2], ignore_index=True)\n\n df1['item_category'] = item_category\n df1 = df1[['fund_symbol', 'item_category', 'item_desc', 'value']]\n return df1", "_____no_output_____" ], [ "def write2disk(df, out_filename):\n df.to_parquet(data_folder+out_filename+'.parquet', engine='auto', compression='snappy',index=False)\n df.to_csv(data_folder+out_filename+'.csv', index=False)", "_____no_output_____" ], [ "def print_df_details(df):\n print(df.shape[0])\n print()\n print(df.dropna(axis=0).head())", "_____no_output_____" ], [ "mf_df = pd.read_parquet(data_folder+'mf.parquet')", "_____no_output_____" ], [ "print_df_details(mf_df)", "23783\n\n fund_symbol quote_type region fund_short_name \\\n0 AAAAX MutualFund US DWS RREEF Real Assets Fund - Cl \n1 AAAEX MutualFund US AllianzGI Health Sciences Fund \n2 AAAFX MutualFund US None \n3 AAAGX MutualFund US Thrivent Large Cap Growth Fund \n4 AAAHX MutualFund US None \n\n fund_long_name currency \\\n0 DWS RREEF Real Assets Fund - Class A USD \n1 Virtus AllianzGI Health Sciences Fund Class P USD \n2 American Century One Choice Blend+ 2015 Portfo... USD \n3 Thrivent Large Cap Growth Fund Class A USD \n4 American Century One Choice Blend+ 2015 Portfo... USD \n\n initial_investment subsequent_investment fund_category \\\n0 1000.0 50.0 World Allocation \n1 1000000.0 NaN Health \n2 2500.0 50.0 Target-Date 2015 \n3 2000.0 50.0 Large Growth \n4 5000000.0 NaN Target-Date 2015 \n\n fund_family ... peer_environment_avg \\\n0 DWS ... 5.05 \n1 Virtus ... 1.43 \n2 American Century Investments ... NaN \n3 Thrivent Funds ... 2.70 \n4 American Century Investments ... NaN \n\n peer_environment_max social_score peer_social_min peer_social_avg \\\n0 10.58 7.43 5.98 9.07 \n1 3.27 12.96 9.52 12.87 \n2 NaN NaN NaN NaN \n3 5.81 10.13 7.25 10.14 \n4 NaN NaN NaN NaN \n\n peer_social_max governance_score peer_governance_min peer_governance_avg \\\n0 11.30 5.43 4.26 7.14 \n1 15.08 8.40 4.96 7.68 \n2 NaN NaN NaN NaN \n3 11.97 8.03 5.30 7.54 \n4 NaN NaN NaN NaN \n\n peer_governance_max \n0 8.11 \n1 10.30 \n2 NaN \n3 8.90 \n4 NaN \n\n[5 rows x 298 columns]\n" ], [ "key_column = \"fund_symbol\"\n\nweek_52 = [\n \"week52_high_low_change\",\n \"week52_high_low_change_perc\",\n \"week52_high\",\n \"week52_high_change\",\n \"week52_high_change_perc\",\n \"week52_low\",\n \"week52_low_change\",\n \"week52_low_change_perc\"\n]\n\nexp_ratio = [\n \"fund_annual_report_net_expense_ratio\",\n \"category_annual_report_net_expense_ratio\",\n \"fund_prospectus_net_expense_ratio\",\n \"fund_prospectus_gross_expense_ratio\",\n \"fund_max_12b1_fee\",\n \"fund_max_front_end_sales_load\",\n \"category_max_front_end_sales_load\",\n \"fund_max_deferred_sales_load\",\n \"category_max_deferred_sales_load\",\n \"fund_year3_expense_projection\",\n \"fund_year5_expense_projection\",\n \"fund_year10_expense_projection\"\n]\n\nasset_allocation = [\n \"asset_cash\",\n \"asset_stocks\",\n \"asset_bonds\",\n \"asset_others\",\n \"asset_preferred\",\n \"asset_convertible\"\n]\n\nsector_allocation = [\n \"fund_sector_basic_materials\",\n \"fund_sector_communication_services\",\n \"fund_sector_consumer_cyclical\",\n \"fund_sector_consumer_defensive\",\n \"fund_sector_energy\",\n \"fund_sector_financial_services\",\n \"fund_sector_healthcare\",\n \"fund_sector_industrials\",\n \"fund_sector_real_estate\",\n \"fund_sector_technology\",\n \"fund_sector_utilities\"\n]\n\nratio = [\n \"fund_price_book_ratio\",\n \"category_price_book_ratio\",\n \"fund_price_cashflow_ratio\",\n \"category_price_cashflow_ratio\",\n \"fund_price_earning_ratio\",\n \"category_price_earning_ratio\",\n \"fund_price_sales_ratio\",\n \"category_price_sales_ratio\",\n \"fund_median_market_cap\",\n \"category_median_market_cap\",\n \"fund_year3_earnings_growth\",\n \"category_year3_earnings_growth\",\n \"fund_bond_maturity\",\n \"category_bond_maturity\",\n \"fund_bond_duration\",\n \"category_bond_duration\"\n]\n\nbond_rating = [\n \"fund_bonds_us_government\",\n \"fund_bonds_aaa\",\n \"fund_bonds_aa\",\n \"fund_bonds_a\",\n \"fund_bonds_bbb\",\n \"fund_bonds_bb\",\n \"fund_bonds_b\",\n \"fund_bonds_below_b\",\n \"fund_bonds_others\"\n]\n\nreturns = [\n \"fund_return_ytd\",\n \"category_return_ytd\",\n \"fund_return_1month\",\n \"category_return_1month\",\n \"fund_return_3months\",\n \"category_return_3months\",\n \"fund_return_1year\",\n \"category_return_1year\",\n \"fund_return_3years\",\n \"category_return_3years\",\n \"fund_return_5years\",\n \"category_return_5years\",\n \"fund_return_10years\",\n \"category_return_10years\",\n \"fund_return_last_bull_market\",\n \"category_return_last_bull_market\",\n \"fund_return_last_bear_market\",\n \"category_return_last_bear_market\",\n \"years_up\",\n \"years_down\",\n \"quarters_up\",\n \"quarters_down\"\n]\n\nannual_returns = [\n \"fund_return_2020\",\n \"category_return_2020\",\n \"fund_return_2019\",\n \"category_return_2019\",\n \"fund_return_2018\",\n \"category_return_2018\",\n \"fund_return_2017\",\n \"category_return_2017\",\n \"fund_return_2016\",\n \"category_return_2016\",\n \"fund_return_2015\",\n \"category_return_2015\",\n \"fund_return_2014\",\n \"category_return_2014\",\n \"fund_return_2013\",\n \"category_return_2013\",\n \"fund_return_2012\",\n \"category_return_2012\",\n \"fund_return_2011\",\n \"category_return_2011\",\n \"fund_return_2010\",\n \"category_return_2010\",\n \"fund_return_2009\",\n \"category_return_2009\",\n \"fund_return_2008\",\n \"category_return_2008\",\n \"fund_return_2007\",\n \"category_return_2007\",\n \"fund_return_2006\",\n \"category_return_2006\",\n \"fund_return_2005\",\n \"category_return_2005\",\n \"fund_return_2004\",\n \"category_return_2004\",\n \"fund_return_2003\",\n \"category_return_2003\",\n \"fund_return_2002\",\n \"category_return_2002\",\n \"fund_return_2001\",\n \"category_return_2001\",\n \"fund_return_2000\",\n \"category_return_2000\"\n]\n\nquarterly_returns = [\n \"fund_return_2021_q3\",\n \"fund_return_2021_q2\",\n \"fund_return_2021_q1\",\n \"fund_return_2020_q4\",\n \"fund_return_2020_q3\",\n \"fund_return_2020_q2\",\n \"fund_return_2020_q1\",\n \"fund_return_2019_q4\",\n \"fund_return_2019_q3\",\n \"fund_return_2019_q2\",\n \"fund_return_2019_q1\",\n \"fund_return_2018_q4\",\n \"fund_return_2018_q3\",\n \"fund_return_2018_q2\",\n \"fund_return_2018_q1\",\n \"fund_return_2017_q4\",\n \"fund_return_2017_q3\",\n \"fund_return_2017_q2\",\n \"fund_return_2017_q1\",\n \"fund_return_2016_q4\",\n \"fund_return_2016_q3\",\n \"fund_return_2016_q2\",\n \"fund_return_2016_q1\",\n \"fund_return_2015_q4\",\n \"fund_return_2015_q3\",\n \"fund_return_2015_q2\",\n \"fund_return_2015_q1\",\n \"fund_return_2014_q4\",\n \"fund_return_2014_q3\",\n \"fund_return_2014_q2\",\n \"fund_return_2014_q1\",\n \"fund_return_2013_q4\",\n \"fund_return_2013_q3\",\n \"fund_return_2013_q2\",\n \"fund_return_2013_q1\",\n \"fund_return_2012_q4\",\n \"fund_return_2012_q3\",\n \"fund_return_2012_q2\",\n \"fund_return_2012_q1\",\n \"fund_return_2011_q4\",\n \"fund_return_2011_q3\",\n \"fund_return_2011_q2\",\n \"fund_return_2011_q1\",\n \"fund_return_2010_q4\",\n \"fund_return_2010_q3\",\n \"fund_return_2010_q2\",\n \"fund_return_2010_q1\",\n \"fund_return_2009_q4\",\n \"fund_return_2009_q3\",\n \"fund_return_2009_q2\",\n \"fund_return_2009_q1\",\n \"fund_return_2008_q4\",\n \"fund_return_2008_q3\",\n \"fund_return_2008_q2\",\n \"fund_return_2008_q1\",\n \"fund_return_2007_q4\",\n \"fund_return_2007_q3\",\n \"fund_return_2007_q2\",\n \"fund_return_2007_q1\",\n \"fund_return_2006_q4\",\n \"fund_return_2006_q3\",\n \"fund_return_2006_q2\",\n \"fund_return_2006_q1\",\n \"fund_return_2005_q4\",\n \"fund_return_2005_q3\",\n \"fund_return_2005_q2\",\n \"fund_return_2005_q1\",\n \"fund_return_2004_q4\",\n \"fund_return_2004_q3\",\n \"fund_return_2004_q2\",\n \"fund_return_2004_q1\",\n \"fund_return_2003_q4\",\n \"fund_return_2003_q3\",\n \"fund_return_2003_q2\",\n \"fund_return_2003_q1\",\n \"fund_return_2002_q4\",\n \"fund_return_2002_q3\",\n \"fund_return_2002_q2\",\n \"fund_return_2002_q1\",\n \"fund_return_2001_q4\",\n \"fund_return_2001_q3\",\n \"fund_return_2001_q2\",\n \"fund_return_2001_q1\",\n \"fund_return_2000_q4\",\n \"fund_return_2000_q3\",\n \"fund_return_2000_q2\",\n \"fund_return_2000_q1\"\n]\n\nalpha_beta = [\n \"fund_alpha_3years\",\n \"fund_beta_3years\",\n \"fund_mean_annual_return_3years\",\n \"fund_r_squared_3years\",\n \"fund_stdev_3years\",\n \"fund_sharpe_ratio_3years\",\n \"fund_treynor_ratio_3years\",\n \"fund_alpha_5years\",\n \"fund_beta_5years\",\n \"fund_mean_annual_return_5years\",\n \"fund_r_squared_5years\",\n \"fund_stdev_5years\",\n \"fund_sharpe_ratio_5years\",\n \"fund_treynor_ratio_5years\",\n \"fund_alpha_10years\",\n \"fund_beta_10years\",\n \"fund_mean_annual_return_10years\",\n \"fund_r_squared_10years\",\n \"fund_stdev_10years\",\n \"fund_sharpe_ratio_10years\",\n \"fund_treynor_ratio_10years\",\n \"fund_return_category_rank_ytd\",\n \"fund_return_category_rank_1month\",\n \"fund_return_category_rank_3months\",\n \"fund_return_category_rank_1year\",\n \"fund_return_category_rank_3years\",\n \"fund_return_category_rank_5years\",\n \"load_adj_return_1year\",\n \"load_adj_return_3years\",\n \"load_adj_return_5years\",\n \"load_adj_return_10years\"\n]\n", "_____no_output_____" ], [ "# Converting week_52 columns\nweek_52_df = flip_cols2rows(src_df=mf_df, col_list=week_52, item_category='Week 52', key_col=key_column)", "_____no_output_____" ], [ "print_df_details(week_52_df)", "190264\n\n fund_symbol item_category item_desc value\n0 AAAAX Week 52 week52_high_low_change 2.44\n1 AAAEX Week 52 week52_high_low_change 8.53\n2 AAAFX Week 52 week52_high_low_change 0.76\n3 AAAGX Week 52 week52_high_low_change 4.64\n4 AAAHX Week 52 week52_high_low_change 0.77\n" ], [ "write2disk(week_52_df, 'mfd_week_52')", "_____no_output_____" ], [ "# Converting exp_ratio columns\nexp_ratio_df = flip_cols2rows(src_df=mf_df, col_list=exp_ratio, item_category='Expense Ratio', key_col=key_column)", "_____no_output_____" ], [ "print_df_details(exp_ratio_df)", "285396\n\n fund_symbol item_category item_desc value\n0 AAAAX Expense Ratio fund_annual_report_net_expense_ratio 0.0122\n1 AAAEX Expense Ratio fund_annual_report_net_expense_ratio 0.0109\n2 AAAFX Expense Ratio fund_annual_report_net_expense_ratio 0.0058\n3 AAAGX Expense Ratio fund_annual_report_net_expense_ratio 0.0108\n4 AAAHX Expense Ratio fund_annual_report_net_expense_ratio 0.0038\n" ], [ "write2disk(exp_ratio_df, 'mfd_exp_ratio')", "_____no_output_____" ], [ "asset_allocation_df = flip_cols2rows(src_df=mf_df, col_list=asset_allocation, item_category='Asset Allocation', key_col=key_column)", "_____no_output_____" ], [ "print_df_details(asset_allocation_df)", "142698\n\n fund_symbol item_category item_desc value\n0 AAAAX Asset Allocation asset_cash 0.0167\n1 AAAEX Asset Allocation asset_cash 0.0309\n2 AAAFX Asset Allocation asset_cash 0.0920\n3 AAAGX Asset Allocation asset_cash 0.0182\n4 AAAHX Asset Allocation asset_cash 0.0920\n" ], [ "write2disk(asset_allocation_df, 'mfd_asset_allocation')", "_____no_output_____" ], [ "sector_allocation_df = flip_cols2rows(src_df=mf_df, col_list=sector_allocation, item_category='Sector Allocation', key_col=key_column)", "_____no_output_____" ], [ "print_df_details(sector_allocation_df)", "261613\n\n fund_symbol item_category item_desc value\n0 AAAAX Sector Allocation fund_sector_basic_materials 0.1607\n1 AAAEX Sector Allocation fund_sector_basic_materials 0.0368\n2 AAAFX Sector Allocation fund_sector_basic_materials 0.0290\n3 AAAGX Sector Allocation fund_sector_basic_materials 0.0000\n4 AAAHX Sector Allocation fund_sector_basic_materials 0.0290\n" ], [ "write2disk(sector_allocation_df, 'mfd_sector_allocation')", "_____no_output_____" ], [ "ratio_df = flip_cols2rows(src_df=mf_df, col_list=ratio, item_category='Ratio', key_col=key_column)", "_____no_output_____" ], [ "print_df_details(ratio_df)", "380528\n\n fund_symbol item_category item_desc value\n0 AAAAX Ratio fund_price_book_ratio 1.91\n1 AAAEX Ratio fund_price_book_ratio 4.68\n2 AAAFX Ratio fund_price_book_ratio 2.57\n3 AAAGX Ratio fund_price_book_ratio 10.20\n4 AAAHX Ratio fund_price_book_ratio 2.57\n" ], [ "write2disk(ratio_df, 'mfd_ratio')", "_____no_output_____" ], [ "bond_rating_df = flip_cols2rows(src_df=mf_df, col_list=bond_rating, item_category='Bond Rating', key_col=key_column)", "_____no_output_____" ], [ "print_df_details(bond_rating_df)", "214047\n\n fund_symbol item_category item_desc value\n0 AAAAX Bond Rating fund_bonds_us_government NaN\n1 AAAEX Bond Rating fund_bonds_us_government NaN\n2 AAAFX Bond Rating fund_bonds_us_government 0.0\n3 AAAGX Bond Rating fund_bonds_us_government NaN\n4 AAAHX Bond Rating fund_bonds_us_government 0.0\n" ], [ "write2disk(bond_rating_df, 'mfd_bond_rating')", "_____no_output_____" ], [ "returns_df = flip_cols2rows(src_df=mf_df, col_list=returns, item_category='Return', key_col=key_column)", "_____no_output_____" ], [ "print_df_details(returns_df)", "523226\n\n fund_symbol item_category item_desc value\n0 AAAAX Return fund_return_ytd 0.21026\n1 AAAEX Return fund_return_ytd 0.19077\n2 AAAFX Return fund_return_ytd NaN\n3 AAAGX Return fund_return_ytd 0.24559\n4 AAAHX Return fund_return_ytd NaN\n" ], [ "returns_df.info()", "<class 'pandas.core.frame.DataFrame'>\nRangeIndex: 523226 entries, 0 to 523225\nData columns (total 4 columns):\n # Column Non-Null Count Dtype \n--- ------ -------------- ----- \n 0 fund_symbol 523226 non-null object \n 1 item_category 523226 non-null object \n 2 item_desc 523226 non-null object \n 3 value 475925 non-null float64\ndtypes: float64(1), object(3)\nmemory usage: 16.0+ MB\n" ], [ "write2disk(returns_df, 'mfd_returns')", "_____no_output_____" ], [ "annual_returns_df = flip_cols2rows(src_df=mf_df, col_list=annual_returns, item_category='Annual Returns', key_col=key_column)", "_____no_output_____" ], [ "print_df_details(annual_returns_df)", "998886\n\n fund_symbol item_category item_desc value\n0 AAAAX Annual Returns fund_return_2020 0.03703\n1 AAAEX Annual Returns fund_return_2020 NaN\n2 AAAFX Annual Returns fund_return_2020 NaN\n3 AAAGX Annual Returns fund_return_2020 0.42443\n4 AAAHX Annual Returns fund_return_2020 NaN\n" ], [ "write2disk(annual_returns_df, 'mfd_annual_returns')", "_____no_output_____" ], [ "quarterly_returns_df = flip_cols2rows(src_df=mf_df, col_list=quarterly_returns, item_category='Quarterly Returns', key_col=key_column)", "_____no_output_____" ], [ "print_df_details(quarterly_returns_df)", "2069121\n\n fund_symbol item_category item_desc value\n5 AAAIX Quarterly Returns fund_return_2021_q3 -0.00561\n14 AAARX Quarterly Returns fund_return_2021_q3 -0.00773\n17 AAAUX Quarterly Returns fund_return_2021_q3 -0.00450\n21 AABAX Quarterly Returns fund_return_2021_q3 -0.00453\n29 AABOX Quarterly Returns fund_return_2021_q3 -0.00128\n" ], [ "write2disk(quarterly_returns_df, 'mfd_quarterly_returns')", "_____no_output_____" ], [ "alpha_beta_df = flip_cols2rows(src_df=mf_df, col_list=alpha_beta, item_category='Alpha/Beta', key_col=key_column)", "_____no_output_____" ], [ "print_df_details(alpha_beta_df)", "737273\n\n fund_symbol item_category item_desc value\n0 AAAAX Alpha/Beta fund_alpha_3years -1.61\n1 AAAEX Alpha/Beta fund_alpha_3years 6.59\n3 AAAGX Alpha/Beta fund_alpha_3years 4.92\n5 AAAIX Alpha/Beta fund_alpha_3years -0.40\n10 AAANX Alpha/Beta fund_alpha_3years -5.08\n" ], [ "write2disk(alpha_beta_df, 'mfd_alpha_beta')", "_____no_output_____" ], [ "drop_columns = [\n \"week52_high_low_change\",\n \"week52_high_low_change_perc\",\n \"week52_high\",\n \"week52_high_change\",\n \"week52_high_change_perc\",\n \"week52_low\",\n \"week52_low_change\",\n \"week52_low_change_perc\",\n \"fund_annual_report_net_expense_ratio\",\n \"category_annual_report_net_expense_ratio\",\n \"fund_prospectus_net_expense_ratio\",\n \"fund_prospectus_gross_expense_ratio\",\n \"fund_max_12b1_fee\",\n \"fund_max_front_end_sales_load\",\n \"category_max_front_end_sales_load\",\n \"fund_max_deferred_sales_load\",\n \"category_max_deferred_sales_load\",\n \"fund_year3_expense_projection\",\n \"fund_year5_expense_projection\",\n \"fund_year10_expense_projection\",\n \"asset_cash\",\n \"asset_stocks\",\n \"asset_bonds\",\n \"asset_others\",\n \"asset_preferred\",\n \"asset_convertible\",\n \"fund_sector_basic_materials\",\n \"fund_sector_communication_services\",\n \"fund_sector_consumer_cyclical\",\n \"fund_sector_consumer_defensive\",\n \"fund_sector_energy\",\n \"fund_sector_financial_services\",\n \"fund_sector_healthcare\",\n \"fund_sector_industrials\",\n \"fund_sector_real_estate\",\n \"fund_sector_technology\",\n \"fund_sector_utilities\",\n \"fund_price_book_ratio\",\n \"category_price_book_ratio\",\n \"fund_price_cashflow_ratio\",\n \"category_price_cashflow_ratio\",\n \"fund_price_earning_ratio\",\n \"category_price_earning_ratio\",\n \"fund_price_sales_ratio\",\n \"category_price_sales_ratio\",\n \"fund_median_market_cap\",\n \"category_median_market_cap\",\n \"fund_year3_earnings_growth\",\n \"category_year3_earnings_growth\",\n \"fund_bond_maturity\",\n \"category_bond_maturity\",\n \"fund_bond_duration\",\n \"category_bond_duration\",\n \"fund_bonds_us_government\",\n \"fund_bonds_aaa\",\n \"fund_bonds_aa\",\n \"fund_bonds_a\",\n \"fund_bonds_bbb\",\n \"fund_bonds_bb\",\n \"fund_bonds_b\",\n \"fund_bonds_below_b\",\n \"fund_bonds_others\",\n \"fund_return_ytd\",\n \"category_return_ytd\",\n \"fund_return_1month\",\n \"category_return_1month\",\n \"fund_return_3months\",\n \"category_return_3months\",\n \"fund_return_1year\",\n \"category_return_1year\",\n \"fund_return_3years\",\n \"category_return_3years\",\n \"fund_return_5years\",\n \"category_return_5years\",\n \"fund_return_10years\",\n \"category_return_10years\",\n \"fund_return_last_bull_market\",\n \"category_return_last_bull_market\",\n \"fund_return_last_bear_market\",\n \"category_return_last_bear_market\",\n \"years_up\",\n \"years_down\",\n \"quarters_up\",\n \"quarters_down\",\n \"fund_return_2020\",\n \"category_return_2020\",\n \"fund_return_2019\",\n \"category_return_2019\",\n \"fund_return_2018\",\n \"category_return_2018\",\n \"fund_return_2017\",\n \"category_return_2017\",\n \"fund_return_2016\",\n \"category_return_2016\",\n \"fund_return_2015\",\n \"category_return_2015\",\n \"fund_return_2014\",\n \"category_return_2014\",\n \"fund_return_2013\",\n \"category_return_2013\",\n \"fund_return_2012\",\n \"category_return_2012\",\n \"fund_return_2011\",\n \"category_return_2011\",\n \"fund_return_2010\",\n \"category_return_2010\",\n \"fund_return_2009\",\n \"category_return_2009\",\n \"fund_return_2008\",\n \"category_return_2008\",\n \"fund_return_2007\",\n \"category_return_2007\",\n \"fund_return_2006\",\n \"category_return_2006\",\n \"fund_return_2005\",\n \"category_return_2005\",\n \"fund_return_2004\",\n \"category_return_2004\",\n \"fund_return_2003\",\n \"category_return_2003\",\n \"fund_return_2002\",\n \"category_return_2002\",\n \"fund_return_2001\",\n \"category_return_2001\",\n \"fund_return_2000\",\n \"category_return_2000\",\n \"fund_return_2021_q3\",\n \"fund_return_2021_q2\",\n \"fund_return_2021_q1\",\n \"fund_return_2020_q4\",\n \"fund_return_2020_q3\",\n \"fund_return_2020_q2\",\n \"fund_return_2020_q1\",\n \"fund_return_2019_q4\",\n \"fund_return_2019_q3\",\n \"fund_return_2019_q2\",\n \"fund_return_2019_q1\",\n \"fund_return_2018_q4\",\n \"fund_return_2018_q3\",\n \"fund_return_2018_q2\",\n \"fund_return_2018_q1\",\n \"fund_return_2017_q4\",\n \"fund_return_2017_q3\",\n \"fund_return_2017_q2\",\n \"fund_return_2017_q1\",\n \"fund_return_2016_q4\",\n \"fund_return_2016_q3\",\n \"fund_return_2016_q2\",\n \"fund_return_2016_q1\",\n \"fund_return_2015_q4\",\n \"fund_return_2015_q3\",\n \"fund_return_2015_q2\",\n \"fund_return_2015_q1\",\n \"fund_return_2014_q4\",\n \"fund_return_2014_q3\",\n \"fund_return_2014_q2\",\n \"fund_return_2014_q1\",\n \"fund_return_2013_q4\",\n \"fund_return_2013_q3\",\n \"fund_return_2013_q2\",\n \"fund_return_2013_q1\",\n \"fund_return_2012_q4\",\n \"fund_return_2012_q3\",\n \"fund_return_2012_q2\",\n \"fund_return_2012_q1\",\n \"fund_return_2011_q4\",\n \"fund_return_2011_q3\",\n \"fund_return_2011_q2\",\n \"fund_return_2011_q1\",\n \"fund_return_2010_q4\",\n \"fund_return_2010_q3\",\n \"fund_return_2010_q2\",\n \"fund_return_2010_q1\",\n \"fund_return_2009_q4\",\n \"fund_return_2009_q3\",\n \"fund_return_2009_q2\",\n \"fund_return_2009_q1\",\n \"fund_return_2008_q4\",\n \"fund_return_2008_q3\",\n \"fund_return_2008_q2\",\n \"fund_return_2008_q1\",\n \"fund_return_2007_q4\",\n \"fund_return_2007_q3\",\n \"fund_return_2007_q2\",\n \"fund_return_2007_q1\",\n \"fund_return_2006_q4\",\n \"fund_return_2006_q3\",\n \"fund_return_2006_q2\",\n \"fund_return_2006_q1\",\n \"fund_return_2005_q4\",\n \"fund_return_2005_q3\",\n \"fund_return_2005_q2\",\n \"fund_return_2005_q1\",\n \"fund_return_2004_q4\",\n \"fund_return_2004_q3\",\n \"fund_return_2004_q2\",\n \"fund_return_2004_q1\",\n \"fund_return_2003_q4\",\n \"fund_return_2003_q3\",\n \"fund_return_2003_q2\",\n \"fund_return_2003_q1\",\n \"fund_return_2002_q4\",\n \"fund_return_2002_q3\",\n \"fund_return_2002_q2\",\n \"fund_return_2002_q1\",\n \"fund_return_2001_q4\",\n \"fund_return_2001_q3\",\n \"fund_return_2001_q2\",\n \"fund_return_2001_q1\",\n \"fund_return_2000_q4\",\n \"fund_return_2000_q3\",\n \"fund_return_2000_q2\",\n \"fund_return_2000_q1\",\n \"fund_alpha_3years\",\n \"fund_beta_3years\",\n \"fund_mean_annual_return_3years\",\n \"fund_r_squared_3years\",\n \"fund_stdev_3years\",\n \"fund_sharpe_ratio_3years\",\n \"fund_treynor_ratio_3years\",\n \"fund_alpha_5years\",\n \"fund_beta_5years\",\n \"fund_mean_annual_return_5years\",\n \"fund_r_squared_5years\",\n \"fund_stdev_5years\",\n \"fund_sharpe_ratio_5years\",\n \"fund_treynor_ratio_5years\",\n \"fund_alpha_10years\",\n \"fund_beta_10years\",\n \"fund_mean_annual_return_10years\",\n \"fund_r_squared_10years\",\n \"fund_stdev_10years\",\n \"fund_sharpe_ratio_10years\",\n \"fund_treynor_ratio_10years\",\n \"fund_return_category_rank_ytd\",\n \"fund_return_category_rank_1month\",\n \"fund_return_category_rank_3months\",\n \"fund_return_category_rank_1year\",\n \"fund_return_category_rank_3years\",\n \"fund_return_category_rank_5years\",\n \"load_adj_return_1year\",\n \"load_adj_return_3years\",\n \"load_adj_return_5years\",\n \"load_adj_return_10years\"\n]", "_____no_output_____" ], [ "mf_df_basic = mf_df.drop(drop_columns, axis = 1)", "_____no_output_____" ], [ "mf_df_basic.info()", "<class 'pandas.core.frame.DataFrame'>\nRangeIndex: 23783 entries, 0 to 23782\nData columns (total 54 columns):\n # Column Non-Null Count Dtype \n--- ------ -------------- ----- \n 0 fund_symbol 23783 non-null object \n 1 quote_type 23783 non-null object \n 2 region 23783 non-null object \n 3 fund_short_name 22959 non-null object \n 4 fund_long_name 23778 non-null object \n 5 currency 23783 non-null object \n 6 initial_investment 16485 non-null float64\n 7 subsequent_investment 8943 non-null float64\n 8 fund_category 23120 non-null object \n 9 fund_family 23783 non-null object \n 10 exchange_code 23783 non-null object \n 11 exchange_name 23783 non-null object \n 12 exchange_timezone 23783 non-null object \n 13 management_name 23783 non-null object \n 14 management_bio 23304 non-null object \n 15 management_start_date 23783 non-null object \n 16 total_net_assets 23749 non-null float64\n 17 year_to_date_return 23382 non-null float64\n 18 day50_moving_average 23782 non-null float64\n 19 day200_moving_average 23782 non-null float64\n 20 investment_strategy 23783 non-null object \n 21 fund_yield 18686 non-null float64\n 22 morningstar_overall_rating 21976 non-null float64\n 23 morningstar_risk_rating 21976 non-null float64\n 24 inception_date 23783 non-null object \n 25 last_dividend 17282 non-null float64\n 26 last_cap_gain 7 non-null float64\n 27 annual_holdings_turnover 21975 non-null float64\n 28 investment_type 22674 non-null object \n 29 size_type 22674 non-null object \n 30 top10_holdings 23585 non-null object \n 31 top10_holdings_total_assets 23640 non-null float64\n 32 morningstar_return_rating 21976 non-null float64\n 33 returns_as_of_date 23756 non-null object \n 34 sustainability_score 15407 non-null float64\n 35 sustainability_rank 15407 non-null float64\n 36 esg_peer_group 15407 non-null object \n 37 esg_peer_count 15407 non-null float64\n 38 esg_score 15407 non-null float64\n 39 peer_esg_min 15407 non-null float64\n 40 peer_esg_avg 15407 non-null float64\n 41 peer_esg_max 15407 non-null float64\n 42 environment_score 15388 non-null float64\n 43 peer_environment_min 14839 non-null float64\n 44 peer_environment_avg 14839 non-null float64\n 45 peer_environment_max 14839 non-null float64\n 46 social_score 15388 non-null float64\n 47 peer_social_min 14839 non-null float64\n 48 peer_social_avg 14839 non-null float64\n 49 peer_social_max 14839 non-null float64\n 50 governance_score 15388 non-null float64\n 51 peer_governance_min 14839 non-null float64\n 52 peer_governance_avg 14839 non-null float64\n 53 peer_governance_max 14839 non-null float64\ndtypes: float64(33), object(21)\nmemory usage: 9.8+ MB\n" ], [ "write2disk(mf_df_basic, 'mf_basic')", "_____no_output_____" ], [ "# Run this after catting all the mfd files into one\nmf_detail_df = pd.read_csv(data_folder+'mf_detail.csv')\nprint_df_details(mf_detail_df)", "5803052\n\n fund_symbol item_category item_desc value\n0 AAAAX Alpha/Beta fund_alpha_3years -1.61\n1 AAAEX Alpha/Beta fund_alpha_3years 6.59\n3 AAAGX Alpha/Beta fund_alpha_3years 4.92\n5 AAAIX Alpha/Beta fund_alpha_3years -0.40\n10 AAANX Alpha/Beta fund_alpha_3years -5.08\n" ], [ "mf_detail_df.dropna(axis=0, how='any', inplace=True)", "_____no_output_____" ], [ "print_df_details(mf_detail_df)", "3997038\n\n fund_symbol item_category item_desc value\n0 AAAAX Alpha/Beta fund_alpha_3years -1.61\n1 AAAEX Alpha/Beta fund_alpha_3years 6.59\n3 AAAGX Alpha/Beta fund_alpha_3years 4.92\n5 AAAIX Alpha/Beta fund_alpha_3years -0.40\n10 AAANX Alpha/Beta fund_alpha_3years -5.08\n" ], [ "mf_detail_df.groupby(['item_category', 'item_desc']).count()", "_____no_output_____" ], [ "write2disk(mf_detail_df, 'mf_detail_nona')", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb300e255c083362a091ef240805caff55c9ea7e

5,845

ipynb

Jupyter Notebook

data/Sentiment Analysis.ipynb

sampottinger/news_flower

6c1255b867e3687c8a1f843acee898dc776bdc42

[ "MIT" ]

4

2019-08-24T06:22:24.000Z

2021-08-10T03:30:57.000Z

data/Sentiment Analysis.ipynb

sampottinger/news_flower

6c1255b867e3687c8a1f843acee898dc776bdc42

[ "MIT" ]

null

data/Sentiment Analysis.ipynb

sampottinger/news_flower

6c1255b867e3687c8a1f843acee898dc776bdc42

[ "MIT" ]

null

21.02518

105

0.530197

[ [ [ "# Sentiment Analysis Notebook\n\nGenerate the sentiment polarity column and a new CSV file for one day of news articles.", "_____no_output_____" ] ], [ [ "import pandas\nimport textblob", "_____no_output_____" ] ], [ [ "### One Day Sample", "_____no_output_____" ] ], [ [ "articles_data = pandas.read_csv('one_day_sample.csv')", "_____no_output_____" ], [ "def get_avg_polarity(text):\n \"\"\"The text form which to calculate polarity.\n \n Args:\n text (str): The text whose polarity should be calculated.\n Returns:\n float: The average polarity across all sentences.\n \"\"\"\n polarities = list(map(\n lambda sentence: sentence.sentiment.polarity,\n textblob.TextBlob(str(text)).sentences\n ))\n \n if len(polarities) == 0:\n return None\n else:\n return sum(polarities) / len(polarities)", "_____no_output_____" ], [ "articles_data['descriptionPolarity'] = articles_data['description'].apply(get_avg_polarity)", "_____no_output_____" ], [ "articles_data['descriptionPolarity'].plot.hist()", "_____no_output_____" ] ], [ [ "Save results with sentiment", "_____no_output_____" ] ], [ [ "articles_data[['source', 'title', 'descriptionPolarity']].to_csv('articles_with_sentiment.csv')", "_____no_output_____" ], [ "articles_data", "_____no_output_____" ] ], [ [ "Get average for articles by source", "_____no_output_____" ] ], [ [ "sources_ranked = articles_data.groupby('source')['descriptionPolarity'].mean()\\\n .copy()\\\n .reset_index()\\\n .sort_values('descriptionPolarity')", "_____no_output_____" ], [ "sources_ranked.to_csv('sources_ranked.csv')", "_____no_output_____" ], [ "sources_ranked", "_____no_output_____" ] ], [ [ "Some EDA", "_____no_output_____" ] ], [ [ "articles_data.groupby('source')['descriptionPolarity'].mean()", "_____no_output_____" ], [ "articles_data.groupby('source')['descriptionPolarity'].min()", "_____no_output_____" ], [ "articles_data.groupby('source')['descriptionPolarity'].max()", "_____no_output_____" ] ], [ [ "### March Extremes", "_____no_output_____" ] ], [ [ "march_data = pandas.read_csv('march_descriptions.csv')", "_____no_output_____" ], [ "march_data['descriptionPolarity'] = march_data['description'].apply(get_avg_polarity)", "_____no_output_____" ], [ "min_vals = march_data.groupby('dayOfMarch')['descriptionPolarity'].min().reset_index()", "_____no_output_____" ], [ "max_vals = march_data.groupby('dayOfMarch')['descriptionPolarity'].max().reset_index()", "_____no_output_____" ], [ "joined_vals = pandas.merge(left=min_vals, right=max_vals, on='dayOfMarch', suffixes=['Min', 'Max'])", "_____no_output_____" ], [ "ax = joined_vals.plot.line(\n x='dayOfMarch',\n y=['descriptionPolarityMin', 'descriptionPolarityMax'],\n title='Range of Sentiment (June 2019)',\n color='#007AFF',\n legend=False,\n figsize=(10, 5)\n)\n\nax.set_xlabel('Day of June 2019')\nax.set_ylabel('Sentiment Polarity')", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ] ]

cb301c5a8efec928ea47dd9c501971e13af18cdc

102,580

ipynb

Jupyter Notebook

code/visualization/5_distributions.ipynb

vicb1/miscellaneous

2c9762579abf75ef6cba75d1d1536a693d69e82a

[ "MIT" ]

null

code/visualization/5_distributions.ipynb

vicb1/miscellaneous

2c9762579abf75ef6cba75d1d1536a693d69e82a

[ "MIT" ]

null

code/visualization/5_distributions.ipynb

vicb1/miscellaneous

2c9762579abf75ef6cba75d1d1536a693d69e82a

[ "MIT" ]

null

172.693603

24,488

0.87715

[ [ [ "**[Data Visualization: From Non-Coder to Coder Micro-Course Home Page](https://www.kaggle.com/learn/data-visualization-from-non-coder-to-coder)**\n\n---\n", "_____no_output_____" ], [ "In this tutorial you'll learn all about **histograms** and **density plots**.\n\n# Set up the notebook\n\nAs always, we begin by setting up the coding environment. (_This code is hidden, but you can un-hide it by clicking on the \"Code\" button immediately below this text, on the right._)", "_____no_output_____" ] ], [ [ "\nimport pandas as pd\nimport matplotlib.pyplot as plt\n%matplotlib inline\nimport seaborn as sns\nprint(\"Setup Complete\")", "Setup Complete\n" ] ], [ [ "# Select a dataset\n\nWe'll work with a dataset of 150 different flowers, or 50 each from three different species of iris (*Iris setosa*, *Iris versicolor*, and *Iris virginica*).\n\n![tut4_iris](https://i.imgur.com/RcxYYBA.png)\n\n# Load and examine the data\n\nEach row in the dataset corresponds to a different flower. There are four measurements: the sepal length and width, along with the petal length and width. We also keep track of the corresponding species. ", "_____no_output_____" ] ], [ [ "# Path of the file to read\niris_filepath = \"./input/iris.csv\"\n\n# Read the file into a variable iris_data\niris_data = pd.read_csv(iris_filepath, index_col=\"Id\")\n\n# Print the first 5 rows of the data\niris_data.head()", "_____no_output_____" ] ], [ [ "# Histograms\n\nSay we would like to create a **histogram** to see how petal length varies in iris flowers. We can do this with the `sns.distplot` command. ", "_____no_output_____" ] ], [ [ "# Histogram \nsns.distplot(a=iris_data['Petal Length (cm)'], kde=False)", "_____no_output_____" ] ], [ [ "We customize the behavior of the command with two additional pieces of information:\n- `a=` chooses the column we'd like to plot (_in this case, we chose `'Petal Length (cm)'`_).\n- `kde=False` is something we'll always provide when creating a histogram, as leaving it out will create a slightly different plot.\n\n# Density plots\n\nThe next type of plot is a **kernel density estimate (KDE)** plot. In case you're not familiar with KDE plots, you can think of it as a smoothed histogram. \n\nTo make a KDE plot, we use the `sns.kdeplot` command. Setting `shade=True` colors the area below the curve (_and `data=` has identical functionality as when we made the histogram above_).", "_____no_output_____" ] ], [ [ "# KDE plot \nsns.kdeplot(data=iris_data['Petal Length (cm)'], shade=True)", "_____no_output_____" ] ], [ [ "# 2D KDE plots\n\nWe're not restricted to a single column when creating a KDE plot. We can create a **two-dimensional (2D) KDE plot** with the `sns.jointplot` command.\n\nIn the plot below, the color-coding shows us how likely we are to see different combinations of sepal width and petal length, where darker parts of the figure are more likely. ", "_____no_output_____" ] ], [ [ "# 2D KDE plot\nsns.jointplot(x=iris_data['Petal Length (cm)'], y=iris_data['Sepal Width (cm)'], kind=\"kde\")", "_____no_output_____" ] ], [ [ "Note that in addition to the 2D KDE plot in the center,\n- the curve at the top of the figure is a KDE plot for the data on the x-axis (in this case, `iris_data['Petal Length (cm)']`), and\n- the curve on the right of the figure is a KDE plot for the data on the y-axis (in this case, `iris_data['Sepal Width (cm)']`).", "_____no_output_____" ], [ "# Color-coded plots\n\nFor the next part of the tutorial, we'll create plots to understand differences between the species. To accomplish this, we begin by breaking the dataset into three separate files, with one for each species.", "_____no_output_____" ] ], [ [ "# Paths of the files to read\niris_set_filepath = \"./input/iris_setosa.csv\"\niris_ver_filepath = \"./input/iris_versicolor.csv\"\niris_vir_filepath = \"./input/iris_virginica.csv\"\n\n# Read the files into variables \niris_set_data = pd.read_csv(iris_set_filepath, index_col=\"Id\")\niris_ver_data = pd.read_csv(iris_ver_filepath, index_col=\"Id\")\niris_vir_data = pd.read_csv(iris_vir_filepath, index_col=\"Id\")\n\n# Print the first 5 rows of the Iris versicolor data\niris_ver_data.head()", "_____no_output_____" ] ], [ [ "In the code cell below, we create a different histogram for each species by using the `sns.distplot` command (_as above_) three times. We use `label=` to set how each histogram will appear in the legend.", "_____no_output_____" ] ], [ [ "# Histograms for each species\nsns.distplot(a=iris_set_data['Petal Length (cm)'], label=\"Iris-setosa\", kde=False)\nsns.distplot(a=iris_ver_data['Petal Length (cm)'], label=\"Iris-versicolor\", kde=False)\nsns.distplot(a=iris_vir_data['Petal Length (cm)'], label=\"Iris-virginica\", kde=False)\n\n# Add title\nplt.title(\"Histogram of Petal Lengths, by Species\")\n\n# Force legend to appear\nplt.legend()", "_____no_output_____" ] ], [ [ "In this case, the legend does not automatically appear on the plot. To force it to show (for any plot type), we can always use `plt.legend()`.\n\nWe can also create a KDE plot for each species by using `sns.kdeplot` (_as above_). Again, `label=` is used to set the values in the legend.", "_____no_output_____" ] ], [ [ "# KDE plots for each species\nsns.kdeplot(data=iris_set_data['Petal Length (cm)'], label=\"Iris-setosa\", shade=True)\nsns.kdeplot(data=iris_ver_data['Petal Length (cm)'], label=\"Iris-versicolor\", shade=True)\nsns.kdeplot(data=iris_vir_data['Petal Length (cm)'], label=\"Iris-virginica\", shade=True)\n\n# Add title\nplt.title(\"Distribution of Petal Lengths, by Species\")", "_____no_output_____" ] ], [ [ "One interesting pattern that can be seen in plots is that the plants seem to belong to one of two groups, where _Iris versicolor_ and _Iris virginica_ seem to have similar values for petal length, while _Iris setosa_ belongs in a category all by itself. \n\nIn fact, according to this dataset, we might even be able to classify any iris plant as *Iris setosa* (as opposed to *Iris versicolor* or *Iris virginica*) just by looking at the petal length: if the petal length of an iris flower is less than 2 cm, it's most likely to be *Iris setosa*!", "_____no_output_____" ], [ "# What's next?\n\nPut your new skills to work in a **[coding exercise](https://www.kaggle.com/kernels/fork/2951534)**!", "_____no_output_____" ], [ "---\n**[Data Visualization: From Non-Coder to Coder Micro-Course Home Page](https://www.kaggle.com/learn/data-visualization-from-non-coder-to-coder)**\n\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ] ]

cb3023972a23585945d4fddcb27a4b89d2b12c5d

41,722

ipynb

Jupyter Notebook

embed/result_report_twitch.ipynb

Dibbeding/SNACSprojectOrionRigel

9e503ebe11e63adc9b7b10832ccb0d60594b5a72

[ "BSD-3-Clause" ]

null

embed/result_report_twitch.ipynb

Dibbeding/SNACSprojectOrionRigel

9e503ebe11e63adc9b7b10832ccb0d60594b5a72

[ "BSD-3-Clause" ]

null

embed/result_report_twitch.ipynb

Dibbeding/SNACSprojectOrionRigel

9e503ebe11e63adc9b7b10832ccb0d60594b5a72

[ "BSD-3-Clause" ]

null

69.769231

11,400

0.770864

[ [ [ "## Output data preparation for dataset Twitch\n#### Plots and figures in separate notebook", "_____no_output_____" ] ], [ [ "# IMPORTS\nimport matplotlib.pyplot as plt\nimport numpy as np\nimport csv \nimport networkx as nx\nfrom random import sample\nimport time\nimport math\nimport random\nimport scipy\nimport pandas as pd", "_____no_output_____" ], [ "# Define necessary functions\n\ndef arccosh_og(x): ##note that x*x-1 might be less than zero :( And then log(t) could be negative (negative distance?!?!?!?!)\n t = x + math.sqrt(x * x - 1)\n return math.log(t)\n\ndef arccosh(x):\n t = x + math.sqrt(max(x * x, 1) - 1)\n return max(math.log(t), 0.5)\n \ndef query(coordinates, source, destination, curvature):\n \n if source == destination:\n return 0\n \n sourceCoords = coordinates[source]\n destinationCoords = coordinates[destination]\n\n i = 0\n ts = 1.0\n td = 1.0\n tt = 1.0\n\n for i in range(len(sourceCoords)):\n ts += math.pow(sourceCoords[i], 2)\n td += math.pow(destinationCoords[i], 2)\n tt += (sourceCoords[i] * destinationCoords[i])\n #print(ts, td, tt)\n t = math.sqrt(ts * td) - tt\n #print('t:', t)\n return arccosh(t) * math.fabs(curvature)\n\ndef intersection_similarity(u,v):\n return len(set(u).intersection(set(v)))\n\ndef weighted_intersection_similarity(u,v, alpha):\n similarity = 0\n if len(u)==len(v):\n n = len(u)\n for i in range(n):\n if u[i] in v:\n j = v.index(u[i])\n similarity += (n-abs(i-j))**alpha\n \n else:\n print('not equal vector lengths')\n similarity = -1\n \n return similarity", "_____no_output_____" ], [ "# READ REAL NETWORK - Giant Cconnected Component\n\ndataset = 'large_twitch_edges.csv'\n\ndata = pd.read_csv(dataset, header = 0, sep = ',') \ndata = data[[data.columns[0], data.columns[1]]]\ndata.head()\n\ngraph = nx.from_pandas_edgelist(data, data.columns[0], data.columns[1])\nGcc = sorted(nx.connected_components(graph), key=len, reverse=True)\ngiant = graph.subgraph(Gcc[0])", "_____no_output_____" ], [ "# SPECIFY THESE INPUTS\n\noutput_file_name = 'twitch/out'\npartitions = 1\ncurvature = -1\nnumber_of_nodes = 168114\n\n#######################\n\n\nlandFile = output_file_name + '.land'\ncoordFiles = [output_file_name + str(i) + '.coord' for i in range(partitions)]\n\ncoordinates = dict()\nwith open(landFile) as infile:\n for line in infile:\n linesplit = line.split()\n id = int(linesplit[0])\n coords = [float(c) for c in linesplit[1:]]\n coordinates[id] = coords\n\nfor coordFile in coordFiles:\n with open(coordFile) as infile:\n for line in infile:\n linesplit = line.split()\n id = int(linesplit[0])\n coords = [float(c) for c in linesplit[1:]]\n coordinates[id] = coords\n\n#while True:\n# query_input = input(\"Enter ID of 2 nodes: \")\n \n# if query_input == 'exit' or query_input == 'q' or query_input == 'quit':\n # break\n\n# querysplit = query_input.split()\n# source = int(querysplit[0])\n# destination = int(querysplit[1])\n\n# estimate = query(coordinates, source, destination, curvature)\n# print('Rigel estimates the distance between %d and %d to be %f.\\n' % (source, destination, estimate))\n", "_____no_output_____" ], [ "# Relative errors - approximation: select 'select_count = 1000' nodes from where distances (to all nodes) are calculated\n### This is necessary due to slow EXACT path calculation\n\nresult_avg_path_length_estimated = []\nresult_avg_path_length_exact = []\nresult_radius_estimated = []\nresult_radius_exact = []\nresult_diameter_estimated = []\nresult_diameter_exact = []\ntop_cent_exact = []\ntop_cent_estimate = []\ntop_ecc_exact = []\ntop_ecc_estimate = []\n\n\nfor sed in range(5):\n print('START OF SEED', sed, '.')\n np.random.seed(sed)\n\n select_count = 1000\n selected_nodes = random.sample(range(number_of_nodes), select_count)\n\n relative_errors = dict()\n exact_distances = dict()\n estimated_distances= dict()\n\n avg_path_length_exact = 0\n avg_path_length_estimated = 0\n radius_estimated = number_of_nodes\n diameter_estimated = 0\n radius_exact = number_of_nodes\n diameter_exact = 0\n eccentricites_estimated = []\n eccentricites_exact =[]\n centralities_exact = []\n centralities_estimated = []\n\n\n node_names = list(giant.nodes())\n\n iters = 0\n\n for source in selected_nodes:\n iters += 1\n if iters % int(select_count/10) == 0:\n print('Processed ', 10 * iters / int(select_count/10), '% of total calculations...')\n\n eccentricity_curr_est = 0\n eccentricity_curr_ex = 0\n exact_distances[source] = []\n estimated_distances[source] = []\n relative_errors[source] = []\n for target in selected_nodes:\n #print('points:', source, target)\n if source != target:\n estimate = query(coordinates, source, target, curvature)\n exact = nx.shortest_path_length(giant, node_names[source], node_names[target])\n avg_path_length_estimated += estimate\n avg_path_length_exact += exact\n eccentricity_curr_est = max(eccentricity_curr_est, estimate)\n diameter_estimated = max(diameter_estimated, estimate)\n eccentricity_curr_ex = max(eccentricity_curr_ex,exact)\n diameter_exact = max(diameter_exact,exact)\n relative_errors[source].append(abs(estimate-exact)/exact)\n exact_distances[source].append(exact)\n estimated_distances[source].append(estimate)\n else:\n relative_errors[source].append(0)\n exact_distances[source].append(0)\n estimated_distances[source].append(0)\n radius_estimated = min(eccentricity_curr_est, radius_estimated)\n radius_exact = min(eccentricity_curr_ex, radius_exact)\n eccentricites_estimated.append(0-eccentricity_curr_est)\n eccentricites_exact.append(0-eccentricity_curr_ex)\n centralities_exact.append(0-np.mean(list(exact_distances.values())))\n centralities_estimated.append(0-np.mean(list(estimated_distances.values())))\n\n avg_path_length_estimated = avg_path_length_estimated / (select_count * (select_count - 1) )\n avg_path_length_exact = avg_path_length_exact / (select_count * (select_count - 1) )\n \n result_avg_path_length_estimated.append(avg_path_length_estimated)\n result_avg_path_length_exact.append(avg_path_length_exact)\n result_radius_estimated.append(radius_estimated)\n result_radius_exact.append(radius_exact)\n result_diameter_estimated.append(diameter_estimated)\n result_diameter_exact.append(diameter_exact)\n\n ind = np.argpartition(centralities_exact, -20)[-20:]\n top_cent_exact.append(ind[np.argsort(np.array(centralities_exact)[ind])])\n ind = np.argpartition(centralities_estimated, -20)[-20:]\n top_cent_estimate.append(ind[np.argsort(np.array(centralities_estimated)[ind])])\n ind = np.argpartition(eccentricites_exact, -20)[-20:]\n top_ecc_exact.append(ind[np.argsort(np.array(eccentricites_exact)[ind])])\n ind = np.argpartition(eccentricites_estimated, -20)[-20:]\n top_ecc_estimate.append(ind[np.argsort(np.array(eccentricites_estimated)[ind])])", "START OF SEED 0 .\nProcessed 10.0 % of total calculations...\nProcessed 20.0 % of total calculations...\nProcessed 30.0 % of total calculations...\nProcessed 40.0 % of total calculations...\nProcessed 50.0 % of total calculations...\nProcessed 60.0 % of total calculations...\nProcessed 70.0 % of total calculations...\nProcessed 80.0 % of total calculations...\nProcessed 90.0 % of total calculations...\nProcessed 100.0 % of total calculations...\nSTART OF SEED 1 .\nProcessed 10.0 % of total calculations...\nProcessed 20.0 % of total calculations...\nProcessed 30.0 % of total calculations...\nProcessed 40.0 % of total calculations...\nProcessed 50.0 % of total calculations...\nProcessed 60.0 % of total calculations...\nProcessed 70.0 % of total calculations...\nProcessed 80.0 % of total calculations...\nProcessed 90.0 % of total calculations...\nProcessed 100.0 % of total calculations...\nSTART OF SEED 2 .\nProcessed 10.0 % of total calculations...\nProcessed 20.0 % of total calculations...\nProcessed 30.0 % of total calculations...\nProcessed 40.0 % of total calculations...\nProcessed 50.0 % of total calculations...\nProcessed 60.0 % of total calculations...\nProcessed 70.0 % of total calculations...\nProcessed 80.0 % of total calculations...\nProcessed 90.0 % of total calculations...\nProcessed 100.0 % of total calculations...\nSTART OF SEED 3 .\nProcessed 10.0 % of total calculations...\nProcessed 20.0 % of total calculations...\nProcessed 30.0 % of total calculations...\nProcessed 40.0 % of total calculations...\nProcessed 50.0 % of total calculations...\nProcessed 60.0 % of total calculations...\nProcessed 70.0 % of total calculations...\nProcessed 80.0 % of total calculations...\nProcessed 90.0 % of total calculations...\nProcessed 100.0 % of total calculations...\nSTART OF SEED 4 .\nProcessed 10.0 % of total calculations...\nProcessed 20.0 % of total calculations...\nProcessed 30.0 % of total calculations...\nProcessed 40.0 % of total calculations...\nProcessed 50.0 % of total calculations...\nProcessed 60.0 % of total calculations...\nProcessed 70.0 % of total calculations...\nProcessed 80.0 % of total calculations...\nProcessed 90.0 % of total calculations...\nProcessed 100.0 % of total calculations...\n" ], [ "# estimated metrics\nprint(result_avg_path_length_estimated)\nprint(result_avg_path_length_exact)\nprint(result_radius_estimated)\nprint(result_radius_exact)\nprint(result_diameter_estimated)\nprint(result_diameter_exact)", "[2.6978105188833235, 2.7421731004825065, 2.7006032055157183, 2.659601815194189, 2.7258355169842963]\n[2.8695275275275276, 2.900792792792793, 2.8918318318318317, 2.8433733733733733, 2.894818818818819]\n[3.6907110781397536, 3.6341833100388046, 3.634298811026348, 3.6195945158198266, 3.8630546872697606]\n[4, 4, 4, 4, 4]\n[6.325781820205195, 6.275383422143065, 5.846624383127703, 5.90408804612268, 6.8185055093935185]\n[6, 6, 6, 6, 6]\n" ], [ "# Similarity of top central nodes\nfor i in range(5):\n print('Weighted Centrality similarity of top 20: ', weighted_intersection_similarity(list(top_cent_estimate[i]),list(top_cent_exact[i]),1))\n print('Weighted Eccentricity similarity of top 20: ', weighted_intersection_similarity(list(top_ecc_estimate[i]),list(top_ecc_exact[i]),1))\n print('Centrality similarity of top 20: ', intersection_similarity(list(top_cent_estimate[i]),list(top_cent_exact[i])))\n print('Eccentricity similarity of top 20: ', intersection_similarity(list(top_ecc_estimate[i]),list(top_ecc_exact[i])))", "Weighted Centrality similarity of top 20: 270\nWeighted Eccentricity similarity of top 20: 0\nCentrality similarity of top 20: 17\nEccentricity similarity of top 20: 0\nWeighted Centrality similarity of top 20: 261\nWeighted Eccentricity similarity of top 20: 34\nCentrality similarity of top 20: 15\nEccentricity similarity of top 20: 2\nWeighted Centrality similarity of top 20: 366\nWeighted Eccentricity similarity of top 20: 0\nCentrality similarity of top 20: 19\nEccentricity similarity of top 20: 0\nWeighted Centrality similarity of top 20: 255\nWeighted Eccentricity similarity of top 20: 36\nCentrality similarity of top 20: 16\nEccentricity similarity of top 20: 2\nWeighted Centrality similarity of top 20: 274\nWeighted Eccentricity similarity of top 20: 27\nCentrality similarity of top 20: 15\nEccentricity similarity of top 20: 2\n" ], [ "#save data for later reuse (plotting)\nwith open('twitch_diam_ex.pickle', 'wb') as handle:\n pickle.dump(result_diameter_exact, handle)", "_____no_output_____" ], [ "#Average relative error calculation\nARE_per_source = [np.mean(relative_errors[node]) for node in relative_errors.keys()]\nARE_total = np.mean(ARE_per_source)\nprint('Relative error (approximated): ', ARE_total)", "Relative error (approximated): 0.15914362195131065\n" ], [ "# distribution of relative error in total\n\nrelative_errors_total = []\nfor source in relative_errors.keys():\n relative_errors_total += relative_errors[source]\n #print(source, ': ' ,min(relative_errors[source]))\n\nplt.hist(relative_errors_total, bins = 100)\nplt.title('RE distribution')\nplt.xlabel('RE')\nplt.ylabel('#occurance')\nplt.show()\n\nplt.hist([relative_errors_total[i] for i in range(len(relative_errors_total)) if (relative_errors_total[i] < 1.0 and relative_errors_total[i] > 0.0)], bins = 100)\nplt.title('RE distribution - in [0,1]')\nplt.xlabel('RE')\nplt.ylabel('#occurance')\nplt.show()", "_____no_output_____" ], [ "# Save data for later reuse (plotting)\nwith open('twitch_erdist.pickle', 'wb') as handle:\n pickle.dump([relative_errors_total[i] for i in range(len(relative_errors_total)) if (relative_errors_total[i] < 1.0 and relative_errors_total[i] > 0.0)], handle)\n\nwith open('twitch_cdf.pickle', 'wb') as handle:\n pickle.dump({'bins': bins_count[1:], 'cdf':cdf }, handle)", "_____no_output_____" ], [ "# Cumulative Distribution Function of the Distribution if Relative Errors\n\nbase = [relative_errors_total[i] for i in range(len(relative_errors_total)) if (relative_errors_total[i] < 1.0 and relative_errors_total[i] > 0.0)]\ncount, bins_count = np.histogram(base, bins=1000)\npdf = count / sum(count)\ncdf = np.cumsum(pdf)\nplt.plot(bins_count[1:], cdf, label=\"CDF\")\nplt.title('CDF of Relative Error')\nplt.xlabel('Relative Error')\nplt.ylabel('CDF')\nplt.show()", "_____no_output_____" ] ] ]

[ "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb302967216b0996805f5b148787174e23c6f90b

17,379

ipynb

Jupyter Notebook

agrodem_preprocessing/Agrodem_Prepping.ipynb

babakkhavari/agrodem

8de2559afa5a5d1ea9498e52c4f7eeb35dbad0cc

[ "MIT" ]

3

2020-04-24T17:04:17.000Z

2021-01-17T10:52:08.000Z

agrodem_preprocessing/Agrodem_Prepping.ipynb

babakkhavari/agrodem

8de2559afa5a5d1ea9498e52c4f7eeb35dbad0cc

[ "MIT" ]

39

2019-05-14T13:19:24.000Z

2019-07-23T16:40:56.000Z

agrodem_preprocessing/Agrodem_Prepping.ipynb

babakkhavari/agrodem

8de2559afa5a5d1ea9498e52c4f7eeb35dbad0cc

[ "MIT" ]

10

2019-09-19T13:37:18.000Z

2021-02-09T15:58:17.000Z

36.510504

297

0.494045

[ [ [ "### Irrigation model input file prep\n\nThis code prepares the final input file to the irrigation (agrodem) model. It extracts all necessary attributes to crop locations. It also applies some name fixes as needed for the model to run smoothly.The output dataframe is exported as csv and ready to be used in the irrigation model.\n\n**Original code:** [Alexandros Korkovelos](https://github.com/akorkovelos) & [Konstantinos Pegios](https://github.com/kopegios)<br />\n**Conceptualization & Methodological review :** [Alexandros Korkovelos](https://github.com/akorkovelos)<br />\n**Updates, Modifications:** [Alexandros Korkovelos](https://github.com/akorkovelos)<br />\n**Funding:** The World Bank (contract number: 7190531), [KTH](https://www.kth.se/en/itm/inst/energiteknik/forskning/desa/welcome-to-the-unit-of-energy-systems-analysis-kth-desa-1.197296)", "_____no_output_____" ] ], [ [ "#Import modules and libraries\nimport os\nimport geopandas as gpd\nfrom rasterstats import point_query\nimport logging\nimport pandas as pd\nfrom shapely.geometry import Point, Polygon\nimport gdal\nimport rasterio as rio\nimport fiona\nimport gdal\nimport osr\nimport ogr\nimport rasterio.mask\nimport time\nimport numpy as np\nimport itertools\nimport re\nfrom osgeo import gdal,ogr\nimport struct\nimport csv\nimport tkinter as tk\nfrom tkinter import filedialog, messagebox\nfrom pandas import DataFrame as df\nfrom rasterio.warp import calculate_default_transform, reproject\nfrom rasterio.enums import Resampling\nfrom rasterstats import point_query\nfrom pyproj import Proj\nfrom shapely.geometry import Point, Polygon", "_____no_output_____" ], [ "# Import data \n\nroot = tk.Tk()\nroot.withdraw()\nroot.attributes(\"-topmost\", True)\nmessagebox.showinfo('Agrodem Prepping', 'Open the extracted csv file obtained after running the QGIS plugin - AGRODEM')\ninput_file = filedialog.askopenfilename()\n\n# Import csv as pandas dataframe\ncrop_df = pd.read_csv(input_file)", "_____no_output_____" ], [ "# Fill in Nan values with 0\ncrop_df.fillna(99999,inplace=True)\ncrop_df.head(2)", "_____no_output_____" ], [ "##Dropping unecessary columns\n\ndroping_cols = [\"Pixel\"]\ncrop_df.drop(droping_cols, axis=1, inplace=True)\n\n# New for whole Moz\ncrop_df.rename(columns={'elevation': 'sw_depth',\n 'MaizeArea': 'harv_area'}, inplace=True)\n\n# Adding columns missing\ncrop_df[\"country\"] = \"moz\"\n#maize_gdf[\"admin_1\"] = \"Zambezia\"\ncrop_df[\"curr_yield\"] = \"4500\"\ncrop_df[\"max_yield\"] = \"6000\"\ncrop_df['field_1'] = range(0, 0+len(crop_df))", "_____no_output_____" ] ], [ [ "#### Converting dataframe to geo-dataframe", "_____no_output_____" ] ], [ [ "# Add geometry and convert to spatial dataframe in source CRS\n#crop_df['geometry'] = list(zip(crop_df['lon'], crop_df['lat']))\n#crop_df['geometry'] = crop_df['geometry'].apply(Point)\n\n\ncrop_df['geometry'] = crop_df.apply(lambda x: Point((float(x.lon), float(x.lat))), axis =1)\ncrop_df = gpd.GeoDataFrame(crop_df, geometry ='geometry')\n# Reproject data in to Ordnance Survey GB coordinates\n\ncrop_df.crs=\"+proj=utm +zone=37 +south +datum=WGS84 +units=m +no_defs\"", "_____no_output_____" ], [ "# convert to shapefile\n#write the name you would like to have in the string \"test_final5, you can keep this also as the default name\"\ncrop_df.to_file('test_final5.shp',driver = 'ESRI Shapefile')", "_____no_output_____" ], [ "#export to csv\nmessagebox.showinfo('Agrodem Prepping','Browse to the folder where you want to save geodataframe as a csv file')\npath = filedialog.askdirectory()\nshpname = 'Output'\ncrop_df.to_csv(os.path.join(path,\"{}.csv\".format(shpname)))", "_____no_output_____" ], [ "\nmessagebox.showinfo('Agrodem Prepping', 'Browse to the folder that contains required Raster files for temp, prec and radiance')\n#file location: r\"N:\\Agrodem\\Irrigation_model\\Input_data\\Supporting_Layers\"\nraster_path = filedialog.askdirectory()\nraster_files =[]\nprint (\"Reading independent variables...\")\n\nfor i in os.listdir(raster_path):\n if i.endswith('.tif'):\n raster_files.append(i) \nmessagebox.showinfo('Agrodem Prepping','Open the saved shapefile extracted from the input csv file above ') \nshp_filename = filedialog.askopenfilename()\n\n\nprint (\"Extracting raster values to points...\")\n\nfor i in raster_files:\n print(\"Extracting \" + i + \" values...\")\n src_filename = raster_path + \"\\\\\" + i \n li_values = list()\n\n src_ds=gdal.Open(src_filename) \n gt=src_ds.GetGeoTransform()\n rb=src_ds.GetRasterBand(1)\n ds=ogr.Open(shp_filename)\n lyr=ds.GetLayer()\n \n for feat in lyr:\n geom = feat.GetGeometryRef()\n feat_id = feat.GetField('field_1')\n mx,my=geom.GetX(), geom.GetY() #coord in map units\n\n #Convert from map to pixel coordinates.\n #Only works for geotransforms with no rotation.\n px = int((mx - gt[0]) / gt[1]) #x pixel\n py = int((my - gt[3]) / gt[5]) #y pixel\n\n intval=rb.ReadAsArray(px,py,1,1)\n li_values.append([feat_id, intval[0]])\n \n print (\"Writing \" + i + \" values to csv...\")\n \n #input to the output folder for generated csv files\n \n csvoutpath = r\"C:\\Oluchi\\Irrigation model\\Maize\" \n \n with open(csvoutpath + \"\\\\\" + i.split('.')[0] + i.split('.')[1] + '.csv', 'w') as csvfile:\n wr = csv.writer(csvfile)\n wr.writerows(li_values) \n ", "_____no_output_____" ] ], [ [ "## Merge csv files with crop", "_____no_output_____" ] ], [ [ "#Import data \n\nmessagebox.showinfo('Agrodem Prepping', 'Open the csv file you in which you exported the geodataframe previously')\nfile = filedialog.askopenfilename()\nagrodem_input = pd.read_csv(file)\n", "_____no_output_____" ], [ "csv_files = []\n\nprint (\"Reading csv files...\")\n\nfor i in os.listdir(csvoutpath):\n if i.endswith('.csv'):\n csv_files.append(i) \n\nfor i in csv_files:\n print('Reading...'+ i) \n df_csv = pd.read_csv(csvoutpath + \"//\" + i, index_col=None, header=None)\n df_csv.iloc[:,1] = df_csv.iloc[:,1].astype(str)\n df_csv.iloc[:,1] = df_csv.iloc[:,1].str.replace('[','')\n df_csv.iloc[:,1] = df_csv.iloc[:,1].str.replace(']','')\n columnName = i.split('.')[0]\n \n print(\"Merging...\" + columnName)\n agrodem_input[columnName] = df_csv.iloc[:,1]", "_____no_output_____" ], [ "# Define output path\n# Overwriting the csv file\npath = r\"N:\\Agrodem\\Irrigation_model\\Output_data\\agrodem_input\"\nshpname = \"Cassava_Moz_1km_2030_SG_downscaled_SW.csv\"\n\n#drybeans\ncrop_gdf.to_csv(os.path.join(path,\"{c}\".format(c=shpname)))", "_____no_output_____" ] ], [ [ "### Alternative way of extraction raster value to point (long run)", "_____no_output_____" ] ], [ [ "# Seetting rasters path\n#set_path_4rasters = r\"N:\\Agrodem\\Irrigation_model\\Input_data\\Supporting_Layers\"\n\n#for i in os.listdir(set_path_4rasters):\n# if i.endswith('.tif'):\n# #Check if this keeps the raster name as found with the .tif extension\n# columName = i[:-4]\n# print (columName)\n# print (\"Extracting \" + columName + \" values to points...\")\n# maize_gdf[columName] = point_query(maize_gdf, set_path_4rasters + \"\\\\\" + i)", "_____no_output_____" ], [ "agrodem_input.columns", "_____no_output_____" ] ], [ [ "### Updated names of input files for 30s rasters", "_____no_output_____" ] ], [ [ "# Renaming columns as input file requires\nagrodem_input.rename(columns={'wc20_30s_prec_01': 'prec_1',\n 'wc20_30s_prec_02': 'prec_2', \n 'wc20_30s_prec_03': 'prec_3', \n 'wc20_30s_prec_04': 'prec_4',\n 'wc20_30s_prec_05': 'prec_5', \n 'wc20_30s_prec_06': 'prec_6', \n 'wc20_30s_prec_07': 'prec_7',\n 'wc20_30s_prec_08': 'prec_8', \n 'wc20_30s_prec_09': 'prec_9', \n 'wc20_30s_prec_10': 'prec_10',\n 'wc20_30s_prec_11': 'prec_11', \n 'wc20_30s_prec_12': 'prec_12', \n 'wc20_30s_srad_01': 'srad_1',\n 'wc20_30s_srad_02': 'srad_2', \n 'wc20_30s_srad_03': 'srad_3', \n 'wc20_30s_srad_04': 'srad_4',\n 'wc20_30s_srad_05': 'srad_5', \n 'wc20_30s_srad_06': 'srad_6', \n 'wc20_30s_srad_07': 'srad_7',\n 'wc20_30s_srad_08': 'srad_8', \n 'wc20_30s_srad_09': 'srad_9', \n 'wc20_30s_srad_10': 'srad_10',\n 'wc20_30s_srad_11': 'srad_11', \n 'wc20_30s_srad_12': 'srad_12', \n 'wc20_30s_tavg_01': 'tavg_1',\n 'wc20_30s_tavg_02': 'tavg_2', \n 'wc20_30s_tavg_03': 'tavg_3', \n 'wc20_30s_tavg_04': 'tavg_4',\n 'wc20_30s_tavg_05': 'tavg_5', \n 'wc20_30s_tavg_06': 'tavg_6', \n 'wc20_30s_tavg_07': 'tavg_7',\n 'wc20_30s_tavg_08': 'tavg_8',\n 'wc20_30s_tavg_09': 'tavg_9', \n 'wc20_30s_tavg_10': 'tavg_10',\n 'wc20_30s_tavg_11': 'tavg_11', \n 'wc20_30s_tavg_12': 'tavg_12', \n 'wc20_30s_tmax_01': 'tmax_1',\n 'wc20_30s_tmax_02': 'tmax_2', \n 'wc20_30s_tmax_03': 'tmax_3', \n 'wc20_30s_tmax_04': 'tmax_4',\n 'wc20_30s_tmax_05': 'tmax_5', \n 'wc20_30s_tmax_06': 'tmax_6', \n 'wc20_30s_tmax_07': 'tmax_7',\n 'wc20_30s_tmax_08': 'tmax_8', \n 'wc20_30s_tmax_09': 'tmax_9', \n 'wc20_30s_tmax_10': 'tmax_10',\n 'wc20_30s_tmax_11': 'tmax_11', \n 'wc20_30s_tmax_12': 'tmax_12',\n 'wc20_30s_tmin_01': 'tmin_1',\n 'wc20_30s_tmin_02': 'tmin_2', \n 'wc20_30s_tmin_03': 'tmin_3', \n 'wc20_30s_tmin_04': 'tmin_4',\n 'wc20_30s_tmin_05': 'tmin_5', \n 'wc20_30s_tmin_06': 'tmin_6', \n 'wc20_30s_tmin_07': 'tmin_7',\n 'wc20_30s_tmin_08': 'tmin_8', \n 'wc20_30s_tmin_09': 'tmin_9', \n 'wc20_30s_tmin_10': 'tmin_10',\n 'wc20_30s_tmin_11': 'tmin_11', \n 'wc20_30s_tmin_12': 'tmin_12', \n 'wc20_30s_wind_01': 'wind_1',\n 'wc20_30s_wind_02': 'wind_2', \n 'wc20_30s_wind_03': 'wind_3', \n 'wc20_30s_wind_04': 'wind_4',\n 'wc20_30s_wind_05': 'wind_5', \n 'wc20_30s_wind_06': 'wind_6', \n 'wc20_30s_wind_07': 'wind_7',\n 'wc20_30s_wind_08': 'wind_8', \n 'wc20_30s_wind_09': 'wind_9', \n 'wc20_30s_wind_10': 'wind_10',\n 'wc20_30s_wind_11': 'wind_11', \n 'wc20_30s_wind_12': 'wind_12',\n 'gyga_af_agg_erzd_tawcpf23mm__m_1kmtif': 'awsc',\n 'Surface_Water_Suitability_Moz' : 'sw_suit',\n 'elevationtif': 'elevation',\n 'WTDtif':'gw_depth'}, inplace=True)\n", "_____no_output_____" ], [ "agrodem_input.columns", "_____no_output_____" ], [ "droping_cols = [\"Unnamed: 0\",\"geometry\"]\nagrodem_input.drop(droping_cols, axis=1, inplace=True)", "_____no_output_____" ] ], [ [ "## Exporting gdf into csv (or shapefile, gpkg as needed)", "_____no_output_____" ] ], [ [ "#gpkg\n#agrodem_input.to_file(\"Zambezia_1km.gpkg\", layer='Maize_Inputfile', driver=\"GPKG\")\n\n#shp\n#agrodem_input.to_file(\"Moz_250m_Maize_190920.shp\")\n\n# Define output path\npath = r\"C:\\Oluchi\\Irrigation model\\Output_data\\agrodem_input\\Final_input_files\"\ncsvname = \"agrodem_input_Maize.csv\"\n\n#maize\nagrodem_input.to_csv(os.path.join(path,\"{c}\".format(c=csvname)), index=False)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ] ]

cb302d2150c2a2a1248e590dbe1abff6d7aa9510

254,970

ipynb

Jupyter Notebook

P1.ipynb

nikhilparla/udacity_selfdriving_proj_1

f086575f0c7109a9aeb66792c0ecfd293d0ed941

[ "MIT" ]

null

P1.ipynb

nikhilparla/udacity_selfdriving_proj_1

f086575f0c7109a9aeb66792c0ecfd293d0ed941

[ "MIT" ]

null

P1.ipynb

nikhilparla/udacity_selfdriving_proj_1

f086575f0c7109a9aeb66792c0ecfd293d0ed941

[ "MIT" ]

null

410.57971

116,844

0.933678

[ [ [ "# Self-Driving Car Engineer Nanodegree\n\n\n## Project: **Finding Lane Lines on the Road** \n***\nIn this project, you will use the tools you learned about in the lesson to identify lane lines on the road. You can develop your pipeline on a series of individual images, and later apply the result to a video stream (really just a series of images). Check out the video clip \"raw-lines-example.mp4\" (also contained in this repository) to see what the output should look like after using the helper functions below. \n\nOnce you have a result that looks roughly like \"raw-lines-example.mp4\", you'll need to get creative and try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video \"P1_example.mp4\". Ultimately, you would like to draw just one line for the left side of the lane, and one for the right.\n\nIn addition to implementing code, there is a brief writeup to complete. The writeup should be completed in a separate file, which can be either a markdown file or a pdf document. There is a [write up template](https://github.com/udacity/CarND-LaneLines-P1/blob/master/writeup_template.md) that can be used to guide the writing process. Completing both the code in the Ipython notebook and the writeup template will cover all of the [rubric points](https://review.udacity.com/#!/rubrics/322/view) for this project.\n\n---\nLet's have a look at our first image called 'test_images/solidWhiteRight.jpg'. Run the 2 cells below (hit Shift-Enter or the \"play\" button above) to display the image.\n\n**Note: If, at any point, you encounter frozen display windows or other confounding issues, you can always start again with a clean slate by going to the \"Kernel\" menu above and selecting \"Restart & Clear Output\".**\n\n---", "_____no_output_____" ], [ "**The tools you have are color selection, region of interest selection, grayscaling, Gaussian smoothing, Canny Edge Detection and Hough Tranform line detection. You are also free to explore and try other techniques that were not presented in the lesson. Your goal is piece together a pipeline to detect the line segments in the image, then average/extrapolate them and draw them onto the image for display (as below). Once you have a working pipeline, try it out on the video stream below.**\n\n---\n\n<figure>\n <img src=\"examples/line-segments-example.jpg\" width=\"380\" alt=\"Combined Image\" />\n <figcaption>\n <p></p> \n <p style=\"text-align: center;\"> Your output should look something like this (above) after detecting line segments using the helper functions below </p> \n </figcaption>\n</figure>\n <p></p> \n<figure>\n <img src=\"examples/laneLines_thirdPass.jpg\" width=\"380\" alt=\"Combined Image\" />\n <figcaption>\n <p></p> \n <p style=\"text-align: center;\"> Your goal is to connect/average/extrapolate line segments to get output like this</p> \n </figcaption>\n</figure>", "_____no_output_____" ], [ "**Run the cell below to import some packages. If you get an `import error` for a package you've already installed, try changing your kernel (select the Kernel menu above --> Change Kernel). Still have problems? Try relaunching Jupyter Notebook from the terminal prompt. Also, consult the forums for more troubleshooting tips.** ", "_____no_output_____" ], [ "## Import Packages", "_____no_output_____" ] ], [ [ "#importing some useful packages\nimport matplotlib.pyplot as plt\nimport matplotlib.image as mpimg\nimport numpy as np\nimport cv2\n%matplotlib inline", "_____no_output_____" ] ], [ [ "## Read in an Image", "_____no_output_____" ] ], [ [ "#reading in an image\nimage = mpimg.imread('test_images/solidWhiteRight.jpg')\n\n#printing out some stats and plotting\nprint('This image is:', type(image), 'with dimensions:', image.shape)\nplt.imshow(image) # if you wanted to show a single color channel image called 'gray', for example, call as plt.imshow(gray, cmap='gray')", "This image is: <class 'numpy.ndarray'> with dimensions: (540, 960, 3)\n" ] ], [ [ "## Ideas for Lane Detection Pipeline", "_____no_output_____" ], [ "**Some OpenCV functions (beyond those introduced in the lesson) that might be useful for this project are:**\n\n`cv2.inRange()` for color selection \n`cv2.fillPoly()` for regions selection \n`cv2.line()` to draw lines on an image given endpoints \n`cv2.addWeighted()` to coadd / overlay two images \n`cv2.cvtColor()` to grayscale or change color \n`cv2.imwrite()` to output images to file \n`cv2.bitwise_and()` to apply a mask to an image\n\n**Check out the OpenCV documentation to learn about these and discover even more awesome functionality!**", "_____no_output_____" ], [ "## Helper Functions", "_____no_output_____" ], [ "Below are some helper functions to help get you started. They should look familiar from the lesson!", "_____no_output_____" ] ], [ [ "import math\n\ndef grayscale(img):\n \"\"\"Applies the Grayscale transform\n This will return an image with only one color channel\n but NOTE: to see the returned image as grayscale\n (assuming your grayscaled image is called 'gray')\n you should call plt.imshow(gray, cmap='gray')\"\"\"\n return cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)\n # Or use BGR2GRAY if you read an image with cv2.imread()\n # return cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)\n \ndef canny(img, low_threshold, high_threshold):\n \"\"\"Applies the Canny transform\"\"\"\n return cv2.Canny(img, low_threshold, high_threshold)\n\ndef gaussian_blur(img, kernel_size):\n \"\"\"Applies a Gaussian Noise kernel\"\"\"\n return cv2.GaussianBlur(img, (kernel_size, kernel_size), 0)\n\ndef region_of_interest(img, vertices):\n \"\"\"\n Applies an image mask.\n \n Only keeps the region of the image defined by the polygon\n formed from `vertices`. The rest of the image is set to black.\n `vertices` should be a numpy array of integer points.\n \"\"\"\n #defining a blank mask to start with\n mask = np.zeros_like(img) \n \n #defining a 3 channel or 1 channel color to fill the mask with depending on the input image\n if len(img.shape) > 2:\n channel_count = img.shape[2] # i.e. 3 or 4 depending on your image\n ignore_mask_color = (255,) * channel_count\n else:\n ignore_mask_color = 255\n \n #filling pixels inside the polygon defined by \"vertices\" with the fill color \n cv2.fillPoly(mask, vertices, ignore_mask_color)\n \n #returning the image only where mask pixels are nonzero\n masked_image = cv2.bitwise_and(img, mask)\n return masked_image\n\n\ndef draw_lines(img, lines, color=[255, 0, 0], thickness=2):\n \"\"\"\n NOTE: this is the function you might want to use as a starting point once you want to \n average/extrapolate the line segments you detect to map out the full\n extent of the lane (going from the result shown in raw-lines-example.mp4\n to that shown in P1_example.mp4). \n \n Think about things like separating line segments by their \n slope ((y2-y1)/(x2-x1)) to decide which segments are part of the left\n line vs. the right line. Then, you can average the position of each of \n the lines and extrapolate to the top and bottom of the lane.\n \n This function draws `lines` with `color` and `thickness`. \n Lines are drawn on the image inplace (mutates the image).\n If you want to make the lines semi-transparent, think about combining\n this function with the weighted_img() function below\n \"\"\"\n for line in lines:\n for x1,y1,x2,y2 in line:\n cv2.line(img, (x1, y1), (x2, y2), color, thickness)\n\ndef hough_lines(img, rho, theta, threshold, min_line_len, max_line_gap):\n \"\"\"\n `img` should be the output of a Canny transform.\n \n Returns an image with hough lines drawn.\n \"\"\"\n lines = cv2.HoughLinesP(img, rho, theta, threshold, np.array([]), minLineLength=min_line_len, maxLineGap=max_line_gap)\n line_img = np.zeros((img.shape[0], img.shape[1], 3), dtype=np.uint8)\n draw_lines(line_img, lines)\n return line_img\n\n# Python 3 has support for cool math symbols.\n\ndef weighted_img(img, initial_img, α=0.8, β=1., γ=0.):\n \"\"\"\n `img` is the output of the hough_lines(), An image with lines drawn on it.\n Should be a blank image (all black) with lines drawn on it.\n \n `initial_img` should be the image before any processing.\n \n The result image is computed as follows:\n \n initial_img * α + img * β + γ\n NOTE: initial_img and img must be the same shape!\n \"\"\"\n return cv2.addWeighted(initial_img, α, img, β, γ)", "_____no_output_____" ] ], [ [ "## Test Images\n\nBuild your pipeline to work on the images in the directory \"test_images\" \n**You should make sure your pipeline works well on these images before you try the videos.**", "_____no_output_____" ] ], [ [ "import os\nos.listdir(\"test_images/\")", "_____no_output_____" ] ], [ [ "## Build a Lane Finding Pipeline\n\n", "_____no_output_____" ], [ "Build the pipeline and run your solution on all test_images. Make copies into the `test_images_output` directory, and you can use the images in your writeup report.\n\nTry tuning the various parameters, especially the low and high Canny thresholds as well as the Hough lines parameters.", "_____no_output_____" ] ], [ [ "# TODO: Build your pipeline that will draw lane lines on the test_images\n# then save them to the test_images_output directory.\n\ngray = grayscale(image)\nplt.imshow(gray, cmap='gray')\n\nkernel_size = 3\nblur_gray = gaussian_blur(gray, kernel_size)\n\nlow_threshold = 100\nhigh_threshold = 150\ncanny_out = canny(blur_gray, low_threshold, high_threshold)\nplt.imshow(canny_out, cmap='Greys_r')\n\n# give the vertices of polygon in an array form\nysize = image.shape[0]\nxsize = image.shape[1]\nvertices = np.array([[[100, ysize], [450,325],[525,325], [850,ysize]]], dtype=np.int32)\n\n#Region of interest\nmasked_image = region_of_interest(canny_out, vertices)\nplt.imshow(masked_image, cmap='Greys_r')\n\n#Hough transforms\nimg = masked_image\nrho = 1\ntheta = np.pi/180\nthreshold = 10\nmin_line_len = 10\nmax_line_gap = 2\nline_img = hough_lines(img, rho, theta, threshold, min_line_len, max_line_gap)\nplt.imshow(line_img)\n\nlines = cv2.HoughLinesP(img, rho, theta, threshold, np.array([]),min_line_len, max_line_gap)\n\nweighted_image = weighted_img(line_img, image, α=0.8, β=1., γ=0.)\nplt.imshow(weighted_image)\n\ndraw_lines(weighted_image, lines, color=[255, 0, 0], thickness=5)\nplt.imshow(weighted_image)", "_____no_output_____" ] ], [ [ "## Test on Videos\n\nYou know what's cooler than drawing lanes over images? Drawing lanes over video!\n\nWe can test our solution on two provided videos:\n\n`solidWhiteRight.mp4`\n\n`solidYellowLeft.mp4`\n\n**Note: if you get an import error when you run the next cell, try changing your kernel (select the Kernel menu above --> Change Kernel). Still have problems? Try relaunching Jupyter Notebook from the terminal prompt. Also, consult the forums for more troubleshooting tips.**\n\n**If you get an error that looks like this:**\n```\nNeedDownloadError: Need ffmpeg exe. \nYou can download it by calling: \nimageio.plugins.ffmpeg.download()\n```\n**Follow the instructions in the error message and check out [this forum post](https://discussions.udacity.com/t/project-error-of-test-on-videos/274082) for more troubleshooting tips across operating systems.**", "_____no_output_____" ] ], [ [ "# Import everything needed to edit/save/watch video clips\nfrom moviepy.editor import VideoFileClip\nfrom IPython.display import HTML", "_____no_output_____" ], [ "def process_image(image):\n # NOTE: The output you return should be a color image (3 channel) for processing video below\n # TODO: put your pipeline here,\n # you should return the final output (image where lines are drawn on lanes)\n\n return result", "_____no_output_____" ] ], [ [ "Let's try the one with the solid white lane on the right first ...", "_____no_output_____" ] ], [ [ "white_output = 'test_videos_output/solidWhiteRight.mp4'\n## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video\n## To do so add .subclip(start_second,end_second) to the end of the line below\n## Where start_second and end_second are integer values representing the start and end of the subclip\n## You may also uncomment the following line for a subclip of the first 5 seconds\n##clip1 = VideoFileClip(\"test_videos/solidWhiteRight.mp4\").subclip(0,5)\nclip1 = VideoFileClip(\"test_videos/solidWhiteRight.mp4\")\nwhite_clip = clip1.fl_image(process_image) #NOTE: this function expects color images!!\n%time white_clip.write_videofile(white_output, audio=False)", "_____no_output_____" ] ], [ [ "Play the video inline, or if you prefer find the video in your filesystem (should be in the same directory) and play it in your video player of choice.", "_____no_output_____" ] ], [ [ "HTML(\"\"\"\n<video width=\"960\" height=\"540\" controls>\n <source src=\"{0}\">\n</video>\n\"\"\".format(white_output))", "_____no_output_____" ] ], [ [ "## Improve the draw_lines() function\n\n**At this point, if you were successful with making the pipeline and tuning parameters, you probably have the Hough line segments drawn onto the road, but what about identifying the full extent of the lane and marking it clearly as in the example video (P1_example.mp4)? Think about defining a line to run the full length of the visible lane based on the line segments you identified with the Hough Transform. As mentioned previously, try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video \"P1_example.mp4\".**\n\n**Go back and modify your draw_lines function accordingly and try re-running your pipeline. The new output should draw a single, solid line over the left lane line and a single, solid line over the right lane line. The lines should start from the bottom of the image and extend out to the top of the region of interest.**", "_____no_output_____" ], [ "Now for the one with the solid yellow lane on the left. This one's more tricky!", "_____no_output_____" ] ], [ [ "yellow_output = 'test_videos_output/solidYellowLeft.mp4'\n## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video\n## To do so add .subclip(start_second,end_second) to the end of the line below\n## Where start_second and end_second are integer values representing the start and end of the subclip\n## You may also uncomment the following line for a subclip of the first 5 seconds\n##clip2 = VideoFileClip('test_videos/solidYellowLeft.mp4').subclip(0,5)\nclip2 = VideoFileClip('test_videos/solidYellowLeft.mp4')\nyellow_clip = clip2.fl_image(process_image)\n%time yellow_clip.write_videofile(yellow_output, audio=False)", "_____no_output_____" ], [ "HTML(\"\"\"\n<video width=\"960\" height=\"540\" controls>\n <source src=\"{0}\">\n</video>\n\"\"\".format(yellow_output))", "_____no_output_____" ] ], [ [ "## Writeup and Submission\n\nIf you're satisfied with your video outputs, it's time to make the report writeup in a pdf or markdown file. Once you have this Ipython notebook ready along with the writeup, it's time to submit for review! Here is a [link](https://github.com/udacity/CarND-LaneLines-P1/blob/master/writeup_template.md) to the writeup template file.\n", "_____no_output_____" ], [ "## Optional Challenge\n\nTry your lane finding pipeline on the video below. Does it still work? Can you figure out a way to make it more robust? If you're up for the challenge, modify your pipeline so it works with this video and submit it along with the rest of your project!", "_____no_output_____" ] ], [ [ "challenge_output = 'test_videos_output/challenge.mp4'\n## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video\n## To do so add .subclip(start_second,end_second) to the end of the line below\n## Where start_second and end_second are integer values representing the start and end of the subclip\n## You may also uncomment the following line for a subclip of the first 5 seconds\n##clip3 = VideoFileClip('test_videos/challenge.mp4').subclip(0,5)\nclip3 = VideoFileClip('test_videos/challenge.mp4')\nchallenge_clip = clip3.fl_image(process_image)\n%time challenge_clip.write_videofile(challenge_output, audio=False)", "_____no_output_____" ], [ "HTML(\"\"\"\n<video width=\"960\" height=\"540\" controls>\n <source src=\"{0}\">\n</video>\n\"\"\".format(challenge_output))", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ] ]

cb3036adc87b973edd11c9a2cb86803dc63809b0

59,199

ipynb

Jupyter Notebook

Radio_Modulation_Recognition_Networks.ipynb

LiLee1/Radio-Modulation-Recognition-Networks

5c4026181eeb277f346bb1001d754b9359006f84

[ "MIT" ]

18

2021-04-22T16:12:15.000Z

2022-03-07T09:21:29.000Z

Radio_Modulation_Recognition_Networks.ipynb

LiLee1/Radio-Modulation-Recognition-Networks

5c4026181eeb277f346bb1001d754b9359006f84

[ "MIT" ]

null

Radio_Modulation_Recognition_Networks.ipynb

LiLee1/Radio-Modulation-Recognition-Networks

5c4026181eeb277f346bb1001d754b9359006f84

[ "MIT" ]

8

2021-03-23T00:35:39.000Z

2022-01-13T09:28:28.000Z

33.314012

361

0.489991

[ [ [ "<a href=\"https://colab.research.google.com/github/KristynaPijackova/Radio-Modulation-Recognition-Networks/blob/main/Radio_Modulation_Recognition_Networks.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>", "_____no_output_____" ], [ "# Radio Modulation Recognition Networks\n\n---\n\n**Author: Kristyna Pijackova**\n\n---\n\nThis notebook contains code for my [bachelor thesis](https://www.vutbr.cz/studenti/zav-prace/detail/133594) in the academic year 2020/2021. \n\n---\n\n**The code structure is following:**\n\n\n* **Imports** - Import needed libraries\n* **Defined Functions** - Functions defined for an easier manipulation with the data later on\n* **Accessing the datasets** - you may skip this part and download the datasets elsewhere if you please\n* **Loading Data** - Load the data and divide them into training, validation and test sets\n* **Deep Learning Part** -Contains the architectures, which are prepared to be trained and evaluated\n* **Load Trained Model** - Optionaly you can download the CGDNN model and see how it does on the corresponding dataset\n* **Layer Visualization** - A part of code which was written to visualize the activation maps of the convolutional and recurrent layers\n* **Plotting** - You can plot the confusion matrices in this part \n\n---\n\n**Quick guide to running the document:**\n\nOpen [Google Colab](https://colab.research.google.com/notebooks/intro.ipynb#recent=true) and go to 'GitHub' bookmark. Insert the link to the Github repository. This should open the code for you and allow you to run and adjust it.\n\n* Use `up` and `down` keys to move in the notebook\n* Use `ctrl+enter` to run cell or choose 'Run All' in Runtime to run the whole document at once \n* If you change something in specific cell, it's enough to re-run just the cell to save the changes\n* Hide/show sections of the code with the arrows at side, which are next to some cell code\n* In the top left part yoz can click on the Content icon, which will allow you to navigate easier through this notebook\n\n\n\n\n\n", "_____no_output_____" ], [ "# Imports", "_____no_output_____" ], [ "Import needed libraries", "_____no_output_____" ] ], [ [ "from scipy.io import loadmat\nfrom pandas import factorize\nimport pickle\nimport numpy as np\nimport random\nfrom scipy import signal\n\nfrom matplotlib import pyplot as plt\nfrom sklearn.metrics import confusion_matrix\nimport seaborn as sns\n\nfrom tensorflow.keras.utils import to_categorical\nimport tensorflow as tf\nfrom tensorflow import keras\nfrom tensorflow.keras import backend as K\nfrom tensorflow.keras import layers\nfrom tensorflow.keras.utils import plot_model", "_____no_output_____" ] ], [ [ "Mount to Google Drive (optional)", "_____no_output_____" ] ], [ [ "# Mounting your Google Drive\n\n# from google.colab import drive\n# drive.mount('/content/gdrive', force_remount=True)\n# root_dir = \"/content/gdrive/My Drive/\"", "_____no_output_____" ] ], [ [ "# Defined functions for easier work with data", "_____no_output_____" ], [ "## Functions to load datasets", "_____no_output_____" ] ], [ [ "# VUT Dataset\ndef load_VUT_dataset(dataset_location):\n \"\"\"\n Load dataset and extract needed data\n\n Input: \n dataset_location: specify where the file is stored and its name\n\n Output:\n SNR: list of the SNR range in dataset [-20 to 18]\n X: array of the measured I/Q data [num_of_samples, 128, 2]\n modulations: list of the modulations in this dataset\n one_hot: one_hot encoded data - the other maps the order of the mods\n lbl_SNR: list of each snr (for plotting)\n \"\"\"\n\n # Load the dataset stored as .mat with loadmat fuction from scipy.io\n\n # from scipy.io import loadmat\n dataset = loadmat(dataset_location)\n\n # Point to wanted data\n\n SNR = dataset['SNR']\n X = dataset['X'] \n mods = dataset['mods']\n one_hot = dataset['one_hot'] \n\n # Transpose the structure of X from [:,2,128] to [:,128,2]\n\n X = np.transpose(X[:,:,:],(0,2,1))\n\n # Change the type and structure of output SNR and mods to lists\n\n SNRs = []\n SNR = np.reshape(SNR,-1)\n\n for i in range(SNR.shape[0]):\n snr = SNR[:][i].tolist()\n SNRs.append(snr)\n\n modulations = []\n mods = np.reshape(mods,-1)\n\n for i in range(mods.shape[0]):\n mod = mods[i][0].tolist()\n modulations.append(mod)\n\n # Assign SNR value to each vector\n repeat_n = X.shape[0]/len(mods)/len(SNR)\n repeat_n_mod = len(mods) \n lbl_SNR = np.tile(np.repeat(SNR, repeat_n), repeat_n_mod)\n\n # X = tf.convert_to_tensor(X, dtype=tf.float32)\n # one_hot = tf.convert_to_tensor(one_hot, dtype=tf.float32)\n\n return SNRs, X, modulations, one_hot, lbl_SNR\n", "_____no_output_____" ], [ "# RadioML2016.10a/10b or MIGOU MOD\n\ndef load_dataset(dataset_location):\n \"\"\"\n Load dataset and extract needed data\n\n Input: \n dataset_location: specify where the file is stored and its name\n\n Output:\n snrs: list of the SNR range in dataset [-20 to 18]\n X: array of the measured I/Q data [num_of_samples, 128, 2]\n modulations: list of the modulations in this dataset\n one_hot_encode: one_hot encoded data - the other maps the order of the mods\n lbl_SNR: list of each snr (for plotting)\n \"\"\"\n\n snrs,mods = map(lambda j: sorted(list(set(map(lambda x: x[j], dataset_location.keys())))), [1,0])\n\n X = []; I = []; Q = []; lbl = [];\n\n for mod in mods:\n for snr in snrs:\n X.append(dataset_location[(mod,snr)])\n for i in range(dataset_location[(mod,snr)].shape[0]): \n lbl.append((mod,snr))\n X = np.vstack(X); lbl=np.vstack(lbl)\n\n X = np.transpose(X[:,:,:],(0,2,1))\n\n # One-hot-encoding\n Y = [];\n for i in range(len(lbl)):\n mod = (lbl[i,0])\n Y.append(mod)\n\n mapping = {}\n for x in range(len(mods)):\n mapping[mods[x]] = x\n\n ## integer representation\n for x in range(len(Y)):\n Y[x] = mapping[Y[x]]\n\n one_hot_encode = to_categorical(Y)\n\n # Assign SNR value to each vector\n repeat_n = X.shape[0]/len(mods)/len(snrs)\n repeat_n_mod = len(mods) \n lbl_SNR = np.tile(np.repeat(snrs, repeat_n), repeat_n_mod)\n\n\n\n return snrs, X, mods, one_hot_encode, lbl_SNR", "_____no_output_____" ], [ "# RML2016.10b / just for the way it is saved in my GoogleDrive\n\ndef load_RMLb_dataset(X, lbl):\n mods = np.unique(lbl[:,0])\n snrs = np.unique(lbl[:,1])\n snrs = list(map(int, snrs))\n snrs.sort()\n\n # One-hot encoding\n Y = [];\n for i in range(len(lbl)):\n mod = (lbl[i,0])\n Y.append(mod)\n\n mapping = {}\n for x in range(len(mods)):\n mapping[mods[x]] = x\n\n ## integer representation\n for x in range(len(Y)):\n Y[x] = mapping[Y[x]]\n\n one_hot_encode = to_categorical(Y)\n\n\n # Assign SNR value to each vector\n repeat_n = X.shape[0]/len(mods)/len(snrs)\n repeat_n_mod = len(mods) \n lbl_SNR = np.tile(np.repeat(snrs, repeat_n), repeat_n_mod)\n\n X = X\n\n return snrs, X, mods, one_hot_encode, lbl_SNR\n", "_____no_output_____" ] ], [ [ "## Functions to handle the datasets", "_____no_output_____" ] ], [ [ "def train_test_valid_split(X, one_hot, train_split=0.7, valid_split=0.15, test_split=0.15):\n \n \"\"\"\n Train-Test split the data\n\n Input:\n X: X data\n one_hot: Y data encoded to one_hot\n train_split (default 0.7)\n valid_split (default 0.15)\n test_split (default 0.15)\n train_split : valid_split : test_split - ratio for splitting the dataset\n \n NOTE: the ratio split must be a sum of 1!\n\n Output:\n train_idx: indexes from X assinged to train data\n valid_idx: indexes from X assinged to validation data \n test_idx: indexes from X assinged to test data\n X_train: X data assigned for training\n X_valid: X data assigned for validation\n X_test: X data assigned for testing\n Y_train: one-hot encoded Y data assigned for training\n Y_valid: one-hot encoded Y data assigned for validation\n Y_test: one-hot encoded Y data assigned for testing\n \"\"\"\n\n # Set random seed\n np.random.seed(42)\n random.seed(42)\n\n # Get the number of samples\n n_examples = X.shape[0]\n n_train = int(n_examples * train_split)\n n_valid = int(n_examples * valid_split)\n n_test = int(n_examples * test_split)\n \n # Get indexes of train data\n train_idx = np.random.choice(range(0, n_examples), size=n_train, replace=False)\n\n # Left indexes for valid and test sets\n left_idx= list(set(range(0, n_examples)) - set(train_idx))\n \n # Get indexes for the left indexes of the X data\n val = np.random.choice(range(0, (n_valid+n_test)), size=(n_valid), replace=False)\n test = list(set(range(0, len(left_idx))) - set(val))\n\n # Assign indeces for validation to left indexes\n valid_idx = []\n for i in val:\n val_idx = left_idx[i]\n valid_idx.append(val_idx)\n \n # Get the test set as the rest indexes\n test_idx = []\n for i in test:\n tst_idx = left_idx[i]\n test_idx.append(tst_idx)\n \n # Shuffle the valid_idx and test_idx\n random.shuffle(valid_idx)\n random.shuffle(test_idx)\n\n # Assing the indexes to the X and Y data to create train and test sets\n X_train = X[train_idx]\n X_valid = X[valid_idx]\n X_test = X[test_idx] \n Y_train = one_hot[train_idx]\n Y_valid = one_hot[valid_idx]\n Y_test = one_hot[test_idx] \n\n return train_idx, valid_idx, test_idx, X_train, X_valid, X_test, Y_train, Y_valid, Y_test\n\n", "_____no_output_____" ], [ "def normalize_data(X_train, X_valid, X_test):\n # mean-std normalization\n\n mean = X_train[:,:,:].mean(axis=0)\n X_train[:,:,:] -= mean\n std = X_train[:,:,:].std(axis=0)\n X_train[:,:,:] /= std\n\n\n X_valid[:,:,:] -= mean\n X_valid[:,:,:] /= std\n\n X_test[:,:,:] -= mean\n X_test[:,:,:] /= std\n\n return X_train, X_valid, X_test", "_____no_output_____" ], [ "def return_indices_of_a(a, b):\n \"\"\"\n Compare two lists a, b for same items and return indeces\n of the item in list a\n\n a: List of items, its indeces will be returned\n b: List of items to search for in list a\n\n Credit: https://stackoverflow.com/users/97248/pts ; https://stackoverflow.com/questions/10367020/compare-two-lists-in-python-and-return-indices-of-matched-values\n \"\"\"\n b_set = set(b)\n return [i for i, v in enumerate(a) if v in b_set]", "_____no_output_____" ] ], [ [ "## Functions for plotting", "_____no_output_____" ] ], [ [ "def show_confusion_matrix(validations, predictions, matrix_snr, save=False):\n \"\"\"\n Plot confusion matrix\n\n validations: True Y labels\n predictions: Predicted Y labels of your model\n matrix_snr: SNR information for plot's titel\n \"\"\"\n \n cm = confusion_matrix(validations, predictions)\n # Normalise\n cmn = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]\n fig, ax = plt.subplots(figsize=(10,10))\n sns.heatmap(cmn, cmap='Blues', annot=True, fmt='.2f', xticklabels=mods, yticklabels=mods)\n sns.set(font_scale=1.3)\n if matrix_snr == None:\n plt.title(\"Confusion Matrix\")\n else:\n plt.title(\"Confusion Matrix \\n\" + str(matrix_snr) + \"dB\")\n plt.ylabel('True Label')\n plt.xlabel('Predicted Label')\n if save == True:\n plt.savefig(base_dir + 'Own_dataset/' + str(matrix_snr) + '.png') \n plt.show(block=False)\n ", "_____no_output_____" ], [ "def All_SNR_show_confusion_matrix(X_test, save=False):\n \"\"\"\n Plot confusion matrix of all SNRs in one\n\n X_test: X_test data\n \"\"\"\n prediction = model.predict(X_test)\n\n Y_Pred = []; Y_Test = [];\n\n for i in range(len(prediction[:,0])):\n Y_Pred.append(np.argmax(prediction[i,:]))\n Y_Test.append(np.argmax(Y_test[i]))\n\n show_confusion_matrix(Y_Pred, Y_Test, None, save)", "_____no_output_____" ], [ "def SNR_show_confusion_matrix(in_snr, lbl_SNR, X_test, save=False):\n \"\"\"\n Plot confusion matrices of chosen SNRs\n\n in_snr: must be list of SNRs\n X_test: X_test data\n \"\"\"\n for snr in in_snr:\n matrix_snr = snr\n m_snr = matrix_snr;\n\n Y_Pred = []; Y_Test = []; Y_Pred_SNR = []; Y_Test_SNR = []; \n matrix_snr_index = [];\n\n prediction = model.predict(X_test)\n\n for i in range(len(prediction[:,0])):\n Y_Pred.append(np.argmax(prediction[i,:]))\n Y_Test.append(np.argmax(Y_test[i]))\n\n for i in range(len(lbl_SNR)):\n if int(lbl_SNR[i]) == m_snr:\n matrix_snr_index.append(i)\n\n indeces_of_Y_test = return_indices_of_a(test_idx, matrix_snr_index)\n\n for i in indeces_of_Y_test:\n Y_Pred_SNR.append(Y_Pred[i])\n Y_Test_SNR.append(Y_Test[i])\n show_confusion_matrix(Y_Pred_SNR, Y_Test_SNR, matrix_snr, save)", "_____no_output_____" ], [ "def plot_split_distribution(mods, Y_train, Y_valid, Y_test):\n\n x = np.arange(len(mods)) # the label locations\n width = 1 # the width of the bars\n\n fig, ax = plt.subplots()\n bar1 = ax.bar(x-width*0.3, np.count_nonzero(Y_train == 1, axis=0), width*0.3, label = \"Train\" )\n bar2 = ax.bar(x , np.count_nonzero(Y_valid == 1, axis=0), width*0.3, label = \"Valid\" )\n bar3 = ax.bar(x+width*0.3, np.count_nonzero(Y_test == 1, axis=0), width*0.3, label = \"Test\" )\n\n\n # Add some text for labels, title and custom x-axis tick labels, etc.\n ax.set_ylabel('Distribution')\n ax.set_title('Distribution overview of splitted dataset')\n ax.set_xticks(x)\n ax.set_xticklabels(mods)\n ax.legend(loc='upper center', bbox_to_anchor=(0.5, -0.15),\n fancybox=True, shadow=True, ncol=5)\n\n\n def autolabel(rects):\n \"\"\"Attach a text label above each bar in *rects*, displaying its height.\"\"\"\n for rect in rects:\n height = rect.get_height()\n ax.annotate('{}'.format(height),\n xy=(rect.get_x() + rect.get_width() / 2, height),\n xytext=(0, 0), # 3 points vertical offset\n textcoords=\"offset points\",\n ha='center', va='bottom')\n \n # autolabel(bar1)\n # autolabel(bar2)\n # autolabel(bar3)\n # fig.tight_layout()\n return plt.show()", "_____no_output_____" ], [ "def SNR_accuracy(in_snr, name):\n \"\"\"\n Computes accuracies of chosen SNRs individualy\n \n in_snr: must be list of SNRs\n \"\"\"\n \n acc = []\n for snr in in_snr:\n acc_snr = snr\n idx_acc_snr = []\n\n for i in range(len(test_idx)):\n if int(lbl_SNR[test_idx[i]]) == int(acc_snr):\n idx_acc_snr.append(i)\n\n acc_X_test = X_test[idx_acc_snr]\n # acc_X_f_test = X_f_test[idx_acc_snr]\n acc_Y_test = Y_test[idx_acc_snr]\n\n print('\\nSNR ' + str(acc_snr) + 'dB:')\n accuracy_snr = model.evaluate([acc_X_test], acc_Y_test, batch_size=32, verbose=2)\n acc.append(accuracy_snr)\n\n acc = np.vstack(acc)\n fig = plt.figure()\n ax = fig.add_subplot(1, 1, 1)\n plt.plot(SNR, (acc[:,1]*100), 'steelblue', marker='.', markersize= 15, label = name, linestyle = '-',)\n ax.legend(loc=4, prop={'size': 25})\n\n x_major_ticks = np.arange(-20, 19, 2 )\n ax.set_xticks(x_major_ticks)\n\n y_major_ticks = np.arange(0, 101, 10 )\n y_minor_ticks = np.arange(0, 101, 2)\n ax.set_yticks(y_major_ticks)\n ax.set_yticks(y_minor_ticks, minor=True)\n ax.tick_params(axis='both', which='major', labelsize=20)\n\n ax.grid(which='both',color='lightgray', linestyle='-')\n\n ax.grid(which='minor', alpha=0.2)\n ax.grid(which='major', alpha=0.5)\n\n plt.xlim(-20, 18)\n plt.ylim(0,100)\n plt.title(\"Classification Accuracy\",fontsize=20)\n plt.ylabel('Accuracy (%)',fontsize=20)\n plt.xlabel('SNR (dB)',fontsize=20)\n # plt.savefig(base_dir + name + '.png') \n plt.show()\n\n return acc[:,1]\n", "_____no_output_____" ] ], [ [ "## Functions for visualization of layers", "_____no_output_____" ] ], [ [ "def layer_overview(model):\n\n \"\"\"\n Offers overview of the model's layers and theirs outputs\n\n model: specify trained model you want to have overview of\n \"\"\"\n\n # Names and outputs from layers\n layer_names = [layer.name for layer in model.layers]\n layer_outputs = [layer.output for layer in model.layers[:]]\n\n return layer_names, layer_outputs\n\ndef model_visualization(nth_layer, nth_test_idx, mods, model,\n plot_sample = False, plot_activations = True, \n plot_feature_maps = True):\n \n \"\"\"\n The function provised overview of activation of specific layer and its\n feature maps.\n\n nth_layer: enter number which corresponds with the position of wanted layer \n nth_test_idx: enter number pointing at the test indexes from earlier\n mods: provide variable which holds listed modulations\n model: specify which trained model to load\n plot_sample = False: set to true to plot sample data\n plot_activations = True: plots activation of chosen layer\n plot_feature_maps = True: plots feature map of chosen layer\n \"\"\"\n\n # Sample data for visualization\n test_sample = X_test[nth_test_idx,:,:] # shape [128,2]\n test_sample = test_sample[None] # change to needed [1,128,2]\n SNR = lbl_SNR[test_idx[nth_test_idx]]\n mod = one_hot[test_idx[nth_test_idx]]\n f, u = factorize(mods)\n mod = mod.dot(u)\n\n # Names and outputs from layers\n layer_names = [layer.name for layer in model.layers]\n layer_outputs = [layer.output for layer in model.layers[:]]\n\n ## Activations ##\n\n # define activation model\n activation_model = tf.keras.models.Model(model.input, layer_outputs)\n\n # get the activations of chosen test sample\n activations = activation_model.predict(test_sample)\n\n ## Feature-maps ##\n\n # define feature maps model \n feature_maps_model = tf.keras.models.Model(model.inputs, model.layers[4].output)\n \n # get the activated features\n feature_maps = feature_maps_model.predict(test_sample)\n\n\n # Plot sample\n if plot_sample == True:\n plt.plot(test_sample[0,:,:])\n plt.title(mod + ' ' + str(SNR) + 'dB')\n plt.show()\n\n # Plot activations\n if plot_activations == True:\n activation_layer = activations[nth_layer]\n activation_layer = np.transpose(activation_layer[:,:,:],(0,2,1)) # reshape\n fig, ax = plt.subplots(figsize=(20,10))\n ax.matshow(activation_layer[0,:,:], cmap='viridis')\n # plt.matshow(activation_layer[0,:,:], cmap='viridis')\n plt.title('Activation of layer ' + layer_names[nth_layer])\n ax.grid(False)\n ax.set_xlabel('Lenght of sequence')\n ax.set_ylabel('Filters')\n fig.show()\n plt.savefig(base_dir + 'activations.png')\n plt.savefig(base_dir + 'activations.svg')\n\n # Plot feature maps\n if plot_feature_maps == True:\n n_filters = int(feature_maps.shape[2]/2); ix = 1\n fig = plt.figure(figsize=(25,15))\n for _ in range(n_filters):\n for _ in range(2):\n # specify subplot and turn of axis\n ax =fig.add_subplot(n_filters, 5, ix)\n # ax = plt.subplot(n_filters, 5, ix, )\n ax.set_xticks([])\n ax.set_yticks([])\n # plot filter channel in grayscale\n ax.plot(feature_maps[0, :, ix-1])\n ix += 1\n # show the figure\n fig.show()\n plt.savefig(base_dir + 'feature_map.png')\n plt.savefig(base_dir + 'feature_map.svg')", "_____no_output_____" ] ], [ [ "## Transformer", "_____no_output_____" ] ], [ [ "def position_encoding_init(n_position, emb_dim):\n ''' Init the sinusoid position encoding table '''\n\n # keep dim 0 for padding token position encoding zero vector\n position_enc = np.array([\n [pos / np.power(10000, 2 * (j // 2) / emb_dim) for j in range(emb_dim)]\n if pos != 0 else np.zeros(emb_dim) for pos in range(n_position)])\n \n\n position_enc[1:, 0::2] = np.sin(position_enc[1:, 0::2]) # dim 2i\n position_enc[1:, 1::2] = np.cos(position_enc[1:, 1::2]) # dim 2i+1\n \n return position_enc", "_____no_output_____" ], [ "# Transformer Block\nclass TransformerBlock(layers.Layer):\n def __init__(self, embed_dim, num_heads, ff_dim, rate=0.1):\n super(TransformerBlock, self).__init__()\n self.att = layers.MultiHeadAttention(num_heads=num_heads, key_dim=embed_dim)\n self.ffn = keras.Sequential(\n [layers.Dense(ff_dim, activation=\"relu\"), layers.Dense(embed_dim),]\n )\n self.layernorm1 = layers.LayerNormalization(epsilon=1e-6)\n self.layernorm2 = layers.LayerNormalization(epsilon=1e-6)\n self.dropout1 = layers.Dropout(rate)\n self.dropout2 = layers.Dropout(rate)\n\n def call(self, inputs, training):\n attn_output = self.att(inputs, inputs)\n attn_output = self.dropout1(attn_output, training=training)\n out1 = self.layernorm1(inputs + attn_output)\n ffn_output = self.ffn(out1)\n ffn_output = self.dropout2(ffn_output, training=training)\n return self.layernorm2(out1 + ffn_output)", "_____no_output_____" ] ], [ [ "# Access the datasets\n\nWith the following cells, you can easily access the datasets. However, if you end up using them for your work, do not forget to credit the original authors! More info is provided for each of them below.", "_____no_output_____" ] ], [ [ "# Uncomment the following line, if needed, to download the datasets\n# !conda install -y gdown", "_____no_output_____" ] ], [ [ "## RadioML Datasets\n\n\n* O'shea, Timothy J., and Nathan West. \"Radio machine learning dataset generation with gnu radio.\" Proceedings of the GNU Radio Conference. Vol. 1. No. 1. 2016.\n\n* The datasets are available at: https://www.deepsig.ai/datasets \n\n* All datasets provided by Deepsig Inc. are licensed under the Creative Commons Attribution - [NonCommercial - ShareAlike 4.0 License (CC BY-NC-SA 4.0)](https://creativecommons.org/licenses/by-nc-sa/4.0/).\n\nBoth datasets are left unchanged, however, the RadioML2016.10b version is not stored as the original data, but is already splitted into X and labels\n", "_____no_output_____" ] ], [ [ "# RadioML2016.10a stored as the original pkl file\n!gdown --id 1aus-u2xSKETW9Yv5Q-QG9tz9Xnbj5yHV", "_____no_output_____" ], [ "dataset_pkl = open('RML2016.10a_dict.pkl','rb')\nRML_dataset_location = pickle.load(dataset_pkl, encoding='bytes')", "_____no_output_____" ], [ "# RadioML2016.10b stored in X.pkl and label.pkl\n!gdown --id 10OdxNvtSbOm58t-MMHZcmSMqzEWDSpAr\n!gdown --id 1-MvVKNmTfqyfYD_usvAfEcizzBX0eEpE", "_____no_output_____" ], [ "RMLb_X_data_file = open('X.pkl','rb')\nRMLb_labels_file = open('labels.pkl', 'rb')\nRMLb_X = pickle.load(RMLb_X_data_file, encoding='bytes')\nRMLb_lbl = pickle.load(RMLb_labels_file, encoding='ascii') ", "_____no_output_____" ] ], [ [ "## Migou-Mod Dataset\n\n\n* Utrilla, Ramiro (2020), “MIGOU-MOD: A dataset of modulated radio signals acquired with MIGOU, a low-power IoT experimental platform”, Mendeley Data, V1, doi: 10.17632/fkwr8mzndr.1\n\n* The dataset is available at: https://data.mendeley.com/datasets/fkwr8mzndr/1 \n\n* The dataset is licensed under the Creative Commons Attribution - [NonCommercial - ShareAlike 4.0 License (CC BY-NC-SA 4.0)](https://creativecommons.org/licenses/by-nc-sa/4.0/).\n\nThe following version of the dataset contain only a fraction of the original samples (550,000 samples compared to 8.8 million samples in the original dataset)\n", "_____no_output_____" ] ], [ [ "# Migou-Mod Dataset - 550,000 samples \n!gdown --id 1-CIL3bD4o9ylBkD0VZkGd5n1-8_RTRvs", "_____no_output_____" ], [ "MIGOU_dataset_pkl = open('dataset_25.pkl','rb')\nMIGOU_dataset_location = pickle.load(MIGOU_dataset_pkl, encoding='bytes')", "_____no_output_____" ] ], [ [ "## VUT Dataset\n\nThis dataset was generated in MATLAB with 1000 samples per SNR value and each modulation type. It includes three QAM modulation schemes and further OFDM, GFDM, and FBMC modulations which are not included in previous datasets. To mimic the RadioML dataset, the data are represented as 2x128 vectors of I/Q signals in the SNR range from -20 dB to 18 dB.", "_____no_output_____" ] ], [ [ "# VUT Dataset\n!gdown --id 1G5WsgUze8qfuSzy6Edg_4qRIiAx_YUc4", "_____no_output_____" ], [ "VUT_dataset_location = 'NEW_Dataset_05_02_2021.mat'", "_____no_output_____" ] ], [ [ "# Load the data", "_____no_output_____" ], [ "## VUT Dataset\n\n", "_____no_output_____" ] ], [ [ "SNR, X, mods, one_hot, lbl_SNR = load_VUT_dataset(VUT_dataset_location)", "_____no_output_____" ], [ "train_idx, valid_idx, test_idx, X_train, X_valid, X_test, Y_train, Y_valid, Y_test = train_test_valid_split(X, one_hot, train_split=0.7, valid_split=0.15, test_split=0.15)", "_____no_output_____" ], [ "plot_split_distribution(mods, Y_train, Y_valid, Y_test)", "_____no_output_____" ] ], [ [ "## DeepSig Dataset", "_____no_output_____" ] ], [ [ "# 10a\n# SNR, X, modulations, one_hot, lbl_SNR = load_dataset(RML_dataset_location)\n\n# 10b\nSNR, X, modulations, one_hot, lbl_SNR = load_RMLb_dataset(RMLb_X, RMLb_lbl)", "_____no_output_____" ], [ "mods = []\nfor i in range(len(modulations)):\n modu = modulations[i].decode('utf-8')\n mods.append(modu)", "_____no_output_____" ], [ "train_idx, valid_idx, test_idx, X_train, X_valid, X_test, Y_train, Y_valid, Y_test = train_test_valid_split(X, one_hot, train_split=0.7, valid_split=0.15, test_split=0.15)", "_____no_output_____" ], [ "plot_split_distribution(mods, Y_train, Y_valid, Y_test)", "_____no_output_____" ], [ "# X_train, X_valid, X_test = normalize_data(X_train, X_valid, X_test)", "_____no_output_____" ] ], [ [ "## MIGOU-MOD", "_____no_output_____" ] ], [ [ "SNR, X, mods, one_hot, lbl_SNR = load_dataset(MIGOU_dataset_location)", "_____no_output_____" ], [ "train_idx, valid_idx, test_idx, X_train, X_valid, X_test, Y_train, Y_valid, Y_test = train_test_valid_split(X, one_hot, train_split=0.7, valid_split=0.15, test_split=0.15)", "_____no_output_____" ], [ "plot_split_distribution(mods, Y_train, Y_test, Y_test)", "_____no_output_____" ] ], [ [ "# Architectures for training", "_____no_output_____" ], [ "## CNN", "_____no_output_____" ] ], [ [ "\ncnn_in = keras.layers.Input(shape=(128,2))\ncnn = keras.layers.ZeroPadding1D(padding=4)(cnn_in)\ncnn = keras.layers.Conv1D(filters=50, kernel_size=8, activation='relu')(cnn)\ncnn = keras.layers.MaxPool1D(pool_size=2)(cnn)\ncnn = keras.layers.Conv1D(filters=50, kernel_size=8, activation='relu')(cnn)\ncnn = keras.layers.MaxPool1D(pool_size=2)(cnn)\ncnn = keras.layers.Conv1D(filters=50, kernel_size=4, activation='relu')(cnn)\ncnn = keras.layers.Dropout(rate=0.6)(cnn)\ncnn = keras.layers.MaxPool1D(pool_size=2)(cnn)\ncnn = keras.layers.Flatten()(cnn)\ncnn = keras.layers.Dense(70, activation='selu')(cnn)\ncnn_out = keras.layers.Dense(len(mods), activation='softmax')(cnn)\n\nmodel_cnn = keras.models.Model(cnn_in, cnn_out)\n\ncallbacks = [\n keras.callbacks.ModelCheckpoint(\n \"cnn_model.h5\", save_best_only=True, monitor=\"val_loss\"),\n keras.callbacks.ReduceLROnPlateau(\n monitor=\"val_loss\", factor=0.3, patience=3, min_lr=0.00007),\n keras.callbacks.EarlyStopping(monitor=\"val_loss\", patience=5, verbose=1)]\n\noptimizer = keras.optimizers.Adam(learning_rate=0.0007)\n\nmodel_cnn.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])", "_____no_output_____" ], [ "# model_cldnn.summary()", "_____no_output_____" ], [ "tf.keras.backend.clear_session()\nhistory = model_cnn.fit(X_train, Y_train, batch_size=128, epochs=4, verbose=2, validation_data= (X_valid, Y_valid), callbacks=callbacks)\n", "_____no_output_____" ], [ "model = keras.models.load_model(\"cnn_model.h5\")\n\ntest_loss, test_acc = model.evaluate(X_test, Y_test)\n\nprint(\"Test accuracy\", test_acc)\nprint(\"Test loss\", test_loss)", "_____no_output_____" ], [ "SNR_accuracy(SNR, 'CNN')", "_____no_output_____" ] ], [ [ "## CLDNN", "_____no_output_____" ] ], [ [ "layer_in = keras.layers.Input(shape=(128,2))\nlayer = keras.layers.Conv1D(filters=64, kernel_size=8, activation='relu')(layer_in)\nlayer = keras.layers.MaxPool1D(pool_size=2)(layer)\nlayer = keras.layers.LSTM(64, return_sequences=True,)(layer)\nlayer = keras.layers.Dropout(0.4)(layer)\nlayer = keras.layers.LSTM(64, return_sequences=True,)(layer)\nlayer = keras.layers.Dropout(0.4)(layer)\nlayer = keras.layers.Flatten()(layer)\nlayer_out = keras.layers.Dense(len(mods), activation='softmax')(layer)\n\nmodel_cldnn = keras.models.Model(layer_in, layer_out)\n\noptimizer = keras.optimizers.Adam(learning_rate=0.0007)\n\ncallbacks = [\n keras.callbacks.ModelCheckpoint(\n \"cldnn_model.h5\", save_best_only=True, monitor=\"val_loss\"),\n keras.callbacks.ReduceLROnPlateau(\n monitor=\"val_loss\", factor=0.4, patience=5, min_lr=0.000007),\n keras.callbacks.EarlyStopping(monitor=\"val_loss\", patience=8, verbose=1)]\n\nmodel_cldnn.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])", "_____no_output_____" ], [ "# model_cldnn.summary()", "_____no_output_____" ], [ "tf.keras.backend.clear_session()\nhistory = model_cldnn.fit(X_train, Y_train, batch_size=128, epochs=100, verbose=2, validation_data= (X_valid, Y_valid), callbacks=callbacks)\n# history = model_iq.fit(X_train, Y_train, batch_size=128, epochs=100, verbose=2, validation_split=0.15, callbacks=callbacks)\n", "_____no_output_____" ], [ "model = keras.models.load_model(\"cldnn_model.h5\")\n\ntest_loss, test_acc = model.evaluate(X_test, Y_test)\n\nprint(\"Test accuracy\", test_acc)\nprint(\"Test loss\", test_loss)", "_____no_output_____" ], [ "SNR_accuracy(SNR, 'CLDNN')", "_____no_output_____" ] ], [ [ "## GGDNN", "_____no_output_____" ] ], [ [ "layer_in = keras.layers.Input(shape=(128,2)) \nlayer = keras.layers.Conv1D(filters=80, kernel_size=(12), activation='relu')(layer_in)\nlayer = keras.layers.MaxPool1D(pool_size=(2))(layer)\nlayer = keras.layers.GRU(40, return_sequences=True)(layer)\nlayer = keras.layers.GaussianDropout(0.4)(layer)\nlayer = keras.layers.GRU(40, return_sequences=True)(layer)\nlayer = keras.layers.GaussianDropout(0.4)(layer)\nlayer = keras.layers.Flatten()(layer)\nlayer_out = keras.layers.Dense(10, activation='softmax')(layer)\n\nmodel_CGDNN = keras.models.Model(layer_in, layer_out)\n\noptimizer = keras.optimizers.Adam(learning_rate=0.002)\n\ncallbacks = [\n keras.callbacks.ModelCheckpoint(\n \"cgdnn_model.h5\", save_best_only=True, monitor=\"val_loss\"),\n keras.callbacks.ReduceLROnPlateau(\n monitor=\"val_loss\", factor=0.4, patience=4, min_lr=0.000007),\n keras.callbacks.EarlyStopping(monitor=\"val_loss\", patience=10, verbose=1)]\n\nmodel_CGDNN.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])", "_____no_output_____" ], [ "# model_CGDNN.summary()", "_____no_output_____" ], [ "tf.keras.backend.clear_session()\nhistory = model_CGDNN.fit(X_train, Y_train, batch_size=128, epochs=100, verbose=2, validation_data=(X_valid,Y_valid), callbacks=callbacks)", "_____no_output_____" ], [ "model = keras.model_CGDNN.load_model(\"cgdnn_model.h5\")\n\ntest_loss, test_acc = model.evaluate(X_test, Y_test)\n\nprint(\"Test accuracy\", test_acc)\nprint(\"Test loss\", test_loss)\n\nSNR_accuracy(SNR, 'CLGDNN')", "_____no_output_____" ] ], [ [ "## MCTransformer", "_____no_output_____" ] ], [ [ "embed_dim = 64 # Embedding size for each token\nnum_heads = 4 # Number of attention heads\nff_dim = 16 # Hidden layer size in feed forward network inside transformer\n\ninputs = keras.layers.Input(shape=(128,2))\nx = keras.layers.Conv1D(filters=embed_dim, kernel_size=8, activation='relu')(inputs)\nx = keras.layers.MaxPool1D(pool_size=2)(x)\nx = keras.layers.LSTM(embed_dim, return_sequences=True,)(x)\nx = keras.layers.Dropout(0.4)(x)\n\npos_emb = position_encoding_init(60,64)\nx_pos = x+pos_emb\n\ntransformer_block = TransformerBlock(embed_dim, num_heads, ff_dim)\nx = transformer_block(x_pos)\n\nx = layers.GlobalAveragePooling1D()(x)\nx = layers.Dropout(0.1)(x)\nx = layers.Dense(20, activation=\"relu\")(x)\nx = layers.Dropout(0.1)(x)\noutputs = layers.Dense(len(mods), activation=\"softmax\")(x)\n\nmodel_MCT = keras.Model(inputs=inputs, outputs=outputs)", "_____no_output_____" ], [ "# model_MCT.summary()", "_____no_output_____" ], [ "optimizer = keras.optimizers.SGD(learning_rate=0.03)\nmodel_MCT.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])", "_____no_output_____" ], [ "history = model_MCT.fit(X_train, Y_train, batch_size=16, epochs=20, validation_data= (X_valid, Y_valid))", "_____no_output_____" ] ], [ [ "Uncomment and lower the learning rate, if the validation loss doesn't improve.", "_____no_output_____" ] ], [ [ "# optimizer = keras.optimizers.SGD(learning_rate=0.01)\n# model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])\n# history = model.fit(X_train, Y_train, batch_size=16, epochs=10, validation_data= (X_valid, Y_valid))", "_____no_output_____" ], [ "# optimizer = keras.optimizers.SGD(learning_rate=0.005)\n# model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])\n# history = model.fit(X_train, Y_train, batch_size=16, epochs=10, validation_data= (X_valid, Y_valid))", "_____no_output_____" ], [ "# optimizer = keras.optimizers.SGD(learning_rate=0.001)\n# model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])\n# history = model.fit(X_train, Y_train, batch_size=128, epochs=10, validation_data= (X_valid, Y_valid))", "_____no_output_____" ], [ "test_loss, test_acc = model_MCT.evaluate(X_test, Y_test)\n\nprint(\"Test accuracy\", test_acc)\nprint(\"Test loss\", test_loss)\nSNR_accuracy(SNR, 'MCT')", "_____no_output_____" ] ], [ [ "# Load saved CGDNN models", "_____no_output_____" ], [ "Download the models", "_____no_output_____" ] ], [ [ "# # RadioML2016.10a\n\n# !gdown --id 1h0iVzR0qEPEwcUEPKM3hBGF46uXQEs_l\n\n# # RadioML2016.10b\n# !gdown --id 1XCPOHF8ZeSC61qR1hrFKhgUxPHbpHg6R\n\n# # Migou-Mod Dataset\n# !gdown --id 1s4Uz5KlkLVO9lQyrJwVTW_754RNkigoC\n\n# # VUT Dataset\n# !gdown --id 1DWr1uDzz7m7rEfcKWXZXJpJ692EC0vBw", "_____no_output_____" ] ], [ [ "Uncomment wanted model \n\nDon't forget you also need to load the right dataset before predicting ", "_____no_output_____" ] ], [ [ "# RadioML2016.10a\n# model = tf.keras.models.load_model(\"cgd_model_10a.h5\")\n\n# RadioML2016.10b\n# model = tf.keras.models.load_model(\"cgd_model_10b.h5\")\n\n# Migou-Mod Dataset\n# model = tf.keras.models.load_model(\"CGD_MIGOU.h5\")\n\n# VUT Dataset\n# model = tf.keras.models.load_model(\"CGD_VUT.h5\")\n\n# model.summary()", "_____no_output_____" ], [ "# prediction = model.predict([X_test[:,:,:]])\n\n# Y_Pred = []; Y_Test = []; Y_Pred_SNR = []; Y_Test_SNR = []; \n# for i in range(len(prediction[:,0])):\n# Y_Pred.append(np.argmax(prediction[i,:]))\n# Y_Test.append(np.argmax(Y_test[i]))\n\n# Y_Pred[:20], Y_Test[:20]", "_____no_output_____" ] ], [ [ "\n# Visualize activation and feature map ", "_____no_output_____" ] ], [ [ "model_visualization(1,9000, mods, model)", "_____no_output_____" ] ], [ [ "# Plot Confusion Matrix", "_____no_output_____" ] ], [ [ "All_SNR_show_confusion_matrix([X_test], save=False)", "_____no_output_____" ], [ "SNR_show_confusion_matrix(mods, lbl_SNR[:], X_test, save=False)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ] ]

cb3038cfeea3f8f71f9ceac50364e6d880f5efc7

15,312

ipynb

Jupyter Notebook

.ipynb_checkpoints/Letcode_11_01-checkpoint.ipynb

yujingma45/Letcode

03b1f8165cea6ff8311b718a5c4ccac0e86e02db

[ "MIT" ]

null

.ipynb_checkpoints/Letcode_11_01-checkpoint.ipynb

yujingma45/Letcode

03b1f8165cea6ff8311b718a5c4ccac0e86e02db

[ "MIT" ]

null

.ipynb_checkpoints/Letcode_11_01-checkpoint.ipynb

yujingma45/Letcode

03b1f8165cea6ff8311b718a5c4ccac0e86e02db

[ "MIT" ]

null

25.908629

178

0.452847

[ [ [ "## Hash Table", "_____no_output_____" ] ], [ [ "### 1_TWO SUM", "_____no_output_____" ] ], [ [ "# interesting way is dictionary comprehension\ndict = dict((key, value) for (key, value) in iterable)\ndict = dict(key:value for key in iterable)", "_____no_output_____" ], [ "# two way hash:\n# remeber the number sum combinations \ndef twoSum( nums, target):\n \"\"\"\n :type nums: List[int]\n :type target: int\n :rtype: List[int]\n \"\"\"\n num_dict={}\n #t_minus_n = [target - i for i in nums]\n if nums.count(target/2)==2:\n result = [i for i,j in enumerate(nums) if j==target/2]\n else:\n comb = list(zip(nums,[target - i for i in nums]))\n #(1,2)!=(2,1) so we can use to see if both 2,1 in the nums list\n # like the parentheses question\n print(comb)\n for num in comb:\n # tuple can be hashed(used as keys), not list\n if num[0]!=num[1]:\n num_dict[num]=num_dict.get(num,0)+1 \n result = [i for i,j in enumerate(comb) if num_dict.get(j[::-1],0)==1]\n # need to check if they have opposit\n # only can enumerate give all the index\n return result", "_____no_output_____" ], [ "# one pass hash - keeping remeber the position, until onece trace back \ndef twoSum( nums, target):\n \"\"\"\n :type nums: List[int]\n :type target: int\n :rtype: List[int]\n \"\"\"\n \n num_dict = {}\n for key,value in enumerate(nums):\n com = target - value \n print(com)\n print(num_dict)\n if num_dict.__contains__(com):\n print(num_dict)\n return [num_dict.get(com), key] # at this time key is the current key\n # the next time would be a trigger to extract the previous one\n num_dict[value] = key # if not exist put down the position\n", "_____no_output_____" ], [ "def twoSum(self, nums, target):\n num_dict={}\n for pos, num in enumerate(nums):\n com = target - num\n if num_dict.get(com,None)!=None:\n return [num_dict[com],pos]\n num_dict[num]=pos\n ", "_____no_output_____" ] ], [ [ "### 136._SingleNum", "_____no_output_____" ] ], [ [ "# using set\ndef singleNumber(nums):\n return 2*sum(set(nums))-sum(nums)", "_____no_output_____" ], [ "lists=[4,1,2,1,2]\nsingleNumber(lists)", "_____no_output_____" ], [ "def singleNumber2(nums):\n res = 0\n for num in nums:\n res = res^ num\n print(res)\n return res\n\n# https://stackoverflow.com/questions/14526584/what-does-the-xor-operator-do\n# the number who are not single would be take out later as a mask\n# only left the single number", "_____no_output_____" ], [ "singleNumber2(nums)", "4\n5\n7\n6\n4\n" ] ], [ [ "### xor \n\n^ is the Python bitwise XOR operator. \n\nXOR stands for exclusive OR. It is used in cryptography because it let's you 'flip' the bits using a mask in a reversable operation:\n\n", "_____no_output_____" ] ], [ [ "print(10 ^ 5)\nprint(15 ^ 5)", "15\n10\n" ] ], [ [ "where 5 is the mask; (input XOR mask) **XOR mask gives you the input again**.", "_____no_output_____" ], [ "### 217._ contains duplicate", "_____no_output_____" ] ], [ [ "class Solution:\n def containsDuplicate(self, nums):\n \"\"\"\n :type nums: List[int]\n :rtype: bool\n \"\"\"\n num_dict={}\n for num in nums: \n if num in num_dict:\n return True\n else:\n num_dict[num]=1\n return False \n", "_____no_output_____" ], [ "class Solution:\n def containsDuplicate(self, nums):\n \"\"\"\n :type nums: List[int]\n :rtype: bool\n \"\"\"\n return len(set(nums))!= len(nums)\n", "_____no_output_____" ] ], [ [ "### 219._ contains duplicate II\nThis one has some misleading message. The closest numbers should have the distance less or equal than k. Not all the distances between duplicates should at most k", "_____no_output_____" ] ], [ [ "def containsNearbyDuplicate(self, nums, k):\n \"\"\"\n :type nums: List[int]\n :type k: int\n :rtype: bool\n \"\"\"\n if nums==[]: return False\n if len(nums)==len(set(nums)): return False\n num_dict={i:[] for i in nums}\n min_dist= len(nums)\n for i in range(0,len(nums)):\n key= nums[i]\n num_dict[key].append(i)\n if len(num_dict[key])>1:\n min_dist=min(min_dist,(num_dict[key])[-1]-num_dict[key][-2])\n return min_dist<=k", "_____no_output_____" ] ], [ [ "The first solution has a big disadvantage:\n1. Need to create a dict with all the key into it, not necessary\n2. we only need check dist(two close duplicated number)<=k, So we don't actually need remeber the failed index, we just need to calculate distance with the nearest one. \n\nSo I did 2nd:", "_____no_output_____" ] ], [ [ "def containsNearbyDuplicate(nums, k):\n \"\"\"\n :type nums: List[int]\n :type k: int\n :rtype: bool\n \"\"\"\n if nums==[]: return False\n if len(nums)==len(set(nums)): return False\n num_dict={}\n for i in range(0,len(nums)):\n key= nums[i]\n if (key in num_dict) and (i -num_dict[key]<=k):\n return True\n else:\n num_dict[key] = i # only remeber the lastest one\n return False", "_____no_output_____" ], [ "containsNearbyDuplicate([1,2,3,1,1], 1)", "{1: 0}\n{1: 0, 2: 1}\n{1: 0, 2: 1, 3: 2}\n{1: 3, 2: 1, 3: 2}\n" ] ], [ [ "For solution 2, we don't need to retrive all the num[i], we can use enumerate, don't need else, return will break it:", "_____no_output_____" ] ], [ [ "def containsNearbyDuplicate(nums, k):\n \"\"\"\n :type nums: List[int]\n :type k: int\n :rtype: bool\n \"\"\"\n if nums==[] or len(nums)==len(set(nums)) or k<0: return False\n # use the condition to eliminate all unexpect situation\n num_dict={}\n for i,num in enumerate(nums):\n if (num in num_dict) and (i -num_dict[num]<=k):\n return True\n num_dict[num] = i # only remeber the lastest one\n return False ", "_____no_output_____" ] ], [ [ "Truns out mine(solution 1) is faster..., reduced the loop key. So I modified my solution 1 to, make it simpler and elegant:", "_____no_output_____" ] ], [ [ "def containsNearbyDuplicate(self, nums, k):\n \"\"\"\n :type nums: List[int]\n :type k: int\n :rtype: bool\n \"\"\"\n if nums==[] or len(nums)==len(set(nums)) or k<0: return False\n num_dict={i:[] for i in nums}\n min_dist= len(nums)\n for i in range(0,len(nums)):\n key= nums[i]\n num_dict[key].append(i)\n if len(num_dict[key])>1:\n min_dist=min(min_dist,(num_dict[key])[-1]-num_dict[key][-2])\n return min_dist<=k", "_____no_output_____" ] ], [ [ "### 242._ Valid Anagram", "_____no_output_____" ] ], [ [ "# using array/set\ndef isAnagram(self, s, t):\n \"\"\"\n :type s: str\n :type t: str\n :rtype: bool\n \"\"\"\n if len(s)!=len(t): return False\n if set(s)!=set(t): return False\n\n return sorted(s)==sorted(t)", "_____no_output_____" ], [ "# using hash table1\ndef isAnagram(self, s, t):\n \"\"\"\n :type s: str\n :type t: str\n :rtype: bool\n \"\"\"\n if len(s)!=len(t): return False\n if set(s)!=set(t): return False\n s_dict,t_dict={},{}\n for char in s:\n s_dict[char] = s_dict.get(char,0)+1\n\n for char in t:\n t_dict[char] = t_dict.get(char,0)+1\n return s_dict==t_dict", "_____no_output_____" ], [ "# using hash table2 - not quite fast.. since we rewrite the same dict\ndef isAnagram(self, s, t):\n \"\"\"\n :type s: str\n :type t: str\n :rtype: bool\n \"\"\"\n if len(s)!=len(t) or set(s)!=set(t): return False\n char_dict = {}\n for char in s:\n char_dict [char] = char_dict.get(char,0)+1\n for char in t:\n char_dict[char] = char_dict[char]-1\n return all(value == 0 for value in char_dict.values())", "_____no_output_____" ], [ "## Turns out the best solution using ... count... so I tried two:", "_____no_output_____" ], [ "def isAnagram(self, s, t):\n \"\"\"\n :type s: str\n :type t: str\n :rtype: bool\n \"\"\"\n return all(s.count(c) == t.count(c) for c in \"abcdefghijklmnopqrstuvwxyz\")", "_____no_output_____" ], [ "## give an early break if count doesn't match\n\ndef isAnagram(self, s, t):\n \"\"\"\n :type s: str\n :type t: str\n :rtype: bool\n \"\"\"\n l = \"abcdefghijklmnopqrstuvwxyz\"\n for c in l:\n if s.count(c) != t.count(c): return False\n return True", "_____no_output_____" ] ], [ [ "### all(iterable)\n\nThe all() method returns:\n\nTrue - If all elements in an iterable are true\nFalse - If any element in an iterable is false\nhttps://stackoverflow.com/questions/35253971/how-to-check-if-all-values-of-a-dictionary-are-0-in-python\n\n### str.count(\"substr\")", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code" ], [ "markdown" ] ]

cb307c0355512aa037004bec75a31669df2a09a5

15,409

ipynb

Jupyter Notebook

docs_src/jekyll_metadata.ipynb

bhollan/fastai_docs

b06a06bec8080c9f1fa856ec8b70322bf89c8e54

[ "Apache-2.0" ]

null

docs_src/jekyll_metadata.ipynb

bhollan/fastai_docs

b06a06bec8080c9f1fa856ec8b70322bf89c8e54

[ "Apache-2.0" ]

null

docs_src/jekyll_metadata.ipynb

bhollan/fastai_docs

b06a06bec8080c9f1fa856ec8b70322bf89c8e54

[ "Apache-2.0" ]

null

22.044349

119

0.551301

[ [ [ "%reload_ext autoreload\n%autoreload 2", "_____no_output_____" ], [ "from fastai.gen_doc.gen_notebooks import *\nfrom pathlib import Path", "_____no_output_____" ] ], [ [ "### To update this notebook", "_____no_output_____" ], [ "Run `tools/sgen_notebooks.py", "_____no_output_____" ], [ "Or run below: \nYou need to make sure to refresh right after", "_____no_output_____" ] ], [ [ "import glob\nfor f in Path().glob('*.ipynb'):\n generate_missing_metadata(f)", "_____no_output_____" ] ], [ [ "# Metadata generated below", "_____no_output_____" ] ], [ [ "update_nb_metadata('torch_core.ipynb',\n summary='Basic functions using pytorch',\n title='torch_core')", "_____no_output_____" ], [ "update_nb_metadata('gen_doc.convert2html.ipynb',\n summary='Converting the documentation notebooks to HTML pages',\n title='gen_doc.convert2html')", "_____no_output_____" ], [ "update_nb_metadata('metrics.ipynb',\n summary='Useful metrics for training',\n title='metrics')", "_____no_output_____" ], [ "update_nb_metadata('callbacks.fp16.ipynb',\n summary='Training in mixed precision implementation',\n title='callback.fp16')", "_____no_output_____" ], [ "update_nb_metadata('callbacks.general_sched.ipynb',\n summary='Implementation of a flexible training API',\n title='callbacks.general_sched')", "_____no_output_____" ], [ "update_nb_metadata('text.ipynb',\n keywords='fastai',\n summary='Application to NLP, including ULMFiT fine-tuning',\n title='text')", "_____no_output_____" ], [ "update_nb_metadata('callback.ipynb',\n summary='Implementation of the callback system',\n title='callback')", "_____no_output_____" ], [ "update_nb_metadata('tabular.models.ipynb',\n keywords='fastai',\n summary='Model for training tabular/structured data',\n title='tabular.model')", "_____no_output_____" ], [ "update_nb_metadata('callbacks.mixup.ipynb',\n summary='Implementation of mixup',\n title='callbacks.mixup')", "_____no_output_____" ], [ "update_nb_metadata('applications.ipynb',\n summary='Types of problems you can apply the fastai library to',\n title='applications')", "_____no_output_____" ], [ "update_nb_metadata('vision.data.ipynb',\n summary='Basic dataset for computer vision and helper function to get a DataBunch',\n title='vision')", "_____no_output_____" ], [ "update_nb_metadata('overview.ipynb',\n summary='Overview of the core modules',\n title='overview')", "_____no_output_____" ], [ "update_nb_metadata('training.ipynb',\n keywords='fastai',\n summary='Overview of fastai training modules, including Learner, metrics, and callbacks',\n title='training')", "_____no_output_____" ], [ "update_nb_metadata('text.transform.ipynb',\n summary='NLP data processing; tokenizes text and creates vocab indexes',\n title='text.transform')", "_____no_output_____" ], [ "update_nb_metadata('jekyll_metadata.ipynb')", "_____no_output_____" ], [ "update_nb_metadata('collab.ipynb',\n summary='Application to collaborative filtering',\n title='collab')", "_____no_output_____" ], [ "update_nb_metadata('text.learner.ipynb',\n summary='Easy access of language models and ULMFiT',\n title='text.learner')", "_____no_output_____" ], [ "update_nb_metadata('gen_doc.nbdoc.ipynb',\n summary='Helper function to build the documentation',\n title='gen_doc.nbdoc')", "_____no_output_____" ], [ "update_nb_metadata('vision.learner.ipynb',\n summary='`Learner` support for computer vision',\n title='vision.learner')", "_____no_output_____" ], [ "update_nb_metadata('core.ipynb',\n summary='Basic helper functions for the fastai library',\n title='core')", "_____no_output_____" ], [ "update_nb_metadata('fastai_typing.ipynb',\n keywords='fastai',\n summary='Type annotations names',\n title='fastai_typing')", "_____no_output_____" ], [ "update_nb_metadata('gen_doc.gen_notebooks.ipynb',\n summary='Generation of documentation notebook skeletons from python module',\n title='gen_doc.gen_notebooks')", "_____no_output_____" ], [ "update_nb_metadata('basic_train.ipynb',\n summary='Learner class and training loop',\n title='basic_train')", "_____no_output_____" ], [ "update_nb_metadata('gen_doc.ipynb',\n keywords='fastai',\n summary='Documentation modules overview',\n title='gen_doc')", "_____no_output_____" ], [ "update_nb_metadata('callbacks.rnn.ipynb',\n summary='Implementation of a callback for RNN training',\n title='callbacks.rnn')", "_____no_output_____" ], [ "update_nb_metadata('callbacks.one_cycle.ipynb',\n summary='Implementation of the 1cycle policy',\n title='callbacks.one_cycle')", "_____no_output_____" ], [ "update_nb_metadata('tta.ipynb',\n summary='Module brings TTA (Test Time Functionality) to the `Learner` class. Use `learner.TTA()` instead',\n title='tta')", "_____no_output_____" ], [ "update_nb_metadata('vision.ipynb',\n summary='Application to Computer Vision',\n title='vision')", "_____no_output_____" ], [ "update_nb_metadata('vision.transform.ipynb',\n summary='List of transforms for data augmentation in CV',\n title='vision.transform')", "_____no_output_____" ], [ "update_nb_metadata('callbacks.lr_finder.ipynb',\n summary='Implementation of the LR Range test from Leslie Smith',\n title='callbacks.lr_finder')", "_____no_output_____" ], [ "update_nb_metadata('text.data.ipynb',\n summary='Basic dataset for NLP tasks and helper functions to create a DataBunch',\n title='text.data')", "_____no_output_____" ], [ "update_nb_metadata('text.models.ipynb',\n summary='Implementation of the AWD-LSTM and the RNN models',\n title='text.models')", "_____no_output_____" ], [ "update_nb_metadata('tabular.data.ipynb',\n summary='Base class to deal with tabular data and get a DataBunch',\n title='tabular.data')", "_____no_output_____" ], [ "update_nb_metadata('callbacks.ipynb',\n keywords='fastai',\n summary='Callbacks implemented in the fastai library',\n title='callbacks')", "_____no_output_____" ], [ "update_nb_metadata('train.ipynb',\n summary='Extensions to Learner that easily implement Callback',\n title='train')", "_____no_output_____" ], [ "update_nb_metadata('callbacks.hooks.ipynb',\n summary='Implement callbacks using hooks',\n title='callbacks.hooks')", "_____no_output_____" ], [ "update_nb_metadata('text.models.qrnn.ipynb')", "_____no_output_____" ], [ "update_nb_metadata('vision.image.ipynb',\n summary='Image class, variants and internal data augmentation pipeline',\n title='vision.image')", "_____no_output_____" ], [ "update_nb_metadata('vision.models.unet.ipynb',\n summary='Dynamic Unet that can use any pretrained model as a backbone.',\n title='vision.models.unet')", "_____no_output_____" ], [ "update_nb_metadata('vision.models.ipynb',\n keywords='fastai',\n summary='Overview of the models used for CV in fastai',\n title='vision.models')", "_____no_output_____" ], [ "update_nb_metadata('gen_doc.sgen_notebooks.ipynb',\n keywords='fastai',\n summary='Script to generate notebooks and update html',\n title='gen_doc.sgen_notebooks')", "_____no_output_____" ], [ "update_nb_metadata('tabular.transform.ipynb',\n summary='Transforms to clean and preprocess tabular data',\n title='tabular.transform')", "_____no_output_____" ], [ "update_nb_metadata('data.ipynb',\n summary='Basic classes to contain the data for model training.',\n title='data')", "_____no_output_____" ], [ "update_nb_metadata('index.ipynb',\n keywords='fastai',\n toc='false')", "_____no_output_____" ], [ "update_nb_metadata('layers.ipynb',\n summary='Provides essential functions to building and modifying `Model` architectures.',\n title='layers')", "_____no_output_____" ], [ "update_nb_metadata('tabular.ipynb',\n keywords='fastai',\n summary='Application to tabular/structured data',\n title='tabular')", "_____no_output_____" ], [ "update_nb_metadata('tmp.ipynb')", "_____no_output_____" ], [ "update_nb_metadata('Untitled.ipynb')", "_____no_output_____" ] ] ]

[ "code", "markdown", "code", "markdown", "code" ]

[ [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb307d395c891a151460949c4589d83f0f1d3da1

7,192

ipynb

Jupyter Notebook

src/Untitled1.ipynb

seungtaek94/CenterNet

6ac40e9642386c68e982960d4460da6b3cd236c4

[ "MIT" ]

null

src/Untitled1.ipynb

seungtaek94/CenterNet

6ac40e9642386c68e982960d4460da6b3cd236c4

[ "MIT" ]

null

src/Untitled1.ipynb

seungtaek94/CenterNet

6ac40e9642386c68e982960d4460da6b3cd236c4

[ "MIT" ]

null

39.086957

137

0.455228

[ [ [ "from lib.opts import opts\nfrom lib.models.model import create_model, load_model\nfrom types import MethodType\nimport torch.onnx as onnx\nimport torch\n\nfrom torch.onnx import OperatorExportTypes\nfrom collections import OrderedDict", "_____no_output_____" ], [ "def pose_dla_forward(self, x):\n x = self.base(x)\n x = self.dla_up(x)\n y = []\n for i in range(self.last_level - self.first_level):\n y.append(x[i].clone())\n self.ida_up(y, 0, len(y))\n ret = [] ## change dict to list\n for head in self.heads:\n ret.append(self.__getattr__(head)(y[-1]))\n return ret\n## for dla34v0\ndef dlav0_forward(self, x):\n x = self.base(x)\n x = self.dla_up(x[self.first_level:])\n # x = self.fc(x)\n # y = self.softmax(self.up(x))\n ret = [] ## change dict to list\n for head in self.heads:\n ret.append(self.__getattr__(head)(x))\n return ret\n## for resdcn\ndef resnet_dcn_forward(self, x):\n x = self.conv1(x)\n x = self.bn1(x)\n x = self.relu(x)\n x = self.maxpool(x)\n\n x = self.layer1(x)\n x = self.layer2(x)\n x = self.layer3(x)\n x = self.layer4(x)\n x = self.deconv_layers(x)\n ret = [] ## change dict to list\n for head in self.heads:\n ret.append(self.__getattr__(head)(x))\n return ret", "_____no_output_____" ], [ "forward = {'dla':pose_dla_forward,'dlav0':dlav0_forward,'resdcn':resnet_dcn_forward}", "_____no_output_____" ], [ "opt = opts().init() ## change lib/opts.py add_argument('task', default='ctdet'....) to add_argument('--task', default='ctdet'....)", "usage: ipykernel_launcher.py [-h] [--dataset DATASET] [--exp_id EXP_ID]\n [--test] [--debug DEBUG] [--demo DEMO]\n [--load_model LOAD_MODEL] [--resume]\n [--gpus GPUS] [--num_workers NUM_WORKERS]\n [--not_cuda_benchmark] [--seed SEED]\n [--print_iter PRINT_ITER] [--hide_data_time]\n [--save_all] [--metric METRIC]\n [--vis_thresh VIS_THRESH]\n [--debugger_theme {white,black}] [--arch ARCH]\n [--head_conv HEAD_CONV] [--down_ratio DOWN_RATIO]\n [--input_res INPUT_RES] [--input_h INPUT_H]\n [--input_w INPUT_W] [--lr LR] [--lr_step LR_STEP]\n [--num_epochs NUM_EPOCHS]\n [--batch_size BATCH_SIZE]\n [--master_batch_size MASTER_BATCH_SIZE]\n [--num_iters NUM_ITERS]\n [--val_intervals VAL_INTERVALS] [--trainval]\n [--flip_test] [--test_scales TEST_SCALES] [--nms]\n [--K K] [--not_prefetch_test] [--fix_res]\n [--keep_res] [--not_rand_crop] [--shift SHIFT]\n [--scale SCALE] [--rotate ROTATE] [--flip FLIP]\n [--no_color_aug] [--aug_rot AUG_ROT]\n [--aug_ddd AUG_DDD] [--rect_mask]\n [--kitti_split KITTI_SPLIT] [--mse_loss]\n [--reg_loss REG_LOSS] [--hm_weight HM_WEIGHT]\n [--off_weight OFF_WEIGHT] [--wh_weight WH_WEIGHT]\n [--hp_weight HP_WEIGHT]\n [--hm_hp_weight HM_HP_WEIGHT]\n [--dep_weight DEP_WEIGHT]\n [--dim_weight DIM_WEIGHT]\n [--rot_weight ROT_WEIGHT]\n [--peak_thresh PEAK_THRESH] [--norm_wh]\n [--dense_wh] [--cat_spec_wh] [--not_reg_offset]\n [--agnostic_ex] [--scores_thresh SCORES_THRESH]\n [--center_thresh CENTER_THRESH]\n [--aggr_weight AGGR_WEIGHT] [--dense_hp]\n [--not_hm_hp] [--not_reg_hp_offset]\n [--not_reg_bbox] [--eval_oracle_hm]\n [--eval_oracle_wh] [--eval_oracle_offset]\n [--eval_oracle_kps] [--eval_oracle_hmhp]\n [--eval_oracle_hp_offset] [--eval_oracle_dep]\n task\nipykernel_launcher.py: error: unrecognized arguments: -f\n" ], [ "opt.arch = 'dla_34'\nopt.heads = OrderedDict([('hm', 80), ('reg', 2), ('wh', 2)])\nopt.head_conv = 256 if 'dla' in opt.arch else 64\nprint(opt)\nmodel = create_model(opt.arch, opt.heads, opt.head_conv)\nmodel.forward = MethodType(forward[opt.arch.split('_')[0]], model)\nload_model(model, '../models/ctdet_coco_dla_2x.pth')\nmodel.eval()\nmodel.cuda()\ninput = torch.zeros([1, 3, 512, 512]).cuda()\nonnx.export(model, input, \"ctdet_coco_dla_2x.onnx\", verbose=True,\n operator_export_type=OperatorExportTypes.ONNX)", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code" ] ]

cb30842bc3039abe57c48e968558196f7f1e0507

4,367

ipynb

Jupyter Notebook

4/greed/min_platforms.ipynb

ZacksAmber/Udacity-Data-Structure-Algorithms

b5e008ab111b6bc9765acd58d7e1771852eb1d30

[ "MIT" ]

1

2021-09-27T10:18:14.000Z

4/greed/min_platforms.ipynb

ZacksAmber/Udacity-Data-Structure-Algorithms

b5e008ab111b6bc9765acd58d7e1771852eb1d30

[ "MIT" ]

null

4/greed/min_platforms.ipynb

ZacksAmber/Udacity-Data-Structure-Algorithms

b5e008ab111b6bc9765acd58d7e1771852eb1d30

[ "MIT" ]

null

30.971631

326

0.585757

[ [ [ "## Problem Statement\n\nGiven arrival and departure times of trains on a single day in a railway platform, **find out the minimum number of platforms required** so that no train has to wait for the other(s) to leave. *In other words, when a train is about to arrive, at least one platform must be available to accommodate it.* \n\nYou will be given arrival and departure times both in the form of a list. The size of both the lists will be equal, with each common index representing the same train. Note: Time `hh:mm` would be written as integer `hhmm` for e.g. `9:30` would be written as `930`. Similarly, `13:45` would be given as `1345`\n\n**Example:**<br>\nInput: A schedule of 6 trains:\n```\narrival = [900, 940, 950, 1100, 1500, 1800]\ndeparture = [910, 1200, 1120, 1130, 1900, 2000]\n```\nExpected output: Minimum number of platforms required = 3\n", "_____no_output_____" ], [ "### The greedy approach: \nSort the schedule, and make sure when a train arrives or depart, keep track of the required number of platforms. We will have iterator `i` and `j` traversing the arrival and departure lists respectively. At any moment, the difference `(i - j)` will provide us the required number of platforms. \n \nAt the time of either arrival or departure of a train, if `i^th` arrival is scheduled before the `j^th` departure, increment the `platform_required` and `i` as well. Otherwise, decrement `platform_required` count, and increase `j`. Keep track of the **max** value of `platform_required` ever, as the expected result. \n \n", "_____no_output_____" ] ], [ [ "def min_platforms(arrival, departure):\n \"\"\"\n :param: arrival - list of arrival time\n :param: departure - list of departure time\n TODO - complete this method and return the minimum number of platforms (int) required\n so that no train has to wait for other(s) to leave\n \"\"\"\n return", "_____no_output_____" ] ], [ [ "<span class=\"graffiti-highlight graffiti-id_khuho24-id_mgzo0p4\"><i></i><button>Show Solution</button></span>", "_____no_output_____" ] ], [ [ "def test_function(test_case):\n arrival = test_case[0]\n departure = test_case[1]\n solution = test_case[2]\n \n output = min_platforms(arrival, departure)\n if output == solution:\n print(\"Pass\")\n else:\n print(\"Fail\")", "_____no_output_____" ], [ "arrival = [900, 940, 950, 1100, 1500, 1800]\ndeparture = [910, 1200, 1120, 1130, 1900, 2000]\ntest_case = [arrival, departure, 3]\n\ntest_function(test_case)", "_____no_output_____" ], [ "arrival = [200, 210, 300, 320, 350, 500]\ndeparture = [230, 340, 320, 430, 400, 520]\ntest_case = [arrival, departure, 2]\ntest_function(test_case)", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ] ]

cb308a6e2e737314c4af4b33d9d94bf906ae3a8f

107,119

ipynb

Jupyter Notebook

Course5_Seq/week1/rnn/.ipynb_checkpoints/Building_a_Recurrent_Neural_Network_Step_by_Step_v3b-checkpoint.ipynb

ShiqianShen/Deep-learning-coursera

83eeadc95d0dd5ae78cba2da8a827e87292a5d53

[ "MIT" ]

null

Course5_Seq/week1/rnn/.ipynb_checkpoints/Building_a_Recurrent_Neural_Network_Step_by_Step_v3b-checkpoint.ipynb

ShiqianShen/Deep-learning-coursera

83eeadc95d0dd5ae78cba2da8a827e87292a5d53

[ "MIT" ]

null

Course5_Seq/week1/rnn/.ipynb_checkpoints/Building_a_Recurrent_Neural_Network_Step_by_Step_v3b-checkpoint.ipynb

ShiqianShen/Deep-learning-coursera

83eeadc95d0dd5ae78cba2da8a827e87292a5d53

[ "MIT" ]

null

42.933467

573

0.519646

[ [ [ "# Building your Recurrent Neural Network - Step by Step\n\nWelcome to Course 5's first assignment! In this assignment, you will implement key components of a Recurrent Neural Network in numpy.\n\nRecurrent Neural Networks (RNN) are very effective for Natural Language Processing and other sequence tasks because they have \"memory\". They can read inputs $x^{\\langle t \\rangle}$ (such as words) one at a time, and remember some information/context through the hidden layer activations that get passed from one time-step to the next. This allows a unidirectional RNN to take information from the past to process later inputs. A bidirectional RNN can take context from both the past and the future. \n\n**Notation**:\n- Superscript $[l]$ denotes an object associated with the $l^{th}$ layer. \n\n- Superscript $(i)$ denotes an object associated with the $i^{th}$ example. \n\n- Superscript $\\langle t \\rangle$ denotes an object at the $t^{th}$ time-step. \n \n- **Sub**script $i$ denotes the $i^{th}$ entry of a vector.\n\nExample: \n- $a^{(2)[3]<4>}_5$ denotes the activation of the 2nd training example (2), 3rd layer [3], 4th time step <4>, and 5th entry in the vector.\n\n#### Pre-requisites\n* We assume that you are already familiar with `numpy`. \n* To refresh your knowledge of numpy, you can review course 1 of this specialization \"Neural Networks and Deep Learning\". \n * Specifically, review the week 2 assignment [\"Python Basics with numpy (optional)\"](https://www.coursera.org/learn/neural-networks-deep-learning/item/Zh0CU).\n \n \n#### Be careful when modifying the starter code\n* When working on graded functions, please remember to only modify the code that is between the\n```Python\n#### START CODE HERE\n```\nand\n```Python\n#### END CODE HERE\n```\n* In particular, Be careful to not modify the first line of graded routines. These start with:\n```Python\n# GRADED FUNCTION: routine_name\n```\n* The automatic grader (autograder) needs these to locate the function.\n* Even a change in spacing will cause issues with the autograder. \n* It will return 'failed' if these are modified or missing.\"", "_____no_output_____" ], [ "## <font color='darkblue'>Updates for 3b</font>\n\n#### If you were working on the notebook before this update...\n* The current notebook is version \"3b\".\n* You can find your original work saved in the notebook with the previous version name (\"v3a\") \n* To view the file directory, go to the menu \"File->Open\", and this will open a new tab that shows the file directory.\n\n#### List of updates\n\n* `rnn_cell_backward`\n - fixed error in equations\n - harmonize rnn backward diagram with rnn_forward diagram and fixed Wax multiple (changed from at to xt).\n - clarified dba batch as summing 'm' examples\n - aligned equations\n* `lstm_cell_backward`\n - aligned equations\n* `lstm_forward`\n - fixed typo, Wb to bf\n* `lstm_cell_forward`\n - changed c_next_tmp.shape to a_next_tmp.shape in test case\n - clarified dbxx batch as summing 'm' examples", "_____no_output_____" ], [ "Let's first import all the packages that you will need during this assignment.", "_____no_output_____" ] ], [ [ "import numpy as np\nfrom rnn_utils import *", "_____no_output_____" ] ], [ [ "## 1 - Forward propagation for the basic Recurrent Neural Network\n\nLater this week, you will generate music using an RNN. The basic RNN that you will implement has the structure below. In this example, $T_x = T_y$. ", "_____no_output_____" ], [ "<img src=\"images/RNN.png\" style=\"width:500;height:300px;\">\n<caption><center> **Figure 1**: Basic RNN model </center></caption>", "_____no_output_____" ], [ "### Dimensions of input $x$\n\n#### Input with $n_x$ number of units\n* For a single timestep of a single input example, $x^{(i) \\langle t \\rangle }$ is a one-dimensional input vector.\n* Using language as an example, a language with a 5000 word vocabulary could be one-hot encoded into a vector that has 5000 units. So $x^{(i)\\langle t \\rangle}$ would have the shape (5000,). \n* We'll use the notation $n_x$ to denote the number of units in a single timestep of a single training example.", "_____no_output_____" ], [ "#### Time steps of size $T_{x}$\n* A recurrent neural network has multiple time steps, which we'll index with $t$.\n* In the lessons, we saw a single training example $x^{(i)}$ consist of multiple time steps $T_x$. For example, if there are 10 time steps, $T_{x} = 10$", "_____no_output_____" ], [ "#### Batches of size $m$\n* Let's say we have mini-batches, each with 20 training examples. \n* To benefit from vectorization, we'll stack 20 columns of $x^{(i)}$ examples.\n* For example, this tensor has the shape (5000,20,10). \n* We'll use $m$ to denote the number of training examples. \n* So the shape of a mini-batch is $(n_x,m,T_x)$", "_____no_output_____" ], [ "#### 3D Tensor of shape $(n_{x},m,T_{x})$\n* The 3-dimensional tensor $x$ of shape $(n_x,m,T_x)$ represents the input $x$ that is fed into the RNN.\n\n#### Taking a 2D slice for each time step: $x^{\\langle t \\rangle}$\n* At each time step, we'll use a mini-batches of training examples (not just a single example).\n* So, for each time step $t$, we'll use a 2D slice of shape $(n_x,m)$.\n* We're referring to this 2D slice as $x^{\\langle t \\rangle}$. The variable name in the code is `xt`.", "_____no_output_____" ], [ "### Definition of hidden state $a$\n\n* The activation $a^{\\langle t \\rangle}$ that is passed to the RNN from one time step to another is called a \"hidden state.\"\n\n### Dimensions of hidden state $a$\n\n* Similar to the input tensor $x$, the hidden state for a single training example is a vector of length $n_{a}$.\n* If we include a mini-batch of $m$ training examples, the shape of a mini-batch is $(n_{a},m)$.\n* When we include the time step dimension, the shape of the hidden state is $(n_{a}, m, T_x)$\n* We will loop through the time steps with index $t$, and work with a 2D slice of the 3D tensor. \n* We'll refer to this 2D slice as $a^{\\langle t \\rangle}$. \n* In the code, the variable names we use are either `a_prev` or `a_next`, depending on the function that's being implemented.\n* The shape of this 2D slice is $(n_{a}, m)$", "_____no_output_____" ], [ "### Dimensions of prediction $\\hat{y}$\n* Similar to the inputs and hidden states, $\\hat{y}$ is a 3D tensor of shape $(n_{y}, m, T_{y})$.\n * $n_{y}$: number of units in the vector representing the prediction.\n * $m$: number of examples in a mini-batch.\n * $T_{y}$: number of time steps in the prediction.\n* For a single time step $t$, a 2D slice $\\hat{y}^{\\langle t \\rangle}$ has shape $(n_{y}, m)$.\n* In the code, the variable names are:\n - `y_pred`: $\\hat{y}$ \n - `yt_pred`: $\\hat{y}^{\\langle t \\rangle}$", "_____no_output_____" ], [ "Here's how you can implement an RNN: \n\n**Steps**:\n1. Implement the calculations needed for one time-step of the RNN.\n2. Implement a loop over $T_x$ time-steps in order to process all the inputs, one at a time. ", "_____no_output_____" ], [ "## 1.1 - RNN cell\n\nA recurrent neural network can be seen as the repeated use of a single cell. You are first going to implement the computations for a single time-step. The following figure describes the operations for a single time-step of an RNN cell. \n\n<img src=\"images/rnn_step_forward_figure2_v3a.png\" style=\"width:700px;height:300px;\">\n<caption><center> **Figure 2**: Basic RNN cell. Takes as input $x^{\\langle t \\rangle}$ (current input) and $a^{\\langle t - 1\\rangle}$ (previous hidden state containing information from the past), and outputs $a^{\\langle t \\rangle}$ which is given to the next RNN cell and also used to predict $\\hat{y}^{\\langle t \\rangle}$ </center></caption>\n\n#### rnn cell versus rnn_cell_forward\n* Note that an RNN cell outputs the hidden state $a^{\\langle t \\rangle}$. \n * The rnn cell is shown in the figure as the inner box which has solid lines. \n* The function that we will implement, `rnn_cell_forward`, also calculates the prediction $\\hat{y}^{\\langle t \\rangle}$\n * The rnn_cell_forward is shown in the figure as the outer box that has dashed lines.", "_____no_output_____" ], [ "**Exercise**: Implement the RNN-cell described in Figure (2).\n\n**Instructions**:\n1. Compute the hidden state with tanh activation: $a^{\\langle t \\rangle} = \\tanh(W_{aa} a^{\\langle t-1 \\rangle} + W_{ax} x^{\\langle t \\rangle} + b_a)$.\n2. Using your new hidden state $a^{\\langle t \\rangle}$, compute the prediction $\\hat{y}^{\\langle t \\rangle} = softmax(W_{ya} a^{\\langle t \\rangle} + b_y)$. We provided the function `softmax`.\n3. Store $(a^{\\langle t \\rangle}, a^{\\langle t-1 \\rangle}, x^{\\langle t \\rangle}, parameters)$ in a `cache`.\n4. Return $a^{\\langle t \\rangle}$ , $\\hat{y}^{\\langle t \\rangle}$ and `cache`\n\n#### Additional Hints\n* [numpy.tanh](https://www.google.com/search?q=numpy+tanh&rlz=1C5CHFA_enUS854US855&oq=numpy+tanh&aqs=chrome..69i57j0l5.1340j0j7&sourceid=chrome&ie=UTF-8)\n* We've created a `softmax` function that you can use. It is located in the file 'rnn_utils.py' and has been imported.\n* For matrix multiplication, use [numpy.dot](https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html)\n\n", "_____no_output_____" ] ], [ [ "# GRADED FUNCTION: rnn_cell_forward\n\ndef rnn_cell_forward(xt, a_prev, parameters):\n \"\"\"\n Implements a single forward step of the RNN-cell as described in Figure (2)\n\n Arguments:\n xt -- your input data at timestep \"t\", numpy array of shape (n_x, m).\n a_prev -- Hidden state at timestep \"t-1\", numpy array of shape (n_a, m)\n parameters -- python dictionary containing:\n Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)\n Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)\n Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)\n ba -- Bias, numpy array of shape (n_a, 1)\n by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)\n Returns:\n a_next -- next hidden state, of shape (n_a, m)\n yt_pred -- prediction at timestep \"t\", numpy array of shape (n_y, m)\n cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)\n \"\"\"\n \n # Retrieve parameters from \"parameters\"\n Wax = parameters[\"Wax\"]\n Waa = parameters[\"Waa\"]\n Wya = parameters[\"Wya\"]\n ba = parameters[\"ba\"]\n by = parameters[\"by\"]\n \n ### START CODE HERE ### (≈2 lines)\n # compute next activation state using the formula given above\n a_next = None\n # compute output of the current cell using the formula given above\n yt_pred = None\n ### END CODE HERE ###\n \n # store values you need for backward propagation in cache\n cache = (a_next, a_prev, xt, parameters)\n \n return a_next, yt_pred, cache", "_____no_output_____" ], [ "np.random.seed(1)\nxt_tmp = np.random.randn(3,10)\na_prev_tmp = np.random.randn(5,10)\nparameters_tmp = {}\nparameters_tmp['Waa'] = np.random.randn(5,5)\nparameters_tmp['Wax'] = np.random.randn(5,3)\nparameters_tmp['Wya'] = np.random.randn(2,5)\nparameters_tmp['ba'] = np.random.randn(5,1)\nparameters_tmp['by'] = np.random.randn(2,1)\n\na_next_tmp, yt_pred_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp)\nprint(\"a_next[4] = \\n\", a_next_tmp[4])\nprint(\"a_next.shape = \\n\", a_next_tmp.shape)\nprint(\"yt_pred[1] =\\n\", yt_pred_tmp[1])\nprint(\"yt_pred.shape = \\n\", yt_pred_tmp.shape)", "_____no_output_____" ] ], [ [ "**Expected Output**: \n```Python\na_next[4] = \n [ 0.59584544 0.18141802 0.61311866 0.99808218 0.85016201 0.99980978\n -0.18887155 0.99815551 0.6531151 0.82872037]\na_next.shape = \n (5, 10)\nyt_pred[1] =\n [ 0.9888161 0.01682021 0.21140899 0.36817467 0.98988387 0.88945212\n 0.36920224 0.9966312 0.9982559 0.17746526]\nyt_pred.shape = \n (2, 10)\n\n```", "_____no_output_____" ], [ "## 1.2 - RNN forward pass \n\n- A recurrent neural network (RNN) is a repetition of the RNN cell that you've just built. \n - If your input sequence of data is 10 time steps long, then you will re-use the RNN cell 10 times. \n- Each cell takes two inputs at each time step:\n - $a^{\\langle t-1 \\rangle}$: The hidden state from the previous cell.\n - $x^{\\langle t \\rangle}$: The current time-step's input data.\n- It has two outputs at each time step:\n - A hidden state ($a^{\\langle t \\rangle}$)\n - A prediction ($y^{\\langle t \\rangle}$)\n- The weights and biases $(W_{aa}, b_{a}, W_{ax}, b_{x})$ are re-used each time step. \n - They are maintained between calls to rnn_cell_forward in the 'parameters' dictionary.\n\n\n<img src=\"images/rnn_forward_sequence_figure3_v3a.png\" style=\"width:800px;height:180px;\">\n<caption><center> **Figure 3**: Basic RNN. The input sequence $x = (x^{\\langle 1 \\rangle}, x^{\\langle 2 \\rangle}, ..., x^{\\langle T_x \\rangle})$ is carried over $T_x$ time steps. The network outputs $y = (y^{\\langle 1 \\rangle}, y^{\\langle 2 \\rangle}, ..., y^{\\langle T_x \\rangle})$. </center></caption>\n", "_____no_output_____" ], [ "**Exercise**: Code the forward propagation of the RNN described in Figure (3).\n\n**Instructions**:\n* Create a 3D array of zeros, $a$ of shape $(n_{a}, m, T_{x})$ that will store all the hidden states computed by the RNN.\n* Create a 3D array of zeros, $\\hat{y}$, of shape $(n_{y}, m, T_{x})$ that will store the predictions. \n - Note that in this case, $T_{y} = T_{x}$ (the prediction and input have the same number of time steps).\n* Initialize the 2D hidden state `a_next` by setting it equal to the initial hidden state, $a_{0}$.\n* At each time step $t$:\n - Get $x^{\\langle t \\rangle}$, which is a 2D slice of $x$ for a single time step $t$.\n - $x^{\\langle t \\rangle}$ has shape $(n_{x}, m)$\n - $x$ has shape $(n_{x}, m, T_{x})$\n - Update the 2D hidden state $a^{\\langle t \\rangle}$ (variable name `a_next`), the prediction $\\hat{y}^{\\langle t \\rangle}$ and the cache by running `rnn_cell_forward`.\n - $a^{\\langle t \\rangle}$ has shape $(n_{a}, m)$\n - Store the 2D hidden state in the 3D tensor $a$, at the $t^{th}$ position.\n - $a$ has shape $(n_{a}, m, T_{x})$\n - Store the 2D $\\hat{y}^{\\langle t \\rangle}$ prediction (variable name `yt_pred`) in the 3D tensor $\\hat{y}_{pred}$ at the $t^{th}$ position.\n - $\\hat{y}^{\\langle t \\rangle}$ has shape $(n_{y}, m)$\n - $\\hat{y}$ has shape $(n_{y}, m, T_x)$\n - Append the cache to the list of caches.\n* Return the 3D tensor $a$ and $\\hat{y}$, as well as the list of caches.\n\n#### Additional Hints\n- [np.zeros](https://docs.scipy.org/doc/numpy/reference/generated/numpy.zeros.html)\n- If you have a 3 dimensional numpy array and are indexing by its third dimension, you can use array slicing like this: `var_name[:,:,i]`.", "_____no_output_____" ] ], [ [ "# GRADED FUNCTION: rnn_forward\n\ndef rnn_forward(x, a0, parameters):\n \"\"\"\n Implement the forward propagation of the recurrent neural network described in Figure (3).\n\n Arguments:\n x -- Input data for every time-step, of shape (n_x, m, T_x).\n a0 -- Initial hidden state, of shape (n_a, m)\n parameters -- python dictionary containing:\n Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)\n Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)\n Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)\n ba -- Bias numpy array of shape (n_a, 1)\n by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)\n\n Returns:\n a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)\n y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)\n caches -- tuple of values needed for the backward pass, contains (list of caches, x)\n \"\"\"\n \n # Initialize \"caches\" which will contain the list of all caches\n caches = []\n \n # Retrieve dimensions from shapes of x and parameters[\"Wya\"]\n n_x, m, T_x = x.shape\n n_y, n_a = parameters[\"Wya\"].shape\n \n ### START CODE HERE ###\n \n # initialize \"a\" and \"y_pred\" with zeros (≈2 lines)\n a = None\n y_pred = None\n \n # Initialize a_next (≈1 line)\n a_next = None\n \n # loop over all time-steps of the input 'x' (1 line)\n for t in range(None):\n # Update next hidden state, compute the prediction, get the cache (≈2 lines)\n xt = None\n a_next, yt_pred, cache = None\n # Save the value of the new \"next\" hidden state in a (≈1 line)\n a[:,:,t] = None\n # Save the value of the prediction in y (≈1 line)\n y_pred[:,:,t] = None\n # Append \"cache\" to \"caches\" (≈1 line)\n None\n \n ### END CODE HERE ###\n \n # store values needed for backward propagation in cache\n caches = (caches, x)\n \n return a, y_pred, caches", "_____no_output_____" ], [ "np.random.seed(1)\nx_tmp = np.random.randn(3,10,4)\na0_tmp = np.random.randn(5,10)\nparameters_tmp = {}\nparameters_tmp['Waa'] = np.random.randn(5,5)\nparameters_tmp['Wax'] = np.random.randn(5,3)\nparameters_tmp['Wya'] = np.random.randn(2,5)\nparameters_tmp['ba'] = np.random.randn(5,1)\nparameters_tmp['by'] = np.random.randn(2,1)\n\na_tmp, y_pred_tmp, caches_tmp = rnn_forward(x_tmp, a0_tmp, parameters_tmp)\nprint(\"a[4][1] = \\n\", a_tmp[4][1])\nprint(\"a.shape = \\n\", a_tmp.shape)\nprint(\"y_pred[1][3] =\\n\", y_pred_tmp[1][3])\nprint(\"y_pred.shape = \\n\", y_pred_tmp.shape)\nprint(\"caches[1][1][3] =\\n\", caches_tmp[1][1][3])\nprint(\"len(caches) = \\n\", len(caches_tmp))", "_____no_output_____" ] ], [ [ "**Expected Output**:\n\n```Python\na[4][1] = \n [-0.99999375 0.77911235 -0.99861469 -0.99833267]\na.shape = \n (5, 10, 4)\ny_pred[1][3] =\n [ 0.79560373 0.86224861 0.11118257 0.81515947]\ny_pred.shape = \n (2, 10, 4)\ncaches[1][1][3] =\n [-1.1425182 -0.34934272 -0.20889423 0.58662319]\nlen(caches) = \n 2\n```", "_____no_output_____" ], [ "Congratulations! You've successfully built the forward propagation of a recurrent neural network from scratch. \n\n#### Situations when this RNN will perform better:\n- This will work well enough for some applications, but it suffers from the vanishing gradient problems. \n- The RNN works best when each output $\\hat{y}^{\\langle t \\rangle}$ can be estimated using \"local\" context. \n- \"Local\" context refers to information that is close to the prediction's time step $t$.\n- More formally, local context refers to inputs $x^{\\langle t' \\rangle}$ and predictions $\\hat{y}^{\\langle t \\rangle}$ where $t'$ is close to $t$.\n\nIn the next part, you will build a more complex LSTM model, which is better at addressing vanishing gradients. The LSTM will be better able to remember a piece of information and keep it saved for many timesteps. ", "_____no_output_____" ], [ "## 2 - Long Short-Term Memory (LSTM) network\n\nThe following figure shows the operations of an LSTM-cell.\n\n<img src=\"images/LSTM_figure4_v3a.png\" style=\"width:500;height:400px;\">\n<caption><center> **Figure 4**: LSTM-cell. This tracks and updates a \"cell state\" or memory variable $c^{\\langle t \\rangle}$ at every time-step, which can be different from $a^{\\langle t \\rangle}$. \nNote, the $softmax^{*}$ includes a dense layer and softmax</center></caption>\n\nSimilar to the RNN example above, you will start by implementing the LSTM cell for a single time-step. Then you can iteratively call it from inside a \"for-loop\" to have it process an input with $T_x$ time-steps. ", "_____no_output_____" ], [ "### Overview of gates and states\n\n#### - Forget gate $\\mathbf{\\Gamma}_{f}$\n\n* Let's assume we are reading words in a piece of text, and plan to use an LSTM to keep track of grammatical structures, such as whether the subject is singular (\"puppy\") or plural (\"puppies\"). \n* If the subject changes its state (from a singular word to a plural word), the memory of the previous state becomes outdated, so we \"forget\" that outdated state.\n* The \"forget gate\" is a tensor containing values that are between 0 and 1.\n * If a unit in the forget gate has a value close to 0, the LSTM will \"forget\" the stored state in the corresponding unit of the previous cell state.\n * If a unit in the forget gate has a value close to 1, the LSTM will mostly remember the corresponding value in the stored state.\n\n##### Equation\n\n$$\\mathbf{\\Gamma}_f^{\\langle t \\rangle} = \\sigma(\\mathbf{W}_f[\\mathbf{a}^{\\langle t-1 \\rangle}, \\mathbf{x}^{\\langle t \\rangle}] + \\mathbf{b}_f)\\tag{1} $$\n\n##### Explanation of the equation:\n\n* $\\mathbf{W_{f}}$ contains weights that govern the forget gate's behavior. \n* The previous time step's hidden state $[a^{\\langle t-1 \\rangle}$ and current time step's input $x^{\\langle t \\rangle}]$ are concatenated together and multiplied by $\\mathbf{W_{f}}$. \n* A sigmoid function is used to make each of the gate tensor's values $\\mathbf{\\Gamma}_f^{\\langle t \\rangle}$ range from 0 to 1.\n* The forget gate $\\mathbf{\\Gamma}_f^{\\langle t \\rangle}$ has the same dimensions as the previous cell state $c^{\\langle t-1 \\rangle}$. \n* This means that the two can be multiplied together, element-wise.\n* Multiplying the tensors $\\mathbf{\\Gamma}_f^{\\langle t \\rangle} * \\mathbf{c}^{\\langle t-1 \\rangle}$ is like applying a mask over the previous cell state.\n* If a single value in $\\mathbf{\\Gamma}_f^{\\langle t \\rangle}$ is 0 or close to 0, then the product is close to 0.\n * This keeps the information stored in the corresponding unit in $\\mathbf{c}^{\\langle t-1 \\rangle}$ from being remembered for the next time step.\n* Similarly, if one value is close to 1, the product is close to the original value in the previous cell state.\n * The LSTM will keep the information from the corresponding unit of $\\mathbf{c}^{\\langle t-1 \\rangle}$, to be used in the next time step.\n \n##### Variable names in the code\nThe variable names in the code are similar to the equations, with slight differences. \n* `Wf`: forget gate weight $\\mathbf{W}_{f}$\n* `bf`: forget gate bias $\\mathbf{b}_{f}$\n* `ft`: forget gate $\\Gamma_f^{\\langle t \\rangle}$", "_____no_output_____" ], [ "#### Candidate value $\\tilde{\\mathbf{c}}^{\\langle t \\rangle}$\n* The candidate value is a tensor containing information from the current time step that **may** be stored in the current cell state $\\mathbf{c}^{\\langle t \\rangle}$.\n* Which parts of the candidate value get passed on depends on the update gate.\n* The candidate value is a tensor containing values that range from -1 to 1.\n* The tilde \"~\" is used to differentiate the candidate $\\tilde{\\mathbf{c}}^{\\langle t \\rangle}$ from the cell state $\\mathbf{c}^{\\langle t \\rangle}$.\n\n##### Equation\n$$\\mathbf{\\tilde{c}}^{\\langle t \\rangle} = \\tanh\\left( \\mathbf{W}_{c} [\\mathbf{a}^{\\langle t - 1 \\rangle}, \\mathbf{x}^{\\langle t \\rangle}] + \\mathbf{b}_{c} \\right) \\tag{3}$$\n\n##### Explanation of the equation\n* The 'tanh' function produces values between -1 and +1.\n\n\n##### Variable names in the code\n* `cct`: candidate value $\\mathbf{\\tilde{c}}^{\\langle t \\rangle}$", "_____no_output_____" ], [ "#### - Update gate $\\mathbf{\\Gamma}_{i}$\n\n* We use the update gate to decide what aspects of the candidate $\\tilde{\\mathbf{c}}^{\\langle t \\rangle}$ to add to the cell state $c^{\\langle t \\rangle}$.\n* The update gate decides what parts of a \"candidate\" tensor $\\tilde{\\mathbf{c}}^{\\langle t \\rangle}$ are passed onto the cell state $\\mathbf{c}^{\\langle t \\rangle}$.\n* The update gate is a tensor containing values between 0 and 1.\n * When a unit in the update gate is close to 1, it allows the value of the candidate $\\tilde{\\mathbf{c}}^{\\langle t \\rangle}$ to be passed onto the hidden state $\\mathbf{c}^{\\langle t \\rangle}$\n * When a unit in the update gate is close to 0, it prevents the corresponding value in the candidate from being passed onto the hidden state.\n* Notice that we use the subscript \"i\" and not \"u\", to follow the convention used in the literature.\n\n##### Equation\n\n$$\\mathbf{\\Gamma}_i^{\\langle t \\rangle} = \\sigma(\\mathbf{W}_i[a^{\\langle t-1 \\rangle}, \\mathbf{x}^{\\langle t \\rangle}] + \\mathbf{b}_i)\\tag{2} $$ \n\n##### Explanation of the equation\n\n* Similar to the forget gate, here $\\mathbf{\\Gamma}_i^{\\langle t \\rangle}$, the sigmoid produces values between 0 and 1.\n* The update gate is multiplied element-wise with the candidate, and this product ($\\mathbf{\\Gamma}_{i}^{\\langle t \\rangle} * \\tilde{c}^{\\langle t \\rangle}$) is used in determining the cell state $\\mathbf{c}^{\\langle t \\rangle}$.\n\n##### Variable names in code (Please note that they're different than the equations)\nIn the code, we'll use the variable names found in the academic literature. These variables don't use \"u\" to denote \"update\".\n* `Wi` is the update gate weight $\\mathbf{W}_i$ (not \"Wu\") \n* `bi` is the update gate bias $\\mathbf{b}_i$ (not \"bu\")\n* `it` is the forget gate $\\mathbf{\\Gamma}_i^{\\langle t \\rangle}$ (not \"ut\")", "_____no_output_____" ], [ "#### - Cell state $\\mathbf{c}^{\\langle t \\rangle}$\n\n* The cell state is the \"memory\" that gets passed onto future time steps.\n* The new cell state $\\mathbf{c}^{\\langle t \\rangle}$ is a combination of the previous cell state and the candidate value.\n\n##### Equation\n\n$$ \\mathbf{c}^{\\langle t \\rangle} = \\mathbf{\\Gamma}_f^{\\langle t \\rangle}* \\mathbf{c}^{\\langle t-1 \\rangle} + \\mathbf{\\Gamma}_{i}^{\\langle t \\rangle} *\\mathbf{\\tilde{c}}^{\\langle t \\rangle} \\tag{4} $$\n\n##### Explanation of equation\n* The previous cell state $\\mathbf{c}^{\\langle t-1 \\rangle}$ is adjusted (weighted) by the forget gate $\\mathbf{\\Gamma}_{f}^{\\langle t \\rangle}$\n* and the candidate value $\\tilde{\\mathbf{c}}^{\\langle t \\rangle}$, adjusted (weighted) by the update gate $\\mathbf{\\Gamma}_{i}^{\\langle t \\rangle}$\n\n##### Variable names and shapes in the code\n* `c`: cell state, including all time steps, $\\mathbf{c}$ shape $(n_{a}, m, T)$\n* `c_next`: new (next) cell state, $\\mathbf{c}^{\\langle t \\rangle}$ shape $(n_{a}, m)$\n* `c_prev`: previous cell state, $\\mathbf{c}^{\\langle t-1 \\rangle}$, shape $(n_{a}, m)$", "_____no_output_____" ], [ "#### - Output gate $\\mathbf{\\Gamma}_{o}$\n\n* The output gate decides what gets sent as the prediction (output) of the time step.\n* The output gate is like the other gates. It contains values that range from 0 to 1.\n\n##### Equation\n\n$$ \\mathbf{\\Gamma}_o^{\\langle t \\rangle}= \\sigma(\\mathbf{W}_o[\\mathbf{a}^{\\langle t-1 \\rangle}, \\mathbf{x}^{\\langle t \\rangle}] + \\mathbf{b}_{o})\\tag{5}$$ \n\n##### Explanation of the equation\n* The output gate is determined by the previous hidden state $\\mathbf{a}^{\\langle t-1 \\rangle}$ and the current input $\\mathbf{x}^{\\langle t \\rangle}$\n* The sigmoid makes the gate range from 0 to 1.\n\n\n##### Variable names in the code\n* `Wo`: output gate weight, $\\mathbf{W_o}$\n* `bo`: output gate bias, $\\mathbf{b_o}$\n* `ot`: output gate, $\\mathbf{\\Gamma}_{o}^{\\langle t \\rangle}$", "_____no_output_____" ], [ "#### - Hidden state $\\mathbf{a}^{\\langle t \\rangle}$\n\n* The hidden state gets passed to the LSTM cell's next time step.\n* It is used to determine the three gates ($\\mathbf{\\Gamma}_{f}, \\mathbf{\\Gamma}_{u}, \\mathbf{\\Gamma}_{o}$) of the next time step.\n* The hidden state is also used for the prediction $y^{\\langle t \\rangle}$.\n\n##### Equation\n\n$$ \\mathbf{a}^{\\langle t \\rangle} = \\mathbf{\\Gamma}_o^{\\langle t \\rangle} * \\tanh(\\mathbf{c}^{\\langle t \\rangle})\\tag{6} $$\n\n##### Explanation of equation\n* The hidden state $\\mathbf{a}^{\\langle t \\rangle}$ is determined by the cell state $\\mathbf{c}^{\\langle t \\rangle}$ in combination with the output gate $\\mathbf{\\Gamma}_{o}$.\n* The cell state state is passed through the \"tanh\" function to rescale values between -1 and +1.\n* The output gate acts like a \"mask\" that either preserves the values of $\\tanh(\\mathbf{c}^{\\langle t \\rangle})$ or keeps those values from being included in the hidden state $\\mathbf{a}^{\\langle t \\rangle}$\n\n##### Variable names and shapes in the code\n* `a`: hidden state, including time steps. $\\mathbf{a}$ has shape $(n_{a}, m, T_{x})$\n* 'a_prev`: hidden state from previous time step. $\\mathbf{a}^{\\langle t-1 \\rangle}$ has shape $(n_{a}, m)$\n* `a_next`: hidden state for next time step. $\\mathbf{a}^{\\langle t \\rangle}$ has shape $(n_{a}, m)$ ", "_____no_output_____" ], [ "#### - Prediction $\\mathbf{y}^{\\langle t \\rangle}_{pred}$\n* The prediction in this use case is a classification, so we'll use a softmax.\n\nThe equation is:\n$$\\mathbf{y}^{\\langle t \\rangle}_{pred} = \\textrm{softmax}(\\mathbf{W}_{y} \\mathbf{a}^{\\langle t \\rangle} + \\mathbf{b}_{y})$$\n\n##### Variable names and shapes in the code\n* `y_pred`: prediction, including all time steps. $\\mathbf{y}_{pred}$ has shape $(n_{y}, m, T_{x})$. Note that $(T_{y} = T_{x})$ for this example.\n* `yt_pred`: prediction for the current time step $t$. $\\mathbf{y}^{\\langle t \\rangle}_{pred}$ has shape $(n_{y}, m)$", "_____no_output_____" ], [ "### 2.1 - LSTM cell\n\n**Exercise**: Implement the LSTM cell described in the Figure (4).\n\n**Instructions**:\n1. Concatenate the hidden state $a^{\\langle t-1 \\rangle}$ and input $x^{\\langle t \\rangle}$ into a single matrix: \n\n$$concat = \\begin{bmatrix} a^{\\langle t-1 \\rangle} \\\\ x^{\\langle t \\rangle} \\end{bmatrix}$$ \n\n2. Compute all the formulas 1 through 6 for the gates, hidden state, and cell state.\n3. Compute the prediction $y^{\\langle t \\rangle}$.\n", "_____no_output_____" ], [ "#### Additional Hints\n* You can use [numpy.concatenate](https://docs.scipy.org/doc/numpy/reference/generated/numpy.concatenate.html). Check which value to use for the `axis` parameter.\n* The functions `sigmoid()` and `softmax` are imported from `rnn_utils.py`.\n* [numpy.tanh](https://docs.scipy.org/doc/numpy/reference/generated/numpy.tanh.html)\n* Use [np.dot](https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html) for matrix multiplication.\n* Notice that the variable names `Wi`, `bi` refer to the weights and biases of the **update** gate. There are no variables named \"Wu\" or \"bu\" in this function.", "_____no_output_____" ] ], [ [ "# GRADED FUNCTION: lstm_cell_forward\n\ndef lstm_cell_forward(xt, a_prev, c_prev, parameters):\n \"\"\"\n Implement a single forward step of the LSTM-cell as described in Figure (4)\n\n Arguments:\n xt -- your input data at timestep \"t\", numpy array of shape (n_x, m).\n a_prev -- Hidden state at timestep \"t-1\", numpy array of shape (n_a, m)\n c_prev -- Memory state at timestep \"t-1\", numpy array of shape (n_a, m)\n parameters -- python dictionary containing:\n Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)\n bf -- Bias of the forget gate, numpy array of shape (n_a, 1)\n Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)\n bi -- Bias of the update gate, numpy array of shape (n_a, 1)\n Wc -- Weight matrix of the first \"tanh\", numpy array of shape (n_a, n_a + n_x)\n bc -- Bias of the first \"tanh\", numpy array of shape (n_a, 1)\n Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)\n bo -- Bias of the output gate, numpy array of shape (n_a, 1)\n Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)\n by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)\n \n Returns:\n a_next -- next hidden state, of shape (n_a, m)\n c_next -- next memory state, of shape (n_a, m)\n yt_pred -- prediction at timestep \"t\", numpy array of shape (n_y, m)\n cache -- tuple of values needed for the backward pass, contains (a_next, c_next, a_prev, c_prev, xt, parameters)\n \n Note: ft/it/ot stand for the forget/update/output gates, cct stands for the candidate value (c tilde),\n c stands for the cell state (memory)\n \"\"\"\n\n # Retrieve parameters from \"parameters\"\n Wf = parameters[\"Wf\"] # forget gate weight\n bf = parameters[\"bf\"]\n Wi = parameters[\"Wi\"] # update gate weight (notice the variable name)\n bi = parameters[\"bi\"] # (notice the variable name)\n Wc = parameters[\"Wc\"] # candidate value weight\n bc = parameters[\"bc\"]\n Wo = parameters[\"Wo\"] # output gate weight\n bo = parameters[\"bo\"]\n Wy = parameters[\"Wy\"] # prediction weight\n by = parameters[\"by\"]\n \n # Retrieve dimensions from shapes of xt and Wy\n n_x, m = xt.shape\n n_y, n_a = Wy.shape\n\n ### START CODE HERE ###\n # Concatenate a_prev and xt (≈1 line)\n concat = None\n\n # Compute values for ft (forget gate), it (update gate),\n # cct (candidate value), c_next (cell state), \n # ot (output gate), a_next (hidden state) (≈6 lines)\n ft = None # forget gate\n it = None # update gate\n cct = None # candidate value\n c_next = None # cell state\n ot = None # output gate\n a_next = None # hidden state\n \n # Compute prediction of the LSTM cell (≈1 line)\n yt_pred = None\n ### END CODE HERE ###\n\n # store values needed for backward propagation in cache\n cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)\n\n return a_next, c_next, yt_pred, cache", "_____no_output_____" ], [ "np.random.seed(1)\nxt_tmp = np.random.randn(3,10)\na_prev_tmp = np.random.randn(5,10)\nc_prev_tmp = np.random.randn(5,10)\nparameters_tmp = {}\nparameters_tmp['Wf'] = np.random.randn(5, 5+3)\nparameters_tmp['bf'] = np.random.randn(5,1)\nparameters_tmp['Wi'] = np.random.randn(5, 5+3)\nparameters_tmp['bi'] = np.random.randn(5,1)\nparameters_tmp['Wo'] = np.random.randn(5, 5+3)\nparameters_tmp['bo'] = np.random.randn(5,1)\nparameters_tmp['Wc'] = np.random.randn(5, 5+3)\nparameters_tmp['bc'] = np.random.randn(5,1)\nparameters_tmp['Wy'] = np.random.randn(2,5)\nparameters_tmp['by'] = np.random.randn(2,1)\n\na_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp)\nprint(\"a_next[4] = \\n\", a_next_tmp[4])\nprint(\"a_next.shape = \", a_next_tmp.shape)\nprint(\"c_next[2] = \\n\", c_next_tmp[2])\nprint(\"c_next.shape = \", c_next_tmp.shape)\nprint(\"yt[1] =\", yt_tmp[1])\nprint(\"yt.shape = \", yt_tmp.shape)\nprint(\"cache[1][3] =\\n\", cache_tmp[1][3])\nprint(\"len(cache) = \", len(cache_tmp))", "_____no_output_____" ] ], [ [ "**Expected Output**:\n\n```Python\na_next[4] = \n [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482\n 0.76566531 0.34631421 -0.00215674 0.43827275]\na_next.shape = (5, 10)\nc_next[2] = \n [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942\n 0.76449811 -0.0981561 -0.74348425 -0.26810932]\nc_next.shape = (5, 10)\nyt[1] = [ 0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381\n 0.00943007 0.12666353 0.39380172 0.07828381]\nyt.shape = (2, 10)\ncache[1][3] =\n [-0.16263996 1.03729328 0.72938082 -0.54101719 0.02752074 -0.30821874\n 0.07651101 -1.03752894 1.41219977 -0.37647422]\nlen(cache) = 10\n```", "_____no_output_____" ], [ "### 2.2 - Forward pass for LSTM\n\nNow that you have implemented one step of an LSTM, you can now iterate this over this using a for-loop to process a sequence of $T_x$ inputs. \n\n<img src=\"images/LSTM_rnn.png\" style=\"width:500;height:300px;\">\n<caption><center> **Figure 5**: LSTM over multiple time-steps. </center></caption>\n\n**Exercise:** Implement `lstm_forward()` to run an LSTM over $T_x$ time-steps. \n\n**Instructions**\n* Get the dimensions $n_x, n_a, n_y, m, T_x$ from the shape of the variables: `x` and `parameters`.\n* Initialize the 3D tensors $a$, $c$ and $y$.\n - $a$: hidden state, shape $(n_{a}, m, T_{x})$\n - $c$: cell state, shape $(n_{a}, m, T_{x})$\n - $y$: prediction, shape $(n_{y}, m, T_{x})$ (Note that $T_{y} = T_{x}$ in this example).\n - **Note** Setting one variable equal to the other is a \"copy by reference\". In other words, don't do `c = a', otherwise both these variables point to the same underlying variable.\n* Initialize the 2D tensor $a^{\\langle t \\rangle}$ \n - $a^{\\langle t \\rangle}$ stores the hidden state for time step $t$. The variable name is `a_next`.\n - $a^{\\langle 0 \\rangle}$, the initial hidden state at time step 0, is passed in when calling the function. The variable name is `a0`.\n - $a^{\\langle t \\rangle}$ and $a^{\\langle 0 \\rangle}$ represent a single time step, so they both have the shape $(n_{a}, m)$ \n - Initialize $a^{\\langle t \\rangle}$ by setting it to the initial hidden state ($a^{\\langle 0 \\rangle}$) that is passed into the function.\n* Initialize $c^{\\langle t \\rangle}$ with zeros. \n - The variable name is `c_next`. \n - $c^{\\langle t \\rangle}$ represents a single time step, so its shape is $(n_{a}, m)$\n - **Note**: create `c_next` as its own variable with its own location in memory. Do not initialize it as a slice of the 3D tensor $c$. In other words, **don't** do `c_next = c[:,:,0]`.\n* For each time step, do the following:\n - From the 3D tensor $x$, get a 2D slice $x^{\\langle t \\rangle}$ at time step $t$.\n - Call the `lstm_cell_forward` function that you defined previously, to get the hidden state, cell state, prediction, and cache.\n - Store the hidden state, cell state and prediction (the 2D tensors) inside the 3D tensors.\n - Also append the cache to the list of caches.", "_____no_output_____" ] ], [ [ "# GRADED FUNCTION: lstm_forward\n\ndef lstm_forward(x, a0, parameters):\n \"\"\"\n Implement the forward propagation of the recurrent neural network using an LSTM-cell described in Figure (4).\n\n Arguments:\n x -- Input data for every time-step, of shape (n_x, m, T_x).\n a0 -- Initial hidden state, of shape (n_a, m)\n parameters -- python dictionary containing:\n Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)\n bf -- Bias of the forget gate, numpy array of shape (n_a, 1)\n Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)\n bi -- Bias of the update gate, numpy array of shape (n_a, 1)\n Wc -- Weight matrix of the first \"tanh\", numpy array of shape (n_a, n_a + n_x)\n bc -- Bias of the first \"tanh\", numpy array of shape (n_a, 1)\n Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)\n bo -- Bias of the output gate, numpy array of shape (n_a, 1)\n Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)\n by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)\n \n Returns:\n a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)\n y -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)\n c -- The value of the cell state, numpy array of shape (n_a, m, T_x)\n caches -- tuple of values needed for the backward pass, contains (list of all the caches, x)\n \"\"\"\n\n # Initialize \"caches\", which will track the list of all the caches\n caches = []\n \n ### START CODE HERE ###\n Wy = parameters['Wy'] # saving parameters['Wy'] in a local variable in case students use Wy instead of parameters['Wy']\n # Retrieve dimensions from shapes of x and parameters['Wy'] (≈2 lines)\n n_x, m, T_x = None\n n_y, n_a = None\n \n # initialize \"a\", \"c\" and \"y\" with zeros (≈3 lines)\n a = None\n c = None\n y = None\n \n # Initialize a_next and c_next (≈2 lines)\n a_next = None\n c_next = None\n \n # loop over all time-steps\n for t in range(None):\n # Get the 2D slice 'xt' from the 3D input 'x' at time step 't'\n xt = None\n # Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)\n a_next, c_next, yt, cache = None\n # Save the value of the new \"next\" hidden state in a (≈1 line)\n a[:,:,t] = None\n # Save the value of the next cell state (≈1 line)\n c[:,:,t] = None\n # Save the value of the prediction in y (≈1 line)\n y[:,:,t] = None\n # Append the cache into caches (≈1 line)\n None\n \n ### END CODE HERE ###\n \n # store values needed for backward propagation in cache\n caches = (caches, x)\n\n return a, y, c, caches", "_____no_output_____" ], [ "np.random.seed(1)\nx_tmp = np.random.randn(3,10,7)\na0_tmp = np.random.randn(5,10)\nparameters_tmp = {}\nparameters_tmp['Wf'] = np.random.randn(5, 5+3)\nparameters_tmp['bf'] = np.random.randn(5,1)\nparameters_tmp['Wi'] = np.random.randn(5, 5+3)\nparameters_tmp['bi']= np.random.randn(5,1)\nparameters_tmp['Wo'] = np.random.randn(5, 5+3)\nparameters_tmp['bo'] = np.random.randn(5,1)\nparameters_tmp['Wc'] = np.random.randn(5, 5+3)\nparameters_tmp['bc'] = np.random.randn(5,1)\nparameters_tmp['Wy'] = np.random.randn(2,5)\nparameters_tmp['by'] = np.random.randn(2,1)\n\na_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp)\nprint(\"a[4][3][6] = \", a_tmp[4][3][6])\nprint(\"a.shape = \", a_tmp.shape)\nprint(\"y[1][4][3] =\", y_tmp[1][4][3])\nprint(\"y.shape = \", y_tmp.shape)\nprint(\"caches[1][1][1] =\\n\", caches_tmp[1][1][1])\nprint(\"c[1][2][1]\", c_tmp[1][2][1])\nprint(\"len(caches) = \", len(caches_tmp))", "_____no_output_____" ] ], [ [ "**Expected Output**:\n\n```Python\na[4][3][6] = 0.172117767533\na.shape = (5, 10, 7)\ny[1][4][3] = 0.95087346185\ny.shape = (2, 10, 7)\ncaches[1][1][1] =\n [ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139\n 0.41005165]\nc[1][2][1] -0.855544916718\nlen(caches) = 2\n```", "_____no_output_____" ], [ "Congratulations! You have now implemented the forward passes for the basic RNN and the LSTM. When using a deep learning framework, implementing the forward pass is sufficient to build systems that achieve great performance. \n\nThe rest of this notebook is optional, and will not be graded.", "_____no_output_____" ], [ "## 3 - Backpropagation in recurrent neural networks (OPTIONAL / UNGRADED)\n\nIn modern deep learning frameworks, you only have to implement the forward pass, and the framework takes care of the backward pass, so most deep learning engineers do not need to bother with the details of the backward pass. If however you are an expert in calculus and want to see the details of backprop in RNNs, you can work through this optional portion of the notebook. \n\nWhen in an earlier [course](https://www.coursera.org/learn/neural-networks-deep-learning/lecture/0VSHe/derivatives-with-a-computation-graph) you implemented a simple (fully connected) neural network, you used backpropagation to compute the derivatives with respect to the cost to update the parameters. Similarly, in recurrent neural networks you can calculate the derivatives with respect to the cost in order to update the parameters. The backprop equations are quite complicated and we did not derive them in lecture. However, we will briefly present them below. ", "_____no_output_____" ], [ "Note that this notebook does not implement the backward path from the Loss 'J' backwards to 'a'. This would have included the dense layer and softmax which are a part of the forward path. This is assumed to be calculated elsewhere and the result passed to rnn_backward in 'da'. It is further assumed that loss has been adjusted for batch size (m) and division by the number of examples is not required here.", "_____no_output_____" ], [ "This section is optional and ungraded. It is more difficult and has fewer details regarding its implementation. This section only implements key elements of the full path.", "_____no_output_____" ], [ "### 3.1 - Basic RNN backward pass\n\nWe will start by computing the backward pass for the basic RNN-cell and then in the following sections, iterate through the cells.\n\n<img src=\"images/rnn_backward_overview_3a_1.png\" style=\"width:500;height:300px;\"> <br>\n<caption><center> **Figure 6**: RNN-cell's backward pass. Just like in a fully-connected neural network, the derivative of the cost function $J$ backpropagates through the time steps of the RNN by following the chain-rule from calculus. Internal to the cell, the chain-rule is also used to calculate $(\\frac{\\partial J}{\\partial W_{ax}},\\frac{\\partial J}{\\partial W_{aa}},\\frac{\\partial J}{\\partial b})$ to update the parameters $(W_{ax}, W_{aa}, b_a)$. The operation can utilize the cached results from the forward path. </center></caption>", "_____no_output_____" ], [ "Recall from lecture, the shorthand for the partial derivative of cost relative to a variable is dVariable. For example, $\\frac{\\partial J}{\\partial W_{ax}}$ is $dW_{ax}$. This will be used throughout the remaining sections.", "_____no_output_____" ], [ "\n<img src=\"images/rnn_cell_backward_3a_c.png\" style=\"width:800;height:500px;\"> <br>\n<caption><center> **Figure 7**: This implementation of rnn_cell_backward does **not** include the output dense layer and softmax which are included in rnn_cell_forward. \n\n$da_{next}$ is $\\frac{\\partial{J}}{\\partial a^{\\langle t \\rangle}}$ and includes loss from previous stages and current stage output logic. The addition shown in green will be part of your implementation of rnn_backward. </center></caption>", "_____no_output_____" ], [ "##### Equations\nTo compute the rnn_cell_backward you can utilize the following equations. It is a good exercise to derive them by hand. Here, $*$ denotes element-wise multiplication while the absence of a symbol indicates matrix multiplication.\n\n\\begin{align}\n\\displaystyle a^{\\langle t \\rangle} &= \\tanh(W_{ax} x^{\\langle t \\rangle} + W_{aa} a^{\\langle t-1 \\rangle} + b_{a})\\tag{-} \\\\[8pt]\n\\displaystyle \\frac{\\partial \\tanh(x)} {\\partial x} &= 1 - \\tanh^2(x) \\tag{-} \\\\[8pt]\n\\displaystyle {dW_{ax}} &= (da_{next} * ( 1-\\tanh^2(W_{ax}x^{\\langle t \\rangle}+W_{aa} a^{\\langle t-1 \\rangle} + b_{a}) )) x^{\\langle t \\rangle T}\\tag{1} \\\\[8pt]\n\\displaystyle dW_{aa} &= (da_{next} * ( 1-\\tanh^2(W_{ax}x^{\\langle t \\rangle}+W_{aa} a^{\\langle t-1 \\rangle} + b_{a}) )) a^{\\langle t-1 \\rangle T}\\tag{2} \\\\[8pt]\n\\displaystyle db_a& = \\sum_{batch}( da_{next} * ( 1-\\tanh^2(W_{ax}x^{\\langle t \\rangle}+W_{aa} a^{\\langle t-1 \\rangle} + b_{a}) ))\\tag{3} \\\\[8pt]\n\\displaystyle dx^{\\langle t \\rangle} &= { W_{ax}}^T (da_{next} * ( 1-\\tanh^2(W_{ax}x^{\\langle t \\rangle}+W_{aa} a^{\\langle t-1 \\rangle} + b_{a}) ))\\tag{4} \\\\[8pt]\n\\displaystyle da_{prev} &= { W_{aa}}^T(da_{next} * ( 1-\\tanh^2(W_{ax}x^{\\langle t \\rangle}+W_{aa} a^{\\langle t-1 \\rangle} + b_{a}) ))\\tag{5}\n\\end{align}\n\n", "_____no_output_____" ], [ "#### Implementing rnn_cell_backward\nThe results can be computed directly by implementing the equations above. However, the above can optionally be simplified by computing 'dz' and utlilizing the chain rule. \nThis can be further simplified by noting that $\\tanh(W_{ax}x^{\\langle t \\rangle}+W_{aa} a^{\\langle t-1 \\rangle} + b_{a})$ was computed and saved in the forward pass. \n\nTo calculate dba, the 'batch' above is a sum across all 'm' examples (axis= 1). Note that you should use the keepdims = True option.\n\nIt may be worthwhile to review Course 1 [Derivatives with a computational graph](https://www.coursera.org/learn/neural-networks-deep-learning/lecture/0VSHe/derivatives-with-a-computation-graph) through [Backpropagation Intuition](https://www.coursera.org/learn/neural-networks-deep-learning/lecture/6dDj7/backpropagation-intuition-optional), which decompose the calculation into steps using the chain rule. \nMatrix vector derivatives are described [here](http://cs231n.stanford.edu/vecDerivs.pdf), though the equations above incorporate the required transformations.\n\nNote rnn_cell_backward does __not__ include the calculation of loss from $y \\langle t \\rangle$, this is incorporated into the incoming da_next. This is a slight mismatch with rnn_cell_forward which includes a dense layer and softmax. \n\nNote: in the code: \n$\\displaystyle dx^{\\langle t \\rangle}$ is represented by dxt, \n$\\displaystyle d W_{ax}$ is represented by dWax, \n$\\displaystyle da_{prev}$ is represented by da_prev, \n$\\displaystyle dW_{aa}$ is represented by dWaa, \n$\\displaystyle db_{a}$ is represented by dba, \ndz is not derived above but can optionally be derived by students to simplify the repeated calculations.\n", "_____no_output_____" ] ], [ [ "def rnn_cell_backward(da_next, cache):\n \"\"\"\n Implements the backward pass for the RNN-cell (single time-step).\n\n Arguments:\n da_next -- Gradient of loss with respect to next hidden state\n cache -- python dictionary containing useful values (output of rnn_cell_forward())\n\n Returns:\n gradients -- python dictionary containing:\n dx -- Gradients of input data, of shape (n_x, m)\n da_prev -- Gradients of previous hidden state, of shape (n_a, m)\n dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)\n dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)\n dba -- Gradients of bias vector, of shape (n_a, 1)\n \"\"\"\n \n # Retrieve values from cache\n (a_next, a_prev, xt, parameters) = cache\n \n # Retrieve values from parameters\n Wax = parameters[\"Wax\"]\n Waa = parameters[\"Waa\"]\n Wya = parameters[\"Wya\"]\n ba = parameters[\"ba\"]\n by = parameters[\"by\"]\n\n ### START CODE HERE ###\n # compute the gradient of the loss with respect to z (optional) (≈1 line)\n dz = None\n\n # compute the gradient of the loss with respect to Wax (≈2 lines)\n dxt = None\n dWax = None\n\n # compute the gradient with respect to Waa (≈2 lines)\n da_prev = None\n dWaa = None\n\n # compute the gradient with respect to b (≈1 line)\n dba = None\n\n ### END CODE HERE ###\n \n # Store the gradients in a python dictionary\n gradients = {\"dxt\": dxt, \"da_prev\": da_prev, \"dWax\": dWax, \"dWaa\": dWaa, \"dba\": dba}\n \n return gradients", "_____no_output_____" ], [ "np.random.seed(1)\nxt_tmp = np.random.randn(3,10)\na_prev_tmp = np.random.randn(5,10)\nparameters_tmp = {}\nparameters_tmp['Wax'] = np.random.randn(5,3)\nparameters_tmp['Waa'] = np.random.randn(5,5)\nparameters_tmp['Wya'] = np.random.randn(2,5)\nparameters_tmp['ba'] = np.random.randn(5,1)\nparameters_tmp['by'] = np.random.randn(2,1)\n\na_next_tmp, yt_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp)\n\nda_next_tmp = np.random.randn(5,10)\ngradients_tmp = rnn_cell_backward(da_next_tmp, cache_tmp)\nprint(\"gradients[\\\"dxt\\\"][1][2] =\", gradients_tmp[\"dxt\"][1][2])\nprint(\"gradients[\\\"dxt\\\"].shape =\", gradients_tmp[\"dxt\"].shape)\nprint(\"gradients[\\\"da_prev\\\"][2][3] =\", gradients_tmp[\"da_prev\"][2][3])\nprint(\"gradients[\\\"da_prev\\\"].shape =\", gradients_tmp[\"da_prev\"].shape)\nprint(\"gradients[\\\"dWax\\\"][3][1] =\", gradients_tmp[\"dWax\"][3][1])\nprint(\"gradients[\\\"dWax\\\"].shape =\", gradients_tmp[\"dWax\"].shape)\nprint(\"gradients[\\\"dWaa\\\"][1][2] =\", gradients_tmp[\"dWaa\"][1][2])\nprint(\"gradients[\\\"dWaa\\\"].shape =\", gradients_tmp[\"dWaa\"].shape)\nprint(\"gradients[\\\"dba\\\"][4] =\", gradients_tmp[\"dba\"][4])\nprint(\"gradients[\\\"dba\\\"].shape =\", gradients_tmp[\"dba\"].shape)", "_____no_output_____" ] ], [ [ "**Expected Output**:\n\n<table>\n <tr>\n <td>\n **gradients[\"dxt\"][1][2]** =\n </td>\n <td>\n -1.3872130506\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dxt\"].shape** =\n </td>\n <td>\n (3, 10)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"da_prev\"][2][3]** =\n </td>\n <td>\n -0.152399493774\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"da_prev\"].shape** =\n </td>\n <td>\n (5, 10)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWax\"][3][1]** =\n </td>\n <td>\n 0.410772824935\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWax\"].shape** =\n </td>\n <td>\n (5, 3)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWaa\"][1][2]** = \n </td>\n <td>\n 1.15034506685\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWaa\"].shape** =\n </td>\n <td>\n (5, 5)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dba\"][4]** = \n </td>\n <td>\n [ 0.20023491]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dba\"].shape** = \n </td>\n <td>\n (5, 1)\n </td>\n </tr>\n</table>", "_____no_output_____" ], [ "#### Backward pass through the RNN\n\nComputing the gradients of the cost with respect to $a^{\\langle t \\rangle}$ at every time-step $t$ is useful because it is what helps the gradient backpropagate to the previous RNN-cell. To do so, you need to iterate through all the time steps starting at the end, and at each step, you increment the overall $db_a$, $dW_{aa}$, $dW_{ax}$ and you store $dx$.\n\n**Instructions**:\n\nImplement the `rnn_backward` function. Initialize the return variables with zeros first and then loop through all the time steps while calling the `rnn_cell_backward` at each time timestep, update the other variables accordingly.", "_____no_output_____" ], [ "* Note that this notebook does not implement the backward path from the Loss 'J' backwards to 'a'. \n * This would have included the dense layer and softmax which are a part of the forward path. \n * This is assumed to be calculated elsewhere and the result passed to rnn_backward in 'da'. \n * You must combine this with the loss from the previous stages when calling rnn_cell_backward (see figure 7 above).\n* It is further assumed that loss has been adjusted for batch size (m).\n * Therefore, division by the number of examples is not required here.", "_____no_output_____" ] ], [ [ "def rnn_backward(da, caches):\n \"\"\"\n Implement the backward pass for a RNN over an entire sequence of input data.\n\n Arguments:\n da -- Upstream gradients of all hidden states, of shape (n_a, m, T_x)\n caches -- tuple containing information from the forward pass (rnn_forward)\n \n Returns:\n gradients -- python dictionary containing:\n dx -- Gradient w.r.t. the input data, numpy-array of shape (n_x, m, T_x)\n da0 -- Gradient w.r.t the initial hidden state, numpy-array of shape (n_a, m)\n dWax -- Gradient w.r.t the input's weight matrix, numpy-array of shape (n_a, n_x)\n dWaa -- Gradient w.r.t the hidden state's weight matrix, numpy-arrayof shape (n_a, n_a)\n dba -- Gradient w.r.t the bias, of shape (n_a, 1)\n \"\"\"\n \n ### START CODE HERE ###\n \n # Retrieve values from the first cache (t=1) of caches (≈2 lines)\n (caches, x) = None\n (a1, a0, x1, parameters) = None\n \n # Retrieve dimensions from da's and x1's shapes (≈2 lines)\n n_a, m, T_x = None\n n_x, m = None\n \n # initialize the gradients with the right sizes (≈6 lines)\n dx = None\n dWax = None\n dWaa = None\n dba = None\n da0 = None\n da_prevt = None\n \n # Loop through all the time steps\n for t in reversed(range(None)):\n # Compute gradients at time step t. \n # Remember to sum gradients from the output path (da) and the previous timesteps (da_prevt) (≈1 line)\n gradients = None\n # Retrieve derivatives from gradients (≈ 1 line)\n dxt, da_prevt, dWaxt, dWaat, dbat = gradients[\"dxt\"], gradients[\"da_prev\"], gradients[\"dWax\"], gradients[\"dWaa\"], gradients[\"dba\"]\n # Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines)\n dx[:, :, t] = None\n dWax += None\n dWaa += None\n dba += None\n \n # Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line) \n da0 = None\n ### END CODE HERE ###\n\n # Store the gradients in a python dictionary\n gradients = {\"dx\": dx, \"da0\": da0, \"dWax\": dWax, \"dWaa\": dWaa,\"dba\": dba}\n \n return gradients", "_____no_output_____" ], [ "np.random.seed(1)\nx_tmp = np.random.randn(3,10,4)\na0_tmp = np.random.randn(5,10)\nparameters_tmp = {}\nparameters_tmp['Wax'] = np.random.randn(5,3)\nparameters_tmp['Waa'] = np.random.randn(5,5)\nparameters_tmp['Wya'] = np.random.randn(2,5)\nparameters_tmp['ba'] = np.random.randn(5,1)\nparameters_tmp['by'] = np.random.randn(2,1)\n\na_tmp, y_tmp, caches_tmp = rnn_forward(x_tmp, a0_tmp, parameters_tmp)\nda_tmp = np.random.randn(5, 10, 4)\ngradients_tmp = rnn_backward(da_tmp, caches_tmp)\n\nprint(\"gradients[\\\"dx\\\"][1][2] =\", gradients_tmp[\"dx\"][1][2])\nprint(\"gradients[\\\"dx\\\"].shape =\", gradients_tmp[\"dx\"].shape)\nprint(\"gradients[\\\"da0\\\"][2][3] =\", gradients_tmp[\"da0\"][2][3])\nprint(\"gradients[\\\"da0\\\"].shape =\", gradients_tmp[\"da0\"].shape)\nprint(\"gradients[\\\"dWax\\\"][3][1] =\", gradients_tmp[\"dWax\"][3][1])\nprint(\"gradients[\\\"dWax\\\"].shape =\", gradients_tmp[\"dWax\"].shape)\nprint(\"gradients[\\\"dWaa\\\"][1][2] =\", gradients_tmp[\"dWaa\"][1][2])\nprint(\"gradients[\\\"dWaa\\\"].shape =\", gradients_tmp[\"dWaa\"].shape)\nprint(\"gradients[\\\"dba\\\"][4] =\", gradients_tmp[\"dba\"][4])\nprint(\"gradients[\\\"dba\\\"].shape =\", gradients_tmp[\"dba\"].shape)", "_____no_output_____" ] ], [ [ "**Expected Output**:\n\n<table>\n <tr>\n <td>\n **gradients[\"dx\"][1][2]** =\n </td>\n <td>\n [-2.07101689 -0.59255627 0.02466855 0.01483317]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dx\"].shape** =\n </td>\n <td>\n (3, 10, 4)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"da0\"][2][3]** =\n </td>\n <td>\n -0.314942375127\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"da0\"].shape** =\n </td>\n <td>\n (5, 10)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWax\"][3][1]** =\n </td>\n <td>\n 11.2641044965\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWax\"].shape** =\n </td>\n <td>\n (5, 3)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWaa\"][1][2]** = \n </td>\n <td>\n 2.30333312658\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWaa\"].shape** =\n </td>\n <td>\n (5, 5)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dba\"][4]** = \n </td>\n <td>\n [-0.74747722]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dba\"].shape** = \n </td>\n <td>\n (5, 1)\n </td>\n </tr>\n</table>", "_____no_output_____" ], [ "## 3.2 - LSTM backward pass", "_____no_output_____" ], [ "### 3.2.1 One Step backward\nThe LSTM backward pass is slightly more complicated than the forward pass.\n\n<img src=\"images/LSTM_cell_backward_rev3a_c2.png\" style=\"width:500;height:400px;\"> <br>\n<caption><center> **Figure 8**: lstm_cell_backward. Note the output functions, while part of the lstm_cell_forward, are not included in lstm_cell_backward </center></caption>\n\nThe equations for the LSTM backward pass are provided below. (If you enjoy calculus exercises feel free to try deriving these from scratch yourself.)", "_____no_output_____" ], [ "### 3.2.2 gate derivatives\nNote the location of the gate derivatives ($\\gamma$..) between the dense layer and the activation function (see graphic above). This is convenient for computing parameter derivatives in the next step. \n\\begin{align}\nd\\gamma_o^{\\langle t \\rangle} &= da_{next}*\\tanh(c_{next}) * \\Gamma_o^{\\langle t \\rangle}*\\left(1-\\Gamma_o^{\\langle t \\rangle}\\right)\\tag{7} \\\\[8pt]\ndp\\widetilde{c}^{\\langle t \\rangle} &= \\left(dc_{next}*\\Gamma_u^{\\langle t \\rangle}+ \\Gamma_o^{\\langle t \\rangle}* (1-\\tanh^2(c_{next})) * \\Gamma_u^{\\langle t \\rangle} * da_{next} \\right) * \\left(1-\\left(\\widetilde c^{\\langle t \\rangle}\\right)^2\\right) \\tag{8} \\\\[8pt]\nd\\gamma_u^{\\langle t \\rangle} &= \\left(dc_{next}*\\widetilde{c}^{\\langle t \\rangle} + \\Gamma_o^{\\langle t \\rangle}* (1-\\tanh^2(c_{next})) * \\widetilde{c}^{\\langle t \\rangle} * da_{next}\\right)*\\Gamma_u^{\\langle t \\rangle}*\\left(1-\\Gamma_u^{\\langle t \\rangle}\\right)\\tag{9} \\\\[8pt]\nd\\gamma_f^{\\langle t \\rangle} &= \\left(dc_{next}* c_{prev} + \\Gamma_o^{\\langle t \\rangle} * (1-\\tanh^2(c_{next})) * c_{prev} * da_{next}\\right)*\\Gamma_f^{\\langle t \\rangle}*\\left(1-\\Gamma_f^{\\langle t \\rangle}\\right)\\tag{10}\n\\end{align}\n### 3.2.3 parameter derivatives \n\n$ dW_f = d\\gamma_f^{\\langle t \\rangle} \\begin{bmatrix} a_{prev} \\\\ x_t\\end{bmatrix}^T \\tag{11} $\n$ dW_u = d\\gamma_u^{\\langle t \\rangle} \\begin{bmatrix} a_{prev} \\\\ x_t\\end{bmatrix}^T \\tag{12} $\n$ dW_c = dp\\widetilde c^{\\langle t \\rangle} \\begin{bmatrix} a_{prev} \\\\ x_t\\end{bmatrix}^T \\tag{13} $\n$ dW_o = d\\gamma_o^{\\langle t \\rangle} \\begin{bmatrix} a_{prev} \\\\ x_t\\end{bmatrix}^T \\tag{14}$\n\nTo calculate $db_f, db_u, db_c, db_o$ you just need to sum across all 'm' examples (axis= 1) on $d\\gamma_f^{\\langle t \\rangle}, d\\gamma_u^{\\langle t \\rangle}, dp\\widetilde c^{\\langle t \\rangle}, d\\gamma_o^{\\langle t \\rangle}$ respectively. Note that you should have the `keepdims = True` option.\n\n$\\displaystyle db_f = \\sum_{batch}d\\gamma_f^{\\langle t \\rangle}\\tag{15}$\n$\\displaystyle db_u = \\sum_{batch}d\\gamma_u^{\\langle t \\rangle}\\tag{16}$\n$\\displaystyle db_c = \\sum_{batch}d\\gamma_c^{\\langle t \\rangle}\\tag{17}$\n$\\displaystyle db_o = \\sum_{batch}d\\gamma_o^{\\langle t \\rangle}\\tag{18}$\n\nFinally, you will compute the derivative with respect to the previous hidden state, previous memory state, and input.\n\n$ da_{prev} = W_f^T d\\gamma_f^{\\langle t \\rangle} + W_u^T d\\gamma_u^{\\langle t \\rangle}+ W_c^T dp\\widetilde c^{\\langle t \\rangle} + W_o^T d\\gamma_o^{\\langle t \\rangle} \\tag{19}$\n\nHere, to account for concatenation, the weights for equations 19 are the first n_a, (i.e. $W_f = W_f[:,:n_a]$ etc...)\n\n$ dc_{prev} = dc_{next}*\\Gamma_f^{\\langle t \\rangle} + \\Gamma_o^{\\langle t \\rangle} * (1- \\tanh^2(c_{next}))*\\Gamma_f^{\\langle t \\rangle}*da_{next} \\tag{20}$\n\n$ dx^{\\langle t \\rangle} = W_f^T d\\gamma_f^{\\langle t \\rangle} + W_u^T d\\gamma_u^{\\langle t \\rangle}+ W_c^T dp\\widetilde c^{\\langle t \\rangle} + W_o^T d\\gamma_o^{\\langle t \\rangle}\\tag{21} $\n\nwhere the weights for equation 21 are from n_a to the end, (i.e. $W_f = W_f[:,n_a:]$ etc...)\n\n**Exercise:** Implement `lstm_cell_backward` by implementing equations $7-21$ below. \n \n \nNote: In the code:\n\n$d\\gamma_o^{\\langle t \\rangle}$ is represented by `dot`, \n$dp\\widetilde{c}^{\\langle t \\rangle}$ is represented by `dcct`, \n$d\\gamma_u^{\\langle t \\rangle}$ is represented by `dit`, \n$d\\gamma_f^{\\langle t \\rangle}$ is represented by `dft`\n", "_____no_output_____" ] ], [ [ "def lstm_cell_backward(da_next, dc_next, cache):\n \"\"\"\n Implement the backward pass for the LSTM-cell (single time-step).\n\n Arguments:\n da_next -- Gradients of next hidden state, of shape (n_a, m)\n dc_next -- Gradients of next cell state, of shape (n_a, m)\n cache -- cache storing information from the forward pass\n\n Returns:\n gradients -- python dictionary containing:\n dxt -- Gradient of input data at time-step t, of shape (n_x, m)\n da_prev -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)\n dc_prev -- Gradient w.r.t. the previous memory state, of shape (n_a, m, T_x)\n dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)\n dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)\n dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)\n dWo -- Gradient w.r.t. the weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)\n dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)\n dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)\n dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)\n dbo -- Gradient w.r.t. biases of the output gate, of shape (n_a, 1)\n \"\"\"\n\n # Retrieve information from \"cache\"\n (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache\n \n ### START CODE HERE ###\n # Retrieve dimensions from xt's and a_next's shape (≈2 lines)\n n_x, m = None\n n_a, m = None\n \n # Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)\n dot = None\n dcct = None\n dit = None\n dft = None\n \n # Compute parameters related derivatives. Use equations (11)-(18) (≈8 lines)\n dWf = None\n dWi = None\n dWc = None\n dWo = None\n dbf = None\n dbi = None\n dbc = None\n dbo = None\n\n # Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (19)-(21). (≈3 lines)\n da_prev = None\n dc_prev = None\n dxt = None\n ### END CODE HERE ###\n \n # Save gradients in dictionary\n gradients = {\"dxt\": dxt, \"da_prev\": da_prev, \"dc_prev\": dc_prev, \"dWf\": dWf,\"dbf\": dbf, \"dWi\": dWi,\"dbi\": dbi,\n \"dWc\": dWc,\"dbc\": dbc, \"dWo\": dWo,\"dbo\": dbo}\n\n return gradients", "_____no_output_____" ], [ "np.random.seed(1)\nxt_tmp = np.random.randn(3,10)\na_prev_tmp = np.random.randn(5,10)\nc_prev_tmp = np.random.randn(5,10)\nparameters_tmp = {}\nparameters_tmp['Wf'] = np.random.randn(5, 5+3)\nparameters_tmp['bf'] = np.random.randn(5,1)\nparameters_tmp['Wi'] = np.random.randn(5, 5+3)\nparameters_tmp['bi'] = np.random.randn(5,1)\nparameters_tmp['Wo'] = np.random.randn(5, 5+3)\nparameters_tmp['bo'] = np.random.randn(5,1)\nparameters_tmp['Wc'] = np.random.randn(5, 5+3)\nparameters_tmp['bc'] = np.random.randn(5,1)\nparameters_tmp['Wy'] = np.random.randn(2,5)\nparameters_tmp['by'] = np.random.randn(2,1)\n\na_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp)\n\nda_next_tmp = np.random.randn(5,10)\ndc_next_tmp = np.random.randn(5,10)\ngradients_tmp = lstm_cell_backward(da_next_tmp, dc_next_tmp, cache_tmp)\nprint(\"gradients[\\\"dxt\\\"][1][2] =\", gradients_tmp[\"dxt\"][1][2])\nprint(\"gradients[\\\"dxt\\\"].shape =\", gradients_tmp[\"dxt\"].shape)\nprint(\"gradients[\\\"da_prev\\\"][2][3] =\", gradients_tmp[\"da_prev\"][2][3])\nprint(\"gradients[\\\"da_prev\\\"].shape =\", gradients_tmp[\"da_prev\"].shape)\nprint(\"gradients[\\\"dc_prev\\\"][2][3] =\", gradients_tmp[\"dc_prev\"][2][3])\nprint(\"gradients[\\\"dc_prev\\\"].shape =\", gradients_tmp[\"dc_prev\"].shape)\nprint(\"gradients[\\\"dWf\\\"][3][1] =\", gradients_tmp[\"dWf\"][3][1])\nprint(\"gradients[\\\"dWf\\\"].shape =\", gradients_tmp[\"dWf\"].shape)\nprint(\"gradients[\\\"dWi\\\"][1][2] =\", gradients_tmp[\"dWi\"][1][2])\nprint(\"gradients[\\\"dWi\\\"].shape =\", gradients_tmp[\"dWi\"].shape)\nprint(\"gradients[\\\"dWc\\\"][3][1] =\", gradients_tmp[\"dWc\"][3][1])\nprint(\"gradients[\\\"dWc\\\"].shape =\", gradients_tmp[\"dWc\"].shape)\nprint(\"gradients[\\\"dWo\\\"][1][2] =\", gradients_tmp[\"dWo\"][1][2])\nprint(\"gradients[\\\"dWo\\\"].shape =\", gradients_tmp[\"dWo\"].shape)\nprint(\"gradients[\\\"dbf\\\"][4] =\", gradients_tmp[\"dbf\"][4])\nprint(\"gradients[\\\"dbf\\\"].shape =\", gradients_tmp[\"dbf\"].shape)\nprint(\"gradients[\\\"dbi\\\"][4] =\", gradients_tmp[\"dbi\"][4])\nprint(\"gradients[\\\"dbi\\\"].shape =\", gradients_tmp[\"dbi\"].shape)\nprint(\"gradients[\\\"dbc\\\"][4] =\", gradients_tmp[\"dbc\"][4])\nprint(\"gradients[\\\"dbc\\\"].shape =\", gradients_tmp[\"dbc\"].shape)\nprint(\"gradients[\\\"dbo\\\"][4] =\", gradients_tmp[\"dbo\"][4])\nprint(\"gradients[\\\"dbo\\\"].shape =\", gradients_tmp[\"dbo\"].shape)", "_____no_output_____" ] ], [ [ "**Expected Output**:\n\n<table>\n <tr>\n <td>\n **gradients[\"dxt\"][1][2]** =\n </td>\n <td>\n 3.23055911511\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dxt\"].shape** =\n </td>\n <td>\n (3, 10)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"da_prev\"][2][3]** =\n </td>\n <td>\n -0.0639621419711\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"da_prev\"].shape** =\n </td>\n <td>\n (5, 10)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dc_prev\"][2][3]** =\n </td>\n <td>\n 0.797522038797\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dc_prev\"].shape** =\n </td>\n <td>\n (5, 10)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWf\"][3][1]** = \n </td>\n <td>\n -0.147954838164\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWf\"].shape** =\n </td>\n <td>\n (5, 8)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWi\"][1][2]** = \n </td>\n <td>\n 1.05749805523\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWi\"].shape** = \n </td>\n <td>\n (5, 8)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWc\"][3][1]** = \n </td>\n <td>\n 2.30456216369\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWc\"].shape** = \n </td>\n <td>\n (5, 8)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWo\"][1][2]** = \n </td>\n <td>\n 0.331311595289\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWo\"].shape** = \n </td>\n <td>\n (5, 8)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbf\"][4]** = \n </td>\n <td>\n [ 0.18864637]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbf\"].shape** = \n </td>\n <td>\n (5, 1)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbi\"][4]** = \n </td>\n <td>\n [-0.40142491]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbi\"].shape** = \n </td>\n <td>\n (5, 1)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbc\"][4]** = \n </td>\n <td>\n [ 0.25587763]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbc\"].shape** = \n </td>\n <td>\n (5, 1)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbo\"][4]** = \n </td>\n <td>\n [ 0.13893342]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbo\"].shape** = \n </td>\n <td>\n (5, 1)\n </td>\n </tr>\n</table>", "_____no_output_____" ], [ "### 3.3 Backward pass through the LSTM RNN\n\nThis part is very similar to the `rnn_backward` function you implemented above. You will first create variables of the same dimension as your return variables. You will then iterate over all the time steps starting from the end and call the one step function you implemented for LSTM at each iteration. You will then update the parameters by summing them individually. Finally return a dictionary with the new gradients. \n\n**Instructions**: Implement the `lstm_backward` function. Create a for loop starting from $T_x$ and going backward. For each step call `lstm_cell_backward` and update the your old gradients by adding the new gradients to them. Note that `dxt` is not updated but is stored.", "_____no_output_____" ] ], [ [ "def lstm_backward(da, caches):\n \n \"\"\"\n Implement the backward pass for the RNN with LSTM-cell (over a whole sequence).\n\n Arguments:\n da -- Gradients w.r.t the hidden states, numpy-array of shape (n_a, m, T_x)\n caches -- cache storing information from the forward pass (lstm_forward)\n\n Returns:\n gradients -- python dictionary containing:\n dx -- Gradient of inputs, of shape (n_x, m, T_x)\n da0 -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)\n dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)\n dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)\n dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)\n dWo -- Gradient w.r.t. the weight matrix of the save gate, numpy array of shape (n_a, n_a + n_x)\n dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)\n dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)\n dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)\n dbo -- Gradient w.r.t. biases of the save gate, of shape (n_a, 1)\n \"\"\"\n\n # Retrieve values from the first cache (t=1) of caches.\n (caches, x) = caches\n (a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]\n \n ### START CODE HERE ###\n # Retrieve dimensions from da's and x1's shapes (≈2 lines)\n n_a, m, T_x = None\n n_x, m = None\n \n # initialize the gradients with the right sizes (≈12 lines)\n dx = None\n da0 = None\n da_prevt = None\n dc_prevt = None\n dWf = None\n dWi = None\n dWc = None\n dWo = None\n dbf = None\n dbi = None\n dbc = None\n dbo = None\n \n # loop back over the whole sequence\n for t in reversed(range(None)):\n # Compute all gradients using lstm_cell_backward\n gradients = None\n # Store or add the gradient to the parameters' previous step's gradient\n da_prevt = None\n dc_prevt = None\n dx[:,:,t] = None\n dWf += None\n dWi += None\n dWc += None\n dWo += None\n dbf += None\n dbi += None\n dbc += None\n dbo += None\n # Set the first activation's gradient to the backpropagated gradient da_prev.\n da0 = None\n \n ### END CODE HERE ###\n\n # Store the gradients in a python dictionary\n gradients = {\"dx\": dx, \"da0\": da0, \"dWf\": dWf,\"dbf\": dbf, \"dWi\": dWi,\"dbi\": dbi,\n \"dWc\": dWc,\"dbc\": dbc, \"dWo\": dWo,\"dbo\": dbo}\n \n return gradients", "_____no_output_____" ], [ "np.random.seed(1)\nx_tmp = np.random.randn(3,10,7)\na0_tmp = np.random.randn(5,10)\n\nparameters_tmp = {}\nparameters_tmp['Wf'] = np.random.randn(5, 5+3)\nparameters_tmp['bf'] = np.random.randn(5,1)\nparameters_tmp['Wi'] = np.random.randn(5, 5+3)\nparameters_tmp['bi'] = np.random.randn(5,1)\nparameters_tmp['Wo'] = np.random.randn(5, 5+3)\nparameters_tmp['bo'] = np.random.randn(5,1)\nparameters_tmp['Wc'] = np.random.randn(5, 5+3)\nparameters_tmp['bc'] = np.random.randn(5,1)\nparameters_tmp['Wy'] = np.zeros((2,5)) # unused, but needed for lstm_forward\nparameters_tmp['by'] = np.zeros((2,1)) # unused, but needed for lstm_forward\n\na_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp)\n\nda_tmp = np.random.randn(5, 10, 4)\ngradients_tmp = lstm_backward(da_tmp, caches_tmp)\n\nprint(\"gradients[\\\"dx\\\"][1][2] =\", gradients_tmp[\"dx\"][1][2])\nprint(\"gradients[\\\"dx\\\"].shape =\", gradients_tmp[\"dx\"].shape)\nprint(\"gradients[\\\"da0\\\"][2][3] =\", gradients_tmp[\"da0\"][2][3])\nprint(\"gradients[\\\"da0\\\"].shape =\", gradients_tmp[\"da0\"].shape)\nprint(\"gradients[\\\"dWf\\\"][3][1] =\", gradients_tmp[\"dWf\"][3][1])\nprint(\"gradients[\\\"dWf\\\"].shape =\", gradients_tmp[\"dWf\"].shape)\nprint(\"gradients[\\\"dWi\\\"][1][2] =\", gradients_tmp[\"dWi\"][1][2])\nprint(\"gradients[\\\"dWi\\\"].shape =\", gradients_tmp[\"dWi\"].shape)\nprint(\"gradients[\\\"dWc\\\"][3][1] =\", gradients_tmp[\"dWc\"][3][1])\nprint(\"gradients[\\\"dWc\\\"].shape =\", gradients_tmp[\"dWc\"].shape)\nprint(\"gradients[\\\"dWo\\\"][1][2] =\", gradients_tmp[\"dWo\"][1][2])\nprint(\"gradients[\\\"dWo\\\"].shape =\", gradients_tmp[\"dWo\"].shape)\nprint(\"gradients[\\\"dbf\\\"][4] =\", gradients_tmp[\"dbf\"][4])\nprint(\"gradients[\\\"dbf\\\"].shape =\", gradients_tmp[\"dbf\"].shape)\nprint(\"gradients[\\\"dbi\\\"][4] =\", gradients_tmp[\"dbi\"][4])\nprint(\"gradients[\\\"dbi\\\"].shape =\", gradients_tmp[\"dbi\"].shape)\nprint(\"gradients[\\\"dbc\\\"][4] =\", gradients_tmp[\"dbc\"][4])\nprint(\"gradients[\\\"dbc\\\"].shape =\", gradients_tmp[\"dbc\"].shape)\nprint(\"gradients[\\\"dbo\\\"][4] =\", gradients_tmp[\"dbo\"][4])\nprint(\"gradients[\\\"dbo\\\"].shape =\", gradients_tmp[\"dbo\"].shape)", "_____no_output_____" ] ], [ [ "**Expected Output**:\n\n<table>\n <tr>\n <td>\n **gradients[\"dx\"][1][2]** =\n </td>\n <td>\n [0.00218254 0.28205375 -0.48292508 -0.43281115]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dx\"].shape** =\n </td>\n <td>\n (3, 10, 4)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"da0\"][2][3]** =\n </td>\n <td>\n 0.312770310257\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"da0\"].shape** =\n </td>\n <td>\n (5, 10)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWf\"][3][1]** = \n </td>\n <td>\n -0.0809802310938\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWf\"].shape** =\n </td>\n <td>\n (5, 8)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWi\"][1][2]** = \n </td>\n <td>\n 0.40512433093\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWi\"].shape** = \n </td>\n <td>\n (5, 8)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWc\"][3][1]** = \n </td>\n <td>\n -0.0793746735512\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWc\"].shape** = \n </td>\n <td>\n (5, 8)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWo\"][1][2]** = \n </td>\n <td>\n 0.038948775763\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dWo\"].shape** = \n </td>\n <td>\n (5, 8)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbf\"][4]** = \n </td>\n <td>\n [-0.15745657]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbf\"].shape** = \n </td>\n <td>\n (5, 1)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbi\"][4]** = \n </td>\n <td>\n [-0.50848333]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbi\"].shape** = \n </td>\n <td>\n (5, 1)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbc\"][4]** = \n </td>\n <td>\n [-0.42510818]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbc\"].shape** = \n </td>\n <td>\n (5, 1)\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbo\"][4]** = \n </td>\n <td>\n [ -0.17958196]\n </td>\n </tr>\n <tr>\n <td>\n **gradients[\"dbo\"].shape** = \n </td>\n <td>\n (5, 1)\n </td>\n </tr>\n</table>", "_____no_output_____" ], [ "### Congratulations !\n\nCongratulations on completing this assignment. You now understand how recurrent neural networks work! \n\nLet's go on to the next exercise, where you'll use an RNN to build a character-level language model.\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ] ]

cb308b95b46f2b436848514e8f8430f3a3bed6f3

81,182

ipynb

Jupyter Notebook

notebooks/AH_2.0_Data_Exploration.ipynb

AkashHaldankar/Portuguese_Bank

873c9358a1b9e09ae4b9468316741fe3a49b5c47

[ "MIT" ]

null

notebooks/AH_2.0_Data_Exploration.ipynb

AkashHaldankar/Portuguese_Bank

873c9358a1b9e09ae4b9468316741fe3a49b5c47

[ "MIT" ]

null

notebooks/AH_2.0_Data_Exploration.ipynb

AkashHaldankar/Portuguese_Bank

873c9358a1b9e09ae4b9468316741fe3a49b5c47

[ "MIT" ]

null

73.136937

12,472

0.723301

[ [ [ "import pandas as pd\nimport matplotlib.pyplot as plt\nimport seaborn as sns\nfrom sklearn.model_selection import train_test_split\nfrom sklearn.ensemble import RandomForestClassifier\nimport matplotlib.pyplot as plt\nfrom statsmodels.graphics.mosaicplot import mosaic", "_____no_output_____" ], [ "path = '/home/akash/greyatom/Hackathon_1/Portuguese_Bank/data/raw/bank-additional.csv'", "_____no_output_____" ], [ "bank_data_full = pd.read_csv(path,sep=';')", "_____no_output_____" ], [ "bank_data_full.head()", "_____no_output_____" ], [ "bank_data_full.info()", "<class 'pandas.core.frame.DataFrame'>\nRangeIndex: 4119 entries, 0 to 4118\nData columns (total 21 columns):\nage 4119 non-null int64\njob 4119 non-null object\nmarital 4119 non-null object\neducation 4119 non-null object\ndefault 4119 non-null object\nhousing 4119 non-null object\nloan 4119 non-null object\ncontact 4119 non-null object\nmonth 4119 non-null object\nday_of_week 4119 non-null object\nduration 4119 non-null int64\ncampaign 4119 non-null int64\npdays 4119 non-null int64\nprevious 4119 non-null int64\npoutcome 4119 non-null object\nemp.var.rate 4119 non-null float64\ncons.price.idx 4119 non-null float64\ncons.conf.idx 4119 non-null float64\neuribor3m 4119 non-null float64\nnr.employed 4119 non-null float64\ny 4119 non-null object\ndtypes: float64(5), int64(5), object(11)\nmemory usage: 675.9+ KB\n" ], [ "rename_cols = {'emp.var.rate':'emp_var_rate','cons.price.idx':'cons_price_idx','cons.conf.idx':'cons_conf_idx','nr.employed':'nr_employed'}\nbank_data_full.rename(columns=rename_cols,inplace=True)", "_____no_output_____" ], [ "bank_data_full_category = bank_data_full.select_dtypes(include=['object_'])", "_____no_output_____" ], [ "bank_data_full_category.head()", "_____no_output_____" ], [ "bank_data_full_numeric = bank_data_full.select_dtypes(include=['number'])", "_____no_output_____" ], [ "bank_data_full_numeric.head()", "_____no_output_____" ], [ "bank_data_full_numeric.describe()", "_____no_output_____" ], [ "bank_data_full_category.describe()", "_____no_output_____" ], [ "bank_data_full['month'].value_counts().plot(kind='bar')", "_____no_output_____" ], [ "bank_data_full['marital'].value_counts().plot(kind='bar')", "_____no_output_____" ], [ "bank_data_full['education'].value_counts().plot(kind='bar')", "_____no_output_____" ], [ "bank_data_full['default'].value_counts().plot(kind='bar')", "_____no_output_____" ], [ "bank_data_full['housing'].value_counts().plot(kind='bar')", "_____no_output_____" ], [ "bank_data_full['loan'].value_counts().plot(kind='bar')", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code", "code" ] ]

cb30917a7767d3000b8f1dbb8f560766295e9850

136,307

ipynb

Jupyter Notebook

demo/.ipynb_checkpoints/comparison_fftconv_spatialconv-checkpoint.ipynb

mtyhon/ckconv

056ec93c039e8bcda89f07ff9fdece3e7373b0bf

[ "MIT" ]

74

2021-02-04T14:28:49.000Z

2022-03-23T16:12:18.000Z

demo/.ipynb_checkpoints/comparison_fftconv_spatialconv-checkpoint.ipynb

mtyhon/ckconv

056ec93c039e8bcda89f07ff9fdece3e7373b0bf

[ "MIT" ]

7

2021-02-28T03:29:12.000Z

2022-02-16T14:33:06.000Z

demo/.ipynb_checkpoints/comparison_fftconv_spatialconv-checkpoint.ipynb

mtyhon/ckconv

056ec93c039e8bcda89f07ff9fdece3e7373b0bf

[ "MIT" ]

6

2021-02-12T14:43:15.000Z

2021-08-11T02:42:31.000Z

211.986003

42,280

0.650752

[ [ [ "# Comparison FFTConv & SpatialConv\n\nIn this notebook, we compare the speed and the error of utilizing fft and spatial convolutions. \n\nIn particular, we will:\n* Perform a forward and backward pass on a small network utilizing different types of convolution.\n* Analyze their speed and their error response w.r.t. spatial convolutions. \n\nLet's go! First, we import some packages:", "_____no_output_____" ] ], [ [ "# Append .. to path\nimport os,sys\nckconv_source = os.path.join(os.getcwd(), '..')\nif ckconv_source not in sys.path:\n sys.path.append(ckconv_source)\n\nimport torch\nimport ckconv\nimport matplotlib.pyplot as plt", "_____no_output_____" ], [ "causal_fftconv = ckconv.nn.functional.causal_fftconv\ncausal_conv = ckconv.nn.functional.causal_conv", "_____no_output_____" ] ], [ [ "First we create a (long) input signal and define the convolutional kernels. ", "_____no_output_____" ] ], [ [ "input_size = 2000\nno_channels = 20\nbatch_size = 3\n\n# Input signal\nsignal = torch.randn(batch_size, no_channels, input_size).cuda()\nsignal.normal_(0, 0.01)\n\n# Conv. kernels:\nkernel1 = torch.nn.Parameter(torch.randn(20, 20, input_size)).cuda()\nkernel2 = torch.nn.Parameter(torch.randn(20, 20, input_size)).cuda()\nkernel3 = torch.nn.Parameter(torch.randn(20, 20, input_size)).cuda()\nkernel1.data.normal_(0, 0.01)\nkernel2.data.normal_(0, 0.01)\nkernel3.data.normal_(0, 0.01)\n\nprint()", "\n" ] ], [ [ "Now, we perform the forward pass:", "_____no_output_____" ] ], [ [ "# With spatialconv\ny1 = torch.relu(causal_conv(signal, kernel1))\ny2 = torch.relu(causal_conv(y1, kernel2))\ny3 = causal_conv(y2, kernel3)", "_____no_output_____" ], [ "# With fftconv (double)\ny1_dfft = torch.relu(causal_fftconv(signal, kernel1, double_precision=True))\ny2_dfft = torch.relu(causal_fftconv(y1_dfft, kernel2, double_precision=True))\ny3_dfft = causal_fftconv(y2_dfft, kernel3, double_precision=True)", "_____no_output_____" ], [ "# With fftconv (float)\ny1_fft = torch.relu(causal_fftconv(signal, kernel1, double_precision=False))\ny2_fft = torch.relu(causal_fftconv(y1_fft, kernel2, double_precision=False))\ny3_fft = causal_fftconv(y2_fft, kernel3, double_precision=False)", "_____no_output_____" ], [ "plt.figure(figsize=(6.4,5))\nplt.title('Result Conv. Network with Spatial Convolutions')\nplt.plot(y3.detach().cpu().numpy()[0, 0, :])\nplt.show()\n\nfig, axs = plt.subplots(1, 2,figsize=(15,5))\n\n\naxs[0].set_title('Spatial - FFT (Float precision)')\naxs[0].plot(y3.detach().cpu().numpy()[0, 0, :] - y3_fft.detach().cpu().numpy()[0, 0, :])\n\naxs[1].set_title('Spatial - FFT (Double precision)')\naxs[1].plot(y3.detach().cpu().numpy()[0, 0, :] - y3_dfft.detach().cpu().numpy()[0, 0, :])\n\nplt.show()\n\nprint('Abs Error Mean. Float: {} , Double: {}'.format(torch.abs(y3 - y3_fft).mean(), torch.abs(y3 - y3_dfft).mean()))\nprint('Abs Error Std Dev. Float: {} , Double: {}'.format(torch.abs(y3 - y3_fft).std(), torch.abs(y3 - y3_dfft).std()))", "_____no_output_____" ] ], [ [ "We observe that the error is very small. \n\n\n### Speed analysis\n\nNow, we analyze their speed:", "_____no_output_____" ] ], [ [ "# With spatialconv\n\nwith torch.autograd.profiler.profile(use_cuda=True) as prof:\n y1 = torch.relu(causal_conv(signal, kernel1))\n y2 = torch.relu(causal_conv(y1, kernel2))\n y3 = causal_conv(y2, kernel3)\n y3 = y3.sum()\n y3.backward()\n \nprint(prof)\n\n# Self CPU time total: 103.309ms\n# CUDA time total: 103.847ms\n ", "------------------------------------------- ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ \n Name Self CPU % Self CPU CPU total % CPU total CPU time avg Self CUDA Self CUDA % CUDA total CUDA time avg # of Calls \n------------------------------------------- ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ \n aten::constant_pad_nd 0.04% 42.114us 0.11% 118.304us 118.304us 35.360us 0.03% 184.224us 184.224us 1 \n aten::empty 0.01% 11.538us 0.01% 11.538us 11.538us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.03% 33.639us 0.03% 33.639us 33.639us 108.928us 0.10% 108.928us 108.928us 1 \n aten::narrow 0.00% 4.260us 0.01% 11.081us 11.081us 1.024us 0.00% 1.024us 1.024us 1 \n aten::slice 0.00% 3.340us 0.01% 6.821us 6.821us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 3.481us 0.00% 3.481us 3.481us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.02% 19.932us 0.02% 19.932us 19.932us 38.912us 0.04% 38.912us 38.912us 1 \n aten::constant_pad_nd 0.02% 18.745us 0.05% 48.187us 48.187us 6.144us 0.01% 22.528us 22.528us 1 \n aten::empty 0.00% 4.607us 0.00% 4.607us 4.607us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.01% 9.692us 0.01% 9.692us 9.692us 5.120us 0.00% 5.120us 5.120us 1 \n aten::narrow 0.00% 2.900us 0.01% 5.417us 5.417us 2.048us 0.00% 2.048us 2.048us 1 \n aten::slice 0.00% 1.495us 0.00% 2.517us 2.517us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.022us 0.00% 1.022us 1.022us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.01% 9.726us 0.01% 9.726us 9.726us 9.216us 0.01% 9.216us 9.216us 1 \n aten::conv1d 0.01% 7.424us 0.17% 173.560us 173.560us 1.888us 0.00% 7.242ms 7.242ms 1 \n aten::convolution 0.01% 7.755us 0.16% 166.136us 166.136us 4.096us 0.00% 7.240ms 7.240ms 1 \n aten::_convolution 0.02% 25.339us 0.15% 158.381us 158.381us 38.015us 0.04% 7.236ms 7.236ms 1 \n aten::contiguous 0.00% 2.579us 0.00% 2.579us 2.579us 0.928us 0.00% 0.928us 0.928us 1 \n aten::unsqueeze 0.01% 6.777us 0.01% 8.094us 8.094us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.317us 0.00% 1.317us 1.317us 0.000us 0.00% 0.000us 0.000us 1 \n aten::unsqueeze 0.01% 5.847us 0.01% 6.889us 6.889us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.042us 0.00% 1.042us 1.042us 0.000us 0.00% 0.000us 0.000us 1 \n aten::contiguous 0.00% 2.825us 0.00% 2.825us 2.825us 0.992us 0.00% 0.992us 0.992us 1 \n aten::cudnn_convolution 0.08% 86.972us 0.10% 100.891us 100.891us 7.194ms 6.93% 7.196ms 7.196ms 1 \n aten::empty 0.00% 3.284us 0.00% 3.284us 3.284us 0.000us 0.00% 0.000us 0.000us 1 \n aten::contiguous 0.00% 2.626us 0.00% 2.626us 2.626us 0.960us 0.00% 0.960us 0.960us 1 \n aten::resize_ 0.00% 1.498us 0.00% 1.498us 1.498us 0.000us 0.00% 0.000us 0.000us 1 \n aten::contiguous 0.00% 1.973us 0.00% 1.973us 1.973us 1.024us 0.00% 1.024us 1.024us 1 \n aten::resize_ 0.00% 0.367us 0.00% 0.367us 0.367us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.460us 0.00% 0.460us 0.460us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.254us 0.00% 0.254us 0.254us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.350us 0.00% 0.350us 0.350us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.252us 0.00% 0.252us 0.252us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.00% 2.855us 0.00% 2.855us 2.855us 0.000us 0.00% 0.000us 0.000us 1 \n aten::squeeze 0.01% 10.307us 0.01% 11.764us 11.764us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.457us 0.00% 1.457us 1.457us 0.000us 0.00% 0.000us 0.000us 1 \n aten::relu 0.02% 24.209us 0.05% 53.008us 53.008us 4.096us 0.00% 9.216us 9.216us 1 \n aten::threshold 0.02% 23.637us 0.03% 28.799us 28.799us 5.120us 0.00% 5.120us 5.120us 1 \n aten::empty 0.00% 5.162us 0.00% 5.162us 5.162us 0.000us 0.00% 0.000us 0.000us 1 \n aten::constant_pad_nd 0.03% 33.860us 0.08% 78.135us 78.135us 7.136us 0.01% 60.416us 60.416us 1 \n aten::empty 0.01% 5.659us 0.01% 5.659us 5.659us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.01% 14.076us 0.01% 14.076us 14.076us 13.344us 0.01% 13.344us 13.344us 1 \n aten::narrow 0.00% 4.683us 0.01% 8.784us 8.784us 1.024us 0.00% 1.024us 1.024us 1 \n aten::slice 0.00% 2.448us 0.00% 4.101us 4.101us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.653us 0.00% 1.653us 1.653us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.02% 15.756us 0.02% 15.756us 15.756us 38.912us 0.04% 38.912us 38.912us 1 \n aten::constant_pad_nd 0.03% 30.662us 0.07% 71.049us 71.049us 6.145us 0.01% 25.600us 25.600us 1 \n aten::empty 0.00% 4.341us 0.00% 4.341us 4.341us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.01% 12.660us 0.01% 12.660us 12.660us 5.120us 0.00% 5.120us 5.120us 1 \n aten::narrow 0.00% 4.853us 0.01% 9.009us 9.009us 1.024us 0.00% 1.024us 1.024us 1 \n aten::slice 0.00% 2.505us 0.00% 4.156us 4.156us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.651us 0.00% 1.651us 1.651us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.01% 14.377us 0.01% 14.377us 14.377us 13.312us 0.01% 13.312us 13.312us 1 \n aten::conv1d 0.01% 7.960us 0.18% 181.944us 181.944us 2.049us 0.00% 8.762ms 8.762ms 1 \n aten::convolution 0.01% 8.419us 0.17% 173.984us 173.984us 2.048us 0.00% 8.760ms 8.760ms 1 \n aten::_convolution 0.03% 26.869us 0.16% 165.565us 165.565us 4.096us 0.00% 8.758ms 8.758ms 1 \n aten::contiguous 0.00% 3.757us 0.00% 3.757us 3.757us 2.048us 0.00% 2.048us 2.048us 1 \n aten::unsqueeze 0.01% 10.482us 0.01% 12.148us 12.148us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.666us 0.00% 1.666us 1.666us 0.000us 0.00% 0.000us 0.000us 1 \n aten::unsqueeze 0.01% 6.818us 0.01% 7.780us 7.780us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 0.962us 0.00% 0.962us 0.962us 0.000us 0.00% 0.000us 0.000us 1 \n aten::contiguous 0.00% 4.545us 0.00% 4.545us 4.545us 1.024us 0.00% 1.024us 1.024us 1 \n aten::cudnn_convolution 0.08% 79.635us 0.10% 99.906us 99.906us 8.749ms 8.42% 8.751ms 8.751ms 1 \n aten::empty 0.00% 4.758us 0.00% 4.758us 4.758us 0.000us 0.00% 0.000us 0.000us 1 \n aten::contiguous 0.00% 4.122us 0.00% 4.122us 4.122us 1.024us 0.00% 1.024us 1.024us 1 \n aten::resize_ 0.00% 1.190us 0.00% 1.190us 1.190us 0.000us 0.00% 0.000us 0.000us 1 \n aten::contiguous 0.00% 3.299us 0.00% 3.299us 3.299us 1.024us 0.00% 1.024us 1.024us 1 \n aten::resize_ 0.00% 0.731us 0.00% 0.731us 0.731us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.648us 0.00% 0.648us 0.648us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.538us 0.00% 0.538us 0.538us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.472us 0.00% 0.472us 0.472us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.376us 0.00% 0.376us 0.376us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.00% 4.137us 0.00% 4.137us 4.137us 0.000us 0.00% 0.000us 0.000us 1 \n aten::squeeze 0.01% 9.096us 0.01% 10.560us 10.560us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.464us 0.00% 1.464us 1.464us 0.000us 0.00% 0.000us 0.000us 1 \n aten::relu 0.02% 23.134us 0.05% 47.255us 47.255us 4.093us 0.00% 9.214us 9.214us 1 \n aten::threshold 0.02% 19.495us 0.02% 24.121us 24.121us 5.121us 0.00% 5.121us 5.121us 1 \n aten::empty 0.00% 4.626us 0.00% 4.626us 4.626us 0.000us 0.00% 0.000us 0.000us 1 \n aten::constant_pad_nd 0.03% 34.739us 0.08% 80.064us 80.064us 6.048us 0.01% 61.438us 61.438us 1 \n aten::empty 0.00% 4.657us 0.00% 4.657us 4.657us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.01% 14.946us 0.01% 14.946us 14.946us 15.455us 0.01% 15.455us 15.455us 1 \n aten::narrow 0.01% 5.204us 0.01% 9.397us 9.397us 1.023us 0.00% 1.023us 1.023us 1 \n aten::slice 0.00% 2.421us 0.00% 4.193us 4.193us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.772us 0.00% 1.772us 1.772us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.02% 16.325us 0.02% 16.325us 16.325us 38.912us 0.04% 38.912us 38.912us 1 \n aten::constant_pad_nd 0.04% 38.619us 0.36% 376.817us 376.817us 8.191us 0.01% 21.504us 21.504us 1 \n aten::empty 0.28% 290.495us 0.28% 290.495us 290.495us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.02% 20.506us 0.02% 20.506us 20.506us 4.096us 0.00% 4.096us 4.096us 1 \n aten::narrow 0.01% 5.559us 0.01% 10.178us 10.178us 1.023us 0.00% 1.023us 1.023us 1 \n aten::slice 0.00% 2.637us 0.00% 4.619us 4.619us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.982us 0.00% 1.982us 1.982us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.02% 17.019us 0.02% 17.019us 17.019us 8.193us 0.01% 8.193us 8.193us 1 \n aten::conv1d 0.01% 9.426us 0.19% 192.025us 192.025us 2.051us 0.00% 7.831ms 7.831ms 1 \n aten::convolution 0.01% 9.059us 0.18% 182.599us 182.599us 2.047us 0.00% 7.828ms 7.828ms 1 \n aten::_convolution 0.03% 29.486us 0.17% 173.540us 173.540us 5.121us 0.00% 7.826ms 7.826ms 1 \n aten::contiguous 0.00% 3.977us 0.00% 3.977us 3.977us 1.023us 0.00% 1.023us 1.023us 1 \n aten::unsqueeze 0.01% 10.656us 0.01% 12.540us 12.540us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.884us 0.00% 1.884us 1.884us 0.000us 0.00% 0.000us 0.000us 1 \n aten::unsqueeze 0.01% 5.928us 0.01% 6.801us 6.801us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 0.873us 0.00% 0.873us 0.873us 0.000us 0.00% 0.000us 0.000us 1 \n------------------------------------------- ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ \nSelf CPU time total: 103.309ms\nCUDA time total: 103.847ms\n\n" ], [ "# With fft and double precision\n\nwith torch.autograd.profiler.profile(use_cuda=True) as prof:\n y1_dfft = torch.relu(causal_fftconv(signal, kernel1, double_precision=True))\n y2_dfft = torch.relu(causal_fftconv(y1_dfft, kernel2, double_precision=True))\n y3_dfft = causal_fftconv(y2_dfft, kernel3, double_precision=True)\n y3_dfft = y3_dfft.sum()\n y3_dfft.backward()\n \nprint(prof)\n\n# Self CPU time total: 32.416ms\n# CUDA time total: 31.895ms", "----------------------------------- ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ \n Name Self CPU % Self CPU CPU total % CPU total CPU time avg Self CUDA Self CUDA % CUDA total CUDA time avg # of Calls \n----------------------------------- ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ \n aten::constant_pad_nd 0.13% 42.500us 0.34% 110.639us 110.639us 37.312us 0.12% 178.912us 178.912us 1 \n aten::empty 0.03% 10.307us 0.03% 10.307us 10.307us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.09% 28.164us 0.09% 28.164us 28.164us 100.640us 0.32% 100.640us 100.640us 1 \n aten::narrow 0.01% 4.271us 0.03% 10.603us 10.603us 2.048us 0.01% 2.048us 2.048us 1 \n aten::slice 0.01% 3.179us 0.02% 6.332us 6.332us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.01% 3.153us 0.01% 3.153us 3.153us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.06% 19.065us 0.06% 19.065us 19.065us 38.912us 0.12% 38.912us 38.912us 1 \n aten::constant_pad_nd 0.06% 18.016us 0.14% 45.904us 45.904us 7.168us 0.02% 22.528us 22.528us 1 \n aten::empty 0.01% 3.872us 0.01% 3.872us 3.872us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.03% 9.435us 0.03% 9.435us 9.435us 5.120us 0.02% 5.120us 5.120us 1 \n aten::narrow 0.01% 2.948us 0.02% 5.353us 5.353us 2.048us 0.01% 2.048us 2.048us 1 \n aten::slice 0.00% 1.402us 0.01% 2.405us 2.405us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.003us 0.00% 1.003us 1.003us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.03% 9.228us 0.03% 9.228us 9.228us 8.192us 0.03% 8.192us 8.192us 1 \n aten::constant_pad_nd 0.09% 29.481us 0.20% 66.276us 66.276us 6.176us 0.02% 72.704us 72.704us 1 \n aten::empty 0.02% 5.155us 0.02% 5.155us 5.155us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.04% 13.320us 0.04% 13.320us 13.320us 26.592us 0.08% 26.592us 26.592us 1 \n aten::narrow 0.01% 3.207us 0.02% 6.527us 6.527us 1.024us 0.00% 1.024us 1.024us 1 \n aten::slice 0.01% 1.718us 0.01% 3.320us 3.320us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.602us 0.00% 1.602us 1.602us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.04% 11.793us 0.04% 11.793us 11.793us 38.912us 0.12% 38.912us 38.912us 1 \n aten::to 0.02% 7.955us 0.10% 33.131us 33.131us 2.048us 0.01% 22.528us 22.528us 1 \n aten::empty_strided 0.02% 7.054us 0.02% 7.054us 7.054us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.06% 18.122us 0.06% 18.122us 18.122us 20.480us 0.06% 20.480us 20.480us 1 \n aten::to 0.02% 5.759us 0.08% 26.911us 26.911us 2.048us 0.01% 78.848us 78.848us 1 \n aten::empty_strided 0.01% 3.922us 0.01% 3.922us 3.922us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.05% 17.230us 0.05% 17.230us 17.230us 76.800us 0.24% 76.800us 76.800us 1 \n aten::fft_rfft 0.06% 19.102us 0.30% 97.055us 97.055us 7.168us 0.02% 189.440us 189.440us 1 \n aten::reshape 0.01% 4.305us 0.03% 9.378us 9.378us 1.024us 0.00% 1.024us 1.024us 1 \n aten::view 0.02% 5.073us 0.02% 5.073us 5.073us 0.000us 0.00% 0.000us 0.000us 1 \n aten::_fft_with_size 0.14% 44.173us 0.15% 49.822us 49.822us 177.152us 0.56% 177.152us 177.152us 1 \n aten::stride 0.00% 0.919us 0.00% 0.919us 0.919us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.315us 0.00% 0.315us 0.315us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.01% 2.808us 0.01% 2.808us 2.808us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.00% 1.607us 0.00% 1.607us 1.607us 0.000us 0.00% 0.000us 0.000us 1 \n aten::reshape 0.01% 3.388us 0.02% 7.838us 7.838us 1.024us 0.00% 1.024us 1.024us 1 \n aten::view 0.01% 4.450us 0.01% 4.450us 4.450us 0.000us 0.00% 0.000us 0.000us 1 \n aten::view_as_complex 0.03% 10.915us 0.03% 10.915us 10.915us 3.072us 0.01% 3.072us 3.072us 1 \n aten::fft_rfft 0.05% 15.225us 0.97% 315.250us 315.250us 7.168us 0.02% 971.776us 971.776us 1 \n aten::reshape 0.01% 3.429us 0.03% 8.641us 8.641us 1.024us 0.00% 1.024us 1.024us 1 \n aten::view 0.02% 5.212us 0.02% 5.212us 5.212us 0.000us 0.00% 0.000us 0.000us 1 \n aten::_fft_with_size 0.13% 41.173us 0.84% 270.787us 270.787us 959.488us 3.01% 959.488us 959.488us 1 \n aten::stride 0.00% 0.444us 0.00% 0.444us 0.444us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.258us 0.00% 0.258us 0.258us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.01% 2.636us 0.01% 2.636us 2.636us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.70% 226.276us 0.70% 226.276us 226.276us 0.000us 0.00% 0.000us 0.000us 1 \n aten::reshape 0.01% 3.443us 0.03% 9.739us 9.739us 1.024us 0.00% 1.024us 1.024us 1 \n aten::view 0.02% 6.296us 0.02% 6.296us 6.296us 0.000us 0.00% 0.000us 0.000us 1 \n aten::view_as_complex 0.03% 10.858us 0.03% 10.858us 10.858us 3.072us 0.01% 3.072us 3.072us 1 \n aten::conj 0.02% 5.377us 0.12% 39.245us 39.245us 2.048us 0.01% 117.760us 117.760us 1 \n aten::_conj 0.04% 13.418us 0.10% 33.868us 33.868us 4.096us 0.01% 115.712us 115.712us 1 \n aten::empty 0.00% 1.573us 0.00% 1.573us 1.573us 0.000us 0.00% 0.000us 0.000us 1 \n aten::conj 0.05% 15.241us 0.06% 18.877us 18.877us 111.616us 0.35% 111.616us 111.616us 1 \n aten::resize_ 0.01% 3.636us 0.01% 3.636us 3.636us 0.000us 0.00% 0.000us 0.000us 1 \n aten::unsqueeze 0.02% 6.718us 0.02% 7.832us 7.832us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.114us 0.00% 1.114us 1.114us 0.000us 0.00% 0.000us 0.000us 1 \n aten::unsqueeze 0.01% 4.176us 0.01% 4.762us 4.762us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 0.586us 0.00% 0.586us 0.586us 0.000us 0.00% 0.000us 0.000us 1 \n aten::mul 0.13% 40.837us 0.59% 191.019us 191.019us 377.856us 1.18% 377.856us 377.856us 1 \n aten::empty 0.46% 150.182us 0.46% 150.182us 150.182us 0.000us 0.00% 0.000us 0.000us 1 \n aten::sum 0.10% 30.856us 0.11% 34.901us 34.901us 540.672us 1.70% 540.672us 540.672us 1 \n aten::empty 0.01% 3.022us 0.01% 3.022us 3.022us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 1.023us 0.00% 1.023us 1.023us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fft_irfft 0.05% 16.142us 0.45% 146.073us 146.073us 5.152us 0.02% 226.304us 226.304us 1 \n aten::view_as_real 0.04% 11.540us 0.04% 11.540us 11.540us 4.064us 0.01% 4.064us 4.064us 1 \n aten::reshape 0.01% 3.448us 0.03% 8.381us 8.381us 1.024us 0.00% 1.024us 1.024us 1 \n aten::view 0.02% 4.933us 0.02% 4.933us 4.933us 0.000us 0.00% 0.000us 0.000us 1 \n aten::_fft_with_size 0.12% 39.672us 0.32% 102.321us 102.321us 175.168us 0.55% 214.016us 214.016us 1 \n aten::stride 0.00% 0.446us 0.00% 0.446us 0.446us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.265us 0.00% 0.265us 0.265us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.271us 0.00% 0.271us 0.271us 0.000us 0.00% 0.000us 0.000us 1 \n aten::clone 0.02% 7.656us 0.10% 33.421us 33.421us 2.048us 0.01% 21.504us 21.504us 1 \n aten::empty_like 0.01% 2.554us 0.02% 5.236us 5.236us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.01% 2.682us 0.01% 2.682us 2.682us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.06% 20.529us 0.06% 20.529us 20.529us 19.456us 0.06% 19.456us 19.456us 1 \n aten::empty 0.01% 2.715us 0.01% 2.715us 2.715us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.01% 1.810us 0.01% 1.810us 1.810us 0.000us 0.00% 0.000us 0.000us 1 \n aten::div_ 0.07% 23.721us 0.07% 23.721us 23.721us 17.344us 0.05% 17.344us 17.344us 1 \n aten::reshape 0.01% 3.046us 0.02% 7.689us 7.689us 2.048us 0.01% 2.048us 2.048us 1 \n aten::view 0.01% 4.643us 0.01% 4.643us 4.643us 0.000us 0.00% 0.000us 0.000us 1 \n aten::to 0.02% 6.284us 0.09% 30.066us 30.066us 3.072us 0.01% 21.504us 21.504us 1 \n aten::empty_strided 0.02% 5.441us 0.02% 5.441us 5.441us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.06% 18.341us 0.06% 18.341us 18.341us 18.432us 0.06% 18.432us 18.432us 1 \n aten::slice 0.02% 5.599us 0.02% 6.541us 6.541us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 0.942us 0.00% 0.942us 0.942us 0.000us 0.00% 0.000us 0.000us 1 \n aten::slice 0.01% 3.224us 0.01% 3.733us 3.733us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 0.509us 0.00% 0.509us 0.509us 0.000us 0.00% 0.000us 0.000us 1 \n aten::slice 0.01% 2.995us 0.01% 3.625us 3.625us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 0.630us 0.00% 0.630us 0.630us 0.000us 0.00% 0.000us 0.000us 1 \n aten::relu 0.05% 15.368us 0.10% 33.710us 33.710us 4.096us 0.01% 16.384us 16.384us 1 \n aten::threshold 0.05% 15.497us 0.06% 18.342us 18.342us 12.288us 0.04% 12.288us 12.288us 1 \n aten::empty 0.01% 2.845us 0.01% 2.845us 2.845us 0.000us 0.00% 0.000us 0.000us 1 \n aten::constant_pad_nd 0.06% 20.194us 0.15% 47.134us 47.134us 6.176us 0.02% 61.440us 61.440us 1 \n aten::empty 0.01% 2.410us 0.01% 2.410us 2.410us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.03% 9.573us 0.03% 9.573us 9.573us 15.360us 0.05% 15.360us 15.360us 1 \n aten::narrow 0.01% 2.965us 0.02% 5.289us 5.289us 1.024us 0.00% 1.024us 1.024us 1 \n aten::slice 0.00% 1.391us 0.01% 2.324us 2.324us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 0.933us 0.00% 0.933us 0.933us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.03% 9.668us 0.03% 9.668us 9.668us 38.880us 0.12% 38.880us 38.880us 1 \n aten::constant_pad_nd 0.06% 18.625us 0.13% 43.036us 43.036us 6.144us 0.02% 21.504us 21.504us 1 \n----------------------------------- ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ \nSelf CPU time total: 32.416ms\nCUDA time total: 31.895ms\n\n" ], [ "# With fft and float precision\nwith torch.autograd.profiler.profile(use_cuda=True) as prof:\n y1_fft = torch.relu(causal_fftconv(signal, kernel1, double_precision=False))\n y2_fft = torch.relu(causal_fftconv(y1_fft, kernel2, double_precision=False))\n y3_fft = causal_fftconv(y2_fft, kernel3, double_precision=False)\n y3_fft = y3_fft.sum()\n y3_fft.backward()\n\nprint(prof)\n\n# Self CPU time total: 12.797ms\n# CUDA time total: 13.138ms", "----------------------------------- ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ \n Name Self CPU % Self CPU CPU total % CPU total CPU time avg Self CUDA Self CUDA % CUDA total CUDA time avg # of Calls \n----------------------------------- ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ \n aten::constant_pad_nd 0.33% 41.982us 0.84% 107.540us 107.540us 36.288us 0.28% 167.168us 167.168us 1 \n aten::empty 0.08% 9.863us 0.08% 9.863us 9.863us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.21% 26.432us 0.21% 26.432us 26.432us 94.016us 0.72% 94.016us 94.016us 1 \n aten::narrow 0.03% 4.281us 0.08% 10.216us 10.216us 1.024us 0.01% 1.024us 1.024us 1 \n aten::slice 0.02% 3.026us 0.05% 5.935us 5.935us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.02% 2.909us 0.02% 2.909us 2.909us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.15% 19.047us 0.15% 19.047us 19.047us 35.840us 0.27% 35.840us 35.840us 1 \n aten::constant_pad_nd 0.15% 19.710us 0.39% 50.039us 50.039us 22.176us 0.17% 49.152us 49.152us 1 \n aten::empty 0.04% 4.544us 0.04% 4.544us 4.544us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.07% 9.579us 0.07% 9.579us 9.579us 5.120us 0.04% 5.120us 5.120us 1 \n aten::narrow 0.02% 3.185us 0.05% 6.481us 6.481us 7.744us 0.06% 7.744us 7.744us 1 \n aten::slice 0.02% 2.171us 0.03% 3.296us 3.296us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.01% 1.125us 0.01% 1.125us 1.125us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.08% 9.725us 0.08% 9.725us 9.725us 14.112us 0.11% 14.112us 14.112us 1 \n aten::constant_pad_nd 0.18% 23.479us 0.42% 53.280us 53.280us 18.080us 0.14% 77.472us 77.472us 1 \n aten::empty 0.03% 3.547us 0.03% 3.547us 3.547us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.08% 10.079us 0.08% 10.079us 10.079us 24.576us 0.19% 24.576us 24.576us 1 \n aten::narrow 0.03% 3.326us 0.05% 6.911us 6.911us 2.048us 0.02% 2.048us 2.048us 1 \n aten::slice 0.02% 2.589us 0.03% 3.585us 3.585us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.01% 0.996us 0.01% 0.996us 0.996us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.07% 9.264us 0.07% 9.264us 9.264us 32.768us 0.25% 32.768us 32.768us 1 \n aten::fft_rfft 0.21% 26.662us 0.91% 116.350us 116.350us 12.256us 0.09% 109.664us 109.664us 1 \n aten::reshape 0.06% 8.166us 0.13% 16.873us 16.873us 20.480us 0.16% 20.480us 20.480us 1 \n aten::view 0.07% 8.707us 0.07% 8.707us 8.707us 0.000us 0.00% 0.000us 0.000us 1 \n aten::_fft_with_size 0.37% 47.168us 0.42% 53.883us 53.883us 71.680us 0.55% 71.680us 71.680us 1 \n aten::stride 0.00% 0.624us 0.00% 0.624us 0.624us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.337us 0.00% 0.337us 0.337us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.03% 3.475us 0.03% 3.475us 3.475us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.02% 2.279us 0.02% 2.279us 2.279us 0.000us 0.00% 0.000us 0.000us 1 \n aten::reshape 0.03% 3.258us 0.06% 7.477us 7.477us 1.024us 0.01% 1.024us 1.024us 1 \n aten::view 0.03% 4.219us 0.03% 4.219us 4.219us 0.000us 0.00% 0.000us 0.000us 1 \n aten::view_as_complex 0.09% 11.455us 0.09% 11.455us 11.455us 4.224us 0.03% 4.224us 4.224us 1 \n aten::fft_rfft 0.12% 15.130us 0.65% 83.181us 83.181us 7.904us 0.06% 219.104us 219.104us 1 \n aten::reshape 0.03% 3.353us 0.07% 8.681us 8.681us 12.544us 0.10% 12.544us 12.544us 1 \n aten::view 0.04% 5.328us 0.04% 5.328us 5.328us 0.000us 0.00% 0.000us 0.000us 1 \n aten::_fft_with_size 0.27% 34.825us 0.31% 40.011us 40.011us 193.536us 1.47% 193.536us 193.536us 1 \n aten::stride 0.00% 0.424us 0.00% 0.424us 0.424us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.251us 0.00% 0.251us 0.251us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.02% 2.696us 0.02% 2.696us 2.696us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.01% 1.815us 0.01% 1.815us 1.815us 0.000us 0.00% 0.000us 0.000us 1 \n aten::reshape 0.03% 3.228us 0.06% 8.306us 8.306us 1.024us 0.01% 1.024us 1.024us 1 \n aten::view 0.04% 5.078us 0.04% 5.078us 5.078us 0.000us 0.00% 0.000us 0.000us 1 \n aten::view_as_complex 0.09% 11.053us 0.09% 11.053us 11.053us 4.096us 0.03% 4.096us 4.096us 1 \n aten::conj 0.05% 6.124us 0.33% 42.391us 42.391us 2.080us 0.02% 56.320us 56.320us 1 \n aten::_conj 0.11% 14.155us 0.28% 36.267us 36.267us 5.088us 0.04% 54.240us 54.240us 1 \n aten::empty 0.01% 1.907us 0.01% 1.907us 1.907us 0.000us 0.00% 0.000us 0.000us 1 \n aten::conj 0.12% 15.772us 0.16% 20.205us 20.205us 49.152us 0.37% 49.152us 49.152us 1 \n aten::resize_ 0.03% 4.433us 0.03% 4.433us 4.433us 0.000us 0.00% 0.000us 0.000us 1 \n aten::unsqueeze 0.05% 6.533us 0.06% 7.672us 7.672us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.01% 1.139us 0.01% 1.139us 1.139us 0.000us 0.00% 0.000us 0.000us 1 \n aten::unsqueeze 0.03% 3.990us 0.04% 4.601us 4.601us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 0.611us 0.00% 0.611us 0.611us 0.000us 0.00% 0.000us 0.000us 1 \n aten::mul 0.22% 27.674us 0.24% 30.894us 30.894us 158.688us 1.21% 158.688us 158.688us 1 \n aten::empty 0.03% 3.220us 0.03% 3.220us 3.220us 0.000us 0.00% 0.000us 0.000us 1 \n aten::sum 0.22% 27.754us 0.24% 31.030us 31.030us 90.112us 0.69% 90.112us 90.112us 1 \n aten::empty 0.02% 2.496us 0.02% 2.496us 2.496us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.01% 0.780us 0.01% 0.780us 0.780us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fft_irfft 0.13% 16.192us 1.21% 154.366us 154.366us 5.120us 0.04% 60.416us 60.416us 1 \n aten::view_as_real 0.09% 11.538us 0.09% 11.538us 11.538us 3.072us 0.02% 3.072us 3.072us 1 \n aten::reshape 0.03% 3.574us 0.07% 9.000us 9.000us 1.024us 0.01% 1.024us 1.024us 1 \n aten::view 0.04% 5.426us 0.04% 5.426us 5.426us 0.000us 0.00% 0.000us 0.000us 1 \n aten::_fft_with_size 0.33% 42.598us 0.85% 109.049us 109.049us 32.768us 0.25% 50.176us 50.176us 1 \n aten::stride 0.00% 0.457us 0.00% 0.457us 0.457us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.256us 0.00% 0.256us 0.256us 0.000us 0.00% 0.000us 0.000us 1 \n aten::stride 0.00% 0.264us 0.00% 0.264us 0.264us 0.000us 0.00% 0.000us 0.000us 1 \n aten::clone 0.06% 7.805us 0.27% 34.453us 34.453us 2.976us 0.02% 10.240us 10.240us 1 \n aten::empty_like 0.02% 3.048us 0.05% 6.330us 6.330us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.03% 3.282us 0.03% 3.282us 3.282us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.16% 20.318us 0.16% 20.318us 20.318us 7.264us 0.06% 7.264us 7.264us 1 \n aten::empty 0.02% 2.447us 0.02% 2.447us 2.447us 0.000us 0.00% 0.000us 0.000us 1 \n aten::empty 0.02% 2.076us 0.02% 2.076us 2.076us 0.000us 0.00% 0.000us 0.000us 1 \n aten::div_ 0.21% 26.498us 0.21% 26.498us 26.498us 7.168us 0.05% 7.168us 7.168us 1 \n aten::reshape 0.03% 3.499us 0.07% 8.587us 8.587us 1.024us 0.01% 1.024us 1.024us 1 \n aten::view 0.04% 5.088us 0.04% 5.088us 5.088us 0.000us 0.00% 0.000us 0.000us 1 \n aten::to 0.02% 2.688us 0.02% 2.688us 2.688us 1.024us 0.01% 1.024us 1.024us 1 \n aten::slice 0.04% 5.642us 0.05% 6.612us 6.612us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.01% 0.970us 0.01% 0.970us 0.970us 0.000us 0.00% 0.000us 0.000us 1 \n aten::slice 0.03% 3.479us 0.03% 3.937us 3.937us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 0.458us 0.00% 0.458us 0.458us 0.000us 0.00% 0.000us 0.000us 1 \n aten::slice 0.03% 3.242us 0.03% 3.840us 3.840us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.00% 0.598us 0.00% 0.598us 0.598us 0.000us 0.00% 0.000us 0.000us 1 \n aten::relu 0.12% 15.263us 0.27% 34.608us 34.608us 4.096us 0.03% 15.360us 15.360us 1 \n aten::threshold 0.13% 16.490us 0.15% 19.345us 19.345us 11.264us 0.09% 11.264us 11.264us 1 \n aten::empty 0.02% 2.855us 0.02% 2.855us 2.855us 0.000us 0.00% 0.000us 0.000us 1 \n aten::constant_pad_nd 0.17% 21.340us 0.38% 49.082us 49.082us 6.144us 0.05% 57.344us 57.344us 1 \n aten::empty 0.02% 2.349us 0.02% 2.349us 2.349us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.08% 9.607us 0.08% 9.607us 9.607us 14.336us 0.11% 14.336us 14.336us 1 \n aten::narrow 0.03% 3.222us 0.04% 5.498us 5.498us 1.024us 0.01% 1.024us 1.024us 1 \n aten::slice 0.01% 1.307us 0.02% 2.276us 2.276us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.01% 0.969us 0.01% 0.969us 0.969us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.08% 10.288us 0.08% 10.288us 10.288us 35.840us 0.27% 35.840us 35.840us 1 \n aten::constant_pad_nd 0.16% 19.926us 0.35% 44.556us 44.556us 8.192us 0.06% 21.504us 21.504us 1 \n aten::empty 0.02% 2.497us 0.02% 2.497us 2.497us 0.000us 0.00% 0.000us 0.000us 1 \n aten::fill_ 0.06% 8.097us 0.06% 8.097us 8.097us 5.120us 0.04% 5.120us 5.120us 1 \n aten::narrow 0.02% 3.166us 0.04% 5.441us 5.441us 1.024us 0.01% 1.024us 1.024us 1 \n aten::slice 0.01% 1.371us 0.02% 2.275us 2.275us 0.000us 0.00% 0.000us 0.000us 1 \n aten::as_strided 0.01% 0.904us 0.01% 0.904us 0.904us 0.000us 0.00% 0.000us 0.000us 1 \n aten::copy_ 0.07% 8.595us 0.07% 8.595us 8.595us 7.168us 0.05% 7.168us 7.168us 1 \n aten::constant_pad_nd 0.15% 19.135us 0.34% 43.290us 43.290us 6.176us 0.05% 66.560us 66.560us 1 \n aten::empty 0.02% 2.539us 0.02% 2.539us 2.539us 0.000us 0.00% 0.000us 0.000us 1 \n----------------------------------- ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ \nSelf CPU time total: 12.797ms\nCUDA time total: 13.138ms\n\n" ] ], [ [ "We see that whilst the error is minimal, the gains in speed are extreme (10 times faster for kernels and inputs of size 2000).", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ] ]

cb309e9130312afb77c4ad058e02604fedcb1a47

18,567

ipynb

Jupyter Notebook

site/zh-cn/beta/tutorials/estimators/premade_estimators.ipynb

crypdra/docs

41ab06fd14b3a3dff933bb80b19ce46c7c5781cf

[ "Apache-2.0" ]

2

2019-10-25T18:51:16.000Z

2019-10-25T18:51:18.000Z

site/zh-cn/beta/tutorials/estimators/premade_estimators.ipynb

crypdra/docs

41ab06fd14b3a3dff933bb80b19ce46c7c5781cf

[ "Apache-2.0" ]

null

site/zh-cn/beta/tutorials/estimators/premade_estimators.ipynb

crypdra/docs

41ab06fd14b3a3dff933bb80b19ce46c7c5781cf

[ "Apache-2.0" ]

null

30.239414

304

0.50886

[ [ [ "##### Copyright 2019 The TensorFlow Authors.", "_____no_output_____" ] ], [ [ "#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n# you may not use this file except in compliance with the License.\n# You may obtain a copy of the License at\n#\n# https://www.apache.org/licenses/LICENSE-2.0\n#\n# Unless required by applicable law or agreed to in writing, software\n# distributed under the License is distributed on an \"AS IS\" BASIS,\n# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n# See the License for the specific language governing permissions and\n# limitations under the License.", "_____no_output_____" ] ], [ [ "# 预创建的 Estimators", "_____no_output_____" ], [ "<table class=\"tfo-notebook-buttons\" align=\"left\">\n <td>\n <a target=\"_blank\" href=\"https://tensorflow.google.cn/beta/tutorials/estimators/premade_estimators\"><img src=\"https://tensorflow.google.cn/images/tf_logo_32px.png\" />在 tensorFlow.google.cn 上查看</a>\n </td>\n <td>\n <a target=\"_blank\" href=\"https://colab.research.google.com/github/tensorflow/docs/blob/master/site/zh-cn/beta/tutorials/estimators/premade_estimators.ipynb\"><img src=\"https://tensorflow.google.cn/images/colab_logo_32px.png\" />在 Google Colab 中运行</a>\n </td>\n <td>\n <a target=\"_blank\" href=\"https://github.com/tensorflow/docs/blob/master/site/zh-cn/beta/tutorials/estimators/premade_estimators.ipynb\"><img src=\"https://tensorflow.google.cn/images/GitHub-Mark-32px.png\" />在 GitHub 上查看源代码</a>\n </td>\n <td>\n <a href=\"https://storage.googleapis.com/tensorflow_docs/docs/site/zh-cn/beta/tutorials/estimators/premade_estimators.ipynb\"><img src=\"https://tensorflow.google.cn/images/download_logo_32px.png\" />下载 notebook</a>\n </td>\n</table>", "_____no_output_____" ], [ "Note: 我们的 TensorFlow 社区翻译了这些文档。因为社区翻译是尽力而为，所以无法保证它们是最准确的，并且反映了最新的\n[官方英文文档](https://www.tensorflow.org/?hl=en)。如果您有改进此翻译的建议，请提交 pull request 到\n[tensorflow/docs](https://github.com/tensorflow/docs) GitHub 仓库。要志愿地撰写或者审核译文，请加入\n[[email protected] Google Group](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-zh-cn)。", "_____no_output_____" ], [ "\n本教程将向您展示如何使用 Estimators 解决 Tensorflow 中的鸢尾花（Iris）分类问题。Estimator 是 Tensorflow 完整模型的高级表示，它被设计用于轻松扩展和异步训练。更多细节请参阅 [Estimators](https://tensorflow.google.cn/guide/estimators)。\n\n请注意，在 Tensorflow 2.0 中，[Keras API](https://tensorflow.google.cn/guide/keras) 可以完成许多相同的任务，而且被认为是一个更易学习的API。如果您刚刚开始入门，我们建议您从 Keras 开始。有关 Tensorflow 2.0 中可用高级API的更多信息，请参阅 [Keras标准化](https://medium.com/tensorflow/standardizing-on-keras-guidance-on-high-level-apis-in-tensorflow-2-0-bad2b04c819a)。\n", "_____no_output_____" ], [ "## 首先要做的事\n\n为了开始，您将首先导入 Tensorflow 和一系列您需要的库。\n", "_____no_output_____" ] ], [ [ "from __future__ import absolute_import, division, print_function, unicode_literals\n\ntry:\n # Colab only\n %tensorflow_version 2.x\nexcept Exception:\n pass\n\nimport tensorflow as tf\n\nimport pandas as pd", "_____no_output_____" ] ], [ [ "## 数据集\n\n本文档中的示例程序构建并测试了一个模型，该模型根据[花萼](https://en.wikipedia.org/wiki/Sepal)和[花瓣](https://en.wikipedia.org/wiki/Petal)的大小将鸢尾花分成三种物种。\n\n您将使用鸢尾花数据集训练模型。该数据集包括四个特征和一个[标签](https://developers.google.com/machine-learning/glossary/#label)。这四个特征确定了单个鸢尾花的以下植物学特征：\n\n* 花萼长度\n* 花萼宽度\n* 花瓣长度\n* 花瓣宽度\n\n根据这些信息，您可以定义一些有用的常量来解析数据：\n", "_____no_output_____" ] ], [ [ "CSV_COLUMN_NAMES = ['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth', 'Species']\nSPECIES = ['Setosa', 'Versicolor', 'Virginica']", "_____no_output_____" ] ], [ [ "接下来，使用 Keras 与 Pandas 下载并解析鸢尾花数据集。注意为训练和测试保留不同的数据集。", "_____no_output_____" ] ], [ [ "train_path = tf.keras.utils.get_file(\n \"iris_training.csv\", \"https://storage.googleapis.com/download.tensorflow.org/data/iris_training.csv\")\ntest_path = tf.keras.utils.get_file(\n \"iris_test.csv\", \"https://storage.googleapis.com/download.tensorflow.org/data/iris_test.csv\")\n\ntrain = pd.read_csv(train_path, names=CSV_COLUMN_NAMES, header=0)\ntest = pd.read_csv(test_path, names=CSV_COLUMN_NAMES, header=0)", "_____no_output_____" ] ], [ [ "通过检查数据您可以发现有四列浮点型特征和一列 int32 型标签。", "_____no_output_____" ] ], [ [ "train.head()", "_____no_output_____" ] ], [ [ "对于每个数据集都分割出标签，模型将被训练来预测这些标签。", "_____no_output_____" ] ], [ [ "train_y = train.pop('Species')\ntest_y = test.pop('Species')\n\n# 标签列现已从数据中删除\ntrain.head()", "_____no_output_____" ] ], [ [ "## Estimator 编程概述\n\n现在您已经设定好了数据，您可以使用 Tensorflow Estimator 定义模型。Estimator 是从 `tf.estimator.Estimator` 中派生的任何类。Tensorflow提供了一组`tf.estimator`(例如，`LinearRegressor`)来实现常见的机器学习算法。此外，您可以编写您自己的[自定义 Estimator](https://tensorflow.google.cn/guide/custom_estimators)。入门阶段我们建议使用预创建的 Estimator。\n\n为了编写基于预创建的 Estimator 的 Tensorflow 项目，您必须完成以下工作：\n\n* 创建一个或多个输入函数\n* 定义模型的特征列\n* 实例化一个 Estimator，指定特征列和各种超参数。\n* 在 Estimator 对象上调用一个或多个方法，传递合适的输入函数以作为数据源。\n\n我们来看看这些任务是如何在鸢尾花分类中实现的。\n", "_____no_output_____" ], [ "## 创建输入函数\n\n您必须创建输入函数来提供用于训练、评估和预测的数据。\n\n**输入函数**是一个返回 `tf.data.Dataset` 对象的函数，此对象会输出下列含两个元素的元组：\n\n* [`features`](https://developers.google.com/machine-learning/glossary/#feature)——Python字典，其中：\n * 每个键都是特征名称\n * 每个值都是包含此特征所有值的数组\n* `label` 包含每个样本的[标签](https://developers.google.com/machine-learning/glossary/#label)的值的数组。\n\n为了向您展示输入函数的格式，请查看下面这个简单的实现：\n", "_____no_output_____" ] ], [ [ "def input_evaluation_set():\n features = {'SepalLength': np.array([6.4, 5.0]),\n 'SepalWidth': np.array([2.8, 2.3]),\n 'PetalLength': np.array([5.6, 3.3]),\n 'PetalWidth': np.array([2.2, 1.0])}\n labels = np.array([2, 1])\n return features, labels", "_____no_output_____" ] ], [ [ "\n您的输入函数可以以您喜欢的方式生成 `features` 字典与 `label` 列表。但是，我们建议使用 Tensorflow 的 [Dataset API](https://tensorflow.google.cn/guide/datasets)，该 API 可以用来解析各种类型的数据。\n\nDataset API 可以为您处理很多常见情况。例如，使用 Dataset API，您可以轻松地从大量文件中并行读取记录，并将它们合并为单个数据流。\n\n为了简化此示例，我们将使用 [pandas](https://pandas.pydata.org/) 加载数据，并利用此内存数据构建输入管道。\n", "_____no_output_____" ] ], [ [ "def input_fn(features, labels, training=True, batch_size=256):\n \"\"\"An input function for training or evaluating\"\"\"\n # 将输入转换为数据集。\n dataset = tf.data.Dataset.from_tensor_slices((dict(features), labels))\n\n # 如果在训练模式下混淆并重复数据。\n if training:\n dataset = dataset.shuffle(1000).repeat()\n \n return dataset.batch(batch_size)\n", "_____no_output_____" ] ], [ [ "## 定义特征列（feature columns）\n\n[**特征列（feature columns）**](https://developers.google.com/machine-learning/glossary/#feature_columns)是一个对象，用于描述模型应该如何使用特征字典中的原始输入数据。当您构建一个 Estimator 模型的时候，您会向其传递一个特征列的列表，其中包含您希望模型使用的每个特征。`tf.feature_column` 模块提供了许多为模型表示数据的选项。\n\n对于鸢尾花问题，4 个原始特征是数值，因此我们将构建一个特征列的列表，以告知 Estimator 模型将 4 个特征都表示为 32 位浮点值。故创建特征列的代码如下所示：\n", "_____no_output_____" ] ], [ [ "# 特征列描述了如何使用输入。\nmy_feature_columns = []\nfor key in train.keys():\n my_feature_columns.append(tf.feature_column.numeric_column(key=key))", "_____no_output_____" ] ], [ [ "特征列可能比上述示例复杂得多。您可以从[指南](https://tensorflow.google.cn/guide/feature_columns)获取更多关于特征列的信息。\n\n我们已经介绍了如何使模型表示原始特征，现在您可以构建 Estimator 了。\n", "_____no_output_____" ], [ "## 实例化 Estimator\n\n鸢尾花为题是一个经典的分类问题。幸运的是，Tensorflow 提供了几个预创建的 Estimator 分类器，其中包括：\n\n* `tf.estimator.DNNClassifier` 用于多类别分类的深度模型\n* `tf.estimator.DNNLinearCombinedClassifier` 用于广度与深度模型\n* `tf.estimator.LinearClassifier` 用于基于线性模型的分类器\n\n对于鸢尾花问题，`tf.estimator.LinearClassifier` 似乎是最好的选择。您可以这样实例化该 Estimator：\n", "_____no_output_____" ] ], [ [ "# 构建一个拥有两个隐层，隐藏节点分别为 30 和 10 的深度神经网络。\nclassifier = tf.estimator.DNNClassifier(\n feature_columns=my_feature_columns,\n # 隐层所含结点数量分别为 30 和 10.\n hidden_units=[30, 10],\n # 模型必须从三个类别中做出选择。\n n_classes=3)", "_____no_output_____" ] ], [ [ " ## 训练、评估和预测\n\n我们已经有一个 Estimator 对象，现在可以调用方法来执行下列操作：\n\n* 训练模型。\n* 评估经过训练的模型。\n* 使用经过训练的模型进行预测。", "_____no_output_____" ], [ "### 训练模型\n\n通过调用 Estimator 的 `Train` 方法来训练模型，如下所示：", "_____no_output_____" ] ], [ [ "# 训练模型。\nclassifier.train(\n input_fn=lambda: input_fn(train, train_y, training=True),\n steps=5000)", "_____no_output_____" ] ], [ [ "注意将 ` input_fn` 调用封装在 [`lambda`](https://docs.python.org/3/tutorial/controlflow.html) 中以获取参数，同时提供不带参数的输入函数，如 Estimator 所预期的那样。`step` 参数告知该方法在训练多少步后停止训练。\n", "_____no_output_____" ], [ "### 评估经过训练的模型\n\n现在模型已经经过训练，您可以获取一些关于模型性能的统计信息。代码块将在测试数据上对经过训练的模型的准确率（accuracy）进行评估：\n", "_____no_output_____" ] ], [ [ "eval_result = classifier.evaluate(\n input_fn=lambda: input_fn(test, test_y, training=False))\n\nprint('\\nTest set accuracy: {accuracy:0.3f}\\n'.format(**eval_result))", "_____no_output_____" ] ], [ [ "与对 `train` 方法的调用不同，我们没有传递 `steps` 参数来进行评估。用于评估的 `input_fn` 只生成一个 [epoch](https://developers.google.com/machine-learning/glossary/#epoch) 的数据。\n\n`eval_result` 字典亦包含 `average_loss`（每个样本的平均误差），`loss`（每个 mini-batch 的平均误差）与 Estimator 的 `global_step`（经历的训练迭代次数）值。 ", "_____no_output_____" ], [ "### 利用经过训练的模型进行预测（推理）\n\n我们已经有一个经过训练的模型，可以生成准确的评估结果。我们现在可以使用经过训练的模型，根据一些无标签测量结果预测鸢尾花的品种。与训练和评估一样，我们使用单个函数调用进行预测：", "_____no_output_____" ] ], [ [ "# 由模型生成预测\nexpected = ['Setosa', 'Versicolor', 'Virginica']\npredict_x = {\n 'SepalLength': [5.1, 5.9, 6.9],\n 'SepalWidth': [3.3, 3.0, 3.1],\n 'PetalLength': [1.7, 4.2, 5.4],\n 'PetalWidth': [0.5, 1.5, 2.1],\n}\n\ndef input_fn(features, batch_size=256):\n \"\"\"An input function for prediction.\"\"\"\n # 将输入转换为无标签数据集。\n return tf.data.Dataset.from_tensor_slices(dict(features)).batch(batch_size)\n\npredictions = classifier.predict(\n input_fn=lambda: input_fn(predict_x))", "_____no_output_____" ] ], [ [ "`predict` 方法返回一个 Python 可迭代对象，为每个样本生成一个预测结果字典。以下代码输出了一些预测及其概率：", "_____no_output_____" ] ], [ [ "for pred_dict, expec in zip(predictions, expected):\n class_id = pred_dict['class_ids'][0]\n probability = pred_dict['probabilities'][class_id]\n\n print('Prediction is \"{}\" ({:.1f}%), expected \"{}\"'.format(\n SPECIES[class_id], 100 * probability, expec))", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ] ]

cb30a70a4d994527db64bea50a17045185bf4e8f

492,331

ipynb

Jupyter Notebook

notebooks/active_learning/fb-01-probabilistic approaches/02-GP_with_sklearn.ipynb

MetaExp/backend

9e37257ed40a1c90ffb7212d3f756a8da201e3bd

[ "MIT" ]

1

2018-01-25T21:22:12.000Z

notebooks/active_learning/fb-01-probabilistic approaches/02-GP_with_sklearn.ipynb

MetaExp/backend

9e37257ed40a1c90ffb7212d3f756a8da201e3bd

[ "MIT" ]

57

2018-01-24T15:38:40.000Z

2018-04-20T08:48:38.000Z

notebooks/active_learning/fb-01-probabilistic approaches/02-GP_with_sklearn.ipynb

MetaExp/backend

9e37257ed40a1c90ffb7212d3f756a8da201e3bd

[ "MIT" ]

null

1,857.85283

72,862

0.947137

[ [ [ "## [Experiments] Uncertainty Sampling with a 1D Gaussian Process as model\n\nFirst, we define a prior probablility for a model.\nThe GaussianRegressor approximates this model using an optimization method (probably similar to EM) for a given data input.\nThe resulting model has a mean and a certainty.\nWe use these to determine the next data point that should be labeled and critizise the data set.", "_____no_output_____" ] ], [ [ "%matplotlib inline\nfrom sklearn.gaussian_process import GaussianProcessRegressor\nfrom sklearn.gaussian_process.kernels import (RBF, Matern, RationalQuadratic,\n ExpSineSquared, DotProduct,\n ConstantKernel)\nimport math\nimport numpy as np\nfrom matplotlib import pyplot as plt", "_____no_output_____" ], [ "size = 100\nkernel = 1.0 * RBF(length_scale=1.0,length_scale_bounds=(1e-1,10.0))\ngp = GaussianProcessRegressor(kernel=kernel)", "_____no_output_____" ], [ "# plot prior probability of model\nplt.figure(figsize=(8, 8))\nplt.subplot(2, 1, 1)\nX_ = np.linspace(0, 5, size)\ny_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)\nplt.plot(X_, y_mean, 'k', lw=3, zorder=9)\nplt.fill_between(X_, y_mean - y_std, y_mean + y_std,\n alpha=0.2, color='k')\ny_samples = gp.sample_y(X_[:, np.newaxis], 10)\nplt.plot(X_, y_samples, lw=1)\nplt.xlim(0, 5)\nplt.ylim(-3, 3)\nplt.title(\"Prior (kernel: %s)\" % kernel, fontsize=12)", "_____no_output_____" ], [ "# Generate data and fit GP\nrng = np.random.RandomState(4)\nX = np.linspace(0, 5, 100)[:, np.newaxis]\ny = np.sin((X[:, 0] - 2.5) ** 2)", "_____no_output_____" ], [ "budget = 10\nrequested_X = []\nrequested_y = []\n\n# init model with random data point\nstart = np.random.choice(np.arange(size))\nrequested_X.append(X[start])\nrequested_y.append(y[start])\ngp.fit(requested_X, requested_y)\ny_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)\n\nfor index in range(2,10):\n max_std = np.unravel_index(np.argmax(y_std, axis=None), y_std.shape)\n requested_X.append(X[max_std])\n requested_y.append(y[max_std])\n \n gp.fit(requested_X, requested_y)\n y_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)\n \n plt.plot(X_, y_mean, 'k', lw=3, zorder=9)\n plt.fill_between(X_, y_mean - y_std, y_mean + y_std,\n alpha=0.2, color='k')\n\n y_samples = gp.sample_y(X_[:, np.newaxis], 7)\n plt.plot(X_, y_samples, lw=1)\n plt.plot(X_, y, lw=2,color='b',zorder =8, dashes=[1,1],)\n plt.scatter(requested_X, requested_y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))\n plt.xlim(0, 5)\n plt.ylim(-3, 3)\n plt.title(\"%s examles: Posterior (kernel: %s)\\n Log-Likelihood: %.3f\"\n % (index, gp.kernel_, gp.log_marginal_likelihood(gp.kernel_.theta)),\n fontsize=12)\n plt.show()", "_____no_output_____" ] ], [ [ "Note how the new data point we aquired after 9 iterations completely changed the certainty about our model.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ] ]

cb30bcbb95adef2331a73011e551d30e639fcf15

134,798

ipynb

Jupyter Notebook

Day 3/.ipynb_checkpoints/Distributions_Tutorial1-checkpoint.ipynb

Abuton/10-Academy-5days-Challenge

97188d5d0122265a8216ec35ef8ffb67db1f3e39

[ "Apache-2.0" ]

1

2021-01-23T11:36:19.000Z

Day 3/.ipynb_checkpoints/Distributions_Tutorial1-checkpoint.ipynb

Abuton/10-Academy-5days-Challenge

97188d5d0122265a8216ec35ef8ffb67db1f3e39

[ "Apache-2.0" ]

null

Day 3/.ipynb_checkpoints/Distributions_Tutorial1-checkpoint.ipynb

Abuton/10-Academy-5days-Challenge

97188d5d0122265a8216ec35ef8ffb67db1f3e39

[ "Apache-2.0" ]

null

154.054857

40,788

0.88571

[ [ [ "# Probability Distribution: \n\nIn [probability theory](https://en.wikipedia.org/wiki/Probability_theory) and [statistics](https://en.wikipedia.org/wiki/statistics), a probability distribution is a [mathematical function](https://en.wikipedia.org/wiki/Function_(mathematics)) that, stated in simple terms, can be thought of as providing the probabilities of occurrence of different possible outcomes in an experiment. \n\nIn more technical terms, the probability distribution is a description of a random phenomenon in terms of the probabilities of events. Examples of random phenomena can include the results of an experiment or survey. A probability distribution is defined in terms of an underlying sample space, which is the set of all possible outcomes of the random phenomenon being observed.\n\n\n### Discrete and Continuous Distributions\n\nProbability distributions are generally divided into two classes. A __discrete probability distribution__ (applicable to the scenarios where the set of possible outcomes is discrete, such as a coin toss or a roll of dice) can be encoded by a discrete list of the probabilities of the outcomes, known as a [probability mass function](https://en.wikipedia.org/wiki/Probability_mass_function). On the other hand, a __continuous probability distribution__ (applicable to the scenarios where the set of possible outcomes can take on values in a continuous range (e.g. real numbers), such as the temperature on a given day) is typically described by probability density functions (with the probability of any individual outcome actually being 0). Such distributions are generally described with the help of [probability density functions](https://en.wikipedia.org/wiki/Probability_density_function).\n\n### In this notebook, we discuss about most important distributions\n* **Bernoulli distribution**\n* **Binomial distribution**\n* **Poisson distribution**\n* **Normal distribution**", "_____no_output_____" ], [ "#### Some Essential Terminologies\n\n* __Mode__: for a discrete random variable, the value with highest probability (the location at which the probability mass function has its peak); for a continuous random variable, a location at which the probability density function has a local peak.\n* __Support__: the smallest closed set whose complement has probability zero.\n* __Head__: the range of values where the pmf or pdf is relatively high.\n* __Tail__: the complement of the head within the support; the large set of values where the pmf or pdf is relatively low.\n* __Expected value or mean__: the weighted average of the possible values, using their probabilities as their weights; or the continuous analog thereof.\n* __Median__: the value such that the set of values less than the median, and the set greater than the median, each have probabilities no greater than one-half.\n* __Variance__: the second moment of the pmf or pdf about the mean; an important measure of the dispersion of the distribution.\n* __Standard deviation__: the square root of the variance, and hence another measure of dispersion.\n\n* __Symmetry__: a property of some distributions in which the portion of the distribution to the left of a specific value is a mirror image of the portion to its right.\n* __Skewness__: a measure of the extent to which a pmf or pdf \"leans\" to one side of its mean. The third standardized moment of the distribution.\n* __Kurtosis__: a measure of the \"fatness\" of the tails of a pmf or pdf. The fourth standardized moment of the distribution.\n\n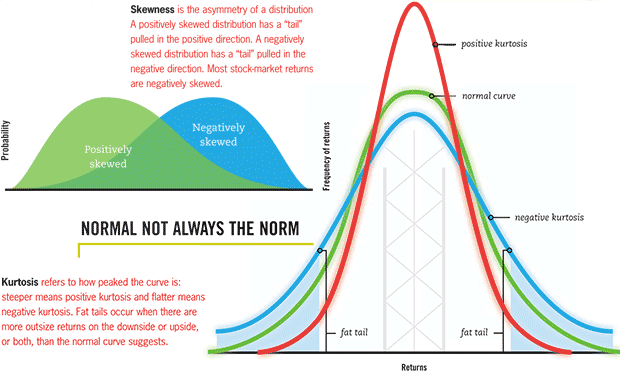![kurtosis](https://anotherbloodybullshitblog.files.wordpress.com/2016/01/normal-not-always-the-norm.gif?w=809)", "_____no_output_____" ], [ "## Bernoulii distribution\n\nThe Bernoulli distribution, named after Swiss mathematician [Jacob Bernoulli](https://en.wikipedia.org/wiki/Jacob_Bernoulli), is the probability distribution of a random variable which takes the value 1 with probability $p$ and the value 0 with probability $q = 1 − p$ — i.e., the probability distribution of any single experiment that asks a ___yes–no question___; the question results in a boolean-valued outcome, a single bit of information whose value is success/yes/true/one with probability $p$ and failure/no/false/zero with probability $q$. This distribution has only two possible outcomes and a single trial.\n\nIt can be used to represent a coin toss where 1 and 0 would represent \"head\" and \"tail\" (or vice versa), respectively. In particular, unfair coins would have $p ≠ 0.5$.\n\nThe probability mass function $f$ of this distribution, over possible outcomes $k$, is\n\n$${\\displaystyle f(k;p)={\\begin{cases}p&{\\text{if }}k=1,\\\\[6pt]1-p&{\\text{if }}k=0.\\end{cases}}}$$", "_____no_output_____" ] ], [ [ "import numpy as np\nfrom matplotlib import pyplot as plt\nfrom numpy import random\nimport seaborn as sns", "_____no_output_____" ], [ "from scipy.stats import bernoulli", "_____no_output_____" ] ], [ [ "#### Generate random variates", "_____no_output_____" ] ], [ [ "# p=0.5 i.e. fair coin\ns=bernoulli.rvs(p=0.5,size=10)\ns", "_____no_output_____" ], [ "plt.hist(s)", "_____no_output_____" ], [ "# p=0.2 i.e. more tails than heads\nbernoulli.rvs(p=0.2,size=10)", "_____no_output_____" ], [ "# p=0.8 i.e. more heads than tails\nbernoulli.rvs(p=0.8,size=10)", "_____no_output_____" ] ], [ [ "#### Mean, variance, skew, and kurtosis", "_____no_output_____" ] ], [ [ "print(\"A fair coin is spinning...\\n\"+\"-\"*30)\npr=0.5 # Fair coin toss probability\nmean, var, skew, kurt = bernoulli.stats(p=pr, moments='mvsk')\nprint(\"Mean:\",mean)\nprint(\"Variance:\",var)\nprint(\"Skew:\",skew)\nprint(\"Kurtosis:\",kurt)\nprint(\"\\nNow a biased coin is spinning...\\n\"+\"-\"*35)\npr=0.7 # Biased coin toss probability\nmean, var, skew, kurt = bernoulli.stats(p=pr, moments='mvsk')\nprint(\"Mean:\",mean)\nprint(\"Variance:\",var)\nprint(\"Skew:\",skew)\nprint(\"Kurtosis:\",kurt)", "A fair coin is spinning...\n------------------------------\nMean: 0.5\nVariance: 0.25\nSkew: 0.0\nKurtosis: -2.0\n\nNow a biased coin is spinning...\n-----------------------------------\nMean: 0.7\nVariance: 0.21000000000000002\nSkew: -0.8728715609439702\nKurtosis: -1.2380952380952361\n" ] ], [ [ "#### Standard deviation, mean, median", "_____no_output_____" ] ], [ [ "print(\"\\nA biased coin with likelihood 0.3 is spinning...\\n\"+\"-\"*50)\npr=0.3\nprint(\"Std. dev:\",bernoulli.std(p=pr))\nprint(\"Mean:\",bernoulli.mean(p=pr))\nprint(\"Median:\",bernoulli.median(p=pr))", "\nA biased coin with likelihood 0.3 is spinning...\n--------------------------------------------------\nStd. dev: 0.458257569496\nMean: 0.3\nMedian: 0.0\nEntropy: 0.6108643020548935\n" ] ], [ [ "## Binomial distribution\n\nThe Binomial Distribution can instead be thought as the sum of outcomes of an event following a Bernoulli distribution. The Binomial Distribution is therefore used in binary outcome events and the probability of success and failure is the same in all the successive trials. This distribution takes two parameters as inputs: the number of times an event takes place and the probability assigned to one of the two classes.\n\nThe binomial distribution is frequently used to model the number of successes in a sample of size n drawn with replacement from a population of size N. A simple example of a Binomial Distribution in action can be the toss of a biased/unbiased coin repeated a certain amount of times.\n\nIn general, if the random variable $X$ follows the binomial distribution with parameters n ∈ ℕ and p ∈ [0,1], we write X ~ B(n, p). The probability of getting exactly $k$ successes in $n$ trials is given by the probability mass function:\n\n$${\\Pr(k;n,p)=\\Pr(X=k)={n \\choose k}p^{k}(1-p)^{n-k}}$$\n\nfor k = 0, 1, 2, ..., n, where\n\n$${\\displaystyle {\\binom {n}{k}}={\\frac {n!}{k!(n-k)!}}}$$", "_____no_output_____" ] ], [ [ "from scipy.stats import binom", "_____no_output_____" ] ], [ [ "#### Generate random variates", "_____no_output_____" ], [ "8 coins are flipped (or 1 coin is flipped 8 times), each with probability of success (1) of 0.25 This trial/experiment is repeated for 10 times", "_____no_output_____" ] ], [ [ "k=binom.rvs(8,0.25,size=10)\nprint(\"Number of success for each trial:\",k)\nprint(\"Average of the success:\", np.mean(k))", "Number of success for each trial: [2 3 4 1 1 2 3 0 0 2]\nAverage of the success: 1.8\n" ], [ "sns.distplot(binom.rvs(n=10, p=0.5, size=1000), hist=True, kde=False)\n\nplt.show()", "_____no_output_____" ], [ "print(\"A fair coin is spinning 5 times\\n\"+\"-\"*35)\npr=0.5 # Fair coin toss probability\nn=5\nmean, var, skew, kurt = binom.stats(n=n,p=pr, moments='mvsk')\nprint(\"Mean:\",mean)\nprint(\"Variance:\",var)\nprint(\"Skew:\",skew)\nprint(\"Kurtosis:\",kurt)\nprint(\"\\nNow a biased coin is spinning 5 times...\\n\"+\"-\"*45)\npr=0.7 # Biased coin toss probability\nn=5\nmean, var, skew, kurt = binom.stats(n=n,p=pr, moments='mvsk')\nprint(\"Mean:\",mean)\nprint(\"Variance:\",var)\nprint(\"Skew:\",skew)\nprint(\"Kurtosis:\",kurt)", "A fair coin is spinning 5 times\n-----------------------------------\nMean: 2.5\nVariance: 1.25\nSkew: 0.0\nKurtosis: -0.4\n\nNow a biased coin is spinning 5 times...\n---------------------------------------------\nMean: 3.5\nVariance: 1.0500000000000003\nSkew: -0.39036002917941315\nKurtosis: -0.24761904761904757\n" ] ], [ [ "#### Standard deviation, mean, median", "_____no_output_____" ] ], [ [ "n=5\npr=0.7\nprint(\"\\n{} biased coins with likelihood {} are spinning...\\n\".format(n,pr)+\"-\"*50)\nprint(\"Std. dev:\",binom.std(n=n,p=pr))\nprint(\"Mean:\",binom.mean(n=n,p=pr))\nprint(\"Median:\",binom.median(n=n,p=pr))", "\n5 biased coins with likelihood 0.7 are spinning...\n--------------------------------------------------\nStd. dev: 1.02469507659596\nMean: 3.5\nMedian: 4.0\n" ] ], [ [ "#### Visualize the probability mass function (pmf)", "_____no_output_____" ] ], [ [ "n=40\npr=0.5\nrv = binom(n,pr)\nx=np.arange(0,41,1)\npmf1 = rv.pmf(x)\n\nn=40\npr=0.15\nrv = binom(n,pr)\nx=np.arange(0,41,1)\npmf2 = rv.pmf(x)\n\nn=50\npr=0.6\nrv = binom(n,pr)\nx=np.arange(0,41,1)\npmf3 = rv.pmf(x)\n\nplt.figure(figsize=(12,6))\nplt.title(\"Probability mass function: $\\\\binom{n}{k}\\, p^k (1-p)^{n-k}$\\n\",fontsize=20)\nplt.scatter(x,pmf1)\nplt.scatter(x,pmf2)\nplt.scatter(x,pmf3,c='k')\nplt.legend([\"$n=40, p=0.5$\",\"$n=40, p=0.3$\",\"$n=50, p=0.6$\"],fontsize=15)\nplt.xlabel(\"Number of successful trials ($k$)\",fontsize=15)\nplt.ylabel(\"Probability of success\",fontsize=15)\nplt.xticks(fontsize=15)\nplt.yticks(fontsize=15)\nplt.grid(True)\nplt.show()", "_____no_output_____" ] ], [ [ "## Poisson Distribution\n\nThe Poisson distribution, is a discrete probability distribution that expresses the probability that an event might happen or not knowing how often it usually occurs.\n\nPoisson Distributions are for example frequently used by insurance companies to conduct risk analysis (eg. predict the number of car crash accidents within a predefined time span) to decide car insurance pricing.\n\nOther examples that may follow a Poisson include\n\n* number of phone calls received by a call center per hour \n* The number of patients arriving in an emergency room between 10 and 11 pm", "_____no_output_____" ] ], [ [ "from scipy.stats import poisson", "_____no_output_____" ] ], [ [ "#### Display probability mass function (pmf)\n\nAn event can occur 0, 1, 2, … times in an interval. The average number of events in an interval is designated $\\lambda$. This is the event rate, also called the rate parameter. The probability of observing k events in an interval is given by the equation\n\n${\\displaystyle P(k{\\text{ events in interval}})=e^{-\\lambda }{\\frac {\\lambda ^{k}}{k!}}}$\n\nwhere,\n\n${\\lambda}$ is the average number of events per interval\n\ne is the number 2.71828... (Euler's number) the base of the natural logarithms\n\nk takes values 0, 1, 2, …\nk! = k × (k − 1) × (k − 2) × … × 2 × 1 is the factorial of k.", "_____no_output_____" ], [ "#### Generate random variates", "_____no_output_____" ] ], [ [ "la=5\nr = poisson.rvs(mu=la, size=20)\nprint(\"Random variates with lambda={}: {}\".format(la,r))\n\nla=0.5\nr = poisson.rvs(mu=la, size=20)\nprint(\"Random variates with lambda={}: {}\".format(la,r))", "Random variates with lambda=5: [6 8 7 2 6 9 8 7 3 5 5 4 2 4 5 1 6 6 6 5]\nRandom variates with lambda=0.5: [2 0 0 0 0 1 0 0 0 1 0 1 0 1 1 0 0 0 0 0]\n" ], [ "data_poisson = poisson.rvs(mu=3, size=10000)\n\nsns.distplot(data_poisson, kde=False)\n\nplt.show()", "_____no_output_____" ], [ "print(\"For small lambda\\n\"+\"-\"*25)\nla=0.5\nmean, var, skew, kurt = poisson.stats(mu=la, moments='mvsk')\nprint(\"Mean:\",mean)\nprint(\"Variance:\",var)\nprint(\"Skew:\",skew)\nprint(\"Kurtosis:\",kurt)\nprint(\"\\nNow for large lambda\\n\"+\"-\"*30)\nla=5\nmean, var, skew, kurt = poisson.stats(mu=la, moments='mvsk')\nprint(\"Mean:\",mean)\nprint(\"Variance:\",var)\nprint(\"Skew:\",skew)\nprint(\"Kurtosis:\",kurt)", "For small lambda\n-------------------------\nMean: 0.5\nVariance: 0.5\nSkew: 1.4142135623730951\nKurtosis: 2.0\n\nNow for large lambda\n------------------------------\nMean: 5.0\nVariance: 5.0\nSkew: 0.4472135954999579\nKurtosis: 0.2\n" ] ], [ [ "#### Standard deviation, mean, median", "_____no_output_____" ] ], [ [ "la=5\nprint(\"For lambda = {}\\n-------------------------\".format(la))\nprint(\"Std. dev:\",poisson.std(mu=la))\nprint(\"Mean:\",poisson.mean(mu=la))\nprint(\"Median:\",poisson.median(mu=la))", "For lambda = 5\n-------------------------\nStd. dev: 2.23606797749979\nMean: 5.0\nMedian: 5.0\n" ] ], [ [ "#### For the complete list of functions and methods please [see this link](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.poisson.html#scipy.stats.poisson).", "_____no_output_____" ], [ "## Normal (Gaussian) distribution\n\nIn probability theory, the normal (or Gaussian or Gauss or Laplace–Gauss) distribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.\n\nThe normal distribution is useful because of the **[central limit theorem](https://en.wikipedia.org/wiki/Central_limit_theorem)**. In its most general form, under some conditions (which include finite variance), it states that **averages of samples of observations of random variables independently drawn from independent distributions converge in distribution to the normal**, that is, they become normally distributed when the number of observations is sufficiently large. \n\nPhysical quantities that are expected to be the sum of many independent processes (such as measurement errors) often have distributions that are nearly normal. Moreover, many results and methods (such as propagation of uncertainty and least squares parameter fitting) can be derived analytically in explicit form when the relevant variables are normally distributed.\n\n### PDF\n\nThe probability density function (PDF) is given by,\n$$ f(x\\mid \\mu ,\\sigma ^{2})={\\frac {1}{\\sqrt {2\\pi \\sigma ^{2}}}}e^{-{\\frac {(x-\\mu )^{2}}{2\\sigma ^{2}}}} $$\nwhere,\n- $\\mu$ is the mean or expectation of the distribution (and also its median and mode),\n- $\\sigma$ is the standard deviation, and $\\sigma^2$ is the variance.", "_____no_output_____" ] ], [ [ "from scipy.stats import norm", "_____no_output_____" ], [ "x = np.linspace(-3, 3, num = 100)\nconstant = 1.0 / np.sqrt(2*np.pi)\npdf_normal_distribution = constant * np.exp((-x**2) / 2.0)\n\nfig, ax = plt.subplots(figsize=(10, 5));\nax.plot(x, pdf_normal_distribution);\nax.set_ylim(0);\nax.set_title('Normal Distribution', size = 20);\nax.set_ylabel('Probability Density', size = 20)", "_____no_output_____" ], [ "mu, sigma = 0.5, 0.1\n\ns = np.random.normal(mu, sigma, 1000)\n\n# create the bins and the histogram\ncount, bins, ignored = plt.hist(s, 20, normed=True)\n\n# plot the distribution curve\n\nplt.plot(bins, 1/(sigma*np.sqrt(2*np.pi))*np.exp( -(bins - mu)**2 / (2*sigma**2)), linewidth = 3, color = \"y\")\n \nplt.show() ", "C:\\Users\\HP PC\\anaconda3\\lib\\site-packages\\ipykernel_launcher.py:10: MatplotlibDeprecationWarning: \nThe 'normed' kwarg was deprecated in Matplotlib 2.1 and will be removed in 3.1. Use 'density' instead.\n # Remove the CWD from sys.path while we load stuff.\n" ], [ "a1 = np.random.normal(loc=0,scale=np.sqrt(0.2),size=100000)\na2 = np.random.normal(loc=0,scale=1.0,size=100000)\na3 = np.random.normal(loc=0,scale=np.sqrt(5),size=100000)\na4 = np.random.normal(loc=-2,scale=np.sqrt(0.5),size=100000)", "_____no_output_____" ], [ "plt.figure(figsize=(8,5))\nplt.hist(a1,density=True,bins=100,color='blue',alpha=0.5)\nplt.hist(a2,density=True,bins=100,color='red',alpha=0.5)\nplt.hist(a3,density=True,bins=100,color='orange',alpha=0.5)\nplt.hist(a4,density=True,bins=100,color='green',alpha=0.5)\nplt.xlim(-7,7)\nplt.show()", "_____no_output_____" ] ], [ [ "## References\n\nhttps://www.w3schools.com/python/numpy_random_normal.asp\n\nhttps://towardsdatascience.com/probability-distributions-in-data-science-cce6e64873a7\n\nhttps://statisticsbyjim.com/basics/probabilitydistributions/#:~:text=A%20probability%20distribution%20is%20a,on%20the%20underlying%20probability%20distribution.\n\nhttps://bolt.mph.ufl.edu/6050-6052/unit-3b/binomial-random-variables/", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ] ]

cb30c8473205977c91072491dae4dfec224b39ed

104,814

ipynb

Jupyter Notebook

ai1/labs/AI1_02.ipynb

derekgbridge/artificial_intelligence

f81d55444adc480aa3e4b826df009be3fbc89ff3

[ "MIT" ]

21

2020-09-28T16:11:09.000Z

2022-02-01T17:48:41.000Z

ai1/labs/AI1_02.ipynb

derekgbridge/artificial_intelligence

f81d55444adc480aa3e4b826df009be3fbc89ff3

[ "MIT" ]

null

ai1/labs/AI1_02.ipynb

derekgbridge/artificial_intelligence

f81d55444adc480aa3e4b826df009be3fbc89ff3

[ "MIT" ]

4

2021-09-08T09:00:50.000Z

2021-10-11T09:41:41.000Z

36.546025

1,521

0.453785

[ [ [ "<h1>02 Pandas</h1>\n$\\newcommand{\\Set}[1]{\\{#1\\}}$ \n$\\newcommand{\\Tuple}[1]{\\langle#1\\rangle}$ \n$\\newcommand{\\v}[1]{\\pmb{#1}}$ \n$\\newcommand{\\cv}[1]{\\begin{bmatrix}#1\\end{bmatrix}}$ \n$\\newcommand{\\rv}[1]{[#1]}$ \n$\\DeclareMathOperator{\\argmax}{arg\\,max}$ \n$\\DeclareMathOperator{\\argmin}{arg\\,min}$ \n$\\DeclareMathOperator{\\dist}{dist}$\n$\\DeclareMathOperator{\\abs}{abs}$", "_____no_output_____" ] ], [ [ "%load_ext autoreload\n%autoreload 2\n%matplotlib inline", "_____no_output_____" ], [ "import pandas as pd\nimport numpy as np\nimport matplotlib.pyplot as plt", "_____no_output_____" ] ], [ [ "<h1>Series</h1>\n<p>\n A Series is like a 1D array. The values in the Series have an index, which, by default, uses consecutive \n integers from 0.\n</p>", "_____no_output_____" ] ], [ [ "s = pd.Series([2, 4, -12, 0, 2])\ns", "_____no_output_____" ] ], [ [ "<p>\n You can get its shape and dtype as we did with numpy arrays:\n</p>", "_____no_output_____" ] ], [ [ "s.shape", "_____no_output_____" ], [ "s.dtype", "_____no_output_____" ] ], [ [ "<p>\n You can get the values as a numpy array:\n</p>", "_____no_output_____" ] ], [ [ "s.values", "_____no_output_____" ] ], [ [ "<p>\n You can access by index and by slicing, as in Python:\n</p>", "_____no_output_____" ] ], [ [ "s[3]", "_____no_output_____" ], [ "s[1:3]", "_____no_output_____" ], [ "s[1:]", "_____no_output_____" ] ], [ [ "<p>\n A nice feature is Boolean indexing, where you extract values using a list of Booleans (not square brackets \n twice) and it returns the values that correspond to the Trues in the list:\n</p>", "_____no_output_____" ] ], [ [ "s[[True, True, False, False, True]]", "_____no_output_____" ] ], [ [ "<p>\n Operators are vectorized, similar to numpy:\n</p>", "_____no_output_____" ] ], [ [ "s * 2", "_____no_output_____" ], [ "s > 0", "_____no_output_____" ] ], [ [ "<p>\n The next example is neat. It combines a vectorized operator with the idea of Boolean indexing:\n</p>", "_____no_output_____" ] ], [ [ "s[s > 0]", "_____no_output_____" ] ], [ [ "<p>\n There are various methods, as you would expect, many building out from numpy e.g.:\n</p>", "_____no_output_____" ] ], [ [ "s.sum()", "_____no_output_____" ], [ "s.mean()", "_____no_output_____" ], [ "s.unique()", "_____no_output_____" ], [ "s.value_counts()", "_____no_output_____" ] ], [ [ "<p>\n One method is astype, which can do data type conversions:\n</p>", "_____no_output_____" ] ], [ [ "s.astype(float)", "_____no_output_____" ] ], [ [ "<h1>DataFrame</h1>\n<p>\n A DataFrame is a table of data, comprising rows and columns. The rows and columns both have an index. If\n you want more dimensions (we won't), then they support hierarchical indexing.\n</p>\n<p>\n There are various ways of creating a DataFrame, e.g. supply to its constructor a dictionary of equal-sized\n lists:\n</p>", "_____no_output_____" ] ], [ [ "df = pd.DataFrame({'a' : [1, 2, 3], 'b' : [4, 5, 6], 'c' : [7, 8, 9]})\ndf", "_____no_output_____" ] ], [ [ "<p>\n The keys of the dictionary became the column index, and it assigned integers to the other index. \n</p>\n<p>\n But, instead of looking at all the possible ways of doing this, we'll be reading the data in from a CSV file.\n We will assume that the first line of the file contains headers. These become the column indexes.\n</p>", "_____no_output_____" ] ], [ [ "df = pd.read_csv('../datasets/dataset_stop_and_searchA.csv')", "_____no_output_____" ], [ "df", "_____no_output_____" ] ], [ [ "<p>\n Notice when the CSV file has an empty value (a pair of consecutive commas), then Pandas treats this as NaN,\n which is a float. \n</p>", "_____no_output_____" ], [ "<p>\n A useful method at this point is describe:\n</p>", "_____no_output_____" ] ], [ [ "df.describe(include='all')", "_____no_output_____" ] ], [ [ "<p>\n We can also get the column headers, row index, shape and dtypes (not dtype):\n</p>", "_____no_output_____" ] ], [ [ "df.columns", "_____no_output_____" ], [ "df.index", "_____no_output_____" ], [ "df.shape", "_____no_output_____" ], [ "df.dtypes", "_____no_output_____" ] ], [ [ "<p>\n You can retrieve a whole column, as a Series, using column indexing:\n</p>", "_____no_output_____" ] ], [ [ "df['Suspect-ethnicity']", "_____no_output_____" ] ], [ [ "<p>\n Now you have a Series, you might use the unique or value_counts methods that we looked at earlier.\n</p>", "_____no_output_____" ] ], [ [ "df['Suspect-ethnicity'].unique()", "_____no_output_____" ], [ "df['Suspect-ethnicity'].value_counts()", "_____no_output_____" ] ], [ [ "<p>\n If you ask for more than one column, then you must give them as a list (note the nested brackets). \n Then, the result is not a Series, but a DataFrame:\n</p>", "_____no_output_____" ] ], [ [ "df[['Suspect-ethnicity', 'Officer-ethnicity']]", "_____no_output_____" ] ], [ [ "<p> \n How do we get an individual row? The likelihood of wanting this in this module is small. \n</p>\n<p>\n If you do need to get an individual row, you cannot do indexing using square brackets, because that \n notation is for columns.\n</p>\n<p>\n The iloc and loc methods are probably what you would use. iloc retrieves by position. So df.iloc[0]\n retrieves the first row. loc, on the other hand, retrieves by label, so df.loc[0] retrieves the row\n whose label in the row index is 0. Confusing, huh? Ordinarily, they'll be the same.\n</p>", "_____no_output_____" ] ], [ [ "df.iloc[4]", "_____no_output_____" ], [ "df.loc[4]", "_____no_output_____" ] ], [ [ "<p>\n But sometimes the position and the label in the row index will not correspond. This can happen, for example,\n after shuffling the rows of the DataFrame or after deleting a row (see example later).\n</p>", "_____no_output_____" ], [ "<p>\n In any case, we're much more likely to want to select several rows (hence a DataFrame) using Boolean indexing,\n defined by a Boolean expression. We use a Boolean expression that defines a Series and then use that\n to index the DataFrame.\n</p>\n<p>\n As an example, here's a Boolean expression:\n</p>", "_____no_output_____" ] ], [ [ "df['Officer-ethnicity'] == 'Black'", "_____no_output_____" ] ], [ [ "<p>\n And here we use that Boolean expression to extract rows:\n</p>", "_____no_output_____" ] ], [ [ "df[df['Officer-ethnicity'] == 'Black']", "_____no_output_____" ] ], [ [ "<p>\n In our Boolean expressions, we can do and, or and not (&, |, ~), but note that this often requires\n extra parentheses, e.g.\n</p>", "_____no_output_____" ] ], [ [ "df[(df['Officer-ethnicity'] == 'Black') & (df['Object-of-search'] == 'Stolen goods')]", "_____no_output_____" ] ], [ [ "<p>\n We can use this idea to delete rows.\n</p>\n<p>\n We use Boolean indexing as above to select the rows we want to keep. Then we assign that dataframe back\n to the original variable.\n</p>\n<p>\n For example, let's delete all male suspects, in other words, keep all female suspects:\n</p>", "_____no_output_____" ] ], [ [ "df = df[df['Gender'] == 'Female'].copy()", "_____no_output_____" ], [ "df", "_____no_output_____" ] ], [ [ "<p>\n This example also illustrates the point from earlier about the difference between position (iloc) and\n label in the row index (loc).\n</p>", "_____no_output_____" ] ], [ [ "df.iloc[0]", "_____no_output_____" ], [ "df.loc[0] # raises an exception", "_____no_output_____" ], [ "df.iloc[11] # raises an exception", "_____no_output_____" ], [ "df.loc[11]", "_____no_output_____" ] ], [ [ "<p>\n This is often a source of errors when writing Pandas. So one tip is, whenever you perform an operation\n that has the potential to change the row index, then reset the index so that it corresponds to the\n positions:\n</p>", "_____no_output_____" ] ], [ [ "df.reset_index(drop=True, inplace=True)", "_____no_output_____" ], [ "df", "_____no_output_____" ] ], [ [ "<p>\n Deleting columns can be done in the same way as we deleted rows, i.e. extract the ones you want to keep\n and then assign the result back to the original variable, e.g.:\n</p>", "_____no_output_____" ] ], [ [ "df = df[['Gender', 'Age', 'Object-of-search', 'Outcome']].copy()", "_____no_output_____" ], [ "df", "_____no_output_____" ] ], [ [ "<p>\n But deletion can also be done using the drop method. If axis=0 (default), you're deleting rows.\n If axis=1, you're deleting columns (and this time you name the column you want to delete), e.g.:\n</p>", "_____no_output_____" ] ], [ [ "df.drop(\"Age\", axis=1, inplace=True)", "_____no_output_____" ], [ "df", "_____no_output_____" ] ], [ [ "<p>\n One handy variant is dropna with axis=0, which can be used to delete rows that contains NaN. We may see\n an example of this and a few other methods in our lectures and futuer labs. But, for now, we have enough\n for you to tackle something interesting.\n</p>", "_____no_output_____" ], [ "<h1>Exercise</h1>\n<p>\n I've a larger file that contains all stop-and-searches by the Metropolitan Police for about a year \n (mid-2018 to mid-2019).\n</p>\n<p>\n Read it in:\n</p>", "_____no_output_____" ] ], [ [ "df = pd.read_csv('../datasets/dataset_stop_and_searchB.csv')", "_____no_output_____" ], [ "df.shape", "_____no_output_____" ] ], [ [ "<p>\n Using this larger dataset, your job is to answer this question: Are the Metropolitan Police racist?\n</p>", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ] ]

cb30cae70c18958834d07e0568adbe9aabb18a45

4,631

ipynb

Jupyter Notebook

Instagram/Instagram_Post_image_and_caption.ipynb

srini047/awesome-notebooks

2a5b771b37b62090de5311d61dce8495fae7b59f

[ "BSD-3-Clause" ]

null

Instagram/Instagram_Post_image_and_caption.ipynb

srini047/awesome-notebooks

2a5b771b37b62090de5311d61dce8495fae7b59f

[ "BSD-3-Clause" ]

null

Instagram/Instagram_Post_image_and_caption.ipynb

srini047/awesome-notebooks

2a5b771b37b62090de5311d61dce8495fae7b59f

[ "BSD-3-Clause" ]

null

20.311404

296

0.513496

[ [ [ "<img width=\"10%\" alt=\"Naas\" src=\"https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160\"/>", "_____no_output_____" ], [ "# Instagram - Post image and caption\n<a href=\"https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/Instagram/Instagram_Post_image_and_caption.ipynb\" target=\"_parent\"><img src=\"https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg\"/></a>", "_____no_output_____" ], [ "**Tags:** #instagram #snippet", "_____no_output_____" ], [ "**Author:** [Jeremy Ravenel](https://www.linkedin.com/in/ACoAAAJHE7sB5OxuKHuzguZ9L6lfDHqw--cdnJg/)", "_____no_output_____" ], [ "## Input", "_____no_output_____" ], [ "### Import libraries", "_____no_output_____" ] ], [ [ "try:\n from instabot import Bot\nexcept:\n pip install instabot --user\n from instabot import Bot\nimport naas", "_____no_output_____" ] ], [ [ "### Setup your Instagram", "_____no_output_____" ] ], [ [ "# Credentials\nusername = \"USERNAME\"\npassword = \"PASSWORD\"\n\n# Instragram outputs\nimage_path = \"demo.jpg\"\ncaption = \"Naas is doing this.\"", "_____no_output_____" ] ], [ [ "## Model", "_____no_output_____" ], [ "### Connect to your instagram account", "_____no_output_____" ] ], [ [ "bot = Bot()\nbot.login(username=username, \n password=password) ", "_____no_output_____" ] ], [ [ "## Output", "_____no_output_____" ], [ "### Upload photo", "_____no_output_____" ] ], [ [ "bot.upload_photo(image_path,\n caption=caption) ", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ] ]

cb30cb9bb84033804a157cbb3687161218228203

7,602

ipynb

Jupyter Notebook

dl-waterloo/lec03.ipynb

JasonWayne/course-notes

feff7a0636e7f8f2353c1dea24fe25296a8b33c3

[ "MIT" ]

null

dl-waterloo/lec03.ipynb

JasonWayne/course-notes

feff7a0636e7f8f2353c1dea24fe25296a8b33c3

[ "MIT" ]

null

dl-waterloo/lec03.ipynb

JasonWayne/course-notes

feff7a0636e7f8f2353c1dea24fe25296a8b33c3

[ "MIT" ]

null

18.586797

206

0.50934

[ [ [ "##### 1", "_____no_output_____" ], [ "![1](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0001.jpg)", "_____no_output_____" ], [ "##### 2", "_____no_output_____" ], [ "![2](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0002.jpg)", "_____no_output_____" ], [ "##### 3", "_____no_output_____" ], [ "![3](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0003.jpg)", "_____no_output_____" ], [ "##### 4", "_____no_output_____" ], [ "![4](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0004.jpg)", "_____no_output_____" ], [ "and no similarity information included", "_____no_output_____" ], [ "##### 5", "_____no_output_____" ], [ "![5](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0005.jpg)", "_____no_output_____" ], [ "纵向d表示单词数，横向n表示文档数，即$ d = vocab size $\n\n左边$U$矩阵的每一行就是每一个单词的K维表示，右边$V^T$矩阵每一列就是每一篇文档的$K$维表示\n\n这就是Latent Sementic Index(Analysis)的做法\n这与PCA的区别就是，这里没有减均值的操作（Centeralize)。\n\n为什么不减均值？因为这里矩阵中的每一个数，其实是表示某个词在某篇文章中的出现频次，减去均值，那必然有很多词被表示成了负数，这是没有意义的。\n\n教授举了图像的例子。对于图像矩阵做SVD，同样，行是像素点，列是某一个图片，那么，在SVD分解后，U矩阵的每一列单独拿出来，仍然可以看成是某一种图像，如果做了Centeralization，那就什么都不是了。那文本做了SVD之后，对于U的每一列，就相当于是一个Topic，上面的数字表示每一个词在当前这个topic的出现频率；对于V的每一列，则表示每一篇文章，分别由哪几个主题，以什么比例组成。\n\n教授补充：对于一个非负矩阵，SVD分解的结果会出现负值。所以现在有了Non negative matrix factorization的方法。\n\n这里还有点乱。\n\n只有Non negatie matrix factorization之后的结果，才可以看成主题模型那样的理解，因为没有负值；而PCA和SVD都会出现负值，所以不能那样理解。", "_____no_output_____" ], [ "##### 6", "_____no_output_____" ], [ "![6](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0006.jpg)", "_____no_output_____" ], [ "##### 7", "_____no_output_____" ], [ "![7](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0007.jpg)", "_____no_output_____" ], [ "out of sample 就是没出现过的，不在训练集中的", "_____no_output_____" ], [ "##### 8", "_____no_output_____" ], [ "![8](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0008.jpg)", "_____no_output_____" ], [ "##### 9", "_____no_output_____" ], [ "![9](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0009.jpg)", "_____no_output_____" ], [ "##### 10", "_____no_output_____" ], [ "![10](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0010.jpg)", "_____no_output_____" ], [ "##### 11", "_____no_output_____" ], [ "![11](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0011.jpg)", "_____no_output_____" ], [ "Glove directly used, word2vec indirectly used this\n\n这里的每一列(或者行，因为是对称的）表示一个词的window", "_____no_output_____" ], [ "##### 12", "_____no_output_____" ], [ "![12](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0012.jpg)", "_____no_output_____" ], [ "##### 13", "_____no_output_____" ], [ "![13](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0013.jpg)", "_____no_output_____" ], [ "##### 14", "_____no_output_____" ], [ "![14](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0014.jpg)", "_____no_output_____" ], [ "这里的length of window表达有歧义，其实是在说input layer只有一个值是1，其它都是零。正常理解的length ＝ 1，是会有两个值为1.\n", "_____no_output_____" ], [ "##### 15", "_____no_output_____" ], [ "![15](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0015.jpg)", "_____no_output_____" ], [ "##### 16", "_____no_output_____" ], [ "![16](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0016.jpg)", "_____no_output_____" ], [ "##### 17", "_____no_output_____" ], [ "![17](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0017.jpg)", "_____no_output_____" ], [ "##### 18", "_____no_output_____" ], [ "![18](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0018.jpg)", "_____no_output_____" ], [ "##### 19", "_____no_output_____" ], [ "![19](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0019.jpg)", "_____no_output_____" ], [ "##### 20", "_____no_output_____" ], [ "![20](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0020.jpg)", "_____no_output_____" ], [ "##### 21", "_____no_output_____" ], [ "![21](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0021.jpg)", "_____no_output_____" ], [ "##### 22", "_____no_output_____" ], [ "![22](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0022.jpg)", "_____no_output_____" ], [ "##### 23", "_____no_output_____" ], [ "![23](http://7xqhfk.com1.z0.glb.clouddn.com/dl-waterloo/lec03/0023.jpg)", "_____no_output_____" ] ] ]

[ "markdown" ]

[ [ "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown", "markdown" ] ]

cb30dde3bd0616a5e1be324f7531a69799b7aa1f

188,793

ipynb

Jupyter Notebook

Traffic_Light_Classifier.ipynb

rajathkmanjunath/Traffic-Light-Classifier

45cd1c4deb6cbd0bbb6d58929915d52f75f875a3

[ "MIT" ]

null

Traffic_Light_Classifier.ipynb

rajathkmanjunath/Traffic-Light-Classifier

45cd1c4deb6cbd0bbb6d58929915d52f75f875a3

[ "MIT" ]

null

Traffic_Light_Classifier.ipynb

rajathkmanjunath/Traffic-Light-Classifier

45cd1c4deb6cbd0bbb6d58929915d52f75f875a3

[ "MIT" ]

null

178.78125

29,532

0.892189

[ [ [ "# Traffic Light Classifier\n---\n\nIn this project, you’ll use your knowledge of computer vision techniques to build a classifier for images of traffic lights! You'll be given a dataset of traffic light images in which one of three lights is illuminated: red, yellow, or green.\n\nIn this notebook, you'll pre-process these images, extract features that will help us distinguish the different types of images, and use those features to classify the traffic light images into three classes: red, yellow, or green. The tasks will be broken down into a few sections:\n\n1. **Loading and visualizing the data**. \n The first step in any classification task is to be familiar with your data; you'll need to load in the images of traffic lights and visualize them!\n\n2. **Pre-processing**. \n The input images and output labels need to be standardized. This way, you can analyze all the input images using the same classification pipeline, and you know what output to expect when you eventually classify a *new* image.\n \n3. **Feature extraction**. \n Next, you'll extract some features from each image that will help distinguish and eventually classify these images.\n \n4. **Classification and visualizing error**. \n Finally, you'll write one function that uses your features to classify *any* traffic light image. This function will take in an image and output a label. You'll also be given code to determine the accuracy of your classification model. \n \n5. **Evaluate your model**.\n To pass this project, your classifier must be >90% accurate and never classify any red lights as green; it's likely that you'll need to improve the accuracy of your classifier by changing existing features or adding new features. I'd also encourage you to try to get as close to 100% accuracy as possible!\n \nHere are some sample images from the dataset (from left to right: red, green, and yellow traffic lights):\n<img src=\"images/all_lights.png\" width=\"50%\" height=\"50%\">\n", "_____no_output_____" ], [ "---\n### *Here's what you need to know to complete the project:*\n\nSome template code has already been provided for you, but you'll need to implement additional code steps to successfully complete this project. Any code that is required to pass this project is marked with **'(IMPLEMENTATION)'** in the header. There are also a couple of questions about your thoughts as you work through this project, which are marked with **'(QUESTION)'** in the header. Make sure to answer all questions and to check your work against the [project rubric](https://review.udacity.com/#!/rubrics/1213/view) to make sure you complete the necessary classification steps!\n\nYour project submission will be evaluated based on the code implementations you provide, and on two main classification criteria.\nYour complete traffic light classifier should have:\n1. **Greater than 90% accuracy**\n2. ***Never* classify red lights as green**\n", "_____no_output_____" ], [ "# 1. Loading and Visualizing the Traffic Light Dataset\n\nThis traffic light dataset consists of 1484 number of color images in 3 categories - red, yellow, and green. As with most human-sourced data, the data is not evenly distributed among the types. There are:\n* 904 red traffic light images\n* 536 green traffic light images\n* 44 yellow traffic light images\n\n*Note: All images come from this [MIT self-driving car course](https://selfdrivingcars.mit.edu/) and are licensed under a [Creative Commons Attribution-ShareAlike 4.0 International License](https://creativecommons.org/licenses/by-sa/4.0/).*", "_____no_output_____" ], [ "### Import resources\n\nBefore you get started on the project code, import the libraries and resources that you'll need.", "_____no_output_____" ] ], [ [ "import cv2 # computer vision library\nimport helpers # helper functions\n\nimport random\nimport numpy as np\nimport matplotlib.pyplot as plt\nimport matplotlib.image as mpimg # for loading in images\n\n%matplotlib inline", "_____no_output_____" ] ], [ [ "## Training and Testing Data\n\nAll 1484 of the traffic light images are separated into training and testing datasets. \n\n* 80% of these images are training images, for you to use as you create a classifier.\n* 20% are test images, which will be used to test the accuracy of your classifier.\n* All images are pictures of 3-light traffic lights with one light illuminated.\n\n## Define the image directories\n\nFirst, we set some variables to keep track of some where our images are stored:\n\n IMAGE_DIR_TRAINING: the directory where our training image data is stored\n IMAGE_DIR_TEST: the directory where our test image data is stored", "_____no_output_____" ] ], [ [ "# Image data directories\nIMAGE_DIR_TRAINING = \"traffic_light_images/training/\"\nIMAGE_DIR_TEST = \"traffic_light_images/test/\"", "_____no_output_____" ] ], [ [ "## Load the datasets\n\nThese first few lines of code will load the training traffic light images and store all of them in a variable, `IMAGE_LIST`. This list contains the images and their associated label (\"red\", \"yellow\", \"green\"). \n\nYou are encouraged to take a look at the `load_dataset` function in the helpers.py file. This will give you a good idea about how lots of image files can be read in from a directory using the [glob library](https://pymotw.com/2/glob/). The `load_dataset` function takes in the name of an image directory and returns a list of images and their associated labels. \n\nFor example, the first image-label pair in `IMAGE_LIST` can be accessed by index: \n``` IMAGE_LIST[0][:]```.\n", "_____no_output_____" ] ], [ [ "# Using the load_dataset function in helpers.py\n# Load training data\nIMAGE_LIST = helpers.load_dataset(IMAGE_DIR_TRAINING)\n", "_____no_output_____" ] ], [ [ "## Visualize the Data\n\nThe first steps in analyzing any dataset are to 1. load the data and 2. look at the data. Seeing what it looks like will give you an idea of what to look for in the images, what kind of noise or inconsistencies you have to deal with, and so on. This will help you understand the image dataset, and **understanding a dataset is part of making predictions about the data**.", "_____no_output_____" ], [ "---\n### Visualize the input images\n\nVisualize and explore the image data! Write code to display an image in `IMAGE_LIST`:\n* Display the image\n* Print out the shape of the image \n* Print out its corresponding label\n\nSee if you can display at least one of each type of traffic light image – red, green, and yellow — and look at their similarities and differences.", "_____no_output_____" ] ], [ [ "plt.imshow(IMAGE_LIST[750][0])\nplt.show()\n\n## TODO: Write code to display an image in IMAGE_LIST (try finding a yellow traffic light!)\nprint(IMAGE_LIST[750][0].shape)\nprint(IMAGE_LIST[750][1])\n## TODO: Print out 1. The shape of the image and 2. The image's label\n\n# The first image in IMAGE_LIST is displayed below (without information about shape or label)\nselected_image = IMAGE_LIST[0][0]\nplt.imshow(selected_image)\nplt.show()", "_____no_output_____" ] ], [ [ "# 2. Pre-process the Data\n\nAfter loading in each image, you have to standardize the input and output!\n\n### Input\n\nThis means that every input image should be in the same format, of the same size, and so on. We'll be creating features by performing the same analysis on every picture, and for a classification task like this, it's important that **similar images create similar features**! \n\n### Output\n\nWe also need the output to be a label that is easy to read and easy to compare with other labels. It is good practice to convert categorical data like \"red\" and \"green\" to numerical data.\n\nA very common classification output is a 1D list that is the length of the number of classes - three in the case of red, yellow, and green lights - with the values 0 or 1 indicating which class a certain image is. For example, since we have three classes (red, yellow, and green), we can make a list with the order: [red value, yellow value, green value]. In general, order does not matter, we choose the order [red value, yellow value, green value] in this case to reflect the position of each light in descending vertical order.\n\nA red light should have the label: [1, 0, 0]. Yellow should be: [0, 1, 0]. Green should be: [0, 0, 1]. These labels are called **one-hot encoded labels**.\n\n*(Note: one-hot encoding will be especially important when you work with [machine learning algorithms](https://machinelearningmastery.com/how-to-one-hot-encode-sequence-data-in-python/)).*\n\n<img src=\"images/processing_steps.png\" width=\"80%\" height=\"80%\">\n", "_____no_output_____" ], [ "---\n<a id='task2'></a>\n### (IMPLEMENTATION): Standardize the input images\n\n* Resize each image to the desired input size: 32x32px.\n* (Optional) You may choose to crop, shift, or rotate the images in this step as well.\n\nIt's very common to have square input sizes that can be rotated (and remain the same size), and analyzed in smaller, square patches. It's also important to make all your images the same size so that they can be sent through the same pipeline of classification steps!", "_____no_output_____" ] ], [ [ "# This function should take in an RGB image and return a new, standardized version\ndef standardize_input(image):\n standard_im = cv2.resize(image, (32,32))\n return standard_im\nplt.imshow(IMAGE_LIST[0][0])\nplt.show()\nplt.imshow(standardize_input(IMAGE_LIST[0][0]))", "_____no_output_____" ] ], [ [ "## Standardize the output\n\nWith each loaded image, we also specify the expected output. For this, we use **one-hot encoding**.\n\n* One-hot encode the labels. To do this, create an array of zeros representing each class of traffic light (red, yellow, green), and set the index of the expected class number to 1. \n\nSince we have three classes (red, yellow, and green), we have imposed an order of: [red value, yellow value, green value]. To one-hot encode, say, a yellow light, we would first initialize an array to [0, 0, 0] and change the middle value (the yellow value) to 1: [0, 1, 0].\n", "_____no_output_____" ], [ "---\n<a id='task3'></a>\n### (IMPLEMENTATION): Implement one-hot encoding", "_____no_output_____" ] ], [ [ "def one_hot_encode(label):\n \n ## TODO: Create a one-hot encoded label that works for all classes of traffic lights\n one_hot_encoded = [0,0,0] \n if(label == 'red'):\n one_hot_encoded[0] = 1\n \n elif(label == 'yellow'):\n one_hot_encoded[1] = 1\n \n elif(label == 'green'):\n one_hot_encoded[2] = 1\n \n return one_hot_encoded\n", "_____no_output_____" ] ], [ [ "### Testing as you Code\n\nAfter programming a function like this, it's a good idea to test it, and see if it produces the expected output. **In general, it's good practice to test code in small, functional pieces, after you write it**. This way, you can make sure that your code is correct as you continue to build a classifier, and you can identify any errors early on so that they don't compound.\n\nAll test code can be found in the file `test_functions.py`. You are encouraged to look through that code and add your own testing code if you find it useful!\n\nOne test function you'll find is: `test_one_hot(self, one_hot_function)` which takes in one argument, a one_hot_encode function, and tests its functionality. If your one_hot_label code does not work as expected, this test will print ot an error message that will tell you a bit about why your code failed. Once your code works, this should print out TEST PASSED.", "_____no_output_____" ] ], [ [ "# Importing the tests\nimport test_functions\ntests = test_functions.Tests()\n\n# Test for one_hot_encode function\ntests.test_one_hot(one_hot_encode)\n", "_____no_output_____" ] ], [ [ "## Construct a `STANDARDIZED_LIST` of input images and output labels.\n\nThis function takes in a list of image-label pairs and outputs a **standardized** list of resized images and one-hot encoded labels.\n\nThis uses the functions you defined above to standardize the input and output, so those functions must be complete for this standardization to work!\n", "_____no_output_____" ] ], [ [ "def standardize(image_list):\n \n # Empty image data array\n standard_list = []\n\n # Iterate through all the image-label pairs\n for item in image_list:\n image = item[0]\n label = item[1]\n\n # Standardize the image\n standardized_im = standardize_input(image)\n\n # One-hot encode the label\n one_hot_label = one_hot_encode(label) \n\n # Append the image, and it's one hot encoded label to the full, processed list of image data \n standard_list.append((standardized_im, one_hot_label))\n \n return standard_list\n\n# Standardize all training images\nSTANDARDIZED_LIST = standardize(IMAGE_LIST)", "_____no_output_____" ] ], [ [ "## Visualize the standardized data\n\nDisplay a standardized image from STANDARDIZED_LIST and compare it with a non-standardized image from IMAGE_LIST. Note that their sizes and appearance are different!", "_____no_output_____" ] ], [ [ "## TODO: Display a standardized image and its label\nplt.imshow(IMAGE_LIST[0][0])\nplt.show()\nimage = standardize(IMAGE_LIST)\nplt.imshow(image[0][0])\nplt.show()", "_____no_output_____" ] ], [ [ "# 3. Feature Extraction\n\nYou'll be using what you now about color spaces, shape analysis, and feature construction to create features that help distinguish and classify the three types of traffic light images.\n\nYou'll be tasked with creating **one feature** at a minimum (with the option to create more). The required feature is **a brightness feature using HSV color space**:\n\n1. A brightness feature.\n - Using HSV color space, create a feature that helps you identify the 3 different classes of traffic light.\n - You'll be asked some questions about what methods you tried to locate this traffic light, so, as you progress through this notebook, always be thinking about your approach: what works and what doesn't?\n\n2. (Optional): Create more features! \n\nAny more features that you create are up to you and should improve the accuracy of your traffic light classification algorithm! One thing to note is that, to pass this project you must **never classify a red light as a green light** because this creates a serious safety risk for a self-driving car. To avoid this misclassification, you might consider adding another feature that specifically distinguishes between red and green lights.\n\nThese features will be combined near the end of his notebook to form a complete classification algorithm.", "_____no_output_____" ], [ "## Creating a brightness feature \n\nThere are a number of ways to create a brightness feature that will help you characterize images of traffic lights, and it will be up to you to decide on the best procedure to complete this step. You should visualize and test your code as you go.\n\nPictured below is a sample pipeline for creating a brightness feature (from left to right: standardized image, HSV color-masked image, cropped image, brightness feature):\n\n<img src=\"images/feature_ext_steps.png\" width=\"70%\" height=\"70%\">\n", "_____no_output_____" ], [ "## RGB to HSV conversion\n\nBelow, a test image is converted from RGB to HSV colorspace and each component is displayed in an image.", "_____no_output_____" ] ], [ [ "# Convert and image to HSV colorspace\n# Visualize the individual color channels\n\nimage_num = 0\ntest_im = STANDARDIZED_LIST[image_num][0]\ntest_label = STANDARDIZED_LIST[image_num][1]\n\n# Convert to HSV\nhsv = cv2.cvtColor(test_im, cv2.COLOR_RGB2HSV)\n\n# Print image label\nprint('Label [red, yellow, green]: ' + str(test_label))\n\n# HSV channels\nh = hsv[:,:,0]\ns = hsv[:,:,1]\nv = hsv[:,:,2]\n\n# Plot the original image and the three channels\nf, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(20,10))\nax1.set_title('Standardized image')\nax1.imshow(test_im)\nax2.set_title('H channel')\nax2.imshow(h, cmap='gray')\nax3.set_title('S channel')\nax3.imshow(s, cmap='gray')\nax4.set_title('V channel')\nax4.imshow(v, cmap='gray')\n", "Label [red, yellow, green]: [1, 0, 0]\n" ] ], [ [ "---\n<a id='task7'></a>\n### (IMPLEMENTATION): Create a brightness feature that uses HSV color space\n\nWrite a function that takes in an RGB image and returns a 1D feature vector and/or single value that will help classify an image of a traffic light. The only requirement is that this function should apply an HSV colorspace transformation, the rest is up to you. \n\nFrom this feature, you should be able to estimate an image's label and classify it as either a red, green, or yellow traffic light. You may also define helper functions if they simplify your code.", "_____no_output_____" ] ], [ [ "## This feature should use HSV colorspace values\ndef create_feature(rgb_image):\n hsv = cv2.cvtColor(rgb_image, cv2.COLOR_RGB2HSV)\n \n# apply red mask on the upper, yellow mask on the middle and the green mask on the lower\n\n low_s = int(np.mean(hsv[:,:,1]))\n low_v = int(np.mean(hsv[:,:,2]))\n high_v = 255\n high_h = 255\n red_lower = np.array([150,low_s,low_v])\n red_upper = np.array([180, high_h, high_v])\n\n \n green_lower = np.array([75, low_s, low_v])\n green_upper = np.array([100, high_h, high_v])\n \n yellow_lower = np.array([15, low_s, low_v])\n yellow_upper = np.array([70, high_h,high_v])\n \n red_mask = cv2.inRange(hsv, red_lower, red_upper)\n\n red_count = np.count_nonzero(red_mask)\n \n yellow_mask = cv2.inRange(hsv, yellow_lower, yellow_upper)\n yellow_count = np.count_nonzero(yellow_mask)\n \n green_mask = cv2.inRange(hsv, green_lower, green_upper)\n green_count = np.count_nonzero(green_mask)\n\n return [red_count, yellow_count, green_count]", "_____no_output_____" ] ], [ [ "## (QUESTION 1): How do the features you made help you distinguish between the 3 classes of traffic light images?", "_____no_output_____" ], [ "**Answer:**\n* converted the image to hsv color space to extract the features.\n* The hue component of the image indicates which color and as the traffic signal pixels have higher value component. \n* After tweaking with the thresholds for the mask, set the one resulting in maximum accuracy.\n* the mask is created and the number of non zero pixels in the mask is counted.\n* the mask (Red, green or Yellow) containing the maximum number of non zero components is sent to the one hot encoder.\n* The one hot encoder returns the encoded value of the color.", "_____no_output_____" ], [ "# 4. Classification and Visualizing Error\n\nUsing all of your features, write a function that takes in an RGB image and, using your extracted features, outputs whether a light is red, green or yellow as a one-hot encoded label. This classification function should be able to classify any image of a traffic light!\n\nYou are encouraged to write any helper functions or visualization code that you may need, but for testing the accuracy, make sure that this `estimate_label` function returns a one-hot encoded label.", "_____no_output_____" ], [ "---\n<a id='task8'></a>\n### (IMPLEMENTATION): Build a complete classifier ", "_____no_output_____" ] ], [ [ "# This function should take in RGB image input\n# Analyze that image using your feature creation code and output a one-hot encoded label\ndef estimate_label(rgb_image):\n standardized_image = standardize_input(rgb_image) \n rgb_count = create_feature(standardized_image)\n predicted_label = []\n if(rgb_count[2] > rgb_count[1]) and (rgb_count[2] > rgb_count[0]):\n predicted_label = one_hot_encode('green')\n \n elif(rgb_count[1] > rgb_count[0]) and (rgb_count[1] > rgb_count[2]):\n predicted_label = one_hot_encode('yellow')\n \n else:\n predicted_label = one_hot_encode('red')\n \n return predicted_label", "_____no_output_____" ] ], [ [ "## Testing the classifier\n\nHere is where we test your classification algorithm using our test set of data that we set aside at the beginning of the notebook! This project will be complete once you've pogrammed a \"good\" classifier.\n\nA \"good\" classifier in this case should meet the following criteria (and once it does, feel free to submit your project):\n1. Get above 90% classification accuracy.\n2. Never classify a red light as a green light. \n\n### Test dataset\n\nBelow, we load in the test dataset, standardize it using the `standardize` function you defined above, and then **shuffle** it; this ensures that order will not play a role in testing accuracy.\n", "_____no_output_____" ] ], [ [ "# Using the load_dataset function in helpers.py\n# Load test data\nTEST_IMAGE_LIST = helpers.load_dataset(IMAGE_DIR_TEST)\n\n# Standardize the test data\nSTANDARDIZED_TEST_LIST = standardize(TEST_IMAGE_LIST)\n\n# Shuffle the standardized test data\nrandom.shuffle(STANDARDIZED_TEST_LIST)", "_____no_output_____" ] ], [ [ "## Determine the Accuracy\n\nCompare the output of your classification algorithm (a.k.a. your \"model\") with the true labels and determine the accuracy.\n\nThis code stores all the misclassified images, their predicted labels, and their true labels, in a list called `MISCLASSIFIED`. This code is used for testing and *should not be changed*.", "_____no_output_____" ] ], [ [ "65# Constructs a list of misclassified images given a list of test images and their labels\n# This will throw an AssertionError if labels are not standardized (one-hot encoded)\n\ndef get_misclassified_images(test_images):\n # Track misclassified images by placing them into a list\n misclassified_images_labels = []\n\n # Iterate through all the test images\n # Classify each image and compare to the true label\n for image in test_images:\n\n # Get true data\n im = image[0]\n true_label = image[1]\n assert(len(true_label) == 3), \"The true_label is not the expected length (3).\"\n\n # Get predicted label from your classifier\n predicted_label = estimate_label(im)\n assert(len(predicted_label) == 3), \"The predicted_label is not the expected length (3).\"\n\n # Compare true and predicted labels \n if(predicted_label != true_label):\n # If these labels are not equal, the image has been misclassified\n misclassified_images_labels.append((im, predicted_label, true_label))\n \n # Return the list of misclassified [image, predicted_label, true_label] values\n return misclassified_images_labels\n\n\n# Find all misclassified images in a given test set\nMISCLASSIFIED = get_misclassified_images(STANDARDIZED_TEST_LIST)\n\n# Accuracy calculations\ntotal = len(STANDARDIZED_TEST_LIST)\nnum_correct = total - len(MISCLASSIFIED)\naccuracy = num_correct/total\n\nprint('Accuracy: ' + str(accuracy))\nprint(\"Number of misclassified images = \" + str(len(MISCLASSIFIED)) +' out of '+ str(total))\n", "Accuracy: 0.9764309764309764\nNumber of misclassified images = 7 out of 297\n" ] ], [ [ "---\n<a id='task9'></a>\n### Visualize the misclassified images\n\nVisualize some of the images you classified wrong (in the `MISCLASSIFIED` list) and note any qualities that make them difficult to classify. This will help you identify any weaknesses in your classification algorithm.", "_____no_output_____" ] ], [ [ "# Visualize misclassified example(s)\n\nfor i in MISCLASSIFIED:\n plt.imshow(i[0])\n plt.show()\n print(i[1], i[2])", "_____no_output_____" ] ], [ [ "---\n<a id='question2'></a>\n## (Question 2): After visualizing these misclassifications, what weaknesses do you think your classification algorithm has? Please note at least two.", "_____no_output_____" ], [ "**Answer:** \n* The considering the filter on the whole image results in considering the background component. Some images have dominant backgrounds hence resulting in misclassification.\n* Some images have arrow signal which result in less number of pixels. Hence with a very small background, there are chances of misclassification.", "_____no_output_____" ], [ "## Test if you classify any red lights as green\n\n**To pass this project, you must not classify any red lights as green!** Classifying red lights as green would cause a car to drive through a red traffic light, so this red-as-green error is very dangerous in the real world. \n\nThe code below lets you test to see if you've misclassified any red lights as green in the test set. **This test assumes that `MISCLASSIFIED` is a list of tuples with the order: [misclassified_image, predicted_label, true_label].**\n\nNote: this is not an all encompassing test, but its a good indicator that, if you pass, you are on the right track! This iterates through your list of misclassified examples and checks to see if any red traffic lights have been mistakenly labelled [0, 1, 0] (green).", "_____no_output_____" ] ], [ [ "# Importing the tests\nimport test_functions\ntests = test_functions.Tests()\n\nif(len(MISCLASSIFIED) > 0):\n # Test code for one_hot_encode function\n tests.test_red_as_green(MISCLASSIFIED)\nelse:\n print(\"MISCLASSIFIED may not have been populated with images.\")\n", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown", "markdown" ], [ "code" ] ]

cb30e18fdfdb4343df1624761bb987944d2bd428

18,505

ipynb

Jupyter Notebook

tutorials/tutorial01_sumo.ipynb

leehoon7/flow

5b52d8ad766ef1f34628621dcb413f099e6d34d2

[ "MIT" ]

71

2017-10-17T06:14:07.000Z

2022-03-04T12:26:37.000Z

tutorials/tutorial01_sumo.ipynb

tungngovn/flow

92b16feee3ee62cc176aa047dbb89d3b164b972a

[ "MIT" ]

9

2017-10-13T02:45:35.000Z

2018-08-04T18:03:27.000Z

tutorials/tutorial01_sumo.ipynb

leehoon7/flow

5b52d8ad766ef1f34628621dcb413f099e6d34d2

[ "MIT" ]

17

2018-01-27T06:20:57.000Z

2021-07-31T02:26:04.000Z

39.881466

653

0.661173

[ [ [ "# Tutorial 01: Running Sumo Simulations\n\nThis tutorial walks through the process of running non-RL traffic simulations in Flow. Simulations of this form act as non-autonomous baselines and depict the behavior of human dynamics on a network. Similar simulations may also be used to evaluate the performance of hand-designed controllers on a network. This tutorial focuses primarily on the former use case, while an example of the latter may be found in `exercise07_controllers.ipynb`.\n\nIn this exercise, we simulate a initially perturbed single lane ring road. We witness in simulation that as time advances the initially perturbations do not dissipate, but instead propagates and expands until vehicles are forced to periodically stop and accelerate. For more information on this behavior, we refer the reader to the following article [1].\n\n## 1. Components of a Simulation\nAll simulations, both in the presence and absence of RL, require two components: a *scenario*, and an *environment*. Scenarios describe the features of the transportation network used in simulation. This includes the positions and properties of nodes and edges constituting the lanes and junctions, as well as properties of the vehicles, traffic lights, inflows, etc. in the network. Environments, on the other hand, initialize, reset, and advance simulations, and act the primary interface between the reinforcement learning algorithm and the scenario. Moreover, custom environments may be used to modify the dynamical features of an scenario.\n\n## 2. Setting up a Scenario\nFlow contains a plethora of pre-designed scenarios used to replicate highways, intersections, and merges in both closed and open settings. All these scenarios are located in flow/scenarios. In order to recreate a ring road network, we begin by importing the scenario `LoopScenario`.", "_____no_output_____" ] ], [ [ "from flow.scenarios.loop import LoopScenario", "_____no_output_____" ] ], [ [ "This scenario, as well as all other scenarios in Flow, is parametrized by the following arguments: \n* name\n* vehicles\n* net_params\n* initial_config\n* traffic_lights\n\nThese parameters allow a single scenario to be recycled for a multitude of different network settings. For example, `LoopScenario` may be used to create ring roads of variable length with a variable number of lanes and vehicles.\n\n### 2.1 Name\nThe `name` argument is a string variable depicting the name of the scenario. This has no effect on the type of network created.", "_____no_output_____" ] ], [ [ "name = \"ring_example\"", "_____no_output_____" ] ], [ [ "### 2.2 VehicleParams\nThe `VehicleParams` class stores state information on all vehicles in the network. This class is used to identify the dynamical behavior of a vehicle and whether it is controlled by a reinforcement learning agent. Morover, information pertaining to the observations and reward function can be collected from various get methods within this class.\n\nThe initial configuration of this class describes the number of vehicles in the network at the start of every simulation, as well as the properties of these vehicles. We begin by creating an empty `VehicleParams` object.", "_____no_output_____" ] ], [ [ "from flow.core.params import VehicleParams\n\nvehicles = VehicleParams()", "_____no_output_____" ] ], [ [ "Once this object is created, vehicles may be introduced using the `add` method. This method specifies the types and quantities of vehicles at the start of a simulation rollout. For a description of the various arguements associated with the `add` method, we refer the reader to the following documentation ([VehicleParams.add](https://flow.readthedocs.io/en/latest/flow.core.html?highlight=vehicleparam#flow.core.params.VehicleParams)).\n\nWhen adding vehicles, their dynamical behaviors may be specified either by the simulator (default), or by user-generated models. For longitudinal (acceleration) dynamics, several prominent car-following models are implemented in Flow. For this example, the acceleration behavior of all vehicles will be defined by the Intelligent Driver Model (IDM) [2].", "_____no_output_____" ] ], [ [ "from flow.controllers.car_following_models import IDMController", "_____no_output_____" ] ], [ [ "Another controller we define is for the vehicle's routing behavior. For closed network where the route for any vehicle is repeated, the `ContinuousRouter` controller is used to perpetually reroute all vehicles to the initial set route.", "_____no_output_____" ] ], [ [ "from flow.controllers.routing_controllers import ContinuousRouter", "_____no_output_____" ] ], [ [ "Finally, we add 22 vehicles of type \"human\" with the above acceleration and routing behavior into the `Vehicles` class.", "_____no_output_____" ] ], [ [ "vehicles.add(\"human\",\n acceleration_controller=(IDMController, {}),\n routing_controller=(ContinuousRouter, {}),\n num_vehicles=22)", "_____no_output_____" ] ], [ [ "### 2.3 NetParams\n\n`NetParams` are network-specific parameters used to define the shape and properties of a network. Unlike most other parameters, `NetParams` may vary drastically depending on the specific network configuration, and accordingly most of its parameters are stored in `additional_params`. In order to determine which `additional_params` variables may be needed for a specific scenario, we refer to the `ADDITIONAL_NET_PARAMS` variable located in the scenario file.", "_____no_output_____" ] ], [ [ "from flow.scenarios.loop import ADDITIONAL_NET_PARAMS\n\nprint(ADDITIONAL_NET_PARAMS)", "_____no_output_____" ] ], [ [ "Importing the `ADDITIONAL_NET_PARAMS` dict from the ring road scenario, we see that the required parameters are:\n\n* **length**: length of the ring road\n* **lanes**: number of lanes\n* **speed**: speed limit for all edges\n* **resolution**: resolution of the curves on the ring. Setting this value to 1 converts the ring to a diamond.\n\n\nAt times, other inputs may be needed from `NetParams` to recreate proper network features/behavior. These requirements can be founded in the scenario's documentation. For the ring road, no attributes are needed aside from the `additional_params` terms. Furthermore, for this exercise, we use the scenario's default parameters when creating the `NetParams` object.", "_____no_output_____" ] ], [ [ "from flow.core.params import NetParams\n\nnet_params = NetParams(additional_params=ADDITIONAL_NET_PARAMS)", "_____no_output_____" ] ], [ [ "### 2.4 InitialConfig\n\n`InitialConfig` specifies parameters that affect the positioning of vehicle in the network at the start of a simulation. These parameters can be used to limit the edges and number of lanes vehicles originally occupy, and provide a means of adding randomness to the starting positions of vehicles. In order to introduce a small initial disturbance to the system of vehicles in the network, we set the `perturbation` term in `InitialConfig` to 1m.", "_____no_output_____" ] ], [ [ "from flow.core.params import InitialConfig\n\ninitial_config = InitialConfig(spacing=\"uniform\", perturbation=1)", "_____no_output_____" ] ], [ [ "### 2.5 TrafficLightParams\n\n`TrafficLightParams` are used to describe the positions and types of traffic lights in the network. These inputs are outside the scope of this tutorial, and instead are covered in `exercise06_traffic_lights.ipynb`. For our example, we create an empty `TrafficLightParams` object, thereby ensuring that none are placed on any nodes.", "_____no_output_____" ] ], [ [ "from flow.core.params import TrafficLightParams\n\ntraffic_lights = TrafficLightParams()", "_____no_output_____" ] ], [ [ "## 3. Setting up an Environment\n\nSeveral envionrments in Flow exist to train autonomous agents of different forms (e.g. autonomous vehicles, traffic lights) to perform a variety of different tasks. These environments are often scenario or task specific; however, some can be deployed on an ambiguous set of scenarios as well. One such environment, `AccelEnv`, may be used to train a variable number of vehicles in a fully observable network with a *static* number of vehicles.", "_____no_output_____" ] ], [ [ "from flow.envs.loop.loop_accel import AccelEnv", "_____no_output_____" ] ], [ [ "Although we will not be training any autonomous agents in this exercise, the use of an environment allows us to view the cumulative reward simulation rollouts receive in the absence of autonomy.\n\nEnvrionments in Flow are parametrized by three components:\n* `EnvParams`\n* `SumoParams`\n* `Scenario`\n\n### 3.1 SumoParams\n`SumoParams` specifies simulation-specific variables. These variables include the length a simulation step (in seconds) and whether to render the GUI when running the experiment. For this example, we consider a simulation step length of 0.1s and activate the GUI.\n\nAnother useful parameter is `emission_path`, which is used to specify the path where the emissions output will be generated. They contain a lot of information about the simulation, for instance the position and speed of each car at each time step. If you do not specify any emission path, the emission file will not be generated. More on this in Section 5.", "_____no_output_____" ] ], [ [ "from flow.core.params import SumoParams\n\nsumo_params = SumoParams(sim_step=0.1, render=True, emission_path='data')", "_____no_output_____" ] ], [ [ "### 3.2 EnvParams\n\n`EnvParams` specify environment and experiment-specific parameters that either affect the training process or the dynamics of various components within the scenario. Much like `NetParams`, the attributes associated with this parameter are mostly environment specific, and can be found in the environment's `ADDITIONAL_ENV_PARAMS` dictionary.", "_____no_output_____" ] ], [ [ "from flow.envs.loop.loop_accel import ADDITIONAL_ENV_PARAMS\n\nprint(ADDITIONAL_ENV_PARAMS)", "_____no_output_____" ] ], [ [ "Importing the `ADDITIONAL_ENV_PARAMS` variable, we see that it consists of only one entry, \"target_velocity\", which is used when computing the reward function associated with the environment. We use this default value when generating the `EnvParams` object.", "_____no_output_____" ] ], [ [ "from flow.core.params import EnvParams\n\nenv_params = EnvParams(additional_params=ADDITIONAL_ENV_PARAMS)", "_____no_output_____" ] ], [ [ "## 4. Setting up and Running the Experiment\nOnce the inputs to the scenario and environment classes are ready, we are ready to set up a `Experiment` object.", "_____no_output_____" ] ], [ [ "from flow.core.experiment import Experiment", "_____no_output_____" ] ], [ [ "These objects may be used to simulate rollouts in the absence of reinforcement learning agents, as well as acquire behaviors and rewards that may be used as a baseline with which to compare the performance of the learning agent. In this case, we choose to run our experiment for one rollout consisting of 3000 steps (300 s).\n\n**Note**: When executing the below code, remeber to click on the <img style=\"display:inline;\" src=\"img/play_button.png\"> Play button after the GUI is rendered.", "_____no_output_____" ] ], [ [ "# create the scenario object\nscenario = LoopScenario(name=\"ring_example\",\n vehicles=vehicles,\n net_params=net_params,\n initial_config=initial_config,\n traffic_lights=traffic_lights)\n\n# create the environment object\nenv = AccelEnv(env_params, sumo_params, scenario)\n\n# create the experiment object\nexp = Experiment(env)\n\n# run the experiment for a set number of rollouts / time steps\n_ = exp.run(1, 3000, convert_to_csv=True)", "_____no_output_____" ] ], [ [ "As we can see from the above simulation, the initial perturbations in the network instabilities propogate and intensify, eventually leading to the formation of stop-and-go waves after approximately 180s.\n\n## 5. Visualizing Post-Simulation\n\nOnce the simulation is done, a .xml file will be generated in the location of the specified `emission_path` in `SumoParams` (assuming this parameter has been specified) under the name of the scenario. In our case, this is:", "_____no_output_____" ] ], [ [ "import os\n\nemission_location = os.path.join(exp.env.sim_params.emission_path, exp.env.scenario.name)\nprint(emission_location + '-emission.xml')", "_____no_output_____" ] ], [ [ "The .xml file contains various vehicle-specific parameters at every time step. This information is transferred to a .csv file if the `convert_to_csv` parameter in `exp.run()` is set to True. This file looks as follows:", "_____no_output_____" ] ], [ [ "import pandas as pd\n\npd.read_csv(emission_location + '-emission.csv')", "_____no_output_____" ] ], [ [ "As you can see, each row contains vehicle information for a certain vehicle (specified under the *id* column) at a certain time (specified under the *time* column). These information can then be used to plot various representations of the simulation, examples of which can be found in the `flow/visualize` folder.", "_____no_output_____" ], [ "## 6. Modifying the Simulation\nThis tutorial has walked you through running a single lane ring road experiment in Flow. As we have mentioned before, these simulations are highly parametrizable. This allows us to try different representations of the task. For example, what happens if no initial perturbations are introduced to the system of homogenous human-driven vehicles?\n\n```\ninitial_config = InitialConfig()\n```\n\nIn addition, how does the task change in the presence of multiple lanes where vehicles can overtake one another?\n\n```\nnet_params = NetParams(\n additional_params={\n 'length': 230, \n 'lanes': 2, \n 'speed_limit': 30, \n 'resolution': 40\n }\n)\n```\n\nFeel free to experiment with all these problems and more!\n\n## Bibliography\n[1] Sugiyama, Yuki, et al. \"Traffic jams without bottlenecks—experimental evidence for the physical mechanism of the formation of a jam.\" New journal of physics 10.3 (2008): 033001.\n\n[2] Treiber, Martin, Ansgar Hennecke, and Dirk Helbing. \"Congested traffic states in empirical observations and microscopic simulations.\" Physical review E 62.2 (2000): 1805.", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ] ]

cb30efb3adf7085e5e4b7b6404f57f5ebc21e82a

9,579

ipynb

Jupyter Notebook

python-scripts/data_analytics_learn/link_pandas/Ex_Files_Pandas_Data/Exercise Files/05_06/Final/.ipynb_checkpoints/Data Frame Plots-checkpoint.ipynb

adityaka/misc_scripts

b28f71eb9b7eb429b44aeb9cb34f12355023125e

[ "BSD-3-Clause" ]

1

2018-01-16T18:21:07.000Z

python-scripts/data_analytics_learn/link_pandas/Ex_Files_Pandas_Data/Exercise Files/05_06/Final/.ipynb_checkpoints/Data Frame Plots-checkpoint.ipynb

adityaka/misc_scripts

b28f71eb9b7eb429b44aeb9cb34f12355023125e

[ "BSD-3-Clause" ]

1

2017-05-09T07:13:52.000Z

2017-06-12T05:24:08.000Z

python-scripts/data_analytics_learn/link_pandas/Ex_Files_Pandas_Data/Exercise Files/05_06/Final/.ipynb_checkpoints/Data Frame Plots-checkpoint.ipynb

adityaka/misc_scripts

b28f71eb9b7eb429b44aeb9cb34f12355023125e

[ "BSD-3-Clause" ]

1

2021-09-03T14:17:00.000Z

24.007519

205

0.471239

[ [ [ "### Data Frame Plots\ndocumentation: http://pandas.pydata.org/pandas-docs/stable/visualization.html", "_____no_output_____" ] ], [ [ "import pandas as pd\nimport numpy as np\nimport matplotlib.pyplot as plt\nplt.style.use('ggplot')", "_____no_output_____" ] ], [ [ "The plot method on Series and DataFrame is just a simple wrapper around plt.plot()\n\nIf the index consists of dates, it calls gcf().autofmt_xdate() to try to format the x-axis nicely as show in the plot window.", "_____no_output_____" ] ], [ [ "ts = pd.Series(np.random.randn(1000), index=pd.date_range('1/1/2000', periods=1000))\nts = ts.cumsum()\nts.plot()\nplt.show() ", "_____no_output_____" ] ], [ [ "On DataFrame, plot() is a convenience to plot all of the columns, and include a legend within the plot.", "_____no_output_____" ] ], [ [ "df = pd.DataFrame(np.random.randn(1000, 4), index=pd.date_range('1/1/2016', periods=1000), columns=list('ABCD'))\ndf = df.cumsum()\nplt.figure()\ndf.plot()\nplt.show()", "_____no_output_____" ] ], [ [ "You can plot one column versus another using the x and y keywords in plot():", "_____no_output_____" ] ], [ [ "df3 = pd.DataFrame(np.random.randn(1000, 2), columns=['B', 'C']).cumsum()\ndf3['A'] = pd.Series(list(range(len(df))))\ndf3.plot(x='A', y='B')\nplt.show()", "_____no_output_____" ], [ "df3.tail()", "_____no_output_____" ] ], [ [ "### Plots other than line plots\nPlotting methods allow for a handful of plot styles other than the default Line plot. These methods can be provided as the kind keyword argument to plot(). These include:\n\n- ‘bar’ or ‘barh’ for bar plots\n- ‘hist’ for histogram\n- ‘box’ for boxplot\n- ‘kde’ or 'density' for density plots\n- ‘area’ for area plots\n- ‘scatter’ for scatter plots\n- ‘hexbin’ for hexagonal bin plots\n- ‘pie’ for pie plots\n\nFor example, a bar plot can be created the following way:", "_____no_output_____" ] ], [ [ "plt.figure()\ndf.ix[5].plot(kind='bar')\nplt.axhline(0, color='k')\nplt.show()", "_____no_output_____" ], [ "df.ix[5]", "_____no_output_____" ] ], [ [ "### stack bar chart", "_____no_output_____" ] ], [ [ "df2 = pd.DataFrame(np.random.rand(10, 4), columns=['a', 'b', 'c', 'd'])\ndf2.plot.bar(stacked=True)\nplt.show()", "_____no_output_____" ] ], [ [ "### horizontal bar chart", "_____no_output_____" ] ], [ [ "df2.plot.barh(stacked=True)\nplt.show()", "_____no_output_____" ] ], [ [ "### box plot", "_____no_output_____" ] ], [ [ "df = pd.DataFrame(np.random.rand(10, 5), columns=['A', 'B', 'C', 'D', 'E'])\ndf.plot.box()\nplt.show()", "_____no_output_____" ] ], [ [ "### area plot", "_____no_output_____" ] ], [ [ "df = pd.DataFrame(np.random.rand(10, 4), columns=['a', 'b', 'c', 'd'])\ndf.plot.area()\nplt.show()", "_____no_output_____" ] ], [ [ "### Plotting with Missing Data\nPandas tries to be pragmatic about plotting DataFrames or Series that contain missing data. Missing values are dropped, left out, or filled depending on the plot type.\n\n| Plot Type | NaN Handling | |\n|----------------|-------------------------|---|\n| Line | Leave gaps at NaNs | |\n| Line (stacked) | Fill 0’s | |\n| Bar | Fill 0’s | |\n| Scatter | Drop NaNs | |\n| Histogram | Drop NaNs (column-wise) | |\n| Box | Drop NaNs (column-wise) | |\n| Area | Fill 0’s | |\n| KDE | Drop NaNs (column-wise) | |\n| Hexbin | Drop NaNs | |\n| Pie | Fill 0’s | |\n\nIf any of these defaults are not what you want, or if you want to be explicit about how missing values are handled, consider using fillna() or dropna() before plotting.", "_____no_output_____" ], [ "### density plot", "_____no_output_____" ] ], [ [ "ser = pd.Series(np.random.randn(1000))\nser.plot.kde()\nplt.show()", "_____no_output_____" ] ], [ [ "### lag plot\nLag plots are used to check if a data set or time series is random. Random data should not exhibit any structure in the lag plot. Non-random structure implies that the underlying data are not random.", "_____no_output_____" ] ], [ [ "from pandas.tools.plotting import lag_plot\nplt.figure()\ndata = pd.Series(0.1 * np.random.rand(1000) + 0.9 * np.sin(np.linspace(-99 * np.pi, 99 * np.pi, num=1000)))\nlag_plot(data)\nplt.show()", "_____no_output_____" ] ], [ [ "### matplotlib gallery\ndocumentation: http://matplotlib.org/gallery.html", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ] ]

cb30fde189d67c9d74bb5389bc01c5fc1f91c876

69,897

ipynb

Jupyter Notebook

notebooks/landlab/overland_flow_driver_for_workshop_may2020.ipynb

csdms/csdms-agm-2020

b0b69f4eab725465e085dc1b316c745400f79190

[ "CC0-1.0" ]

3

2020-05-19T15:26:49.000Z

2020-05-26T17:46:48.000Z

notebooks/landlab/overland_flow_driver_for_workshop_may2020.ipynb

csdms/csdms-agm-2020

b0b69f4eab725465e085dc1b316c745400f79190

[ "CC0-1.0" ]

1

2020-05-20T19:56:58.000Z

2020-05-20T20:30:03.000Z

notebooks/landlab/overland_flow_driver_for_workshop_may2020.ipynb

csdms/csdms-2020

b0b69f4eab725465e085dc1b316c745400f79190

[ "CC0-1.0" ]

1

2021-12-01T00:33:01.000Z

184.912698

13,504

0.911327

[ [ [ "<a href=\"http://landlab.github.io\"><img style=\"float: left\" src=\"../media/landlab_header.png\"></a>", "_____no_output_____" ], [ "# The deAlmeida Overland Flow Component ", "_____no_output_____" ], [ "<hr>\n<small>For more Landlab tutorials, click here: <a href=\"https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html\">https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html</a></small>\n<hr>", "_____no_output_____" ], [ "This notebook illustrates running the deAlmeida overland flow component in an extremely simple-minded way on a real topography, then shows it creating a flood sequence along an inclined surface with an oscillating water surface at one end.\n\nFirst, import what we'll need:", "_____no_output_____" ] ], [ [ "from landlab.components.overland_flow import OverlandFlow\nfrom landlab.plot.imshow import imshow_grid\nfrom landlab.plot.colors import water_colormap\nfrom landlab import RasterModelGrid\nfrom landlab.io.esri_ascii import read_esri_ascii\nfrom matplotlib.pyplot import figure\nimport numpy as np\nfrom time import time\n%matplotlib inline", "_____no_output_____" ] ], [ [ "Pick the initial and run conditions", "_____no_output_____" ] ], [ [ "run_time = 100 # duration of run, (s)\nh_init = 0.1 # initial thin layer of water (m)\nn = 0.01 # roughness coefficient, (s/m^(1/3))\ng = 9.8 # gravity (m/s^2)\nalpha = 0.7 # time-step factor (nondimensional; from Bates et al., 2010)\nu = 0.4 # constant velocity (m/s, de Almeida et al., 2012)\nrun_time_slices = (10, 50, 100)", "_____no_output_____" ] ], [ [ "Elapsed time starts at 1 second. This prevents errors when setting our boundary conditions.", "_____no_output_____" ] ], [ [ "elapsed_time = 1.0", "_____no_output_____" ] ], [ [ "Use Landlab methods to import an ARC ascii grid, and load the data into the field that the component needs to look at to get the data. This loads the elevation data, z, into a \"field\" in the grid itself, defined on the nodes.", "_____no_output_____" ] ], [ [ "rmg, z = read_esri_ascii('Square_TestBasin.asc', name='topographic__elevation')\nrmg.set_closed_boundaries_at_grid_edges(True, True, True, True)\n\n# un-comment these two lines for a \"real\" DEM\n#rmg, z = read_esri_ascii('hugo_site.asc', name='topographic__elevation') \n#rmg.status_at_node[z<0.0] = rmg.BC_NODE_IS_CLOSED\n", "_____no_output_____" ] ], [ [ "We can get at this data with this syntax:", "_____no_output_____" ] ], [ [ "np.all(rmg.at_node['topographic__elevation'] == z)", "_____no_output_____" ] ], [ [ "Note that the boundary conditions for this grid mainly got handled with the final line of those three, but for the sake of completeness, we should probably manually \"open\" the outlet. We can find and set the outlet like this:", "_____no_output_____" ] ], [ [ "my_outlet_node = 100 # This DEM was generated using Landlab and the outlet node ID was known\nrmg.status_at_node[my_outlet_node] = rmg.BC_NODE_IS_FIXED_VALUE", "_____no_output_____" ] ], [ [ "Now initialize a couple more grid fields that the component is going to need:", "_____no_output_____" ] ], [ [ "rmg.add_zeros('surface_water__depth', at='node') # water depth (m)", "_____no_output_____" ], [ "rmg.at_node['surface_water__depth'] += h_init", "_____no_output_____" ] ], [ [ "Let's look at our watershed topography", "_____no_output_____" ] ], [ [ "imshow_grid(rmg, 'topographic__elevation') #, vmin=1650.0)", "_____no_output_____" ] ], [ [ "Now instantiate the component itself", "_____no_output_____" ] ], [ [ "of = OverlandFlow(\n rmg, steep_slopes=True\n) #for stability in steeper environments, we set the steep_slopes flag to True", "_____no_output_____" ] ], [ [ "Now we're going to run the loop that drives the component:", "_____no_output_____" ] ], [ [ "while elapsed_time < run_time:\n # First, we calculate our time step.\n dt = of.calc_time_step()\n # Now, we can generate overland flow.\n of.overland_flow()\n # Increased elapsed time\n print('Elapsed time: ', elapsed_time)\n elapsed_time += dt", "_____no_output_____" ], [ "imshow_grid(rmg, 'surface_water__depth', cmap='Blues')", "_____no_output_____" ] ], [ [ "Now let's get clever, and run a set of time slices:", "_____no_output_____" ] ], [ [ "elapsed_time = 1.\nfor t in run_time_slices:\n while elapsed_time < t:\n # First, we calculate our time step.\n dt = of.calc_time_step()\n # Now, we can generate overland flow.\n of.overland_flow()\n # Increased elapsed time\n elapsed_time += dt\n figure(t)\n imshow_grid(rmg, 'surface_water__depth', cmap='Blues')", "_____no_output_____" ] ], [ [ "### Click here for more <a href=\"https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html\">Landlab tutorials</a>", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown" ]

[ [ "markdown", "markdown", "markdown", "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ] ]

cb3103ec083eefe6a9a00d09f0d5cf73afd42bda

21,866

ipynb

Jupyter Notebook

notebooks/12-2020/modes_of_a_ball_channel_pendulum.ipynb

gbrault/resonance

bf66993a98fbbb857511f83bc072449b98f0b4c2

[ "MIT" ]

31

2017-11-10T16:44:04.000Z

2022-01-13T12:22:02.000Z

notebooks/12-2020/modes_of_a_ball_channel_pendulum.ipynb

gbrault/resonance

bf66993a98fbbb857511f83bc072449b98f0b4c2

[ "MIT" ]

178

2017-07-19T20:16:13.000Z

2020-03-10T04:13:46.000Z

notebooks/12-2020/modes_of_a_ball_channel_pendulum.ipynb

gbrault/resonance

bf66993a98fbbb857511f83bc072449b98f0b4c2

[ "MIT" ]

12

2018-04-05T22:58:43.000Z

2021-01-14T04:06:26.000Z

21.229126

400

0.500046

[ [ [ "# Modes of the Ball-Channel Pendulum Linear Model", "_____no_output_____" ] ], [ [ "import numpy as np\nimport numpy.linalg as la\nimport matplotlib.pyplot as plt\nfrom resonance.linear_systems import BallChannelPendulumSystem", "_____no_output_____" ], [ "%matplotlib widget", "_____no_output_____" ] ], [ [ "A (almost) premade system is available in `resonance`. The only thing missing is the function that calculates the canonical coefficients.", "_____no_output_____" ] ], [ [ "sys = BallChannelPendulumSystem()", "_____no_output_____" ], [ "sys.constants", "_____no_output_____" ], [ "sys.states", "_____no_output_____" ], [ "def can_coeffs(mp, mb, l, g, r):\n M = np.array([[mp * l**2 + mb * r**2, -mb * r**2],\n [-mb * r**2, mb * r**2]])\n C = np.zeros((2, 2))\n K = np.array([[g * l * mp, g * mb * r],\n [g * mb * r, g * mb * r]])\n return M, C, K", "_____no_output_____" ], [ "sys.canonical_coeffs_func = can_coeffs", "_____no_output_____" ] ], [ [ "Once the system is completely defined the mass, damping, and stiffness matrices can be calculated and inspected:", "_____no_output_____" ] ], [ [ "M, C, K = sys.canonical_coefficients()", "_____no_output_____" ], [ "M", "_____no_output_____" ], [ "C", "_____no_output_____" ], [ "K", "_____no_output_____" ] ], [ [ "## Convert to mass normalized form (calculate $\\tilde{\\mathbf{K}}$)\n\nFirst calculate the Cholesky lower triangular decomposition matrix of $\\mathbf{M}$, which is symmetric and postive definite.", "_____no_output_____" ] ], [ [ "L = la.cholesky(M)\nL", "_____no_output_____" ] ], [ [ "The transpose can be computed with `np.transpose()`, `L.transpose()` or `L.T` for short:", "_____no_output_____" ] ], [ [ "np.transpose(L)", "_____no_output_____" ], [ "L.transpose()", "_____no_output_____" ], [ "L.T", "_____no_output_____" ] ], [ [ "Check that $\\mathbf{L}\\mathbf{L}^T$ returns $M$. Note that in Python the `@` operator is used for matrix multiplication. The `*` operator will do elementwise multiplication.", "_____no_output_____" ] ], [ [ "L @ L.T", "_____no_output_____" ] ], [ [ "`inv()` computes the inverse, giving $\\left(\\mathbf{L}^T\\right)^{-1}$:", "_____no_output_____" ] ], [ [ "la.inv(L.T)", "_____no_output_____" ] ], [ [ "$\\mathbf{L}^{-1}\\mathbf{M}\\left(\\mathbf{L}^T\\right)^{-1} = \\mathbf{I}$. Note that the off-diagonal terms are very small numbers. The reason these are not precisely zero is due to floating point arithmetic and the associated truncation errors.", "_____no_output_____" ] ], [ [ "la.inv(L) @ M @ la.inv(L.T)", "_____no_output_____" ] ], [ [ "$\\tilde{\\mathbf{K}} = \\mathbf{L}^{-1}\\mathbf{K}\\left(\\mathbf{L}^T\\right)^{-1}$. Note that this matrix is symmetric. It is guaranteed to be symmetric if $\\mathbf{K}$ is symmetric.", "_____no_output_____" ] ], [ [ "Ktilde = la.inv(L) @ K @ la.inv(L.T)\nKtilde", "_____no_output_____" ] ], [ [ "The entries of $\\tilde{\\mathbf{K}}$ can be accessed as so:", "_____no_output_____" ] ], [ [ "k11 = Ktilde[0, 0]\nk12 = Ktilde[0, 1]\nk21 = Ktilde[1, 0]\nk22 = Ktilde[1, 1]", "_____no_output_____" ] ], [ [ "# Calculate the eigenvalues of $\\tilde{\\mathbf{K}}$\n\nThe eigenvalues of this 2 x 2 matrix are found by forming the characteristic equation from:\n\n$$\\textrm{det}\\left(\\tilde{\\mathbf{K}} - \\lambda \\mathbf{I}\\right) = 0$$\n\nand solving the resulting quadratic polynomial for its roots, which are the eigenvalues.", "_____no_output_____" ] ], [ [ "lam1 = (k11 + k22) / 2 + np.sqrt((k11 + k22)**2 - 4 * (k11 * k22 - k12*k21)) / 2\nlam1", "_____no_output_____" ], [ "lam2 = (k11 + k22) / 2 - np.sqrt((k11 + k22)**2 - 4 * (k11 * k22 - k12*k21)) / 2\nlam2", "_____no_output_____" ] ], [ [ "# Calculate the eigenfrequencies of the system\n\n$\\omega_i = \\sqrt{\\lambda_i}$", "_____no_output_____" ] ], [ [ "omega1 = np.sqrt(lam1)\nomega1", "_____no_output_____" ], [ "omega2 = np.sqrt(lam2)\nomega2", "_____no_output_____" ] ], [ [ "And in Hertz:", "_____no_output_____" ] ], [ [ "fn1 = omega1/2/np.pi\nfn1", "_____no_output_____" ], [ "fn2 = omega2/2/np.pi\nfn2", "_____no_output_____" ] ], [ [ "# Calculate the eigenvectors of $\\tilde{\\mathbf{K}}$\n\nThe eigenvectors can be found by substituting the value for $\\lambda$ into:\n\n$$\\tilde{\\mathbf{K}}\\hat{q}_0 = \\lambda \\hat{q}_0$$\n\nand solving for $\\hat{q}_0$.", "_____no_output_____" ] ], [ [ "v1 = np.array([-k12 / (k11 - lam1), 1])", "_____no_output_____" ], [ "v2 = np.array([-k12 / (k11 - lam2), 1])", "_____no_output_____" ] ], [ [ "Check that they are orthogonal, i.e. the dot product should be zero.", "_____no_output_____" ] ], [ [ "np.dot(v1, v2)", "_____no_output_____" ] ], [ [ "The `norm()` function calculates the Euclidean norm, i.e. the vector's magnitude and the vectors can be normalized like so:", "_____no_output_____" ] ], [ [ "v1_hat = v1 / np.linalg.norm(v1)\nv2_hat = v2 / np.linalg.norm(v2)", "_____no_output_____" ], [ "v1_hat", "_____no_output_____" ], [ "v2_hat", "_____no_output_____" ], [ "np.linalg.norm(v1_hat)", "_____no_output_____" ] ], [ [ "For any size $\\tilde{\\mathbf{K}}$ the `eig()` function can be used to calculate the eigenvalues and the normalized eigenvectors with one function call:", "_____no_output_____" ] ], [ [ "evals, evecs = np.linalg.eig(Ktilde)", "_____no_output_____" ], [ "evals", "_____no_output_____" ], [ "evecs", "_____no_output_____" ] ], [ [ "The columns of `evecs` correspond to the entries of `evals`.", "_____no_output_____" ] ], [ [ "P = evecs\nP", "_____no_output_____" ] ], [ [ "If P contains columns that are orthnormal, then $\\mathbf{P}^T \\mathbf{P} = \\mathbf{I}$. Check this with:", "_____no_output_____" ] ], [ [ "P.T @ P", "_____no_output_____" ] ], [ [ "$\\mathbf{P}$ can be used to find the matrix $\\Lambda$ that decouples the differential equations.", "_____no_output_____" ] ], [ [ "Lam = P.T @ Ktilde @ P\nLam", "_____no_output_____" ] ], [ [ "# Formulate solution to ODEs (simulation)", "_____no_output_____" ], [ "The trajectory of the coordinates can be found with:\n\n$$\n\\bar{c}(t) = \\sum_{i=1}^n c_i \\sin(\\omega_i t + \\phi_i) \\bar{u}_i\n$$\n\nwhere\n\n$$\n\\phi_i = \\arctan \\frac{\\omega_i \\hat{q}_{0i}^T \\bar{q}(0)}{\\hat{q}_{0i}^T \\dot{\\bar{q}}(0)}\n$$\n\nand\n\n$$\nc_i = \\frac{\\hat{q}^T_{0i} \\bar{q}(0)}{\\sin\\phi_i}\n$$\n\n$c_i$ are the modal participation factors and reflect what propotional of each mode is excited given specific initial conditions. If the initial conditions are the eigenmode, $\\bar{u}_i$, the all but the $i$th $c_i$ will be zero.\n\nA matrix $\\mathbf{S} = \\left(\\mathbf{L}^T\\right)^{-1} = \\begin{bmatrix}\\bar{u}_1 \\quad \\bar{u}_2\\end{bmatrix}$ can be computed such that the columns are $\\bar{u}_i$.", "_____no_output_____" ] ], [ [ "S = la.inv(L.T) @ P\nS", "_____no_output_____" ], [ "u1 = S[:, 0]\nu2 = S[:, 1]", "_____no_output_____" ], [ "u1", "_____no_output_____" ], [ "u2", "_____no_output_____" ] ], [ [ "Define the initial coordinates as a scalar factor of the second eigenvector, which sets these values to small angles.", "_____no_output_____" ] ], [ [ "c0 = S[:, 1] / 400\nnp.rad2deg(c0)", "_____no_output_____" ] ], [ [ "Set the initial speeds to zero:", "_____no_output_____" ] ], [ [ "s0 = np.zeros(2)\ns0", "_____no_output_____" ] ], [ [ "The initial mass normalized coordinates and speeds are then:", "_____no_output_____" ] ], [ [ "q0 = L.T @ c0\nq0", "_____no_output_____" ], [ "qd0 = L.T @ s0\nqd0", "_____no_output_____" ] ], [ [ "Calculate the modal freqencies in radians per second.", "_____no_output_____" ] ], [ [ "ws = np.sqrt(evals)\nws", "_____no_output_____" ] ], [ [ "The phase shifts for each mode can be found. Note that it is important to use `arctan2()` so that the quadrant and thus sign of the arc tangent is properly handled.\n\n$$\n\\phi_i = \\arctan \\frac{\\omega_i \\hat{q}_{0i}^T \\bar{q}(0)}{\\hat{q}_{0i}^T \\dot{\\bar{q}}(0)}\n$$", "_____no_output_____" ] ], [ [ "phi1 = np.arctan2(ws * P[:, 0] @ q0, P[:, 0] @ qd0)\nphi1", "_____no_output_____" ], [ "phi2 = np.arctan2(ws * P[:, 1] @ q0, P[:, 1] @ qd0)\nphi2", "_____no_output_____" ] ], [ [ "All $\\phi$'s can be calculated in one line using NumPy's broadcasting feature:", "_____no_output_____" ] ], [ [ "phis = np.arctan2(ws * P.T @ q0, P.T @ qd0)\nphis", "_____no_output_____" ] ], [ [ "The phase shifts for this particular initial condition are $\\pm90$ degrees.", "_____no_output_____" ] ], [ [ "np.rad2deg(phis)", "_____no_output_____" ] ], [ [ "Now calculate the modal participation factors.\n\n$$\nc_i = \\frac{\\hat{q}^T_{0i} \\bar{q}(0)}{\\sin\\phi_i}\n$$", "_____no_output_____" ] ], [ [ "cs = P.T @ q0 / np.sin(phis)\ncs", "_____no_output_____" ] ], [ [ "Note that the first participation factor is zero. This is because we've set the initial coordinate to be a scalar function of the second eigenvector.", "_____no_output_____" ], [ "## Simulate", "_____no_output_____" ] ], [ [ "t = np.linspace(0, 5, num=500)", "_____no_output_____" ], [ "cs[1] * np.sin(ws[1] * t)", "_____no_output_____" ] ], [ [ "The following line will give an error because the dimensions of `u1` are not compatible with the dimensions of the preceding portion. It is possible for a single line to work like this if you take advatnage of NumPy's broadcasting rules. See https://scipy-lectures.org/intro/numpy/operations.html#broadcasting for more info. The `tile()` function is used to repeat `u1` as many times as needed.", "_____no_output_____" ] ], [ [ "# cs[1] * np.sin(ws[1] * t) * u1", "_____no_output_____" ], [ "c1 = cs[1] * np.sin(ws[1] * t) * np.tile(u1, (len(t), 1)).T\nc1.shape", "_____no_output_____" ] ], [ [ "`tile()` can be used to create a 2 x 1000 vector that repeats the vector $\\hat{u}_i$ allowing a single line to calculate the mode contribution.", "_____no_output_____" ], [ "Now use a loop to calculate the contribution of each mode and build the summation of contributions from each mode:", "_____no_output_____" ] ], [ [ "ct = np.zeros((2, len(t))) # 2 x m array to hold coordinates as a function of time\nfor ci, wi, phii, ui in zip(cs, ws, phis, S.T):\n print(ci, wi, phii, ui)\n ct += ci * np.sin(wi * t + phii) * np.tile(ui, (len(t), 1)).T", "_____no_output_____" ], [ "def sim(c0, s0, t):\n \"\"\"Returns the time history of the coordinate vector, c(t) given the initial state and time.\n \n Parameters\n ==========\n c0 : ndarray, shape(n,)\n s0 : ndarray, shape(n,)\n t : ndarray, shape(m,)\n \n Returns\n =======\n c(t) : ndarray, shape(n, m)\n \n \"\"\"\n q0 = L.T @ c0\n qd0 = L.T @ s0\n ws = np.sqrt(evals)\n phis = np.arctan2(ws * P.T @ q0, P.T @ qd0)\n cs = P.T @ q0 / np.sin(phis)\n c = np.zeros((2, 1000))\n for ci, wi, phii, ui in zip(cs, ws, phis, S.T):\n c += ci * np.sin(wi * t + phii) * np.tile(ui, (len(t), 1)).T\n return c", "_____no_output_____" ] ], [ [ "Simulate and plot the first mode:", "_____no_output_____" ] ], [ [ "t = np.linspace(0, 5, num=1000)\n\nc0 = S[:, 0] / np.max(S[:, 0]) * np.deg2rad(10)\ns0 = np.zeros(2)\n\nfig, ax = plt.subplots()\nax.plot(t, np.rad2deg(sim(c0, s0, t).T))\nax.set_xlabel('Time [s]')\nax.set_ylabel('Angle [deg]')\nax.legend([r'$\\theta$', r'$\\phi$'])", "_____no_output_____" ] ], [ [ "Simulate and plot the second mode:", "_____no_output_____" ] ], [ [ "t = np.linspace(0, 5, num=1000)\n\nc0 = S[:, 1] / np.max(S[:, 1]) * np.deg2rad(10)\ns0 = np.zeros(2)\n\nfig, ax = plt.subplots()\nax.plot(t, np.rad2deg(sim(c0, s0, t).T))\nax.set_xlabel('Time [s]')\nax.set_ylabel('Angle [deg]')\nax.legend([r'$\\theta$', r'$\\phi$'])", "_____no_output_____" ] ], [ [ "Compare this to the free response from the system:", "_____no_output_____" ] ], [ [ "sys.coordinates['theta'] = c0[0]\nsys.coordinates['phi'] = c0[1]\n\nsys.speeds['alpha'] = 0\nsys.speeds['beta'] = 0", "_____no_output_____" ], [ "traj = sys.free_response(5.0)", "_____no_output_____" ], [ "traj[['theta', 'phi']].plot()", "_____no_output_____" ], [ "sys.animate_configuration(fps=30, repeat=False)", "_____no_output_____" ] ], [ [ "Simulate with arbitrary initial conditions.", "_____no_output_____" ] ], [ [ "sys.coordinates['theta'] = np.deg2rad(12.0)\nsys.coordinates['phi'] = np.deg2rad(3.0)\ntraj = sys.free_response(5.0)", "_____no_output_____" ], [ "traj[['theta', 'phi']].plot()", "_____no_output_____" ] ] ]

[ "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code", "markdown", "code" ]

[ [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code", "code" ], [ "markdown", "markdown" ], [ "code", "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code" ], [ "markdown" ], [ "code", "code", "code", "code" ], [ "markdown" ], [ "code", "code" ] ]

cb310d1b228665d0dcbb8ccfb926f4c24fcb16f5

220,306

ipynb

Jupyter Notebook

Playground.ipynb

nassarofficial/ssd_keras_double

b1b5db9ec437c07efb86cf1d4afb19741b54c25d

[ "Apache-2.0" ]

null

Playground.ipynb

nassarofficial/ssd_keras_double

b1b5db9ec437c07efb86cf1d4afb19741b54c25d

[ "Apache-2.0" ]

null

Playground.ipynb

nassarofficial/ssd_keras_double

b1b5db9ec437c07efb86cf1d4afb19741b54c25d

[ "Apache-2.0" ]

null

38.528506

1,845

0.589911

[ [ [ "import numpy as np\nimport math\nfrom bounding_box_utils.bounding_box_utils import iou, convert_coordinates\nfrom ssd_encoder_decoder.matching_utils import match_bipartite_greedy, match_multi\nimport tensorflow as tf\nfrom keras import backend as K", "Using TensorFlow backend.\n" ], [ "from bs4 import BeautifulSoup", "_____no_output_____" ], [ "fh = open('/home/nassar/gits/datasets/VOC/Pasadena/ImageSets/Main/norm/trainval_standard.txt','r')\ncounter = 0\nfor x in fh:\n with open('/home/nassar/gits/datasets/VOC/Pasadena/Annotations/'+x[:-1]+'.xml') as f:\n soup = BeautifulSoup(f, 'xml')\n if soup.find('yaw'):\n print(\"yaw: \",soup.yaw.text)\n else:\n print(\"EEEEEEEEEEEEEEEEEEEEE\")\n ", "yaw: 0.9086184085882479\nyaw: 6.252642045269685\nyaw: 3.1278045524990383\nyaw: 0.0143116998663535\nyaw: 3.134785869507015\nyaw: 0.017976891295541593\nyaw: 1.5505505074717623\nyaw: 2.529505684915382\nyaw: 4.646241001734104\nyaw: 1.558928087881335\nyaw: 0.021642082724729686\nyaw: 3.475474139496308\nyaw: 6.181432611788317\nyaw: 4.684638245277981\nyaw: 0.3803072440095644\nyaw: 6.272364265817221\nyaw: 3.114365517258682\nyaw: 3.1257101573966444\nyaw: 1.51738925168387\nyaw: 1.5273376284202378\nyaw: 6.256132703773673\nyaw: 2.260724980108255\nyaw: 1.2716468930030684\nyaw: 0.39426987802551905\nyaw: 1.4196508135721877\nyaw: 2.3513075682867606\nyaw: 6.057514234896719\nyaw: 1.5330972149518192\nyaw: 2.8213247358488336\nyaw: 5.823640115129479\nyaw: 3.2121039553703636\nyaw: 1.5437437233889846\nyaw: 3.141243587739394\nyaw: 3.1361821329086106\nyaw: 4.667184952758037\nyaw: 2.8982937558617836\nyaw: 1.570447260944498\nyaw: 1.5514231720977594\nyaw: 1.5552628964521469\nyaw: 3.519107370796166\nyaw: 1.5320500174006226\nyaw: 0.010821041362364843\nyaw: 3.121870433042257\nyaw: 1.5533430342749535\nyaw: 4.7127380462350885\nyaw: 6.263986685407648\nyaw: 6.265732014659642\nyaw: 6.272887864592819\nyaw: 2.526015026411393\nyaw: 1.5451399867905797\nyaw: 3.131818809778625\nyaw: 4.398055182100511\nyaw: 1.5339698795778163\nyaw: 3.158347814408939\nyaw: 4.695982885415943\nyaw: 3.941127983928396\nyaw: 6.265382948809244\nyaw: 0.39426987802551905\nyaw: 0.0143116998663535\nyaw: 5.457644570986268\nyaw: 5.705132258919064\nyaw: 2.841396022246769\nyaw: 4.691445029360758\nyaw: 1.5531685013497536\nyaw: 1.543569190463785\nyaw: 6.283185307179586\nyaw: 6.117029962389726\nyaw: 1.5240215028414483\nyaw: 3.141243587739394\nyaw: 3.131993342703824\nyaw: 3.5393531901193005\nyaw: 6.24496259656091\nyaw: 3.1089549965774994\nyaw: 1.5578808903301387\nyaw: 3.1463050425701784\nyaw: 4.6965064841915405\nyaw: 5.701990666265475\nyaw: 4.70313873534912\nyaw: 4.7073275255539055\nyaw: 6.272887864592819\nyaw: 3.1185543074634676\nyaw: 4.695633819565544\nyaw: 1.578650308428871\nyaw: 6.2737605292188166\nyaw: 3.1382765280110037\nyaw: 3.1309461451526275\nyaw: 3.6726963449716674\nyaw: 2.2657864349390384\nyaw: 4.055447049934024\nyaw: 1.5730652548224893\nyaw: 2.835112836939589\nyaw: 6.273585996293617\nyaw: 5.799205505601559\nyaw: 3.1478758388969728\nyaw: 3.12396482814465\nyaw: 5.701990666265475\nyaw: 1.6034339838071907\nyaw: 3.1049407392979123\nyaw: 3.4515631287439863\nyaw: 1.1461577197846762\nyaw: 1.5526449025741553\nyaw: 3.1162853794358756\nyaw: 6.252642045269685\nyaw: 3.1248374927706473\nyaw: 6.27585492432121\nyaw: 3.761533603898179\nyaw: 4.588121537642693\nyaw: 6.2638121524824495\nyaw: 1.557706357404939\nyaw: 3.1192524391642658\nyaw: 0.021467549799530253\nyaw: 1.574985116999683\nyaw: 4.7073275255539055\nyaw: 3.7060321336847597\nyaw: 1.5591026208065346\nyaw: 1.5563100940033439\nyaw: 6.277425720648005\nyaw: 1.5585790220309361\nyaw: 2.524967828860196\nyaw: 1.557182758629341\nyaw: 0.024085543677521744\nyaw: 5.704085061367867\nyaw: 3.1159363135854763\nyaw: 3.1281536183494367\nyaw: 0.01832595714594046\nyaw: 0.005759586531581288\nyaw: 6.272538798742421\nyaw: 1.6411330956502679\nyaw: 1.5535175672001527\nyaw: 4.709596453581498\nyaw: 1.6966345658636877\nyaw: 2.702816879638419\nyaw: 4.643797540781312\nyaw: 4.8425905425834666\nyaw: 1.6102407678899684\nyaw: 1.5634659439365202\nyaw: 3.125361091546246\nyaw: 0.004363323129985824\nyaw: 4.702615136573521\nyaw: 2.158448685941387\nyaw: 3.130771612227428\nyaw: 2.5277603556633874\nyaw: 5.694485750481898\nyaw: 0.48781952593241507\nyaw: 6.2584016318012665\nyaw: 1.5924384095196262\nyaw: 3.113318319707485\nyaw: 0.7581710270663367\nyaw: 0.6243042734383717\nyaw: 3.1394982584873996\nyaw: 1.5406021307353945\nyaw: 4.658632839423265\nyaw: 6.279520115750399\nyaw: 4.6799258562975945\nyaw: 1.5498523757709646\nyaw: 6.270444403640027\nyaw: 3.0805061297699914\nyaw: 3.110700325829493\nyaw: 3.148923036448169\nyaw: 2.5321236787933734\nyaw: 0.038571776469074684\nyaw: 2.4886649804187146\nyaw: 4.543615641716838\nyaw: 4.741186913042595\nyaw: 1.5578808903301387\nyaw: 1.5905185473424326\nyaw: 1.7228145046436025\nyaw: 4.693888490313549\nyaw: 6.262241356155654\nyaw: 4.6994735439199316\nyaw: 0.03961897402027128\nyaw: 3.0752701420140083\nyaw: 1.5107570005262918\nyaw: 0.15638150097869194\nyaw: 6.272713331667619\nyaw: 6.255260039147677\nyaw: 1.5550883635269477\nyaw: 2.5104815960686437\nyaw: 1.5477579806685715\nyaw: 0.02495820830351891\nyaw: 4.687954370856769\nyaw: 4.312883114603188\nyaw: 2.723237231886752\nyaw: 3.1264082890974425\nyaw: 4.698949945144334\nyaw: 5.258327970408516\nyaw: 2.5413739238289432\nyaw: 6.264684817108446\nyaw: 1.5550883635269477\nyaw: 6.270793469490426\nyaw: 6.254038308671281\nyaw: 1.5526449025741553\nyaw: 3.130597079302229\nyaw: 6.268175475612434\nyaw: 6.260845092754059\nyaw: 1.5920893436692274\nyaw: 0.9464920533565249\nyaw: 3.121346834266659\nyaw: 4.7073275255539055\nyaw: 3.12099776841626\nyaw: 3.9549160850191507\nyaw: 3.078237201742399\nyaw: 3.9718457787634955\nyaw: 3.1309461451526275\nyaw: 6.197664173831865\nyaw: 5.705655857694662\nyaw: 2.568077461384456\nyaw: 1.5933110741456236\nyaw: 3.133040540255021\nyaw: 4.481656453271039\nyaw: 3.105987936849109\nyaw: 2.5413739238289432\nyaw: 2.4998350876314777\nyaw: 1.5514231720977594\nyaw: 1.5676547341413067\nyaw: 4.671897341738421\nyaw: 4.694935687864747\nyaw: 3.1220449659674565\nyaw: 4.67259547343922\nyaw: 3.115238181884679\nyaw: 3.128851750050235\nyaw: 6.261194158604458\nyaw: 3.11785617576267\nyaw: 1.553692100125352\nyaw: 3.1292008159006333\nyaw: 2.5487043066873194\nyaw: 1.566956602440509\nyaw: 4.707851124329505\nyaw: 1.5557864952277454\nyaw: 3.6646678304124936\nyaw: 4.707152992628707\nyaw: 5.852438047787386\nyaw: 2.444857216193657\nyaw: 1.3857914260834978\nyaw: 2.438224965036078\nyaw: 3.333055272533571\nyaw: 4.205196299755138\nyaw: 6.275505858470811\nyaw: 3.2121039553703636\nyaw: 1.5411257295109928\nyaw: 4.661599899151654\nyaw: 6.269222673163631\nyaw: 4.6368162237733355\nyaw: 6.265382948809244\nyaw: 4.6877798379315685\nyaw: 5.719094892935019\nyaw: 3.1196015050146646\nyaw: 6.251943913568888\nyaw: 0.009599310885968814\nyaw: 4.702440603648323\nyaw: 0.31695179216217023\nyaw: 6.263288553706851\nyaw: 6.0329050924436\nyaw: 4.6322783677181505\nyaw: 2.1516419018586093\nyaw: 1.538682268558201\nyaw: 4.706803926778308\nyaw: 1.5526449025741553\nyaw: 3.1148891160342798\nyaw: 3.1401963901881977\nyaw: 5.362698659677776\nyaw: 1.5489797111449675\nyaw: 2.68396732371688\nyaw: 4.69703008296714\nyaw: 1.5627678122357227\nyaw: 1.5508995733221613\nyaw: 6.272538798742421\nyaw: 6.270793469490426\nyaw: 2.6373670326886316\nyaw: 0.08674286382411817\nyaw: 3.1539844912789525\nyaw: 4.690223298884362\nyaw: 1.8643607069803427\nyaw: 6.272713331667619\nyaw: 1.5503759745465628\nyaw: 3.4609879067047555\nyaw: 5.88804276452807\nyaw: 4.749739026377369\nyaw: 3.1019736795695216\nyaw: 3.8325685044543483\nyaw: 1.5580554232553376\nyaw: 1.5585790220309361\nyaw: 4.698775412219134\nyaw: 6.269222673163631\nyaw: 6.261892290305255\nyaw: 3.1148891160342798\nyaw: 3.124313893995049\nyaw: 1.7055357450488589\nyaw: 3.1463050425701784\nyaw: 2.5274112898129886\nyaw: 6.282661708403988\nyaw: 1.4690436314036273\nyaw: 2.20679430622163\nyaw: 4.041309882992871\nyaw: 6.265382948809244\nyaw: 4.684289179427581\nyaw: 5.879490651193297\nyaw: 3.1148891160342798\nyaw: 6.272364265817221\nyaw: 5.658182902040417\nyaw: 3.1391491926370017\nyaw: 1.5514231720977594\nyaw: 2.8321457772111986\nyaw: 6.241297405131723\nyaw: 6.270444403640027\nyaw: 3.1384510609362035\nyaw: 6.278298385274003\nyaw: 1.5671311353657087\nyaw: 4.7214646924950605\nyaw: 4.69685555004194\nyaw: 4.686209041604775\nyaw: 3.0928979674591517\nyaw: 5.926963606847543\nyaw: 3.12710642079824\nyaw: 4.707152992628707\nyaw: 5.43233729683235\nyaw: 3.414562148601706\nyaw: 3.1080823319515023\nyaw: 4.73699812283781\nyaw: 5.887344632827272\nyaw: 6.270269870714828\nyaw: 3.086265716301573\nyaw: 0.014660765716752367\nyaw: 4.701393406097125\nyaw: 3.1182052416130692\nyaw: 4.697902747593137\nyaw: 4.703487801199518\nyaw: 3.118379774538268\nyaw: 3.484026252831081\nyaw: 4.705582196301912\nyaw: 6.276029457246409\nyaw: 5.189038399104342\nyaw: 6.272015199966823\nyaw: 2.160368548118581\nyaw: 6.283010774254388\nyaw: 3.126233756172243\n" ], [ "a = tf.constant([3, 1, 2, 1])\nb = tf.constant([1, 3, 4, 3])\n\nset1 = tf.cast(a,dtype=tf.int32)\nset2 = tf.cast(b,dtype=tf.int32)\n\nid_pick = tf.sets.set_intersection(set1[None,:], set2[None, :])\n", "_____no_output_____" ], [ "K.eval(id_pick.values[0])", "_____no_output_____" ], [ "a = tf.constant([[0,0,0,1,1]])\nb = tf.constant([[0, 0,0, 1,0,2,1, 0,1, 2]])\n\nfind_match = b - a\n\nindices = tf.transpose(tf.where(tf.equal(find_match, tf.zeros_like(find_match))))[0]\n\nout = tf.gather(a, indices)\n\n", "_____no_output_____" ], [ "s = tf.sets.set_intersection(a[None,:], b[None, :])\n", "_____no_output_____" ], [ "masked_a = tf.where( tf.equal(s, 1), s, tf.zeros_like(s) )", "_____no_output_____" ] ] ]

[ "code" ]

[ [ "code", "code", "code", "code", "code", "code", "code", "code" ] ]